Assessing Extreme Precipitation in Northwest China’s Inland River Basin Under a Novel Low Radiative Forcing Scenario
Abstract
1. Introduction
2. Materials and Methods
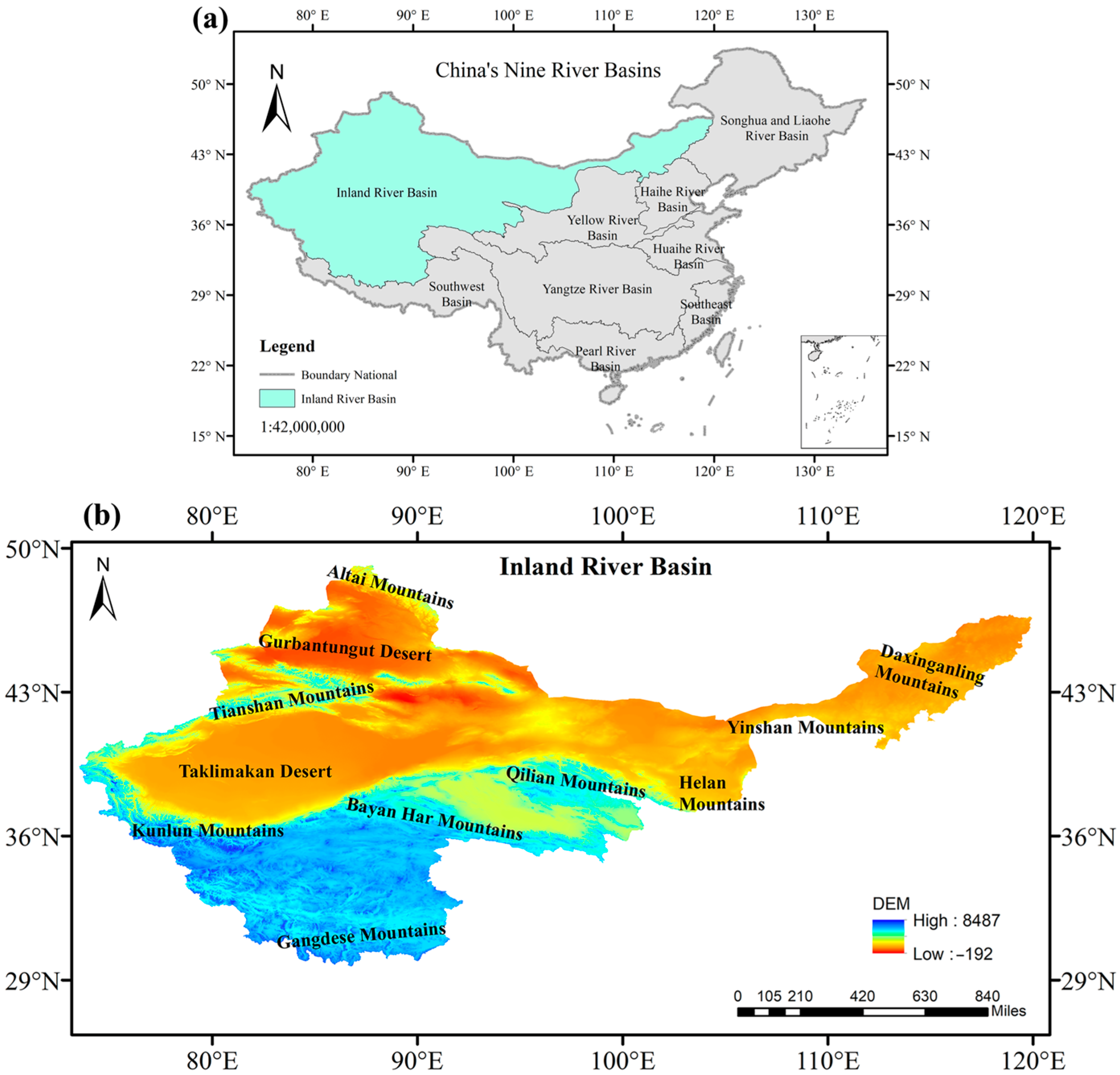
2.1. Study Area
2.2. Data
2.3. Bias Correction
2.4. Precipitation Extreme Indices
3. Results
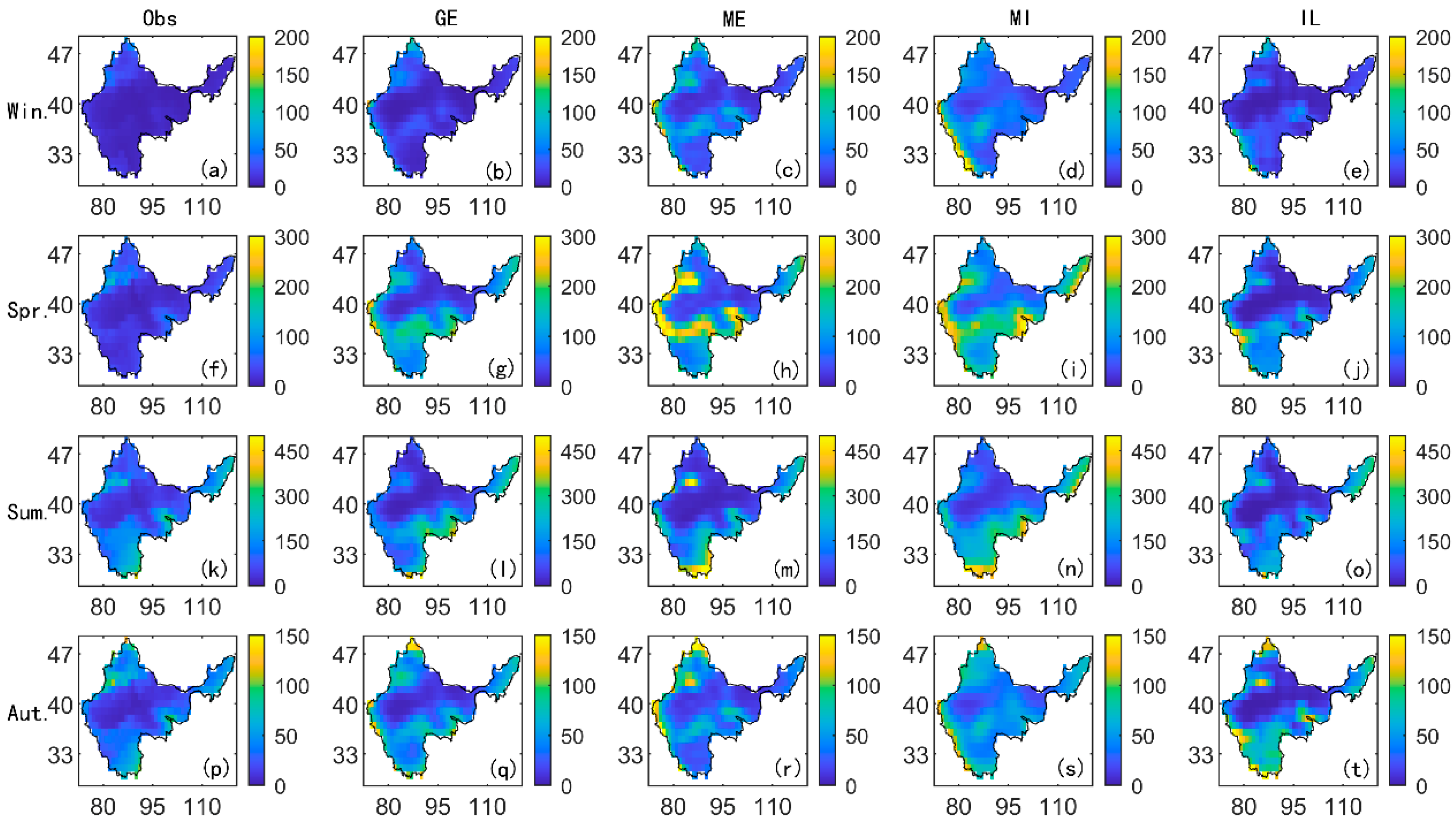
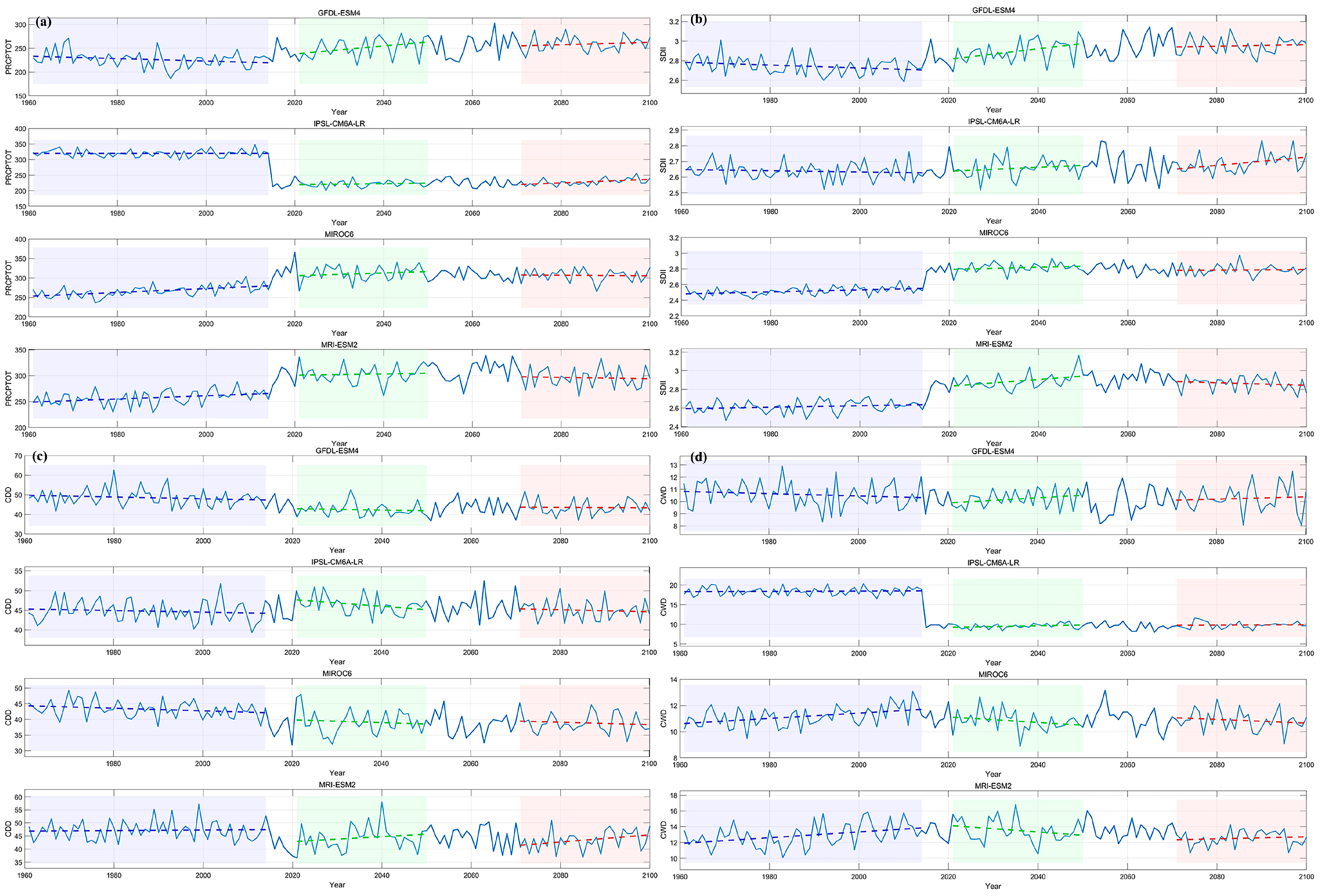
3.1. Seasonality Variability in Historical Data
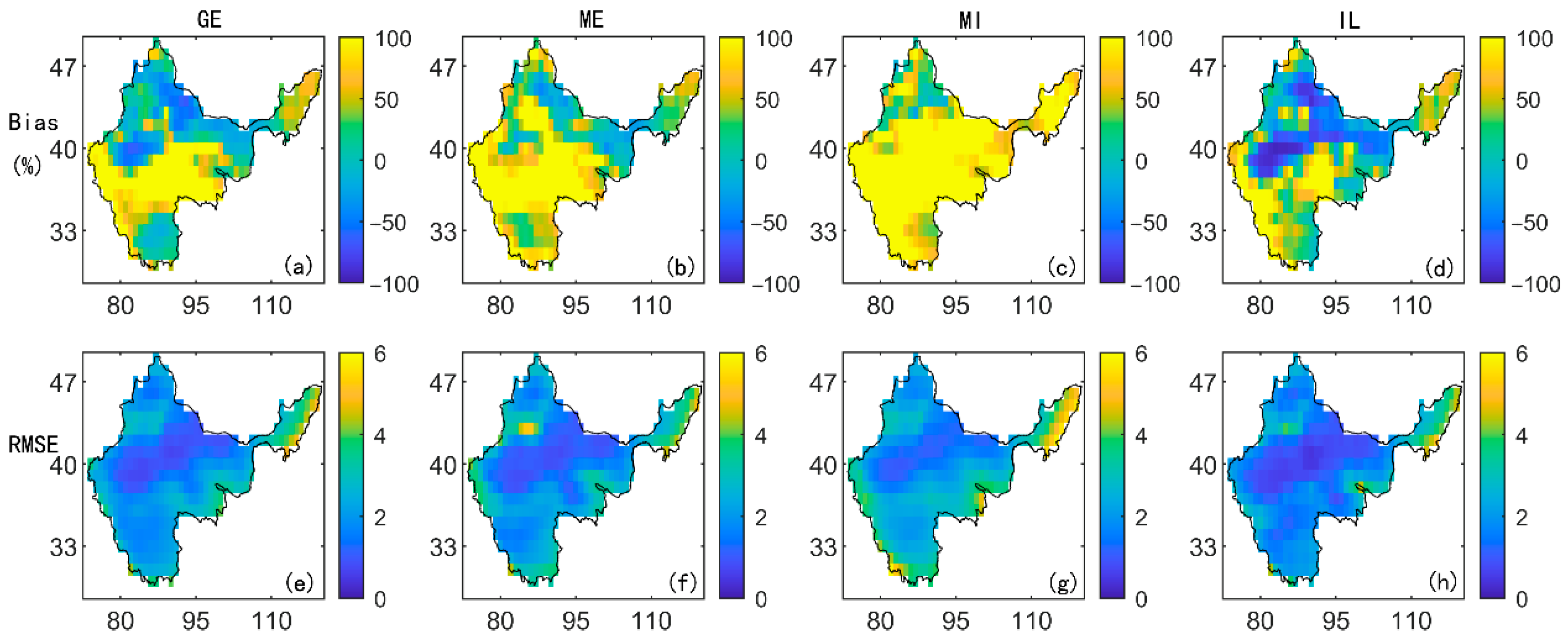
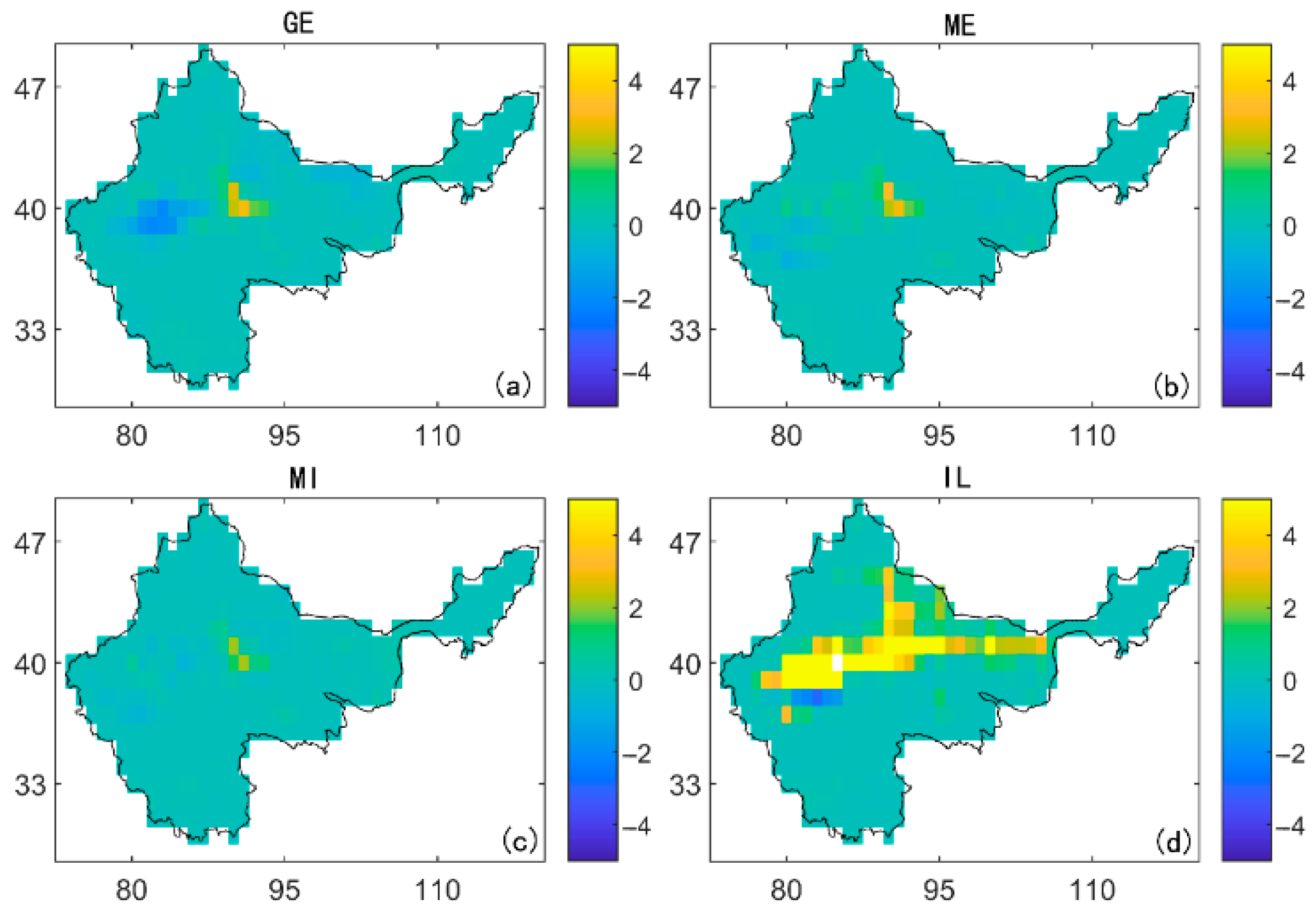
3.2. Model Evaluation and Bias Correction
3.3. Variability in Precipitation Extremes During Historical Events
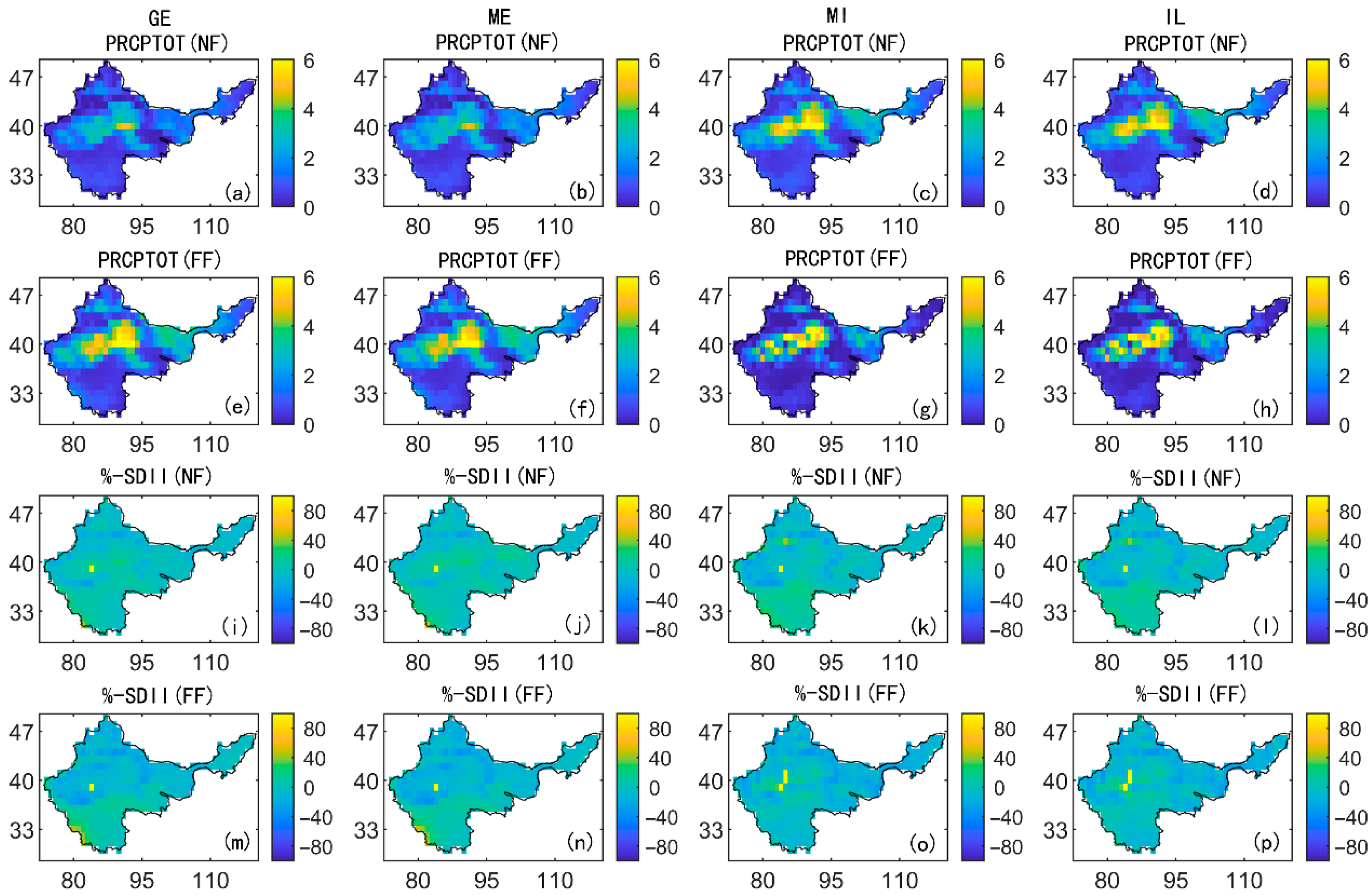
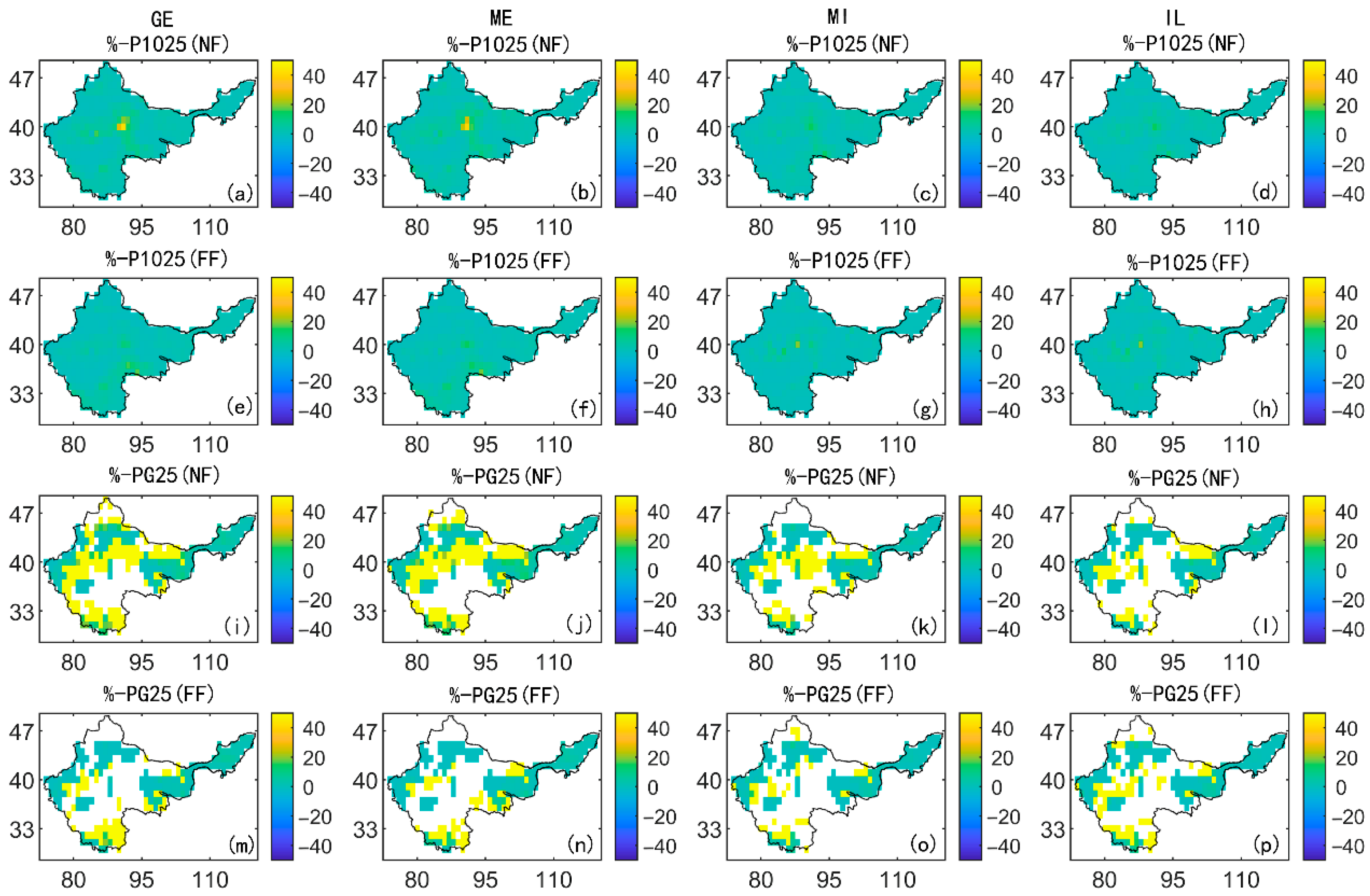
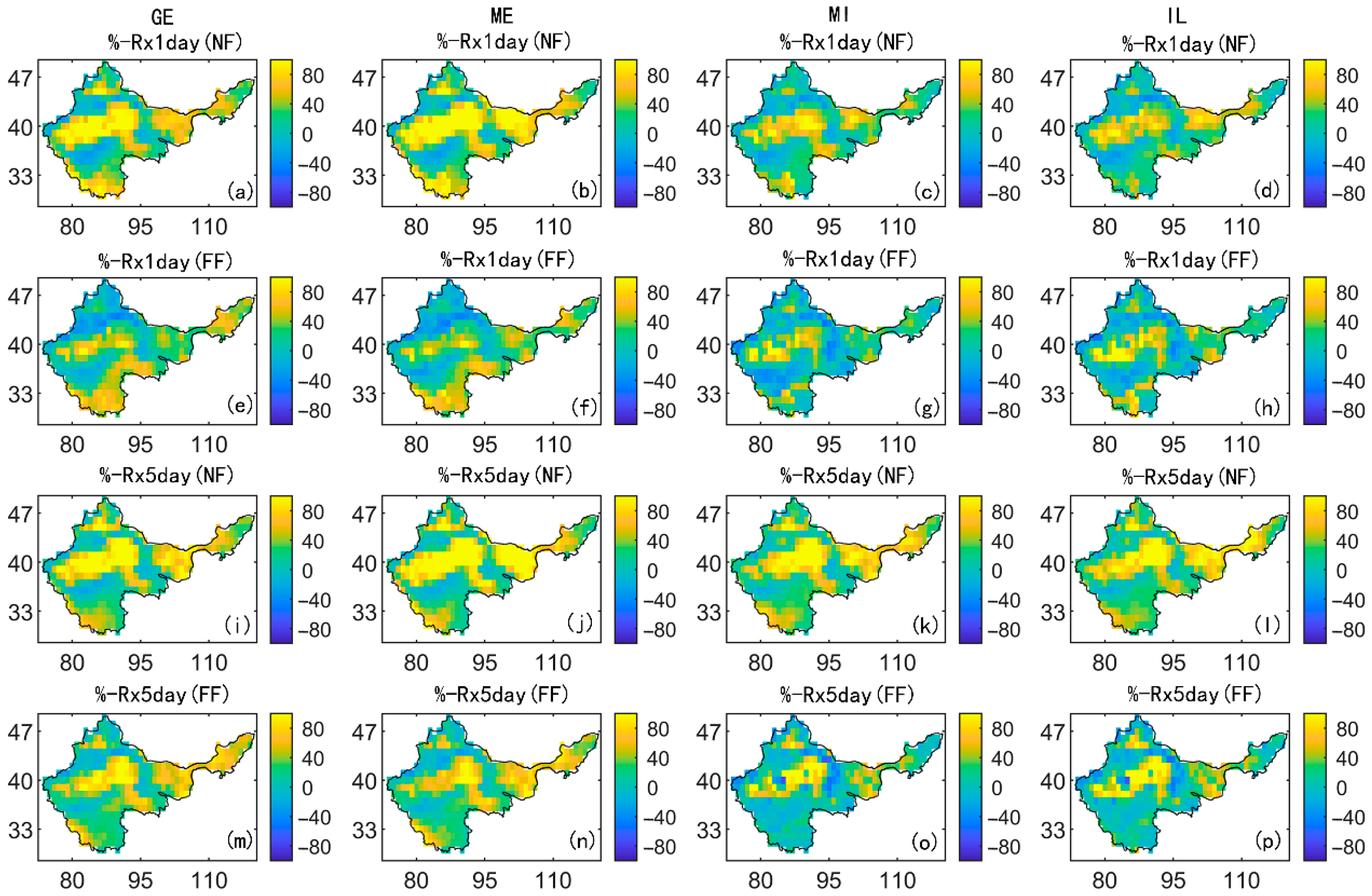
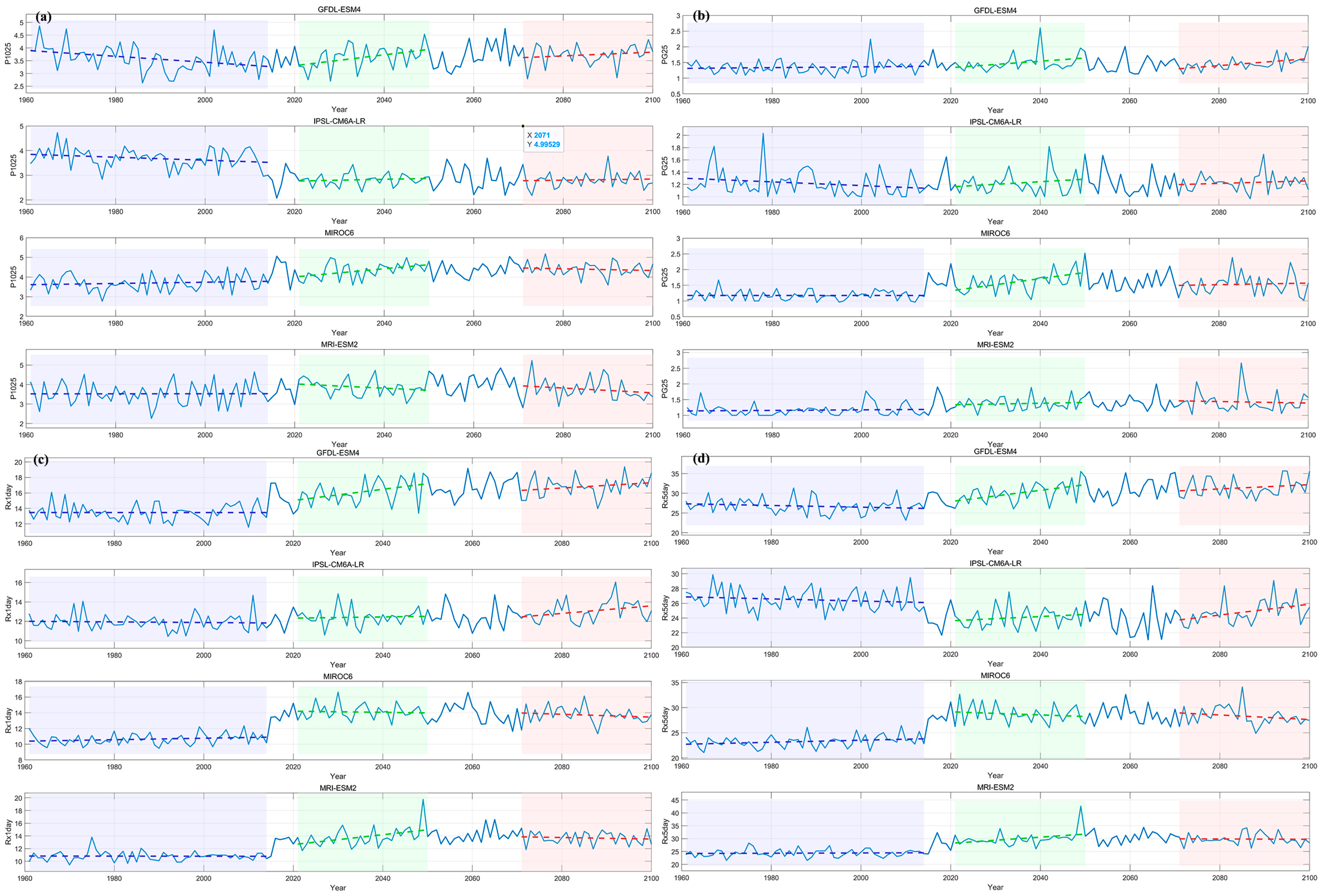
3.4. Analysis of Extreme Precipitation in the Future
4. Discussion
4.1. Model Performance and Uncertainties
4.2. Mechanisms Driving Hydrological Shifts
4.3. Future Trends and Ecological Implications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- White, S.M.; Shelton, C.L.; Gelb, A.W.; Lawson, C.; McGain, F.; Muret, J.; Sherman, J.D. Principles of environmentally-sustainable anaesthesia: A global consensus statement from the World Federation of Societies of Anaesthesiologists. Anaesthesia 2022, 77, 201–212. [Google Scholar] [CrossRef] [PubMed]
- De Nardi, S.; Carnevale, C.; Raccagni, S.; Sangiorgi, L. Climate Change Impact on Cereal Production in Northern Africa: A Comprehensive Modeling and Control Approach. IEEE Access 2025, 13, 5534–5550. [Google Scholar] [CrossRef]
- Berg, P.; Moseley, C.; Haerter, J.O. Strong increase in convective precipitation in response to higher temperatures. Nat. Geosci. 2013, 6, 181–185. [Google Scholar] [CrossRef]
- Donat, M.G.; Lowry, A.L.; Alexander, L.V.; O’Gorman, P.A.; Maher, N. More extreme precipitation in the world’s dry and wet regions. Nat. Clim. Change 2016, 6, 508–515. [Google Scholar] [CrossRef]
- Zhang, W.X.; Zhou, T.J.; Wu, P.L. Anthropogenic amplification of precipitation variability over the past century. Science 2024, 385, 427–432. [Google Scholar] [CrossRef]
- Wang, W.; Zhu, X.; Lu, P.; Zhao, Y.; Chen, Y.; Zhang, S. Spatio-temporal evolution of public opinion on urban flooding: Case study of the 7.20 Henan extreme flood event. Int. J. Disaster Risk Reduct. 2024, 100, 104175. [Google Scholar] [CrossRef]
- Ding, T.; Xie, T.J.; Gao, H.; Zhang, S.Y. Alternation Between the Extreme Drought-Flood Event in the North China Plain in Summer 2024. Int. J. Climatol. 2025, 45, e8831. [Google Scholar] [CrossRef]
- Zhang, W.X.; Zhou, T.J. Increasing impacts from extreme precipitation on population over China with global warming. Sci. Bull. 2020, 65, 243–252. [Google Scholar] [CrossRef]
- Ben Alaya, M.A.; Zwiers, F.W.; Zhang, X. Probable maximum precipitation in a warming climate over North America in CanRCM4 and CRCM5. Clim. Change 2020, 158, 611–629. [Google Scholar] [CrossRef]
- Pendergrass, A.G.; Coleman, D.B.; Deser, C.; Lehner, F.; Rosenbloom, N.; Simpson, I.R. Nonlinear Response of Extreme Precipitation to Warming in CESM1. Geophys. Res. Lett. 2019, 46, 10551–10560. [Google Scholar] [CrossRef]
- Feng, T.C.; Zhu, X.; Dong, W.J. Historical assessment and future projection of extreme precipitation in CMIP6 models: Global and continental. Int. J. Climatol. 2023, 43, 4119–4135. [Google Scholar] [CrossRef]
- Wu, R.G.; You, T.; Hu, K.M. What Formed the North-South Contrasting Pattern of Summer Rainfall Changes over Eastern China? Curr. Clim. Change Rep. 2019, 5, 47–62. [Google Scholar] [CrossRef]
- Monerie, P.A.; Wilcox, L.J.; Turner, A.G. Effects of Anthropogenic Aerosol and Greenhouse Gas Emissions on Northern Hemisphere Monsoon Precipitation: Mechanisms and Uncertainty. J. Clim. 2022, 35, 2305–2326. [Google Scholar] [CrossRef]
- Zhu, H.; Jiang, Z.; Li, L. Projection of climate extremes in China, an incremental exercise from CMIP5 to CMIP6. Science Bulletin 2021, 66, 2528–2537. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Zhao, Y.; Li, J.; Xu, H.; Zhang, C.; Deng, L.; Wang, Y.; Peng, M. Improving CMIP6 Atmospheric River Precipitation Estimation by Cycle-Consistent Generative Adversarial Networks. J. Geophys. Res. Atmos. 2024, 129, e2023JD040698. [Google Scholar] [CrossRef]
- Alexander, L.V.; Fowler, H.J.; Bador, M.; Behrangi, A.; Donat, M.G.; Dunn, R.; Funk, C.; Goldie, J.; Lewis, E.; Rogé, M.; et al. On the use of indices to study extreme precipitation on sub-daily and daily timescales. Environ. Res. Lett. 2019, 14, 125008. [Google Scholar] [CrossRef]
- Bador, M.; Alexander, L.V.; Contractor, S.; Roca, R. Diverse estimates of annual maxima daily precipitation in 22 state-of-the-art quasi-global land observation datasets. Environ. Res. Lett. 2020, 15, 035005. [Google Scholar] [CrossRef]
- Chen, C.-A.; Hsu, H.-H.; Liang, H.-C. Evaluation and comparison of CMIP6 and CMIP5 model performance in simulating the seasonal extreme precipitation in the Western North Pacific and East Asia. Weather. Clim. Extrem. 2021, 31, 100303. [Google Scholar] [CrossRef]
- Xu, H.W.; Chen, H.P.; He, W.Y.; Chen, L.F. Contributions of Anthropogenic Greenhouse Gases and Aerosol Emissions to Changes in Summer Precipitation Over Southern China. J. Geophys. Res.-Atmos. 2024, 129, e2023JD040331. [Google Scholar] [CrossRef]
- Han, T.T.; Guo, X.Y.; Zhou, B.T.; Hao, X. Recent Changes in Heavy Precipitation Events in Northern Central China and Associated Atmospheric Circulation. Asia-Pac. J. Atmos. Sci. 2021, 57, 301–310. [Google Scholar] [CrossRef]
- Xue, S.Y.; Guo, X.H.; He, Y.H.; Cai, H.; Li, J.; Zhu, L.R.; Ye, C. Effects of future climate and land use changes on runoff in tropical regions of China. Sci. Rep. 2024, 14, 30922. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.Q.; Wang, G.J.; Miao, L.J.; Gnyawali, K.R.; Li, S.J.; Amankwah, S.O.Y.; Huang, J.; Lu, J.; Zhan, M. Future drought in CMIP6 projections and the socioeconomic impacts in China. Int. J. Climatol. 2021, 41, 4151–4170. [Google Scholar] [CrossRef]
- Chen, X.G.; Li, Y.; Yao, N.; Liu, D.L.; Liu, Q.Z.; Song, X.Y.; Liu, F.; Pulatov, B.; Meng, Q.; Feng, P. Projected dry/wet regimes in China using SPEI under four SSP-RCPs based on statistically downscaled CMIP6 data. Int. J. Climatol. 2022, 42, 9357–9384. [Google Scholar] [CrossRef]
- Xu, M.; Wang, P.S.; Zhang, X.; Ma, T.; Jin, J.L.; Kang, S.C.; Han, H.; Wu, H.; Hou, Z.; Li, X.; et al. Impacts of glacier shrinkage on peak melt runoff at the sub-basin scale of Northwest China. J. Hydrol. 2025, 654, 132953. [Google Scholar] [CrossRef]
- Han, T.T.; Chen, H.P.; Hao, X.; Wang, H.J. Projected changes in temperature and precipitation extremes over the Silk Road Economic Belt regions by the Coupled Model Intercomparison Project Phase 5 multi-model ensembles. Int. J. Climatol. 2018, 38, 4077–4091. [Google Scholar] [CrossRef]
- Chen, Z.W.; Zhang, X.F.; Chen, J.H. Monitoring Terrestrial Water Storage Changes with the Tongji-Grace2018 Model in the Nine Major River Basins of the Chinese Mainland. Remote Sens. 2021, 13, 1851. [Google Scholar] [CrossRef]
- Guohua, F.; Heshuai, Q.; Xin, W.; Lei, Z. Analysis of spatiotemporal evolution of extreme monthly precipitation in the nine major basins of China in 21st century under climate change. J. Nat. Disasters 2016, 25, 15–25. (In Chinese) [Google Scholar]
- Gupta, V.; Singh, V.; Jain, M.K. Assessment of precipitation extremes in India during the 21st century under SSP1-1.9 mitigation scenarios of CMIP6 GCMs. J. Hydrol. 2020, 590, 125422. [Google Scholar] [CrossRef]
- Wu, J.; Gao, X.J. A gridded daily observation dataset over China region and comparison with the other datasets. Chin. J. Geophys. -Chin. Ed. 2013, 56, 1102–1111. [Google Scholar] [CrossRef]
- Maraun, D. Bias Correction, Quantile Mapping, and Downscaling: Revisiting the Inflation Issue. J. Clim. 2013, 26, 2137–2143. [Google Scholar] [CrossRef]
- Cannon, A.J. Multivariate quantile mapping bias correction: An N-dimensional probability density function transform for climate model simulations of multiple variables. Clim. Dyn. 2017, 50, 31–49. [Google Scholar] [CrossRef]
- Maraun, D.; Widmann, M. Cross-validation of bias-corrected climate simulations is misleading. Hydrol. Earth Syst. Sci. 2018, 22, 4867–4873. [Google Scholar] [CrossRef]
- Li, H.B.; Sheffield, J.; Wood, E.F. Bias correction of monthly precipitation and temperature fields from Intergovernmental Panel on Climate Change AR4 models using equidistant quantile matching. J. Geophys. Res.-Atmos. 2010, 115, 1–20. [Google Scholar] [CrossRef]
- Ren, L.; Xue, L.Q.; Liu, Y.H.; Shi, J.; Han, Q.; Yi, P.F. Study on Variations in Climatic Variables and Their Influence on Runoff in the Manas River Basin, China. Water 2017, 9, 258. [Google Scholar] [CrossRef]
- Wang, W.G.; Ding, Y.M.; Shao, Q.X.; Xu, J.Z.; Jiao, X.Y.; Luo, Y.F.; Yu, Z. Bayesian multi-model projection of irrigation requirement and water use efficiency in three typical rice plantation region of China based on CMIP5. Agric. For. Meteorol. 2017, 232, 89–105. [Google Scholar] [CrossRef]
- Song, X.Y.; Xu, M.; Kang, S.C.; Wang, R.J.; Wu, H. Evaluation and projection of changes in temperature and precipitation over Northwest China based on CMIP6 models. Int. J. Climatol. 2024, 44, 5039–5056. [Google Scholar] [CrossRef]
- Yuan, Y.Y.; Liao, B.Y. Evaluation of multi-source precipitation products for monitoring drought across China. Front. Environ. Sci. 2025, 13, 1524937. [Google Scholar] [CrossRef]
- Wu, Y.; Miao, C.Y.; Slater, L.; Fan, X.W.; Chai, Y.F.; Sorooshian, S. Hydrological Projections under CMIP5 and CMIP6. Bull. Am. Meteorol. Soc. 2024, 105, E2374–E2389. [Google Scholar] [CrossRef]
- Prein, A.F.; Rasmussen, R.; Castro, C.L.; Dai, A.G.; Minder, J. Special issue: Advances in convection-permitting climate modeling. Clim. Dyn. 2020, 55, 1–2. [Google Scholar] [CrossRef]
- Fang, G.H.; Li, Z.; Chen, Y.N.; Liang, W.T.; Zhang, X.Q.; Zhang, Q.F. Projecting the Impact of Climate Change on Runoff in the Tarim River Simulated by the Soil and Water Assessment Tool Glacier Model. Remote Sens. 2023, 15, 3922. [Google Scholar] [CrossRef]
- Xiao, D.; Ren, H.L. Interdecadal changes in synoptic transient eddy activity over the Northeast Pacific and their role in tropospheric Arctic amplification. Clim. Dyn. 2021, 57, 993–1008. [Google Scholar] [CrossRef]
- Li, X.; Peachey, B.; Maeda, N. Global Warming and Anthropogenic Emissions of Water Vapor. Langmuir 2024, 40, 7701–7709. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.H.; Marino, A.; Ji, Y.J. Spatial and Temporal Change Characteristics and Climatic Drivers of Vegetation Productivity and Greenness during the 2001–2020 Growing Seasons on the Qinghai-Tibet Plateau. Land 2024, 13, 1230. [Google Scholar] [CrossRef]


| Abbreviation | Model ID | Country or Union | Spatial Resolution | Time Period | Type and Size |
|---|---|---|---|---|---|
| GE | GFDL-ESM4 | USA | 100 km × 100 km | 1950–2100 | Daily precipitation |
| ME | MRI-ESM2 | Japan | 100 km × 100 km | 1950–2100 | Daily precipitation |
| MI | MIROC6 | Japan | 250 km × 250 km | 1960–2100 | Daily precipitation |
| IL | IPSL-CM6A-LR | France | 250 km × 250 km | 1850–2100 | Daily precipitation |
| Number | Abbreviation | Definition | Unit |
|---|---|---|---|
| 1 | PRCPTOT | Total annual precipitation from days with rainfall ≥ 1 mm | mm |
| 2 | SDII | Mean daily precipitation intensity | mm/day |
| 3 | CDD | Maximum consecutive dry days (<1 mm) | days |
| 4 | CWD | Maximum consecutive wet days (≥1 mm) | days |
| 5 | P1025 | Days with rainfall 10–25 mm | days |
| 6 | PG25 | Days with rainfall > 25 mm | days |
| 7 | Rx1day | Maximum 1-day precipitation | mm |
| 8 | Rx5day | Maximum 5-day cumulative precipitation | mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Xue, L.; Lin, T.; Zhang, P.; Liu, Y. Assessing Extreme Precipitation in Northwest China’s Inland River Basin Under a Novel Low Radiative Forcing Scenario. Water 2025, 17, 2009. https://doi.org/10.3390/w17132009
Yang M, Xue L, Lin T, Zhang P, Liu Y. Assessing Extreme Precipitation in Northwest China’s Inland River Basin Under a Novel Low Radiative Forcing Scenario. Water. 2025; 17(13):2009. https://doi.org/10.3390/w17132009
Chicago/Turabian StyleYang, Mingjie, Lianqing Xue, Tao Lin, Peng Zhang, and Yuanhong Liu. 2025. "Assessing Extreme Precipitation in Northwest China’s Inland River Basin Under a Novel Low Radiative Forcing Scenario" Water 17, no. 13: 2009. https://doi.org/10.3390/w17132009
APA StyleYang, M., Xue, L., Lin, T., Zhang, P., & Liu, Y. (2025). Assessing Extreme Precipitation in Northwest China’s Inland River Basin Under a Novel Low Radiative Forcing Scenario. Water, 17(13), 2009. https://doi.org/10.3390/w17132009







