Research on the Risk of a Multi-Source Hydrological Drought Encounter in the Yangtze River Basin Based on Spatial and Temporal Correlation
Abstract
1. Introduction
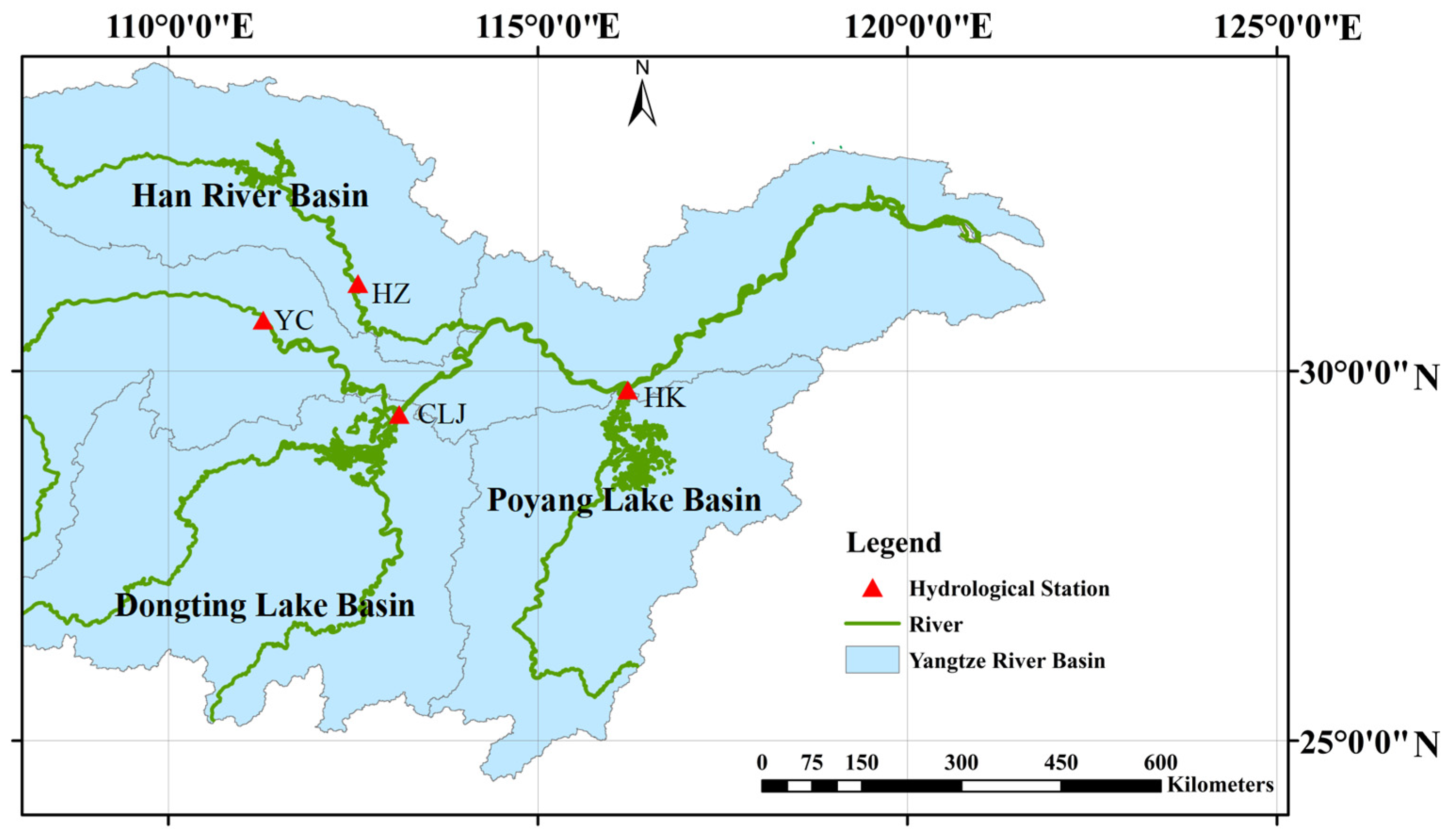
2. Study Area and Data
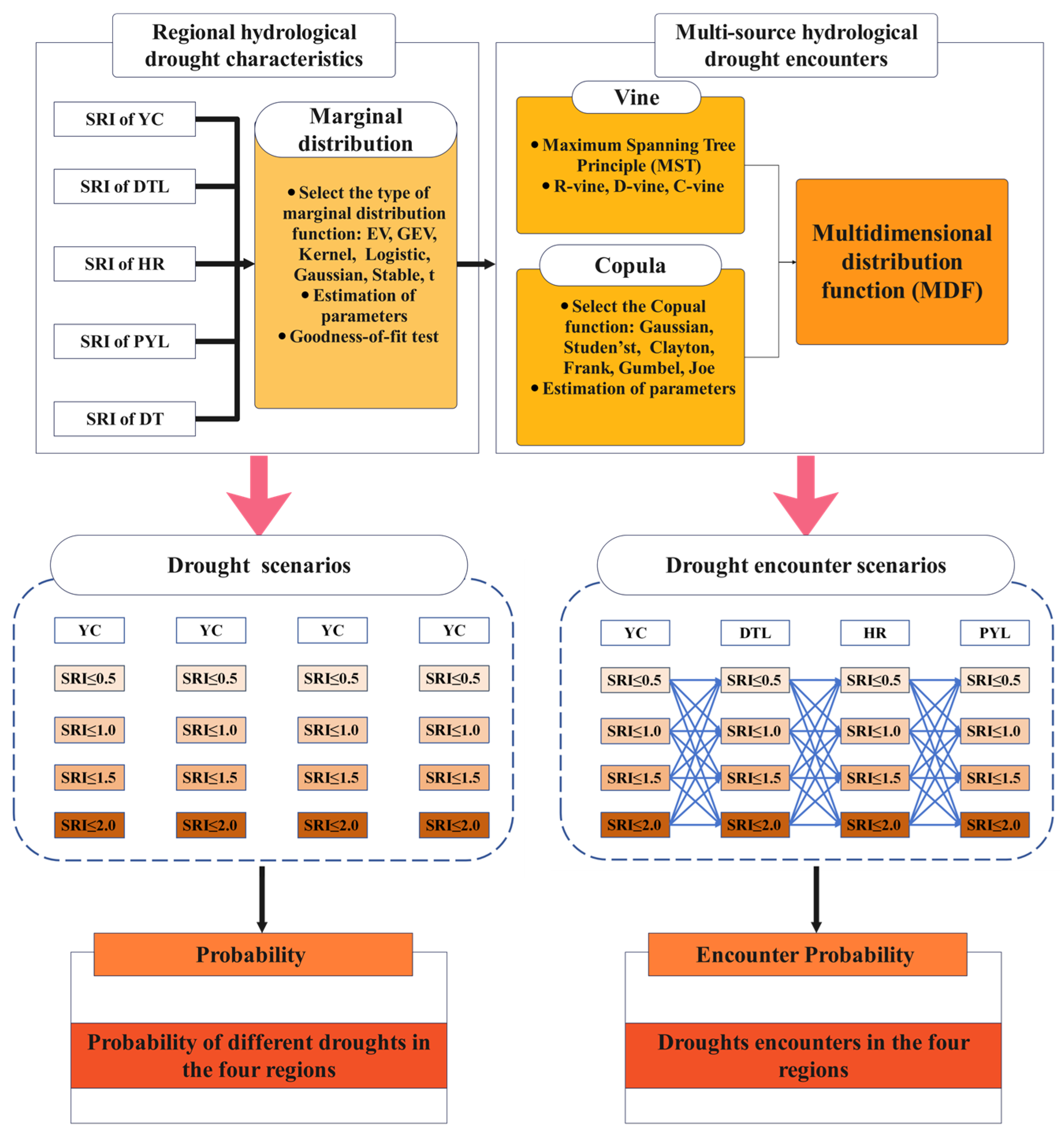
3. Methodology
3.1. Drought Characteristics of Each Region
3.1.1. Drought Index
3.1.2. SRI Distribution Fitting
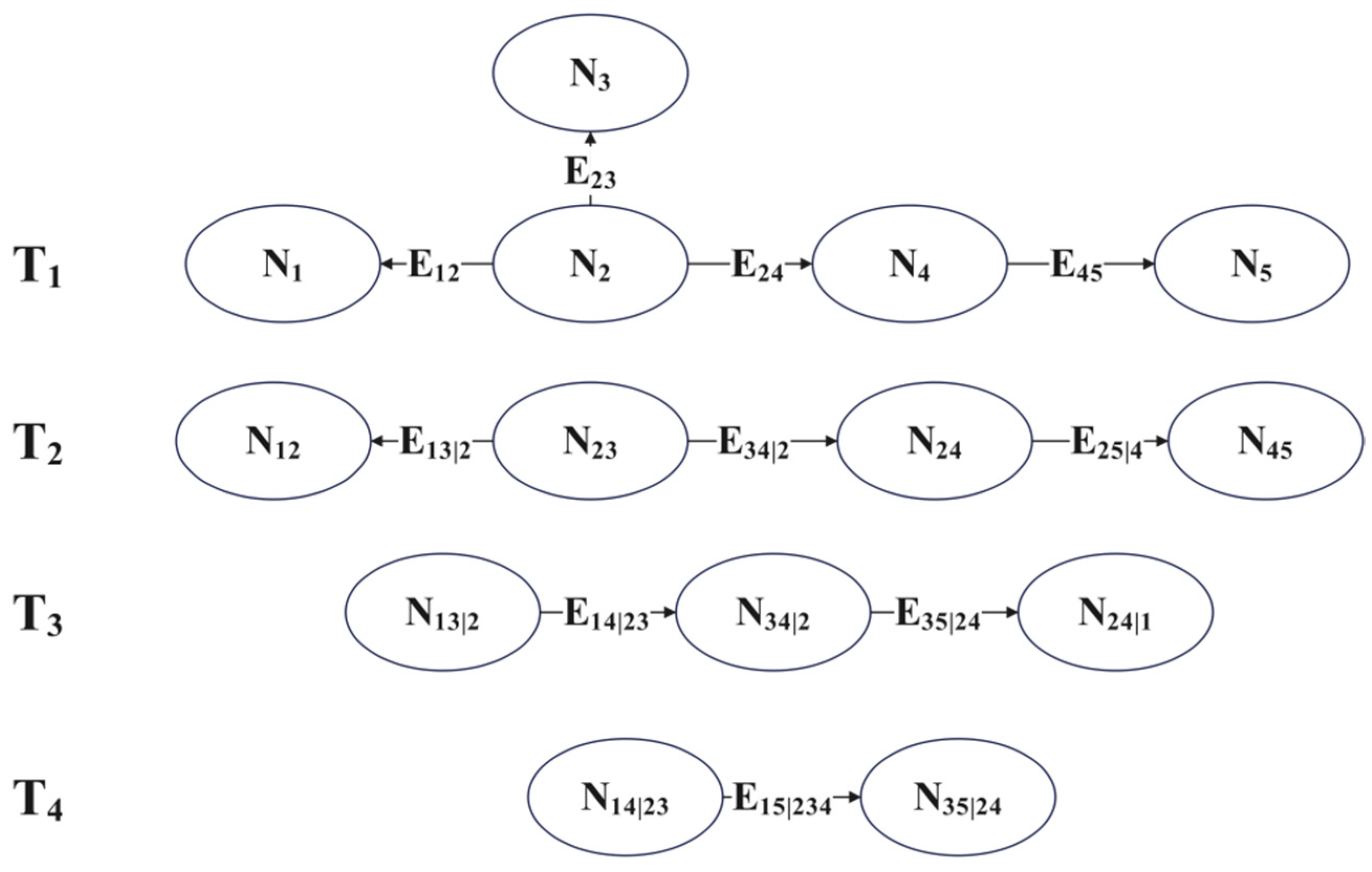
3.2. Multi-Source Hydrologic Drought Encounter Risk Calculation Model
4. Results and Analysis
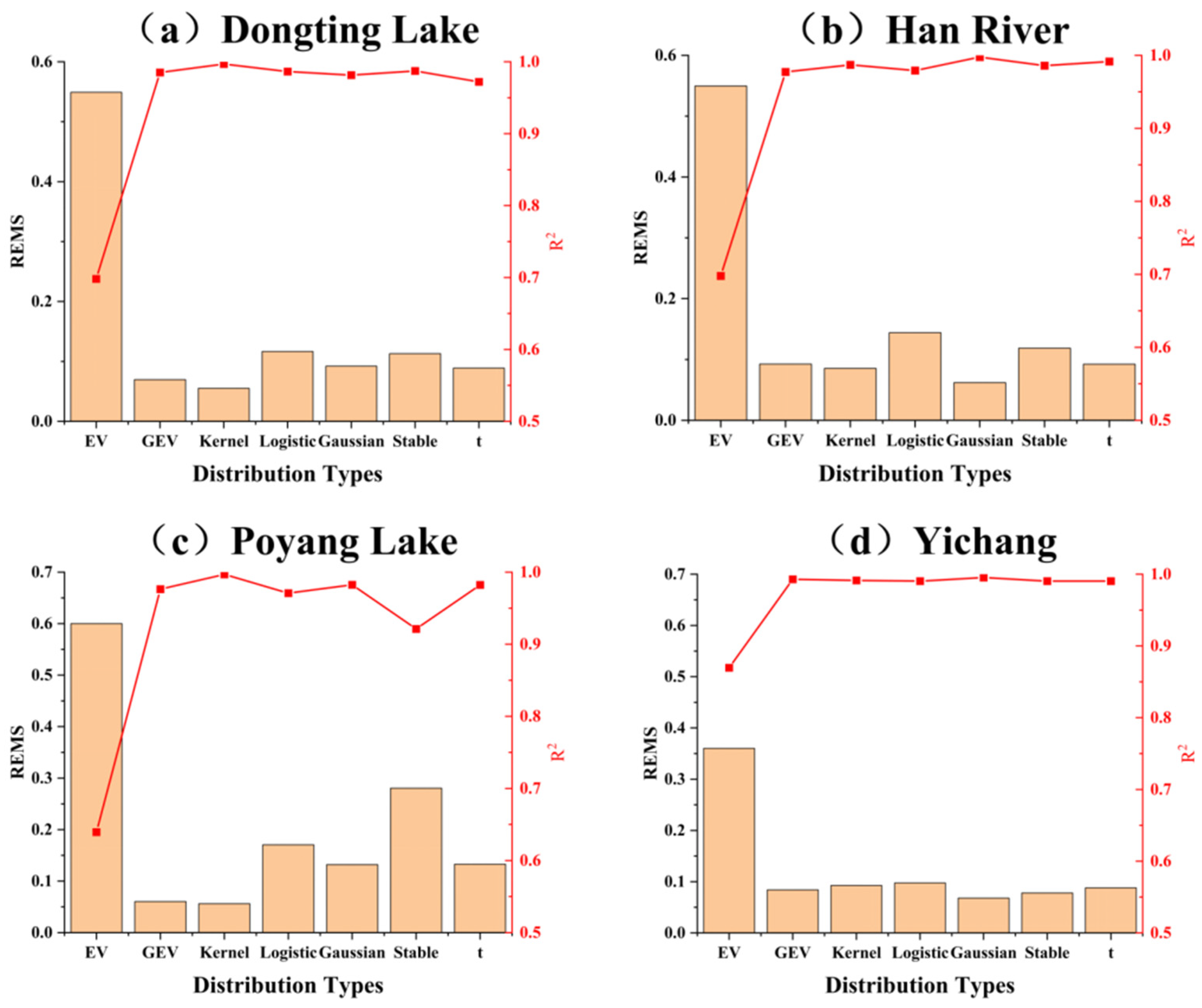
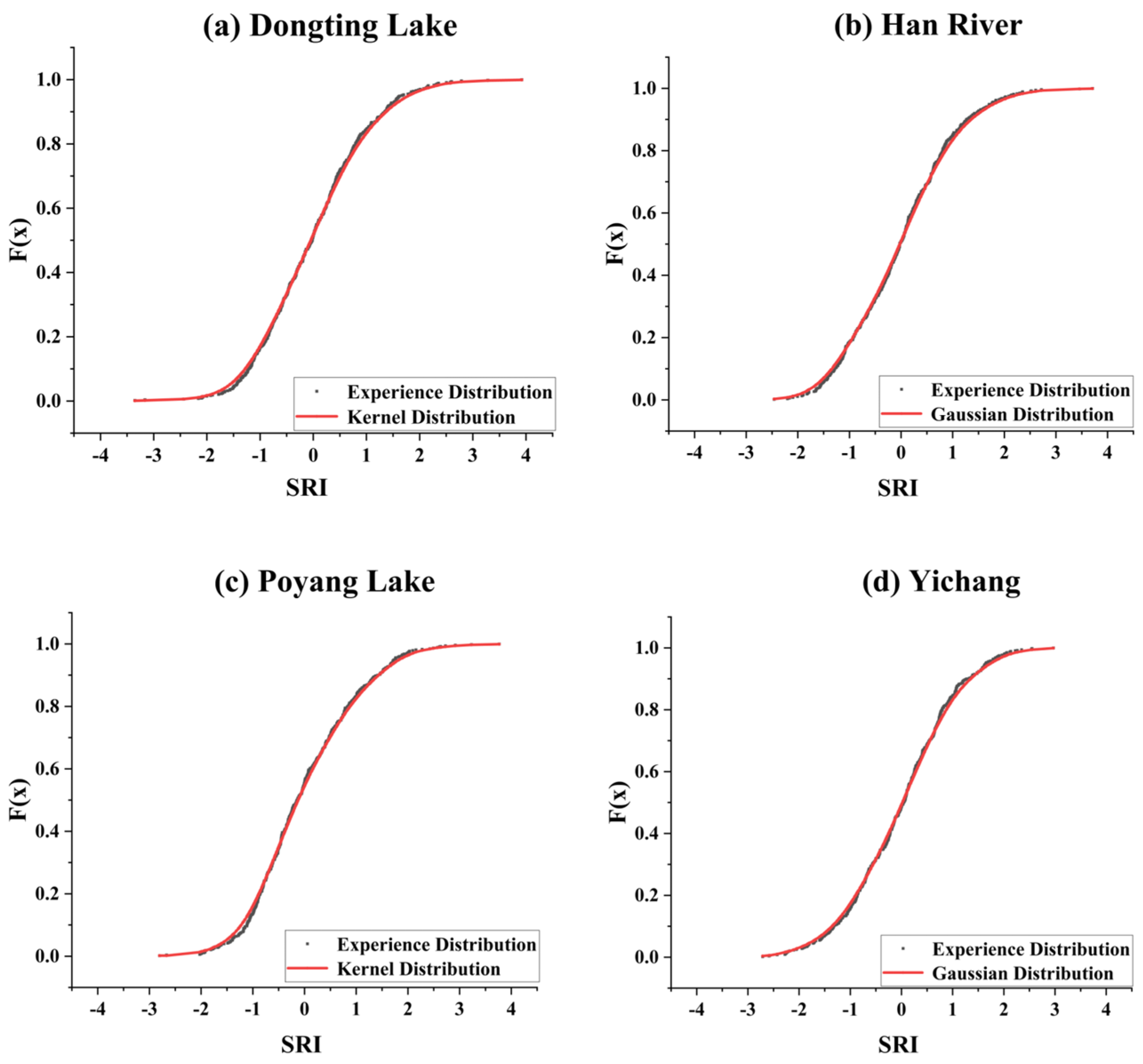
4.1. Fitting the Optimal Marginal Distribution
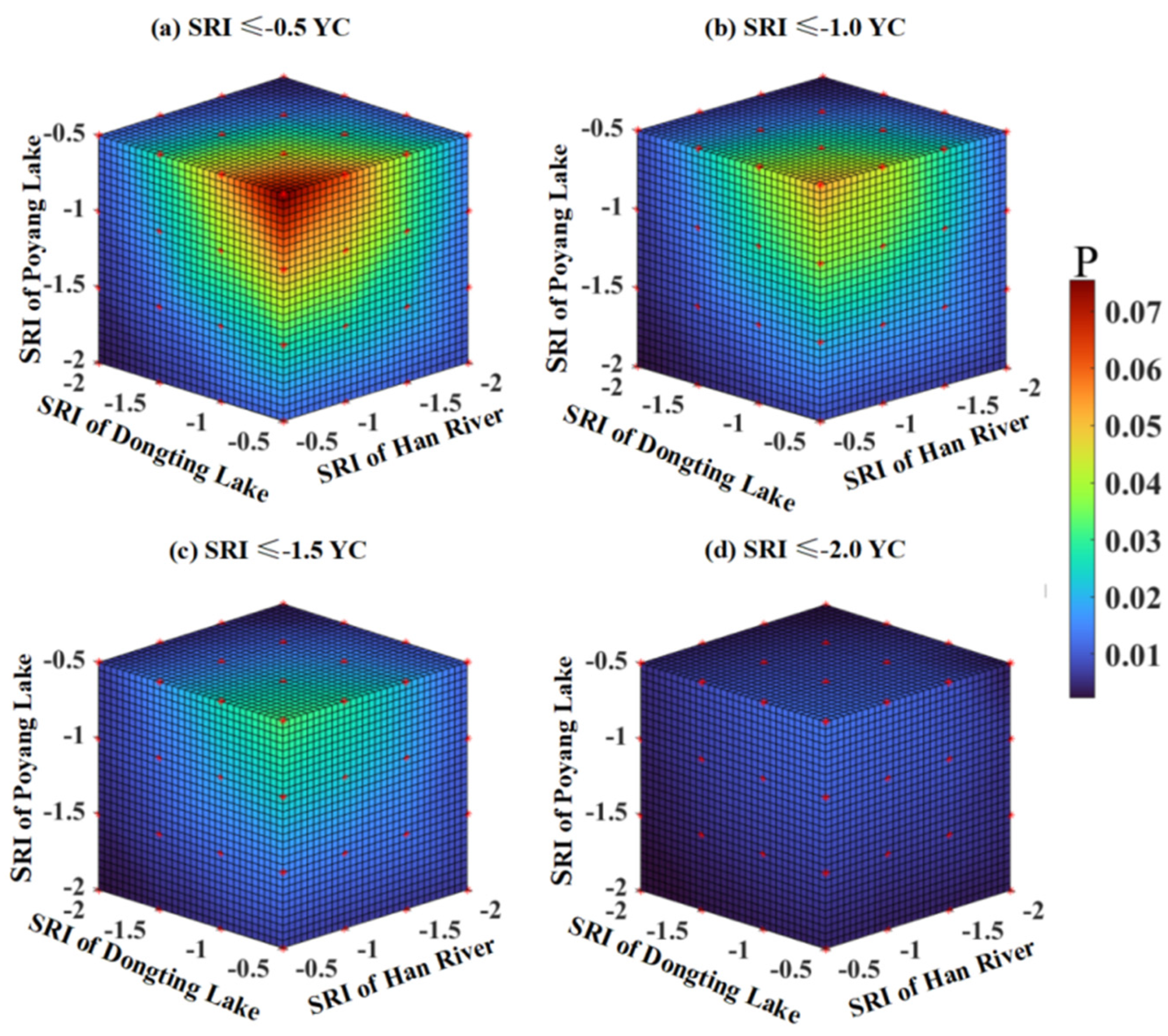
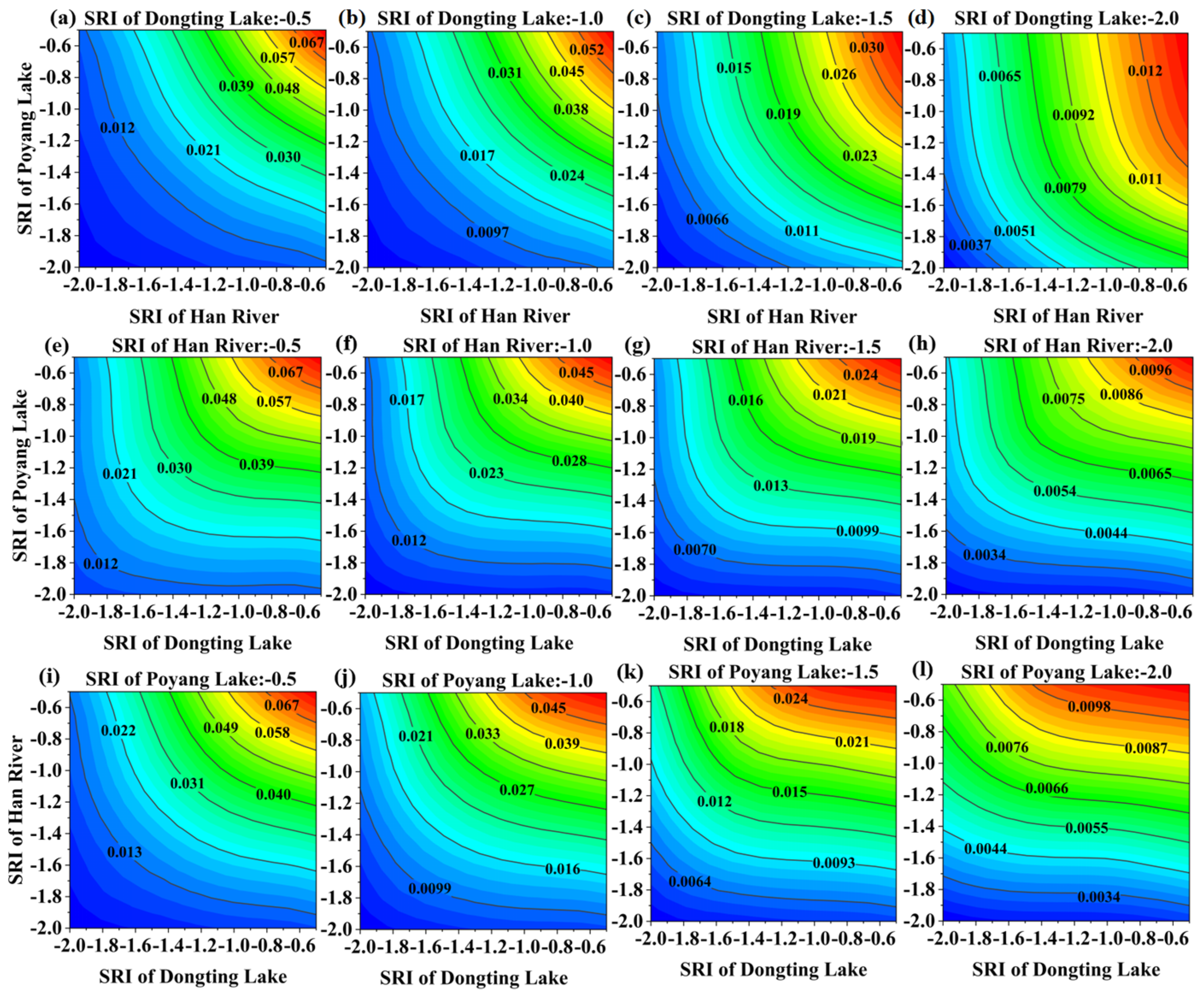
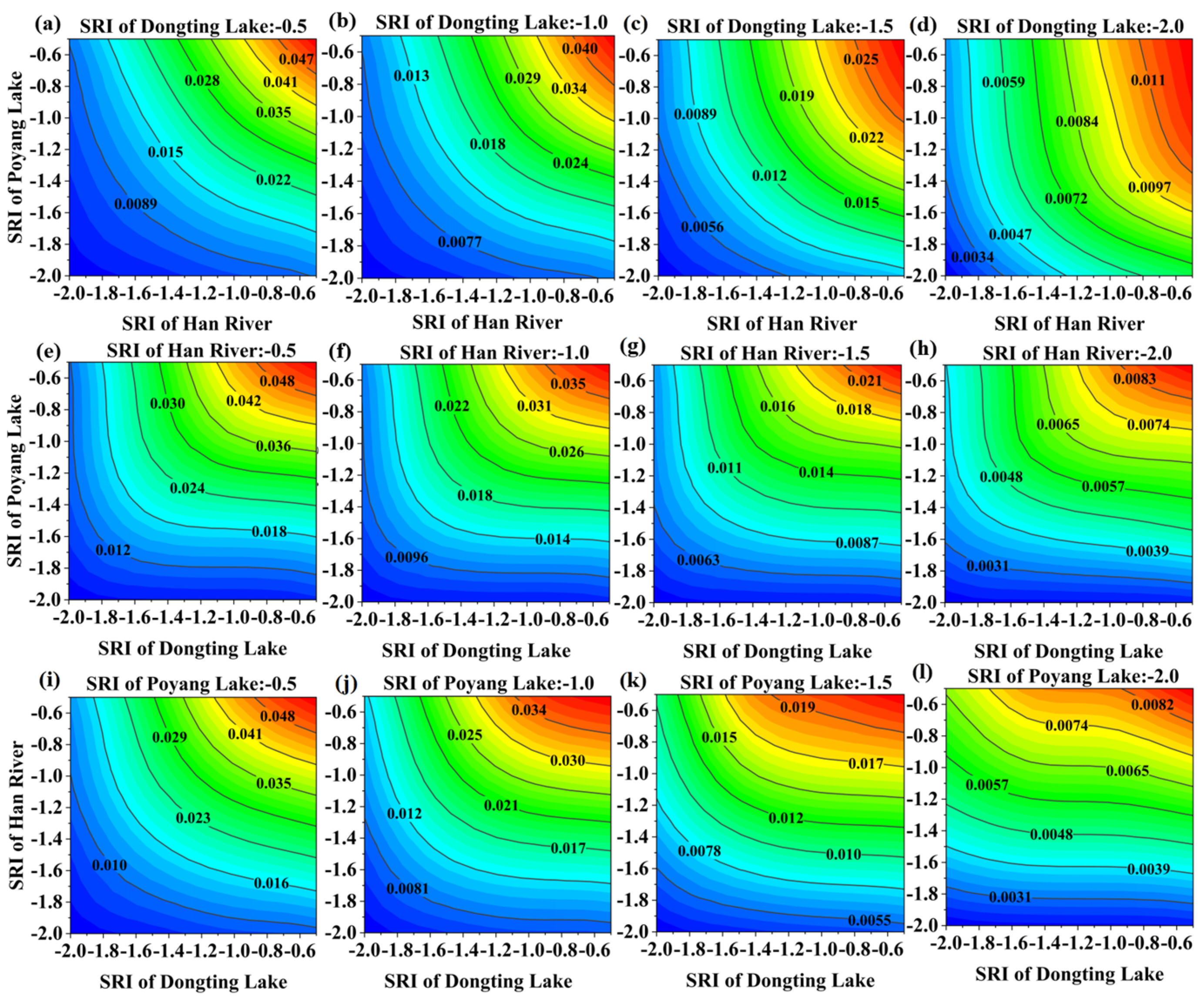
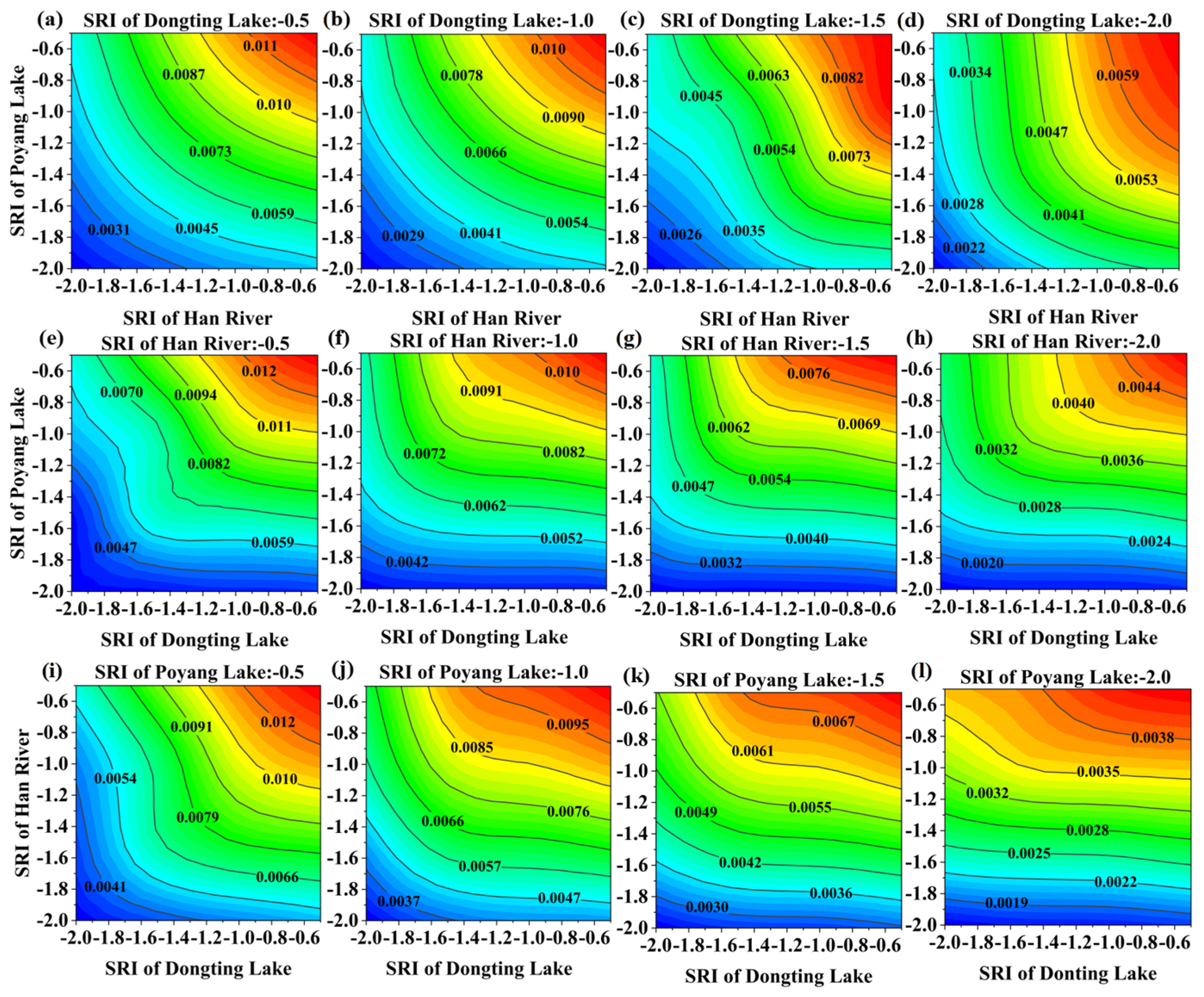
4.2. Jointly Distributed Probabilities
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stott, P. How climate change affects extreme weather events. Science 2016, 352, 1517–1518. [Google Scholar] [CrossRef]
- Zscheischler, J.; Westra, S.; van den Hurk, B.J.J.M.; Seneviratne, S.I.; Ward, P.J.; Pitman, A.; AghaKouchak, A.; Bresch, D.N.; Leonard, M.; Wahl, T.; et al. Future climate risk from compound events. Nat. Clim. Change 2018, 8, 469–477. [Google Scholar] [CrossRef]
- Zscheischler, J.; Seneviratne, S.I. Dependence of drivers affects risks associated with compound events. Sci. Adv. 2017, 3, e1700263. [Google Scholar] [CrossRef]
- Meza, I.; Siebert, S.; Döll, P.; Kusche, J.; Herbert, C.; Eyshi Rezaei, E.; Nouri, H.; Gerdener, H.; Popat, E.; Frischen, J.; et al. Global-scale drought risk assessment for agricultural systems. Nat. Hazard. Earth Syst. 2020, 20, 695–712. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Quiring, S.M.; Peña-Gallardo, M.; Yuan, S.; Domínguez-Castro, F. A review of environmental droughts: Increased risk under global warming? Earth-Sci. Rev. 2020, 201, 102953. [Google Scholar] [CrossRef]
- Zeng, Z.; Wu, W.; Peñuelas, J.; Li, Y.; Jiao, W.; Li, Z.; Ren, X.; Wang, K.; Ge, Q. Increased risk of flash droughts with raised concurrent hot and dry extremes under global warming. Npj Clim. Atmos. Sci. 2023, 6, 134. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, L.; Chen, J.; She, D.; Wang, G.; Zhang, Q.; Xia, J.; Zhang, Y. Projecting Global Drought Risk Under Various SSP-RCP Scenarios. Earth’s Future 2023, 11, e2022EF003420. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, Z.; Singh, V.P.; Zhang, Y.; Feng, S.; Xu, Y.; Hao, F. Drought propagation under global warming: Characteristics, approaches, processes, and controlling factors. Sci. Total Environ. 2022, 838, 156021. [Google Scholar] [CrossRef]
- Xiang, K.; Song, W.; Lu, J.; Zhao, A.; Lu, Y.; Feng, T.; Liu, H.; Gui, R.; Chen, L. Investigating the drought propagation dynamics between meteorological and groundwater drought in the Yellow River Basin, China. J. Hydrol. 2025, 660, 133446. [Google Scholar] [CrossRef]
- Mei, L.; Aru, H.; Tong, S.; Wang, Y.; Guo, E.; Zhang, T.; Yin, S.; Bao, Y. Study on the propagation processes and driving mechanisms of meteorological, hydrological, and agricultural droughts on the Mongolian Plateau. J. Hydrol. 2025, 660, 133511. [Google Scholar] [CrossRef]
- Gao, Y.; Zhao, T.; Tu, T.; Tian, Y.; Zhang, Y.; Liu, Z.; Zheng, Y.; Chen, X.; Wang, H. Spatiotemporal links between meteorological and agricultural droughts impacted by tropical cyclones in China. Sci. Total Environ. 2024, 912, 169119. [Google Scholar] [CrossRef]
- Jiang, T.; Su, X.; Zhang, G.; Zhang, T.; Wu, H. Estimating propagation probability from meteorological to ecological droughts using a hybrid machine learning copula method. Hydrol. Earth Syst. Sci. 2023, 27, 559–576. [Google Scholar] [CrossRef]
- Ge, C.; Sun, P.; Yao, R.; Wang, Y.; Chen, W.; Bian, Y.; Zhang, Q. Characteristics of propagation from meteorological drought to ecological drought in China: Lag and cumulative effects. Atmos. Res. 2024, 304, 107405. [Google Scholar] [CrossRef]
- Li, L.; Peng, Q.; Wang, M.; Cao, Y.; Gu, X.; Cai, H. Quantitative analysis of vegetation drought propagation process and uncertainty in the Yellow River Basin. Agric. Water Manag. 2024, 295, 108775. [Google Scholar] [CrossRef]
- Haile, M.M.; Li, F.; Ai, Z.; Chen, G.; Leng, P. Spatiotemporal characteristics and driving factors of groundwater drought in Nile River Basin (NRB). Catena 2025, 257, 109194. [Google Scholar] [CrossRef]
- Guan, B.; Wang, Q.; Jiang, S.; Zhao, Y.; Li, H.; Chang, H.; Yang, W.; He, G.; Wang, Y. Analysis of the meteorological factors and atmospheric circulation factors over SPEI drought index in Haihe River Basin, China. Atmos. Res. 2025, 325, 108182. [Google Scholar] [CrossRef]
- Luo, Q.; Liu, X.; Wang, K.; Liu, C. Increasingly frequent co-occurrence of drought or pluvial in multiple tributaries of the Yangtze River basin. J. Hydrol. 2024, 633, 131035. [Google Scholar] [CrossRef]
- François, B.; Vrac, M. Time of emergence of compound events: Contribution of univariate and dependence properties. Nat. Hazards Earth Syst. Sci. 2023, 23, 21–44. [Google Scholar] [CrossRef]
- Dong, S.; Jiao, C.; Tao, S. Joint return probability analysis of wind speed and rainfall intensity in typhoon-affected sea area. Nat. Hazards 2017, 86, 1193–1205. [Google Scholar] [CrossRef]
- Yin, C.; Wang, J.; Yu, X.; Li, Y.; Yan, D.; Jian, S. Definition of Extreme Rainfall Events and Design of Rainfall Based on the Copula Function. Water Resour. Manag. 2022, 36, 3759–3778. [Google Scholar] [CrossRef]
- Wang, Y.; Li, C.; Liu, J.; Yu, F.; Qiu, Q.; Tian, J.; Zhang, M. Multivariate Analysis of Joint Probability of Different Rainfall Frequencies Based on Copulas. Water 2017, 9, 198. [Google Scholar] [CrossRef]
- Tosunoğlu, F.; Onof, C. Joint modelling of drought characteristics derived from historical and synthetic rainfalls: Application of Generalized Linear Models and Copulas. J. Hydrol. Reg. Stud. 2017, 14, 167–181. [Google Scholar] [CrossRef]
- Brunner, M.I.; Furrer, R.; Favre, A. Modeling the spatial dependence of floods using the Fisher copula. Hydrol. Earth Syst. Sci. 2019, 23, 107–124. [Google Scholar] [CrossRef]
- Bedford, T.; Cooke, R.M. Probability Density Decomposition for Conditionally Dependent Random Variables Modeled by Vines. Ann. Math. Artif. Intell. 2001, 32, 245–268. [Google Scholar] [CrossRef]
- Ma, F.; Yuan, X. When Will the Unprecedented 2022 Summer Heat Waves in Yangtze River Basin Become Normal in a Warming Climate? Geophys. Res. Lett. 2023, 50, e2022GL101946. [Google Scholar] [CrossRef]
- Li, P.; Yu, Z.; Jiang, P.; Wu, C. Spatiotemporal characteristics of regional extreme precipitation in Yangtze River basin. J. Hydrol. 2021, 603, 126910. [Google Scholar] [CrossRef]
- Yang, P.; Zhang, S.; Xia, J.; Zhan, C.; Cai, W.; Wang, W.; Luo, X.; Chen, N.; Li, J. Analysis of drought and flood alternation and its driving factors in the Yangtze River Basin under climate change. Atmos. Res. 2022, 270, 106087. [Google Scholar] [CrossRef]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35, L02405. [Google Scholar] [CrossRef]
- Yao, N.; Zhao, H.; Li, Y.; Biswas, A.; Feng, H.; Liu, F.; Pulatov, B. National-Scale Variation and Propagation Characteristics of Meteorological, Agricultural, and Hydrological Droughts in China. Remote Sens. 2020, 12, 3407. [Google Scholar] [CrossRef]
- Zhou, Z.; Shi, H.; Fu, Q.; Ding, Y.; Li, T.; Liu, S. Investigating the Propagation From Meteorological to Hydrological Drought by Introducing the Nonlinear Dependence With Directed Information Transfer Index. Water Resour. Res. 2021, 57, e2021WR030028. [Google Scholar] [CrossRef]
- Li, R.; Chen, N.; Zhang, X.; Zeng, L.; Wang, X.; Tang, S.; Li, D.; Niyogi, D. Quantitative analysis of agricultural drought propagation process in the Yangtze River Basin by using cross wavelet analysis and spatial autocorrelation. Agric. For. Meteorol. 2020, 280, 107809. [Google Scholar] [CrossRef]
- Yu, J.; Zou, L.; Xia, J.; Dou, M.; Liu, H.; Zuo, L. Future changes in hydrological drought across the Yangtze River Basin: Identification, spatial–temporal characteristics, and concurrent probability. J. Hydrol. 2023, 625, 130057. [Google Scholar] [CrossRef]
- Joe, H. Families of m-Variate Distributions with Given Margins and m(m-1)/2 Bivariate Dependence Parameters. In Distributions with Fixed Marginals and Related Topics; Lecture Notes-Monograph Series; Institute of Mathematical Statistics: Beachwood, OH, USA, 1996; Volume 28, pp. 120–141. Available online: https://www.jstor.org/stable/4355888 (accessed on 13 March 2024).
- Ni, L.; Wang, D.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J.; Liu, J.; Xie, F. Vine copula selection using mutual information for hydrological dependence modeling. Environ. Res. 2020, 186, 109604. [Google Scholar] [CrossRef]
- Aas, K.; Czado, C.; Frigessi, A.; Bakken, H. Pair-copula constructions of multiple dependence. Insur. Math. Econ. 2009, 44, 182–198. [Google Scholar] [CrossRef]
- Zhu, K.; Kurowicka, D.; Nane, G.F. Common sampling orders of regular vines with application to model selection. Comput. Stat. Data Anal. 2020, 142, 106811. [Google Scholar] [CrossRef]
- Huang, Z.; Chen, X.; Pan, Z.; Gao, R.; Men, J.; Bi, P.; Huang, N.; Zhang, F.; Yang, R. Increasingly frequent and severe dry-to-wet abrupt alteration events are striking the Yangtze River Basin in China. Atmos. Res. 2025, 315, 107926. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, Q.; Song, W.; Tang, S.; Singh, V.P. Hydrological responses of three gorges reservoir region (China) to climate and land use and land cover changes. Nat. Hazards 2025, 121, 1505–1530. [Google Scholar] [CrossRef]
- Xing, L.; Zhao, R.; Sun, H.; Li, M.; Tan, Z. Analysis of drought characteristics and comparison of historical typical years with 2022 drought in the Yangtze River Basin. Nat. Hazards 2024, 120, 3699–3718. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, X.; Chen, N.; Li, B.; Ma, H.; Xu, L.; Li, R.; Niyogi, D. Drought propagation modification after the construction of the Three Gorges Dam in the Yangtze River Basin. J. Hydrol. 2021, 603, 127138. [Google Scholar] [CrossRef]
- Xu, G.; Wu, Y.; Liu, S.; Cheng, S.; Zhang, Y.; Pan, Y.; Wang, L.; Dokuchits, E.Y.; Nkwazema, O.C. How 2022 extreme drought influences the spatiotemporal variations of terrestrial water storage in the Yangtze River Catchment: Insights from GRACE-based drought severity index and in-situ measurements. J. Hydrol. 2023, 626, 130245. [Google Scholar] [CrossRef]
- Wang, H.; Li, Y.P.; Huang, G.H.; Zhang, Q.; Ma, Y.; Li, Y.F. Quantifying Multidimensional Drought Propagation Risks under Climate Change: A Vine-Copula Bayesian Factorial Analysis Method. J. Hydrol. 2024, 637, 131396. [Google Scholar] [CrossRef]
- Qi, G.; Song, J.; Chen, S.; Gong, Y.; Bai, H.; She, D.; Xia, J.; Fu, Y.H. Increasing impacts of compound extreme droughts on vegetation. J. Hydrol. 2025, 660, 133447. [Google Scholar] [CrossRef]
- Wang, L.; He, F.; Zhao, Y.; Wang, J.; Lu, P.; Jia, Y.; Liu, K.; Deng, H.; Cui, H. Inter-basin Water Transfer Will Face Greater Drought Risk in the Future. J. Environ. Manag. 2025, 385, 125649. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wu, Z.; Wang, H.; Yu, Z.; Chen, Y. A hydrological drought risk assessment method based on a four-dimensional Copula function model integrating development andrecovery speed characteristics. Ecol. Indic. 2025, 177, 113751. [Google Scholar] [CrossRef]


| Tree Level | Variable | Optimal Copula Model | |
|---|---|---|---|
| Types of Copula | Parameter Estimates | ||
| First level tree | Dongting Lake, Yichang | Student’s t | [0.82, 5.49] |
| Han River, Yichang | Student’s t | [0.59, 7.93] | |
| Poyang Lake, Dongting Lake | Gumbel | 1.36 | |
| Second level tree | Poyang Lake, Yichang; Dongting Lake | Joe | 1.06 |
| Han River, Dongting Lake; Yichang | Frank | −0.64 | |
| Third level tree | Poyang Lake, Han River; Dongting Lake, Yichang | Gaussian | −0.10 |
| Scenarios | Yichang | Dongting Lake | Han River | Poyang Lake | Joint Cumulative Probability |
|---|---|---|---|---|---|
| 1 | SRI ≤ −2.0 | SRI ≤ −2.0 | SRI ≤ −2.0 | SRI ≤ −2.0 | 0.16% |
| 2 | SRI ≤ −1.5 | SRI ≤ −1.5 | SRI ≤ −1.5 | SRI ≤ −1.5 | 0.71% |
| 3 | SRI ≤ −1.0 | SRI ≤ −1.0 | SRI ≤ −1.0 | SRI ≤ −1.0 | 2.63% |
| 4 | SRI ≤ −0.5 | SRI ≤ −0.5 | SRI ≤ −0.5 | SRI ≤ −0.5 | 7.55% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Wang, H. Research on the Risk of a Multi-Source Hydrological Drought Encounter in the Yangtze River Basin Based on Spatial and Temporal Correlation. Water 2025, 17, 1986. https://doi.org/10.3390/w17131986
Li J, Wang H. Research on the Risk of a Multi-Source Hydrological Drought Encounter in the Yangtze River Basin Based on Spatial and Temporal Correlation. Water. 2025; 17(13):1986. https://doi.org/10.3390/w17131986
Chicago/Turabian StyleLi, Jinbei, and Hao Wang. 2025. "Research on the Risk of a Multi-Source Hydrological Drought Encounter in the Yangtze River Basin Based on Spatial and Temporal Correlation" Water 17, no. 13: 1986. https://doi.org/10.3390/w17131986
APA StyleLi, J., & Wang, H. (2025). Research on the Risk of a Multi-Source Hydrological Drought Encounter in the Yangtze River Basin Based on Spatial and Temporal Correlation. Water, 17(13), 1986. https://doi.org/10.3390/w17131986





