Assessing the Sensitivity of Sociotechnical Water Distribution Systems to Uncertainty in Consumer Behaviors: Social Distancing and Demand Changes During the COVID-19 Pandemic
Abstract
1. Introduction
2. Extension of Previous Research
- Applying a uniform distribution to existing probabilistic parameters in the ABM system.
- Introducing new variables that influence agents’ movement decisions within the network.
- Modifying the distribution of agents among different node types.
- The system remains robust to uncertainty in existing probabilistic parameters, as expected, since it was designed for such variations.
- The system exhibits different behaviors when agent movement is altered.
- The system’s response becomes noticeably different—and even nonlinear—when agent distributions across node types are modified.
- Methods—Details the methodologies used in our analysis.
- Case Study and Scenarios—Describes the various scenarios and conditions applied to assess uncertainty.
- Results—Presents the findings from implementing different uncertainty methods.
- Discussion and Conclusions—Summarizes key insights and implications of our results.
3. Methods
3.1. Overview
3.1.1. Purpose
3.1.2. Entities, State Variables, and Scales
3.1.3. Process Overview and Scheduling
3.2. Design Concepts
3.2.1. Theoretical and Empirical Background
3.2.2. Individual Decision-Making
3.2.3. Interaction
3.2.4. Heterogeneity
3.2.5. Stochasticity
3.2.6. Observation
3.3. Details
3.3.1. Implementation Details
3.3.2. Initialization
3.3.3. Input Data
- COVID-19 transition values.
- Risk perception variables for Bayesian Belief Network (BBN) training.
- Hydraulic network data, including pipes, pumps, tanks, valves, and demand patterns.
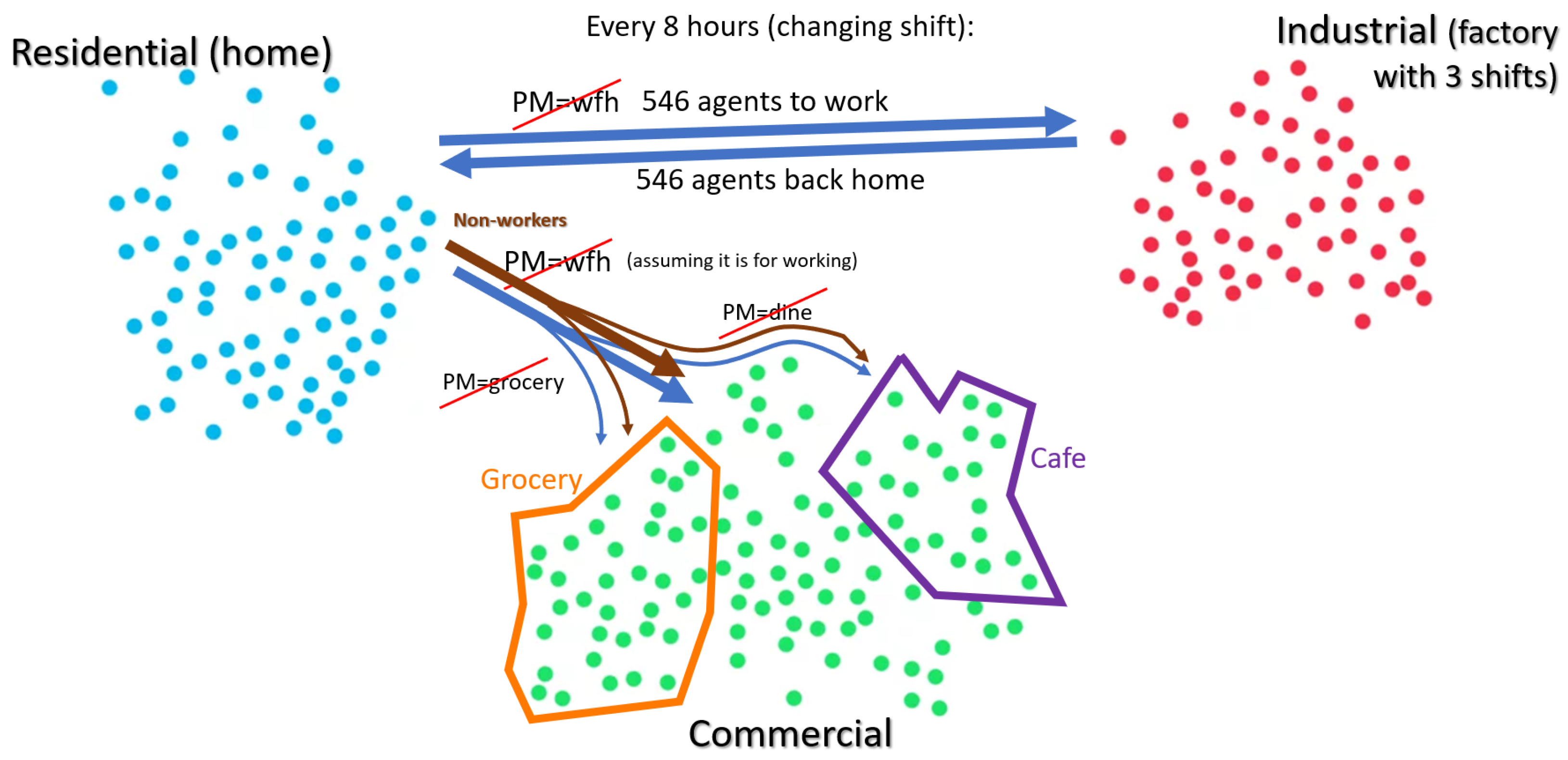
3.3.4. Movement Submodel
- Residential to Commercial Movement: Agents move between residential and commercial nodes based on their prevention measure (PM) adoption:
- –
- Agents not adopting the dine-out PM move to café nodes (subset of commercial nodes).
- –
- Agents not adopting the grocery PM move to grocery nodes (subset of commercial nodes).
- –
- Agents not adopting the work-from-home (WFH) PM move to any commercial node.
Movement from commercial to residential nodes (i.e., returning home) has no restrictions. - Residential to Industrial Movement: Initially, a predefined number of agents (e.g., 1092) are placed at industrial nodes. Every 8 h, half of these agents () are replaced with agents from residential nodes at specific time steps: 1:00, 9:00, and 17:00.Only agents that do not adopt the WFH PM move to industrial nodes. Movement from industrial to residential nodes (returning home) has no restrictions.
3.4. Uncertainty Submodel
- Number of Daily Contacts: Uncertainty is introduced in the number of agents potentially exposed to infectious agents during movement between nodes.
- Exposure Rate: The probability of exposure for selected agents is modeled with uncertainty.
- Media Exposure: The probability of agents consuming COVID-19-related information via television or radio is subject to uncertainty.
- Uncertainty in BBN Output: The BBN output determining PM adoption is probabilistic rather than deterministic. Agents update their status based on this probability, introducing uncertainty.
- Exposed Agents’ Condition: Uncertainty is incorporated into the process of determining the health condition of newly exposed agents.
- Worker Mobility: While movement between node types follows specific rules, exceptions allow agents to move from residential to commercial nodes for non-work-related purposes, with a probabilistic constraint.
- Node Type Distribution: The initial distribution of agents across industrial, café, commercial, and residential nodes is subject to uncertainty.
3.4.1. Uncertainty in COVID-19 Transmission Model
- Exposure rate ().
- Non-residential exposure rate ().
- Probability of listening to the radio ().
- Probability of watching TV ().
3.4.2. Worker Mobility
3.4.3. Node Type Distribution
3.4.4. Statistical Significance
4. Case Study and Scenarios
- 434 residential connections,
- 15 industrial connections,
- 9 commercial connections.
5. Results
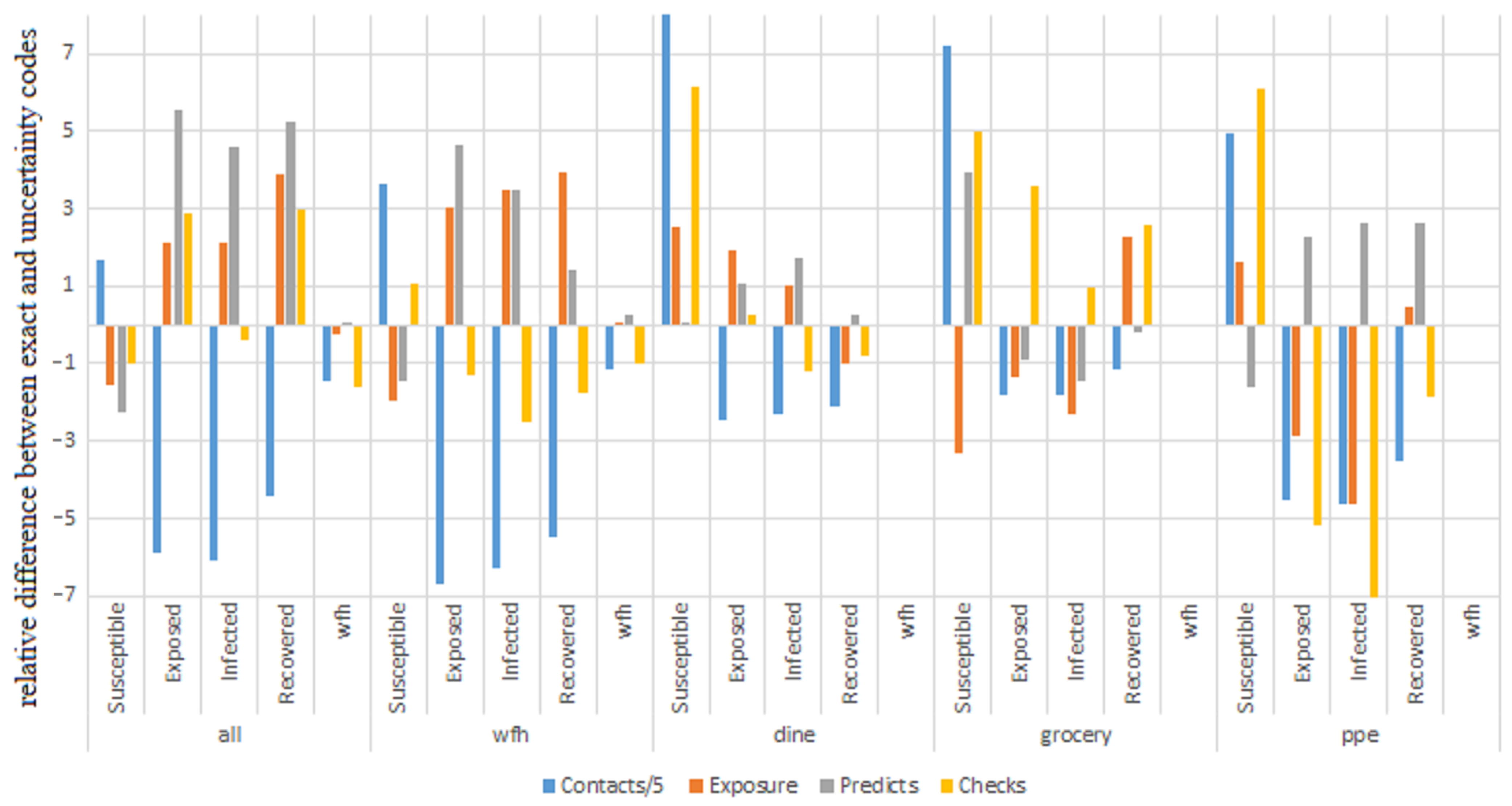
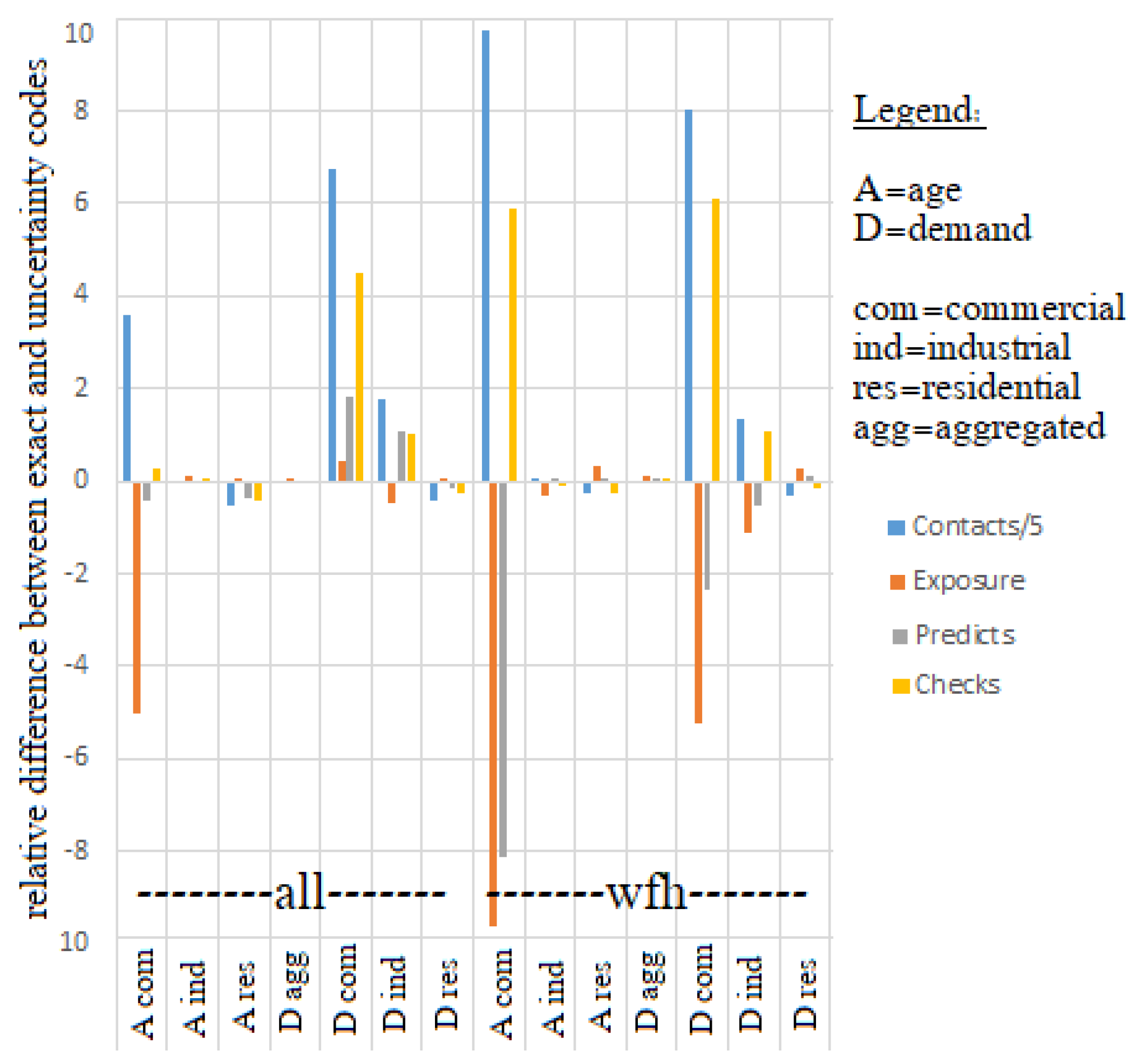
5.1. Sensitivity Analysis of Uncertainty in ABM Parameters
- Age/Demand: Final simulation value difference.
- Susceptible (S), Recovered (R), and Work-from-Home (wfh) in SEIR: Final value difference.
- Exposed (E) and Infected (I): Peak difference.
Analysis
- -
- If is smaller, a random number of agents is selected uniformly from the range to be exposed.
- -
- Otherwise, a random number of agents is selected uniformly from the range to be exposed.
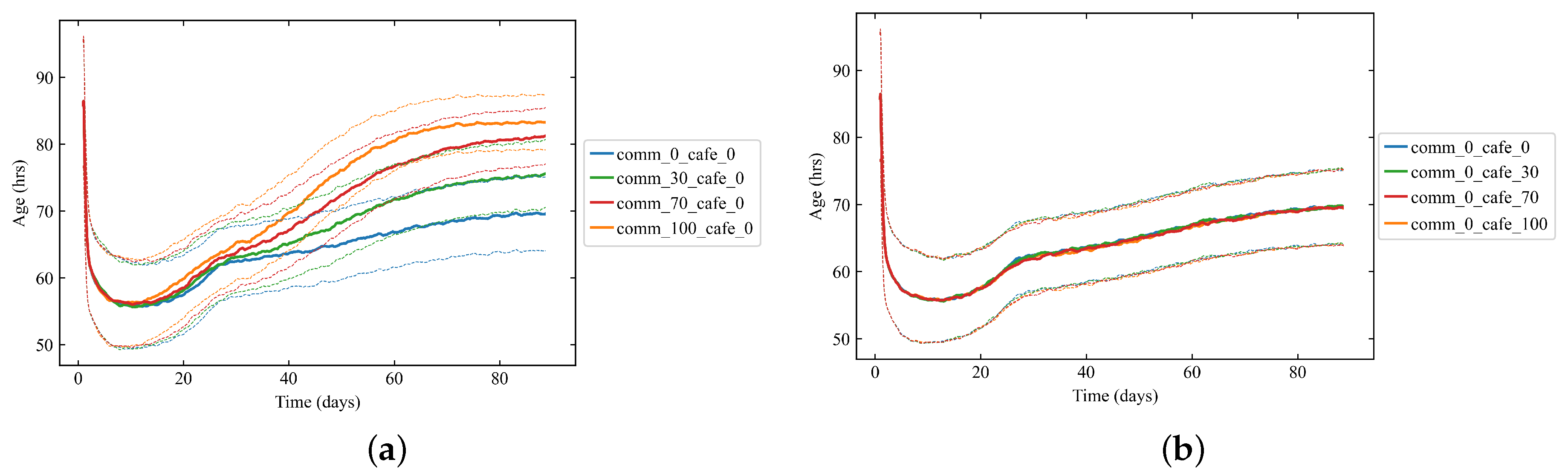
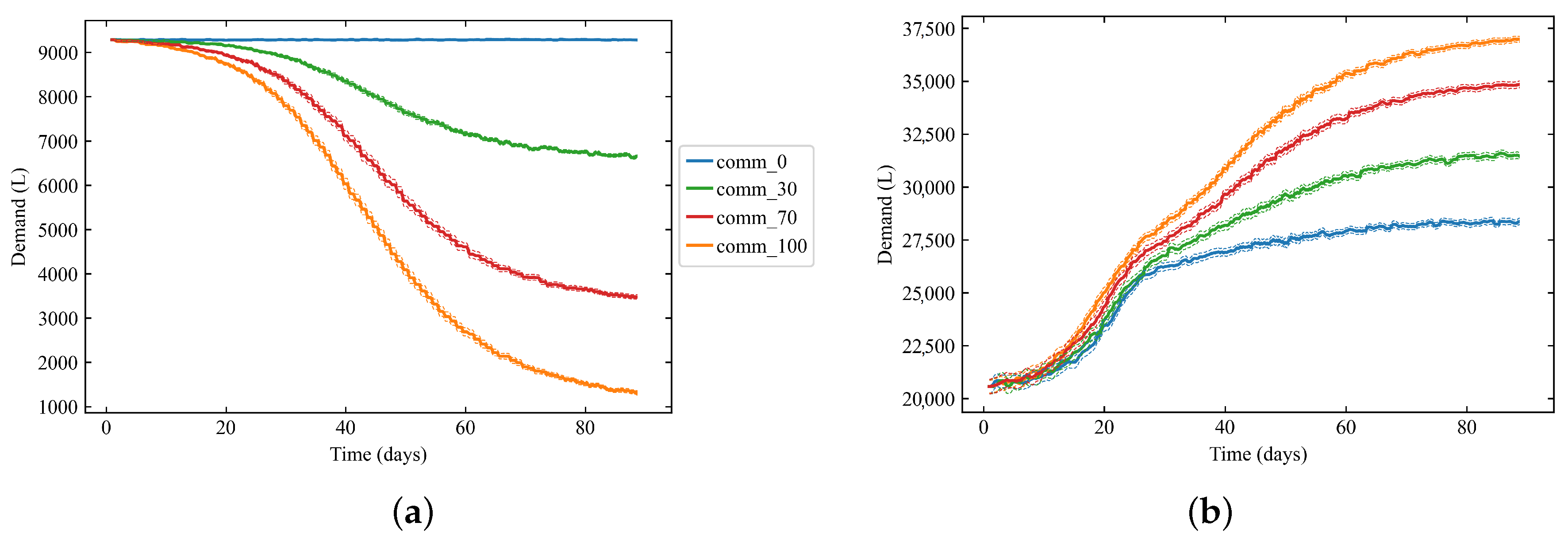
5.2. Adding Non-Workers to Commercial and Café Nodes
Demand Analysis for Varying Commercial Percentages
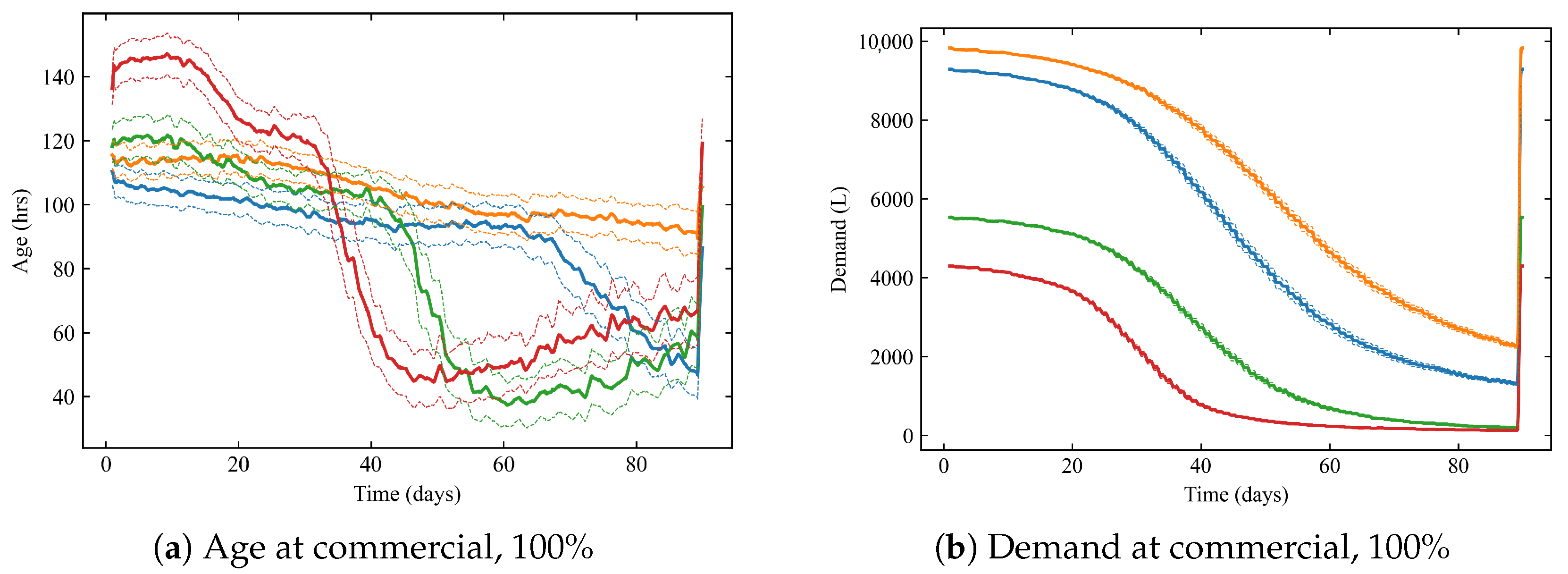
5.3. Changing the Distribution of Agents in the Network
Scenarios for Different Distributions
- Less-ind: Fewer agents in industrial nodes, leading to an increase in cafés, commercial, and, especially, residential nodes.
- Regular: The default distribution, representing a typical city.
- More-ind: More agents in industrial nodes, resulting in fewer in cafés, commercial, and residential areas, resembling an industrial town.
- Much-more-ind: A heavily industrialized area designed primarily for work, with minimal residential accommodations.
6. Discussion
6.1. Results Discussion
6.2. Emergence in Complex Systems
6.3. Applicability to Real-World Systems
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
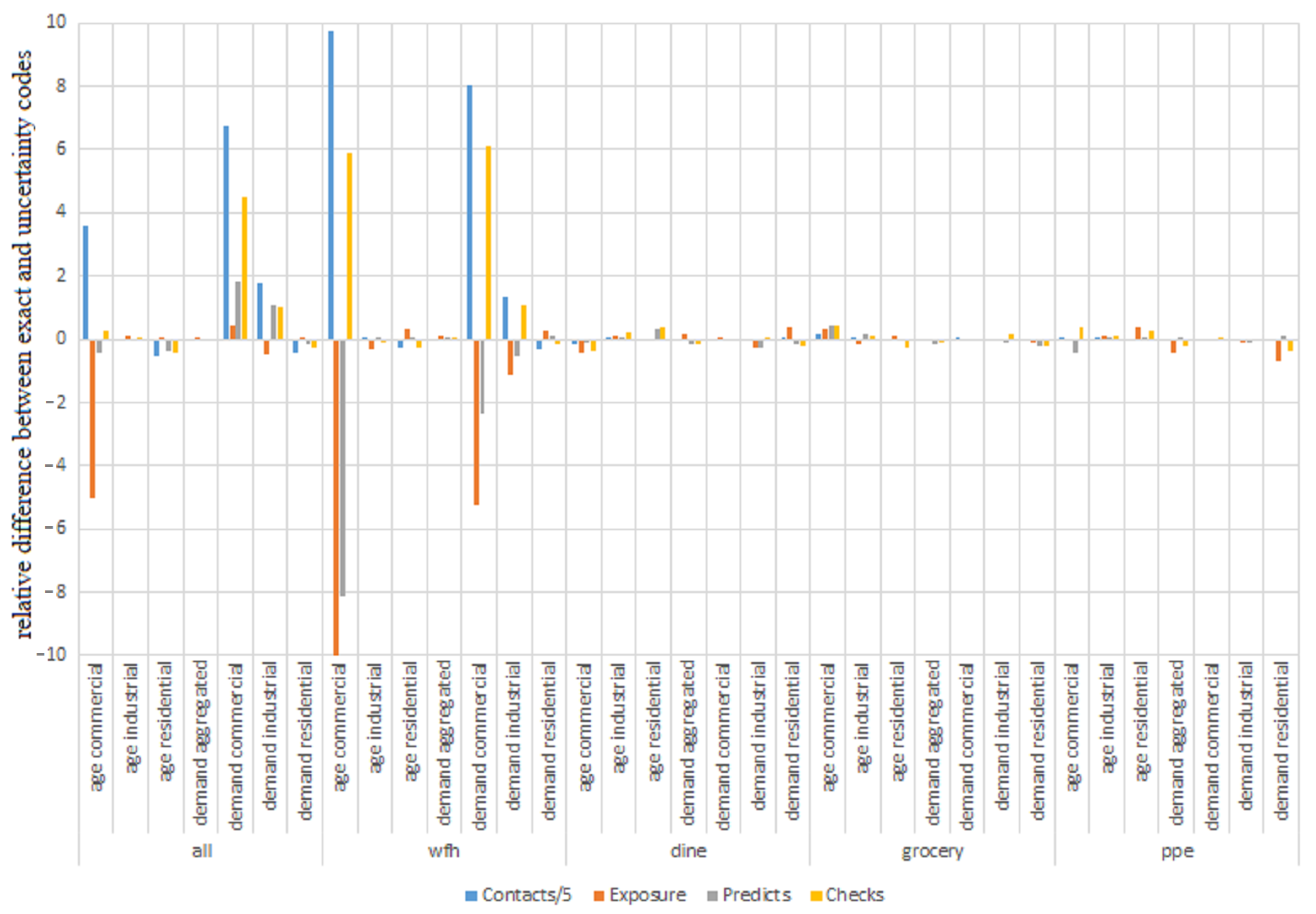
| (a) | ||||||||||
| Exact vs. | all | wfh | ||||||||
| Contacts | 10.87 | −35.10 | −36.44 | −28.82 | −11.73 | 16.06 | −31.95 | −29.37 | −27.45 | −7.12 |
| Exposure | −3.06 | 5.15 | 3.67 | 8.99 | 2.18 | 1.94 | −7.89 | −4.26 | −7.22 | −3.00 |
| Predicts | −1.59 | 7.04 | 2.89 | 7.49 | 1.89 | −0.06 | −0.48 | 0.78 | −2.90 | 0.57 |
| Checks | −0.06 | −1.88 | −5.43 | 1.31 | −0.10 | −2.00 | −0.56 | −0.97 | 0.04 | −0.51 |
| (b) | ||||||||||
| Exact vs. | dine | grocery | ||||||||
| Contacts | 43.17 | −14.71 | −13.14 | −11.27 | 0 | 89.83 | −15.66 | −15.36 | −15.87 | 0 |
| Exposure | 2.84 | −6.08 | −4.92 | −3.11 | 0 | 5.44 | −4.00 | −3.50 | −2.78 | 0 |
| Predicts | −4.52 | 1.90 | 1.83 | 1.70 | 0 | 2.66 | −4.32 | −3.47 | −3.53 | 0 |
| Checks | 6.69 | −0.66 | −2.38 | −1.13 | 0 | 12.62 | −6.49 | −7.42 | −4.36 | 0 |
| (c) | ||||||||||
| Exact vs. | ppe | |||||||||
| Contacts | 20.56 | −17.83 | −16.93 | −15.02 | 0 | |||||
| Exposure | −3.83 | 5.61 | 3.69 | 6.54 | 0 | |||||
| Predicts | -4.63 | 8.08 | 6.24 | 7.48 | 0 | |||||
| Checks | 0.06 | 0.55 | −2.18 | 3.27 | 0 | |||||
| (a) | ||||||||||||||
| Exact vs. | all | wfh | ||||||||||||
| Contacts | 29.68 | 0.68 | −3.33 | −0.92 | 52.60 | 9.70 | −3.75 | 67.30 | −0.52 | −3.44 | 0.72 | 62.56 | 17.39 | −1.68 |
| Exposure | −9.72 | −0.16 | −0.61 | −0.39 | −7.04 | 2.49 | −0.17 | 20.26 | −1.03 | −2.51 | 0.51 | 30.52 | 13.89 | −0.81 |
| Predicts | −15.51 | −0.82 | −0.03 | 0.17 | −10.66 | 1.48 | 0.62 | 10.38 | 0.26 | 0.15 | −0.08 | 5.34 | 1.68 | −0.30 |
| Checks | 1.26 | 0.00 | −0.34 | −0.59 | 1.27 | 2.33 | −0.77 | 6.97 | −0.26 | −1.60 | 0.31 | 7.34 | 11.16 | −0.23 |
| (b) | ||||||||||||||
| Exact vs. | dine | grocery | ||||||||||||
| Contacts | −0.45 | −0.96 | −3.07 | 1.58 | −0.05 | −0.05 | 2.67 | −2.11 | −0.49 | −0.37 | 1.61 | −0.03 | −0.14 | 2.71 |
| Exposure | −1.70 | −0.49 | −1.92 | 1.58 | 0.00 | −0.06 | 2.64 | 0.55 | 0.06 | 0.77 | −0.48 | 0.03 | −0.27 | −0.74 |
| Predicts | −3.04 | −0.48 | −1.00 | 2.82 | −0.02 | −0.10 | 4.73 | 1.33 | 0.28 | −0.11 | −1.75 | −0.04 | −0.01 | −2.88 |
| Checks | −1.24 | −1.16 | −1.74 | 2.11 | −0.02 | 0.07 | 3.51 | −2.75 | −0.84 | −2.92 | 2.91 | −0.04 | −0.04 | 4.85 |
| (c) | ||||||||||||||
| Exact vs. | ppe | |||||||||||||
| Contacts | −1.86 | −0.90 | −2.18 | 2.76 | −0.01 | 0.11 | 4.65 | |||||||
| Exposure | −1.67 | −0.63 | −1.34 | 2.38 | −0.02 | −0.05 | 4.05 | |||||||
| Predicts | −1.54 | −1.13 | −2.56 | 3.63 | 0.00 | −0.25 | 6.20 | |||||||
| Checks | −1.61 | −1.18 | −3.48 | 3.56 | 0.01 | 0.03 | 6.01 | |||||||
| (a) | ||||||||||
| Exact vs. | all | wfh | ||||||||
| Contacts | 8.26 | −29.37 | −30.54 | −22.24 | −7.32 | 18.14 | −33.56 | −31.34 | −27.43 | −5.65 |
| Exposure | −1.53 | 2.12 | 2.11 | 3.90 | −0.27 | −1.97 | 3.01 | 3.47 | 3.91 | 0.03 |
| Predicts | −2.27 | 5.52 | 4.61 | 5.26 | 0.04 | −1.47 | 4.62 | 3.47 | 1.41 | 0.28 |
| Checks | −0.98 | 2.86 | −0.42 | 2.97 | −1.62 | 1.04 | −1.32 | −2.49 | −1.74 | −0.99 |
| (b) | ||||||||||
| Exact vs. | dine | grocery | ||||||||
| Contacts | 41.92 | −12.33 | −11.66 | −10.65 | 0 | 36.00 | −8.95 | −9.01 | −5.84 | 0 |
| Exposure | 2.52 | 1.93 | 1.02 | −0.99 | 0 | −3.32 | −1.36 | −2.33 | 2.27 | 0 |
| Predicts | 0.02 | 1.04 | 1.70 | 0.24 | 0 | 3.92 | −0.88 | −1.47 | −0.21 | 0 |
| Checks | 6.15 | 0.25 | −1.21 | −0.81 | 0 | 5.01 | 3.56 | 0.95 | 2.56 | 0 |
| (c) | ||||||||||
| Exact vs. | ppe | |||||||||
| Contacts | 24.81 | −22.72 | −23.03 | −17.56 | 0 | |||||
| Exposure | 1.64 | −2.88 | −4.60 | 0.44 | 0 | |||||
| Predicts | −1.59 | 2.25 | 2.63 | 2.62 | 0 | |||||
| Checks | 6.11 | −5.20 | −7.29 | −1.88 | 0 | |||||
| (a) | ||||||||||||||
| Exact vs. | all | wfh | ||||||||||||
| Contacts | 17.89 | −0.30 | −2.52 | −0.32 | 33.86 | 8.74 | −2.18 | 48.67 | 0.14 | −1.35 | −0.14 | 40.04 | 6.60 | −1.61 |
| Exposure | −5.05 | 0.12 | 0.05 | 0.03 | 0.42 | −0.47 | 0.02 | −11.72 | −0.31 | 0.33 | 0.09 | −5.23 | −1.14 | 0.29 |
| Predicts | −0.45 | −0.02 | −0.36 | −0.02 | 1.82 | 1.08 | −0.14 | −8.11 | 0.04 | 0.01 | 0.01 | −2.36 | −0.52 | 0.10 |
| Checks | 0.29 | 0.04 | −0.42 | −0.02 | 4.49 | 1.01 | −0.26 | 5.88 | −0.09 | −0.24 | 0.04 | 6.08 | 1.07 | −0.18 |
| (b) | ||||||||||||||
| Exact vs. | dine | grocery | ||||||||||||
| Contacts | −0.71 | 0.02 | −0.34 | −0.01 | 0.00 | −0.10 | 0.01 | 0.73 | 0.11 | −0.32 | −0.07 | 0.03 | −0.03 | −0.12 |
| Exposure | −0.40 | 0.11 | −0.04 | 0.18 | 0.01 | −0.28 | 0.36 | 0.30 | −0.18 | 0.09 | −0.07 | −0.05 | −0.01 | −0.09 |
| Predicts | −0.08 | 0.05 | 0.34 | −0.15 | −0.03 | −0.28 | −0.18 | 0.42 | 0.16 | −0.07 | −0.15 | 0.00 | −0.11 | −0.23 |
| Checks | −0.35 | 0.23 | 0.40 | −0.15 | −0.07 | 0.01 | −0.22 | 0.43 | 0.12 | −0.26 | −0.12 | −0.02 | 0.19 | −0.23 |
| (c) | ||||||||||||||
| Exact vs. | ppe | |||||||||||||
| Contacts | 0.17 | 0.14 | −0.07 | −0.11 | −0.05 | −0.05 | −0.14 | |||||||
| Exposure | −0.04 | 0.11 | 0.36 | −0.44 | 0.00 | −0.10 | −0.71 | |||||||
| Predicts | −0.40 | 0.07 | 0.01 | 0.04 | −0.01 | −0.10 | 0.10 | |||||||
| Checks | 0.37 | 0.09 | 0.27 | −0.22 | 0.03 | −0.01 | −0.38 | |||||||
Appendix B. Process Scheduling Details
- Step H1.
- Agents move between residential and non-residential nodes. Agents move between nodes based on predefined node capacities and node type requirements. Agents are assigned to move to and from non-residential nodes based on an hourly total capacity at each non-residential node.
- Step H2.
- Agents update COVID-19 status indicators. Agents update COVID-19 status indicators, which represent the number of hours an agent spends in the exposed, infected, severe, and symptomatic stages (, , , and , respectively).
- Step H3.
- Agents transmit COVID-19. Infected agents expose susceptible agents when they occupy the same node. When an infected agent moves to a new node, up to 10 susceptible agents at the new node are exposed based on the node’s exposure rate ( for residential nodes, for non-residential nodes in Table A5).
- Step H4.
- Agents update mass media exposure. Agents receive information from TV and radio based on probabilistic estimates that they use each form of media at each hour of the day [11,31] (Table A8). The mass media exposure () is a binary number that is changed from 0 to 1 once an agent receives information about COVID-19 at any time step, based on probabilistic behaviors to use radio and TV.
- Step H5.
- Agents exert water demand. The hourly demand at each node is calculated based on the number of agents at each node as follows:where is the new demand for node N at time t, is the number of agents at node N, is the capacity of node N, and is the base demand.
- Step D1.
- Agents update COVID-19 status. Agents update COVID-19 status state variables (S, , and ) based on their progression through disease stages. Once the time in a stage exceeds an agent’s threshold for that stage (e.g., > , Table A5), the agent updates its COVID-19 status (e.g., ).
- Step D2.
- Agents update personal experience with COVID-19. Once an agent enters the infectious stage (), the agent updates the personal COVID-19 status () from “no” (value of 1) to “doctor confirmed and am still infected” (value of 9) [14].
- Step D3.
- Agents update friends and family COVID-19 status. An agent updates the friends and family COVID-19 status () when a peer agent enters the infectious stage. The value () can increase up to 7 to represent the number of peers in an agent’s network that are infected. A value of seven corresponds to survey responses that the person is “very much affected” by friends or family testing positive or dying from COVID-19 [14].
- Step D4.
- Agents update decision to adopt prevention measures. BBN models are applied to calculate the probability of adopting each prevention measure based on mass media exposure, personal COVID-19 status, and friends and family COVID-19 status (, , and , respectively). Prevention measures include working from home, dining out less, grocery shopping less, and wearing PPE, and bottled-water-buying behaviors are drinking bottled water, cooking with bottled water, and using bottled water for hygiene. Refer to previous work for more information on prevention measures [14,32].
- Step D5.
- Agents update demand patterns. Agents that choose to work from home, dine out less, or grocery-shop less update their demand patterns from a typical diurnal pattern to a pattern that expresses demands uniformly across daylight hours (standard and COVID-19 demand patterns in Table A7).
- Step S1.
- Calculate hydraulic performance of the water distribution system. The unique demand patterns reporting the demands at each node and each hour for the 90-day period are passed to the EPANET simulation using WNTR. Results from the hydraulic simulation for each hourly time step are recorded, including the water age and pressure at each node and the flow rate and direction of flow in each pipe.
Appendix C. State Variables and Parameters
| Parameter | Symbol | Value |
|---|---|---|
| Residential exposure rate | ||
| Non-residential exposure rate | ||
| Probability of listening to radio | Table A8 | |
| Probability of watching TV | Table A8 | |
| Work node | All industrial nodes | |
| Home node | All residential nodes | |
| Exposed stage threshold (days) | ∼ LN | |
| Symptomatic stage threshold (days) | ∼ LN ∼ LN | |
| Infected stage threshold (days) | ||
| Severe stage threshold (days) | ∼ LN ∼ LN | |
| Critical stage threshold (days) | ∼ LN ∼ LN |
| State Variable | Symbol | Value |
|---|---|---|
| COVID-19 status | S | [susceptible, exposed, infected, recovered, dead] |
| Symptomatic status | [Symptomatic, asymptomatic] | |
| Infected status | [mild, severe, critical] | |
| Personal COVID-19 status (BBN input) | ||
| Friends and Family COVID-19 status (BBN input) | ||
| Mass media exposure (BBN input) | ||
| Time in exposed stage (days) | ||
| Time in symptomatic stage (days) | ||
| Time in infected stage (days) | ||
| Time in severe stage (days) | ||
| Time in critical stage (days) | ||
| WFH decision | [Not WFH, WFH] | |
| Dine out less decision | [Dine out, dine out less] | |
| Grocery shop less decision | [Grocery shop, grocery shop less] | |
| PPE decision | [Wear PPE, not wear PPE] |
Appendix D. Supplemental Information
Appendix D.1. Daily Demand Patterns
| Hour | Standard Residential Pattern | COVID-19 Residential Pattern |
|---|---|---|
| 0 | 0.55 | 0.51 |
| 1 | 0.55 | 0.41 |
| 2 | 0.58 | 0.40 |
| 3 | 0.67 | 0.47 |
| 4 | 0.85 | 0.67 |
| 5 | 1.05 | 0.99 |
| 6 | 1.16 | 1.07 |
| 7 | 1.12 | 1.05 |
| 8 | 1.15 | 1.13 |
| 9 | 1.10 | 1.21 |
| 10 | 1.02 | 1.26 |
| 11 | 1.00 | 1.31 |
| 12 | 1.02 | 1.28 |
| 13 | 1.10 | 1.22 |
| 14 | 1.20 | 1.14 |
| 15 | 1.35 | 1.11 |
| 16 | 1.45 | 1.15 |
| 17 | 1.50 | 1.21 |
| 18 | 1.50 | 1.25 |
| 19 | 1.35 | 1.32 |
| 20 | 1.00 | 1.21 |
| 21 | 0.80 | 1.06 |
| 22 | 0.70 | 0.88 |
| 23 | 0.60 | 0.67 |
Appendix D.2. TV and Radio Probabilities
| Daily Time Step | ||
|---|---|---|
| 0 | 0.463 | 4.626 |
| 1 | 0.577 | 0.439 |
| 2 | 0.35 | 0.226 |
| 3 | 0.35 | 0.215 |
| 4 | 0.575 | 0.006 |
| 5 | 8.342 | 0.366 |
| 6 | 20.76 | 4.405 |
| 7 | 24.794 | 17.15 |
| 8 | 4.436 | 12.898 |
| 9 | 4.597 | 8.847 |
| 10 | 0.52 | 0.343 |
| 11 | 4.49 | 0.22 |
| 12 | 8.515 | 4.846 |
| 13 | 8.622 | 0.151 |
| 14 | 8.678 | 0.421 |
| 15 | 12.711 | 0.656 |
| 16 | 12.328 | 0.869 |
| 17 | 8.251 | 15.769 |
| 18 | 4.165 | 21.366 |
| 19 | 0.243 | 17.037 |
| 20 | 0.35 | 27.649 |
| 21 | 0.342 | 35.729 |
| 22 | 0.123 | 31.951 |
| 23 | 0.233 | 9.203 |
Appendix D.3. BBN Figures and Tables
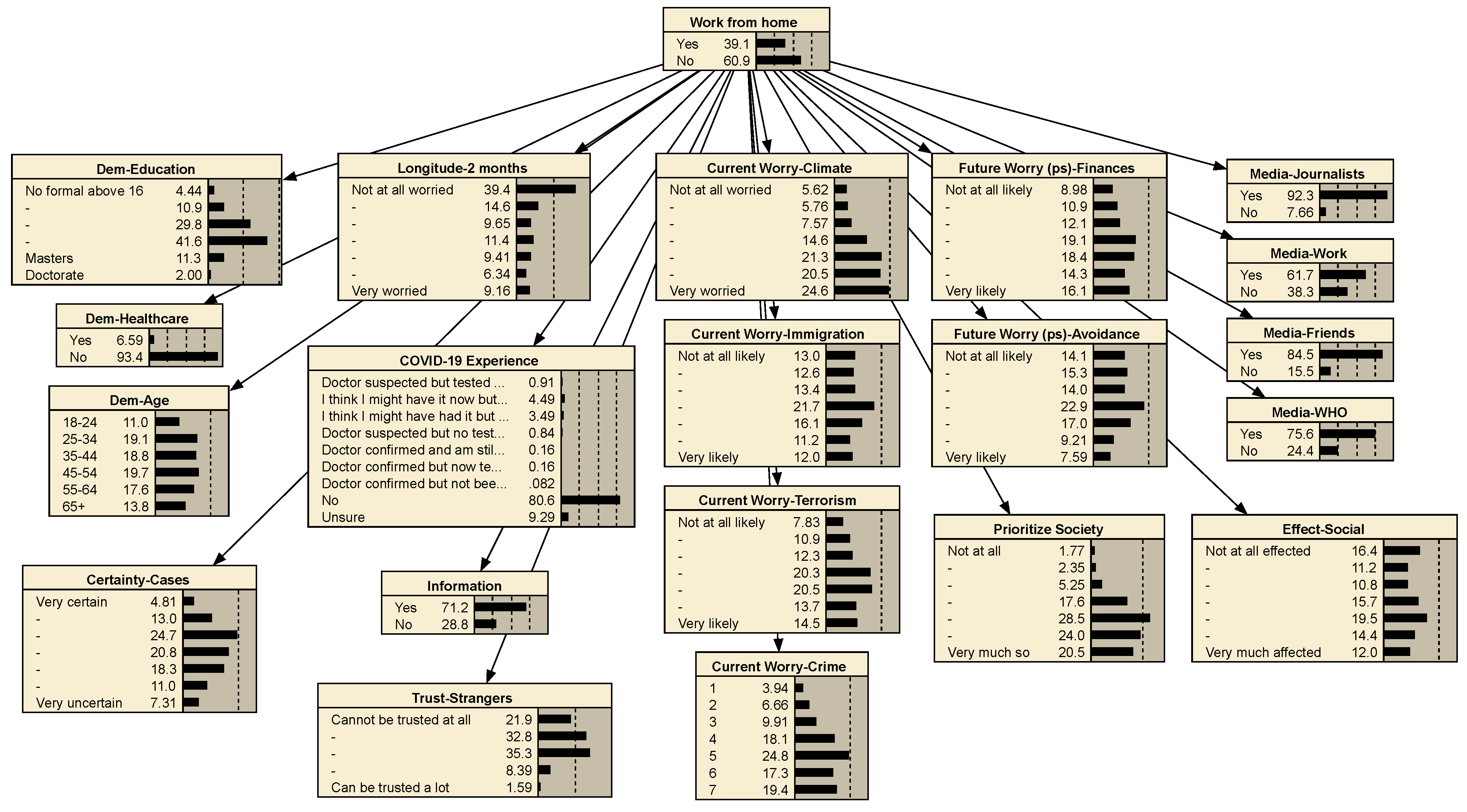
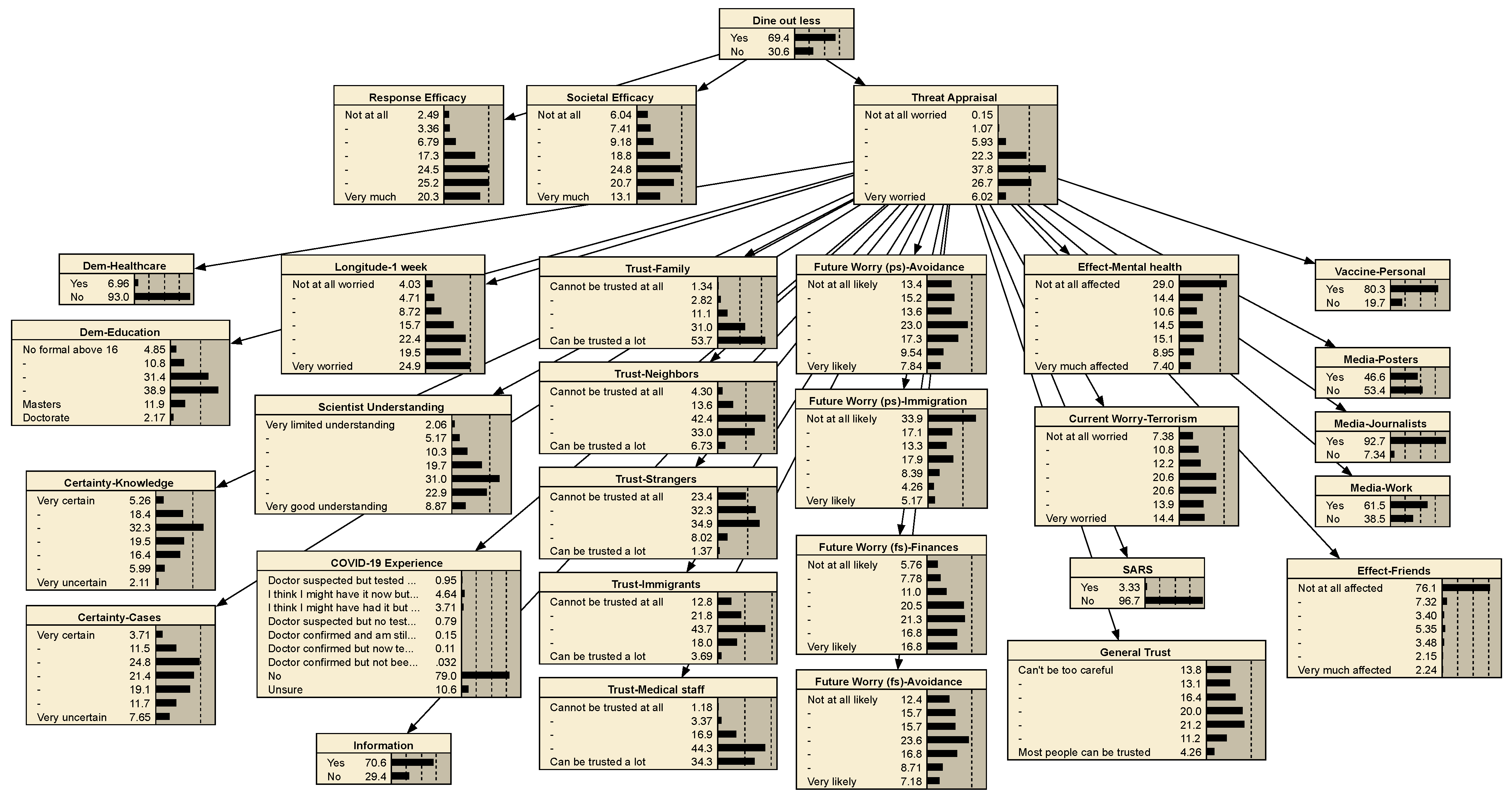
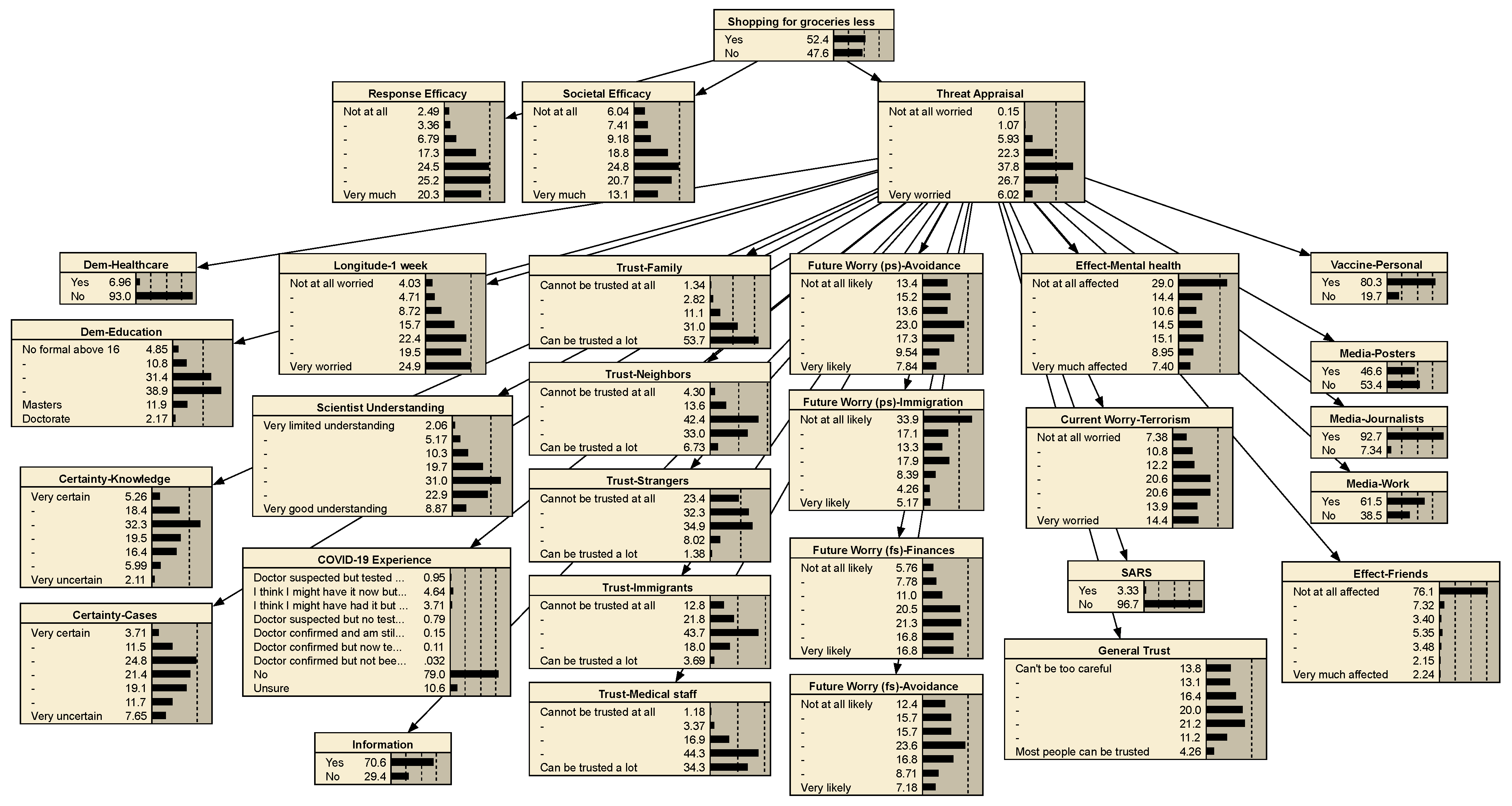
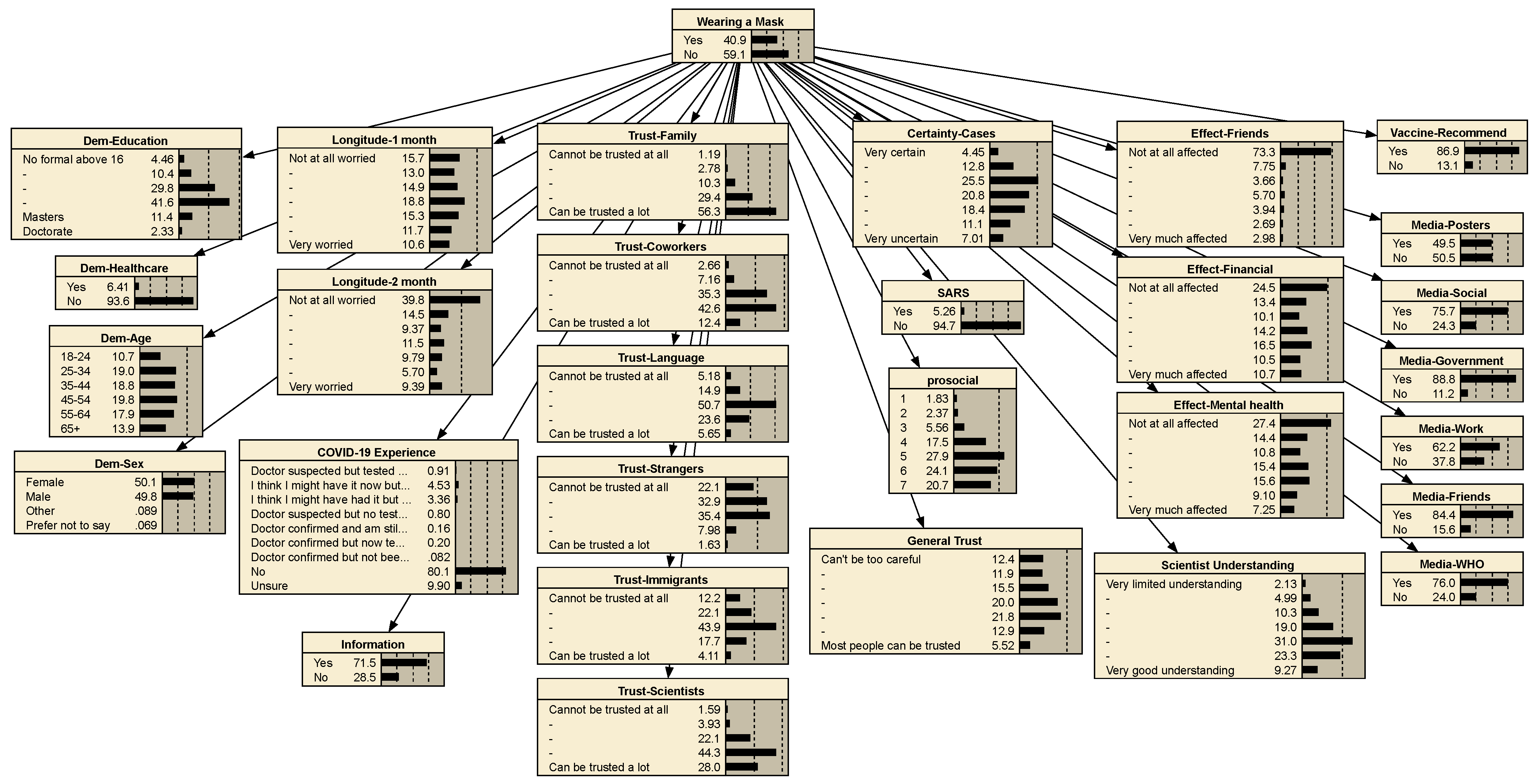
| Variable | Question |
|---|---|
| Trust-Family | How much do you trust people in your family? [5] |
| Trust-Neighbors | How much do you trust people in your neighbourhood? [5] |
| Trust-Coworkers | How much do you trust people you work or study with? [5] |
| Trust-Language | How much do you trust people who speak a different language from you? [5] |
| Trust-Strangers | How much do you trust strangers? [5] |
| Trust-Immigrants | How much do you trust immigrants? [5] |
| Trust-Medical staff | How much do you trust medical doctors and nurses? [5] |
| Trust-Scientists | How much do you trust scientists? [5] |
| Media-Posters | Have you come across information about coronavirus or COVID-19 from: official public posters. [1: yes, 2: no] |
| Media-Social | Have you come across information about coronavirus or COVID-19 from: social media or online blogs from individuals. [1: yes, 2: no] |
| Media-Journalist | Have you come across information about coronavirus or COVID-19 from: journalists and commentators in the media (TV, radio, newspapers). [1: yes, 2: no] |
| Media-Government | Have you come across information about coronavirus or COVID-19 from: government or official sources such as websites or public speeches/broadcasts within the country you are living in. [1: yes, 2: no] |
| Media-Work | Have you come across information about coronavirus or COVID-19 from: official messages from your place of work or education. [1: yes, 2: no] |
| Media-Friends | Have you come across information about coronavirus or COVID-19 from: friends and family. [1: yes, 2: no] |
| Media-WHO | Have you come across information about coronavirus or COVID-19 from: World Health Organisation. [1: yes, 2: no] |
| Current Worry-Climate | How worried are you personally about climate change at present? [7] |
| Current Worry-Immigration | How worried are you personally about immigration at present? [7] |
| Current Worry-Terrorism | How worried are you personally about terrorism at present? [7] |
| Current Worry-Crime | How worried are you personally about crime at present? [7] |
| Future Worry-Finances | How likely do you think it is that [you (ps) OR your friends and family in the country you are currently living in (fs)] will be directly affected by financial problems in the next 6 months? [7] |
| Future Worry-Avoidance | How likely do you think it is that [you (ps) OR your friends and family in the country you are currently living in (fs)] will be directly affected by antisocial behavior by others in the next 6 months? [7] |
| Future Worry-Immigration | How likely do you think it is that [you (ps) OR your friends and family in the country you are currently living in (fs)] will be directly affected by immigration in the next 6 months? [7] |
| Dem-Sex | What is your sex? [1: female, 2: male, 3: other, 4: prefer not to say] |
| Dem-Age | What is your age? [1: 18–24, 2: 25–34, 3: 35–44, 4: 45–54, 5: 55–64, 6: 65+] |
| Dem-Healthcare | Are you a healthcare provider (e.g., doctor, nurse, paramedic, pharmacist, carer)? |
| Dem-Education | Please indicate your highest educational qualification: [1: no formal above 16 to 5: Masters, 9: doctorate] |
| Prioritize Society | To what extent do you think it’s important to do things for the benefit of others and society even if they have some costs to you personally? [7] |
| COVID-19 Experience | Have you ever had, or thought you might have, the coronavirus/COVID-19? [9: unsure, 8: no, 3: I think I might have had it but am recovered, 2: I think I might have it now but not tested, 1: doctor suspected but tested negative, 4: doctor suspected but no test yet, 5: doctor confirmed and am still infected, 6: doctor confirmed but now test negative, 7: doctor confirmed but not been tested again] |
| Longitude-1 week | How worried were you about coronavirus 1 week ago? [7] |
| Longitude-1 month | How worried were you about coronavirus 1 month ago? [7] |
| Longitude-2 months | How worried were you about coronavirus 2 months ago? [7] |
| Effect-Financial | To what extent have you been affected by the coronavirus/COVID-19 in the following ways?— I have experienced financial difficulties as a result of the pandemic [7] |
| Effect-Social | To what extent have you been affected by the coronavirus/COVID-19 in the following ways?—I have experienced social difficulties as a result of the pandemic [7] |
| Effect-Mental health | To what extent have you been affected by the coronavirus/COVID-19 in the following ways?—I have experienced mental health difficulties as a result of the pandemic (e.g., increased anxiety) [7] |
| Effect-Friends | To what extent have you been affected by the coronavirus/COVID-19 in the following ways?—I have friends and family who have tested positive or died from the virus [7] |
| SARS | Have you personally been affected by a previous similar epidemic such as SARS (Severe Acute Respiratory Syndrome), MERS (Middle East Respiratory Syndrome) or Ebola? [1: yes, 2: no] |
| General Trust | Generally speaking, would you say most people can be trusted, or that you can’t be too careful in dealing with people? [7] |
| Information | Have you sought out information specifically about coronavirus/COVID-19? [1: yes, 2: no] |
| Scientist Understanding | To what extent do you think scientists have a good understanding of the coronavirus/COVID-19? [7] |
| Certainty-Knowledge | How certain or uncertain do you think the following are: The current scientific knowledge about the coronavirus/COVID-19? [7] |
| Certainty-Cases | How certain or uncertain do you think the following are: The estimates of the number of cases of coronavirus/COVID-19 worldwide [7] |
| Vaccine-Personal | If a vaccine were to be available for the coronavirus/COVID-19 now: Would you get vaccinated yourself? [1: yes, 2: no] |
| Vaccine-Recommend | If a vaccine were to be available for the coronavirus/COVID-19 now: Would you recommend vulnerable friends and family to get vaccinated? [1: yes, 2: no] |
| Threat Severity (PMT) | How much do you agree or disagree with the following statements?—Getting sick with the coronavirus/COVID-19 can be serious [5] |
| Response Efficacy (PMT) | To what extent do you feel that the personal actions you are taking to try to limit the spread of coronavirus make a difference? [7] |
| Societal Efficacy (PMT) | To what extent do you feel the actions that your country is taking to limit the spread of coronavirus make a difference? [7] |
| Variable | Likert Scale |
|---|---|
| Trust | 1 = Cannot be trusted at all to 5 = Can be trusted a lot |
| Current Worry | 1 = not at all worried to 7 = very worried |
| Future Worry | 1 = not at all likely to 7 = very likely |
| Cultural Cognition | 1 = strongly disagree to 6 = Strongly agree |
| Prioritize Society | 1 = not at all to 7 = very much so |
| Longitude | 1 = not at all worried to 7 = very worried |
| Effect | 1 = not at all affected to 7 = very much affected |
| General Trust | 1 = Can’t be too careful to 7 = Most people can be trusted |
| Scientist Understanding | 1 = very limited understanding to 7 = very good understanding |
| Certainty | 1 = very certain to 7 = very uncertain |
| Country-Affect and Personal-Sick | 1 = strongly disagree to 5 = strongly agree |
| Threat Severity | 1 = strongly disagree to 5 = strongly agree |
| Response Efficacy and Societal Efficacy | 1 = not at all to 7 = very much |
| PM | Accuracy | Recall | Precision | |
|---|---|---|---|---|
| Work from home | 66.5% | 47.9% | 58.7% | 52.8% |
| PPE | 74.4% | 60.0% | 72.6% | 65.7% |
| Dining out less | 95.2% | 72.3% | 71.2% | 82.1% |
| Shopping for groceries less | 69.7% | 61.5% | 60.9% | 64.9% |
References
- Zechman, E.M. Agent-Based Modeling to Simulate Contamination Events and Evaluate Threat Management Strategies in Water Distribution Systems: Agent-Based Modeling to Simulate Contamination Events. Risk Anal. 2011, 31, 758–772. [Google Scholar] [CrossRef]
- Sattler, B.J.; Friesen, J.; Tundis, A.; Pelz, P.F. Modeling and Validation of Residential Water Demand in Agent-Based Models: A Systematic Literature Review. Water 2023, 15, 579. [Google Scholar] [CrossRef]
- Zellner, M.L. Embracing complexity and uncertainty: The potential of agent-based modeling for environmental planning and policy. Plan. Theory Pract. 2008, 9, 437–457. [Google Scholar] [CrossRef]
- Kadinski, L.; Ostfeld, A. Incorporation of COVID-19-Inspired Behaviour into Agent-Based Modelling for Water Distribution Systems’ Contamination Responses. Water 2021, 13, 2863. [Google Scholar] [CrossRef]
- Kerr, C.C.; Stuart, R.M.; Mistry, D.; Abeysuriya, R.G.; Rosenfeld, K.; Hart, G.R.; Núñez, R.C.; Cohen, J.A.; Selvaraj, P.; Hagedorn, B.; et al. Covasim: An agent-based model of COVID-19 dynamics and interventions. Plos Comput. Biol. 2021, 17, e1009149. [Google Scholar] [CrossRef]
- Song, R.; Liu, X.; Zhu, B.; Guo, S. Modeling of Water Distribution System Based on Ten-Minute Accuracy Remote Smart Demand Meters. Water 2022, 14, 1934. [Google Scholar] [CrossRef]
- Baustert, P.; Benetto, E. Uncertainty analysis in agent-based modelling and consequential life cycle assessment coupled models: A critical review. J. Clean. Prod. 2017, 156, 378–394. [Google Scholar] [CrossRef]
- Ligmann-Zielinska, A.; Kramer, D.B.; Spence Cheruvelil, K.; Soranno, P.A. Using uncertainty and sensitivity analyses in socioecological agent-based models to improve their analytical performance and policy relevance. PLoS ONE 2014, 9, e109779. [Google Scholar] [CrossRef]
- Hamis, S.; Stratiev, S.; Powathil, G.G. Uncertainty and sensitivity analyses methods for agent-based mathematical models: An introductory review. In The Physics of Cancer: Research Advances; World Scientific: Singapore, 2021; pp. 1–37. [Google Scholar]
- Sumer, D.; Lansey, K. Effect of uncertainty on water distribution system model design decisions. J. Water Resour. Plan. Manag. 2009, 135, 38–47. [Google Scholar] [CrossRef]
- Shafiee, M.E.; Zechman, E.M. An agent-based modeling framework for sociotechnical simulation of water distribution contamination events. J. Hydroinform. 2013, 15, 862–880. [Google Scholar] [CrossRef]
- Ramsey, E.; Pesantez, J.; Fasaee, M.A.K.; DiCarlo, M.; Monroe, J.; Berglund, E.Z. A Smart Water Grid for Micro-Trading Rainwater: Hydraulic Feasibility Analysis. Water 2020, 12, 3075. [Google Scholar] [CrossRef]
- Kadinski, L.; Berglund, E.; Ostfeld, A. An Agent-Based Model for Contamination Response in Water Distribution Systems during the COVID-19 Pandemic. J. Water Resour. Plan. Manag. 2022, 148, 04022042. [Google Scholar] [CrossRef]
- Vizanko, B.; Kadinski, L.; Ostfeld, A.; Berglund, E.Z. Social distancing, water demand changes, and quality of drinking water during the COVID-19 pandemic. Sustain. Cities Soc. 2024, 102, 105210. [Google Scholar] [CrossRef]
- Hutton, C.J.; Kapelan, Z.; Vamvakeridou-Lyroudia, L.; Savić, D.A. Dealing with uncertainty in water distribution system models: A framework for real-time modeling and data assimilation. J. Water Resour. Plan. Manag. 2014, 140, 169–183. [Google Scholar] [CrossRef]
- Pandey, P.; Dongre, S.; Gupta, R. Probabilistic and fuzzy approaches for uncertainty consideration in water distribution networks–a review. Water Supply 2020, 20, 13–27. [Google Scholar] [CrossRef]
- Kang, D.; Pasha, M.; Lansey, K. Approximate methods for uncertainty analysis of water distribution systems. Urban Water J. 2009, 6, 233–249. [Google Scholar] [CrossRef]
- Pesantez, J.E.; Alghamdi, F.; Sabu, S.; Mahinthakumar, G.; Berglund, E.Z. Using a digital twin to explore water infrastructure impacts during the COVID-19 pandemic. Sustain. Cities Soc. 2022, 77, 103520. [Google Scholar] [CrossRef]
- Matthews, R.B.; Gilbert, N.G.; Roach, A.; Polhill, J.G.; Gotts, N.M. Agent-based land-use models: A review of applications. Landsc. Ecol. 2007, 22, 1447–1459. [Google Scholar] [CrossRef]
- Ferson, S.; Sentz, K. Epistemic uncertainty in agent-based modeling. In Proceedings of the 7th International Workshop on Reliable Engineering Computing, Bochum, Germany, 15–17 June 2016; pp. 65–82. [Google Scholar]
- Kimpton, L.; Challenor, P.; Salter, J. Uncertainty Quantification for Agent Based Models: A Tutorial. arXiv 2024, arXiv:2409.16776. [Google Scholar]
- Anbari, M.J.; Zarghami, M.; Nadiri, A.A. An uncertain agent-based model for socio-ecological simulation of groundwater use in irrigation: A case study of Lake Urmia Basin, Iran. Agric. Water Manag. 2021, 249, 106796. [Google Scholar] [CrossRef]
- Rasekh, A.; Shafiee, M.E.; Zechman, E.; Brumbelow, K. Sociotechnical risk assessment for water distribution system contamination threats. J. Hydroinform. 2014, 16, 531–549. [Google Scholar] [CrossRef]
- Bruch, E.; Atwell, J. Agent-based models in empirical social research. Sociol. Methods Res. 2015, 44, 186–221. [Google Scholar] [CrossRef] [PubMed]
- Klise, K.A.; Hart, D.B.; Moriarty, D.; Bynum, M.L.; Murray, R.; Burkhardt, J.; Haxton, T. Water Network Tool for Resilience (WNTR) User Manual; U.S. Environmental Protection Agency: Washington, DC, USA, 2017; p. 50.
- Rossman, L.A.; Woo, H.; Tryby, M.; Shang, F.; Janke, R.; Haxton, T. EPANET 2.2 User Manual; U.S. Environmental Protection Agency: Washington, DC, USA, 2020; p. 190.
- Brumbelow, K.; Torres, J.; Guikema, S.; Bristow, E.; Kanta, L. Virtual Cities for Water Distribution and Infrastructure System Research. In Proceedings of the World Environmental and Water Resources Congress 2007, Tampa, FL, USA, 15–19 May 2007; pp. 1–7. [Google Scholar] [CrossRef]
- Macal, C.M.; North, M.J. Tutorial on agent-based modelling and simulation. J. Simul. 2010, 4, 151–162. [Google Scholar] [CrossRef]
- Mittal, S.; Rainey, L. Harnessing emergence: The control and design of emergent behavior in system of systems engineering. In Proceedings of the Conference on Summer Computer Simulation, Chicago, IL, USA, 26–29 July 2015; pp. 1–10. [Google Scholar]
- Dryhurst, S.; Schneider, C.R.; Kerr, J.; Freeman, A.L.J.; Recchia, G.; van der Bles, A.M.; Spiegelhalter, D.; van der Linden, S. Risk perceptions of COVID-19 around the world. J. Risk Res. 2020, 23, 994–1006. [Google Scholar] [CrossRef]
- Rogers, G.O.; Sorensen, J.H. Diffusion of Emergency Warning: Comparing Empirical and Simulation Results. In Proceedings of the Risk Analysis: Prospects and Opportunities, Washington, DC, USA, 30 October–2 November 1998; Zervos, C., Knox, K., Abramson, L., Coppock, R., Eds.; Advances in Risk Analysis. National Library of Australia: Boston, MA, USA, 1991; pp. 117–134. [Google Scholar]
- Vizanko, B.; Kadinski, L.; Cummings, C.; Ostfeld, A.; Berglund, E.Z. Modeling prevention behaviors during the COVID-19 pandemic using Bayesian belief networks and protection motivation theory. Risk Anal. 2024, 44, 2198–2223. [Google Scholar] [CrossRef]





| Component | Without Uncertainty | With Uncertainty |
|---|---|---|
| Agent Movement | Expose exactly k agents with probability p | Expose agents with probability |
| Media Exposure | Fixed probability p for agents listening to radio/TV | Probability varies as |
| COVID-19 Status | Probability p for (1) exposure condition and (2) status from BBN output | Probability varies as |
| Worker Mobility | No movement for non-work purposes | Movement allowed from residential to commercial nodes with probability p |
| Node-Type Distribution | Fixed agent distribution | Randomized agent distribution |
| Distribution | Industrial | Café | Commercial | Residential |
|---|---|---|---|---|
| less-ind | 92 | 116 | 1270 | 3128 |
| regular | 1092 | 59 | 939 | 2516 |
| more-ind | 2092 | 27 | 543 | 1944 |
| much-more-ind | 3092 | 20 | 422 | 1071 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Komarovsky, S.; Vizanko, B.; Berglund, E.; Ostfeld, A. Assessing the Sensitivity of Sociotechnical Water Distribution Systems to Uncertainty in Consumer Behaviors: Social Distancing and Demand Changes During the COVID-19 Pandemic. Water 2025, 17, 1965. https://doi.org/10.3390/w17131965
Komarovsky S, Vizanko B, Berglund E, Ostfeld A. Assessing the Sensitivity of Sociotechnical Water Distribution Systems to Uncertainty in Consumer Behaviors: Social Distancing and Demand Changes During the COVID-19 Pandemic. Water. 2025; 17(13):1965. https://doi.org/10.3390/w17131965
Chicago/Turabian StyleKomarovsky, Shimon, Brent Vizanko, Emily Berglund, and Avi Ostfeld. 2025. "Assessing the Sensitivity of Sociotechnical Water Distribution Systems to Uncertainty in Consumer Behaviors: Social Distancing and Demand Changes During the COVID-19 Pandemic" Water 17, no. 13: 1965. https://doi.org/10.3390/w17131965
APA StyleKomarovsky, S., Vizanko, B., Berglund, E., & Ostfeld, A. (2025). Assessing the Sensitivity of Sociotechnical Water Distribution Systems to Uncertainty in Consumer Behaviors: Social Distancing and Demand Changes During the COVID-19 Pandemic. Water, 17(13), 1965. https://doi.org/10.3390/w17131965







