Abstract
Accurately predicting streamflow using process-based models remains challenging due to uncertainties in model parameters and the complex nature of streamflow generation. Data-driven approaches, however, offer feasible alternatives, avoiding the need for physical process representation. This study introduces a hybrid deep learning framework, CNN-GRU-BiLSTM, for daily streamflow prediction. This model integrates convolutional neural networks (CNN), gated recurrent units (GRU), and bidirectional long short-term memory (BiLSTM) networks to leverage their complementary strengths. When applied to the Neuse River Basin (NRB) (North Carolina, USA), the proposed model achieved strong predictive performance, yielding a root mean square (RMSE) of 11.8 m3/s (compared to an average streamflow of 132.7 m3/s), and a mean absolute error (MAE) of 8.7 m3/s, and a Nash–Sutcliffe efficiency (NSE) of 0.994 for the testing dataset. Similar performance trends were observed in the training and validation phases. A comparative analysis against seven other deep learning and hybrid models of similar complexity highlighted the outstanding performance of the CNN-GRU-BiLSTM model across all flood events. Furthermore, its stability, robustness, and transferability were evaluated in a seasonal dataset, peak floods, and different locations along the river. These findings underscore the potential of hybrid deep learning models and reinforce the effectiveness of integrating multiple data-driven techniques for streamflow prediction in regions where precipitation is the dominant driver of streamflow.
1. Introduction
Streamflow prediction is essential for flood control, water resource management, and hydropower generation. The models for streamflow prediction can be divided into two categories: process-based models and data-driven models [1,2]. Understanding runoff-generating mechanisms, channel transport, and parametrization of these physical processes are the basics for developing process-based models. Process-based hydrological models rely on topographic data, soil moisture, land use, and land cover. Furthermore, a long record of hydrometeorological data is required to calibrate the model parameters [3,4]. The complicated interaction between multiple kinds of errors might further reduce forecast accuracy, and the uncertainty from precipitation and hydrology also influences streamflow forecasting [5]. These limitations, together with the issue of uncertainty, have troubled the operational adoption of process-based models [6,7].
In contrast, data-driven models offer several advantages over physical models, including minimal reliance on extensive physical data, faster computation, adaptability to nonlinear systems, and greater flexibility and scalability [8,9,10]. Deep learning models are typical examples of data-driven models and have been widely used in streamflow prediction in different physiographic regions [11]. For example, Shu et al. (2021) [12] explored CNN for monthly streamflow forecasting at Huanren Reservoir and Xiangjiaba hydropower station, China, leveraging its feature extraction capability compared with ANN (artificial neural network) and ELM (extreme learning machine) models. Results showed that CNN outperformed both models, demonstrating outstanding accuracy and stability. Wang et al., 2022 [13], applied LSTM (long short-term memory model) to predict daily streamflow at two stations in the Mississippi River Basin, Iowa, USA. They used the bootstrap method to enhance uncertainty qualifications to make LSTM a reliable tool for streamflow prediction. Deep learning models have been increasingly used and show good prediction skills [14,15,16].
Hybrid deep learning models have also gained increasing attention in streamflow prediction due to their ability to integrate multiple architectures for improved accuracy, stability, transferability, generalizability, and robustness [5,17,18,19]. Kilinc and Yurtsever, 2022 [20], highlight the importance of hybrid models in streamflow forecasting by proposing GWO-GRU hybrid models for the Seyhan Basin, Turkey. The hybrid model outperformed benchmark models (linear regression and single GRU), achieving higher accuracy and improved predictive performance. A comparative study between single and hybrid deep learning models in hourly streamflow forecasting [21] proposes a hybrid model in the Andun Basin, China, integrating DIFF (first order difference), FFNN (feed-forward neural network), and LSTM. This model outperforms five machine learning models (multiple linear regression (MLR), autoregression (AR), autoregressive moving average (ARMA), autoregressive integrated moving average (ARIMA), and FFNN) and four statistical models (LSTM, FFNN-LSTM, DIFF-FFNN, DIFF-LSTM), achieving high accuracy. Fang et al., 2024 [22], developed a CNN-Transformer-LSTM (CTL) hybrid model for streamflow prediction in the Shule River Basin, China. CTL outperformed Transformer, CNN, LSTM, CNN-Transformer, and Transformer-LSTM across one-month, three-month, and six-month horizons, indicating the outstanding performance of hybrid models in improving streamflow prediction.
This study proposes a new hybrid streamflow prediction model, the CNN-GRU-BiLSTM network, for daily streamflow prediction. The proposed approach combines CNN, GRU, and BiLSTM to leverage their strengths. To assess its effectiveness, we compare its performance against individual CNN, LSTM, BiLSTM, and GRU models and hybrid models, including CNN-GRU, CNN-BiLSTM, and GRU-BiLSTM. Furthermore, the proposed model is evaluated across seasonal datasets and diverse physiographic regions to test its stability, robustness, and transferability.
2. Approach
2.1. Model Algorithm
We proposed a hybrid model, CNN-GRU-BiLSTM, based on the complementary strengths of its components: the CNN for extracting local temporal features, GRU for efficient sequence learning, and BiLSTM for capturing bidirectional dependencies. Because streamflow data is complicated, we hypothesized that hybridizing these architectures would help the model learn the short-term and long-term patterns effectively.
2.1.1. Convolutional Neural Networks (CNN)
CNN is a deep learning model primarily intended for spatial data processing, such as image analysis. CNN is also useful for time series forecasting because its feature extraction capacity allows convolutional filters to detect temporal correlations within sequential data. CNN’s three fundamental building blocks are convolutional, pooling, and fully connected layers [23]. However, pooling layers are not used in this study because pooling reduces the temporal dimension, which could lead to information loss in time series data [24,25,26].
2.1.2. Gated Recurrent Unit (GRU)
In the hybrid CNN-GRU-BiLSTM model, CNN provides input to the GRU layer. GRU, with a typical structure shown in Figure 1, is a recurrent neural network (RNN) intended for sequential data processing that captures temporal dependencies using its gating mechanism. It comprises update and reset gates that control the flow of information by calculating how much previous data should be stored or discarded, preventing the frequent vanishing gradient concerns in deep networks. The GRU’s hidden states efficiently encode sequential dependencies, resulting in effective feature transformation before transferring the processed information to the BiLSTM layer. GRU is computationally efficient compared to LSTM, making it practical for capturing short-term variations in precipitation patterns [27].
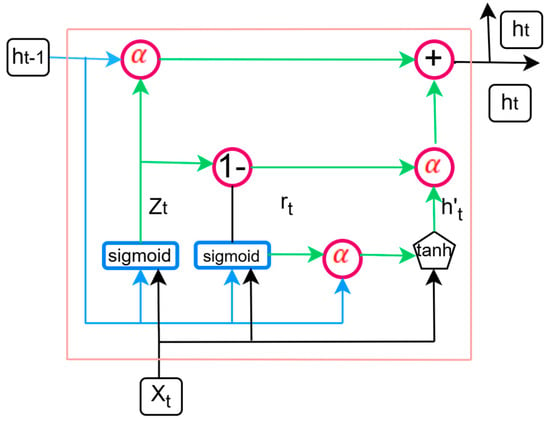
Figure 1.
A typical structure of a GRU cell [28].
In the GRU architecture, the memory cell’s output () at the time step functions as the input for the subsequent cell and a factor in decision-making [21,29]. The update gate () determines how much of the prior hidden state is kept and carried over to the next stage. The reset gate () determines how much of the previous information to forget. The candidate’s hidden state () is calculated by mixing the current input with the reset-modulated previous hidden state, where and + denote element-wise multiplication and addition, respectively. The real hidden state output () combines the new candidate state with the old hidden state based on the update gate’s value. Sigmoid is an activation function that produces values from 0 to 1. The tanh activation function is used to generate a candidate hidden state.
2.1.3. Bidirectional Long Short-Term Memory (BiLSTM)
The BiLSTM network is an advanced RNN variant that processes sequential data in forward and backward directions, capturing dependencies from previous and future time steps. Unlike a standard LSTM network, which only accesses past information, BiLSTM overcomes this limitation through forward and backward data flows [30]. BiLSTM improves the hybrid model’s capacity to discover complicated sequential links that unidirectional architectures may overlook [31]. The structure of a BiLSTM neural network is shown in Figure 2.
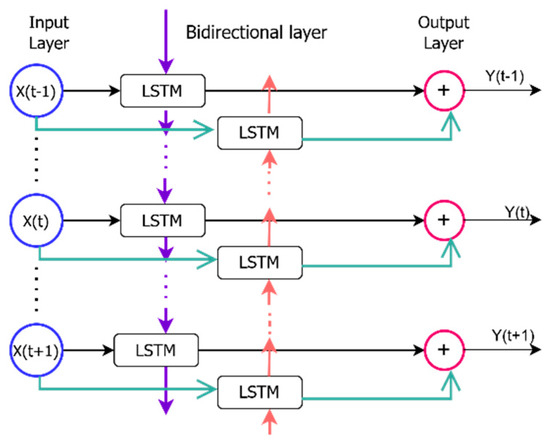
Figure 2.
The structure of a BiLSTM neural network [28].
A standard LSTM network comprises a series of memory cells arranged sequentially. Each cell is interconnected through two essential components called the hidden state () and the cell state (). The hidden state captures short-term memory, and the cell state retains long-term memory [28,29]. These two states at a time step are defined by the following equations:
where , and denote the forget gate, input gate, and output gate values at time step t, respectively. The function δ represents sigmoid activation, is the candidate of the cell state value, and are weight matrices, and ∝ represents the element-wise multiplication. These gates enable the model to learn which information to retain, update, or discard.
2.1.4. CNN-GRU-BiLSTM Model
This hybrid model uses CNN for feature extraction, GRU for short-term dependency learning, and BiLSTM to capture long-range bidirectional dependencies, resulting in strong time series forecasting with minimum information loss. A summary of the roles of each component in the proposed hybrid model is presented in Table 1. The diagram, Figure 3, visualizes how data moves through the hybrid model and how each component contributes to streamflow prediction. The fully connected layer consisted of the dense and the output layers. The dense layer is the final decision-making component, combining extracted features and learned temporal patterns to generate the final streamflow prediction. The output layer comprises a single neuron (dense (1)) for regression, providing the final streamflow estimate.

Table 1.
Summary of the proposed hybrid model components and their roles.

Figure 3.
Diagram Representing Workflow.
Regarding the potential risk of overfitting due to the complexity of the proposed CNN-GRU-BiLSTM model and the relatively limited training data size, we have employed regularization techniques (dropout layers, early stopping, and batch normalization) during model training to improve generalizability of the model and mitigate overfitting.
2.2. Data Preparation and Model Evaluation
In this study, daily time-step precipitation data were collected from 18 spatially distributed stations within the watershed. To represent spatial variability, we combined the precipitation time series from all 18 stations into a single multivariate input matrix for each time step. This allowed the model to learn the spatial distribution of rainfall across the watershed. We further applied a sliding window approach for the temporal dimension. Three consecutive days of precipitation data (time steps) from all 18 stations were utilized to predict the streamflow for the following day. Consequently, the input tensor for the CNN-GRU-BiLSTM model had the 3D shape (samples, time steps, spatial features). This enables the model to learn spatial and temporal dependencies effectively.
Cleaning, converting, and arranging raw data into a format appropriate for modeling is known as data pre-processing. The Partial Auto-Correlation Function (PACF) is used to determine the optimal time lag for constructing the input series. PACF calculates the correlation between a time series and its lagged values after removing the effect of any shorter lags. It helps in deciding the direct relationship between observations made at various time intervals [21]. An augmented Dickey–Fuller (ADF) test was used to guarantee stationarity. It is a statistical test used to determine whether a time series is stationary by checking for the presence of a unit root [32,33,34]. To put all dataset features on a uniform scale, data standardization was also carried out using Minmax Scalar (Equation (11)) [35,36]. The data series was split into training, validation, and testing sets to support the development of a robust and reliable time series model following a commonly used practice, a 70%, 15%, and 15%, respectively, after being converted into a supervised learning format and restructured into samples, time steps, and features appropriate for the model application [8].
The data is normalized using the Minmax Scalar function before the training process to make model inputs consistent and speed up the convergence during the model training. The Minmax Scalar function is represented by Equation (11), where x is the original value in the dataset, , and are the minimum and maximum values of the feature in the dataset, respectively, and is the normalized value after applying the MinMaxScaling.
where X is the original value in the dataset. The and are the minimum and maximum values of the feature in the dataset, respectively. is the normalized value after applying MinMaxScaling.
The grid search method was applied to each constituent of the proposed hybrid model (CNN-GRU-BiLSTM) to systematically find the optimal hyperparameters, number of hidden layers, and neuron node. Each component of the hybrid model was developed and evaluated for performance. Then, they were integrated to explore and leverage their complementary strengths to enhance the efficiency of the separate models.
The evaluation metrics used in this study to quantify the model’s predictive accuracy include mean absolute error (MAE), root mean squared error (RMSE), and Nash–Sutcliffe efficiency (NSE). The following equations represent these metrics.
where , , and are observed, predicted, and average observed values, respectively. The is the number of observations in the test data.
3. Study Area and Data
We tested the performance of the data-driven model for streamflow forecast in the Neuse River Basin (NRB), located in North Carolina, USA. The basin extends across three physiographic regions: coastal plain, plain, and piedmont. The NRB in North Carolina covers 14,582 km2 and is the state’s third-largest river basin. Its topography ranges from 276 m in the upper reaches to sea level downstream. The flow of surface water is heavily influenced by precipitation, with the upper basin receiving an average of 1143 mm of rainfall annually and the downstream receiving 1524 mm (https://www.deq.nc.gov/about/divisions/water-resources/water-planning/basin-planning-branch, accessed on 10 January 2025). Precipitation data were obtained from 18 rain gauge stations in the basin. The streamflow data was collected from the coastal plain area, lower part of the Neuse River (source: United States Geological Survey (USGS) website, data (accessed on 28 October 2024)). The spatial distribution of the stations, the basin boundary, and the physiographic regions are shown in Figure 4.
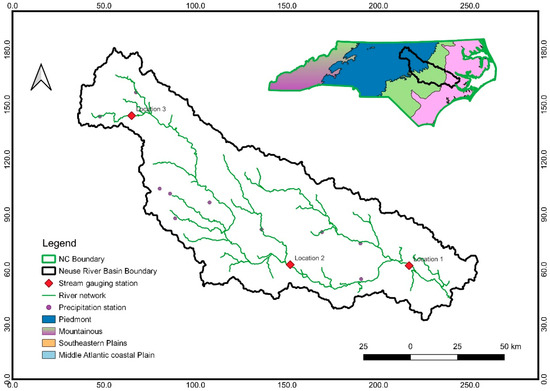
Figure 4.
Study area: Neuse River Basin (NRB), North Carolina, USA.
4. Results and Discussions
This study utilized daily precipitation as the input variable and streamflow as the output. While many physical factors influence streamflow, including climate conditions and land use changes, precipitation is the dominant driver in the study area. Consequently, this research aims to explore a stable, robust, and transferable data-driven model to simulate and predict streamflow in regions where precipitation primarily governs runoff.
In the proposed hybrid model, CNN-GRU-BiLSTM, pooling layers were excluded from the CNN model to avoid reducing the temporal resolution and losing important time-dependent information [24,25]. Instead, all extracted features are passed directly into the sequential layers. In the CNN-GRU-BiLSTM model, the CNN component first extracts short-term patterns, which are then processed by the GRU layer to capture medium-range dependencies. No dense layer is placed between CNN and GRU to preserve the temporal features. A fully connected layer is used only after the BiLSTM layer to ensure that complex sequential patterns captured in forward and backward directions are fully learned before the final regression output is generated.
The model concludes with fully connected dense layers that merge the identified features and temporal dependencies to produce a single regression output. It is configured using the Adam optimizer with mean squared error as the loss metric. To mitigate the risk of overfitting, early stopping is employed during the training process. The training is performed on the designated training dataset, while validation and testing are conducted on separate datasets. An overview of the model’s algorithm is provided in Table 2.

Table 2.
Algorithm of the CNN-GRU-BiLSTM model.
In the model training, a batch size of 32 was used for up to 100 epochs, employing the Adam optimizer and mean squared error (MSE) as the loss function. Regularization techniques such as a dropout rate of 0.2 and early stopping with a patience of four epochs were utilized to prevent overfitting. The activation functions included tanh in the recurrent layers. The training and validation loss plots (learning curves) for the proposed CNN-GRU-BiLSTM model are shown in Figure 5, which demonstrates that the model converges well and generalizes effectively without significant overfitting.
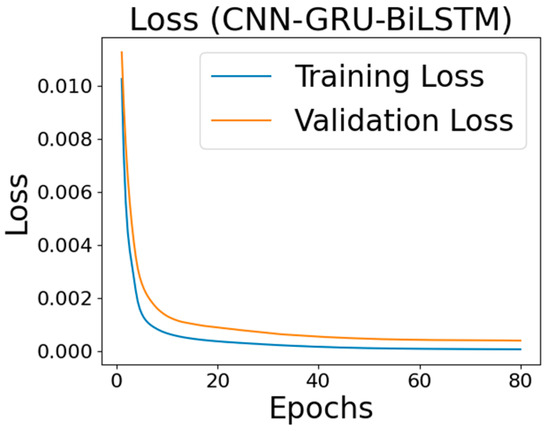
Figure 5.
Training and validation loss plot for the CNN-GRU-BiLSTM hybrid model.
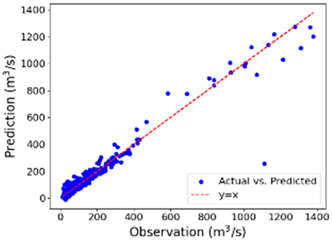
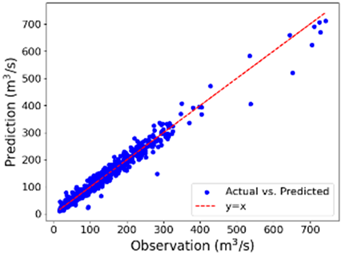
Figure 6 displays the final prediction scatter plot of the CNN-GRU-BiLSTM model for both the training and testing sets. The model’s predictions closely match the observed values for both datasets. The trained model successfully captures extremely high streamflow events in the testing set that were absent in the training set. This demonstrates the model’s ability to generalize effectively, the same as a previous study by Yong Lin et al., 2021 [5].
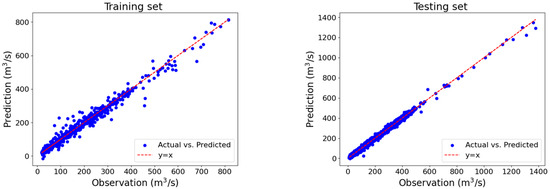
Figure 6.
Scatter plot for the training and testing set by CNN-GRU-BiLSTM.
To evaluate the performance of the proposed CNN-GRU-BiLSTM model, we compared it against four individual deep learning models. These are a convolutional neural network (CNN), a gated recurrent unit (GRU), a long short-term memory (LSTM), and a bidirectional LSTM (BiLSTM). Furthermore, to assess the benefits of combining two components, we included three hybrid models in the comparison: CNN-GRU, GRU-BiLSTM, and CNN-BiLSTM. Based on the evaluation metrics, the CNN-GRU-BiLSTM model outperformed all other models in the training and testing datasets (See Table 2 and Table 3).

Table 3.
Metrics and training time for the models in the training and testing set.
All models performed well in the testing and training sets. However, the CNN-BiLSTM performed the worst among all seven models. Having a different treatment to this hybrid model by adding a GRU between the two models helps improve the model’s performance. For example, RMSE is reduced by 68.02% from 36.9 m3/s in the CNN-BiLSTM model to 11.8 m3/s in the CNN-GRU-BiLSTM model. The combination of CNN, GRU, and BiLSTM leads to improvement over CNN, GRU, and BiLSTM alone, and different combinations such as CNN-GRU, GRU-BiLSTM, and CNN-BiLSTM are shown by a reduction of RMSE and MAE and an increase of NSE. The CNN-GRU-BiLSTM model is outstanding compared to all the other seven deep learning models, with an RMSE of 11.8 m3/s, MAE of 5.1 m3/s, and NSE of 0.994 to the testing set. This is because the watershed has relatively consistent hydrological patterns, and the quality and density of the input data allow the hybrid model to learn short-term and long-term dependencies efficiently.
Furthermore, we have compared the models based on the training time to assess their computational efficiency. The training times (in seconds) for CNN, LSTM, GRU, BiLSTM, CNN-GRU, GRU-BiLSTM, CNN-BiLSTM, and CNN-GRU-BiLSTM were 45.3, 52.1, 61.4, 72.3, 79.8, 81.3, 93.1, and 95.6, respectively. As expected, more complex hybrid models require longer training durations. The CNN-GRU-BiLSTM model achieved the best overall performance in terms of accuracy; however, it had the highest training time (95.6 s). Simpler models train relatively faster, though with slightly lower predictive accuracy. This highlights a trade-off between model complexity and computational cost. This trade-off should be considered in practical applications depending on resource availability and accuracy requirements. The performance comparison among these eight models can also be visualized in Figure 7.
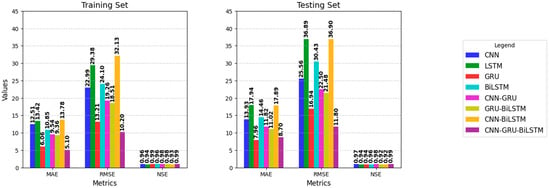
Figure 7.
Bar chart showing metric values for the training and testing sets.
The bar chart for the metric values (Figure 7) reveals that all models achieve NSE values ranging from 0.96 to 0.99 for training and testing sets, indicating comparable model performance. The variations in MAE and RMSE between the training and testing sets span from 5.1 to 13.78 and 8.7 to 17.94 for MAE and 10.20 to 32.13 and 11.8 to 36.9 for RMSE, respectively, based on an average flow rate of 132.70 m3/s. The proposed model achieved the least MAE and RMSE values in both cases. Overall, the key distinction among the models lies in their capacity to minimize errors, with hybrid models displaying a significant advantage over single architecture in most cases.
Furthermore, we divided the dataset into four seasons, fall (23 September–21 December), winter (22 December–19 March), spring (20 March–20 June), and summer (21 June–September), and evaluated the performance of the CNN-GRU-BiLSTM model in predicting the streamflow. The proposed hybrid model (as shown in Table 4) can accurately predict streamflow across different seasons, implying the model’s stability. However, the performance in predicted streamflow for the winter season shows a decrease in NSE value (from 0.968 to 0.899) for the testing set compared to the training set. Still, the MAE and RMSE values are comparable among the seasonal and yearly datasets.

Table 4.
Metrics values for the seasonal training and testing dataset.
The error is high for the seasonal data (Table 4) compared to the full-year data (Table 3) due to short record length, reduced variability, and disrupted temporal dependencies. Seasonal subsets contain fewer data points, which limits the model’s ability to generalize, increases the risk of overfitting, and reduces the diversity of patterns in the training data. Furthermore, seasonal data may break term dependencies. For example, streamflow in early winter may depend on rainfall from the previous fall that occurs late in the season. If the model is trained only on winter data, it misses those prior influences, which can degrade predictive performance.
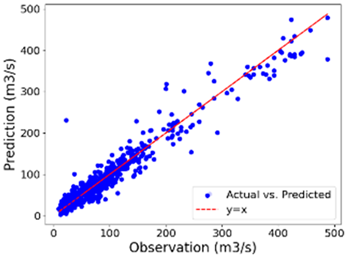
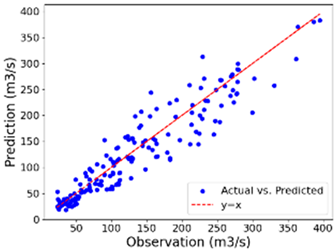
Scatter plots visualizing observation versus reciprocation, both in training and testing datasets, are shown in Table 5.

Table 5.
Scatter plots for the four seasons in training and testing.
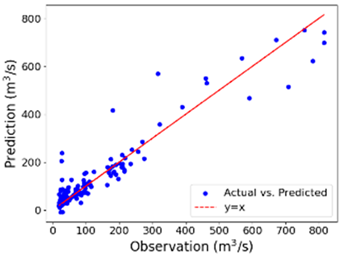
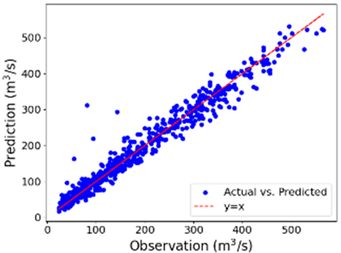
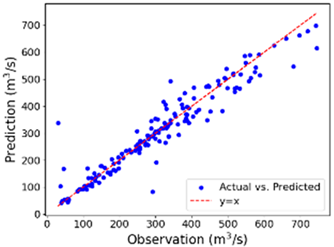
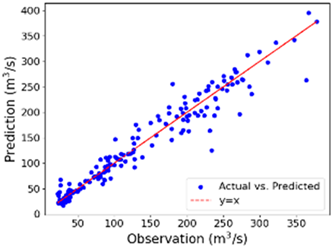
The river’s middle and upper course flows were selected to evaluate the proposed model’s ability to capture streamflow’s spatial and temporal variations. The average flows at the middle and upper course of the river for the same duration (2010–2021) are 75.41 m3/s and 6.65 m3/s, respectively. These flows are smaller by 43.2% and 94.98% from the average flow rate where the proposed model was trained and created. The lower course of the river is on the coastal plain, the middle course is in the plain region, and the upper course is in the Piedmont area, implying that these three locations are in different physiographic environments, though they are in the same watershed (Figure 4). As shown in Figure 8, the hybrid model can reasonably reproduce spatial and temporal flows (especially the middle course flow), depicting the model’s transferability and robustness. The other models are not as generalizable and robust as the proposed model when trained on different datasets, especially in the middle course, where the flow dynamics are complex compared to the lower and upper classes of the river. This implies that the proposed model learned and simulated the flow dynamics in the middle and predicted efficiently.
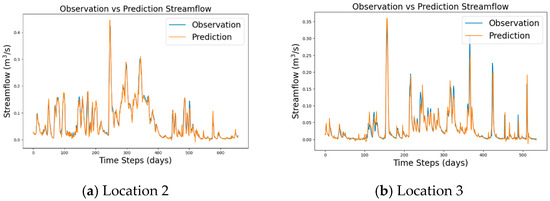
Figure 8.
Observed versus predicted streamflow at (a) middle and (b) upper Neuse River.
This study introduces a CNN-GRU-BiLSTM hybrid model that offers improved robustness compared to individual and dual-combination models. Its adaptable architecture makes it suitable for application in other river basins with similar data availability, supporting diverse hydroclimatic conditions. As climate change alters precipitation trends, the model can serve as a tool to analyze potential impacts on streamflow and water supply. With precipitation as its main input, the model effectively captures climate-driven variations in streamflow, providing insights essential for adaptive water resource planning. Its forecasting strength also supports institutional efforts to develop sustainable and informed water management policies.
Figure 9 compares observed and predicted streamflow at location 1 for two flood events. It demonstrates the CNN-GRU-BiLSTM model’s ability to capture streamflow variations. The percent bias (PBIAS) for the flood events is 4.14 and 2.97 for Event 1 and Event 2, respectively. The hybrid model effectively replicates flood fluctuations over time for different flood types, highlighting its stability and robustness.
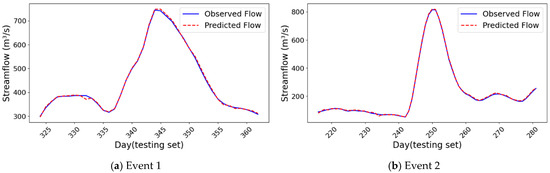
Figure 9.
Observed versus predicted streamflow at location 1 for two peak flood events.
5. Conclusions
A hybrid model, CNN-GRU-BiLSTM, is proposed in this study to improve streamflow prediction for daily streamflow from daily precipitation data. The model consists of CNN, GRU, and BiLSTM networks. The hybrid model is compared with four single models and three combinations of its component models. In addition, the proposed model was tested for seasonal datasets, peak flood events, and other datasets in different physiographic regions but within the same watershed to explore the model’s stability, robustness, and transferability.
The prediction results show that the hybrid models are more stable, robust, and transferable than the single models. The prediction of the model combining CNN-GRU and GRU-BiLSTM is more stable, robust, and generalized than the single models, namely CNN, GRU, BiLSTM, and LSTM. The GRU method in the proposed model (CNN-GRU-BiLSTM) can effectively improve the performance of the CNN-BiLSTM model, the worst-performing model of all the single and hybrid models. The CNN-GRU-BiLSTM model proposed in this paper can improve the time series data-based streamflow predictions from precipitation.
To explore the model’s transferability further, it is advisable to test it on a different watershed with different hydrological setups. In addition, applying different standardization techniques and activation functions might help investigate how the model reacts to different approaches. Further, we plan to consider incorporating techniques such as SHAP values in future work to assess the relative influence of spatial inputs from different stations.
Author Contributions
Conceptualization, H.W. and M.J.; methodology, H.W.; software, H.W.; validation, M.J. and H.W.; formal analysis, H.W.; investigation, H.W.; resources, M.J.; data curation, H.W.; writing—original draft preparation, H.W.; writing—review and editing, M.J.; visualization, H.W.; supervision, M.J.; project administration, M.J.; funding acquisition, M.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The datasets presented in this article are not readily available because the data are part of an ongoing study. Requests to access the datasets should be directed to USGS database.
Acknowledgments
We would like to thank the individuals who supported this work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Parisouj, P.; Mokari, E.; Mohebzadeh, H.; Goharnejad, H.; Jun, C.; Oh, J.; Bateni, S.M. Physics-Informed Data-Driven Model for Predicting Streamflow: A Case Study of the Voshmgir Basin, Iran. Appl. Sci. 2022, 12, 7464. [Google Scholar] [CrossRef]
- Chen, S.; Huang, J.; Huang, J.-C. Improving daily streamflow simulations for data-scarce watersheds using the coupled SWAT-LSTM approach. J. Hydrol. 2023, 622, 129734. [Google Scholar] [CrossRef]
- Beven, K. Deep learning, hydrological processes and the uniqueness of place. Hydrol. Process. 2020, 34, 3608–3613. [Google Scholar] [CrossRef]
- Yang, S.; Yang, D.; Chen, J.; Santisirisomboon, J.; Lu, W.; Zhao, B. A physical process and machine learning combined hydrological model for daily streamflow simulations of large watersheds with limited observation data. J. Hydrol. 2020, 590, 125206. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, D.; Wang, G.; Qiu, J.; Long, K.; Du, Y.; Xie, H.; Wei, Z.; Shangguan, W.; Dai, Y. A hybrid deep learning algorithm and its application to streamflow prediction. J. Hydrol. 2021, 601, 126636. [Google Scholar] [CrossRef]
- Özdoğan-Sarıkoç, G.; Dadaser-Celik, F. Physically based vs. data-driven models for streamflow and reservoir volume prediction at a data-scarce semi-arid basin. Environ. Sci. Pollut. Res. 2024, 31, 39098–39119. [Google Scholar] [CrossRef]
- Li, B.; Sun, T.; Tian, F.; Ni, G. Enhancing process-based hydrological models with embedded neural networks: A hybrid approach. J. Hydrol. 2023, 625, 130107. [Google Scholar] [CrossRef]
- Latif, S.D.; Ahmed, A.N. Streamflow Prediction Utilizing Deep Learning and Machine Learning Algorithms for Sustainable Water Supply Management. Water Resour. Manag. 2023, 37, 3227–3241. [Google Scholar] [CrossRef]
- Hu, X.; Shi, L.; Lin, G.; Lin, L. Comparison of physical-based, data-driven and hybrid modeling approaches for evapotranspiration estimation. J. Hydrol. 2021, 601, 126592. [Google Scholar] [CrossRef]
- Hauswirth, S.M.; Bierkens, M.F.; Beijk, V.; Wanders, N. The potential of data driven approaches for quantifying hydrological extremes. Adv. Water Resour. 2021, 155, 104017. [Google Scholar] [CrossRef]
- Ng, K.; Huang, Y.; Koo, C.; Chong, K.; El-Shafie, A.; Ahmed, A.N. A review of hybrid deep learning applications for streamflow forecasting. J. Hydrol. 2023, 625, 130141. [Google Scholar] [CrossRef]
- Shu, X.; Ding, W.; Peng, Y.; Wang, Z.; Wu, J.; Li, M. Monthly Streamflow Forecasting Using Convolutional Neural Network. Water Resour. Manag. 2021, 35, 5089–5104. [Google Scholar] [CrossRef]
- Wang, Z.; Si, Y.; Chu, H. Daily Streamflow Prediction and Uncertainty Using a Long Short-Term Memory (LSTM) Network Coupled with Bootstrap. Water Resour. Manag. 2022, 36, 4575–4590. [Google Scholar] [CrossRef]
- Latif, S.D.; Ahmed, A.N. A review of deep learning and machine learning techniques for hydrological inflow forecasting. Environ. Dev. Sustain. 2023, 25, 12189–12216. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, H.; Bai, M.; Xu, Y.; Dong, S.; Rao, H.; Ming, W. A Comprehensive Review of Methods for Hydrological Forecasting Based on Deep Learning. Water 2024, 16, 1407. [Google Scholar] [CrossRef]
- Tiwari, M.K.; Deo, R.C.; Adamowski, J.F. Short-term flood forecasting using artificial neural networks, extreme learning machines, and M5 model tree. In Advances in Streamflow Forecasting; Elsevier: Amsterdam, The Netherlands, 2021; pp. 263–279. [Google Scholar] [CrossRef]
- Ougahi, J.H.; Rowan, J.S. Enhanced streamflow forecasting using hybrid modelling integrating glacio-hydrological outputs, deep learning and wavelet transformation. Sci. Rep. 2025, 15, 2762. [Google Scholar] [CrossRef] [PubMed]
- Yu, Q.; Jiang, L.; Wang, Y.; Liu, J. Enhancing streamflow simulation using hybridized machine learning models in a semi-arid basin of the Chinese loess Plateau. J. Hydrol. 2023, 617, 129115. [Google Scholar] [CrossRef]
- He, M.; Jiang, S.; Ren, L.; Cui, H.; Du, S.; Zhu, Y.; Qin, T.; Yang, X.; Fang, X.; Xu, C.-Y. Exploring the performance and interpretability of hybrid hydrologic model coupling physical mechanisms and deep learning. J. Hydrol. 2025, 649, 132440. [Google Scholar] [CrossRef]
- Kilinc, H.C.; Yurtsever, A. Short-Term Streamflow Forecasting Using Hybrid Deep Learning Model Based on Grey Wolf Algorithm for Hydrological Time Series. Sustainability 2022, 14, 3352. [Google Scholar] [CrossRef]
- Vatanchi, S.M.; Etemadfard, H.; Maghrebi, M.F.; Shad, R. A Comparative Study on Forecasting of Long-term Daily Streamflow using ANN, ANFIS, BiLSTM and CNN-GRU-LSTM. Water Resour. Manag. 2023, 37, 4769–4785. [Google Scholar] [CrossRef]
- Fang, J.; Yang, L.; Wen, X.; Li, W.; Yu, H.; Zhou, T. A deep learning-based hybrid approach for multi-time-ahead streamflow prediction in an arid region of Northwest China. Hydrol. Res. 2024, 55, 180–204. [Google Scholar] [CrossRef]
- Pokharel, S.; Roy, T. A parsimonious setup for streamflow forecasting using CNN-LSTM. J. Hydroinform. 2024, 26, 2751–2761. [Google Scholar] [CrossRef]
- Jin, X.; Yu, X.; Wang, X.; Bai, Y.; Su, T.; Kong, J. Prediction for Time Series with CNN and LSTM. In Proceedings of the 11th International Conference on Modelling, Identification and Control (ICMIC2019), Tianjin, China, 13–15 July 2019; Lecture Notes in Electrical, Engineering. Wang, R., Chen, Z., Zhang, W., Zhu, Q., Eds.; Springer: Singapore, 2020; Volume 582, pp. 631–641. [Google Scholar] [CrossRef]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Coupling a hybrid CNN-LSTM deep learning model with a Boundary Corrected Maximal Overlap Discrete Wavelet Transform for multiscale Lake water level forecasting. J. Hydrol. 2021, 598, 126196. [Google Scholar] [CrossRef]
- Kumshe, U.M.M.; Abdulhamid, Z.M.; Mala, B.A.; Muazu, T.; Muhammad, A.U.; Sangary, O.; Ba, A.F.; Tijjani, S.; Adam, J.M.; Ali, M.A.H.; et al. Improving Short-term Daily Streamflow Forecasting Using an Autoencoder Based CNN-LSTM Model. Water Resour. Manag. 2024, 38, 5973–5989. [Google Scholar] [CrossRef]
- ArunKumar, K.; Kalaga, D.V.; Kumar, C.M.S.; Kawaji, M.; Brenza, T.M. Comparative analysis of Gated Recurrent Units (GRU), long Short-Term memory (LSTM) cells, autoregressive Integrated moving average (ARIMA), seasonal autoregressive Integrated moving average (SARIMA) for forecasting COVID-19 trends. Alex. Eng. J. 2022, 61, 7585–7603. [Google Scholar] [CrossRef]
- Le, X.-H.; Nguyen, D.-H.; Jung, S.; Yeon, M.; Lee, G. Comparison of Deep Learning Techniques for River Streamflow Forecasting. IEEE Access 2021, 9, 71805–71820. [Google Scholar] [CrossRef]
- Zhang, X.; Qi, Y.; Liu, F.; Li, H.; Sun, S. Enhancing daily streamflow simulation using the coupled SWAT-BiLSTM approach for climate change impact assessment in Hai-River Basin. Sci. Rep. 2023, 13, 15169. [Google Scholar] [CrossRef]
- Workneh, H.A.; Jha, M.K. Utilizing Deep Learning Models to Predict Streamflow. Water 2025, 17, 756. [Google Scholar] [CrossRef]
- Wei, Q.; Yang, J.; Fu, F.; Xue, L. Dynamic classification and attention mechanism-based bidirectional long short-term memory network for daily runoff prediction in Aksu River basin, Northwest China. J. Environ. Manag. 2025, 374, 124121. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, D.; Bao, J.; Yong, Q. Multi-step Ahead Time Series Forecasting for Different Data Patterns Based on LSTM Recurrent Neural Network. In Proceedings of the 2017 14th Web Information Systems and Applications Conference (WISA), Liuzhou, China, 11–12 November 2017; pp. 305–310. [Google Scholar] [CrossRef]
- Sun, X.; Li, Z.; Tian, Q. Assessment of hydrological drought based on nonstationary runoff data. Hydrol. Res. 2020, 51, 894–910. [Google Scholar] [CrossRef]
- Xie, T.; Zhang, G.; Hou, J.; Xie, J.; Lv, M.; Liu, F. Hybrid forecasting model for non-stationary daily runoff series: A case study in the Han River Basin, China. J. Hydrol. 2019, 577, 123915. [Google Scholar] [CrossRef]
- Rathnayake, D.; Perera, P.B.; Eranga, H.; Ishwara, M. Generalization of LSTM CNN ensemble profiling method with time-series data normalization and regularization. In Proceedings of the 2021 21st International Conference on Advances in ICT for Emerging Regions (ICter), Colombo, Sri Lanka, 2–3 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Nifa, K.; Boudhar, A.; Ouatiki, H.; Elyoussfi, H.; Bargam, B.; Chehbouni, A. Deep Learning Approach with LSTM for Daily Streamflow Prediction in a Semi-Arid Area: A Case Study of Oum Er-Rbia River Basin, Morocco. Water 2023, 15, 262. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).