Identifying Worst Transient Cases and Optimizing Surge Protection for Existing Water Networks
Abstract
1. Introduction
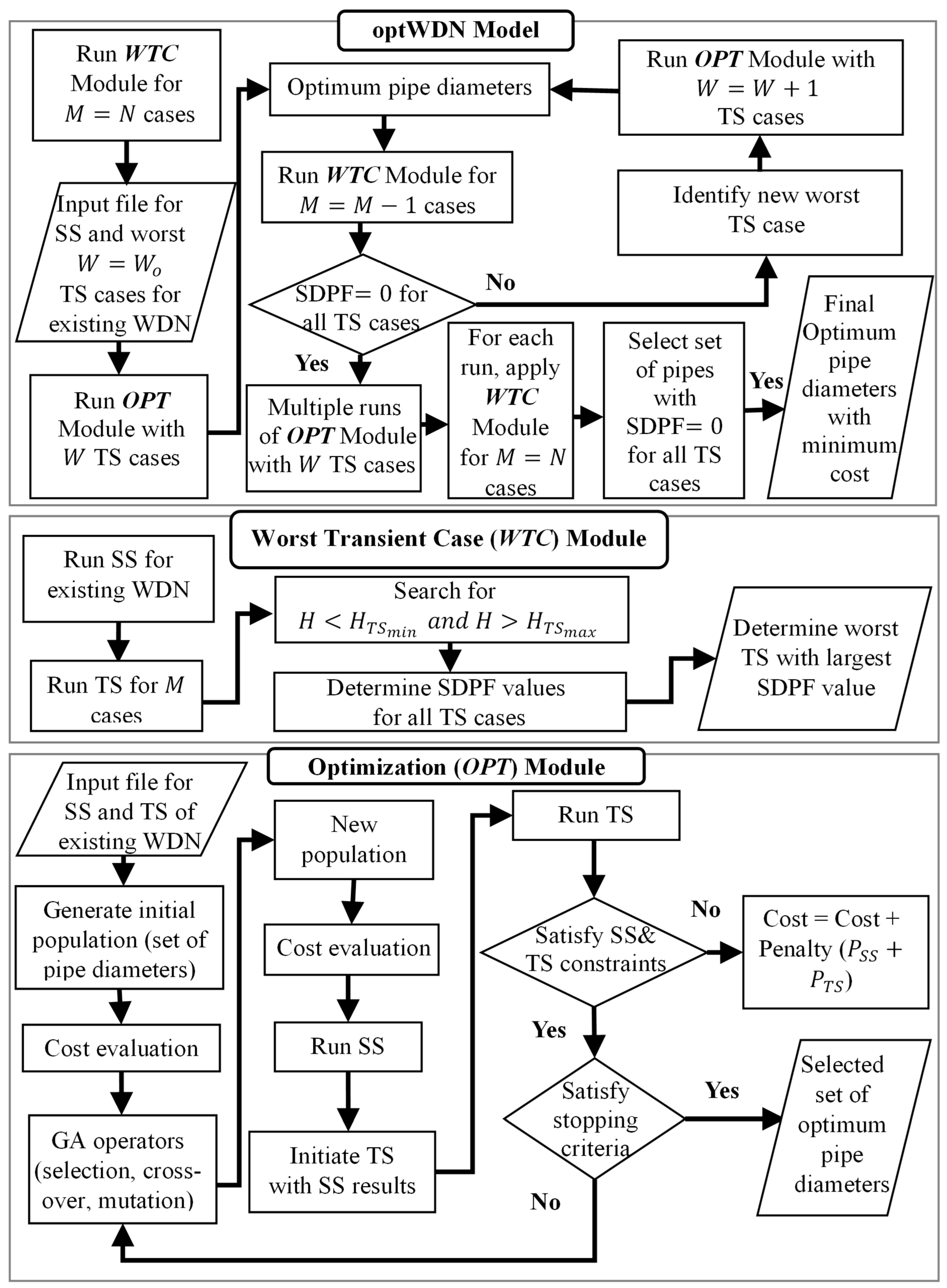
2. Model Formulation
2.1. Model Scope and Components
2.2. Steady-State Simulator
2.3. Transient Simulator
2.4. Optimization Module
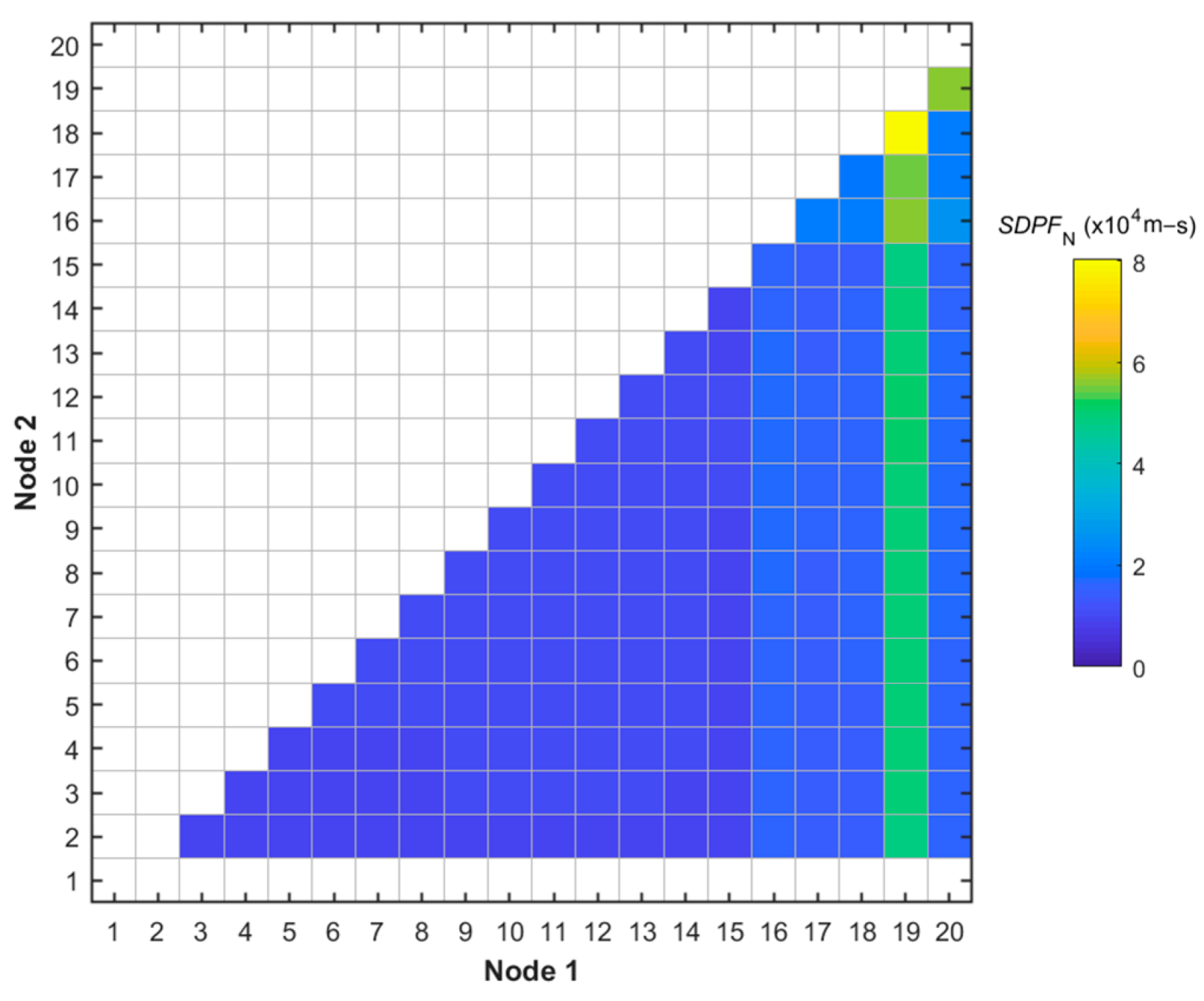
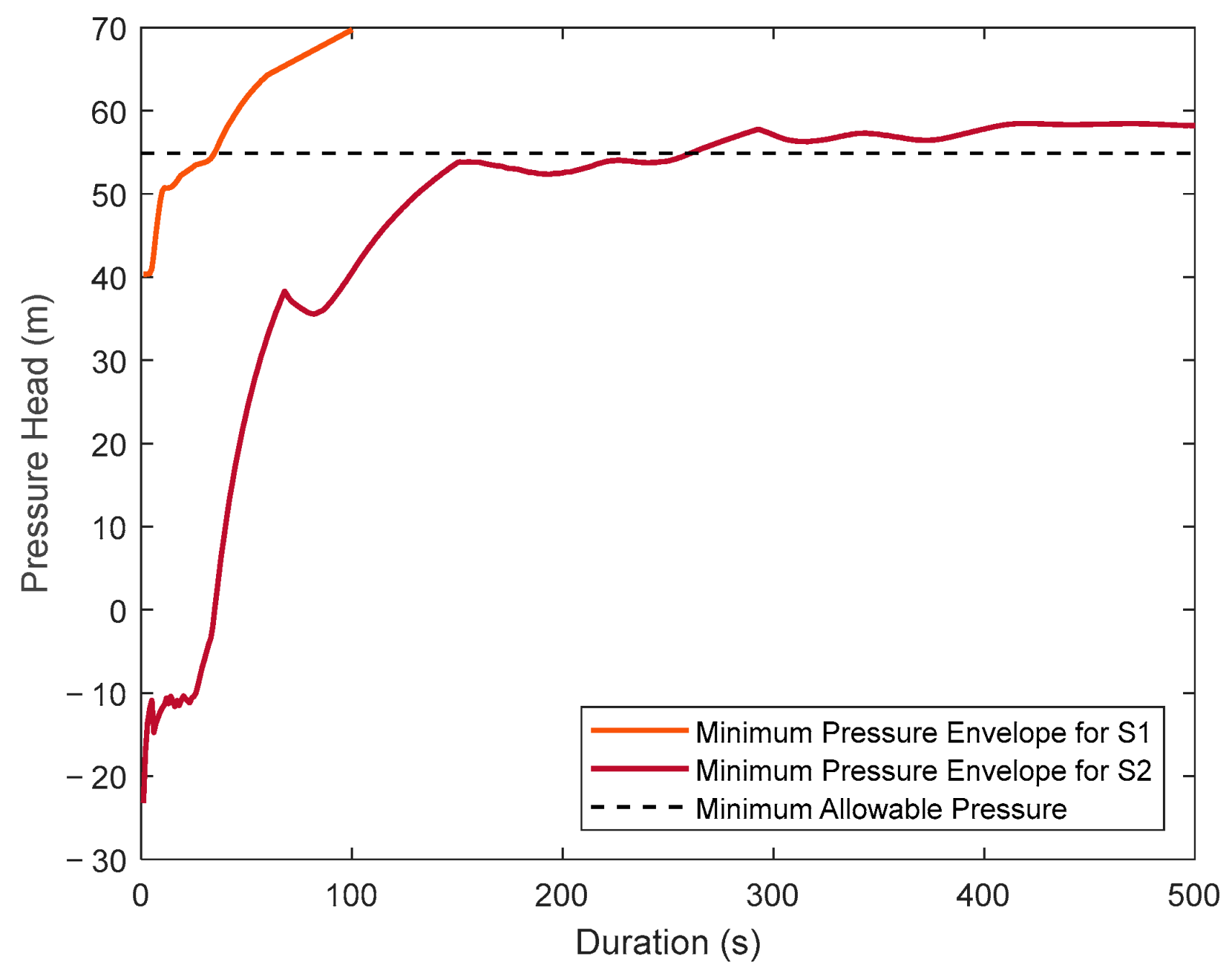
2.5. Worst Transient Case (WTC) Module
3. Model Validation and Application
3.1. Case Study Description
3.2. Model Parameters
3.3. Model Validation
3.4. Testing Model Performance
3.5. Examining the Effect of Gradual Demand Increase
4. Results and Discussion
4.1. Validation of Transient Simulator
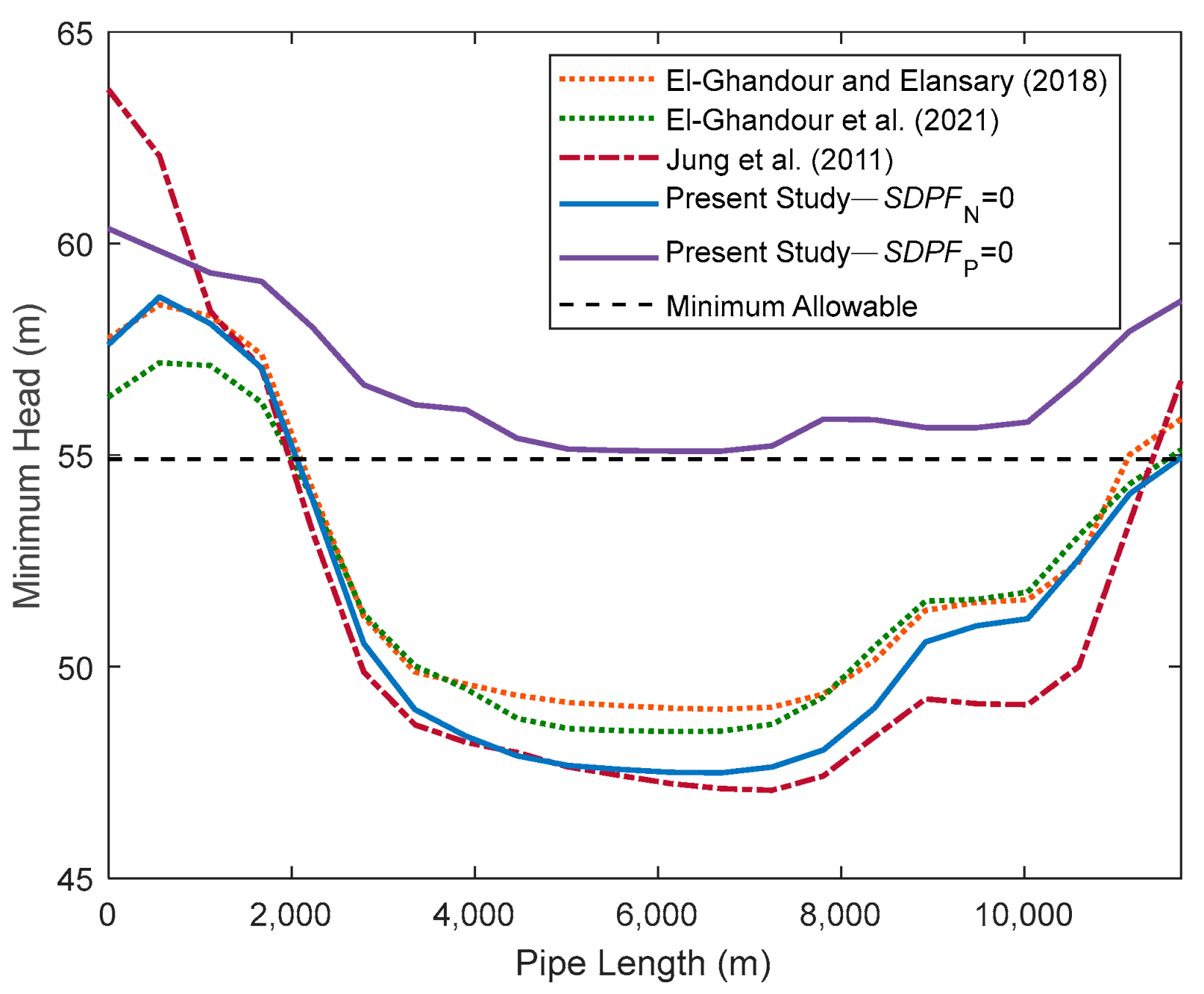
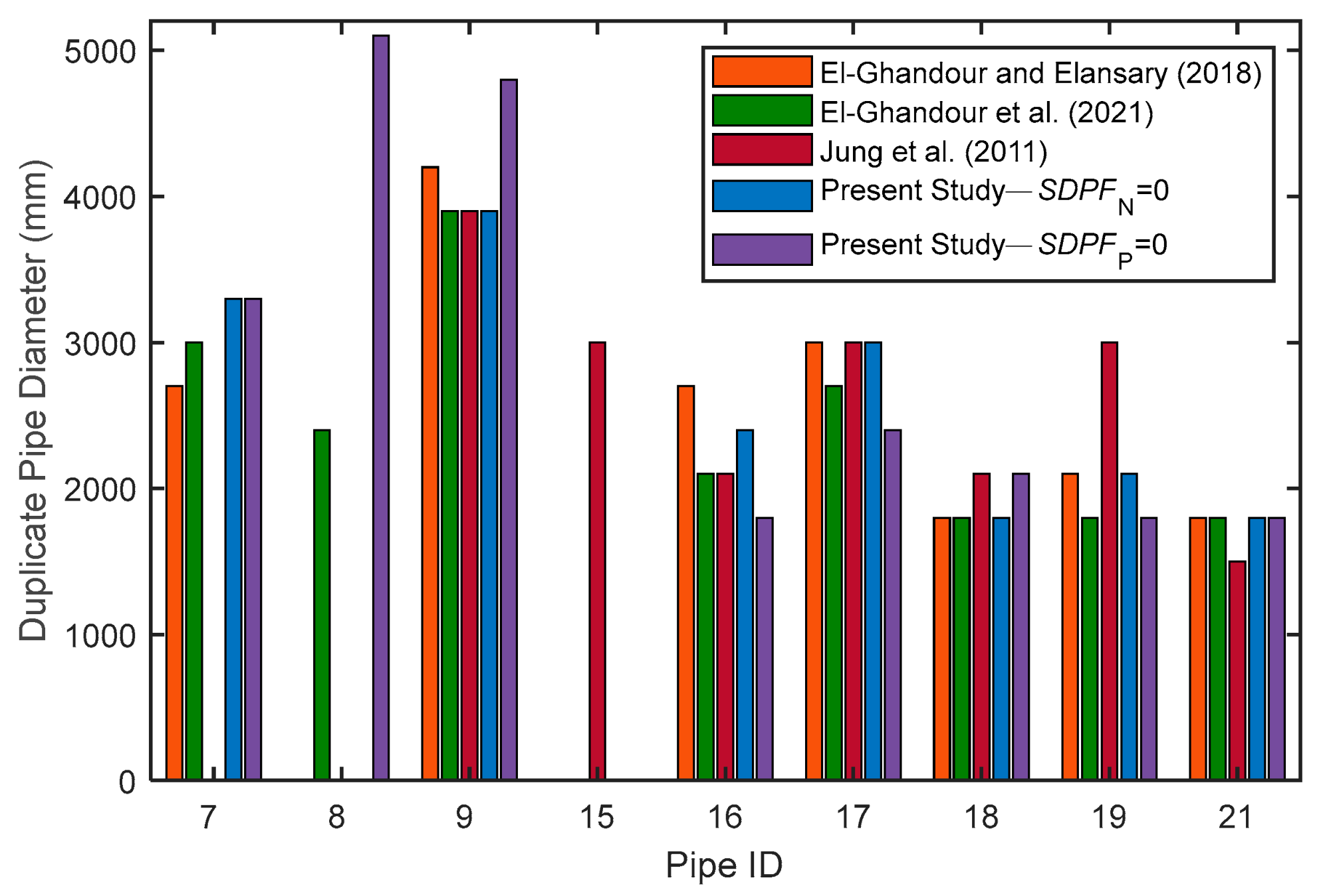
4.2. Validation of Optimization Module
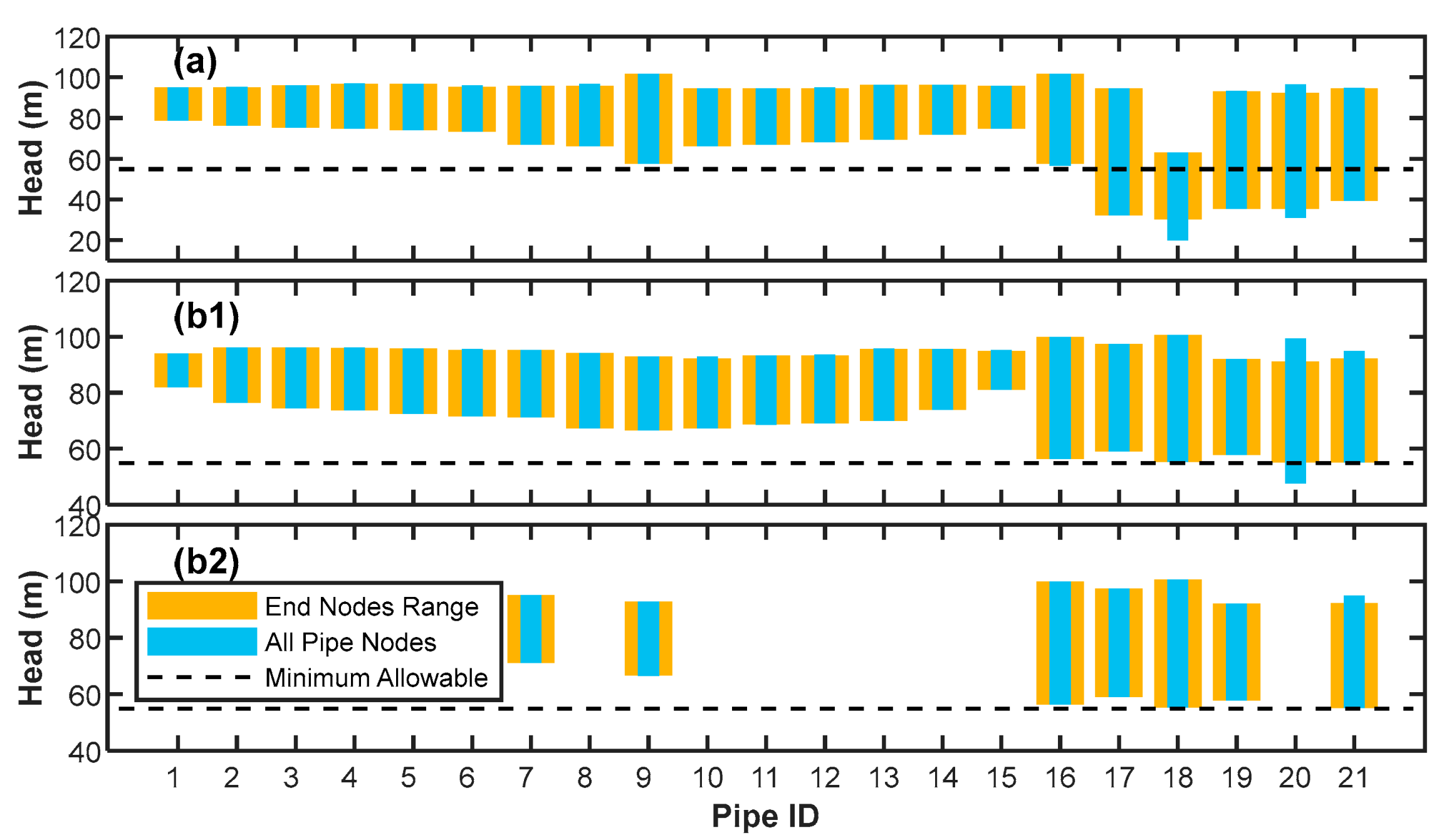
4.3. Validation of Worst Transient Case Module
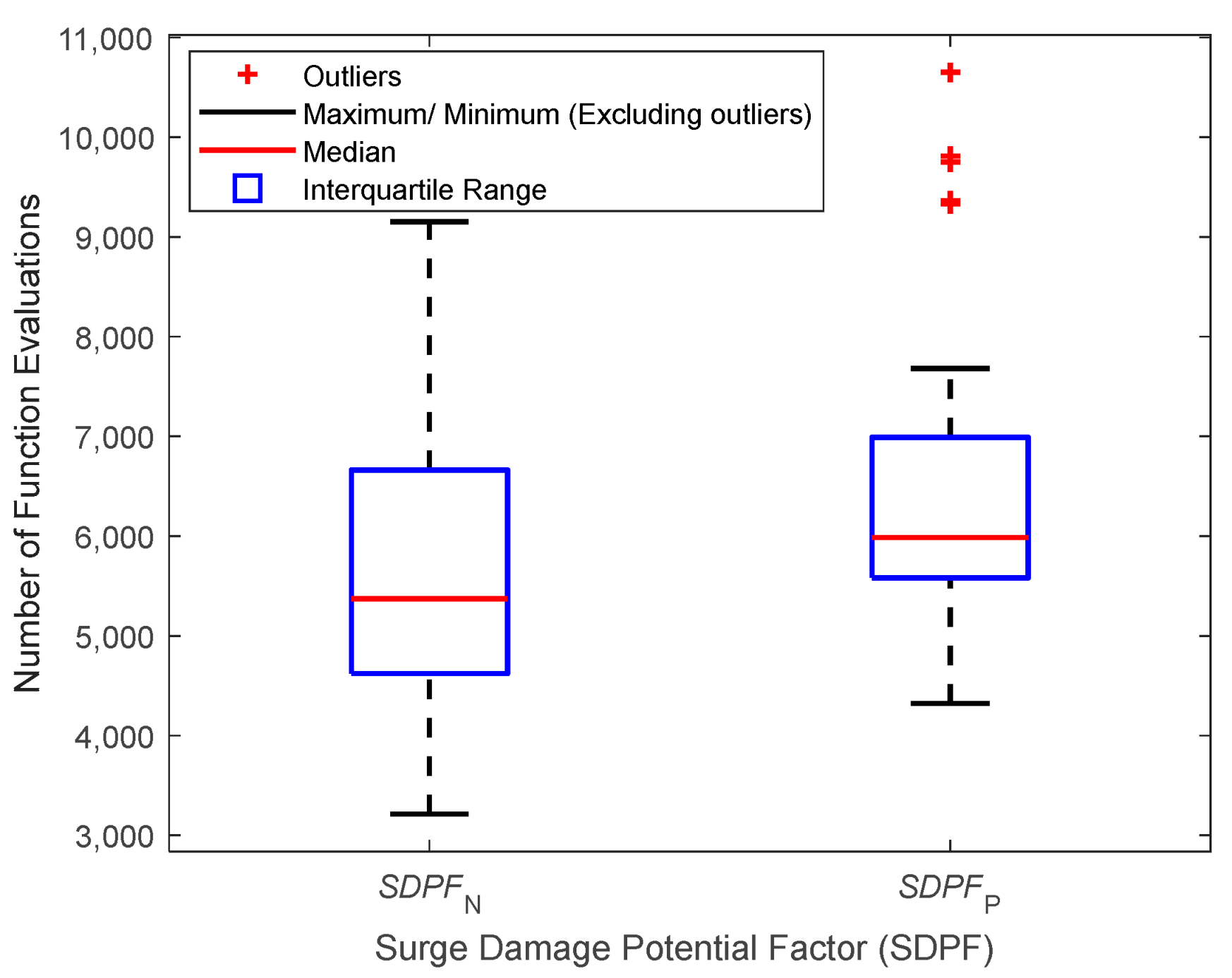
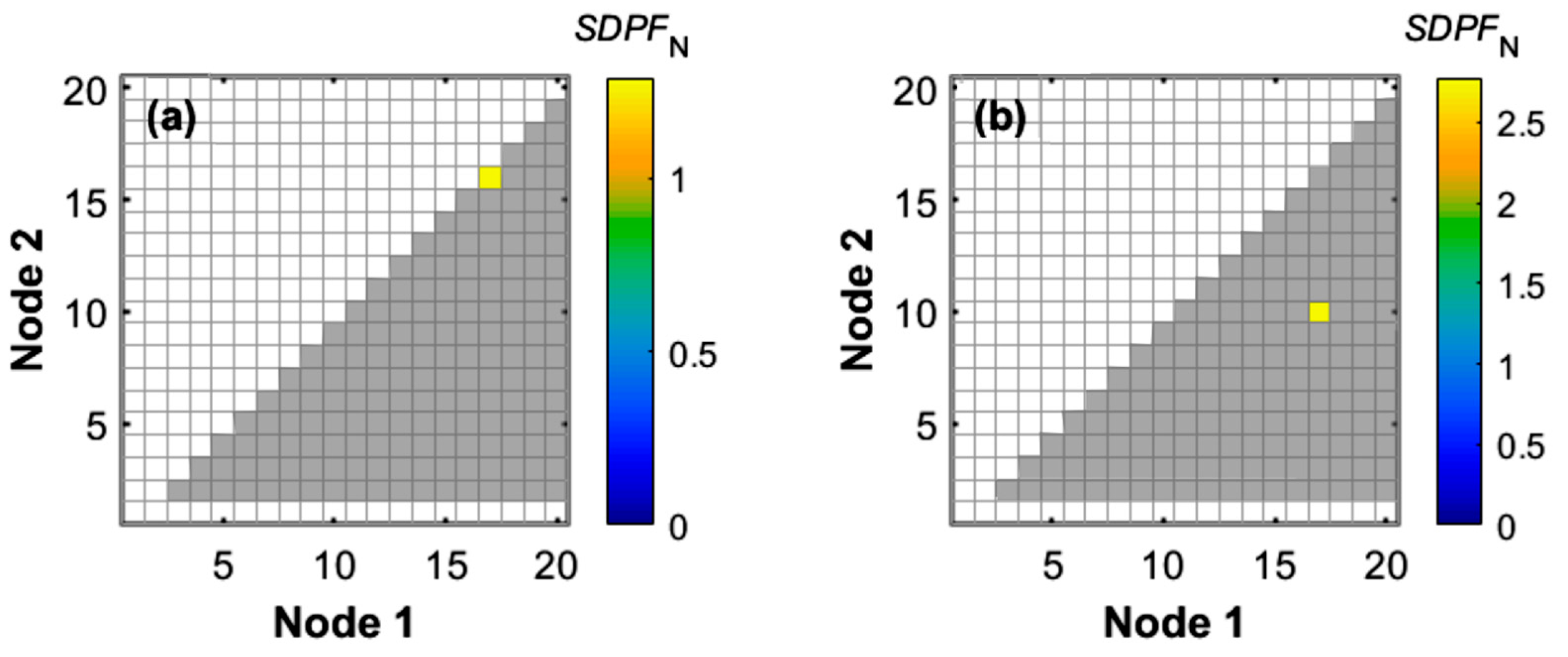
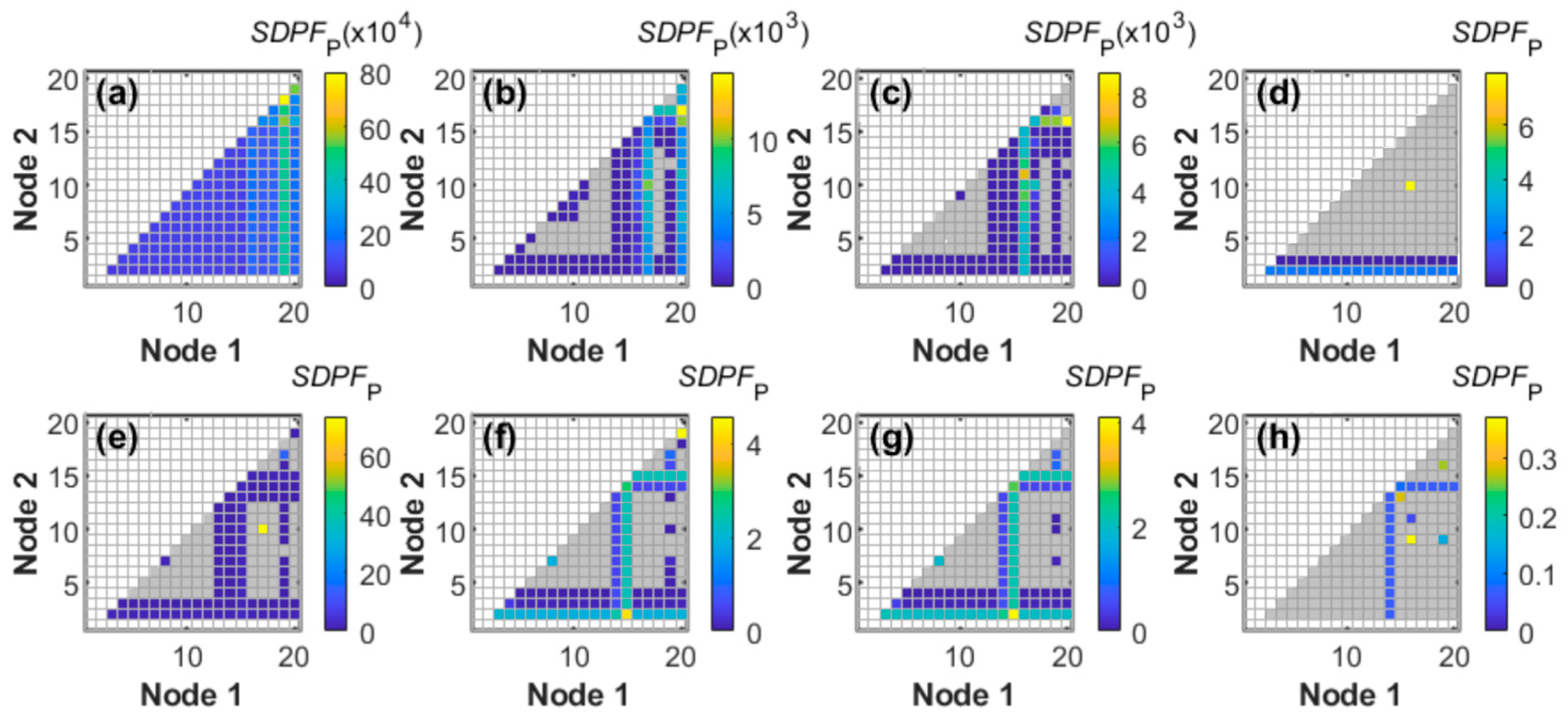
4.4. Effect of SDPF Calculation Approach
4.5. Optimum Protection for Worst Transient Cases
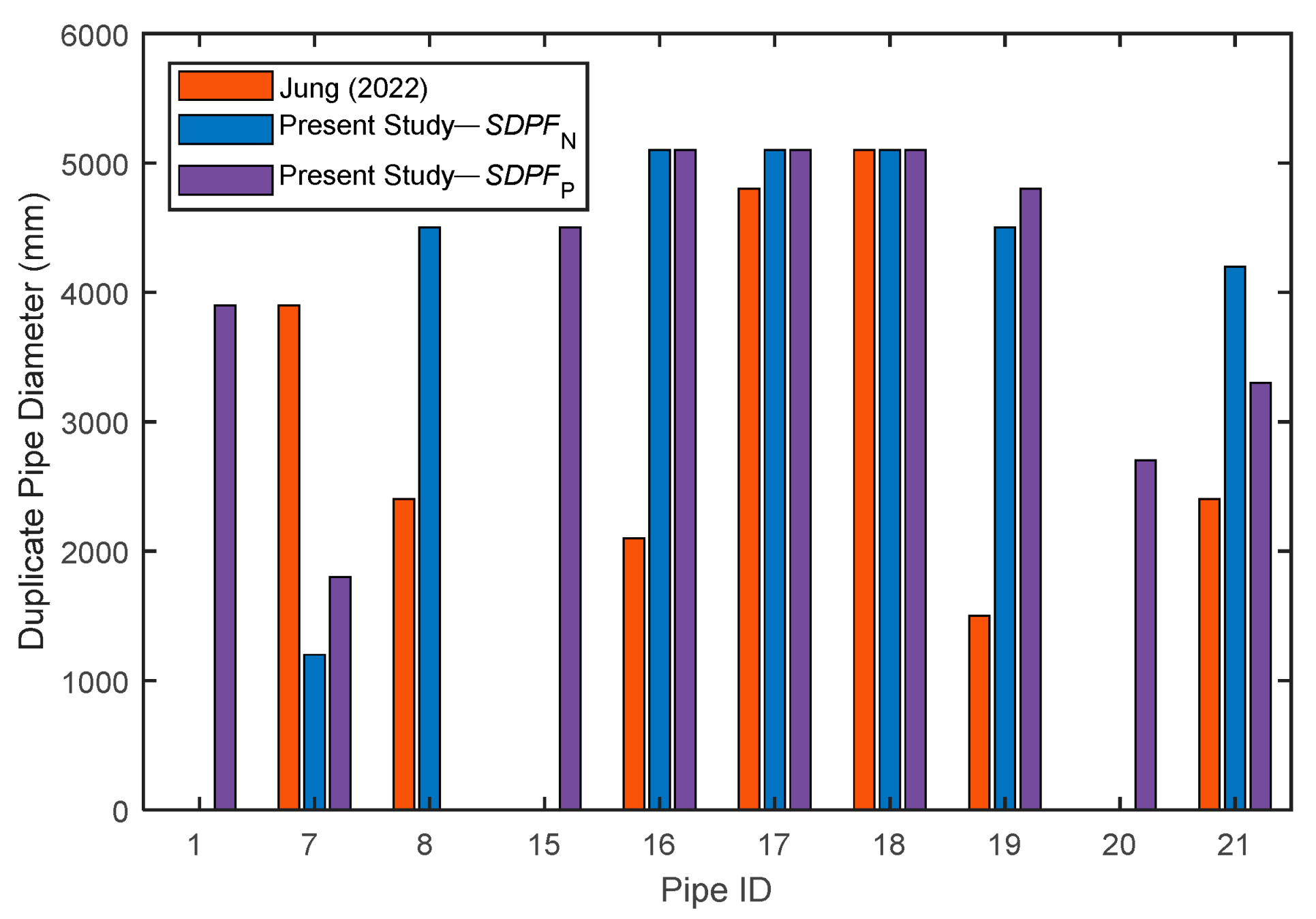
4.6. Cost Reduction for Surge Protection
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Pipe ID | Jung et al. [34] | ||
|---|---|---|---|
| 7 | - | 3300 | 3300 |
| 8 | - | - | 5100 |
| 9 | 3900 | 3900 | 4800 |
| 15 | 3000 | - | - |
| 16 | 2100 | 2400 | 1800 |
| 17 | 3000 | 3000 | 2400 |
| 18 | 2100 | 1800 | 2100 |
| 19 | 3000 | 2100 | 1800 |
| 21 | 1500 | 1800 | 1800 |
| Total optimized pipe Cost (million USD) | 49.1 | 46.37 | 52.83 |
| Pipe ID | Jung [18] | ||
|---|---|---|---|
| 1 | - | - | 3900 |
| 7 | 3900 | 1200 | 1800 |
| 8 | 2400 | 4500 | - |
| 15 | - | - | 4500 |
| 16 | 2100 | 5100 | 5100 |
| 17 | 4800 | 5100 | 5100 |
| 18 | 5100 | 5100 | 5100 |
| 19 | 1500 | 4500 | 4800 |
| 20 | - | - | 2700 |
| 21 | 2400 | 4200 | 3300 |
| Total optimized pipe Cost (million USD) | 70 | 102.11 | 122.24 |
References
- Zhou, X.; Gao, D.Y.; Simpson, A.R. Optimal design of water distribution networks by a discrete state transition algorithm. Eng. Optim. 2016, 48, 603–628. [Google Scholar] [CrossRef]
- El-Ghandour, H.A.; Elbeltagi, E. Comparison of five evolutionary algorithms for optimization of water distribution networks. J. Comput. Civ. Eng. 2018, 32, 04017066. [Google Scholar] [CrossRef]
- Maier, H.R.; Simpson, A.R.; Zecchin, A.C.; Foong, W.K.; Phang, K.Y.; Seah, H.Y.; Tan, C.L. Ant colony optimization for design of water distribution systems. J. Water Resour. Plan. Manag. 2003, 129, 200–209. [Google Scholar] [CrossRef]
- Zecchin, A.C.; Simpson, A.R.; Maier, H.R.; Nixon, J.B. Parametric study for an ant algorithm applied to water distribution system optimization. IEEE Trans. Evol. Comput. 2005, 9, 175–191. [Google Scholar] [CrossRef]
- Zecchin, A.C.; Maier, H.R.; Simpson, A.R.; Leonard, M.; Nixon, J.B. Ant colony optimization applied to water distribution system design: Comparative study of five algorithms. J. Water Resour. Plan. Manag. 2007, 133, 87–92. [Google Scholar] [CrossRef]
- Mehdi, D.; Massoud, T. Optimal renovation planning of water distribution networks considering hydraulic and quality reliability indices. Urban Water J. 2019, 16, 249–258. [Google Scholar]
- Babu, K.J.; Vijayalakshmi, D.P. Self-adaptive PSO-GA hybrid model for combinatrial water distribution network design. J. Pipeline Syst. Eng. Pract. 2013, 4, 57–67. [Google Scholar] [CrossRef]
- Ezzeldin, R.M.; Djebedjian, B.; Saafan, T. Integer discrete particle swarm optimization of water distribution networks. J. Pipeline Syst. Eng. Pract. 2014, 5, 04013013. [Google Scholar] [CrossRef]
- Surco, D.F.; Vecchi, T.P.; Ravagnani, M.A. Optimization of water distribution networks using a modified particle swarm optimization algorithm. Water Sci. Technol. Water Supply 2018, 18, 660–678. [Google Scholar] [CrossRef]
- Ezzeldin, R.M.; Djebedjian, B. Optimal design of water distribution networks using whale optimization algorithm. Urban Water J. 2020, 17, 14–22. [Google Scholar] [CrossRef]
- Vasan, A.; Simonovic, S.P. Optimization of water distribution network design using differential evolution. J. Water Resour. Plan. Manag. 2010, 136, 279–287. [Google Scholar] [CrossRef]
- Mansouri, R.; Torabi, H.; Hoseini, M.; Morshedzadeh, H. Optimization of the water distribution networks with differential evolution (DE) and mixed integer linear programming (MILP). J. Water Resour. Prot. 2015, 7, 715. [Google Scholar] [CrossRef][Green Version]
- Yazdi, J.; Choi, Y.H.; Kim, J.H. Non-dominated sorting harmony search differential evolution (NS-HS-DE): A hybrid algorithm for multi-objective design of water distribution networks. Water 2017, 9, 587. [Google Scholar] [CrossRef]
- Jung, B.S.; Karney, B.W. Revisiting Transient Optimization of Water Supply Systems. In Proceedings of the 38th IAHR World Congress Panama, Panama City, Panama, 1–6 September 2019. [Google Scholar]
- El-Ghandour, H.A.; Elansary, A.S. Optimal selection of pressure relief valve parameters for surge pressure control in water distribution systems. Urban Water J. 2019, 16, 269–276. [Google Scholar] [CrossRef]
- Kim, H.; Kim, S. Optimization of pressure relief valve for pipeline system under transient induced cavitation condition. Urban Water J. 2019, 16, 718–726. [Google Scholar] [CrossRef]
- Huang, Y.; Zheng, F.; Duan, H.F.; Zhang, Q. Multi-objective optimal design of water distribution networks accounting for transient impacts. Water Resour. Manag. 2020, 34, 1517–1534. [Google Scholar] [CrossRef]
- Jung, B.S. Water Distribution System Optimization Accounting for Worst-Case Transient Loadings. J. Environ. Inform. Lett. 2022, 7, 20–29. [Google Scholar] [CrossRef]
- Sangroula, U.; Han, K.H.; Koo, K.M.; Gnawali, K.; Yum, K.T. Optimization of water distribution networks using genetic algorithm based SOP–WDN program. Water 2022, 14, 851. [Google Scholar] [CrossRef]
- Ghobadian, R.; Mohammadi, K. Optimal design and cost analysis of water distribution networks based on pressure-dependent leakage using NSGA-II. Appl. Water Sci. 2023, 13, 92. [Google Scholar] [CrossRef]
- Naidu, M.N.; Vasan, A.; Varma, M.R.; Patil, M.B. Multiobjective design of water distribution networks using modified NSGA-II algorithm. Water Supply 2023, 23, 1220–1233. [Google Scholar] [CrossRef]
- Djebedjian, B.; Mohamed, M.S.; Mondy, A.G.; Rayan, M.A. Cost optimization of water distribution systems subjected to water hammer. In Proceedings of the Thirteenth International Water Technology Conference, Hurghada, Egypt, 12–15 March 2009; pp. 491–513. [Google Scholar]
- El-Ghandour, H.A.; Elansary, A.S. Optimal transient network rehabilitation using multi-objective ant colony optimization algorithm. Urban Water J. 2018, 15, 645–653. [Google Scholar] [CrossRef]
- Jung, B.S.; Karney, B.W. Pipeline Optimization Accounting For Transient Conditions: Exploring The Connections Between System Configuration, Operation, And Surge Protection. In Proceedings of the World Environmental and Water Resources Congress 2013: Showcasing the Future, Cincinnati, OH, USA, 19–23 May 2013; pp. 903–912. [Google Scholar]
- El-Ghandour, H.A.; Elabd, S.M.; Elbeltagi, E. Assessment of optimal water distribution systems design under steady-state and transient conditions due to pipe roughness uncertainty. Ain Shams Eng. J. 2021, 12, 465–473. [Google Scholar] [CrossRef]
- Jung, B.S.; Karney, B.W. Hydraulic optimization of transient protection devices using GA and PSO approaches. Water Resour. Plan. Manag. 2006, 132, 44–52. [Google Scholar] [CrossRef]
- Jung, B.S.; Karney, B.W. Systematic surge protection for worst-case transient loadings in water distribution systems. J. Hydraul. Eng. 2009, 135, 218–223. [Google Scholar] [CrossRef]
- Skulovich, O.; Bent, R.; Judi, D.; Perelman, L.S.; Ostfeld, A. Piece-wise mixed integer programming for optimal sizing of surge control devices in water distribution systems. Water Resour. Res. 2015, 51, 4391–4408. [Google Scholar] [CrossRef]
- Skulovich, O.; Perelman, L.; Ostfeld, A. Modeling and optimizing hydraulic transients in water distribution systems. Procedia Eng. 2014, 70, 1558–1565. [Google Scholar] [CrossRef]
- Skulovich, O.; Perelman, L.; Ostfeld, A. Optimal closure of system actuators for transient control: An analytical approach. J. Hydroinform. 2016, 18, 393–408. [Google Scholar] [CrossRef]
- Bohorquez, J.; Saldarriaga, J. Valve operation optimization for minimizing transient flow effects in water distribution systems (WDS): Application to main pipes in Bogota, Colombia. In Proceedings of the World Environmental and Water Resources Congress, Austin, TX, USA, 17–21 May 2015; pp. 890–901. [Google Scholar]
- Carvajal, J.D.; Bohorquez, J. Estimation of Marginal Time in Water Distribution Systems for Valve Closure Considering Transient Flow Effects: (149). In Proceedings of the WDSA/CCWI Joint Conference Proceedings, Kingston, ON, Canada, 23–25 July 2018; Volume 1. [Google Scholar]
- Jung, B.S.; Karney, B.W. Fluid transients and pipeline optimization using GA and PSO: The diameter connection. Urban Water J. 2004, 1, 167–176. [Google Scholar] [CrossRef]
- Jung, B.S.; Boulos, P.F.; Altman, T. Optimal transient network design: A multi-objective approach. J. Am. Water Work. Ass. 2011, 103, 118–127. [Google Scholar] [CrossRef]
- Walski, T.M. Not So Fast!: Close Hydrants Slowly. Opflow 2009, 35, 14–16. [Google Scholar] [CrossRef]
- Lingireddy, S.; Ormsbee, L.E.; Kamojjala, S.; Hall, A.M. How Slow Is Slow? Managing Fire Hydrant Operation for Protecting Water Infrastructure. AWWA Water Sci. 2022, 4, e1290. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET 2: Users Manual; United States Environmental Protection Agency: Washington, DC, USA, 2000. [Google Scholar]
- Larock, B.E.; Jeppson, R.W.; Watters, G.Z. Hydraulics of Pipeline Systems; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Wylie, E.B.; Streeter, V.L. Fluid Transients in Systems; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Chaudhry, M.H. Applied Hydraulic Transients New York; Springer: Berlin/Heidelberg, Germany, 2014; Volume 415, pp. 31–42. [Google Scholar]
- Xing, L.; Sela, L. Transient simulations in water distribution networks: TSNet python package. Adv. Eng. Softw. 2020, 149, 102884. [Google Scholar] [CrossRef]
- Dandy, G.C.; Simpson, A.R.; Murphy, L.J. An improved genetic algorithm for pipe network optimization. Water Resour. Res. 1996, 32, 449–458. [Google Scholar] [CrossRef]
- Eusuff, M.M.; Lansey, K.E. Optimization of water distribution network design using the shuffled frog leaping algorithm. J. Water Resour. Plan. Manag. 2003, 129, 210–225. [Google Scholar] [CrossRef]
- Yazdi, J.; Hokmabadi, A.; JaliliGhazizadeh, M.R. Optimal Size and Placement of Water Hammer Protective Devices in Water Conveyance Pipelines. Water Resour. Manag. 2019, 33, 569–590. [Google Scholar] [CrossRef]
- Lee, J.S.; Zeng, W.; Lambert, M.; Hilditch, T.; Gong, J. Fatigue analysis of metallic-plastic-metallic pipeline systems: A numerical study. Results Eng. 2023, 17, 100986. [Google Scholar] [CrossRef]
- Jara-Arriagada, C.; Stoianov, I. Pressure-induced fatigue failures in cast iron water supply pipes. Eng. Fail. Anal. 2024, 155, 107731. [Google Scholar] [CrossRef]
- Konstantinou, C.; Jara-Arriagada, C.; Stoianov, I. Investigating the impact of cumulative pressure-induced stress on machine learning models for pipe breaks. Water Resour. Manag. 2024, 38, 603–619. [Google Scholar] [CrossRef]
- Rao, S.S. Reliability-Based Design; McGraw-Hill: New York, NY, USA, 1992. [Google Scholar]
- McCuen, R.H.; Knight, Z.; Cutter, A.G. Evaluation of the Nash–Sutcliffe efficiency index. J. Hydrol. Eng. 2006, 11, 597–602. [Google Scholar] [CrossRef]

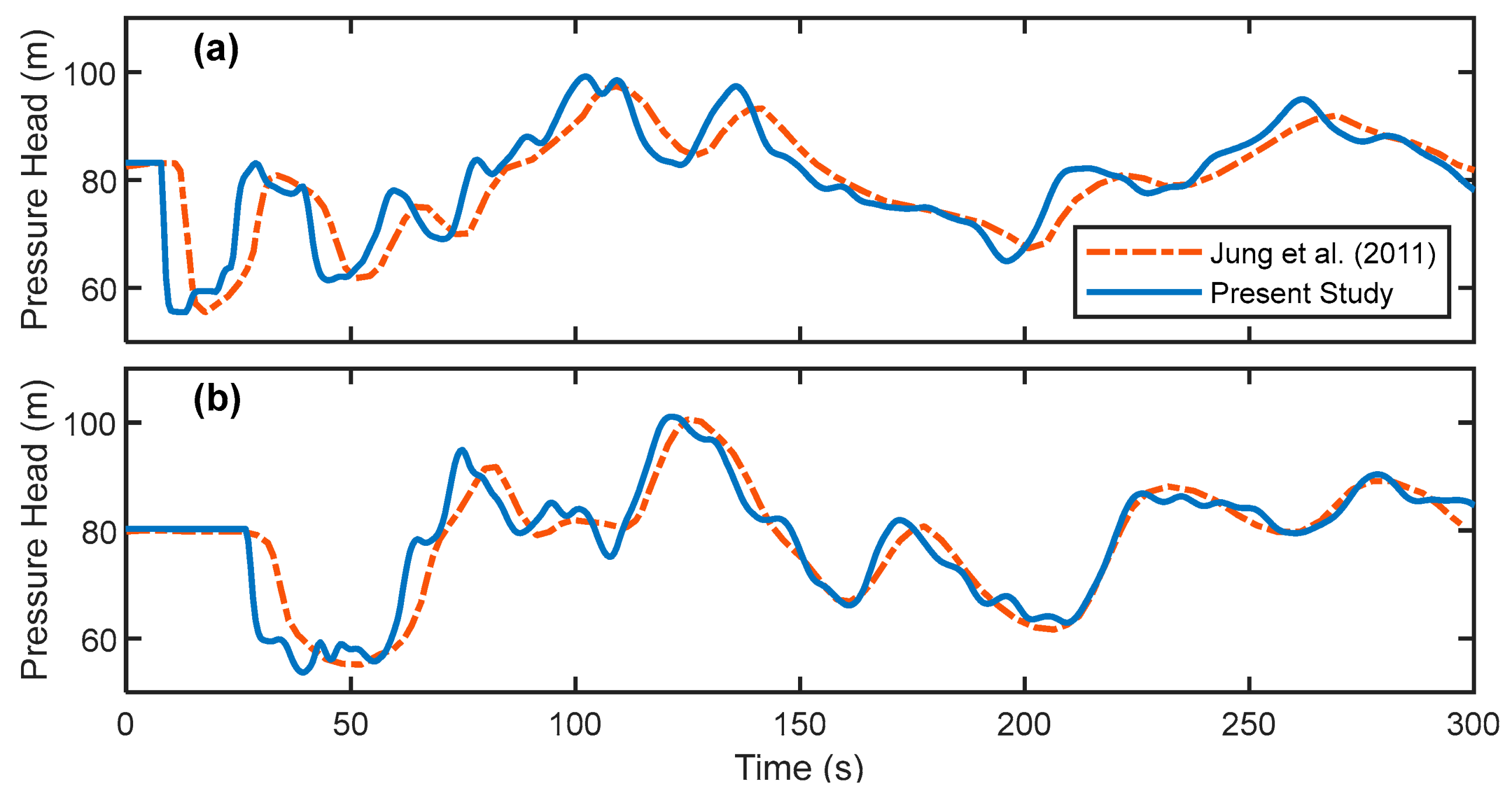
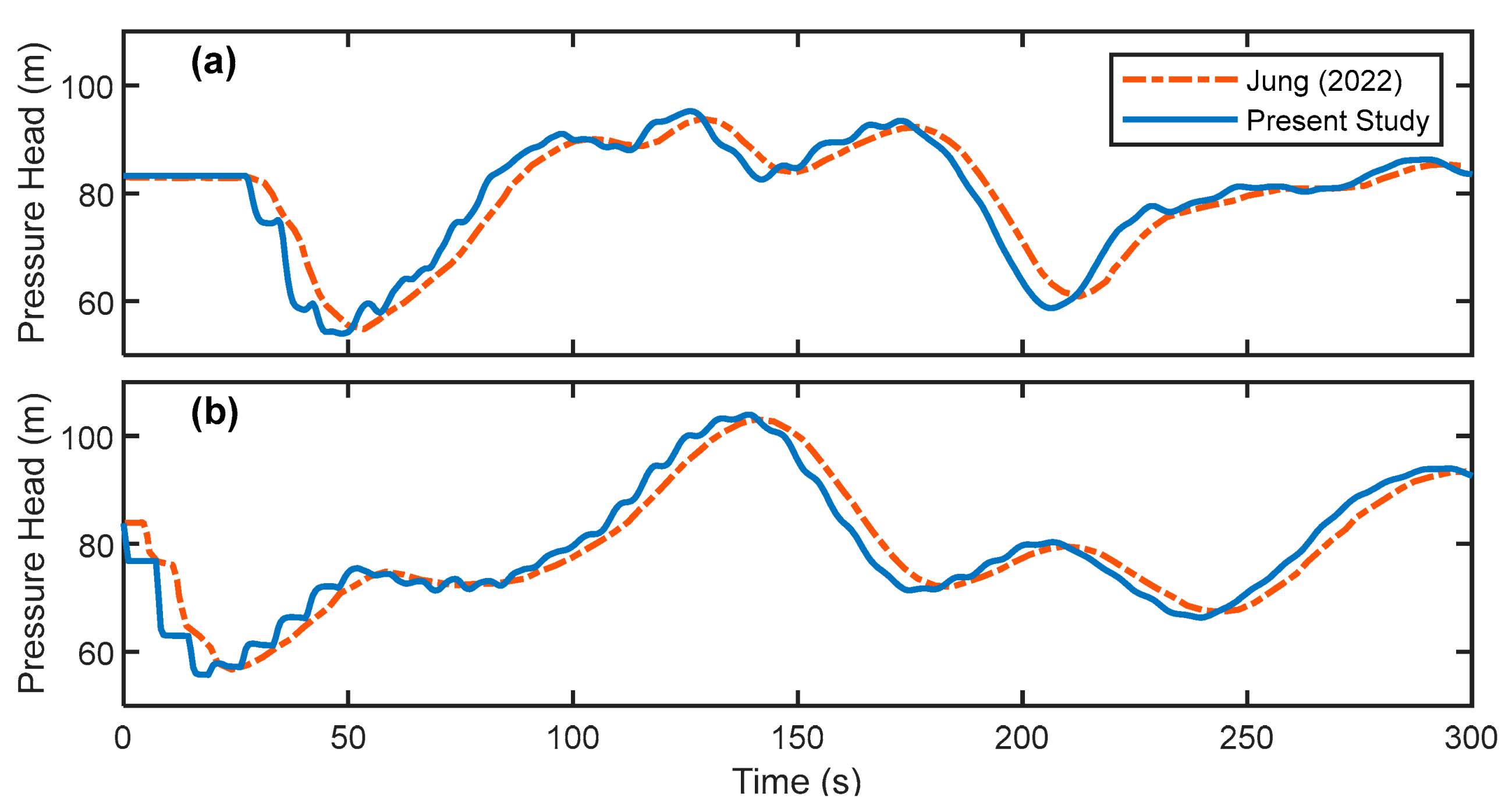
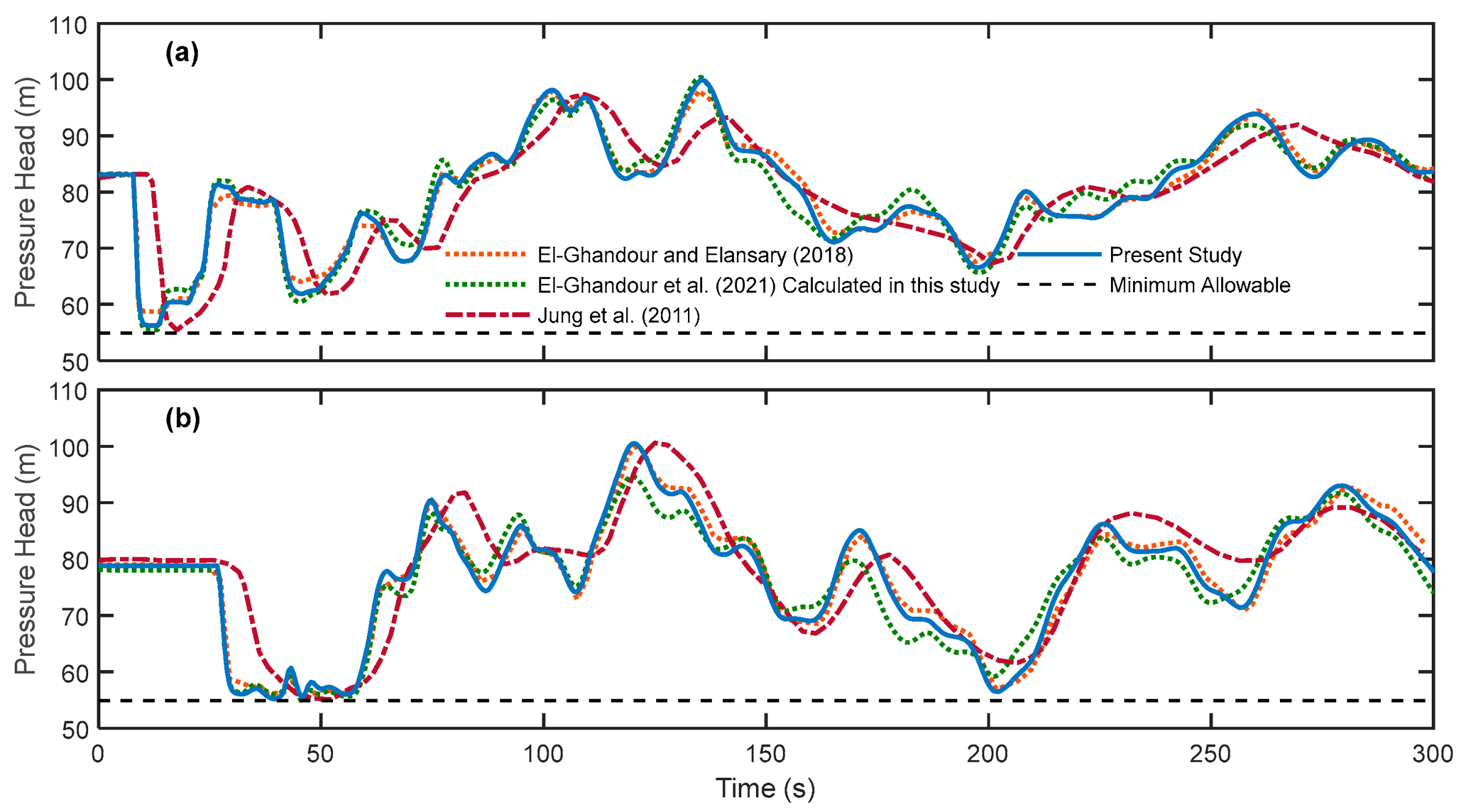



| Pipe Number | Dany et al. [38] | Ghandour and Elbeltagi [2] | Maier et al. [3] | Eusuff and Lansay [43] |
|---|---|---|---|---|
| 7 | - | - | 3600 | 3300 |
| 15 | 3000 | 3000 | - | - |
| 16 | 2100 | 2100 | 2400 | 2400 |
| 17 | 2400 | 2400 | 2400 | 2400 |
| 18 | 2100 | 2100 | 2100 | 2100 |
| 19 | 1800 | 1800 | 3000 | 1800 |
| 21 | 1800 | 1800 | 1500 | 1800 |
| Total Cost (million USD) | 38.79 | 38.79 | 38.64 | 38.13 |
| Population Size | 20 | 30 | 50 | 100 |
|---|---|---|---|---|
| (%) | 3.34 | 3.34 | 3.34 | 3.34 |
| (%) | 13.3 | 15.4 | 5.5 | 2.7 |
| (%) | 95.70 | 95.52 | 95.30 | 95.00 |
| Run Cycle | Number of Worst Transient Cases | Module | over All 171 Cases | Total Duplicate Pipe Cost (Million USD) | |
|---|---|---|---|---|---|
| 0 | 0 | - | 171 | 80.5 103 | - |
| 1 | 1 | (18, 19) | 63 | 1.32 103 | 73.68 |
| 2 | 2 | (18, 19); (17, 20) | 28 | 0.19 103 | 97.30 |
| 3 | 3 | (18, 19); (17, 20); (16, 20) | 3 | 2.81 | 103.65 |
| 4 | 4 | (18, 19); (17, 20); (16, 20); (19, 20) | 15 | 90.0 | 95.29 |
| 5 | 5 | (18, 19); (17, 20); (16, 20); (19, 20); (10, 17) | 3 | 13.1 | 142.46 |
| 6 | 6 | (18, 19); (17, 20); (16, 20); (19, 20); (10, 17); (16, 19) | 2 | 1.47 | 104.47 |
| 7 | 7 | (18, 19); (17, 20); (16, 20); (19, 20); (10, 17); (16, 19); (16, 17) | 1 | 0.47 | 108.75 |
| 8 | 8 | (18, 19); (17, 20); (16, 20); (19, 20); (10, 17); (16, 19); (16, 17); (7, 8) | 0 | 0 | 103.36 |
| 30 GA independent trial runs | (18, 19); (17, 20); (16, 20); (19, 20); (10, 17); (16, 19); (16, 17); (7, 8) | 0 | 0 | 102.11 | |
| Run Cycle | Number of Worst Transient Cases | Module | over All 171 Cases | Total Duplicate Pipe Cost (Million USD) | |
|---|---|---|---|---|---|
| 0 | 0 | - | 171 | 80.5 103 | - |
| 1 | 9 | (18, 19) & (19, 20) & (16, 19) & (17, 19) & (12, 19) & (11, 19) & (9, 19) & (10, 19) & (13, 19) | 1 | 1.29 | 113.04 |
| 2 | 10 | (18, 19) & (19, 20) & (16, 19) & (17, 19) & (12, 19) & (11, 19) & (9, 19) & (10, 19) & (13, 19) & (16, 17) | 1 | 2.77 | 107.58 |
| 3 | 11 | (18, 19) & (19, 20) & (16, 19) & (17, 19) & (12, 19) & (11, 19) & (9, 19) & (10, 19) & (13, 19) & (16, 17) & (10, 17) | 0 | 0 | 114.68 |
| 30 GA independent trial runs | (18, 19) & (19, 20) & (16, 19) & (17, 19) & (12, 19) & (11, 19) & (9, 19) & (10, 19) & (13, 19) & (16, 17) & (10, 17) | 0 | 0 | 102.26 | |
| Run Cycle | Number of Worst Transient Cases | Module | for All 171 Cases | Total Duplicate Pipe Cost (Million USD) | |
|---|---|---|---|---|---|
| 0 | 0 | - | 171 | 802,284.7 | - |
| 1 | 1 | (18, 19) | 124 | 14,507 | 87.67 |
| 2 | 2 | (18, 19); (17, 20) | 115 | 8943.62 | 97.90 |
| 3 | 3 | (18, 19); (17, 20); (16, 20) | 36 | 7.95 | 134.44 |
| 4 | 4 | (18, 19); (17, 20); (16, 20); (10, 16) | 93 | 73.24 | 112.17 |
| 5 | 5 | (18, 19); (17, 20); (16, 20); (10, 16); (10, 17) | 90 | 4.58 | 115.31 |
| 6 | 6 | (18, 19); (17, 20); (16, 20); (10, 16); (10, 17); (19, 20) | 86 | 4.11 | 118.00 |
| 7 | 7 | (18, 19); (17, 20); (16, 20); (10, 16); (10, 17); (19, 20) (2, 15) | 23 | 0.37 | 130.59 |
| 8 | 8 | (18, 19); (17, 20); (16, 20); (10, 16); (10, 17); (19, 20) (2, 15); (9, 16) | 0 | 0 | 138.54 |
| 30 GA independent trial runs | (18, 19); (17, 20); (16, 20); (10, 16); (10, 17); (19, 20) (2, 15); (9, 16) | 0 | 0 | 122.24 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, H.M.; Imam, Y.E.; El-Ghandour, H.A.; Elansary, A.S. Identifying Worst Transient Cases and Optimizing Surge Protection for Existing Water Networks. Water 2025, 17, 1816. https://doi.org/10.3390/w17121816
Ahmed HM, Imam YE, El-Ghandour HA, Elansary AS. Identifying Worst Transient Cases and Optimizing Surge Protection for Existing Water Networks. Water. 2025; 17(12):1816. https://doi.org/10.3390/w17121816
Chicago/Turabian StyleAhmed, Hossam Mohamed, Yehya Emad Imam, Hamdy Ahmed El-Ghandour, and Amgad Saad Elansary. 2025. "Identifying Worst Transient Cases and Optimizing Surge Protection for Existing Water Networks" Water 17, no. 12: 1816. https://doi.org/10.3390/w17121816
APA StyleAhmed, H. M., Imam, Y. E., El-Ghandour, H. A., & Elansary, A. S. (2025). Identifying Worst Transient Cases and Optimizing Surge Protection for Existing Water Networks. Water, 17(12), 1816. https://doi.org/10.3390/w17121816





