A Novel Mountain Shadow Removal Method Based on an Inverted Exponential Function Model for Flood Disaster Monitoring
Abstract
1. Introduction
- Adaptive Thresholding: The model applies dynamic threshold segmentation for slope values, enhancing its adaptability across different terrain conditions.
- Efficiency and Simplicity: The model operates efficiently on the GEE platform, enabling rapid execution to support timely flood disaster response.
- Water Body Integrity: The method effectively removes mountain shadows while preserving mountainous water bodies, making it suitable for flood monitoring in mountainous regions.
2. Study Area and Dataset
2.1. Study Area
2.2. Dataset
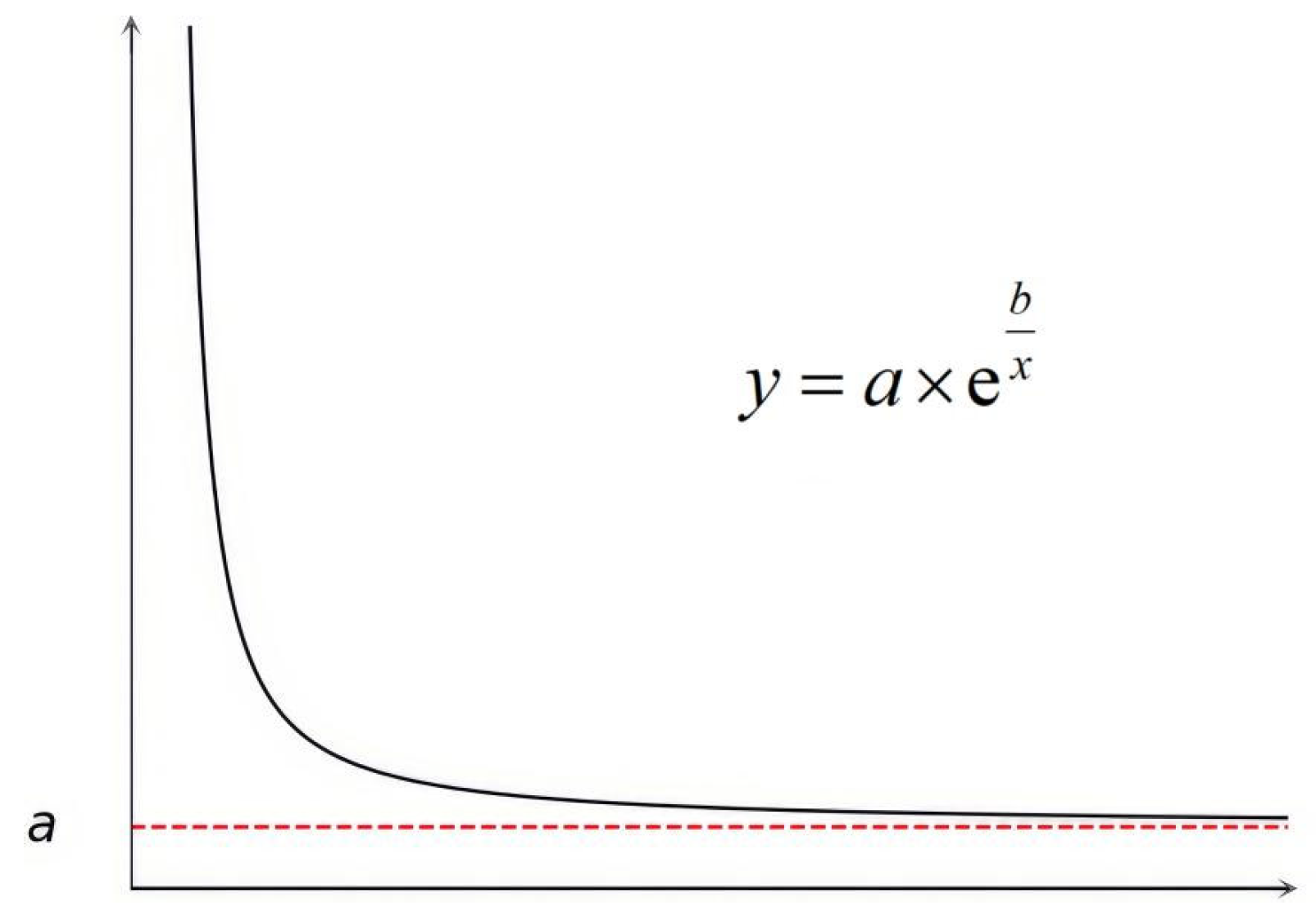
3. Methodology
3.1. Pre-Processing
3.1.1. Sample Point Generation
3.1.2. Removal of Outliers in Sample Points
3.1.3. Coordinate System Transformation and Calculation of Boundary Midpoints
3.2. Processing
3.3. Post-Processing
3.4. Mountain Shadow Removal and Accuracy Evaluation
4. Results and Analysis
4.1. Results and Analysis of the IESRM
4.1.1. Results of the IESRM
4.1.2. Accuracy Analysis of the IESRM Training Set
4.2. Analysis of Mountain Shadow Removal Results in the Study Area
4.2.1. Accuracy Analysis of the IESRM Validation Set
4.2.2. Accuracy Analysis for Different Terrain
4.3. Quantitative Analysis
4.4. Comparison of Different Methods
5. Conclusions
- Accuracy evaluations were conducted in three regions with geographically diverse regions (Mentougou District, Fangshan District, and Zhuozhou City). Despite the complex terrain of Fangshan District, which posed significant challenges for shadow removal, the ultimate processing outcomes results were still satisfactory, achieving an overall accuracy and Kappa coefficient of 94.51% and 0.86, respectively. These results underscore the model’s applicability and robustness under complex terrain conditions.
- Compared to the mechanism formation method and the HAND method, the inverted exponential function model demonstrated the superior performance, achieving an overall accuracy and Kappa coefficient of 96.46% and 0.89, respectively. The application of this model to flood disaster detection significantly reduces the interference of mountain shadows.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bhatt, C.M.; Rao, G.S.; Farooq, M.; Manjusree, P.; Shukla, A.; Sharma, S.V.S.P.; Kulkarni, S.S.; Begum, A.; Bhanumurthy, V.; Diwakar, P.G.; et al. Satellite-based assessment of the catastrophic Jhelum floods of September 2014, Jammu & Kashmir, India. Geomat. Nat. Hazards Risk 2016, 8, 309–327. [Google Scholar] [CrossRef]
- Hamidi, E.; Peter, B.G.; Munoz, D.F.; Moftakhari, H.; Moradkhani, H. Fast Flood Extent Monitoring With SAR Change Detection Using Google Earth Engine. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4201419. [Google Scholar] [CrossRef]
- Wang, R. Design optimization of PV power station with complex terrain—A case study of mountain PV project in Shaanxi. Eng. J. Wuhan Univ. 2023, 56, 1–5. [Google Scholar]
- Huang, M.; Wang, Y.; Jin, S.; Chen, Q. Spatial-Temporal Variations and Severity of the 2020 Catastrophic Floods in the Yangtze River Basin from Sentinel-1 SAR Data. Water 2024, 16, 3445. [Google Scholar] [CrossRef]
- Rogers, J.S.; Maneta, M.M.; Sain, S.R.; Madaus, L.E.; Hacker, J.P. The role of climate and population change in global flood exposure and vulnerability. Nat. Commun. 2025, 16, 1287. [Google Scholar] [CrossRef] [PubMed]
- Toma, A.; Șandric, I.; Mihai, B.-A. Flooded area detection and mapping from Sentinel-1 imagery. Complementary approaches and comparative performance evaluation. Eur. J. Remote Sens. 2024, 57, 2414004. [Google Scholar] [CrossRef]
- Costache, R.; Arabameri, A.; Elkhrachy, I.; Ghorbanzadeh, O.; Pham, Q.B. Detection of areas prone to flood risk using state-of-the-art machine learning models. Geomat. Nat. Hazards Risk 2021, 12, 1488–1507. [Google Scholar] [CrossRef]
- Jiao, Z.; Zhang, Z.; Wu, L. SAR-based dynamic information retrieving of the Beijing-Tianjin-Hebei flood-inundation happened in July 2023, North China. Geomat. Nat. Hazards Risk 2024, 15, 2366361. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, P.; Chen, L.; Xu, M.; Guo, X.; Zhao, L. A new multi-source remote sensing image sample dataset with high resolution for flood area extraction: GF-FloodNet. Int. J. Digit. Earth 2023, 16, 2522–2554. [Google Scholar] [CrossRef]
- Vanama, V.S.K.; Rao, Y.S.; Bhatt, C.M. Change detection based flood mapping using multi-temporal Earth Observation satellite images: 2018 flood event of Kerala, India. Eur. J. Remote Sens. 2021, 54, 42–58. [Google Scholar] [CrossRef]
- Vanama, V.S.K.; Rao, Y.S.; Bhatt, C.M. Rapid monitoring of cyclone induced flood through an automated approach using multi–temporal Earth Observation (EO) images in RSS CloudToolbox platform. Eur. J. Remote Sens. 2021, 54, 589–609. [Google Scholar] [CrossRef]
- Feng, Q.; Niu, B.; Ren, Y.; Su, S.; Wang, J.; Shi, H.; Yang, J.; Han, M. A 10-m national-scale map of ground-mounted photovoltaic power stations in China of 2020. Sci. Data 2024, 11, 198. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Wang, Z.; He, G. AP Shadow Net: A Remote Sensing Shadow Removal Network Based on Atmospheric Transport and Poisson’s Equation. Entropy 2022, 24, 1301. [Google Scholar] [CrossRef] [PubMed]
- Cian, F.; Delgado Blasco, J.M.; Ivanescu, C. Improving rapid flood impact assessment: An enhanced multi-sensor approach including a new flood mapping method based on Sentinel-2 data. J. Environ. Manag. 2024, 369, 122326. [Google Scholar] [CrossRef]
- Yang, C.-J.; Wei, Y.-M.; Wang, S.-Y.; Zhou, Q.-L. Extracting the flood extent from SAR imagery on basis of DEM. J. Nat. Disasters 2002, 11, 121–125. [Google Scholar]
- Prasath, V.S.; Haddad, O. Radar shadow detection in synthetic aperture radar images using digital elevation model and projections. J. Appl. Remote Sens. 2014, 8, 083628. [Google Scholar] [CrossRef]
- Bioresita, F.; Puissant, A.; Stumpf, A.; Malet, J.-P. A Method for Automatic and Rapid Mapping of Water Surfaces from Sentinel-1 Imagery. Remote Sens. 2018, 10, 217. [Google Scholar] [CrossRef]
- Sghaier, M.O.; Hadzagic, M.; Patera, J. Fusion of SAR and multispectral satellite images using multiscale analysis and dempster-shafer theory for flood extent extraction. In Proceedings of the 2019 22th International Conference on Information Fusion (FUSION), Ottawa, ON, Canada, 2–5 July 2019; pp. 1–8. [Google Scholar]
- Gao, H.X.; Chen, B.; Sun, H.Q. Research progress and prospect of flood detection based on SAR satellite images. J. Geo-Inf. Sci. 2023, 25, 1933–1953. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, S. Automatic monitoring of surface water dynamics using Sentinel-1 and Sentinel-2 data with Google Earth Engine. Int. J. Appl. Earth Obs. Geoinf. 2022, 113, 103010. [Google Scholar] [CrossRef]
- DeVries, B.; Huang, C.; Armston, J.; Huang, W.; Jones, J.W.; Lang, M.W. Rapid and robust monitoring of flood events using Sentinel-1 and Landsat data on the Google Earth Engine. Remote Sens. Environ. 2020, 240, 111664. [Google Scholar] [CrossRef]
- Wang, J.; Wang, F.; Wang, S.; Zhou, Y.; Ji, J.; Wang, Z.; Zhao, Q.; Liu, L. Flood Monitoring in the Middle and Lower Basin of the Yangtze River Using Google Earth Engine and Machine Learning Methods. ISPRS Int. J. Geo-Inf. 2023, 12, 129. [Google Scholar] [CrossRef]
- Cian, F.; Marconcini, M.; Ceccato, P. Normalized Difference Flood Index for rapid flood mapping: Taking advantage of EO big data. Remote Sens. Environ. 2018, 209, 712–730. [Google Scholar] [CrossRef]
- Liu, Y.C.; Gao, Y.N. Surface water extraction in Yangtze River Basin based on sentinel time series image. Natl. Remote Sens. Bull. 2022, 26, 372. [Google Scholar] [CrossRef]
- Hansana, P.; Guo, X.; Zhang, S.; Kang, X.; Li, S. Flood Analysis Using Multi-Scale Remote Sensing Observations in Laos. Remote Sens. 2023, 15, 3166. [Google Scholar] [CrossRef]
- Farhadi, H.; Ebadi, H.; Kiani, A.; Asgary, A. Introducing a new index for flood mapping using Sentinel-2 imagery (SFMI). Comput. Geosci. 2025, 194, 105742. [Google Scholar] [CrossRef]
- Lin, L.; Di, L.; Tang, J.; Yu, E.; Zhang, C.; Rahman, M.S.; Shrestha, R.; Kang, L. Improvement and Validation of NASA/MODIS NRT Global Flood Mapping. Remote Sens. 2019, 11, 205. [Google Scholar] [CrossRef]
- Ticehurst, C.; Karim, F. Towards developing comparable optical and SAR remote sensing inundation mapping with hydrodynamic modelling. Int. J. Remote Sens. 2023, 44, 2912–2935. [Google Scholar] [CrossRef]
- Li, C.Y.; Liu, J.Q.; Liu, X.X.; Li, S.T.; Kang, X.D. Flood monitoring and analysis based on time-series SAR image for complex area. Natl. Remote Sens. Bull. 2024, 28, 346–358. [Google Scholar] [CrossRef]
- Shadoud, M.A.; Khalil, A.; Kotaridis, I.; Husein, H.H.; Costache, R. Morphometric analysis for flash flood hazard mapping: A case study of the Abu Al-Ward River Basin. DYSONA-Appl. Sci. 2025, 6, 398–410. [Google Scholar] [CrossRef]
- Moxon, S.D.G. Mapping Mangrove Forests: Processing and Visualization of Multi-Sensor Earth Observation Data for the Colombian Pacific Coast. Master’s Thesis, Palacký University Olomouc, Olomouc, Czech Republic, 2021. [Google Scholar]
- Liu, C.T.; Feng, Q.L.; Jin, D.J. Application of random forest and Sentinel—1/2 in the information extraction of impervious layers in Dongying City. Remote Sens. Nat. Resour. 2021, 33, 253–261. [Google Scholar] [CrossRef]
- Jia, S.C.; Xue, D.J.; Li, C.G.; Zheng, J.; Li, W.Q. Study on new method for water area information extraction based on Sentinel-1 data. People’s Yangtze River 2019, 50, 213–217. [Google Scholar]
- Saleh, T.; Weng, X.; Holail, S.; Hao, C.; Xia, G.-S. DAM-Net: Flood detection from SAR imagery using differential attention metric-based vision transformers. ISPRS J. Photogramm. Remote Sens. 2024, 212, 440–453. [Google Scholar] [CrossRef]
- Tan, W.; Qin, N.; Zhang, Y.; McGrath, H.; Fortin, M.; Li, J. A rapid high-resolution multi-sensory urban flood mapping framework via DEM upscaling. Remote Sens. Environ. 2024, 301, 113956. [Google Scholar] [CrossRef]
- Vinutha, H.; Poornima, B.; Sagar, B. Detection of outliers using interquartile range technique from intrusion dataset. In Information and Decision Sciences: Proceedings of the 6th International Conference on FICTA; Springer: Singapore, 2018; pp. 511–518. [Google Scholar]
- Zhao, C.; Yang, J. A Robust Skewed Boxplot for Detecting Outliers in Rainfall Observations in Real-Time Flood Forecasting. Adv. Meteorol. 2019, 2019, 1795673. [Google Scholar] [CrossRef]
- Zhao, B.; Sui, H.; Liu, J. Siam-DWENet: Flood inundation detection for SAR imagery using a cross-task transfer siamese network. Int. J. Appl. Earth Obs. Geoinf. 2023, 116, 103132. [Google Scholar] [CrossRef]
- Kim, Y.; Lee, M.-J. Rapid Change Detection of Flood Affected Area after Collapse of the Laos Xe-Pian Xe-Namnoy Dam Using Sentinel-1 GRD Data. Remote Sens. 2020, 12, 1978. [Google Scholar] [CrossRef]
- Liang, J.; Liu, D. A local thresholding approach to flood water delineation using Sentinel-1 SAR imagery. ISPRS J. Photogramm. Remote Sens. 2020, 159, 53–62. [Google Scholar] [CrossRef]
- Fayed, H.A.; Atiya, A.F. Speed up grid-search for parameter selection of support vector machines. Appl. Soft Comput. 2019, 80, 202–210. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Riazi, M.; Khosravi, K.; Shahedi, K.; Ahmad, S.; Jun, C.; Bateni, S.M.; Kazakis, N. Enhancing flood susceptibility modeling using multi-temporal SAR images, CHIRPS data, and hybrid machine learning algorithms. Sci. Total Environ. 2023, 871, 162066. [Google Scholar] [CrossRef]
- Myint, S.W.; Gober, P.; Brazel, A.; Grossman-Clarke, S.; Weng, Q. Per-pixel vs. object-based classification of urban land cover extraction using high spatial resolution imagery. Remote Sens. Environ. 2011, 115, 1145–1161. [Google Scholar] [CrossRef]
- Kropatsch, W.G.; Strobl, D. The generation of SAR layover and shadow maps from digital elevation models. IEEE Trans. Geosci. Remote Sens. 1990, 28, 98–107. [Google Scholar] [CrossRef]
- Li, J.; Yang, X.; Lei, Y.; Chang, T.; Zhang, J.; Peng, Y. Probabilistic structure analysis of fluctuating wind speed based on field measurement of super typhoon Doksuri. J. Wind. Eng. Ind. Aerodyn. 2024, 253, 105878. [Google Scholar] [CrossRef]
- Shahtahmassebi, A.; Yang, N.; Wang, K.; Moore, N.; Shen, Z. Review of shadow detection and de-shadowing methods in remote sensing. Chin. Geogr. Sci. 2013, 23, 403–420. [Google Scholar] [CrossRef]
- Wan, L.; Liu, M.; Wang, F.; Zhang, T.; You, H.J. Automatic extraction of flood inundation areas from SAR images: A case study of Jilin, China during the 2017 flood disaster. Int. J. Remote Sens. 2019, 40, 5050–5077. [Google Scholar] [CrossRef]
- Huth, J.; Gessner, U.; Klein, I.; Yesou, H.; Lai, X.; Oppelt, N.; Kuenzer, C. Analyzing Water Dynamics Based on Sentinel-1 Time Series—A Study for Dongting Lake Wetlands in China. Remote Sens. 2020, 12, 1761. [Google Scholar] [CrossRef]
- Wu, S.H.; Wu, Y.Q.; Zhou, J.J. SAR River Image Segmentation Based on Reciprocal Gray Entropy and Improved Chan-Vese Model. Acta Geod. Cartogr. Sin. 2015, 44, 1255–1262. [Google Scholar] [CrossRef]
- Nagai, H.; Abe, T.; Ohki, M. SAR-Based Flood Monitoring for Flatland with Frequently Fluctuating Water Surfaces: Proposal for the Normalized Backscatter Amplitude Difference Index (NoBADI). Remote Sens. 2021, 13, 4136. [Google Scholar] [CrossRef]
- Huang, M.; Jin, S. Backscatter characteristics analysis for flood mapping using multi-temporal Sentinel-1 images. Remote Sens. 2022, 14, 3838. [Google Scholar] [CrossRef]
- Tavus, B.; Kocaman, S. Flood Mapping in Mountainous Areas Using Sentinel-1 & 2 Data and Glcm Features. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, 1575–1580. [Google Scholar] [CrossRef]
- Bayer, T.; Winter, R.; Schreier, G. Terrain influences in SAR backscatter and attempts to their correction. IEEE Trans. Geosci. Remote Sens. 1991, 29, 451–462. [Google Scholar] [CrossRef]
- Rincón, D.; Khan, U.T.; Armenakis, C. Flood risk mapping using GIS and multi-criteria analysis: A greater Toronto area case study. Geosciences 2018, 8, 275. [Google Scholar] [CrossRef]
- Clement, M.A.; Kilsby, C.G.; Moore, P. Multi-temporal synthetic aperture radar flood mapping using change detection. J. Flood Risk Manag. 2017, 11, 152–168. [Google Scholar] [CrossRef]
- Zhou, T.; Fu, H.; Sun, C.; Wang, S. Shadow Detection and Compensation from Remote Sensing Images under Complex Urban Conditions. Remote Sens. 2021, 13, 699. [Google Scholar] [CrossRef]
- Demissie, B.; Vanhuysse, S.; Grippa, T.; Flasse, C.; Wolff, E. Using Sentinel-1 and Google Earth Engine cloud computing for detecting historical flood hazards in tropical urban regions: A case of Dar es Salaam. Geomat. Nat. Hazards Risk 2023, 14, 2202296. [Google Scholar] [CrossRef]
- Peter, B.G.; Cohen, S.; Lucey, R.; Munasinghe, D.; Raney, A.; Brakenridge, G.R. Google Earth Engine Implementation of the Floodwater Depth Estimation Tool (FwDET-GEE) for rapid and large scale flood analysis. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1501005. [Google Scholar] [CrossRef]
- Peng, X.; Chen, S.; Miao, Z.; Xu, Y.; Ye, M.; Lu, P. Automatic Flood Monitoring Method with SAR and Optical Data Using Google Earth Engine. Water 2025, 17, 177. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Wang, X.N.; Tian, J.Y.; Li, X.J.; Wang, L.; Gong, H.L.; Chen, B.B.; Li, X.C.; Guo, J.H. Benefits of Google Earth Engine in remote sensing. Natl. Remote Sens. Bull. 2022, 26, 11. [Google Scholar] [CrossRef]
- Twele, A.; Cao, W.; Plank, S.; Martinis, S. Sentinel-1-based flood mapping: A fully automated processing chain. Int. J. Remote Sens. 2016, 37, 2990–3004. [Google Scholar] [CrossRef]
- Eldhuset, K. Combination of stereo SAR and InSAR for DEM generation using TanDEM-X spotlight data. Int. J. Remote Sens. 2017, 38, 4362–4378. [Google Scholar] [CrossRef]








| Dataset | Resolution | Date Acquired | Bands /Polarization | Preprocessing | Purpose |
|---|---|---|---|---|---|
| Sentinel-1 | 10 m | 5 August 2023 | VV/VH | GEE default processing | Flood detection (model input) |
| Sentinel-2 | 10 m | 15 August 2023 | B2, B3, B4 (RGB) | Cloud < 20%, RGB only | Visual interpretation, validation |
| SRTM DEM | 30 m–10 m | — | Elevation only | Bilinear resampling to 10 m | Slope calculation (model input) |
| Metric | Water | Shadow | Overall |
|---|---|---|---|
| Overall Accuracy | - | - | 98.04% |
| Producer Accuracy | 99.34% | 94.30% | - |
| User Accuracy | 98.04% | 98.02% | - |
| Kappa | - | - | 0.95 |
| Metric | Non-Water | Water | Overall |
|---|---|---|---|
| Overall Accuracy | - | - | 96.46% |
| Producer Accuracy | 97.71% | 91.69% | - |
| User Accuracy | 97.82% | 91.30% | - |
| Kappa | - | - | 0.89 |
| Region | Confusion Matrix | Overall Accuracy | Producer’s Accuracy | User’s Accuracy | Kappa Coefficient |
|---|---|---|---|---|---|
| Mentougou District | 98.72% | Non-Water: 99.28% | Non-Water: 99.39% | 0.82 | |
| Water: 84.04% | Water: 81.44% | ||||
| Fangshan District | 94.51% | Non-Water: 97.31% | Non-Water: 95.17% | 0.86 | |
| Water: 87.31% | Water: 92.66% | ||||
| Fangshan District | 96.61% | Non-Water: 96.27% | Non-Water: 98.83% | 0.92 | |
| Water: 97.39% | Water: 91.94% |
| Method | Confusion Matrix | Overall Accuracy | User’s Accuracy | Kappa Coefficient |
|---|---|---|---|---|
| Formation Mechanism Method | 77.72% | Non-Water: 94.37% | 0.47 | |
| Water: 47.85% | ||||
| HAND Method | 94.40% | Non-Water: 97.00% | 0.83 | |
| Water: 84.99% | ||||
| IESRM | 96.46% | Non-Water: 97.82% | 0.89 | |
| Water: 91.30% |
| Compared Methods | b: Correct Only by Baseline | c: Correct Only by IESRM | McNemar’s χ² | p-Value | Statistical Conclusion |
|---|---|---|---|---|---|
| IESRM vs. HAND | 4 | 58 | 45.31 | <0.001 | Significant difference |
| IESRM vs. Formation | 63 | 1563 | 1381.92 | <0.000001 | Significant difference |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, F.; Shi, H.; Wang, S.; Liu, J. A Novel Mountain Shadow Removal Method Based on an Inverted Exponential Function Model for Flood Disaster Monitoring. Water 2025, 17, 1787. https://doi.org/10.3390/w17121787
Meng F, Shi H, Wang S, Liu J. A Novel Mountain Shadow Removal Method Based on an Inverted Exponential Function Model for Flood Disaster Monitoring. Water. 2025; 17(12):1787. https://doi.org/10.3390/w17121787
Chicago/Turabian StyleMeng, Fei, Haitao Shi, Shihan Wang, and Jiantao Liu. 2025. "A Novel Mountain Shadow Removal Method Based on an Inverted Exponential Function Model for Flood Disaster Monitoring" Water 17, no. 12: 1787. https://doi.org/10.3390/w17121787
APA StyleMeng, F., Shi, H., Wang, S., & Liu, J. (2025). A Novel Mountain Shadow Removal Method Based on an Inverted Exponential Function Model for Flood Disaster Monitoring. Water, 17(12), 1787. https://doi.org/10.3390/w17121787







