Regional Flood Frequency Analysis in Northeastern Bangladesh Using L-Moments for Peak Discharge Estimation at Various Return Periods in Ungauged Catchments

Abstract

The Sylhet Division of Bangladesh, highly susceptible to monsoon flooding, requires effective flood risk management to reduce socio-economic losses. Flood frequency analysis is an essential aspect of flood risk management and plays a crucial role in designing hydraulic structures. This study applies regional flood frequency analysis (RFFA) using L-moments to identify homogeneous hydrological regions and estimate extreme flood quantiles. Records from 26 streamflow gauging stations were used, including streamflow data along with corresponding physiographic and climatic characteristic data, obtained from GIS analysis and ERA5 respectively. Most stations showed no significant monotonic trends, temporal correlations, or spatial dependence, supporting the assumptions of stationarity and independence necessary for reliable frequency analysis, which allowed the use of cluster analysis, discordancy measures, heterogeneity tests for regionalization, and goodness-of-fit tests to evaluate candidate distributions. The Generalized Logistic (GLO) distribution performed best, offering robust quantile estimates with narrow confidence intervals. Multiple Non-Linear Regression models, based on catchment area, elevation, and other parameters, reasonably predicted ungauged basin peak discharges (R² = 0.61–0.87; RMSE = 438–2726 m³/s; MAPE = 41–74%) at different return periods, although uncertainty was higher for extreme events. Four homogeneous regions were identified, showing significant differences in hydrological behavior, with two regions yielding stable estimates and two exhibiting greater extreme variability.

1. Introduction

Floods are natural disasters characterized by their type, volume, and duration, with their frequency rising in recent decades, sparking growing concern among scientists and decision-makers [1]. These catastrophic events cause widespread environmental, agricultural, transportation, and infrastructure damage, resulting in fatalities and substantial economic losses [2,3,4,5]. Human activities, such as land use and climate change, have exacerbated flood risks by altering runoff responses in river catchments, intensifying flood vulnerabilities [6]. Factors such as basin size, slope, soil structure, and urbanization further contribute to the severity of floods, as impermeable surfaces and infrastructure disrupt natural flood mitigation processes [7,8]. With the increasing frequency of floods, especially under the impacts of climate change, effective flood frequency analysis has become crucial for managing these disasters [4].

The estimated flood quantiles (e.g., 50-year, 100-year discharge values) derived from frequency analysis are critical for practical engineering and flood risk management applications. These quantiles play a key role in the design of hydraulic structures like dams (typically using a 100-year return period), culverts (often designed for a 50-year flood), and bridges (commonly based on a 50- to 100-year flood) [9]. Specifically, they determine spillway capacity and dam height, ensuring that the infrastructure can safely convey extreme flows without overtopping or structural failure. In floodplain management, flood quantiles inform zoning regulations and the delineation of high-risk areas, thereby restricting development in flood-prone zones and guiding insurance and land-use planning. Furthermore, urban drainage systems—including stormwater networks, culverts, and detention basins—rely on estimates of more frequent events (e.g., 10-year or 25-year floods) to reduce the risk of urban flooding and maintain public safety during intense rainfall events. Accurate flood frequency estimation ensures a reliable understanding of flood behavior, helping to reduce risk and protect communities. However, accurately estimating return periods for rare geophysical events such as extreme floods remains a challenge [10].

To address this, regional flood frequency analysis (RFFA) has emerged as a widely used method, especially when data periods are unequal or records are limited or incomplete [9]. RFFA involves pooling data from multiple sites with similar characteristics, which improves flood rate estimates and compensates for sparse data at specific sites. The RFFA process includes identifying homogeneous regions, selecting appropriate regional frequency distributions, and transferring flood characteristics from gauged to ungauged catchments. In particular, the Probability-Weighted Moment (PWM)/Generalized Extreme Value (GEV) scheme provides more reliable estimates in homogeneous regions, enhancing flood predictions and enabling better risk management strategies [10]. Despite its advantages, RFFA must be applied cautiously, considering data uncertainties such as stationarity, correlation, and sampling variability [11].

The L-moments method is a prominent technique for regional flood frequency analysis (RFFA) that has been successfully applied globally in regions such as Canada [12], Norway [13], Iran [14], India [15], Korea [16], China [17], and Turkey [18]. Building on the Probability-Weighted Moment (PWM) method [19], L-moments allow a more direct interpretation of flood distributions in scale and shape. This method is particularly effective for estimating distributions with more than three parameters, offering more accurate results than single-location data. The two main techniques in RFA, Annual Maximum Series (AMS) and Peak-Over-Threshold (POT) are utilized to estimate flood magnitudes based on different flood event frequencies, with AMS being beneficial for more extended return periods [6]. L-moments significantly improve the reliability of flood discharge predictions, particularly in regions with limited data, making them essential for robust flood frequency analysis and risk management [5].

Although the L-moments method has become popular worldwide, its application in Bangladesh is limited in various studies. Various flood frequency distributions were compared using the L-moments method without applying discordancy and heterogeneity tests, cluster analysis, or Monte Carlo simulation to estimate quantiles [20]. The Log Pearson Type-3 (LP3) distribution was formulated as the best suited to flood frequency analysis of rivers in Bangladesh [21], outperforming other distributions such as Log-Normal and Extreme Value Type-1 (EV1). Based on the characteristics of hydrographs, a flood index was established for the Haor area [22]. Both Powell and Gumbel distributions were used for the Dudhkumar River, and it was observed that both these models provided a good fit, with predicted magnitudes of floods matching well with the observed magnitudes [23]. Several approaches for the Padma River were compared, and it was concluded that Gumbel and Stochastic methods yielded the best flooding estimates, especially for extended return periods [24]. The Hamiltonian Monte Carlo (HMC) method was used on the Generalized Extreme Value (GEV) distribution, illustrating the greater precision of HMC for extreme return periods compared to the Metropolis–Hastings algorithm [25]. Flash floods in the northeast Haor region were analyzed, and the GEV distribution was found to be best for predicting flash flood levels and establishing new flood risk thresholds to protect Boro crops [26]. While different approaches were adopted in these investigations, the L-moments approach was not frequently used, despite its reliability for flood frequency analysis. Our study focuses on the northeastern region of Bangladesh, a flood-prone area due to its hilly terrain, and Haors, which has large tectonic depressions that remain flooded during the monsoon but dry up post-monsoon. Flash floods occur when heavy rainfall in India’s Assam and Meghalaya regions causes floodwaters to quickly move into Bangladesh, affecting the Haor areas within hours [27]. This rapid inundation leaves farmers with little time to harvest their Boro crops, which cover nearly 80% of the Haor areas [28]. Flash floods have caused significant damage to crops, destroying up to 70% of them and leading to substantial economic losses [29]. The devastating floods of 2010 and 2016 affected large areas, with the 2010 flood alone damaging 152,000 ha and causing losses worth BDT 13.18 billion [26]. Despite existing flood control structures, such as embankments and rubber dams, the region faces serious flood risks [30]. The 2022 flash floods, which affected over 7.2 million people and caused extensive damage, further highlight the need for better regional flood prediction and management [31].

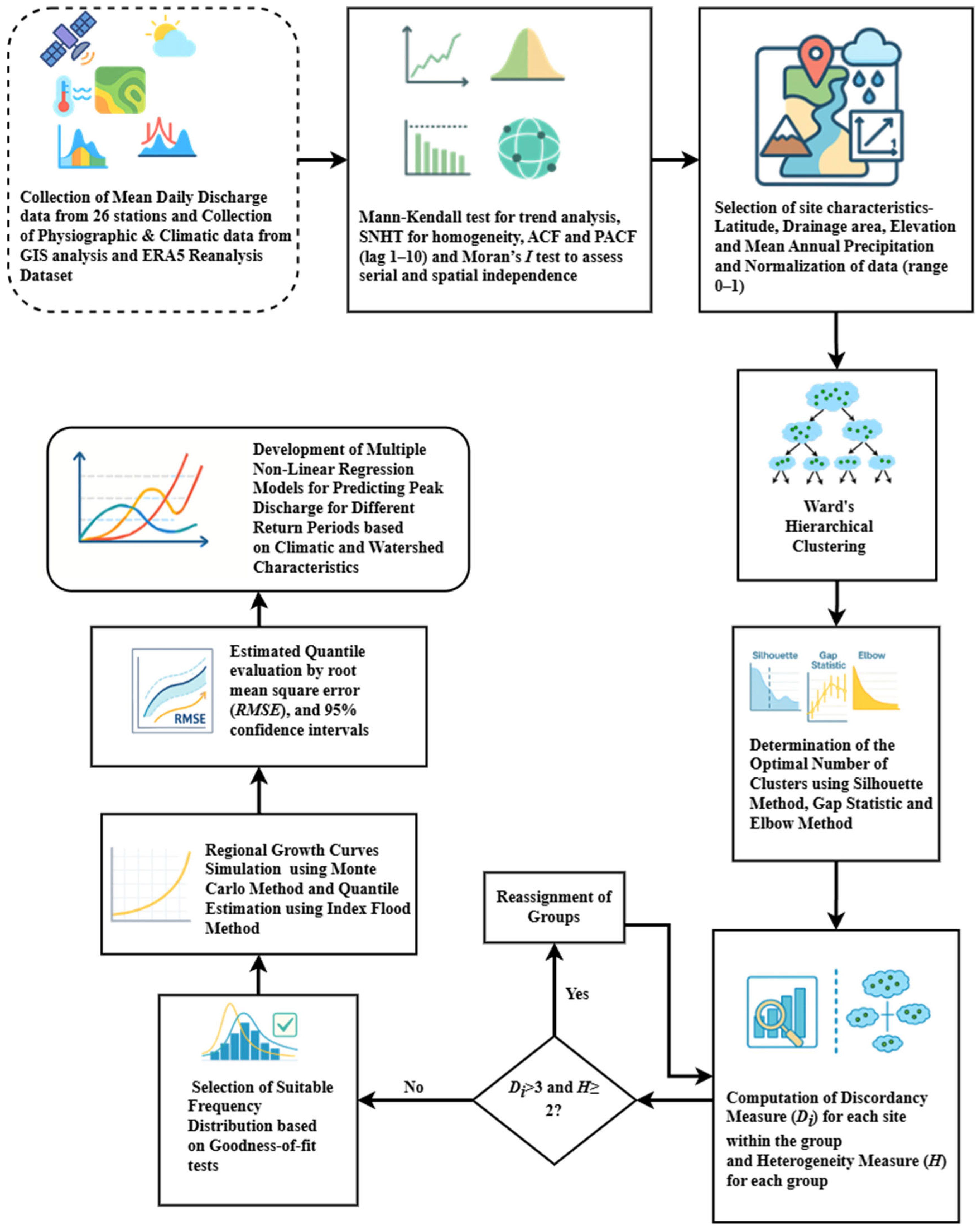
This underscores the importance of our study. This research fills a vital gap by creating and applying a physiographic–statistical framework that effectively advances classical flood frequency analysis (FFA) by combining L-moments-based regional frequency analysis and hierarchical clustering. This method is very effective for our study area since there are only 30 river discharge monitoring stations in the Sylhet Division, and data could be collected from 26 of them. Moreover, many of the discharge observation stations have short and unevenly spaced discharge records, making traditional moment-based methods less reliable. In contrast, L-moments are well-suited for such conditions, as they provide more robust and unbiased estimates even with limited or irregularly spaced data. Behind this methodological enhancement is a multi-step process starting with comprehensive data screening, including the Mann–Kendall test, Standard Normal Homogeneity Test (SNHT), autocorrelation, partial autocorrelation, and Moran’s I test, for ensuring stationarity, independence, and spatial autocorrelation of the annual peak discharge time series, followed by Ward’s hierarchical cluster algorithm based on both hydrological and physiographic watershed properties (drainage area, elevation, mean precipitation, and geographic coordinates) for delineating homogeneous regions, with cluster validity assessed using silhouette width analysis, gap statistics, and the elbow method. The proposed methodology enhances regional homogeneity testing via discordancy measures (D_i statistic) for detecting anomalous stations and heterogeneity measures (H-statistics) derived from Monte Carlo simulations of synthetic regions from Kappa distributions. The selection of probability distribution is optimized by exhaustive goodness-of-fit testing by ${\mathit{Z}}_{\mathit{DIST}}$ statistics between observed and simulated L-kurtosis values of six competing distributions (Generalized Logistic (GLO), Generalized Extreme Value (GEV), Generalized Pareto (GPA), Generalized Normal (GNO), Pearson Type III (PE3), Wakeby (WAK)), and the chosen distribution is also substantiated by Root Mean Square Error (RMSE) analysis and 95% confidence limits based on Monte Carlo simulations. Besides the traditional index flood methods, the study presents several predictive Multiple Non-Linear Regression (MNLR) models for different return periods that incorporate watershed-scale geomorphological predictors (stream order, basin length, elevation, etc.) and climatic predictors in an attempt to enable accurate flood quantile estimation in ungauged basins, where the performance of the model is compared using R² (Coefficient of Determination), RMSE (Root Mean Square Error), and MAPE (Mean Absolute Percentage Error) metrics. The framework’s demonstration application in the Sylhet Division has yielded precise design flood estimates with quantified uncertainty ranges, producing vital input to climate-resilient infrastructure planning. At the same time, its techniques, particularly in cluster validation, hybrid homogeneity testing, and non-linear predictor inclusion, provide a replicable template for flood hazard estimation in similar monsoonal contexts worldwide.

2. Materials and Methods

2.1. Study Area and Data Availability

The present study focuses on the Sylhet Division, located in the northeastern region of Bangladesh, comprising the four administrative districts of Sylhet, Sunamganj, Habiganj, and Moulvibazar. Covering a total area of 12,635.22 km², Sylhet Division accounts for approximately 8.5% of the total area of Bangladesh, and having a population of roughly 11,034,863 people, it has demographic significance. Sylhet Division lies between 23°58′ W to 25°12′ W latitude and 90°56′ E to 92°30′ E longitude. It is bounded by Meghalaya to the north, Tripura and Brahmanbaria district to the south, Assam and Tripura to the east, and Netrakona and Kishoreganj districts to the west. The elevation in the Sylhet Division ranges from 0 m to a maximum of 1620 m, with an average elevation of 88 m [32]. Sylhet Division experiences a tropical monsoon climate, bordering on a humid subtropical climate in higher elevations. The pre-monsoon (March to May), monsoon (June to September), post-monsoon (October to November), and dry winter (December to February) are the primary seasons in this region [33,34]. The region is known for its intense rainfall; the recorded maximum annual rainfall is 4996.03 mm, and the minimum stands at 2041.92 mm, while the average annual temperature is 21.56 °C. From a climatic perspective, the area is classified as having subtropical humid conditions [35]. Sylhet Division is traversed by several major rivers, including the Surma, Meghna, Kushiyara, Jadukata, and Manu. Humid southwesterly flows from the Bay of Bengal are repelled by the mountainous areas of Assam, Meghalaya, and Tripura. Heavy rainfall over the Meghna basin is caused by orographic lifting and other processes [36,37,38,39]. In the past, the Sylhet region has been highly flood-prone, with significant events occurring in 1988, 1998, 2004, 2007, 2017, 2020, and 2022. The floods have varied in intensity, persistence, and socio-economic effects. For instance, the 2004 and 2007 floods caused agricultural losses of BDT 8285.80 million and BDT 3768.64 million, respectively [40]. The floods have also caused huge income and job loss, primarily impacting the rural agrarian community. For the current study, data on the daily discharge of 26 gauging stations and their geographic coordinates (latitude and longitude) were gathered from the Bangladesh Water Development Board (BWDB). Some key physiographic and climatic characteristics of the gauging stations, including Station ID, Station Name, geographic coordinates (latitude and longitude), data availability period, catchment area (km²), Mean Annual Precipitation (MAP in mm), and Mean Annual Temperature (MAT in °C) are summarized in

Table 1. Data summary of 26 streamflow gauging stations.

Station ID	Station Name	Latitude (°)	Longitude (°)	Data Period	Area (km2)	*MAP (mm)	*MAT (°C)
SW264A	Montala	24.0834	91.3506	1998–2024	91	2322.55	24.5
SW135A	JuriCont_Silghat	24.6032	92.12	1990–2012	800	2521.37	24.29
SW341	Chella Sonapur	25.1301	91.6685	1990–2016	511.42	4474.48	17.23
SW280	Sutang Rly. Bridge	24.2828	91.403	1964–2024	246.42	2300.26	24.55
SW157	Ballah	24.0838	91.5961	1999–2023	1142.76	2199.38	24.15
SW67	Kamalganj	24.3558	91.8489	1990–2024	731.08	2241.92	24.12
SW333	Muslimpur	25.1109	91.3914	1996–2023	543.84	4388.25	18.06
SW337	Urargaon	25.1209	91.5936	1990–2016	79.3	4996.03	22.13
SW326	Lubachara	25.0515	92.3085	1985–2022	726.41	3402.17	20.82
SW265	Jaldhup	24.7738	92.1729	1964–2016	2206.57	2630.47	23.98
SW251	Sarighat	25.0939	92.1173	2000–2023	821.7	3578.93	19.34
SW233	Ratnar bhanga (Piyan gang)	25.1624	91.967	1985–2022	844	3981.28	18.15
SW173	Sheola	24.8911	92.1915	1996–2023	25,337.01	2253.36	20.89
SW135	Juri_Silghat	24.5902	92.1177	1964–2022	789.53	2246.75	24.3
SW333A	Dulura	25.1593	91.3878	2003–2024	530	4388.25	18.06
SW233A	Jaflong_Spill	25.1568	92.0167	1994–2024	850	3981.28	18.15
SW332	Islampur	25.1302	91.7538	1988–2016	350.72	4733.84	18.73
SW192	Motiganj	24.3065	91.6822	1964–2023	61.29	2246.75	24.3
SW158.1	Shaistaganj	24.2731	91.4736	1964–2024	1400	2225.64	24.21
SW138	Sofiabad	24.293	91.5465	1964–2024	166.96	2261.9	24.5
SW131.5	Laurergarh Saktiarkhola	25.1891	91.2508	1993–2024	2483.8	3302.25	19.25
SW175.5	Sherpur	24.6303	91.6813	1996–2023	33,855.2	2360.13	21.71
SW266	Kanairghat	24.998	92.2594	2000–2023	1501.7	3377.6	22.01
SW267	Sylhet	24.8879	91.868	2000–2023	1593.12	3377.6	22.01
SW269	Sunamganj	25.0792	91.4121	2000–2023	7176.02	4236.93	21.1
SW201	Monu Rly. Bridge	24.4256	91.9404	1996–2023	2292.71	2041.92	23.83

Note: *MAP (mm) and *MAT (°C) represent the Mean Annual Precipitation (mm) and Mean Annual Temperature (°C), respectively.

. The physiographic characteristics of the gauging stations were extracted using Geographic Information System (GIS) software (ArcGIS Desktop 10.8). Mean Annual Temperature and Mean Annual Precipitation were obtained from monthly ERA5 precipitation and temperature data (ERA5 stands for “ECMWF Reanalysis 5th Generation,” produced by the European Centre for Medium-Range Weather Forecasts), which were extracted using Google Earth Engine (GEE). The dataset covers the period from 1940 to 2024. For each year, the monthly temperature and precipitation values were first averaged to obtain annual means. Then, the Mean Annual Temperature and Mean Annual Precipitation were calculated by averaging these yearly means over the entire 85-year period (1940–2024). The geographical positions of gauging stations utilized for the current study are shown in Figure 1. Figure 2 illustrates the data availability and missing years for each station, highlighting temporal gaps and periods of continuous record.

2.2. Statistical Methods

L-moments are a type of statistical moments based on linear combinations of ordered statistics [41]. Traditional moment-based methods tend to be unreliable, especially with extreme data [11], including difficulty in interpreting the shape information conveyed by higher-order moments (third and beyond), which has prompted the development of better alternatives like L-moments that are more precise and robust [41]. The first four L-moments are described as mean, scale, skewness, and kurtosis, which are linear combinations of the PWMs:

$${\lambda }_1={\beta }_0$$

(1)

$${\lambda }_2=2{\beta }_1-{\beta }_0$$

(2)

$${\lambda }_3=6{\beta }_2-6{\beta }_1+{\beta }_0$$

(3)

$${\lambda }_4=20{\beta }_3-30{\beta }_2+12{\beta }_1-{\beta }_0$$

(4)

and L-moment ratios are defined by Hosking [42] expressed as L-coefficient of variation (L-CV): ${\tau }_2={\displaystyle \frac{{\lambda }_2}{{\lambda }_1}}$, L-skewness (L-CS): ${\tau }_3= {\displaystyle \frac{{\lambda }_3}{{\lambda }_2}}$ and L-kurtosis (L-CK): ${\tau }_4={\displaystyle \frac{{\lambda }_4}{{\lambda }_2}}$. Probability-Weighted Moments (PWMs) are defined by the expression, ${\beta }_r=E[x\cdot F{\left(x\right)}^r]$, where F($x$) is the cumulative distribution function (CDF) of the random variable $X$, and ${\beta }_r$ is the $r^{\mathrm{t}\mathrm{h}}$-order PWM, where $X$ represents data in ascending order [19]. For a sample of size $n$ with ordered data $X_1\le X_2\le \cdots \le X_n$, the sample estimators of the first few PWMs are given by [43]

$${\beta }_0={\displaystyle \frac{1}{n}}{\sum }_{j=1}^n{X}_j$$

(5)

$${\beta }_1={\displaystyle \frac{1}{n}}{\sum }_{j=2}^n{\displaystyle \frac{\left(j-1\right)}{\left(n-1\right)}}{X}_j$$

(6)

$${\beta }_2={\displaystyle \frac{1}{n}}\sum _{j=3}^n{\displaystyle \frac{\left(j-1\right)\left(j-2\right)}{\left(n-1\right)\left(n-2\right)}}{X}_j$$

(7)

The statistic $b_r={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\displaystyle \frac{\left(i-1\right)\left(i-2\right)\cdots \left(i-r\right)}{\left(n-1\right)\left(n-2\right)\cdots \left(n-r\right)}}{x}_{\left(i\right)}$ is an unbiased estimator of ${\beta }_r$ [44]. The first four sample L-moments $l_1,l_2,l_3,$ and $l_4$ can be derived from the unbiased estimators of the sample Probability-Weighted Moments ${\beta }_r$. Using these expressions, $l_1=b_0$, $l_2=2b_1-b_0, l_3=6b_2-6b_1+b_0$, and $l_4=20b_3-30b_2+12b_1-b_0$, and similarly, $t={\displaystyle \frac{l_2}{l_1}}, t_3={\displaystyle \frac{l_3}{l_2}},$ and $t_4={\displaystyle \frac{l_4}{l_2}}$ are the sample L-moments ratios [45]. Regional frequency analysis (RFA) by L-moments consists of four steps: (1) initial data screening, which is the examination of data quality and stationarity; (2) identification of homogeneous regions by classifying sites having similar hydrological properties; (3) selection of a suitable frequency distribution on the basis of goodness-of-fit tests and reliability measures; and (4) estimation of regional flood quantiles using the L-moments approach [42]. Figure 3 depicts the flowchart representing the proposed work.

2.3. Initial Data Screening

An initial screening was performed to ensure the suitability of mean annual peak discharge data from northeast Bangladesh (Sylhet Division) for regional frequency analysis. Stationarity was checked using the nonparametric Mann–Kendall trend test [46,47], while homogeneity was assessed using the Standard Normal Homogeneity Test (SNHT). Serial independence was tested using lag-1 to lag-10 autocorrelation and partial autocorrelation tests, and spatial independence between stations was tested using Moran’s I [48]. For a region to be considered homogeneous, the Annual Maximum Series (AMS) from different stations should be spatially independent; high spatial cross-correlation between stations provides less additional regional information to the site under study than uncorrelated stations [49].

2.3.1. Mann–Kendall Test

The Mann–Kendall (MK) test is a popular nonparametric statistical method for detecting monotonic trends in time series data [50,51,52]. It assesses whether there is a statistically significant trend (either upward or downward) over time without assuming any specific distribution of the data; it also tests the null hypothesis of no trend against the alternative hypothesis of a monotonic trend [53]. For a time series $x_1,x_2,\dots ,x_n$, the test statistic S is calculated by comparing each pair of values:

$$S=\sum _{i=1}^{n-1}\sum _{j=i+1}^n\mathrm{s}\mathrm{g}\mathrm{n}\left(X_j-X_i\right)$$

(8)

where $X_i$ and $X_j$ are data values at times $i$ and $j$ (with $j>i$) and $n$ is the total number of observations. The sign function, $\mathrm{s}\mathrm{g}\mathrm{n}(X_j-X_i)$, is defined as

$$\mathrm{s}\mathrm{g}\mathrm{n}\left(X_j-X_i\right)=\left\{\begin{array}{ll}+1,& \mathrm{i}\mathrm{f} X_j-X_i>0\\ 0,& \mathrm{i}\mathrm{f} X_j-X_i=0\\ -1,& \mathrm{i}\mathrm{f} X_j-X_i<0\end{array}\right.$$

(9)

To determine the statistical significance of the trend, the variance of $S$, denoted $\mathrm{V}\mathrm{a}\mathrm{r}\left(S\right)$, is computed as

$$\mathrm{V}\mathrm{a}\mathrm{r}\left(S\right)={\displaystyle \frac{n\left(n-1\right)\left(2n+5\right)-\sum _{j=1}^m{t}_j\left(t_j-1\right)\left(2t_j+5\right)}{18}}$$

(10)

where $m$ is the number of tied groups and $t_j$ is the tied rank, each with $t_j$ tied points. Using the computed $S$ and its variance, the standardized test statistic $Z$ is determined as follows:

$$Z=\left\{\begin{array}{ll}{\displaystyle \frac{S-1}{\sqrt{\mathrm{V}\mathrm{a}\mathrm{r}\left(S\right)}}},& \mathrm{i}\mathrm{f} S>0\\ 0,& \mathrm{i}\mathrm{f} S=0\\ {\displaystyle \frac{S+1}{\sqrt{\mathrm{V}\mathrm{a}\mathrm{r}\left(S\right)}}},& \mathrm{i}\mathrm{f} S<0\end{array}\right.$$

(11)

A positive Z-value indicates an upward trend, and a negative Z-value indicates a downward trend. The statistical significance of the trend typically would be tested in terms of the p-value associated with it. A p-value of less than or equal to 0.05 is typically considered statistically significant, leading to the null hypothesis of no trend being rejected in favor of the alternative hypothesis of the presence of a trend. Also, Kendall’s Tau ($\tau$) is simply described as a measure of the strength of the correlation of ranks in the dataset [54]. It has values ranging between −1 (perfect negative correlation) and +1 (perfect positive correlation), and its near-zero values reflect no significant association. To test the homogeneity of the time series prior to the detection of the trend, the Standard Normal Homogeneity Test (SNHT) was also employed. The SNHT is a statistical test for detecting changes in the mean value of a time series and is traditionally utilized in climatological and hydrological data quality assessments [55,56,57,58].

2.3.2. Autocorrelation and Partial Autocorrelation Tests

Autocorrelation is a measure of how much a given time series is similar to a lagged copy of itself from one time period to the next. Autocorrelation measures the correlation between observations with a specific time lag and is a fundamental method for identifying patterns, trends, or cycles in time series data [59,60]. Mathematically, the autocorrelation function (ACF) at lag k can be stated as

$${\rho }_k={\displaystyle \frac{\mathrm{Cov}\left(X_t,X_{t-k}\right)}{\sqrt{\mathrm{Var}\left(X_t\right)\cdot \mathrm{Var}\left(X_{t-k}\right)}}}$$

(12)

where $\mathrm{Cov}\left(X_t,X_{t-k}\right)$ is the covariance between observations of the time series values at time $t$ and $t-k$, and $\mathrm{Var}\left(X_t\right)$ and $\mathrm{Var}\left(X_{t-k}\right)$ are the variances at time $t$ and $t-k$, respectively (where k is the lag). The value of ${\rho }_k$ is normalized to lie in the range [−1, 1]. A positive autocorrelation indicates that large (or small) values are followed by values of the same kind, indicating trend or persistence. A negative autocorrelation indicates a reversal, wherein high values will be succeeded by low values and vice versa. A near-zero autocorrelation indicates weak or no serial dependence of observations at the specified lag.

For a stationary time series $\left\{X_t\right\}$, the Partial Autocorrelation Function (PACF) [61,62] at lag $k$, denoted ${\varphi }_{kk}$, is the last coefficient in the Yule–Walker equations for an autoregressive process of order k (AR($k$)):

$$X_t={\varphi }_{k1}{X}_{t-1}+{\varphi }_{k2}{X}_{t-2}+\cdots +{\varphi }_{kk}{X}_{t-k}+{ϵ}_t$$

(13)

where ${ϵ}_t$ is white noise.

The coefficients ${\varphi }_{kj}$ (for $j=1,2,\dots ,k$) are obtained by solving the Yule–Walker system:

$$\left[\begin{array}{cccc}{\rho }_0& {\rho }_1& \cdots & {\rho }_{k-1}\\ {\rho }_1& {\rho }_0& \cdots & {\rho }_{k-2}\\ ⋮& ⋮& \ddots & ⋮\\ {\rho }_{k-1}& {\rho }_{k-2}& \cdots & {\rho }_0\end{array}\right]\left[\begin{array}{c}{\varphi }_{k1}\\ {\varphi }_{k2}\\ ⋮\\ {\varphi }_{kk}\end{array}\right]=\left[\begin{array}{c}{\rho }_1\\ {\rho }_2\\ ⋮\\ {\rho }_k\end{array}\right]$$

(14)

where ${\rho }_j$ is the autocorrelation at lag $j$ and the solution yields ${\varphi }_{kk}$, which is the partial autocorrelation at lag $k$.

2.4. Identification of Homogeneous Regions by Clustering

In order to define homogeneous regions for regional frequency analysis, the following site factors concerning climatic variables, basin characteristics, and location were utilized. They are longitude, latitude, drainage area, elevation, and Mean Annual Precipitation. These variables were selected as they are relevant to hydrological processes and are commonly used in comparable studies [42]. To obtain comparability and prevent analysis from being dominated by larger-scale variables, all the variables were standardized to the range 0–1. The technique employed to cluster the sites by the similarity of these features was Ward’s hierarchical clustering method [63]. The most appropriate number of clusters was found through silhouette widths [64], gap statistics [65], and the elbow method [66]. The utility of these clustering techniques and validation procedures has been shown in several hydrological applications; e.g., silhouette widths have been successfully applied in hierarchical clustering for the delineation of flood estimation zones [67], and cluster analysis in conjunction with distance-based validation procedures has helped evaluate the hydrological similarity of small watersheds [68].

2.5. Discordancy Measure

Discordancy is a statistical measure used under the regional frequency analysis (RFA) method to discern whether any individual site in a collective shows any meaningful divergence from the collective properties. It is used to detect abnormalities or potential inaccuracies within the dataset. A site would be considered discordant if its L-moment ratios, specifically L-CV, L-skewness, and L-kurtosis, show wide divergence from the mean values of the respective ratios for the rest of the sites within the defined region. After homogeneous areas have been determined, a discordancy measure is computed for every location in the specified region. Where a site is discordant with the region as a whole, the reassignment of such a site to a different region needs to be considered. The measure of discordancy for site i is

$$D_i={\displaystyle \frac{N}{3}}{\left(u_i-\overline{\mathrm{u}}\right)}^T{A}^{-1}\left(u_i-\overline{\mathrm{u}}\right)$$

(15)

where $D_i$ is the discordancy value for site i, $N$ is the number of sites in the region, and $u_i$ is the vector of L-moment ratios. For site i, $\overline{\mathrm{u}}$ is the average vector of L-moment ratios for the group, and $A$ is the sample covariance matrix (matrix of sums of squares and cross-products). A site will considered as discordant if its $D_i$ value exceeds a critical threshold $D_i>3$ [42].

2.6. Heterogeneity Measure

The H-statistic is the second measure for assessing regional homogeneity in the context of regional frequency analysis (RFA), providing the quantitative measure of site heterogeneity through a comparison of the variability of the observed sample L-moment ratios (e.g., L-CV, L-skewness, and L-kurtosis) with the variability in a theoretically homogeneous region. This comparison, made through Monte Carlo simulations, provides a statistically sound basis for determining if the observed differences among sites are within acceptable limits for regional analysis. There are three versions of the heterogeneity measure: $H_1$: based on L-CV (${\tau }_2$), $H_2$: based on L-skewness (${\tau }_3$), $H_3$: based on L-kurtosis (${\tau }_4$). Different H-statistic values are interpreted based on threshold criteria summarized in

Table 2. Interpretation of H-statistic values.

H Value	Interpretation
$H<1$	The region is “acceptably homogeneous.”
$1\le H<2$	The region is “possibly heterogeneous.”
$H\ge 2$	The region is “definitely heterogeneous.”

. Each uses a corresponding observed dispersion statistic, denoted as $V_1,V_2,V_3$ computed as weighted standard deviations of the respective L-moment ratios across sites, with weights proportional to the site record lengths.

$$V_1={\left\{{\displaystyle \frac{\sum _{i=1}^N{n}_i{\left(t^{\left(i\right)}-t^R\right)}^2}{\sum _{i=1}^N{n}_i}}\right\}}^{{\displaystyle \frac{1}{2}}}$$

(16)

$$V_2={{\displaystyle \frac{\sum _{i=1}^N{n}_i\left[{\left(t^{\left(i\right)}-t^R\right)}^2+{\left(t_3^{\left(i\right)}-t_3^R\right)}^2\right]}{\sum _{i=1}^N{n}_i}}}^{{\displaystyle \frac{1}{2}}}$$

(17)

$$V_3={{\displaystyle \frac{\sum _{i=1}^N{n}_i\left[{\left(t_3^{\left(i\right)}-t_3^R\right)}^2+{\left(t_4^{\left(i\right)}-t_4^R\right)}^2\right]}{\sum _{i=1}^N{n}_i}}}^{{\displaystyle \frac{1}{2}}}$$

(18)

where $N$ = number of sites, $n_i$ = record length at site $i$, and the sample L-moment ratios are $t_2^{\left(i\right)}$ (L-CV), $t_3^{\left(i\right)}$ (L-skewness), and $t_4^{\left(i\right)}$ (L-kurtosis), The regional average L-moment ratios are $t_2^R$, $t_3^R$, and $t_4^R$. For each $j\in \{1,2,3\}$, the corresponding heterogeneity statistic $H_j$ is defined as

$$H_j={\displaystyle \frac{V_j-{\mu }_{V_j}}{{\sigma }_{V_j}}}$$

(19)

where ${\mu }_{V_j}$ = the mean of $V_j$ values obtained from simulated homogeneous regions, ${\sigma }_{V_j}$ = the standard deviation of those values. The Kappa distribution generates simulations matching the average L-moment ratios of the region, ensuring a flexible representation of hydrological behavior without committing to a specific parametric form [42].

2.7. Selection of Suitable Frequency Distribution Based on Goodness-of-Fit Tests and Reliability Measures

After the homogeneity analysis of the study area, a suitable probability distribution is required for regional frequency analysis (RFA) to identify the best fit for regional frequency analysis and also ensure robust quantile estimates for each location and the regional growth curve; the list of candidate probability distributions for RFA includes Generalized Logistic (GLO), Generalized Extreme Value (GEV), Generalized Pareto (GPA), Generalized Normal (GNO), Pearson Type III (PE3), and Wakeby (WAK) [45]. The goodness-of-fit test is employed to identify the parent probability distribution that closely aligns with the weighted average regional values of L-skewness and L-kurtosis for a proposed group of sites [68]. This test helps validate the appropriateness of a fitted distribution by comparing it with observed regional L-moment statistics. Visualization is often performed by plotting the observed regional values of L-skewness and L-kurtosis and assessing how closely the L-kurtosis of a candidate distribution matches the regional L-kurtosis. The test is based on the $Z_{\mathit{DIST}}$ statistic, which follows an approximately standard normal distribution [43]. The goodness-of-fit statistic is calculated using the following equations:

$${\mathit{Z}}_{DIST}={\displaystyle \frac{{\tau }_4^{DIST}-{\overline{\tau }}_4+{\beta }_4}{{\sigma }_4}}$$

(20)

where “DIST” indicates the candidate distribution, ${\overline{\tau }}_4$ indicates the average L-kurtosis value from observed data, ${\beta }_4$ indicates bias (for regional average sample L-kurtosis), and ${\tau }_4^{DIST}$ indicates the average L-kurtosis value for a fitted distribution computed from a simulation [43].

A candidate distribution is considered a good fit if $\mid {\mathit{Z}}_{\mathit{DIST}}\mid \le 1.64$ corresponds to a confidence level of 90%. If multiple distributions satisfied the goodness-of-fit criteria, the one with the lowest RMSE (Root Mean Square Error) and the narrowest 95% error bound was selected for further analysis [69].

2.8. Quantile Estimation

Quantile estimation is accomplished using the index flood approach, in which it is supposed that all sites in a homogeneous region have the same-shaped frequency distributions but differ by a site-specific scale factor—typically the mean annual flood (index flood) [70]. The at-site flood quantiles are estimated using the regional quantiles derived from the quantile function of the best-fitted regional distribution, expressed by the equation

$$Q_i\left(F\right)=l_1^{\left(i\right)}\cdot q\left(F\right)$$

(21)

where $Q_i\left(F\right)$ is the flood quantile at site $i$ for a given return period (non-exceedance probability $F$), $l_1^{\left(i\right)}$ is the mean of the annual peak flow (APF) at site $i$, and $q\left(F\right)$ is the regional dimensionless quantile obtained from the fitted regional growth curve [9]. The accuracy of estimated flood quantiles is assessed using Monte Carlo simulations for each homogeneous region [42].

For each homogeneous region, a region having the same number of stations, record length at each station, heterogeneity, and regional average L-moment ratios as the observed data were simulated. This procedure was repeated 1000 times to obtain 1000 simulated regions. For each simulation, errors in the simulated growth curve and quantiles were calculated, and then the bias, RMSE (Root Mean Square Error), and 95% error bounds were estimated [71].

2.9. Development of Multiple Non-Linear Regression Models for Predicting Peak Discharge for Different Return Periods Based on Climatic and Watershed Characteristics

To establish a predictive relationship between watershed characteristics and hydrological response parameters (e.g., peak discharge), Multiple Non-Linear Regression (MNLR) analysis was used in this research. Unlike ordinary linear regression, which is based on the assumption of linear relationships among variables, MNLR has the advantage of more flexible functional forms, e.g., power-law or exponential ones that are more consistent with the complexity of hydrologic systems [72].

The general form of the MNLR model used is

$$Y=a\cdot X_1^{b_1}\cdot X_2^{b_2}\cdot \cdots \cdot X_n^{b_n}$$

(22)

where $Y$ is the dependent variable (e.g., 100-year flood discharge, $Q_{100}$), $X_1,X_2,\dots ,X_n$ are the independent variables (e.g., catchment area, Mean Annual Precipitation, stream order, etc.), $a$ is the regression constant, and $b_1,b_2,\dots ,b_n$ are the regression exponents for each predictor. To estimate the coefficients, the model was linearized using a natural logarithmic transformation:

$$ln\left(Y\right)=ln\left(a\right)+b_{1}ln\left(X_1\right)+b_{2}ln\left(X_2\right)+\cdots +b_{n}ln\left(X_n\right)$$

(23)

Standard Ordinary Least Squares (OLS) regression was then applied to the transformed equation [73]. The model’s predictive performance and goodness-of-fit were evaluated using statistical indicators, including the Coefficient of Determination ($R^2$), Root Mean Square Error (RMSE), and Mean Absolute Percentage Error (MAPE) [74]. This approach follows established regional flood frequency analysis and hydrologic modeling methods, where physiographic, climatic, and morphometric watershed variables are commonly used to estimate peak discharge [75,76].

3. Results

3.1. Statistical Tests for Assessing Stationarity and Independence

The Mann–Kendall test and Standard Normal Homogeneity Test (SNHT) were performed on annual peak discharge values of 26 streamflow gauging stations to detect monotonic trends, assess homogeneity, and ascertain data stationarity. If there is a trend, the data are non-stationary and unsuitable for frequency analysis without correction. From the test, it was found that only 5 out of 26 gauge stations exhibited a statistically significant trend at the 95% confidence level (for the Mann–Kendall test, a trend is considered significant if the test statistic Z lies outside the range [−1.96, 1.96] and p-value < 0.05), suggesting non-stationarity for annual peak discharge over time. The remaining 21 stations showed no significant trend (p > 0.05), confirming the stationarity of the dataset and suggesting that frequency analysis can be applied directly. Six stations showed non-homogeneous behavior according to the SNHT (for the SNHT, inhomogeneity is detected if the test statistic exceeds 6.95 and p < 0.05). As most stations exhibit no significant trend, it can be assumed that there is no consistent monotonic trend in the streamflow data at the regional level and that the data can be treated as a stationary series. The lack of substantial trends suggests that annual peak discharge variations at most stations are likely due to short-term variability rather than long-term climatic or anthropogenic changes. The test results are presented in

Table 3. Results of the Mann–Kendall trend test (critical Z = ±1.96, critical p-value (MK) = 0.05) and SNHT (critical value = 6.95, critical p-value (SNHT) = 0.05) at 26 gauge Stations (α = 0.05), evaluated at a 95% confidence level.

Station	Z-Value	p-Value (MK)	Kendall’s Tau	SNHT Statistic	Homogeneous	p-Value (SNHT)
SW131.5	1.3257	0.1849	0.1698	4.0221	TRUE	0.2
SW135A	−0.1788	0.858	−0.0666	3.6729	TRUE	0.2
SW135	−2.5264 *	0.0115 *	−0.2350 *	25.9143 *	FALSE	0.01 *
SW138	−2.2254 *	0.0260 *	−0.2156 *	6.8564	TRUE	0.1
SW157	−1.6114	0.107	−0.2333	12.897 *	FALSE	0.01 *
SW158.1	−2.6223 *	0.0087 *	−0.2349 *	13.4951 *	FALSE	0.01 *
SW173	2.0349 *	0.0418 *	0.2751 *	4.6849	TRUE	0.2
SW175.5	2.8646 *	0.0041 *	0.3862 *	7.4874 *	FALSE	0.05 *
SW192	−1.4577	0.1449	−0.1515	8.3583 *	FALSE	0.05 *
SW201	−1.047	0.295	−0.1428	5.1011	TRUE	0.2
SW233A	1.6656	0.0957	0.2129	3.6703	TRUE	0.2
SW233	−0.8893	0.3737	−0.1216	3.2212	TRUE	0.2
SW251	−0.4216	0.6732	−0.0652	1.1437	TRUE	0.2
SW264A	0.9698	0.3321	0.1384	3.1204	TRUE	0.2
SW265	0.3379	0.7354	0.0384	2.1146	TRUE	0.2
SW266	−0.124	0.9012	−0.0217	1.3569	TRUE	0.2
SW267	1.6872	0.0915	0.25	4.2844	TRUE	0.2
SW269	1.4138	0.1574	0.2101	3.7253	TRUE	0.2
SW280	−1.8115	0.07	−0.2126	5.3187	TRUE	0.2
SW326	−0.8893	0.3737	−0.1216	3.2212	TRUE	0.2
SW332	−1.4192	0.1558	−0.2285	6.2345	TRUE	0.2
SW333A	0.2113	0.8325	0.038	1.3085	TRUE	0.2
SW333	−1.047	0.295	−0.1428	5.1011	TRUE	0.2
SW337	0.3324	0.7395	0.0571	1.3458	TRUE	0.2
SW341	−0.1511	0.8798	−0.0285	4.5678	TRUE	0.2
SW67	0.1136	0.9095	0.0151	12.5919 *	FALSE	0.01 *

Note: * Indicates statistically significant trends.

; marked values indicate statistically significant trends.

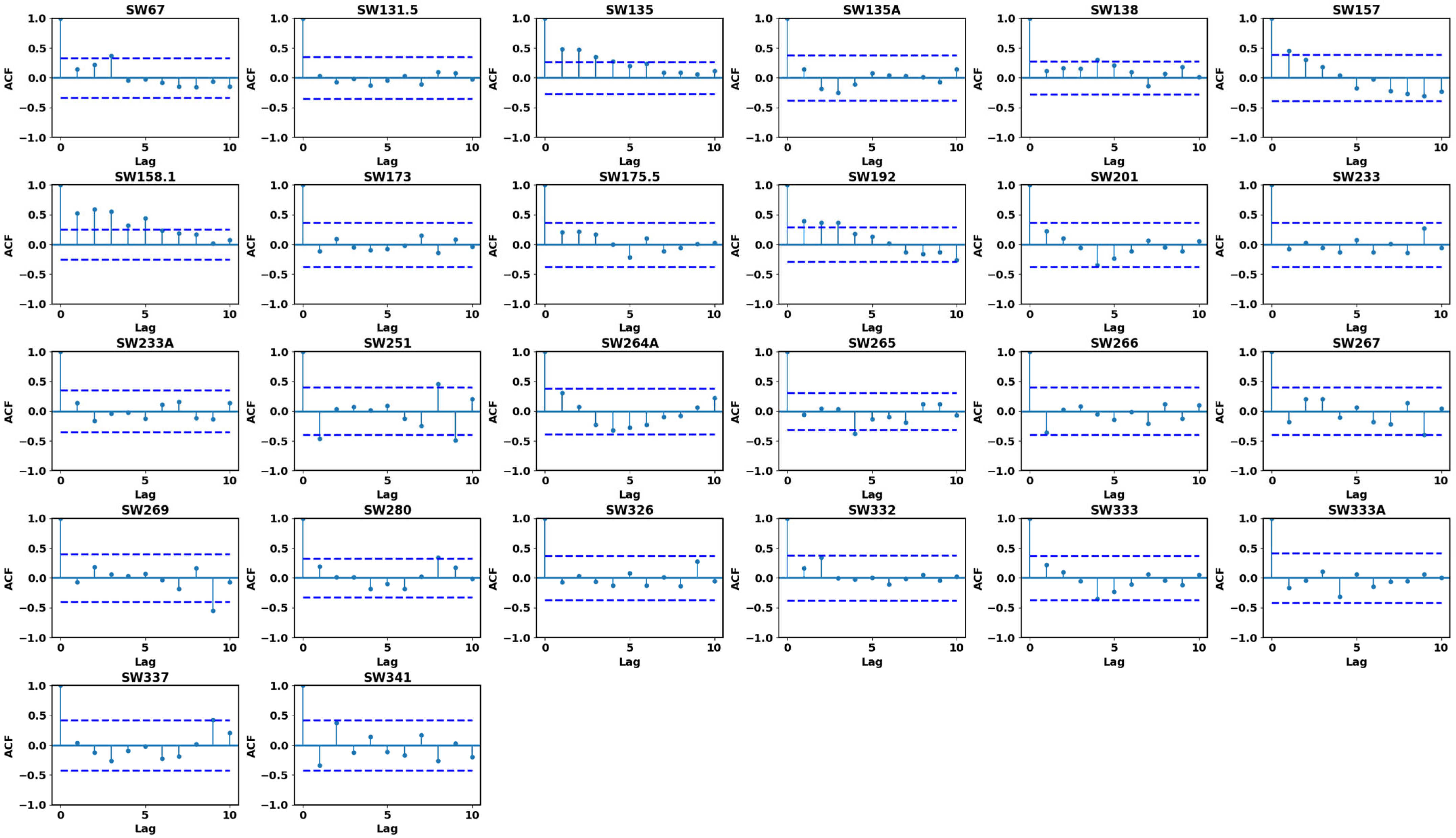
Both autocorrelation and Partial Autocorrelation Function tests were performed to determine how this year’s maximum annual discharge values related to the previous year’s. The test utilized lags of 1 to 10, and the y-axis represented the autocorrelation and partial autocorrelation coefficient while the x-axis represented lag. The 95% confidence level dashed horizontal lines indicate the limits beyond which autocorrelation and partial autocorrelation are significant at the statistical level. For the autocorrelation analysis (ACF) from lag 1 to lag 10, as illustrated in Figure 4, it was observed that most station data do not cross the critical bounds (represented by dashed horizontal lines), indicating no significant autocorrelation in the discharge data at those lags. However, stations such as SW158.1, SW192, and SW135 showed prominent vertical spikes from lag 1 to approximately lag 5, crossing the critical limits. This suggests significant short-term autocorrelation in those stations, implying that past discharge values have a measurable influence on immediate future values. Nonetheless, the insignificance of later lags indicates that this autocorrelation diminishes over time. Most of the autocorrelation values were within boundaries since the data had no significant autocorrelation. The partial autocorrelation analysis (PACF) from lag 1 to lag 10, as illustrated in Figure 5, revealed that the majority of stations remained within the critical bounds across most lags. Certain stations, such as SW135, SW157, SW192, and SW158.1, exhibited notable spikes from lag 1 to lag 2, with values crossing the critical limits, suggesting a significant direct correlation between consecutive years’ discharge values. Importantly, most stations showed minimal partial autocorrelation beyond lag 2, with coefficients generally remaining well within the confidence bounds for higher-order lags. This indicates that while some stations may exhibit direct year-to-year dependence, there is no significant direct relationship between discharge values separated by more than one year when intermediate effects are controlled for. The combined ACF and PACF results demonstrate that the insignificance of correlations at later lags indicates that any existing autocorrelation diminishes over time. Most autocorrelation and partial autocorrelation values were within the critical boundaries, suggesting that yearly flood values are highly independent from year to year across the majority of stations. This pattern reinforces the data independence assumptions underlying flood frequency analysis, justifying the application of standard statistical methods for extreme value analysis of annual maximum discharge data. Also, Moran’s I analysis indicated that cross-correlation between stations was not statistically significant at the 5% level, implying the data series are spatially independent.

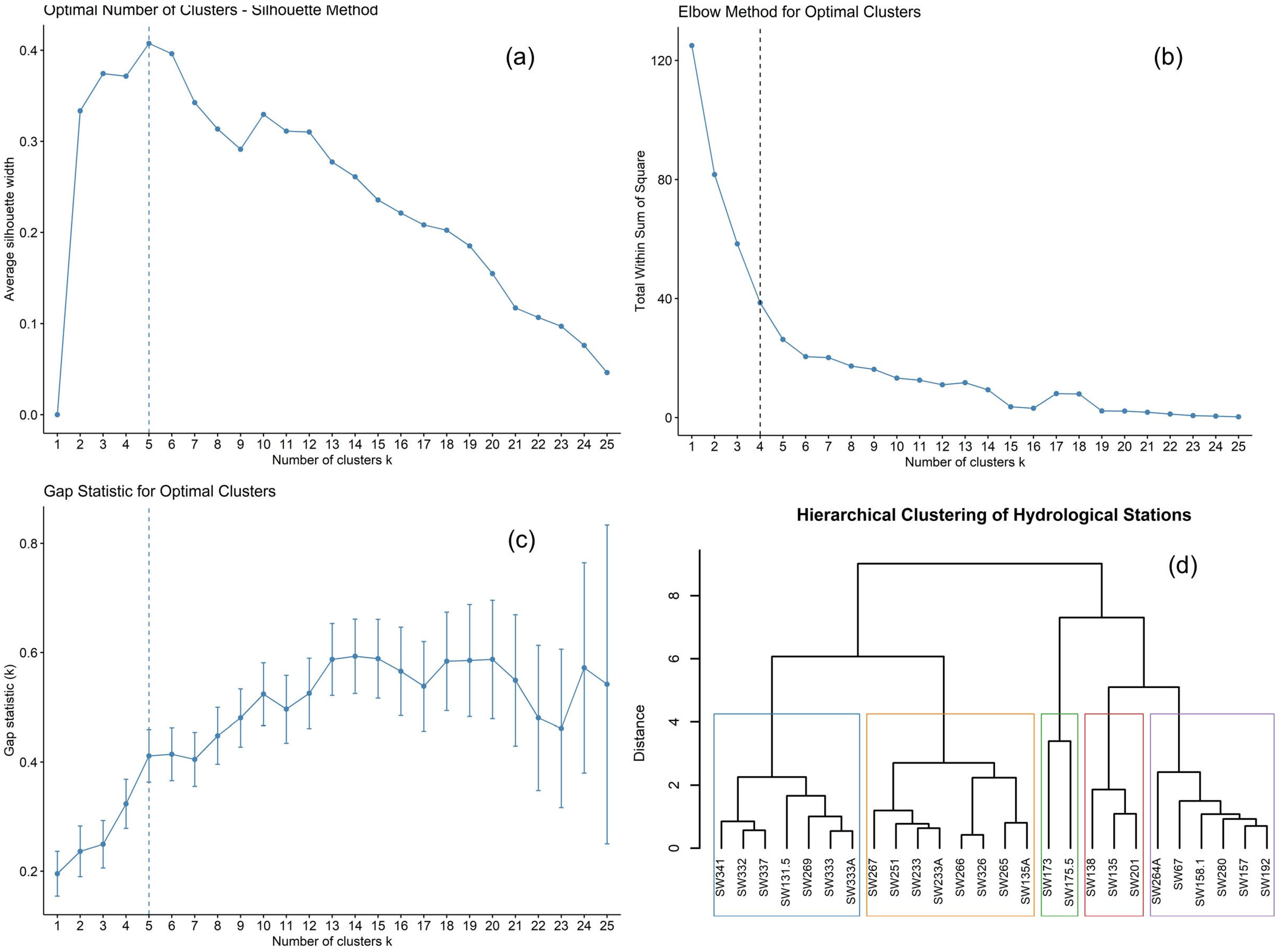
3.2. Initial Grouping by Cluster Analysis

Ward’s hierarchical clustering method was applied to identify homogeneous zones for regional flood frequency analysis (RFFA) using physiographic and climatic parameters, such as latitude, longitude, elevation, catchment area, and Mean Annual Precipitation. A significant drawback of using flood-based statistics to define regions is that such regions may appear statistically homogeneous but may not be hydrologically meaningful or practical for RFFA [77]. Also, regions should not be determined solely based on physiographic characteristics, as these may overlook critical variations in hydrologic response [78]. It is reasonable to include attributes estimated from site measurements, and they should not be strongly correlated with flood values to avoid circular reasoning [42]. Instead, regionalization should use a combination of physical and climatic attributes that are measurable, stable, and not strongly correlated with flood magnitudes—such as catchment area, elevation, Mean Annual Precipitation, and flood seasonality indicators. This approach ensures that the regions are hydrologically meaningful and statistically sound, providing a robust foundation for applying the index flood method and estimating flood quantiles, particularly in data-scarce or ungauged basins.

Several validation techniques were used to identify the optimal number of clusters. The gap statistic and silhouette width suggested five clusters, while the elbow method suggested four as the most suitable number. Overall, the analysis supports the delineation of four to five homogeneous regions. While initial groupings based on these features are informative, the final classification of any region should be confirmed through statistical tests of discordancy and heterogeneity. The results of Ward’s clustering method, showing the optimal number of clusters, are illustrated in the dendrogram shown in Figure 6.

For the first group, with a critical value of 1.92 (D_critical = 1.92), all the included station’s discordancy values are less than this. Notably, SW337 has the least discordancy at 0.17, whereas SW269 is closest to the critical value, with a discordancy of 1.86, indicating no discordant stations in this group. Likewise, the second group, with a D_critical value of 2.14, shows that all stations in this group have discordancy values less than this threshold, with SW251 having the lowest discordancy at 0.34 and SW233A approaching the critical value at 1.81. For group 5, with a D_critical value of 1.65, the discordancy values range from a minimum of 0.67 (SW280) to a maximum of 1.36 (SW264A). For smaller subgroups like group 3 and group 4, the test measures of discordancy are always 1.00, much less than the critical values of 3.00, indicating high agreement within each group. Discordancy and heterogeneity measures are illustrated in

Table 4. Summary of heterogeneity measures and station discordancy values for the five homogeneous groups. Values in the first bracket represent each station’s discordancy values.

Group	Dcritical	Stations Name and Their Discordancy Values (Di)	H1	H2	H3
1	1.92	SW337 (0.17), SW332 (1.74), SW341 (0.91), SW131.5 (1.67), SW269 (1.86), SW333 (0.34), SW333A (0.31)	8.79	6.04	4.48
2	2.14	SW267 (0.68), SW233 (0.94), SW251 (0.34), SW233A (1.81), SW266 (0.99), SW326 (0.68), SW265 (1.51), SW264A (1.04)	4.53	3.55	2.58
3	3	SW173 (1.00), SW175.5 (1.00)	2.06	4.3	3.86
4	3	SW138 (1.00), SW135 (1.00), SW201 (1.00)	6.63	8.94	8.78
5	1.65	SW264A (1.36), SW67 (0.70), SW158.1 (1.04), SW280 (0.67), SW157 (0.93), SW192 (1.30)	1.1	0.08	−0.31

.

In the first group, heterogeneity values vary from 8.79 (H₁) to 4.48 (H₃), indicating significant differences in station streamflow characteristics. This result suggests that although the stations depict overall homogeneity with respect to discordancy, a moderate to high level of variation is observed in their streamflow characteristics, resulting in extreme differences among the stations. These sites span latitudes from 24.0834° to 25.1593°, longitudes from 91.2508° to 91.7538°, and elevations from 8 m (SW135A) to 31 m (SW131.5). Catchment areas range between 350.72 km² (SW332) and 530 km² (SW333A), annual precipitation ranges from 2322.55 mm (SW264A) to 4996.03 mm (SW341), and temperatures range between 18.06 °C (SW333) and 24.50 °C (SW135A).

Contrarily, the second group exhibits comparatively lower heterogeneity values, the highest being 4.53 (H₁) to 2.58 (H₃), pointing towards moderate variation. The stations within this group are more similar to each other than those in the first group. These sites lie between 24.0834° and 25.1624° latitude and between 91.3506° and 92.1729° longitude, with elevations from 21 m to 54 m, basin areas ranging from 726.41 km² (SW326) to 2206.57 km² (SW265), and annual rainfall ranging between 2521.37 mm (SW233A) and 4388.25 mm (SW333). Temperatures vary from 18.06 °C (SW333) to 24.50 °C (SW135A). The third group, composed of SW173 (24.8911° N, 92.1915° E) and SW175.5 (24.6303° N, 91.6813° E), with elevations of 59 m and 28 m, respectively, shows moderate heterogeneity with H₂ = 4.30 and H₁ = 2.06. This group’s catchments vary widely: 25,337.01 km² for SW173 versus 33,855.2 km² for SW175.5, with precipitation around 2253.36 mm (SW173) and 2360.13 mm (SW175.5) and temperatures of 20.89 °C and 21.71 °C, respectively. The fourth group exhibits excessive heterogeneity, with H-values as high as H₃ = 8.78 and H₁ = 6.63. These sites are spread across latitudes of 24.2930° to 24.5902° N and longitudes of 91.5465° to 92.1177° E, with basin areas of 166.96 km² (SW138), 789.53 km² (SW135), and 2292.71 km² (SW201). Precipitation ranges from 2041.92 mm (SW201) to 2261.90 mm (SW138), while temperatures span 23.84 °C to 24.50 °C, indicating notable hydrological and climatic divergence. Lastly, the fifth group is distinguished by its extremely low heterogeneity, with values ranging from H₁ = 1.10 to H₂ = 0.08, signaling a highly homogeneous hydrological response among the stations. These sites are closely clustered between 24.0838° and 25.1301° N and between 91.3506° and 91.8489° E, with elevations from 21 m (SW264A) to 25 m (SW157). Catchment areas are generally modest, between 61.29 km² (SW192) and 1142.76 km² (SW157). Rainfall is also fairly uniform, ranging from 2199.38 mm (SW157) to 4474.48 mm (SW341), and temperature values are consistently between 24.12 °C and 24.55 °C.

In general, although most groups are homogeneous in terms of discordancy (D_i < D_critical), the measures of heterogeneity ($H\ge 2$) indicate a range of variability within the groups. There are groups with high heterogeneity (groups 1 and 4) and groups with minimal variation (group 5).

3.3. Formation of Homogeneous Regions by Discordancy and Heterogeneity Measures

As shown in Table 4, although the discordancy levels were mostly acceptable, the initially high heterogeneity among most groups required an intensive refinement process to achieve more homogeneous regional groupings of the initially clustered homogeneous groups; the final grouping resulted in four well-defined regions exhibiting acceptable homogeneity. This process involved a series of iterations, where the stations were regrouped based on heterogeneity checks and discordancy assessments. In each iteration, the groups were rearranged carefully, and the discordancy and heterogeneity values were recalculated to ensure all regions met the specified standards (i.e., D_i < D_critical and $H\le 2$), as shown in

Table 5. The regional homogeneity assessment results show site groupings, discordancy statistics (D_i), and heterogeneity measures (H₁, H₂, H₃).

Region	Sites (Di) *	Dcrit.	H1	H2	H3
1	SW175.5 (1.00), SW266 (1.00), SW267 (1.00), SW269 (1.00)	3.00	0.94	0.91	1.16
2	SW131.5 (0.60), SW138 (0.88), SW158.1 (1.41), SW192 (0.52), SW332 (1.46), SW233A (1.47), SW333A (0.66)	1.92	1.31	1.76	1.77
3	SW135 (0.46), SW173 (2.10), SW233 (0.15), SW251 (2.16), SW265 (0.46), SW326 (0.15), SW333 (2.26), SW337 (0.26)	2.14	0.34	0.89	1.04
4	SW67 (1.21), SW157 (0.71), SW280 (1.64), SW341 (0.35), SW135A (1.40), SW264A (0.68)	1.65	0.70	0.34	0.26

Note: * Values in the first bracket represent each station’s discordancy values.

.

As shown in Table 5, region 1 consists of four stations: SW175.5, SW266, SW267, and SW269. These stations are geographically confined to a small region and exhibit similar hydrological characteristics. Region 2 comprises seven stations: SW131.5, SW138, SW158.1, SW192, SW332, SW233A, and SW333A. Although these stations are reasonably dispersed across the study area, they share similar runoff characteristics. Region 3 consists of eight stations: SW135, SW173, SW233, SW251, SW265, SW326, SW337, and SW333. This region encompasses a hydrologically heterogeneous region, including upstream and downstream basins, resulting in substantial elevation and basin area variation. Region 4 comprises six stations: SW67, SW157, SW280, SW341, SW135A, and SW264A. Lastly, SW201 could not be assigned to any group and was therefore omitted, as including SW201 in any region caused the discordancy (D_i) and heterogeneity (H) values to exceed their acceptable thresholds, violating the grouping criteria (i.e., D_i < D_critical and $H\le 2$). The final arrangement, as outlined in the table, is the best categorization, in which there were no discordant stations, except for station SW333 of region 3, which slightly surpassed the critical discordancy (D_i (2.26) > D_critical (2.14)) value but passed the heterogeneity test. The location of all four homogeneous regions is shown in Figure 7.

3.4. Goodness-of-Fit Test and Selection of the Best Parent Distribution, Along with the Derivation of the Growth Curve for Each Homogeneous Region

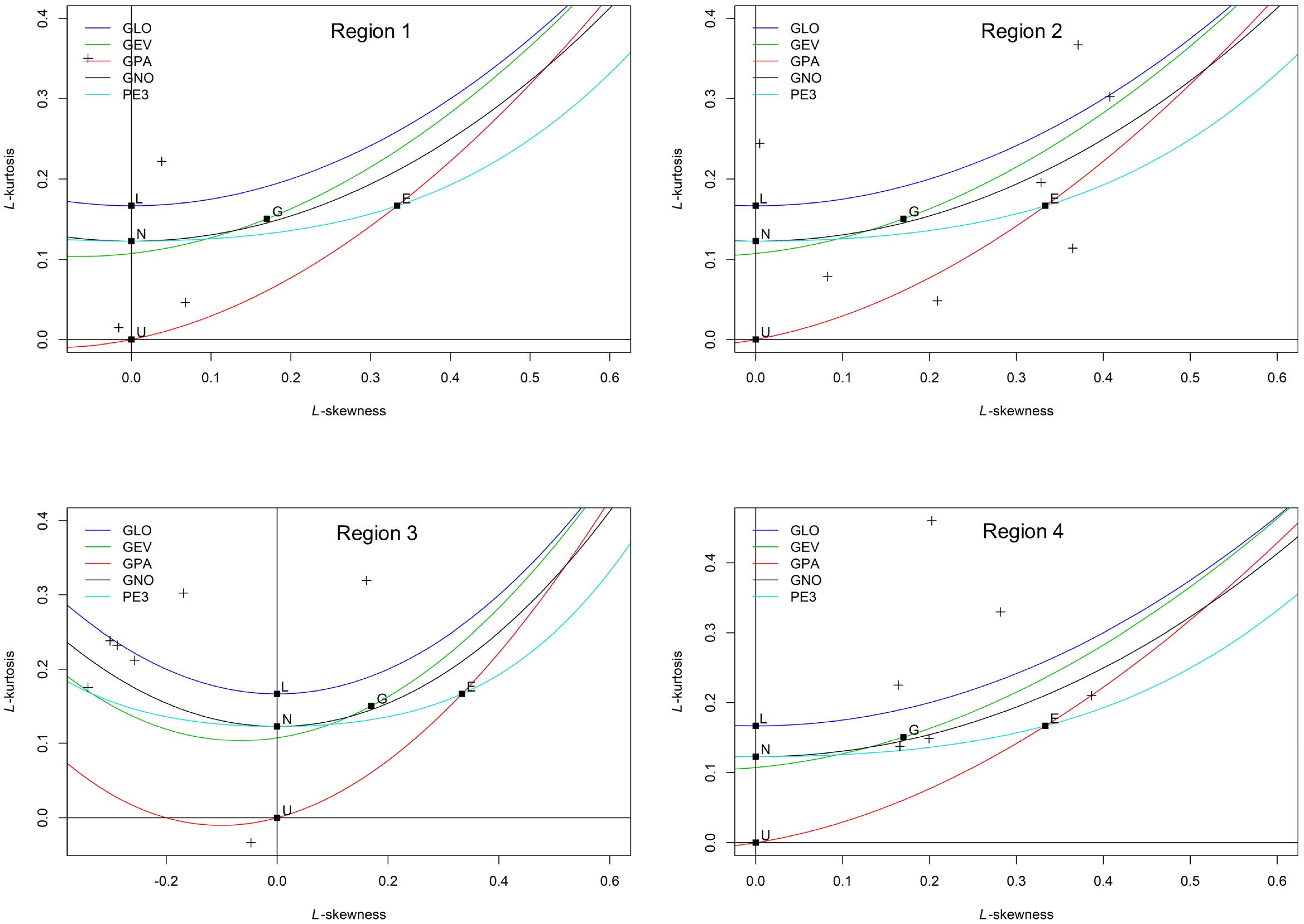
We created L-moment diagrams to assess the probability distributions in the study area. Figure 8 presents a comparison between the observed data and theoretical distribution patterns. However, finding a suitable probability distribution to fit most of the observed regional data is challenging.

The variation in hydrological conditions among sites results in wide-ranging variation in L-moment characteristic values. The single distribution, thus, does not always yield the optimum possible fit for every site. Whereas some datasets perform reasonably well when fitted against the Generalized Extreme Value (GEV) or Pearson Type III distributions, others exhibit extreme disagreement. This suggests that a flexible or site-specific approach to distribution fitting may be necessary to represent the underlying hydrological processes in the region accurately.

To identify suitable parent distributions for each homogeneous region, the good-ness-of-fit statistic ${\mathit{Z}}_{\mathit{DIST}}$ was determined for several candidate distributions: Generalized Logistic (GLO), Generalized Extreme Value (GEV), Generalized Normal (GNO), Generalized Pareto (GPA), and Pearson Type III (PE3). In cases where multiple ${\mathit{Z}}_{\mathit{DIST}}$ values fell within the acceptable range (${\mid \mathit{Z}}_{\mathit{DIST}}\mid \le 1.64$) for a region, a simulation-based approach was adopted to select the most robust distribution [42]. Any distribution with a calculated value not exceeding this threshold was considered a potential candidate, as denoted in

Table 6. Values of Z_DIST statistics for candidate distributions.

Serial No.	Region	GLO	GEV	GNO	PE3	GPA
1	Region 1	0.32	1.20	0.83	0.83	3.97 a
2	Region 2	0.05	0.87	1.37	2.27 a	3.01 a
3	Region 3	1.01	3.55 a	2.44 a	3.02 a	7.28 a
4	Region 4	0.77	1.46	1.79 a	2.39 a	3.18 a

Note: ^a Indicates the calculated values exceeding the critical value of 1.64.

.

Table 7. Regional parameters for the four candidate distributions for L-moments.

Region	Distribution	ξ (Location)	α (Scale)	K (Shape)
Region 1	Gen. Logistic	0.9992	0.045	−0.0112
	Gen. Extreme Value	0.9713	0.0786	0.2638
	Gen. Normal	0.9991	0.0797	−0.0229
	Pearson Type III	1	0.0798	0.0688
Region 2	Gen. Logistic	0.8210	0.3617	−0.2749
	Gen. Extreme Value	0.6193	0.5014	−0.1570
	Gen. Normal	0.8023	0.6350	−0.5729
Region 3	Gen. Logistic	1.0511	0.1483	0.1997
Region 4	Gen. Logistic	0.8471	0.3412	−0.2525
	Gen. Extreme Value	0.6549	0.4816	−0.1246

shows the estimates of the regional parameters for L-moments for the suitable probability distribution.

For regions 1, 2, and 4, more than one distribution passed the critical value in one region. To further narrow down the selection and determine the best distribution, we compared the Root Mean Square Error (RMSE) values and 95% confidence intervals of the regional growth curves for each qualifying distribution. For example, in region 1, the GLO, GEV, GNO, and PE3 distributions all passed the criteria set by the critical value test. Among these distributions, GLO showed the narrowest 95% confidence intervals and lowest RMSE value, particularly for the 50- and 100-year return periods, indicating higher accuracy and less uncertainty in extreme value estimation. Therefore, GLO was selected as the most appropriate distribution for region 1. The same procedure was followed for regions 2, 3, and 4.

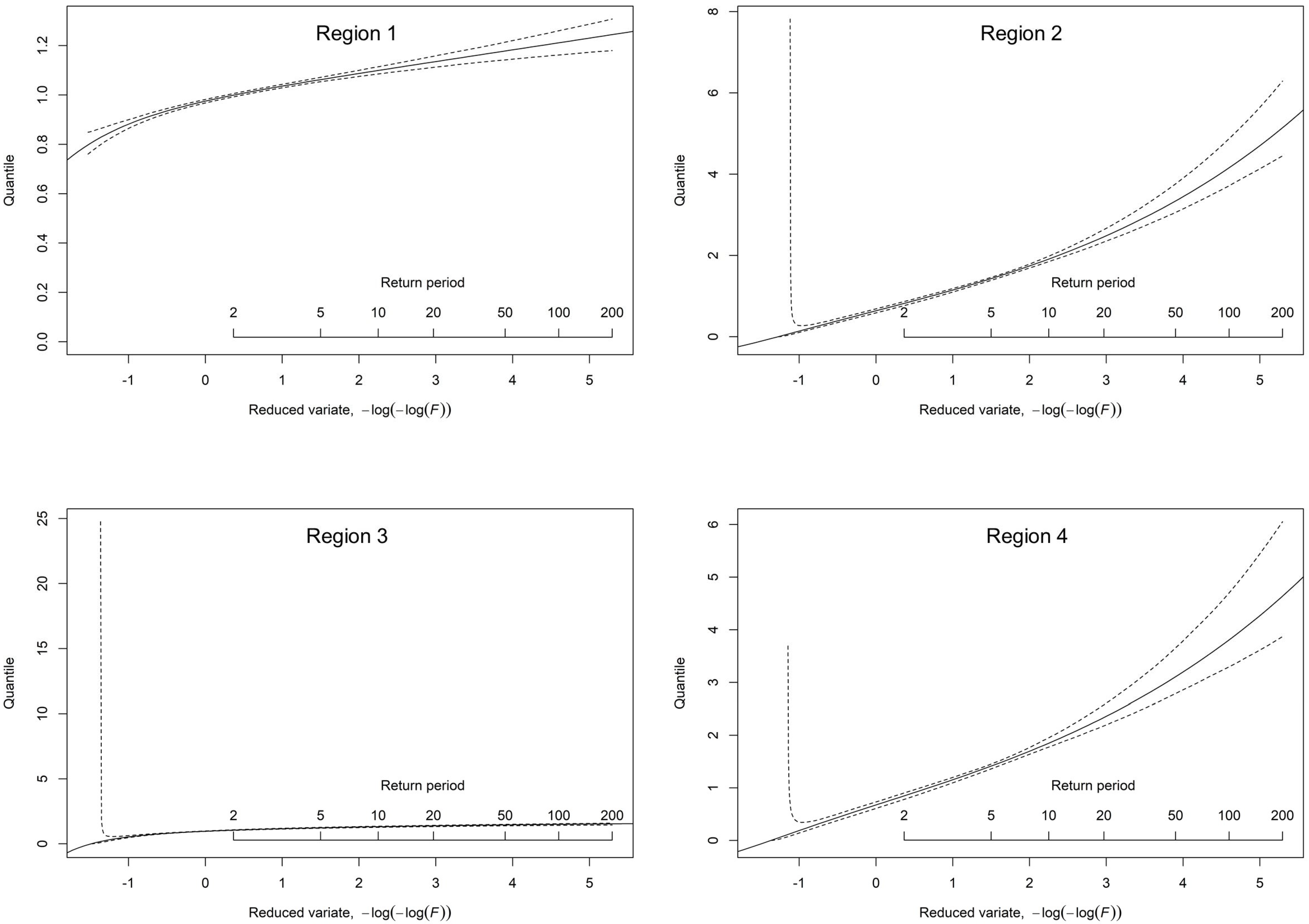
Although more than one distribution passed the initial critical value threshold, GLO always had the lowest RMSE or the smallest and most consistent 95% error bounds for all significant return periods. For this reason, GLO was selected as the best fit for all four regions. Moreover, regional growth curves with 95% error bounds for GLO distribution are given in Figure 9. As presented in

Table 8. Estimated regional quantiles and corresponding accuracy metrics for the four identified homogeneous regions for GLO distribution.

	Return Period	2 Years	5 Years	10 Years	20 Years	50 Years	100 Years	200 Years	1000 Years
Region 1	f	0.5	0.8	0.9	0.95	0.98	0.99	0.995	0.999
	q(F)	0.9991	1.0620	1.0992	1.1338	1.1781	1.2113	1.2445	1.3222
	RMSE	0.0025	0.0082	0.0123	0.0166	0.0243	0.0323	0.0424	0.0740
	Lower Bound	0.9951	1.0526	1.0820	1.1063	1.1337	1.1507	1.1653	1.1884
	Upper Bound	1.0033	1.0773	1.1208	1.1597	1.2077	1.2426	1.2774	1.3575
Region 2	q(F)	0.8210	1.4314	1.9123	2.4612	3.3405	4.1586	5.1431	8.2901
	RMSE	0.0189	0.0856	0.1634	0.2612	0.4621	0.7097	1.0853	2.7769
	Lower Bound	0.7869	1.3347	1.7030	2.0859	2.6369	3.0998	3.6054	4.9954
	Upper Bound	0.8440	1.5995	2.2242	2.9136	3.9559	4.8887	5.9676	9.1964
Region 3	q(F)	1.0511	1.2307	1.3149	1.3813	1.4524	1.4972	1.5358	1.6069
	RMSE	0.0073	0.0517	0.0746	0.0946	0.1204	0.1401	0.1601	0.2068
	Lower Bound	1.0408	1.1577	1.2024	1.2316	1.2560	1.2679	1.2759	1.2813
	Upper Bound	1.0641	1.3186	1.4326	1.5167	1.5997	1.6481	1.6885	1.7572
Region 4	q(F)	0.8471	1.4135	1.8492	2.3379	3.1059	3.8075	4.6387	7.2253
	RMSE	0.0175	0.0677	0.1246	0.1961	0.3499	0.5461	0.8468	2.1913
	Lower Bound	0.8161	1.3418	1.6929	2.0513	2.5513	2.9598	3.4013	4.5394
	Upper Bound	0.8697	1.5481	2.0904	2.6808	3.5651	4.3449	5.2387	7.8847

, quantile estimates across 50-, 100-, 200-, and 1000-year return periods (f = 0.98, 0.99, 0.995, 0.999) reveal significant regional variations in precision and uncertainty. Region 1 demonstrates exceptional stability, with consistently low RMSEs (0.0243 for 50-year, 0.0323 for 100-year, 0.0424 for 200-year, and 0.0740 for 1000-year) and narrow confidence bounds (1.1337–1.2077 for 50-year, 1.1507–1.2426 for 100-year, 1.1653–1.2774 for 200-year, and 1.1884–1.3575 for 1000-year), indicating highly reliable predictions across all return periods. Region 2 shows dramatically increasing uncertainty, with RMSEs surging from 0.4621 (50-year) to 0.7097 (100-year), 1.0853 (200-year), and 2.7769 (1000-year), accompanied by rapidly expanding bounds (2.6369–3.9559 to 3.0998–4.8887 to 3.6054–5.9676 to 4.9954–9.1964), highlighting difficulties in extreme value estimation.

Region 3 maintains moderate precision throughout, with RMSEs ranging from 0.1204 to 0.2068 and bounds (1.2560–1.5997 to 1.2679–1.6481 to 1.2759–1.6885 to 1.2813–1.7572) that suggest reasonable reliability even for rare events. Region 4 exhibits concerning variability, particularly for more extended return periods, with RMSEs climbing from 0.3499 (50-year) to 0.5461 (100-year), 0.8468 (200-year), and 2.1913 (1000-year) and bounds widening significantly (2.5513–3.5651 to 2.9598–4.3449 to 3.4013–5.2387 to 4.5394–7.8847). These patterns underscore critical regional differences in extreme value behavior, with regions 1 and 3 offering relatively stable estimates suitable for precise risk assessment. In contrast, region 2 and region 4 require cautious interpretation and potentially more conservative approaches in engineering and planning applications due to their pronounced uncertainty, especially for 200-year and 1000-year events. Regional flood quantile estimates with associated uncertainty bands across different return periods are plotted in Figure 10.

The log-log return period plot in Figure 10 shows that the regional q(F) curves both intersect and diverge at different return periods, highlighting important hydrological differences among the regions. At lower return periods (around 2 to 5 years), region 3 initially exhibits higher quantile values compared to region 2 and region 4, indicating a greater frequency of moderate events; however, as the return period increases, the curves for regions 2 and 4 rise more steeply and overtake region 3, suggesting a higher magnitude of extreme events in those regions. This crossing pattern implies that the severity of events relative to other regions shifts depending on the frequency of occurrence. Beyond approximately 10 to 20 years, the curves begin to diverge significantly—regions 2 and 4 continue to rise rapidly, while regions 1 and 3 remain relatively flat, indicating lower susceptibility to rare, extreme events. This divergence at higher return periods underscores the need for region-specific planning, as some areas face far greater risks of severe hydrological extremes than others.

3.5. Regional Flood Frequency Relationship for Ungauged Catchments

To estimate the T-year return period flood at a site, the mean annual peak flow must first be determined. However, due to the lack of observed flow data, this site-specific mean cannot be calculated for ungauged catchments. In such cases, developing a relationship between the mean annual peak flows of gauged catchments in the region and their corresponding physiographic and climatic characteristics becomes essential. This regional relationship can then estimate ungauged sites’ mean annual peak flow at different return periods.

At-site annual maximum discharge values for various return periods were derived by multiplying the regional growth curve values by the mean annual peak discharge specific to each site.

Table 9. Estimated maximum flood discharges corresponding to various non-exceedance probabilities (return periods).

Non-Exceedance Probability f (Return Period, Year)
f	0.5	0.8	0.9	0.95	0.98	0.99	0.995	0.999
Station ID	2 Years	5 Years	10 Years	20 Years	50 Years	100 Years	200 Years	1000 Years
SW264A	18.83	31.41	41.10	51.96	69.03	84.63	103.11	160.60
SW135A	125.94	210.14	274.93	347.58	461.77	566.08	689.67	1074.22
SW341	1031.48	1721.04	2251.59	2846.59	3781.80	4636.03	5648.18	8797.55
SW280	47.72	79.62	104.17	131.70	174.97	214.49	261.32	407.04
SW157	263.38	439.46	574.94	726.87	965.68	1183.80	1442.25	2246.44
SW67	91.39	152.49	199.49	252.21	335.08	410.76	500.44	779.49
SW333	166.68	195.17	208.53	219.06	230.34	237.44	243.56	254.84
SW337	541.23	633.74	677.10	711.29	747.92	770.97	790.86	827.48
SW326	811.03	949.64	1014.62	1065.86	1120.75	1155.28	1185.08	1239.95
SW265	428.34	501.55	535.87	562.93	591.92	610.15	625.89	654.88
SW251	987.43	1156.19	1235.30	1297.69	1364.51	1406.55	1442.84	1509.65
SW233	811.03	949.64	1014.62	1065.86	1120.75	1155.28	1185.08	1239.95
SW173	1965.57	2301.51	2458.99	2583.17	2716.19	2799.87	2872.11	3005.10
SW135	1968.63	2305.09	2462.81	2587.19	2720.41	2804.23	2876.58	3009.77
SW333A	486.15	847.56	1132.37	1457.38	1978.08	2462.45	3045.45	4908.90
SW233A	586.20	1022	1365.42	1757.32	2385.18	2969.25	3672.23	5919.20
SW332	1401.72	2443.78	3264.98	4202.07	5703.40	7100.01	8780.95	14,153.86
SW192	40.51	70.62	94.36	121.44	164.83	205.20	253.78	409.06
SW158.1	199.94	348.58	465.72	599.39	813.54	1012.76	1252.53	2018.94
SW138	57.34	99.98	133.57	171.91	233.34	290.48	359.25	579.07
SW131.5	844.89	1473.03	1967.98	2532.82	3437.76	4279.57	5292.76	8531.31
SW175.5	2001.96	2127.87	2202.43	2271.74	2360.45	2426.92	2493.43	2649.13
SW266	1951.70	2074.45	2147.14	2214.71	2301.20	2366.05	2430.84	2582.62
SW267	1748.16	1858.10	1923.21	1983.74	2061.20	2119.25	2177.32	2313.28
SW269	2886.04	3067.55	3175.04	3274.96	3402.85	3498.67	3594.55	3819.03

provides the estimated maximum flood discharges corresponding to each gauging station, reflecting the expected discharge levels for different return intervals. Key geomorphological parameters were extracted using Geographic Information System (GIS) software (ArcGIS Desktop 10.8) and presented in

Table 10. Geomorphological parameters of the watersheds derived from GIS analysis.

Station ID	Total Stream Length (km)	Number of Streams	Perimeter (km)	Main Channel Length (km)	Max Basin Length (km)	Max Stream Order
SW264A	5.79	5	53.87	1.78	17.85	2
SW135A	122.22	21	182.66	19.18	57.89	3
SW341	84.94	9	173.61	22.39	59.11	2
SW280	33.66	5	89.23	20.38	30.7	2
SW157	168.65	37	226.41	17.11	67.57	2
SW67	104.94	21	193.68	24.08	63.5	2
SW333	94.44	7	202.86	29.93	62.99	2
SW337	10.25	1	49.08	10.25	18.41	1
SW326	108.02	17	187.77	15.99	56.92	3
SW265	414.65	43	358.97	29.07	124.04	3
SW251	146.51	11	214.97	36.61	57.45	2
SW233	137.25	15	184.06	33.4	54.89	3
SW173	2644.87	264	1426.02	47.11	378.68	5
SW135	119.4	21	181.15	19.18	57.89	3
SW333A	86.93	7	191	23.71	59.09	2
SW233A	139.71	15	186.23	33.4	54.89	3
SW332	53.72	7	112.65	16.65	40.67	3
SW192	12.06	1	51.5	12.06	17.65	1
SW158.1	232.26	43	294.17	26.15	85.2	3
SW138	26.91	1	94.74	26.91	31.33	1
SW131.5	430.38	51	392.39	36.15	105.25	4
SW175.5	3636.26	360	1616.52	74.07	410.46	5
SW266	276.17	37	277.08	25.64	76.6	3
SW267	340.78	37	434.36	71.75	106.61	3
SW269	762.12	75	683.95	78.48	159.95	5

. These include Total Stream Length and Number of Streams, representing the cumulative length and count of stream segments within the watershed. Additional attributes such as Perimeter, Main Channel Length, Maximum Basin Length, and Maximum Stream Order describe the watershed boundary, principal flow path, longest dimension, and drainage network complexity—factors that significantly influence hydrological response and flood behavior.

Equations for the prediction of peak flood discharge for various return periods were developed using the Multiple Non-Linear Regression (MNLR) model, based on watershed and climatic variables, as shown in

Table 11. Annual maximum flood discharge equations for different return periods.

Return Period	Equation	R2	RMSE	MAPE (%)
Q2	Q = 2.48 × 10−16 × A0.2325 × E1.7621 × TSL−0.3745 × NS1.0083 × P0.6086 × MCL0.0850 × MBL−0.9550 × MSO−0.5222 × MAP3.8834 × MAT1.0942	0.869	438.34	42.68
Q5	Q = 1.68 × 10−11 × A0.1712 × E1.6987 × TSL−0.4499 × NS1.0641 × P0.0461 × MCL0.1968 × MBL−0.4628 × MSO−0.4407 × MAP3.2083 × MAT−0.2086	0.865	522.34	41.00
Q10	Q = 5.81 × 10−9 × A0.1378 × E1.6584 × TSL−0.4958 × NS1.0969 × P−0.2345 × MCL0.2628 × MBL−0.2173 × MSO−0.3964 × MAP2.8488 × MAT−0.8830	0.852	615.60	42.32
Q20	Q = 9.74 × 10−7 × A0.1078 × E1.6195 × TSL−0.5386 × NS1.1269 × P−0.4722 × MCL0.3239 × MBL−0.0096 × MSO−0.3564 × MAP2.5317 × MAT−1.4685	0.833	746.88	45.32
Q50	Q = 4.97 × 10−4 × A0.0702 × E1.5684 × TSL−0.5931 × NS1.1646 × P−0.7521 × MCL0.4018 × MBL0.2351 × MSO−0.3062 × MAP2.1430 × MAT−2.1755	0.797	995.60	49.74
Q100	Q = 4.44 × 10−2 × A0.0425 × E1.5294 × TSL−0.6337 × NS1.1923 × P−0.9482 × MCL0.4599 × MBL0.4065 × MSO−0.2691 × MAP1.8615 × MAT−2.6816	0.762	1253.85	53.95
Q200	Q = 3.52 × A0.0150 × E1.4899 × TSL−0.6740 × NS1.2197 × P−1.1353 × MCL0.5178 × MBL0.5700 × MSO−0.2321 × MAP1.5862 × MAT−3.1723	0.721	1585.62	58.97
Q1000	Q = 6.90 × 104 × A−0.0488 × E1.3965 × TSL−0.7670 × NS1.2821 × P−1.5465 × MCL0.6522 × MBL0.9292 × MSO−0.1463 × MAP0.9612 × MAT−4.2745	0.610	2726.48	73.62

. These equations incorporate key parameters such as area (km²) (A), elevation (m) (E), Total Stream Length (km) (TSL), Number of Streams (NS), Perimeter (km) (P), Main Channel Length (km) (MCL), Maximum Basin Length (km) (MBL), Maximum Stream Order (MSO), Mean Annual Precipitation (mm) (MAP), and Mean Annual Temperature (°C) (MAT) for estimating peak discharge.

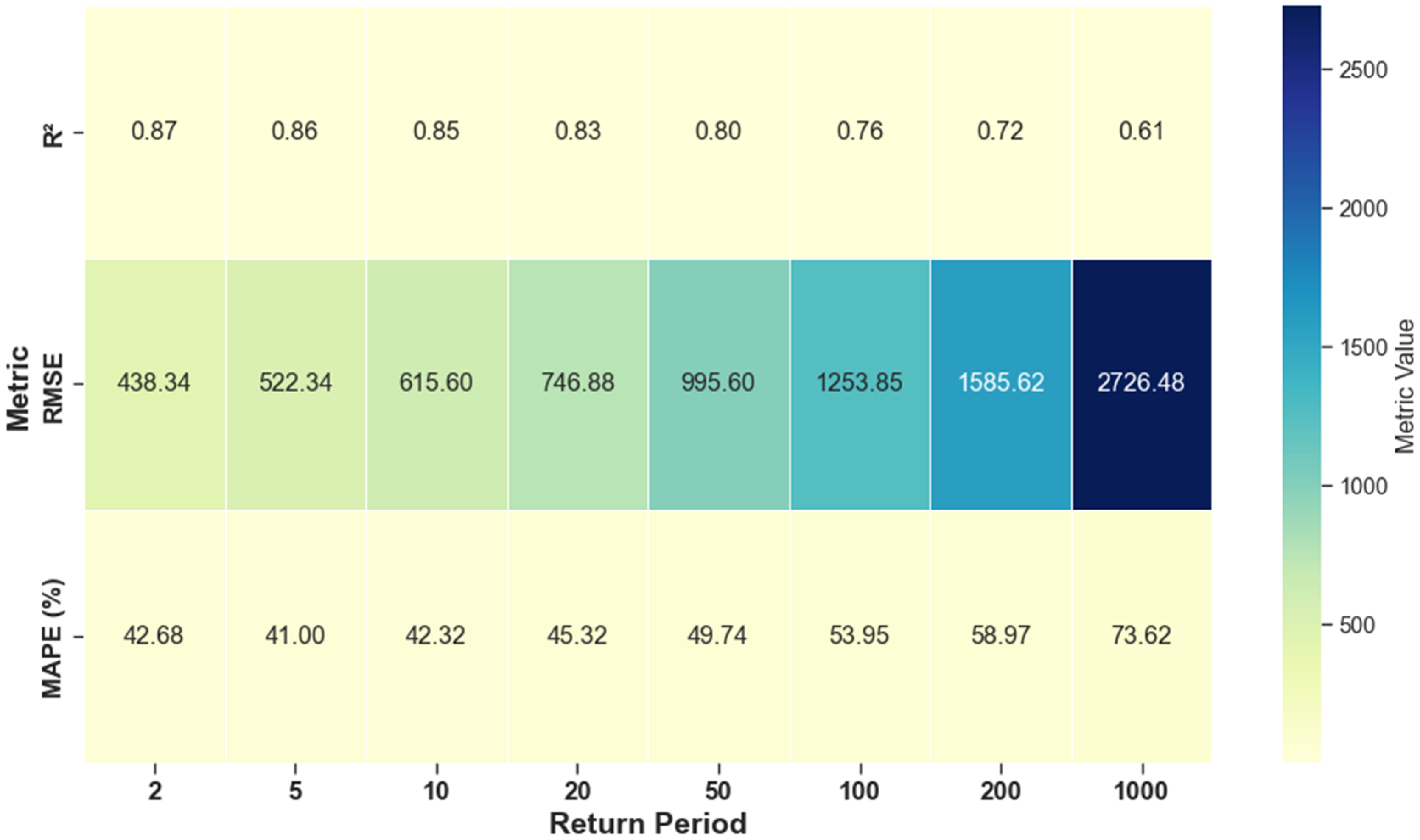
The performance of the models, as indicated by the Coefficient of Determination (R²), Root Mean Square Error (RMSE), and Mean Absolute Percentage Error (MAPE), demonstrates strong predictive accuracy, as illustrated in Figure 11, particularly for lower return periods. Predictive reliability decreases with increasing return periods, reflecting growing uncertainty in extreme flood estimation.

It should be noted that the equations are only applicable to the four homogeneous regions created earlier and are intended for use in both gauged and ungauged catchments within those regions. As the return period increases, predictive performance weakens, evidenced by the decline in R² values and the increase in both RMSE and MAPE (Table 11). The pattern shows the growing uncertainty and complexity in quantifying long-return-period extreme flood events. Lower values of R² and larger errors at longer return periods highlight model limitations in reliability for extreme floods and imply large variance. Hence, these uncertainties and associated errors must be cautiously quantified while utilizing the models, especially for long-return-period events.

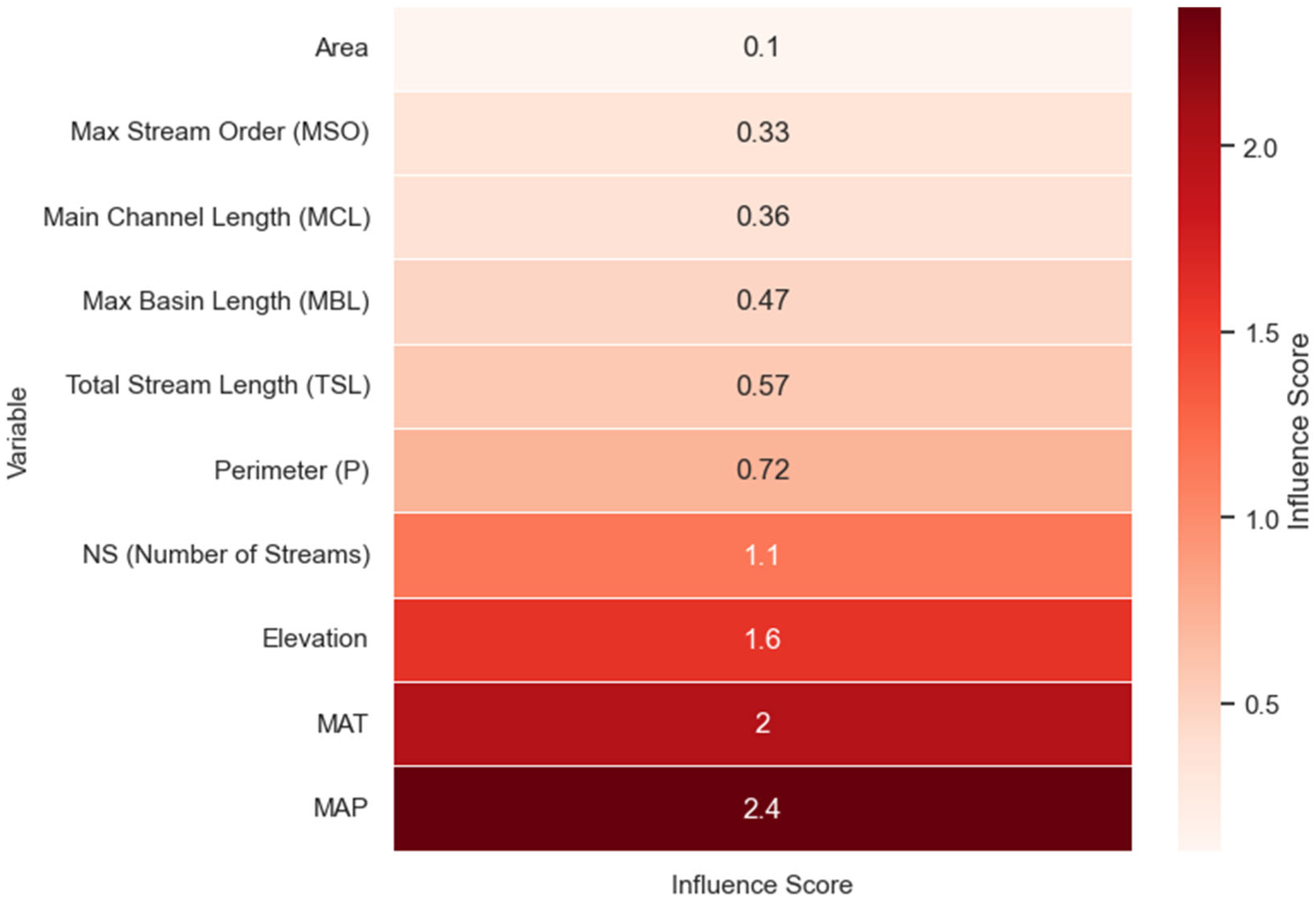
Figure 12 illustrates the average impact of various physiographic and climatic variables on peak discharge, based on the absolute values of exponents in Multiple Non-Linear Regression equations. Among the variables considered, Mean Annual Precipitation and Mean Annual Temperature exhibit the largest effect values, 2.4 and 2.0, respectively, indicating their dominant control on peak discharge. Elevation (1.6), Number of Streams (1.1), and Perimeter (0.72) also reflect comparatively high control. Geometric parameters such as area (0.1), Maximum Stream Order (0.33), and Main Channel Length (0.36) exhibit lower values of influence, reflecting comparatively less impact on peak flow generation. The trend reveals the significant contribution of climatic and topographic factors over the simple morphometric parameters in the formation of flood peaks.

4. Discussion

This study presents a comprehensive framework for regional flood frequency analysis (RFFA) using L-moments in northeastern Bangladesh, addressing critical gaps in existing methodologies by integrating rigorous data screening via the Mann–Kendall test, the Standard Normal Homogeneity Test, autocorrelation, partial autocorrelation, and Moran’s I test to ensure stationarity and spatial independence—an essential step often overlooked [20,21,23,24,25]. This contrasts with earlier assumptions that flood flows strictly follow specific probability distributions, and the current study highlights the importance of flexible, region-specific approaches in flood frequency analysis. In many cases, the scale and shape parameters of the distributions were estimated using the method of moments. A key finding from several studies conducted in Bangladesh is the superiority of the Generalized Logistic (GLO) distribution over traditionally used distributions such as Log-Normal (both two-parameter (LN2) and three-parameter (LN3)), Extreme Value Type-I (EV1), and Log Pearson Type III (LP3) distributions [21]; the Gumbel and Powell method [23]; and Gumbel, Powell, and Ven Te Chow and Stochastic methods [24]. The GLO distribution demonstrated narrower confidence intervals and lower RMSE, providing more reliable quantile estimates across all return periods. The study enhances the initial regional grouping by applying Ward’s hierarchical clustering algorithm, with cluster validity evaluated using silhouette width analysis, gap statistics, and the elbow method. The study strengthens the analysis by incorporating both discordancy measures (D_i statistic) and heterogeneity measures (H-statistics), which were not employed in the previous approach in Bangladesh [20]. For ungauged basins, Multiple Non-Linear Regression (MNLR) models incorporating geomorphologic and climatic predictors—previously unexplored in the context of Bangladesh—achieved strong performance with R² = 0.61–0.87 for 2- to 100-year floods. Although uncertainty increased for extreme events (MAPE = 41–74%, RMSE up to 2726 m³/s for 1000-year floods), the results are consistent with findings from similar studies conducted globally [12]. In contrast, some previous studies outside Bangladesh [16] used only a single predictive variable (area), whereas this study employs 10 geomorphologic and climatic variables to improve prediction accuracy.

5. Conclusions

The present study successfully identified four hydrologically homogeneous regions within the Sylhet Division of Bangladesh using a robust framework integrating L-moments, hierarchical clustering, and physiographic–statistical analysis. This approach addresses critical gaps in regional flood frequency analysis (RFFA) for data-scarce, monsoon-dominated regions, offering scalable solutions for flood risk management. The GLO distribution emerged as the most suitable model across all regions, demonstrating narrow confidence intervals and low Root Mean Square Error (RMSE) values. This contrasts with earlier studies in Bangladesh that favored Log Pearson Type III or Gumbel distributions, highlighting the importance of region-specific methodologies. The superiority of GLO may stem from its flexibility in capturing the tail behavior of flood data in monsoonal climates, where extreme rainfall and rapid runoff responses dominate. The L-moments approach, being less sensitive to outliers than conventional moments, likely enhanced the robustness of distribution selection, particularly in regions with limited data. Multiple Non-Linear Regression models could predict peak discharges in ungauged catchments from geomorphological and climatic predictors. Still, predictive uncertainty increased for extreme events. Future work should incorporate climate change projections to assess non-stationarity, as rising temperatures and intensifying monsoons could alter flood regimes. Expanding the framework to include socio-economic vulnerability metrics could enhance its utility for holistic flood risk management. Overall, this study establishes a replicable L-moments and clustering framework for flood frequency analysis tailored to the complex hydro-climatic setting of northeastern Bangladesh. By identifying region-specific flood behaviors and providing tools for ungauged basins, the findings directly support climate-resilient infrastructure planning and agricultural protection in one of Bangladesh’s most flood-prone regions, and the integration of advanced statistical validation and geospatial techniques sets a precedent for similar monsoonal basins globally, where balancing data limitations with hydrological complexity remains a critical challenge.