Abstract
Rivers play a crucial role in nutrient cycling, yet are increasingly affected by eutrophication due to anthropogenic activities. This study focuses on the Barato River in Hokkaido, Japan, employing an integrated approach of field measurements and Sentinel-2 satellite remote sensing to monitor eutrophication as the river experiencing huge sewage effluents. Key parameters such as chlorophyll-a (Chla), dissolved inorganic nitrogen (DIN), dissolved inorganic phosphorus (DIP), and Secchi Disk Depth (SDD) were analyzed. The developed empirical models showed a strong predictive capability for water quality, particularly for Chla (R2 = 0.87), DIP (R2 = 0.61), and SDD (R2 = 0.82). Seasonal analysis indicated peak Chla concentrations in October, reaching up to 92.4 μg/L, alongside significant decreases in DIN and DIP, suggesting high phytoplankton activity. Advanced machine learning models, specifically back propagation neural networks, improved the prediction accuracy with R2 values up to 0.90 for Chla and 0.83 for DIN. Temporal analyses from 2018 to 2022 consistently revealed the Barato River’s eutrophic state, with severe eutrophication occurring for 33% of the year and moderate for over 50%, emphasizing the ongoing nutrient imbalance. The strong correlation between DIP and Chla highlights phosphorus as the main driver of eutrophication. These findings demonstrate the efficacy of integrating remote sensing and machine learning for dynamic monitoring of river eutrophication, providing critical insights for nutrient management and water quality improvement.
1. Introduction
The health and sustainability of aquatic ecosystems are intricately linked to their nutrient dynamics, previous studies [1,2] shows that eutrophication represents one of the most significant challenges affecting water quality globally. Eutrophication, precipitated by nutrient over-enrichment, frequently results in excessive algal proliferation, diminished dissolved oxygen levels, and substantial water quality degradation, thereby jeopardizing biodiversity and the overall functionality of freshwater systems [3]. Rivers, as dynamic aquatic environments, are integral to urban and rural ecologies, providing essential resources for agriculture, industry, and human consumption [4]. However, the escalating rates of urbanization, industrial discharge, and agricultural activities have markedly intensified the nutrient loads in river systems, contributing to eutrophic conditions [5].
While the eutrophication process naturally occurs over millennia, anthropogenic influences, such as nutrient runoff from agriculture, urban wastewater discharge, and industrial effluents, have accelerated this process, significantly affecting the nutrient balance of numerous aquatic ecosystems [6]. Historically, it was considered that rivers, due to their short hydraulic retention times and continuous flow, were less susceptible to nutrient loading than lakes or reservoirs [7,8]. However, emerging evidence contradicts this hypothesis, demonstrating that rivers can exhibit comparable symptoms of eutrophication, with notable increases in algal biomass and nutrient concentrations [9,10]. This highlights a critical need to address riverine eutrophication as a distinct phenomenon with significant ecological and socio-economic implications.
Globally, river systems have exhibited increasing trends in nutrient concentrations over the past few decades. In numerous regions, instances of severe river eutrophication have been documented, resulting in widespread algal blooms, biodiversity loss, and the deterioration of water quality [11]. Notably, the proliferation of algal blooms in rivers such as the Nakdong in South Korea [12], the Han River in China [13], and the Barwon–Darling in Australia [14] has had far-reaching implications for both water quality and ecosystem health. Refs. [15,16] reported the impact of rice intensification and multi-dike protection systems on surface water quality in the Vietnamese Mekong Delta. These observations indicate a broader issue that, despite the global prevalence of river eutrophication, comprehensive monitoring and assessment remain limited, impeding effective management and mitigation strategies.
Traditional methodologies for monitoring eutrophication, which predominantly rely on field sampling and laboratory analysis, are frequently constrained by spatial and temporal limitations [17]. These approaches, while accurate at specific points, fail to capture the heterogeneity of nutrient dynamics over extensive areas and across seasonal variations. Furthermore, they are resource-intensive, time-consuming, and may not provide timely data for early intervention or policy implementation [18]. Remote sensing technology, with its capacity for large-scale, high-frequency data acquisition, presents a promising alternative for the dynamic monitoring of water quality [19]. By utilizing space-borne platforms such as Sentinel-2, Landsat-8, and MERIS, researchers can assess key eutrophication parameters including Chla, SDD, and nutrient concentrations such as dissolved inorganic nitrogen (DIN) and dissolved inorganic phosphorus (DIP), offering a more comprehensive and efficient approach to monitoring [20]. DIN and DIP are key nutrients influencing aquatic ecosystems. Their elevated concentrations, often linked to anthropogenic sources such as agricultural runoff and wastewater discharge, significantly affect phytoplankton growth [5]. Chla, the principal pigment in phytoplankton, directly reflects the biomass and is widely accepted as a primary indicator of eutrophication [2,5,6,9]. These parameters are interdependent, as nutrient availability (DIN and DIP) regulates algal biomass (Chla), thereby serving as comprehensive indicators of trophic dynamics in the Barato River. Additionally, water transparency, measured by Secchi Disk Depth (SDD), is inversely correlated with phytoplankton biomass and suspended solids, offering a broader perspective on water quality changes [1].
Remote sensing data, particularly from the Sentinel-2 satellite with its high spatial resolution, are well suited to detecting variations in water quality over time and space [21]. However, despite its potential, the application of remote sensing to riverine eutrophication has been insufficiently explored, with the majority of studies focusing on lakes and coastal areas. Furthermore, developing robust inversion models that can accurately relate satellite-derived spectral data to water quality parameters remains a significant challenge, particularly in dynamic and complex river systems [22]. Empirical algorithms and machine learning techniques, such as artificial neural networks, offer opportunities to enhance the accuracy of these models; however, their application in riverine environments is still in the developmental stage and necessitates further validation [23].
To address these gaps, this study focuses on the Barato River in Hokkaido, Japan, as a case study for monitoring eutrophication as the river facing issues with larger amount of sewage effluents of the total flow. Therefore, the study developed an integrated approach combining field-based measurements with remote sensing data for the dynamic monitoring of eutrophication in the river. Specifically, the research aims to (1) assess the current state of eutrophication in the Barato River using key indicators, namely DIN, DIP, Chla, and SDD; (2) develop and validate inversion models for the quantitative evaluation of these indicators utilizing Sentinel-2 data; and (3) provide insights into potential solutions for sustainable water resource management. By advancing the application of remote sensing in riverine eutrophication monitoring, this study seeks to contribute to a more comprehensive understanding of nutrient dynamics and support effective management strategies for river health.
2. Materials and Methods
2.1. Study Area
The Barato River is situated in the northern part of Sapporo, Hokkaido, an area characterized by both developed agriculture and dense urbanization [24]. The river’s flow has been altered historically; it was cut off from the Ishikari River in the 1930s and is now divided into three segments (upper, middle, and lower) due to narrow passages at Yamaguchi Bridge and Kannon Bridge, leading to a slow flow and high occlusion. Such conditions make the river highly susceptible to nutrient buildup and pollution. In addition to receiving a significant portion of domestic wastewater from Sapporo, the river’s water quality is further influenced by two downstream canals—the Ishikari Discharge Canal and the Shimi Canal—which connect to Ishikari Bay and introduce tidal influences that diversify the river’s water characteristics. Despite interventions, including water diversion efforts, the river’s eutrophication remains a persistent problem, as seen through ongoing algal blooms and nutrient imbalances. Given these dynamics, the Barato River presents a complex case study where urban, agricultural, and hydrological factors converge, making it a representative example of semi-enclosed rivers facing similar eutrophication challenges worldwide. Figure 1 illustrates the geographical context of the study, highlighting the location of the Barato River in Hokkaido, Japan, and showcasing specific sampling sites along the river where in-situ data were collected.
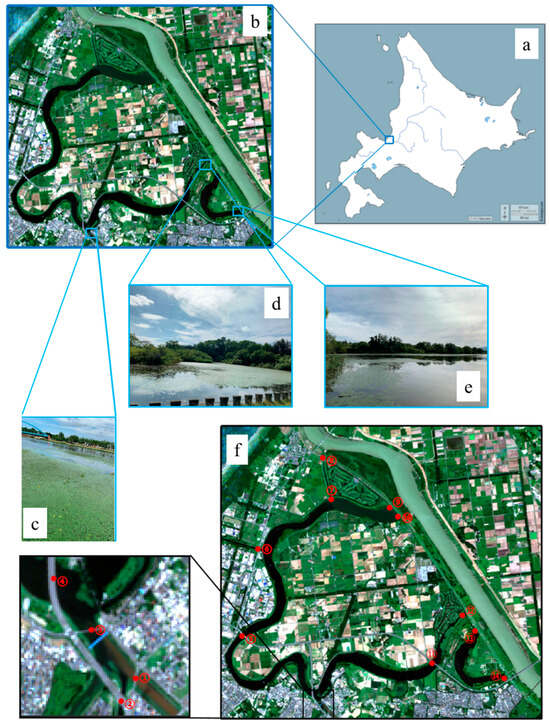
Figure 1.
Study area and sampling sites. (a) Location of Hokkaido, Sapporo, Japan, showing the regional context of the study. (b) Detailed view of the Barato River, the main focus area for water quality analysis. (c–e) Photographs of the sampling sites along the Barato River, illustrating different river segments where in-situ measurements were taken. (f) Detailed sampling locations.
2.2. Datasets
2.2.1. Satellite Data
Sentinel-2 satellite imagery was used in this study for the detection and monitoring of water quality parameters in inland water bodies due to its high spatial resolution and multispectral capabilities. Its temporal resolution and open access policy further facilitated the comprehensive temporal analysis of the Barato River’s eutrophication status. A total of 68 Level-1C (L1C) images were acquired from the U.S. Geological Survey (USGS) database, covering the period between 2018 and 2022. The images were selected in such a way that cloud cover was minimized and winter months were excluded so as to reduce the potential interference from snow and ice. The distribution of images that supported us in carrying out seasonal and annual analyses across the years was as follows: 6 in 2018, 10 in 2019, 12 in 2020, 24 in 2021, and 16 in 2022. Based on satellite data, we have confirmed that the Barato River is in a snow-covered condition from December through March each year as temperatures drop and snowfall impacts the river, making eutrophication problems virtually impossible during this period. However, with the melting of snow and ice in the spring and the gradual rise in temperature, eutrophication is likely to appear from April onwards.
Initially, we performed standard preprocessing steps, including radiometric calibration, geometric correction, and geocoding on the L1C images to ensure data consistency. However, to accurately extract surface reflectance values, atmospheric correction was a pre-requisite and was conducted using the Sen2cor algorithm developed by the European Space Agency (ESA) [25]. The latter applies corrections based on the libRadtran radiative transfer model, converting top-of-atmosphere (TOA) reflectance to surface reflectance by accounting for atmospheric scattering and absorption effects. The corrected Level-2A (L2A) images thus produced were further processed by spatially cropping them to the Barato River region, utilizing the Sentinel Application Platform (SNAP) [26], which facilitated precise spectral analyses of the river’s water quality.
2.2.2. In-Situ Data
We conducted in-situ measurements of water quality parameters to validate satellite-based estimates, calibrate remote sensing models, and improve the accuracy of eutrophication assessments. For this, we performed two field campaigns, one on 31 July 2022 (summer) and another on 9 November 2022 (autumn), at 14 sampling points distributed evenly across the upper, middle, and lower reaches of the Barato River (Figure 1f).
These two dates were chosen for field sampling for the following reasons. Firstly, the Barato River is in a snowmelt state, and the period of time that has sufficient value for eutrophication studies is roughly from the end of March to the end of November each year, while the rest of the year does not have the objective conditions for conducting the study. Within the timeframe suitable for conducting the study, two sampling events were determined to be conducted in July and November to cover different seasons to improve the adaptability of the inversion model, taking into account factors such as the temperature in the area.
The selection of sampling points was based on the following key points: (1) We ensured that all parts of the Barato River were covered as evenly as possible, and that there were sufficient sampling points in the upstream, midstream, and downstream to improve the overall confidence of the results. (2) We considered the feasibility of sampling and selected bridges in several parts of the river as sampling sites to reduce the difficulty of sampling. (3) Based on past data, we increased the number of sampling points in areas prone to eutrophication. We increased the number of sampling points for special areas, such as areas with slow water flow and some degree of lake nature, to ensure that the sampling points had a high degree of characterization. (4) We considered the feasibility of satellite data interpretation. Sampling points were selected as close as possible to the center of the river to ensure that the pixel data of satellite images were within the water body. Key parameters associated with eutrophication, including Chla, DIN, DIP, and SDD, were measured, which are manifested in their ability to represent the degree of eutrophication in water bodies and establish a clear regression relationship with image spectral values. Water samples were collected in sealed test tubes and subsequently transported to our laboratory for precise quantitative analysis. SDD was measured directly in the field using the Secchi Disk method. All the sampling was conducted between 9:00 a.m. and 2:00 p.m. in order to optimize lighting conditions and minimize environmental variability. Both field sampling campaigns were conducted under clear weather conditions to mitigate potential confounding effects from external variables such as turbidity caused by rain or wind. Sampling was performed at the same locations so as to capture the variations in water quality parameters between summer and autumn for seasonal analyses. Descriptive statistics for the water quality parameters revealed through these sampling campaigns after laboratory analysis are provided in Table 1 and Table 2, showing the range and variability observed across seasons.

Table 1.
Descriptive statistics of the optical water quality parameters measured on 31 July 2022.

Table 2.
Descriptive statistics of the optical water quality parameters measured on 9 November 2022.
2.3. Methods
In this study, we adopted a holistic methodological framework, as shown in Figure 2. In this section, we outline the steps taken to achieve the study objectives, including data processing, correlation analysis, empirical model development, and the use of machine learning techniques to enhance model performance. Our method started with a correlation analysis to identify the optimal spectral predictors from Sentinel-2 imagery for each water quality parameter. We then developed empirical models to provide initial parameter estimates. Finally, to enhance model accuracy and account for non-linear relationships, we applied advanced machine learning techniques. In the following subsections, we provide a step-by-step description of each stage of the methodology.
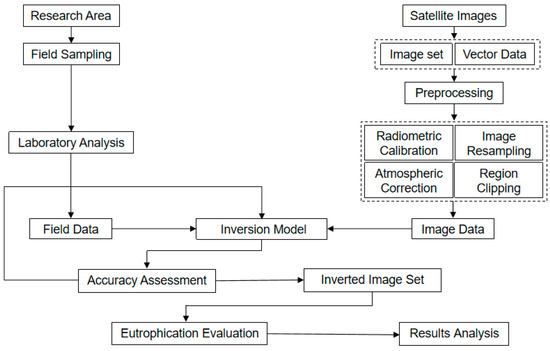
Figure 2.
Flowchart of the overall methodological framework used in this study, showing the integration of field sampling, laboratory analysis, and satellite imagery.
2.3.1. Image Processing and Preprocessing
To ensure accurate spectral analysis of water quality parameters, we subjected the L1C Sentinel-2 images to a series of preprocessing steps, to convert TOA reflectance to surface reflectance, so as to minimize the influence of atmospheric effects on the imagery. For this, we employed the Sen2cor algorithm, which is crucial for correcting atmospheric distortions caused by aerosols, molecular scattering, and gas absorption [27]. It operates by using look-up tables derived from the libRadtran model [28], which accounts for varying atmospheric conditions across the spectral bands of the imagery. This correction process converts the raw TOA reflectance in the L1C images to surface reflectance, producing L2A images that more accurately represent the water surface properties. Following the atmospheric correction, the processed L2A images were further refined by region-specific cropping and isolating the Barato River area from the broader scene captured by the Sentinel-2 satellite. Using the SNAP, the imagery was cropped to focus exclusively on the study area, allowing for precise analysis of water quality and the subsequent development of inversion models.
2.3.2. Inversion of Eutrophication Parameter Concentrations Using Empirical Algorithms
To accurately assess the eutrophication status of the Barato River, we developed inversion models for the key parameters, Chla, DIN, DIP, and SDD, using empirical algorithms. These models were established through a multi-step process including correlation analysis, regression modeling, accuracy assessment, and optimization with machine learning to enhance predictive performance, as detailed below.
Correlation Analysis
Initially, a correlation analysis was performed to identify relationships between spectral values derived from Sentinel-2 imagery and in-situ measurements of water quality parameters [29]. Pearson correlation coefficients were calculated for specific spectral bands and their combinations. The satellite images consist of a total of 13 bands with spatial resolutions of 10, 20, and 60 m. The spectral bands (B2–B7) used in this study are standard in Sentinel-2 datasets, following the European Space Agency’s (ESA) guidelines for multispectral data acquisition. These bands were selected based on their proven efficacy in detecting water quality parameters, as demonstrated in prior studies (e.g., [23]. Detailed band specifications are provided in Table 3.

Table 3.
Wavelength details of the Sentinel satellite.
In this study, separate models were developed for the warm (July) and cold (November) seasons to account for the significant seasonal variability observed in the Barato River. To enhance accuracy, separate models were developed for warm (July) and cold (November) seasons. Within each season, datasets were split into 80% training and 20% validation subsets, ensuring tailored model development for seasonal differences. This staged approach ensures that models are tailored to seasonal differences, enhancing their predictive accuracy while avoiding overlap between training and validation datasets. The best spectral band combinations were determined as Chla: (1/B2) × (1/B4); SDD: ln(B3/B7); DIN: B4/B3; and DIP: (B4/B3) − B5.
Inversion Modeling Based on Empirical Algorithms
Regression models were developed to relate the identified spectral band combinations to the concentration levels of each eutrophication parameter [30]. Initial models used July 2022 (warm season) data for training and November 2022 (cold season) data for validation. However, a staged modeling approach was later implemented, where datasets from each season were split into training (80%) and validation (20%) subsets, so as to enhance the seasonal adaptability. Linear regression was used to derive equations that relate reflectance values to water quality parameter concentrations: Chla—modeled using the combination (1/B2) × (1/B4); DIN—modeled with the band ratio B4/B3; DIP—modeled using (B4/B3) − B5; SDD—modeled through the natural logarithmic transformation ln(B3/B7).
- (a)
- Accuracy assessment
To evaluate the performance of the inversion models developed for the four eutrophication parameters, we used in-situ sampling data collected on 9 November 2022 as a test set [31]. The accuracy of each model was assessed using two statistical metrics: Root Mean Square Error (RMSE) and Mean Absolute Percentage Error (MAPE), defined as follows:
where, is the number of samples, is the predicted value from the inversion model, and is the actual observed value from the field data. RMSE has a range of [0, +∞), where a value of 0 indicates a perfect model with the predicted and true values completely matching. The larger the error, the greater the value of RMSE. MAPE also has a range of [0, + ∞), where a value of 0% signifies a perfect model, and values exceeding 100% indicate a poor-quality model. RMSE and MAPE were calculated for each inversion model, respectively. RMSE quantifies the absolute error between predicted and observed values, with lower values indicating higher accuracy. MAPE provides a percentage-based evaluation, reflecting model reliability across varying scales. Together, these metrics offer a comprehensive assessment of model performance, thereby enabling the evaluation of predictive accuracy across different eutrophication parameters.
- (b)
- Model optimization
- Staged seasonal modeling
Initially, July 2022 (warm season) data were used for training, and November 2022 (cold season) data were used for validation to test the empirical models. Based on observed seasonal variability, a staged modeling approach was later adopted. In this approach, separate models were developed for warm and cold seasons, and datasets within each season were split into training (80%) and validation (20%) subsets. This method enhanced model accuracy through ensuring independent validation and better capturing seasonal differences. For the cool season models, the optimal spectral band combinations were determined: Chla (cool season), 1/B2; DIN (cool season), (1/B3) − (1/B4).
- (c)
- Enhancing inversion accuracy with machine learning
To further enhance the accuracy of the inversion models, a machine learning approach using an artificial neural network (ANN) was implemented. Specifically, a back propagation (BP) neural network was employed to capture non-linear relationships between spectral data and water quality parameters. A BP neural network was selected for its strong non-linear mapping capabilities, making it suitable for the complex relationships inherent in water quality data. Compared to alternative methods such as Support Vector Machines (SVMs), BP is computationally efficient and adaptable to smaller datasets. While overfitting can be a concern, regularization techniques and cross-validation were employed to enhance model robustness and generalizability [32,33]. The model was constructed as a three-layer network, consisting of an input layer, a single hidden layer, and an output layer. The number of nodes in the input layer was determined based on the optimal spectral band combinations identified for each eutrophication parameter from prior correlation analysis. For Chla, five nodes were used for both the warm and cold seasons. For DIN, four nodes were assigned for both warm and cold seasons. DIP required five nodes, and SDD was modeled with six nodes in the input layer.
The number of hidden layer nodes was initially estimated using the following heuristic formula:
where, n is the number of input nodes, m is the number of output nodes (1 in this case), and a is a constant. This heuristic provides a practical starting point for determining network complexity. To address the potential arbitrariness of a, its value was varied within the range [0, 10] during preliminary testing, and the configuration that minimized validation error (measured by RMSE and MAPE) was selected.
Additionally, multiple configurations of hidden nodes (e.g., M values ranging from − 5 to ) were tested systematically. The final configuration, selected based on cross-validated performance, showed optimal predictive accuracy while, at the same time, avoiding overfitting.
The output layer had a single node to predict each specific water quality parameter. For training the model, we used the Levenberg–Marquardt (trainlm) algorithm due to its efficiency for small datasets [34]. The BP neural network models were trained and validated using the collected field and spectral data for each eutrophication parameter, specifically targeting Chla, DIN, DIP, and SDD. To optimize model performance, different nodes in the input layer were used based on the optimal spectral band combinations derived from correlation analyses: 5 nodes for Chla in both warm and cold seasons, 4 nodes for DIN in both warm and cold seasons, 5 nodes for DIP, and 6 nodes for SDD.
- Accuracy assessment
The BP neural network models were also validated using the same field and spectral data, targeting Chla, DIN, DIP, and SDD concentrations. Each model was assessed for performance improvements over traditional linear regression models using R2 values and error metrics (RMSE and MAPE).
2.3.3. Eutrophication Assessment Framework
To comprehensively evaluate the eutrophication status of the Barato River, this study adopted a dual-method approach that combined the Single-Factor Index (Pi) method [35] and the Trophic State Index Modified (TSIM) method [36]. These methods allow for both parameter-specific and holistic evaluations of nutrient levels, providing a detailed understanding of the river’s trophic state over time.
Single-Factor Index (Pi) Method
The Pi method was employed to evaluate the nutrient pollution levels in the river by analyzing two key eutrophication parameters: DIN and DIP. The Pi value for each parameter was calculated using the following formula:
where Ci represents the measured data of DIP, and Si represents the corresponding evaluation standard values.
A Pi value greater than 1 indicates that the concentration of the nutrient exceeds its standard threshold [37], signaling a state of pollution. To further classify the severity of pollution, Pi values were categorized as mild pollution (1 < Pi ≤ 3), moderate pollution (3 < Pi ≤ 6), and severe pollution (Pi > 6). These classifications enabled the assessment of seasonal and annual variations in pollution severity for both DIN and DIP across the study area.
Trophic State Index Modified (TSIM) Method
To provide a holistic assessment of the river’s trophic state, the TSIM method was applied, specifically focusing on Chla as an indicator of overall productivity and nutrient status [38]. The TSIM (Chla) was calculated using the following formula, and the base expression for TSIM is as follows:
where Chl is chlorophyll a concentration, SD is water transparency, and TP is total phosphorus concentration.
TSIM was calculated based on Chla concentrations, following standardized formulas to evaluate eutrophication severity. TSIM values range from 0 to 100, with higher values indicating more severe eutrophic conditions. These calculations were cross-referenced with in-situ measurements to ensure consistency and reliability. TSIM results were interpreted in the context of nutrient management strategies for improving river health [39]. The nutrient status of the study area was assessed based on the following developed nutrient status grading criteria: TSIM < 30 denotes depleted status; 30 ≤ TSIM ≤ 50 represents moderate status; and TSIM > 50 indicates eutrophic conditions. Specifically, 50 < TSIM ≤ 60 corresponds to mild eutrophication, 60 < TSI ≤ 70 represents moderate eutrophication, and TSIM > 70 signifies severe eutrophication. This classification provides a standardized and quantitative measure of the trophic status of the Barato River throughout the year, allowing for comparisons across seasons and years. In this study, TSIM (Chla) was selected as the calculation formula, considering the sampling data, characteristics of the study area, and other relevant factors.
The TSIM (Chla) and Pi values for DIN and DIP were calculated for each month in 2021 and 2022 based on the predicted concentrations obtained from the inversion models. These values were then analyzed to evaluate the temporal trends in eutrophication severity across both years, providing insights into seasonal fluctuations and overall water quality conditions.
3. Results and Discussion
3.1. Inversion of Eutrophication Parameter Concentrations Using Empirical Algorithms
The results of the multi-step process, including correlation analysis, regression modeling, accuracy assessment, and optimization with machine learning to enhance predictive performance, are detailed below.
The results of the correlation analysis indicated a strong relationship between the spectral data and the measured parameters. Notably, the correlation coefficient for Chla was 0.93, indicating a highly robust association, while DIN exhibited a lower but still adequate correlation of 0.72, meeting the requirement of the suitability for inversion modeling (Figure 3).
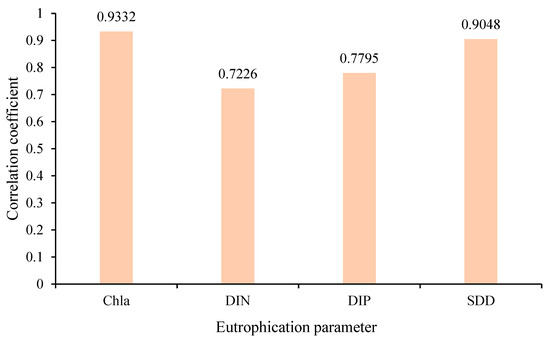
Figure 3.
Correlation coefficients between Sentinel-2 spectral band combinations and in-situ measurements of water quality parameters (Chla, DIN, DIP, and SDD).
Based on the results of the correlation analysis, optimal spectral band combinations were identified for each eutrophication parameter. The relationship between the spectral bands and each eutrophication parameter was derived through linear regression analysis. The developed models are presented below:
For Chla modeling, our regression model utilized the band combination (1/B2) × (1/B4) to predict Chla concentration. We achieved a coefficient of determination R2 of 0.87 (Figure 4a), indicating a strong linear relationship between the spectral reflectance and Chla levels, thereby demonstrating the model’s accuracy in predicting its concentrations. For DIN, the optimal band combination for its estimation was found to be B4/B3, resulting in a regression model with an R2 of 0.52 (Figure 4b). While the correlation in this case was observed to be moderate, it was considered sufficient for providing preliminary estimates of DIN concentration. For DIP, the regression model utilized the combination (B4/B3) −B5, with an R2 of 0.61 (Figure 4c). This model demonstrated an acceptable degree of predictability for its concentrations in the study area. For estimating SDD, the model was developed using the natural logarithmic transformation of the band combination ln(B3/B7), achieving an R2 of 0.82 (Figure 4d). This strong correlation demonstrated that the model is reliable for estimating water transparency. The regression equations and R2 in each model highlight the strength of the relationship between the spectral reflectance of Sentinel-2 bands and the corresponding water quality parameters, and served as the basis for further refinement and validation using independent datasets.
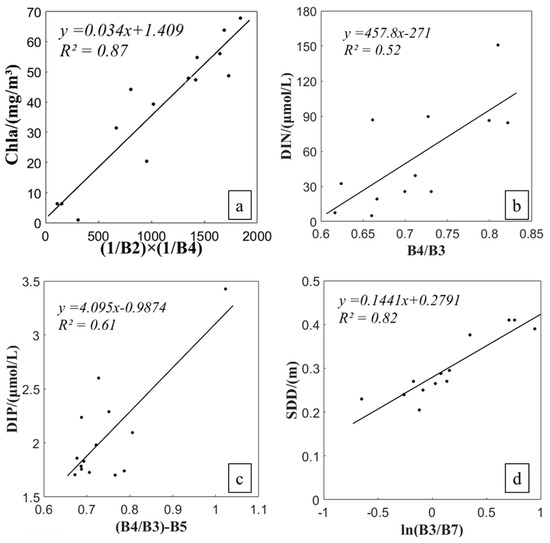
Figure 4.
Empirical regression models for the inversion of eutrophication parameters using Sentinel-2 spectral bands. (a) Chla model based on the combination (1/B2) × (1/B4); (b) DIN model using the band ratio B4/B3; (c) DIP model derived from the combination (B4/B3) − B5; (d) SDD model using the natural logarithmic transformation ln(B3/B7). The strong linear relationships depicted indicate the predictive potential of the spectral band combinations for estimating each eutrophication parameter.
3.1.1. Accuracy Assessment
To evaluate the performance of the inversion models developed for the four eutrophication parameters, we used in-situ sampling data collected on 9 November 2022 as a test set. For each parameter, RMSE and MAPE were calculated using validation subsets within the staged seasonal modeling approach that aimed to ensure that performance metrics reflect independent validation tailored to each season. The results are illustrated in Figure 5a–d. For Chla, the model exhibited a high RMSE of 34.44 μg/L and a MAPE of 190.96% (Figure 5a). These high error values suggest that the Chla model, while showing strong predictive capacity in some conditions, has limitations in adaptability, particularly across different seasonal datasets. For DIP, the model demonstrated high accuracy, with an RMSE of 0.3 μmol/L and a MAPE of 13.1% (Figure 5b), and indicated that the model performs well in predicting DIP concentration, with errors falling within an acceptable range. For DIN, the model showed moderate accuracy, with an RMSE of 127.49 μmol/L and a MAPE of 44.1% (Figure 5c). Although the RMSE indicated a reasonable predictive capacity, the relatively high MAPE suggested that the model’s performance could vary significantly under different conditions. For SDD, the model displayed strong performance with an RMSE of 0.083 m and a MAPE of 18.76% (Figure 5d). These low error values indicated that the model is robust and reliable for estimating water transparency across the study area [40].
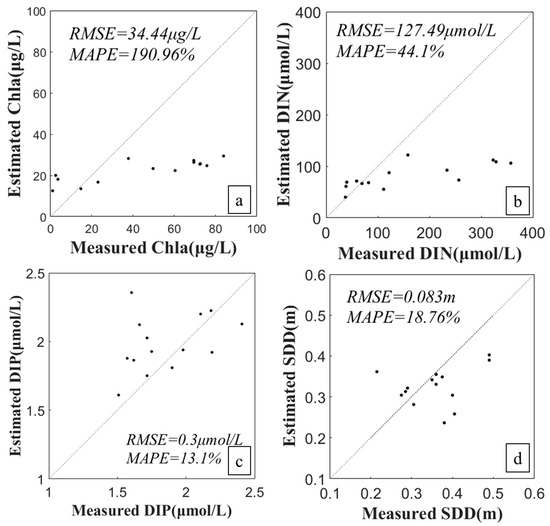
Figure 5.
Accuracy assessment of empirical inversion models for eutrophication parameters. (a) Chla, (b) DIN, (c) DIP, and (d) SDD. Each plot compares the predicted and measured values of the respective parameters, providing an assessment of model accuracy.
Seasonal variations in environmental factors, such as temperature, water temperature, ground cover, and landscape, can significantly impact water quality parameters, affecting the applicability of inversion models across different times of the year [41]. To address this, a staged modeling approach was implemented to enhance model accuracy by accounting for seasonal discrepancies. For Chla and DIN, separate inversion models were developed based on two distinct field sampling trips: the “warm season model,” developed using data collected in July 2022, and the “cool season model,” built from data obtained in November 2022. This approach enabled us to obtain a more precise calibration of the model for each season. Figure 6a,b depict the results of the cool season models for Chla and DIN. The inversion models achieved high R2 with values of 0.70 for Chla and 0.69 for DIN, indicating significantly improved accuracy compared to the original model. The inversion model for Chla in the cool season achieved an R2 of 0.70, demonstrating a strong linear relationship between the spectral band ratio and measured Chla concentrations, thereby improving seasonal adaptability. The model for DIN in the cool season attained an R2 of 0.69, indicating an improved correlation between the predictor variables and actual DIN measurements in the cool season.
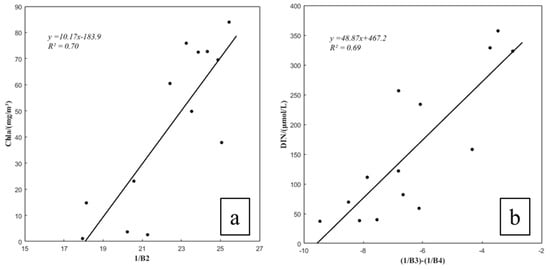
Figure 6.
Staged seasonal modeling results for Chla and DIN. Separate models were developed for warm and cold seasons, with datasets from each season split into training and validation subsets. (a) Cool season inversion model for Chla, using the 1/B2 band combination, achieving an R2 of 0.70, indicating a strong correlation between spectral data and measured Chla concentrations. (b) Cool season inversion model for DIN, based on the (1/B3) − (1/B4) band combination, with an R2 of 0.69, reflecting an improved predictive performance for DIN concentrations in the cool season.
3.1.2. Back Propagation (BP) Neural Network
To enhance the accuracy of inversion models beyond the improvements achieved by staged modeling, we employed a machine learning approach using artificial neural networks (ANNs), specifically the BP neural network. The objective was to overcome the limitations of linear regression models and better capture the non-linear relationships in the water quality parameters. Figure 7a,b show the performance of the BP neural network for predicting Chla concentrations in warm and cold seasons, respectively. The warm season model achieved an R2 value of 0.90, while the cold season model had an R2 of 0.83, indicating a strong correlation between the predicted and measured values in both seasons. Figure 7c,d illustrate the models for DIN during the warm and cold seasons. The R2 values of 0.83 (warm season) and 0.76 (cold season) demonstrate a significant improvement in model accuracy over linear models. For DIP and SDD, Figure 7e,f show R2 values of 0.72 and 0.86, respectively, highlighting the BP neural network’s enhanced predictive capabilities compared to traditional regression approaches.
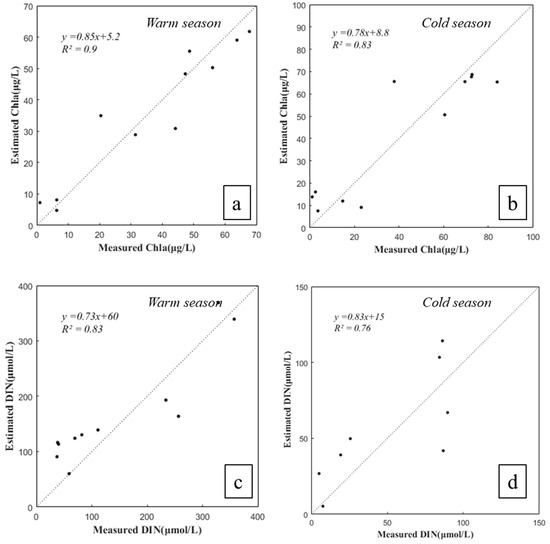
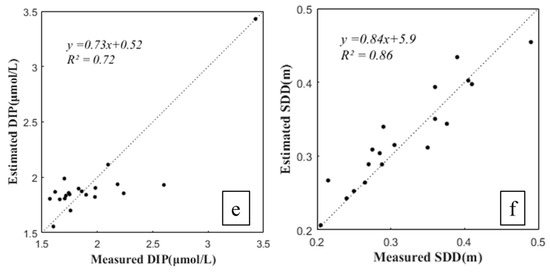
Figure 7.
Performance of BP neural network inversion models for predicting eutrophication parameters. Models were independently trained and validated within warm and cold season datasets. (a) Chla in the warm season, (b) Chla in the cold season, (c) DIN in the warm season, (d) DIN in the cold season, (e) DIP, and (f) SDD. Each plot compares estimated values from the BP neural network models against measured field data, demonstrating significant improvements in model accuracy.
The BP neural network models demonstrated substantial improvements in predictive performance, as evidenced by reductions in both RMSE and MAPE across all eutrophication parameters. For Chla, the warm season model achieved an RMSE of 5.16 μg/L with a MAPE of 9.84%, while the cold season model exhibited an RMSE of 9.77 μg/L and a MAPE of 14.1% (Figure 8a,b). These results indicate an overall enhanced model accuracy when compared to empirical models. The DIN model’s accuracy showed significant gains, with RMSE values dropping to 21.03 μmol/L and 45.07 μmol/L for the warm and cold seasons, respectively, and corresponding MAPE values of 56.01% and 23.88% (Figure 8c,d). The DIP model saw a decrease in RMSE to 0.21 μmol/L and a MAPE reduction to 10.07%, indicating strong predictive accuracy (Figure 8e). Similarly, the SDD model achieved an RMSE of 0.054 m and a MAPE of 14.58%, further underscoring the enhanced precision (Figure 8f).
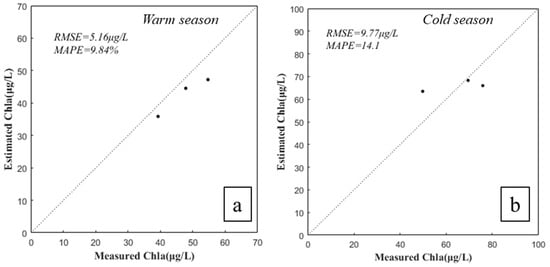
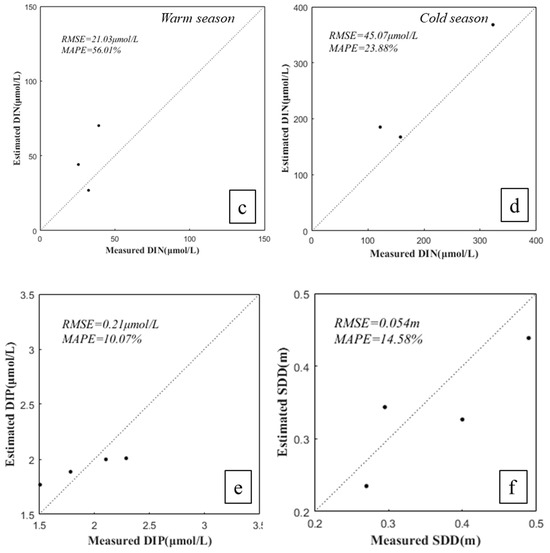
Figure 8.
Accuracy assessment of BP neural network-based inversion models for eutrophication parameters across different seasons. (a) Model performance for Chla in the warm season. (b) Model performance for Chla in the cold season. (c) Model performance for DIN in the warm season. (d) Model performance for DIN in the cold season. (e) Model performance for DIP. (f) Model performance for SDD. These plots indicate the prediction accuracy of the BP neural network models for various water quality parameters.
3.2. Temporal Dynamics of Water Quality Parameters
The Barato River experiences significant seasonal variations due to the local climate. Based on satellite data, the river is confirmed to be in a snow-covered condition from December through March each year. During this period, temperatures drop, and snowfall impacts the river, making eutrophication processes virtually impossible. With the melting of snow and ice in the spring and a gradual rise in temperature, eutrophication dynamics typically appear from April onwards. This study, therefore, focuses on the active eutrophication period spanning April to November, which encompasses the critical nutrient and phytoplankton activity phases.
3.2.1. Dynamic Monitoring in 2021
The developed inversion models were applied to 24 Sentinel-2 images acquired throughout 2021 to analyze the temporal dynamics of four key water quality parameters, Chla, DIN, DIP, and SDD, providing insights into the seasonal trends and interactions among these parameters.
In 2021, Chla concentrations fluctuated seasonally, with peaks in October (92.4 μg/L), indicating heightened phytoplankton activity driven by nutrient availability and favorable seasonal conditions. Notable transitions from April to August reflect dynamic nutrient and environmental interactions influencing growth (Figure 9a).
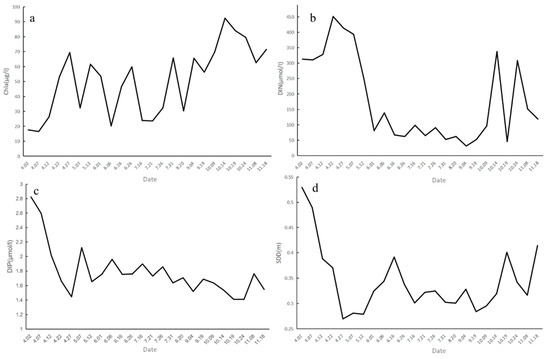
Figure 9.
Temporal dynamics of water quality parameters in 2021. The concentration changes in the four key parameters throughout 2021: (a) Chla in μmol/L; (b) DIN in μmol/L; (c) DIP in μmol/L; (d) SDD in meters.
The temporal trends of DIN and DIP exhibited seasonal variations, with measured data confirming peaks in April (DIN: 451.33 μmol/L; DIP: 2.82 μmol/L) and declines by October (DIN: 45.55 μmol/L; DIP: 1.41 μmol/L). This aligns with modeled trends, demonstrating phytoplankton nutrient uptake and conversion to organic forms. The agreement between modeled and measured values highlights the reliability of the inversion models. The inverse relationship between DIN and DIP levels and Chla concentration underscores the significant role these nutrients play in supporting phytoplankton growth within the study area (Figure 9b,c).
The trends in SDD indicated complex interactions affecting water transparency. While the changes in SDD did not directly correlate with Chla as closely as DIN and DIP did, there was a notable decrease in October, aligning with the peak in Chla. This suggests that increased phytoplankton biomass and suspended matter contributed to reduced water clarity. However, the variability in SDD throughout the year points to additional factors beyond phytoplankton influencing water transparency, such as sediment loading or other particulate matter (Figure 9d).
Normalized trends of Chla, DIN, DIP, and SDD illustrate their interdependence. While visual comparisons with measured data confirm broad alignment, minor deviations suggest transient factors affecting nutrient uptake and phytoplankton growth. The analysis revealed a strong inverse relationship between Chla and nutrient concentrations, particularly DIP (R2 = −0.8211). While this indicates DIP as a primary driver of Chla, visual comparisons with measured data show that local deviations occur due to transient environmental factors. Comparatively, the correlation between Chla and DIN was weaker (−0.1632), further emphasizing the influence of DIP over DIN on phytoplankton dynamics in this river system (Figure 10).
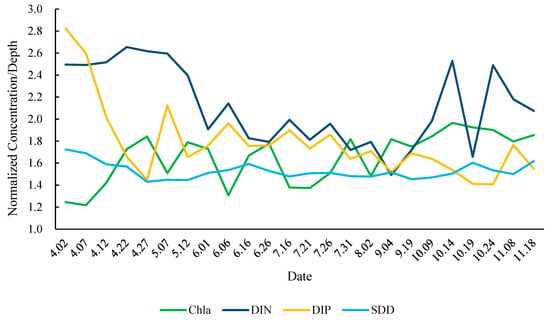
Figure 10.
Temporal trends of normalized water quality parameters in 2021. The graph displays the normalized concentrations of Chla, DIN, DIP, and SDD throughout the year. This graph highlights the relationships and variations between Chla, DIN, DIP, and SDD over time.
In addition to the relationships between Chla and nutrients, a weak to moderate positive correlation was observed between DIN and DIP (0.3335), suggesting some degree of linkage in the behavior of these nutrients over certain periods. The interaction between DIN and DIP may influence their respective availability for phytoplankton uptake and growth [42] (Table 4).

Table 4.
Correlation analysis of inversion results in 2021.
The observed temporal variations in Chla, DIN, DIP, and SDD, along with their correlations, provide a comprehensive picture of the seasonal dynamics of eutrophication in the Barato River. The strong influence of DIP on Chla concentration suggests that phosphorus availability plays a crucial role in phytoplankton growth and subsequent eutrophication events [43]. These findings are vital for water quality monitoring and management, as they underscore the importance of managing nutrient inputs, particularly phosphorus, to mitigate the risk of eutrophication and its associated environmental impacts [44]; they are also critical for understanding the temporal variability of water quality and for guiding future management and policy decisions to improve and maintain river health [45].
3.2.2. Multi-Year Monitoring of Eutrophication (2018–2022)
Modeled after 2021, the changes in water quality parameters from 2018 to 2022 were analyzed separately to identify consistent trends and patterns in the temporal dynamics of eutrophication. Although data availability for 2018 is limited, the trends provide preliminary insights into the eutrophication dynamics. Throughout the year, there is a consistent decrease in DIN and DIP concentrations, with both reaching their lowest levels in October. Conversely, Chla shows an initial decline followed by an upward surge, hitting its lowest point in June and peaking in October. SDD, a measure of water transparency, fluctuates within a narrow range (0.3–0.4 m) and shows a slight increase toward the year’s end. Despite the limited data, a notable negative correlation is observed between Chla and nutrient concentrations (DIN and DIP), suggesting that nutrient depletion is closely associated with increased phytoplankton growth and subsequent Chla concentration rise [46] (Figure 11a–d).
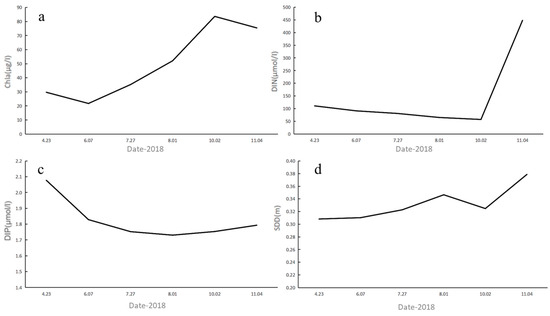
Figure 11.
Temporal changes in water quality parameters of the Barato River in 2018. (a) Chla, (b) DIN, (c) DIP, and (d) SDD.
With an increase in data for 2019, the trends in water quality parameters become more defined. Early in the year, DIN reaches a peak of 603.72 μmol/L in mid-April and then sharply declines by June. After a minor increase in July, it continued to decline, hitting its lowest point (32.39 μmol/L) in October before rebounding in November. DIP follows a similar pattern, reaching a minimum in June, slightly rising in the following months, and dropping to its lowest concentration (1.56 μmol/L) in October. Chla concentration shows a distinct downward trend from April to July, with its lowest value of 14.2 μg/L in mid-July, and subsequently rises to a peak of 91.37 μg/L in early October. SDD records a slow decline, with the lowest transparency (0.26 m) in October. Notably, a strong negative correlation between Chla and the nutrients is established, particularly from June onwards, reinforcing the influence of nutrient dynamics on phytoplankton growth [47] (Figure 12a–d).
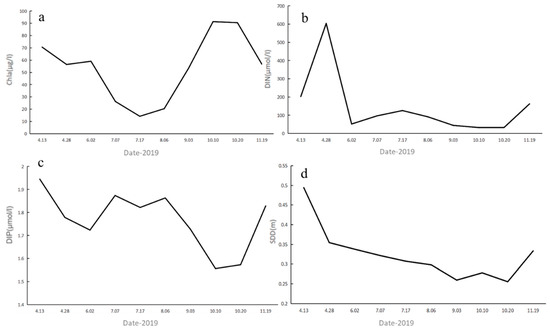
Figure 12.
Temporal changes in water quality parameters of the Barato River in 2019. (a) Chla, (b) DIN, (c) DIP, and (d) SDD.
In 2020, the dataset becomes more robust, allowing for an accurate representation of temporal trends. DIN peaks at 683.66 μmol/L in April and gradually declines, reaching its lowest value (26.35 μmol/L) by late September. DIP reaches its highest concentration (2.58 μmol/L) in March, rapidly decreases, slightly rebounds in July, and finally hits its lowest level by the end of September. Chla exhibits the highest concentration in early November and the lowest in late July, mirroring DIP fluctuations. The correlations between Chla and nutrient concentrations continue to show a significant negative relationship, although with some added variability compared to 2021. This indicates that while nutrient levels directly affect Chla and eutrophication, there is some degree of variability in how these relationships manifest over time (Figure 13a–d).
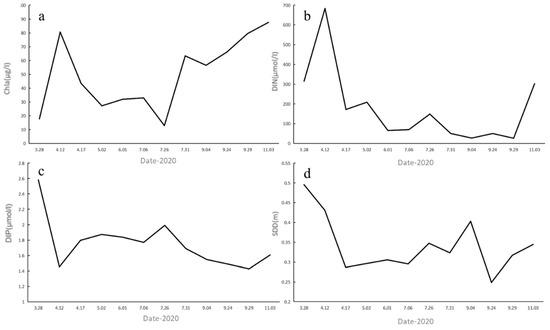
Figure 13.
Temporal changes in water quality parameters of the Barato River in 2020. (a) Chla, (b) DIN, (c) DIP, and (d) SDD.
The data for 2022, being the most extensive and stable, provide a detailed overview of temporal dynamics. DIN starts with high variability, peaking at 275.65 μmol/L in April, and then generally decreases to around 50 μmol/L, stabilizing before rebounding at the year’s end. DIP follows a similar path, peaking at 1.88 μmol/L in April and reaching minimum level in July. Chla displays considerable fluctuations, with multiple peaks in mid-May, late June, early September, and mid-October, reaching its maximum (98.36 μg/L) in early October and its minimum (13.04 μg/L) in late April. SDD shows variation throughout the year, with a marked decline in May followed by an increase in June and slight fluctuations thereafter. These patterns reinforce the persistent eutrophic conditions of the Barato River and the complementary trends between nutrient availability and phytoplankton growth (Figure 14a–d).
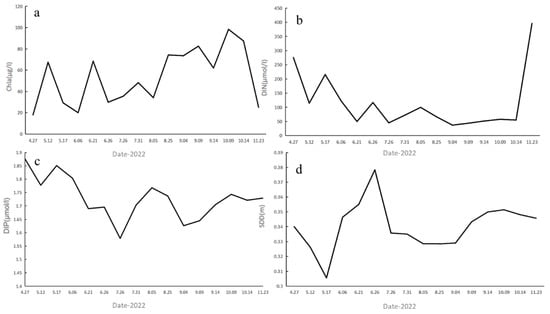
Figure 14.
Temporal changes in water quality parameters of the Barato River in 2022. (a) Chla, (b) DIN, (c) DIP, and (d) SDD.
The multi-year analysis consistently reveals a similar temporal dynamic of eutrophication parameters, including DIN, DIP, Chla, and SDD, across all observed years. A recurring trend is noted where the highest Chla concentrations are reached in October, coinciding with the lowest levels of DIN and DIP. This synchronicity across years underscores a persistent pattern of nutrient depletion due to phytoplankton uptake, culminating in elevated Chla levels, a very good example of eutrophication. Despite some interannual variability, the trend suggested a stable and sustained eutrophic state in the Barato River system. The patterns observed in 2021 are reaffirmed as part of a broader, multi-year phenomenon rather than isolated events. The consistent dynamics between nutrient levels, Chla concentrations, and SDD highlight the river’s long-term eutrophic condition. Measured data corroborate the model’s key trends, highlighting the need for sustained nutrient management to mitigate eutrophication [48,49].
3.3. Evaluation of Eutrophication Status
The results from 2021 indicate that the TSIM for Chla ranged between 55.2 and 74, reflecting a trophic state that fluctuates from slight to severe eutrophication throughout the year. The continuous increase in TSIM values during specific months signifies changes in phytoplankton biomass, aligning with nutrient dynamics in the river [50] (Figure 15a). The Pi index for DIN demonstrates significant variability, ranging from unpolluted to severely polluted states over time, highlighting dynamic nutrient conditions [51] (Figure 15b). In contrast, for DIP it remained consistently in the mild pollution category, indicating a continuous nutrient availability conducive to phytoplankton growth [52] (Figure 15c). Time-based analysis reveals that severe eutrophication occurred 33% of the year, with moderate eutrophication dominating 54% of the time, and slight eutrophication accounting for 13% (Figure 15d). The Pi index distribution for DIN reveals unpolluted conditions for nearly half of the year (48%), with mild pollution spanning 18%, moderate pollution 32%, and severe pollution at 2% (Figure 15e). The DIP values were persistently in mild pollution for the entire year (Figure 15f). These results collectively indicate that in 2021, the Barato River experienced consistent eutrophic conditions, with nutrient concentrations significantly contributing to the observed trophic status.
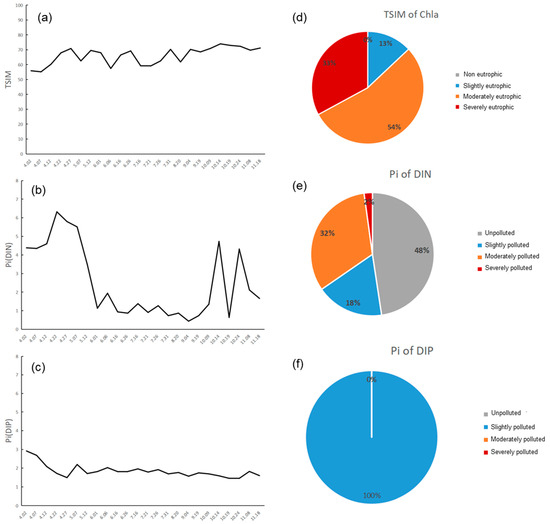
Figure 15.
Temporal dynamics of eutrophication indicators in the Barato River for 2021. (a) TSIM of Chla indicating fluctuations from slight to severe eutrophication throughout the year. (b) Pi for DIN showing significant variability, spanning from unpolluted to severely polluted states. (c) Pi for DIP, which consistently remains in the mild pollution category throughout the year. (d) Pie chart of TSIM illustrating that severe eutrophication occurred for 33% of the year, moderate eutrophication occurred for 54%, and slight eutrophication occurred for 13%. (e) Distribution of Pi for DIN, showing 48% unpolluted, 18% mild pollution, 32% moderate pollution, and 2% severe pollution. (f) Pie chart of Pi for DIP being consistently in a mild pollution state for the entire year, indicating sustained nutrient availability.
The 2022 findings, as illustrated in Figure 16, highlight a largely similar pattern of eutrophication to that observed in 2021. The TSIM (Chla) values ranged from 56.17 to 74.68, closely mirroring the 2021 range, with a slight upward shift in both minimum and maximum values (Figure 16a,b), suggesting the consistent presence of eutrophic conditions throughout the year. The Pi index for DIN (Figure 16e) fluctuated between 0.52 and 5.54 in 2022. The increase in the minimum value compared to 2021 indicated fewer instances of severe pollution. The Pi (DIP), represented in Figure 16c, ranged between 1.63 and 1.94, remaining within the mild pollution category for the entire year. This stability in Pi (DIP) points to a sustained nutrient availability, supporting phytoplankton growth without exacerbating pollution levels [53]. The pie charts (Figure 16d–f) provide a comprehensive time-based breakdown of eutrophication severity. The period of slight eutrophication increased by 2%, from 13% to 15%, while moderate eutrophication decreased by 4%, from 54% to 50%. However, the period classified as severe eutrophication (Figure 16d) experienced a minor increase of 2%, suggesting that while there was a reduction in moderate pollution, severe conditions persisted during certain periods. Additionally, the Pi (DIN) varied throughout the year, with moderate pollution decreasing and mild pollution increasing (Figure 16e), indicating a shift towards reduced nutrient concentrations. The Pi(DIP) values remained relatively stable around 2, consistently reflecting mild pollution throughout the year (Figure 16f), suggesting that despite changes in DIN, the stable DIP concentrations continued to support the eutrophic state. Hence, while the 2022 data suggest some improvement in water quality, particularly in reducing periods of moderate pollution, the persistent nutrient levels (Figure 16a–f) indicate that the river’s overall trophic state remains unchanged, necessitating continued efforts in nutrient management to reduce long-term eutrophication effects [54,55].
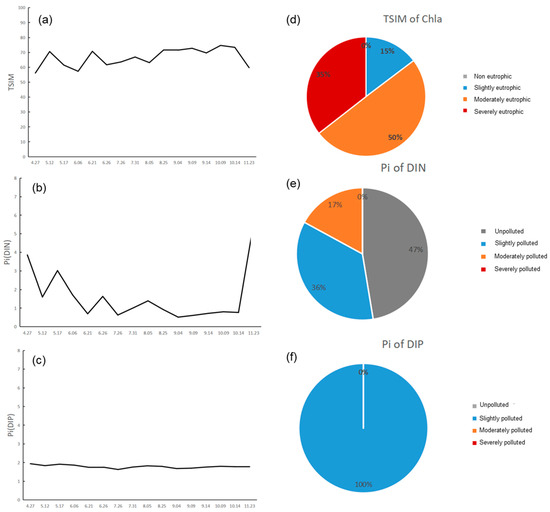
Figure 16.
Temporal dynamics and distribution of eutrophication indicators in the Barato River for 2022. (a) TSIM of Chla showing a consistent eutrophic state throughout the year. (b) TSIM values indicate a slight increase compared to 2021. (c) Pi for DIP, consistently indicating mild pollution throughout the year. (d) Pie chart illustrating TSIM distribution: slight eutrophication accounted for 15%, moderate eutrophication for 50%, and severe eutrophication for 35%. (e) Distribution of Pi for DIN, showing unpolluted conditions for 47% of the year, mild pollution for 36%, and moderate pollution for 17%. (f) Pie chart for Pi of DIP showing 100% mild pollution throughout the year.
3.4. Trends and Implications
The assessment of the Barato River’s eutrophication over 2021 and 2022 revealed a persistent issue with nutrient pollution and trophic imbalance, influenced by the interplay of nutrient availability, biological activity, and environmental conditions [6,56]. The river consistently exhibited eutrophic conditions throughout both years, as evidenced by the high TSIM (Chla) values (Figure 15a for 2021 and Figure 16a for 2022). The trophic state fluctuated mainly between moderate and severe eutrophication, indicating that nutrient levels were sufficient to sustain phytoplankton growth and high Chla concentrations [57]. Notably, severe eutrophication (TSIM > 70) occurred significantly during both years, making up 33% of the time in 2021 and 35% in 2022 (Figure 15d and Figure 16d), highlighting the ongoing environmental risk from nutrient over-enrichment. The temporal variation in eutrophication reflects seasonal patterns, with nutrient spikes (DIN and DIP) contributing to algal blooms and elevated Chla and likely being driven by factors such as agricultural runoff, urban discharge, and natural hydrological processes that influence nutrient delivery and phytoplankton growth [58,59].
The year 2022 depicted slight improvements over 2021, particularly with a shift from moderate to mild pollution (Figure 16d,e). However, these changes were not substantial enough to significantly alter the river’s trophic state. Specifically, the reduction in moderate pollution corresponded to an increase in mild pollution, which may indicate some response to natural processes, yet without a significant decrease in Chla concentrations, the overall eutrophic status persisted. The Pi(DIN) values (Figure 15b for 2021 and Figure 16b for 2022) showed a narrowing range in 2022, with a lower maximum and a higher minimum. This suggests some stabilization in nutrient concentrations, although DIN levels still fluctuated widely, occasionally reaching severe pollution levels. The trend towards milder pollution suggests mitigation efforts may be taking effect, but they have not been sufficient to induce significant improvements in water quality. In contrast, Pi(DIP) remained consistently in the mild pollution category throughout both years (Figure 15c and Figure 16c), indicating a steady supply of DIP, which is essential for phytoplankton proliferation. Given that DIP is a limiting nutrient for many algal species, its persistent availability underpins the eutrophic conditions observed in the river. The steady Pi(DIP) values, approximately around 2, indicate that phosphorus management remains a critical challenge for improving nutrient balance in the Barato River.
The consistent presence of DIP and its mild pollution status throughout both years (Figure 15f and Figure 16f) underscores the inadequacy of current interventions to control phosphorus inputs effectively [60,61]. Managing both point and non-point sources of phosphorus, such as agricultural runoff and wastewater discharge, requires attention to reduce algal growth and mitigate the trophic imbalance [62]. The interplay between DIN and DIP concentrations has vital implications for eutrophication dynamics, and their combined availability at sufficient levels supports phytoplankton growth, preventing either nitrogen or phosphorus from being limiting factors, and sustains the eutrophic conditions of the river [63,64]. The positive correlation between nutrient peaks and elevated Chla levels reinforces the connection between nutrient inputs and biological responses. The observed shift in pollution severity in 2022, where moderate pollution decreased and mild pollution increased (Figure 16d), signals the start of a trend toward good water quality. However, without further reductions in nutrient loads, the risk of reverting to severe eutrophication remains, particularly during periods of high nutrient runoff or low water flow [65,66]. The persistence of eutrophication in the Barato River across both years emphasizes the need for long-term nutrient management strategies [67]. While slight improvements were noted in 2022, they were insufficient to substantially shift the river from its moderate-to-severe eutrophic state. To achieve non-eutrophic conditions, targeted strategies focusing on reducing both nitrogen and phosphorus are essential [68]. Continuous monitoring is imperative to evaluate the effectiveness of interventions, track seasonal changes, and guide progress towards reducing nutrient concentrations, improving water quality, and restoring the river’s ecological balance [69,70].
The Barato River is adjacent to local agricultural land and there are no significant industrial facilities nearby. From the results of the study, it is possible that the eutrophication that occurs from summer to fall each year is related to the use of fertilizers and other chemicals used in local agriculture, i.e., there is a possibility that fertilizers and pesticides are one of the causes of eutrophication in the area because of their eventual flow into the Barato River through the ditches. If this hypothesis is true, further research is needed to verify the mechanisms and impacts of agricultural production on the Barato River. In the meantime, regardless of the source of the eutrophic substances, the current eutrophication problem is clear. Without human intervention, the problem of eutrophication is likely to worsen in the future, eventually affecting the balance of the local ecosystem and its environmental stability. In fact, eutrophication problems are usually progressive, and we have ample experience showing that uncontrolled eutrophication can have serious ecological consequences, and that pre-existing eutrophication symptoms are an important database to confirm the existence of the problem and to provide a basis for intervention. Therefore, we hope that the study of this area can be further developed to identify the possible sources of pollution and to provide the local government or NGOs with a basis for the management of environmental problems. The observed eutrophication patterns have significant ecological implications, including reduced biodiversity and altered aquatic habitats. Nutrient management strategies, such as controlling agricultural runoff and implementing riparian buffer zones, are essential for mitigating these effects. The study highlights the need for integrated approaches combining remote sensing, in-situ measurements, and stakeholder engagement to address eutrophication and enhance ecosystem resilience.
To address the limitations in data collection, we incorporated targeted sampling during the active eutrophication period, complemented by multi-temporal satellite imagery. However, this approach does not provide year-round monitoring due to the snow-covered state of the Barato River from December to March, during which biological activity is minimal, reducing the likelihood of significant eutrophication events. Future studies should expand efforts to include hydrological modeling, which can estimate nutrient fluxes and dynamics during unsampled periods, thereby bridging temporal gaps. Additionally, the application of data assimilation techniques could help refine predictions and improve the overall robustness of eutrophication assessments. Such measures would facilitate a more comprehensive understanding of seasonal variations and interannual trends, providing a valuable framework for the ongoing study of eutrophication dynamics in river system gaps.
4. Conclusions
This study demonstrated the efficacy of integrating Sentinel-2 satellite remote sensing data with in-situ measurements to monitor eutrophication dynamics in the Barato River, Hokkaido, Japan. Through the development of empirical and machine learning-based models, we successfully inverted spectral satellite data to key water quality parameters, specifically Chla, DIN, DIP, and SDD. Our findings revealed that phosphorus, as indicated by DIP concentrations, is a primary driver of eutrophication in this river system, with Chla levels reaching their maxima in the presence of elevated nutrient loads. The machine learning models, particularly artificial neural networks, significantly enhanced the accuracy of parameter prediction compared to traditional regression models, indicating the potential for advanced remote sensing techniques in water quality monitoring. The seasonal and multi-year analysis elucidated persistent eutrophic conditions, with severe and moderate eutrophication predominating throughout the year. The Barato River serves as a representative case study for semi-enclosed rivers experiencing nutrient enrichment from urban, agricultural, and industrial sources. However, this study also exhibits some limitations that warrant consideration in future research. Firstly, the temporal resolution of satellite imagery and in-situ sampling was constrained, potentially overlooking short-term variations in nutrient dynamics and algal blooms. Although machine learning models demonstrated improved predictive performance, the relatively limited dataset for model training may restrict their generalizability across diverse riverine systems or seasons. Additionally, the study primarily focused on the Barato River, and the developed models necessitate further validation in other riverine environments with differing hydrological and nutrient dynamics to establish broader applicability. Moreover, while DIP was identified as a primary nutrient driver, other factors such as organic carbon inputs, turbidity, and sediment transport were not explicitly analyzed, which may have also influenced eutrophication processes. This research highlights the potential of utilizing remote sensing and machine learning as a cost-effective, scalable approach for monitoring eutrophication in river systems. While the models and methodologies developed offer valuable insights for nutrient management, there is a need for continuous monitoring, model validation, and comprehensive assessment of additional factors affecting riverine water quality. Addressing these limitations in future studies will enhance the applicability of these approaches and contribute to the sustainable management of aquatic ecosystems.
Author Contributions
Conceptualization, D.G. and R.A.; methodology, D.G., G.M., R.A., and P.K.; software, D.G., P.K., G.M., and S.A.; validation, D.G., P.K., L.N.G., M.P., and D.J.; formal analysis, D.G., G.M., and P.K.; investigation, D.G., P.K., and R.A.; resources, P.K. and R.A.; data curation, D.G. and G.M.; writing—original draft preparation, D.G., G.M., P.K., and R.A.; writing—review and editing, D.G., G.M., S.A., D.J., L.N.G., M.P., P.K., and R.A.; supervision, P.K. and R.A.; project administration, P.K., S.A., G.M., and R.A.; funding acquisition, S.A. and R.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the Deanship of Scientific Research at King Khalid for funding this work through a large research group (Project group number RGP.2/279/45) and by the Sumitomo grant for Environmental Research number 2330169.
Data Availability Statement
All data produced or examined during the investigation are incorporated in this published publication.
Acknowledgments
We would like to thank Sentinel data hub for providing Sentinel data. The first author would like to express my gratitude to Kudo Isao sensei. It was your generous provision of laboratory equipment that allowed me to carry out sample collection and analysis.
Conflicts of Interest
The authors disclosed no potential conflicts of interest.
References
- Guo, Z.; Boeing, W.J.; Borgomeo, E.; Xu, Y.; Weng, Y. Linking reservoir ecosystems research to the sustainable development goals. Sci. Total Environ. 2021, 781, 146769. [Google Scholar] [CrossRef] [PubMed]
- Primost, J.E.; Peluso, L.; Sasal, M.C.; Bonetto, C.A. Nutrient dynamics in the Paraná River Delta: Relationship to the hydrologic regime and the floodplain wetlands. Limnologica 2022, 94, 125970. [Google Scholar] [CrossRef]
- Sitote, Y.M.; Gebremedhine, M.G. Comprehensive Review of Eutrophication in Freshwater Ecosystems: Causes, Effects, Assessment, and Management Strategies. Preprints 2024. [Google Scholar] [CrossRef]
- Bănăduc, D.; Simić, V.; Cianfaglione, K.; Barinova, S.; Afanasyev, S.; Öktener, A.; McCall, G.; Simić, S.; Curtean-Bănăduc, A. Freshwater as a sustainable resource and generator of secondary resources in the 21st century: Stressors, threats, risks, management and protection strategies, and conservation approaches. Int. J. Environ. Res. Public Health 2022, 19, 16570. [Google Scholar] [CrossRef]
- Costa, D.; Sutter, C.; Shepherd, A.; Jarvie, H.; Wilson, H.; Elliott, J.; Liu, J.; Macrae, M. Impact of climate change on catchment nutrient dynamics: Insights from around the world. Environ. Rev. 2022, 31, 4–25. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Pal, D.B. Nutrients contamination and eutrophication in the river ecosystem. In Ecological Significance of River Ecosystems; Elsevier: Amsterdam, The Netherlands, 2022; pp. 203–216. [Google Scholar]
- Kennedy, R.H.; Walker, W.W. Reservoir nutrient dynamics. In Reservoir Limnology: Ecological Perspectives; Wiley: New York, NY, USA, 1990; pp. 109–131. [Google Scholar]
- Brett, M.T.; Benjamin, M.M. A review and reassessment of lake phosphorus retention and the nutrient loading concept. Freshw. Biol. 2008, 53, 194–211. [Google Scholar] [CrossRef]
- Hilton, J.; O’Hare, M.; Bowes, M.J.; Jones, J.I. How green is my river? A new paradigm of eutrophication in rivers. Sci. Total Environ. 2006, 365, 66–83. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Z. Phytoplankton, dissolved oxygen, and nutrient patterns along a eutrophic river-estuary continuum: Observation and modeling. J. Environ. Manag. 2020, 261, 110233. [Google Scholar] [CrossRef]
- Feng, L.; Wang, Y.; Hou, X.; Qin, B.; Kuster, T.; Qu, F.; Chen, N.; Paerl, H.W.; Zheng, C. Harmful algal blooms in inland waters. Nat. Rev. Earth Environ. 2024, 5, 631–644. [Google Scholar] [CrossRef]
- Kim, K.B.; Jung, M.K.; Tsang, Y.F.; Kwon, H.H. Stochastic modeling of chlorophyll-a for probabilistic assessment and monitoring of algae blooms in the Lower Nakdong River, South Korea. J. Hazard. Mater. 2020, 400, 123066. [Google Scholar] [CrossRef]
- Li, J.; Yin, W.; Jia, H.; Xin, X. Hydrological management strategies for the control of algal blooms in regulated lowland rivers. Hydrol. Process. 2021, 35, e14171. [Google Scholar] [CrossRef]
- Balzer, M.; Facey, J.; Hitchcock, J.; Brooks, A.; Westhorpe, D.; Mitrovic, S. The Importance of Tributary Inflows on Productivity. A Study of the Barwon-Darling River; NSW Department of Planning and Environment: Sydney, Australia, 2021. [Google Scholar]
- Minh, H.V.T.; Avtar, R.; Kumar, P.; Le, K.N.; Kurasaki, M.; Ty, T.V. Impact of rice intensification and urbanization on surface water quality in An Giang using a statistical approach. Water 2020, 12, 1710. [Google Scholar] [CrossRef]
- Minh, H.V.T.; Kurasaki, M.; Ty, T.V.; Tran, D.Q.; Le, K.N.; Avtar, R.; Osaki, M. Effects of multi-dike protection systems on surface water quality in the Vietnamese Mekong Delta. Water 2019, 11, 1010. [Google Scholar] [CrossRef]
- Gray, S.; Hanrahan, G.; McKelvie, I.; Tappin, A.; Tse, F.; Worsfold, P. Flow analysis techniques for spatial and temporal measurement of nutrients in aquatic systems. Environ. Chem. 2006, 3, 3–18. [Google Scholar] [CrossRef]
- Murray, C.; Larson, A.; Goodwill, J.; Wang, Y.; Cardace, D.; Akanda, A.S. Water quality observations from space: A review of critical issues and challenges. Environments 2022, 9, 125. [Google Scholar] [CrossRef]
- Blaen, P.J.; Khamis, K.; Lloyd, C.E.; Bradley, C.; Hannah, D.; Krause, S. Real-time monitoring of nutrients and dissolved organic matter in rivers: Capturing event dynamics, technological opportunities, and future directions. Sci. Total Environ. 2016, 569, 647–660. [Google Scholar] [CrossRef]
- Olmanson, L.G.; Brezonik, P.L.; Bauer, M.E. Remote sensing for regional lake water quality assessment: Capabilities and limitations of current and upcoming satellite systems. In Advances in Watershed Science and Assessment; Springer: Cham, Switzerland, 2015; pp. 111–140. [Google Scholar]
- Pirasteh, S.; Mollaee, S.; Fatholahi, S.N.; Li, J. Estimation of phytoplankton chlorophyll-a concentrations in the Western Basin of Lake Erie using Sentinel-2 and Sentinel-3 data. Can. J. Remote Sens. 2020, 46, 585–602. [Google Scholar] [CrossRef]
- Sagan, V.; Peterson, K.T.; Maimaitijiang, M.; Sidike, P.; Sloan, J.; Greeling, B.A.; Maalouf, S.; Adams, C. Monitoring inland water quality using remote sensing: Potential and limitations of spectral indices, bio-optical simulations, machine learning, and cloud computing. Earth-Sci. Rev. 2020, 205, 103187. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, Y.; Yu, C.; Zhang, Z. Multispectral remote sensing for estimating water quality parameters: A comparative study of inversion methods using unmanned aerial vehicles (UAVs). Sustainability 2023, 15, 10298. [Google Scholar] [CrossRef]
- Naka, M.; Nitta, M. New host and locality records of Gyrodactylus rarus (Monogenea: Gyrodactylidae) from Pungitius tymensis (Gasterosteidae) in Hokkaido, Japan. Biogeography 2021, 23, 80–87. [Google Scholar]
- Tiede, D.; Sudmanns, M.; Augustin, H.; Baraldi, A. Investigating ESA Sentinel-2 products’ systematic cloud cover overestimation in very high altitude areas. Remote Sens. Environ. 2021, 252, 112163. [Google Scholar] [CrossRef]
- Ahmad, M.N.; Shao, Z.; Javed, A. Mapping impervious surface area increase and urban pluvial flooding using Sentinel Application Platform (SNAP) and remote sensing data. Environ. Sci. Pollut. Res. 2023, 30, 125741–125758. [Google Scholar] [CrossRef] [PubMed]
- Bui, Q.T.; Jamet, C.; Vantrepotte, V.; Mériaux, X.; Cauvin, A.; Mograne, M.A. Evaluation of Sentinel-2/MSI atmospheric correction algorithms over two contrasted French coastal waters. Remote Sens. 2022, 14, 1099. [Google Scholar] [CrossRef]
- Gorroño, J.; Guanter, L.; Graf, L.V.; Gascon, F. A software tool for the estimation of uncertainties and spectral error correlation in Sentinel-2 Level-2A data products. EarthArXiv 2023. [Google Scholar] [CrossRef]
- Sent, G.; Biguino, B.; Favareto, L.; Cruz, J.; Sa, C.; Dogliotti, A.I.; Palma, C.; Brotas, V.; Brito, A.C. Deriving water quality parameters using Sentinel-2 imagery: A case study in the Sado Estuary, Portugal. Remote Sens. 2021, 13, 1043. [Google Scholar] [CrossRef]
- Matthews, M.W.; Bernard, S.; Winter, K. Remote sensing of cyanobacteria-dominant algal blooms and water quality parameters in Zeekoevlei, a small hypertrophic lake, using MERIS. Remote Sens. Environ. 2010, 114, 2070–2087. [Google Scholar] [CrossRef]
- Huo, A.; Zhang, J.; Qiao, C.; Li, C.; Xie, J.; Wang, J.; Zhang, X. Multispectral remote sensing inversion for city landscape water eutrophication based on Genetic Algorithm-Support Vector Machine. Water Qual. Res. J. Can. 2014, 49, 285–293. [Google Scholar] [CrossRef]
- Arhonditsis, G.B.; Brett, M.T. Eutrophication model for Lake Washington (USA): Part II—Model calibration and system dynamics analysis. Ecol. Model. 2005, 187, 179–200. [Google Scholar] [CrossRef]
- Elsayed, S.; Ibrahim, H.; Hussein, H.; Elsherbiny, O.; Elmetwalli, A.H.; Moghanm, F.S.; Ghoneim, A.M.; Danish, S.; Datta, R.; Gad, M. Assessment of water quality in Lake Qaroun using ground-based remote sensing data and artificial neural networks. Water 2021, 13, 3094. [Google Scholar] [CrossRef]
- Kumar, D.A.; Murugan, S. Performance analysis of MLPFF neural network back propagation training algorithms for time series data. In Proceedings of the 2014 World Congress on Computing and Communication Technologies, Trichirappalli, India, 27 February–1 March 2014; pp. 114–119. [Google Scholar]
- Reta, G.; Dong, X.; Li, Z.; Bo, H.; Yu, D.; Wan, H.; Su, B. Application of Single Factor and Multi-Factor Pollution Indices Assessment for Human-Impacted River Basins: Water Quality Classification and Pollution Indicators. Nat. Environ. Pollut. Technol. 2019, 18, 1063–1072. [Google Scholar]
- Liu, Q.; Pei, H.; Hu, W.; Xie, J. Assessment of trophic status for Nansi Lake using trophic state index and phytoplankton community. In Proceedings of the 2010 4th International Conference on Bioinformatics and Biomedical Engineering, Chengdu, China, 18–20 June 2010; pp. 1–4. [Google Scholar]
- Wang, L.F.; Bai, Y.X.; Gai, S.N. Single-factor and nemerow multi-factor index to assess heavy metals contamination in soils on railway side of Harbin-Suifenhe Railway in Northeastern China. Appl. Mech. Mater. 2011, 71, 3033–3036. [Google Scholar] [CrossRef]
- Zou, W.; Zhu, G.; Cai, Y.; Vilmi, A.; Xu, H.; Zhu, M.; Gong, Z.; Zhang, Y.; Qin, B. Relationships between nutrient, chlorophyll a and Secchi depth in lakes of the Chinese Eastern Plains ecoregion: Implications for eutrophication management. J. Environ. Manag. 2020, 260, 109923. [Google Scholar] [CrossRef] [PubMed]
- Xing, K.; Guo, H.; Sun, Y.; Huang, Y. Assessment of the spatial-temporal eutrophic character in the Lake Dianchi. J. Geogr. Sci. 2005, 15, 37–43. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Shi, K.; Zhou, Y.; Li, N. Remote sensing estimation of water clarity for various lakes in China. Water Res. 2021, 192, 116844. [Google Scholar] [CrossRef]
- Peng, J.; Jia, J.; Liu, Y.; Li, H.; Wu, J. Seasonal contrast of the dominant factors for spatial distribution of land surface temperature in urban areas. Remote Sens. Environ. 2018, 215, 255–267. [Google Scholar] [CrossRef]
- Wu, B.; Dai, S.; Wen, X.; Qian, C.; Luo, F.; Xu, J.; Wang, X.; Li, Y.; Xi, Y. Chlorophyll-nutrient relationship changes with lake type, season and small-bodied zooplankton in a set of subtropical shallow lakes. Ecol. Indic. 2022, 135, 108571. [Google Scholar] [CrossRef]
- Petkuvienė, J. Phosphorus pool variations in the Curonian lagoon and its implication to eutrophication. Ph.D. Thesis, Klaipėdos Universitetas, Klaipėda, Lithuania, 2015. [Google Scholar]
- Kleinman, P.J.; Sharpley, A.N.; Withers, P.J.; Bergström, L.; Johnson, L.T.; Doody, D.G. Implementing agricultural phosphorus science and management to combat eutrophication. Ambio 2015, 44, 297–310. [Google Scholar] [CrossRef]
- Boesch, D.F.; Brinsfield, R.B.; Magnien, R.E. Chesapeake Bay eutrophication: Scientific understanding, ecosystem restoration, and challenges for agriculture. J. Environ. Qual. 2001, 30, 303–320. [Google Scholar] [CrossRef]
- Fukushima, T.; Matsushita, B. Limiting nutrient and its use efficiency of phytoplankton in a shallow eutrophic lake, Lake Kasumigaura. Hydrobiologia 2021, 848, 3469–3487. [Google Scholar] [CrossRef]
- Jakobsen, H.H.; Markager, S. Carbon-to-chlorophyll ratio for phytoplankton in temperate coastal waters: Seasonal patterns and relationship to nutrients. Limnol. Oceanogr. 2016, 61, 1853–1868. [Google Scholar] [CrossRef]
- Jarvie, H.P.; Sharpley, A.N.; Withers, P.J.; Scott, J.T.; Haggard, B.E.; Neal, C. Phosphorus mitigation to control river eutrophication: Murky waters, inconvenient truths, and “postnormal” science. J. Environ. Qual. 2013, 42, 295–304. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Wang, S.; Ni, Z.; Guo, Y.; Liu, X.; Wang, G.; Li, H. Non-linear dynamics of lake ecosystem in responding to changes of nutrient regimes and climate factors: Case study on Dianchi and Erhai lakes, China. Sci. Total Environ. 2021, 781, 146761. [Google Scholar] [CrossRef]
- Cho, Y.C.; Kang, H.Y.; Son, J.Y.; Kang, T.; Im, J.K. The spatiotemporal eutrophication status and trends in the Paldang Reservoir, Republic of Korea. Sustainability 2023, 16, 373. [Google Scholar] [CrossRef]
- Wang, H.; Wan, X.; Wang, S.; Xia, L.; Song, Y. Assessment of eutrophication characteristics and evaluation of the first-generation eutrophication model in the nearshore waters of Shantou City. Sustainability 2023, 15, 14866. [Google Scholar] [CrossRef]
- Pinckney, J.L.; Paerl, H.W.; Harrington, M.B. Responses of the phytoplankton community growth rate to nutrient pulses in variable estuarine environments. J. Phycol. 1999, 35, 1455–1463. [Google Scholar] [CrossRef]
- Kemp, W.M.; Testa, J.M.; Conley, D.J.; Gilbert, D.; Hagy, J.D. Temporal responses of coastal hypoxia to nutrient loading and physical controls. Biogeosciences 2009, 6, 2985–3008. [Google Scholar] [CrossRef]
- Stutter, M.I.; Graeber, D.; Evans, C.D.; Wade, A.J.; Withers, P.J.A. Balancing macronutrient stoichiometry to alleviate eutrophication. Sci. Total Environ. 2018, 634, 439–447. [Google Scholar] [CrossRef]
- Determan, R.T.; White, J.D.; McKenna, L.W., III. Quantile regression illuminates the successes and shortcomings of long-term eutrophication remediation efforts in an urban river system. Water Res. 2021, 202, 117434. [Google Scholar] [CrossRef]
- Quadra, G.R.; Brovini, E.M. Nutrient Pollution. In The Palgrave Handbook of Global Sustainability; Springer International Publishing: Cham, Switzerland, 2022; pp. 1–21. [Google Scholar]
- Zhao, L.; Zhu, R.; Zhou, Q.; Jeppesen, E.; Yang, K. Trophic status and lake depth play important roles in determining the nutrient-chlorophyll a relationship: Evidence from thousands of lakes globally. Water Res. 2023, 242, 120182. [Google Scholar] [CrossRef]
- Malhadas, M.S.; Mateus, M.D.; Brito, D.; Neves, R. Trophic state evaluation after urban loads diversion in a eutrophic coastal lagoon (Óbidos Lagoon, Portugal): A modeling approach. Hydrobiologia 2014, 740, 231–251. [Google Scholar] [CrossRef]
- Muduli, P.R.; Barik, M.; Acharya, P.; Behera, A.T.; Sahoo, I.B. Variability of Nutrients and Their Stoichiometry in Chilika Lagoon, India. In Coastal Ecosystems: Environmental Importance, Current Challenges and Conservation Measures; Springer Nature Switzerland AG: Cham, Switzerland, 2022; pp. 139–173. [Google Scholar]
- Flaten, D.; Snelgrove, K.; Halket, I.; Buckley, K.; Penn, G.; Akinremi, W.; Wiebe, B.; Tyrchniewicz, E. Acceptable Phosphorus Concentrations in Soils and Impact on the Risk of Phosphorus Transfer from Manure Amended Soils to Surface Waters. Review of Literature for the Manitoba Livestock Manure Management Initiative. 25 April 2006. Available online: https://www.researchgate.net/publication/309673600_Acceptable_Phosphorus_Concentrations_in_Soils_and_Impact_on_the_Risk_of_Phosphorus_Transfer_from_Manure_Amended_Soils_to_Surface_Waters_A_Review_of_Literature_for_the_Manitoba_Livestock_Manure_Managem (accessed on 17 December 2024).
- Liu, W.; Qin, T.; Chen, Y.; Yin, J.; Li, Z.; Wang, H.; Ruan, G.; Zhu, J.; Xiao, H.; Abakumov, E.; et al. Sustainable management strategy for phosphorus in large-scale watersheds based on the coupling model of substance flow analysis and machine learning. Resour. Conserv. Recycl. 2024, 211, 107897. [Google Scholar] [CrossRef]
- Mainstone, C.P.; Parr, W. Phosphorus in rivers—Ecology and management. Sci. Total Environ. 2002, 282, 25–47. [Google Scholar] [CrossRef] [PubMed]
- Raudsepp, U.; Maljutenko, I.; Kõuts, M.; Granhag, L.; Wilewska-Bien, M.; Hassellöv, I.M.; Eriksson, K.M.; Johansson, L.; Jalkanen, J.P.; Karl, M.; et al. Shipborne nutrient dynamics and impact on eutrophication in the Baltic Sea. Sci. Total Environ. 2019, 671, 189–207. [Google Scholar] [CrossRef] [PubMed]
- Jabir, T.; Vipindas, P.V.; Jesmi, Y.; Valliyodan, S.; Parambath, P.M.; Singh, A.; Abdulla, M.H. Nutrient stoichiometry (N:P) controls nitrogen fixation and distribution of diazotrophs in a tropical eutrophic estuary. Mar. Pollut. Bull. 2020, 151, 110799. [Google Scholar] [CrossRef]
- Hamilton, D.P.; Salmaso, N.; Paerl, H.W. Mitigating harmful cyanobacterial blooms: Strategies for control of nitrogen and phosphorus loads. Aquat. Ecol. 2016, 50, 351–366. [Google Scholar] [CrossRef]
- Paerl, H.W.; Havens, K.E.; Xu, H.; Zhu, G.; McCarthy, M.J.; Newell, S.E.; Scott, J.T.; Hall, N.S.; Otten, T.G.; Qin, B. Mitigating eutrophication and toxic cyanobacterial blooms in large lakes: The evolution of a dual nutrient (N and P) reduction paradigm. Hydrobiologia 2020, 847, 4359–4375. [Google Scholar] [CrossRef]
- Bovolo, C.I.; Blenkinsop, S.; Majone, B.; Zambrano-Bigiarini, M.; Fowler, H.J.; Bellin, A.; Burton, A.; Barceló, D.; Grathwohl, P.; Barth, J.A.C. Climate change, water resources and pollution in the Ebro Basin: Towards an integrated approach. In The Ebro River Basin; Springer: Berlin/Heidelberg, Germany, 2011; pp. 295–329. [Google Scholar]
- Cakmak, E.K.; Hartl, M.; Kisser, J.; Cetecioglu, Z. Phosphorus mining from eutrophic marine environments towards a blue economy: The role of bio-based applications. Water Res. 2022, 219, 118505. [Google Scholar] [CrossRef]
- Abbott, B.W.; Moatar, F.; Gauthier, O.; Fovet, O.; Antoine, V.; Ragueneau, O. Trends and seasonality of river nutrients in agricultural catchments: 18 years of weekly citizen science in France. Sci. Total Environ. 2018, 624, 845–858. [Google Scholar] [CrossRef]
- O’Grady, J.; Zhang, D.; O’Connor, N.; Regan, F. A comprehensive review of catchment water quality monitoring using a tiered framework of integrated sensing technologies. Sci. Total Environ. 2021, 765, 142766. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).