Impact of Rain Gauge Density on Flood Forecasting Performance: A PBDHM’s Perspective

Abstract

The structures and parameters of physically-based distributed hydrological models (PBDHMs) can now be established and derived from remote-sensing data with relative ease. When engineers apply PBDHMs for flood forecasting in mesoscale catchments, they encounter varying rain gauge infrastructure conditions. Understanding model performance expectations under varying rain gauge density conditions is crucial for wide PDBHM construction. This study presents a case study of a PBDHM called the Liuxihe Model and examines six rain gauge density scenarios designed based on real-world data to assess the impact of rain gauge density on model flood forecasting performance. The study focuses on a mesoscale catchment in Jiangxi Province, China, covering an area of 2364 km² with 62 rain gauges. The results indicate that models optimized under an adequate rain gauge density condition are less affected by gauge density changes, maintaining accuracy within a range of change. Compared to Kling–Gupta Efficiency (KGE) and Nash–Sutcliffe Efficiency (NSE), the indicators absolute peak time error (APTE) and peak relative error (PRE) are less sensitive to variation in rain gauge density. The study further discusses how rain gauge density changes related to the interpolated rainfall surfaces and parameter optimization, hoping to facilitate the broader application of PBDHMs and offer insights for future practices.

1. Introduction

Flooding resulting from excessive rainfall has been occurring frequently and disasters caused by floods damage people’s lives and property [1], especially for catchments that lack flood monitoring and management. Flood forecasting is a crucial task in catchment management, which falls within the scope of short-term streamflow forecasting, targeting on the hourly time scale, and providing information on flood peak quantity, peak timing, and the flood hydrograph.

It is necessary for flood-prone catchments to set up a flood forecasting system. PBDHMs have a reputation for their interpretability and robustness, which is a feasible and stable component for constructing a catchment flood forecasting system [2]. As disciplines like pedology and remote-sensing developed, more and more high-quality data could be accessed worldwide, and parameters depicting the catchment’s underlying surface characteristics could be derived from public datasets with relative ease. Moreover, the resolution of remote-sensing data has been gradually improving, leading to the advancement in hydrological models into the era of PBDHMs [3,4]. PBDHMs require data such as terrain data, land-use data, and soil data. In the past, acquiring these data was challenging; it was difficult for researchers to obtain the data needed for constructing PBDHMs or the data’s coarse resolution led to suboptimal performance. Nowadays, there is a wealth of terrain data available for constructing PBDHMs. For mesoscale catchment, DEM data with resolutions of 90 m (SRTM DEM), 30 m (ASTER GDEM), or even 12.5 m (TanDEM-X DEM) can be selected according to specific needs, and most of these datasets are freely available and cover global regions [5]. The availability of land-use data for PBDHMs is also extensive, with numerous datasets such as the 30 m CLCD [6], the 10 m Sentinel-2 Global Land Cover Map [7], and many more. Soil-related parameters can also be obtained through remote-sensing technologies; available datasets include soil type database SOTER [8], soil moisture product SMAP [9], and so on. These remote-sensing datasets have significantly advanced the development and widespread application of PBDHMs.

For PBDHMs on flood forecasting, with the combined efforts of many interdisciplinarities, a lot of models were proposed for decision-making on flood prevention and control, such as the SHE [10], VIC [11], HEC-HMS [12], Liuxihe model [13], etc. A PBDHM that describes the catchment’s underlying surface well is robust to respond to various magnitudes of rainfall and has the ability to depict characteristics of a flood that is caused by extreme rainfall accurately.

Once the structure and parameters of the model are determined, for a typical mountainous catchment, inputting rainfall data to the model is sufficient for flood forecasting [14,15]. The preliminary establishment of a PBDHM requires an assessment of the rain gauge infrastructure within the catchment, the rain gauge infrastructure condition in each catchment is constrained by factors such as the local economy and terrain. The observational data from rain gauges measure the rainfall reaching the ground at specific station locations, serving as a crucial source of input data for the model. By using spatial interpolation methods, the rainfall surfaces required for model input are obtained. The density of rain gauges in a catchment is one of the indicators used to measure the condition of the rainfall observation system of a catchment. Investigating the impact of rain gauge density on flood forecasting can provide valuable insights for the construction of flood forecasting models and the development of rain gauge networks within catchments.

In many developing countries, the establishment of rain gauges within river basins is often characterized by poor infrastructure and limited resources. This results in a lack of comprehensive and reliable data, hindering effective water resource management and flood forecasting efforts. Additionally, the sparse distribution of rain gauges exacerbates the challenge of accurately assessing precipitation patterns [16].

There are some studies about rain gauge density’s influence on the hydrological process. Sucozhañay and Célleri [17], Hohmann et al. [18] conclude that gauge density is a key factor affecting model performance. Yin et al. [19] studied the effect of rain station density on hydrological modeling from the perspective of model types. Zeng et al. [20] studied the impact of rain gauge density on runoff simulation from a lumped model perspective. Mishra [21] studied the effect of rain gauge density on the accuracy of rainfall and Prakash et al. [22] proposed a new parameter to access the minimum number of rain gauges necessary for a region to estimate rainfall. However, few studies, if any, have explored how rain gauge density indirectly impacts the performance of PBDHMs in hourly flood forecasting. Since spatial interpolation methods act as the bridge between rainfall observations and the rainfall surfaces used as model inputs, it is essential to investigate the sensitivity of commonly used interpolation methods to changes in rain gauge density. Additionally, parameter calibration/optimization methods provided by PBDHMs help compensate for errors in both input data and model structure to some extent. Therefore, understanding how the impact of rain gauge density propagates through spatial interpolation methods and parameter calibration/optimization is crucial. This knowledge will help answer the question of how the dynamic changes in rain gauge density affect the flood forecasting performance of PBDHMs.

This study set up a PBDHM called the Liuxihe model [13] in a mesoscale catchment located in Jiangxi Province, China to explore the above problems. The study considers three commonly used and representative spatial interpolation methods for rainfall input—Thiessen Polygons (THI), Inverse Distance Weighting (IDW), and Geographically Weighted Regression (GWR)—under varying gauge density conditions. Figure 1 is the flow chart of experiments designed in this study. The study first evaluates the performance of the model using existing gauges with three interpolation methods. Then five rain gauge density conditions are derived from the existing gauge distribution via a sampling algorithm based on gauge distance. These gauge density conditions and spatial interpolation methods consist of 18 scenarios in total. A dataset consisting of 15 flood events is used to compare the models to quantitatively analyze the impact of rain gauge density on model flood forecasting performance. Models using different spatial interpolation settings are optimized and tested separately. This case study hopes to promote PBDHMs construction on mesoscale catchments, especially for catchments with limited gauge infrastructure installed, providing a reference for catchment management agencies on gauge infrastructure development and curves of model performance expectation under varying rain gauge density conditions. A thorough analysis of the PBDHMs for flood forecasting principles is also illustrated, such analyses in this study would be valuable for engineers, hydrologists, or decision-makers working on flood forecasting and related research. The materials, methods, and detailed experimental design and settings of this study are comprehensively described in the following sections.

2. Materials and Methods

2.1. Study Catchment

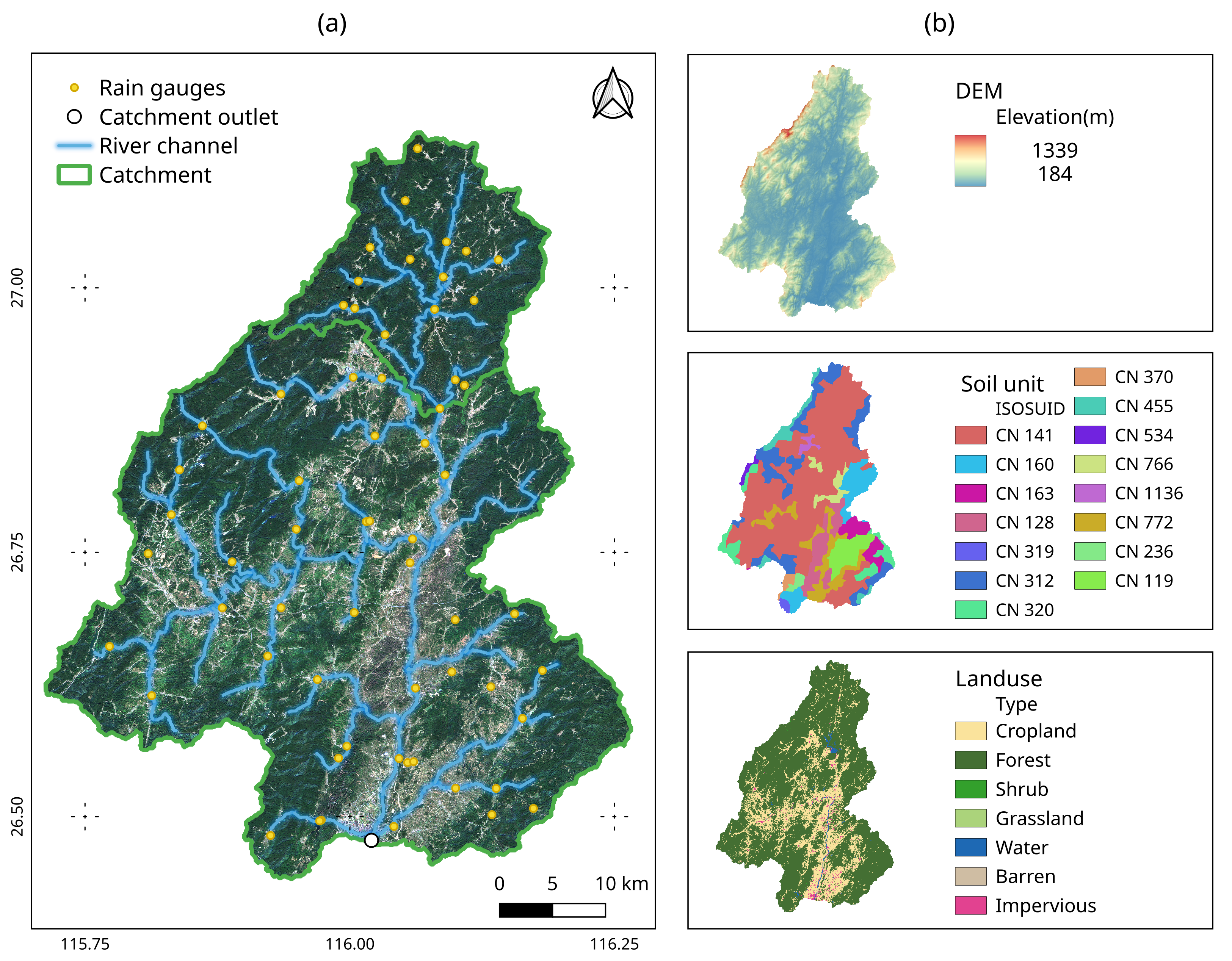
The study catchment is called Ningdu catchment, named after its outlet stations. It is a mesoscale catchment with an area of about 2364 km², located in Jiangxi Province, China (ranging from 26.43° N to 27.14° N, 115.71° E to 116.26° E). Figure 2 is the overview of the Ningdu catchment, showing its river network, rain gauge distribution, DEM, soil type, and land use. The catchment lies between 35 and 693 m in elevation and consists of river networks, which are tributaries of the Mei River. The catchment is located in the subtropical monsoon region, with forest and cropland as the primary land-use types. Human influence on the hydrological processes is relatively limited. According to the SOTER China database [8], there are 15 soil units in the catchment, with Haplic Acrisols being the predominant soil type. The Ningdu catchment is well-managed, it has a 62 rain gauge network, and long-time series hourly rainfall observations for the past few years have been collected.

2.2. Flood Events Data and Model Construction Data

Sixteen typical flood event data (time series of precipitation in each rain gauge and flow observation in catchment outlet) are extracted from the long time series of rain gauge observation from 2013 to 2017.

Table 1. Events data overview.

ID	Event Identifier	Begin Time	Duration (h)	Peak (m3/s)
1	2013-08-21	09:00:00	137	619.0
2	2014-03-01	00:00:00	527	292.3
3	2014-03-26	08:00:00	249	291.5
4	2014-06-16	10:00:00	262	692.6
5	2014-07-13	11:00:00	208	271.4
6	2014-08-11	03:00:00	300	312.3
7	2015-05-27	03:00:00	180	885.6
8	2015-07-01	05:00:00	201	1104.7
9	2015-11-10	14:00:00	300	1140.0
10	2016-06-14	10:00:00	164	919.3
11	2016-07-16	12:00:00	119	965.9
12	2016-11-19 1	12:00:00	254	566.0
13	2016-09-27	18:00:00	182	800.2
14	2017-03-27	22:00:00	172	541.0
15	2017-06-01	05:00:00	228	749.3
16	2017-06-12	08:00:00	317	485.0

Note: ¹ The event used for model parameter optimization.

describes the flood events’ characteristics. The flood event dataset encompasses floods of varying magnitudes, ranging from large to small, and the flood durations span from 119 h to 527 h.

Event 2016-11-19 is chosen for parameter optimization, as it is a medium twin peak flood with a smooth flood hydrograph, which is relatively information-rich and less noisy for model parameter optimization. The other 15 events are used for model performance testing.

The basic structure of the Liuxihe model is constructed by DEM, soil, and land-use remote-sensing products. In this study, the 90 m SRTMv4 dataset [23] is used for the catchment DEM, model parameter slope and flow direction can be calculated from the DEM. For land-use data, a 30 m land-use product by Yang and Huang [6] is warped (resampled and aligned) to the resolution of DEM, and the model slope cell parameter evaporation coefficient and roughness coefficient are estimated according to the land-use of the cell. For soil data, the SOTER China database [8] is used. Soil-related parameters of the model could be calculated by a soil water characteristic calculator developed by Saxton and Rawls [24], according to the profile component of the soil. The initial values of landuse-related and soil-related parameters for the study catchment are provided in the Appendix A.

2.3. Liuxihe Model and Its Parameter Optimization Method

Liuxihe model is a productive PBDHM for mesoscale catchment flood forecasting, which has been applied to flood forecasting in many catchments in Southern China [25,26,27,28,29]. The following is a brief anatomy of the Liuxihe model and further details about the model can be found in [13].

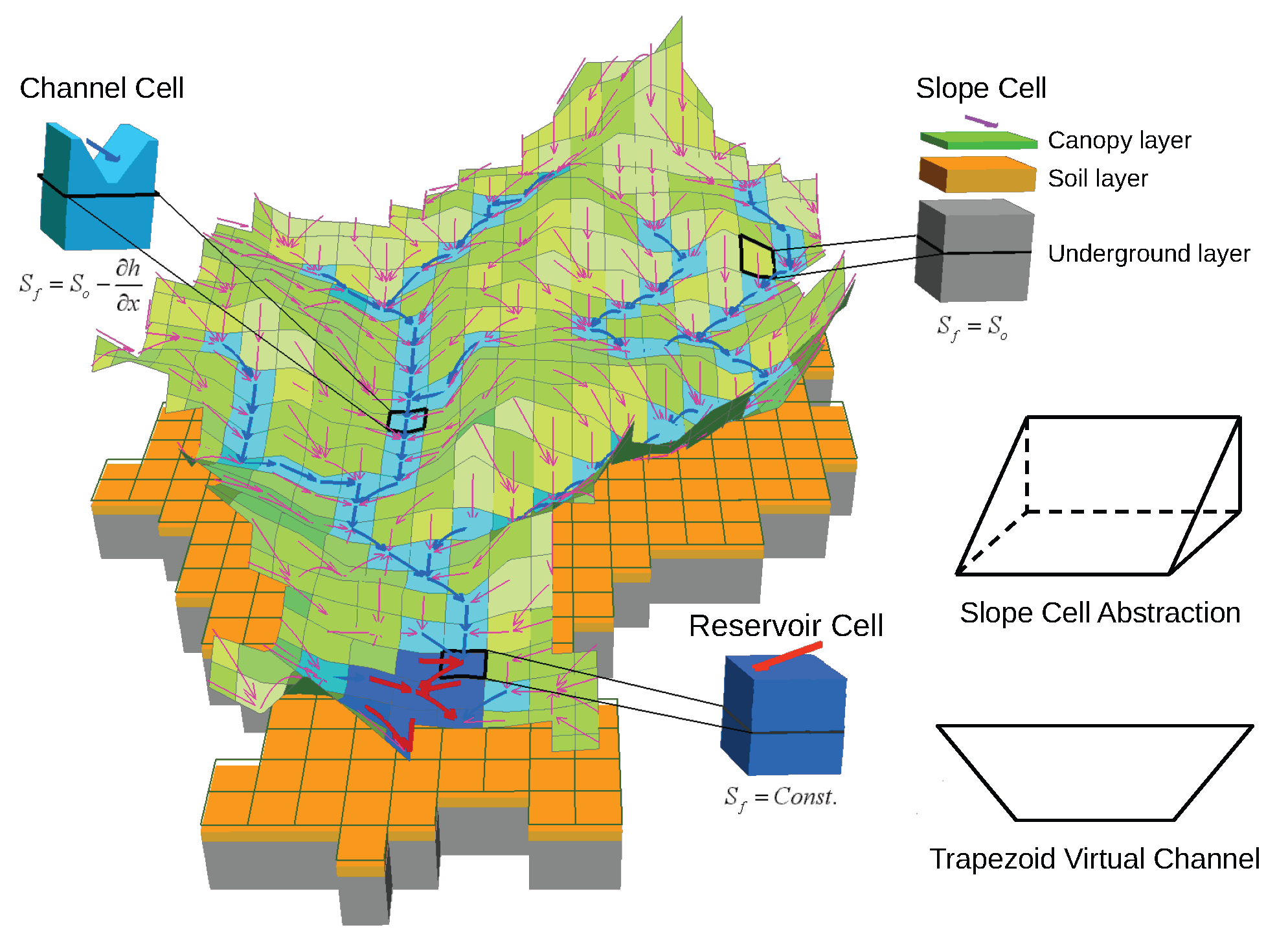
As a PBDHM, the Liuxihe model’s distributed structure is derived from DEM; the grid unit of the DEM is the minimum calculation unit of the model, which is also called cells in the GIS context. Each cell has its attributes, i.e., the model parameters. The Liuxihe model has a few parameters for its simplicity, which fall into four categories, DEM-derived parameters (cell class, slope, flow direction), soil parameters (thickness, saturation hydraulic conductivity, saturated soil water content, field water capacity, wilting point, porosity coefficient, infiltration intensity), land-use parameters (evaporation coefficient, roughness coefficient), and channel parameters (bottom width, bottom slope, side slope, channel roughness). By dividing the catchment into slope cell, channel cell, and reservoir cell horizontally and canopy layer, soil layer, and underground layer vertically, the Liuxihe model couples three subroutines on evaporation, flow generation, and flow convergence to describe the flood process response to a rain event. Figure 3 illustrates the structure of the Liuxihe model.

Though the parameters of PBDHMs derived from remote-sensing data are near to real value, revising the parameters is still needed in model building [30,31], due to the uncertainty in geography data. Many PBDHMs are equipped with parameter optimization/calibration methods [31,32,33], which need observed flow data to tune model parameters responding to rainfall input as close to reality as possible. As with many PBDHMs, the Liuxihe model is equipped with its parameter optimization method [31], which is based on the particle swarm optimization (PSO) algorithm [34]. The Liuxihe Model adopts a scaling law to optimize its parameters. As mentioned earlier, the model’s initial parameters are derived from remote-sensing data, which carry inherent uncertainties. To account for potential deviations, the parameters can be scaled within a range of 0.5 to 1.5 times their initial values and constrained by physical significance. Different particles in the swarm represent the scaling coefficients of the model parameters and move within the solution space. These particles evaluate the quality of their positions using an objective function (also called fit in the PSO context, Equation (1) is used in this study) and adjust their direction and speed accordingly, ultimately converging towards an optimal state. The final optimized model parameters are obtained by multiplying the initial parameters by the scaling coefficients, ensuring that the parameters remain physically meaningful.

$$Fit=\sum _i^N{(Q_{o,i}^2-Q_{s,i}^2)}^2$$

(1)

2.4. Rainfall Spatial Interpolation Methods

There are many spatial interpolation methods to generate a distributed rainfall input from gauge observation point data, but most of them are focused on a day scale or month scale [35,36], or are too complicated for application on an hourly scale. Take Ordinary Kriging, for example, data with weak spatial heterogeneity may face difficulty fitting the semivariogram automatically, resulting in unreliable spatial predictions [37]; this phenomenon often occurs when there are few gauges and minor rainfall, leading to inconsistency in the interpolated rainfall surfaces. In flood forecasting, operators often lack sufficient knowledge to handle these conditions. For these reasons, simple and automatic methods are still commonly used in practice. Considering the ease of use and applicability, this study selects THI, IDW, and GWR for research. They are both representative and widely used in practice. The theoretical backgrounds are briefly introduced below. More detailed information can be found in [38,39,40].

The theory of THI is simple, as in Equation (2), rainfall that occurs in one cell c is generalized the same as its nearest gauges g’s measurement $P\left(g\right)$.

$$P\left(c\right)=P\left(g_{nearest}\right)$$

(2)

IDW assumes that gauges closer to the location of interest have more influence on the estimated value. The method calculates a weighted average of gauge observations, with weights inversely proportional to their distance from the target location, as shown in Equation (3).

$$P\left(c\right)={\displaystyle \frac{{\sum }_i^{N}P\left(g_i\right)D^{-2}(g_i,c)}{{\sum }_i^N{D}^{-2}(g_i,c)}}$$

(3)

where D is a function that describes distances between Cell c and gauge g; the Euclidean distance is commonly used.

GWR accounts for the spatial heterogeneity inherent in rainfall patterns. Unlike traditional regression, GWR accounts for geographic location, allowing coefficients to vary across space. It fits a regression model at each location using nearby observations, weighted by their distance, thus capturing local variations and providing more accurate spatial predictions. For consistency with THI and IDW, who only consider distance in rainfall interpolation, the form of GWR without considering other variables is used in this study. Rainfall in one cell c can be predicted as in Equation (4).

$$P\left(c\right)={\displaystyle \frac{{\sum }_i^{\delta }{w}_{g_i}{\beta }_i}{{\sum }_i^{\delta }{w}_{g_i}}}$$

(4)

where ${\beta }_i$ is the solved regression coefficients, $\delta$ is bandwidth calculated by the AIC method [40], and $w_i$ is the spatial weight which could be calculated by Equation (5).

$$w_{g_i}=\left\{\begin{array}{cc}{(1-{\left({\displaystyle \frac{D(c,g_i)}{\delta }}\right)}^2)}^2,\hfill & D(c,g_i)<\delta \hfill \\ 0,\hfill & D(c,g_i)\ge \delta \hfill \end{array}\right.$$

(5)

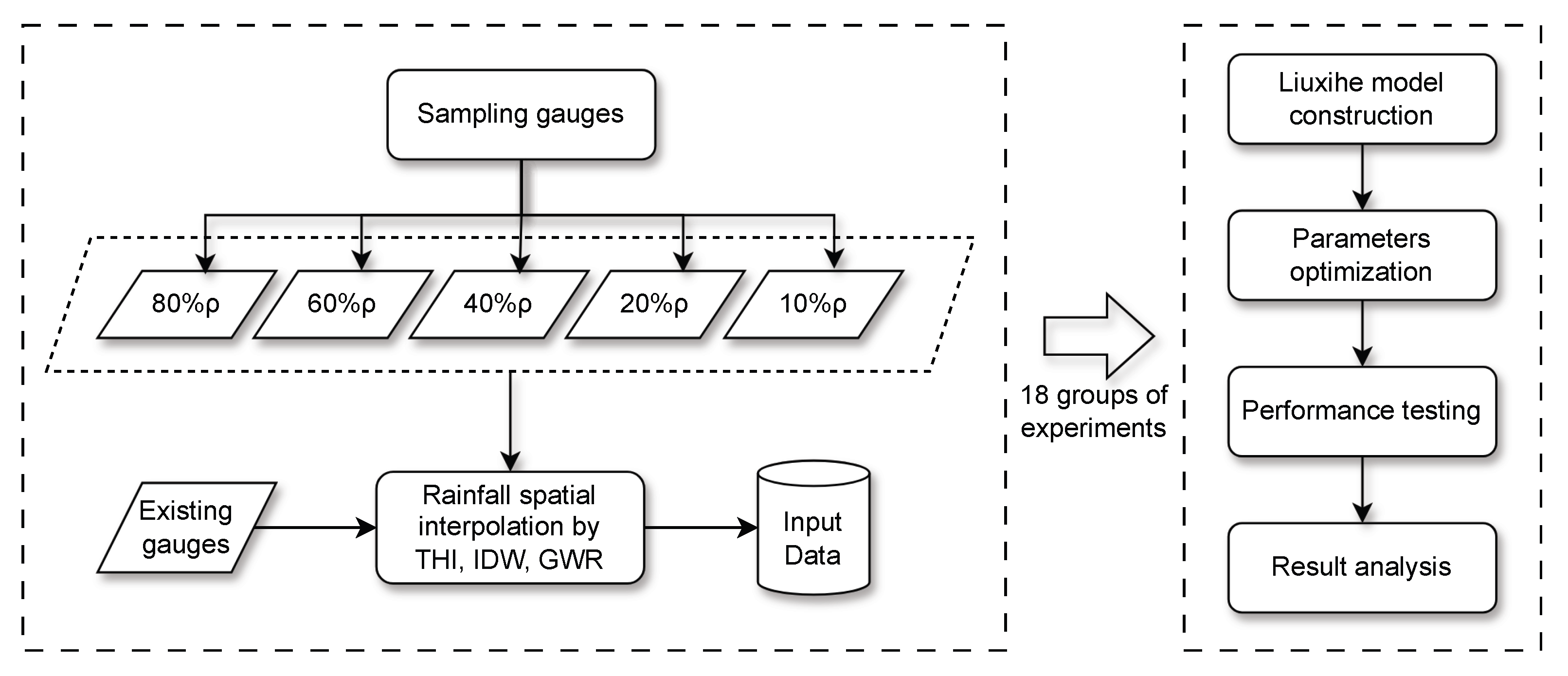
2.5. Experimental Settings

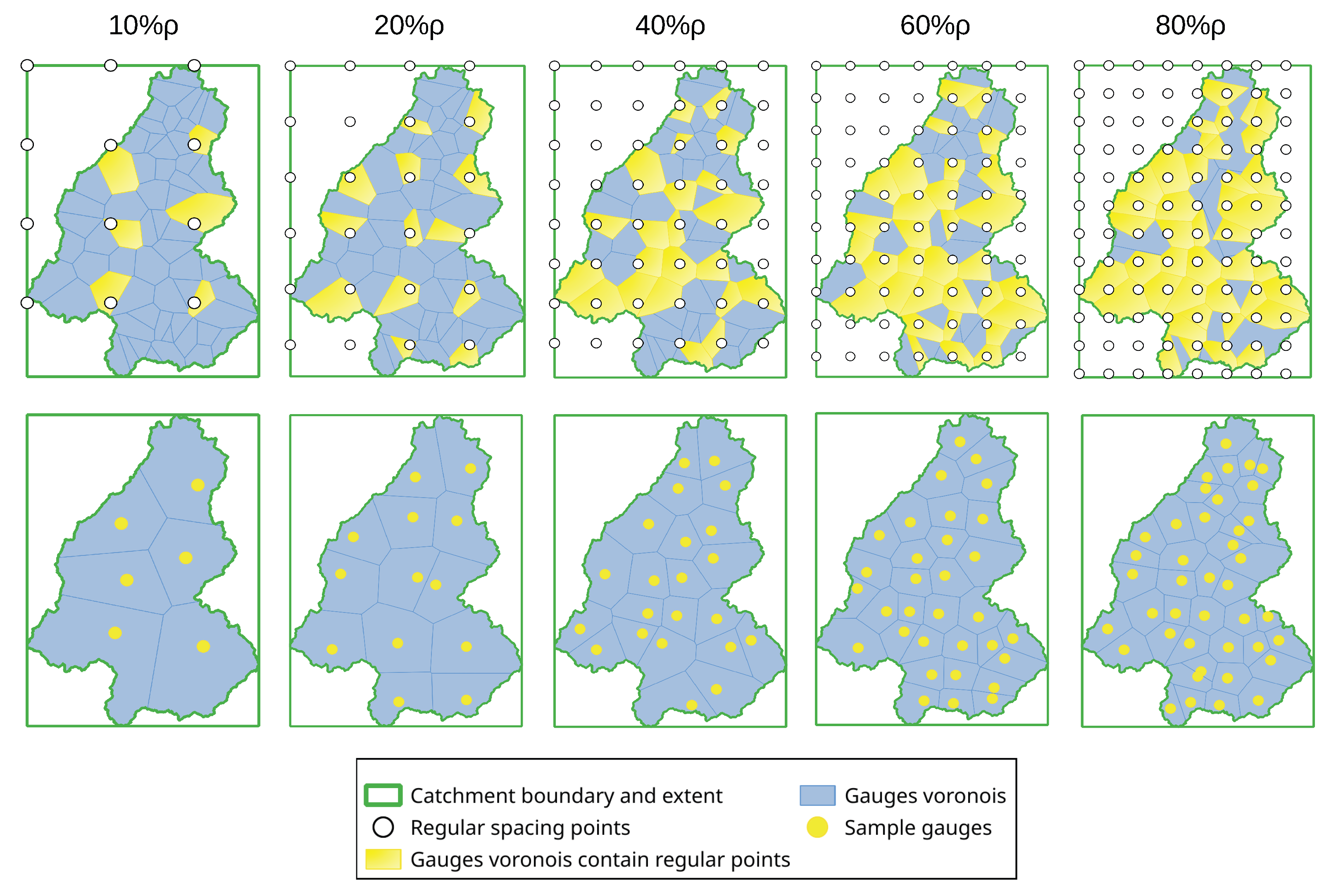
As mentioned earlier in the introduction, five rain gauge density conditions are derived from existing gauge distribution by an algorithm based on the distance of gauges. Algorithm 1 illustrated these procedures and Figure 4 further depicted the process visually.

Algorithm 1 Sampling Scheme

Calculate average gauge distance by $D=\sqrt{{\displaystyle \frac{A}{N}}}$, where $A=$ catchment area and $N=$ number of existing gauges. Generate the Voronoi polygons $\mathcal{P}$ of existing rain gauges (blue polygons in Figure 4). Generate regular spacing point collections ${\mathcal{S}}_i$ (white points in Figure 4) in the catchment extent, with the spacing $D_i={\displaystyle \frac{D}{0.8}},{\displaystyle \frac{D}{0.6}},{\displaystyle \frac{D}{0.4}},{\displaystyle \frac{D}{0.2}},{\displaystyle \frac{D}{0.1}}$. The gauges whose Voronoi polygons are in ${\mathcal{S}}_i\cap \mathcal{P}$ (yellow polygons in Figure 4) are selected as the samples (yellow points in Figure 4).

When installing rain gauges within a catchment, it is common to maximize their effectiveness by distributing rain gauges as evenly as possible when conditions permit. Without considering special circumstances, the density of rain gauges in a catchment can be estimated by dividing the catchment area by the number of gauges. Some GIS tricks can be employed to generate different rain gauge density scenarios. In Algorithm 1, it is assumed that rain gauge density can be measured by the average distance between gauges. By scaling the estimated average distance of existing gauges with factors of 0.8, 0.6, 0.4, 0.2, and 0.1, regular spacing points that mimic the distribution of sampled gauges in these scenarios can be generated. If an existing rain gauge whose Voronoi polygon contains a regular spacing point, this gauge will be chosen to use. This approach simplifies real-world scenarios based on the Voronoi polygon theory. Ultimately, five generated rain gauge density scenarios and 1 existing gauge scenario are present, corresponding to the number of gauges being used are 62, 41, 32, 22, 13, and 6, and the estimated control area of each gauge is 38 km², 57 km², 74 km², 107 km², 182 km², and 394 km², respectively. Notice that from 100% density to 80% density, up to 20 gauges are excluded from the sample. This occurs because existing rain gauges are not perfectly uniformly distributed, some closely spaced gauges are filtered out by the algorithm.

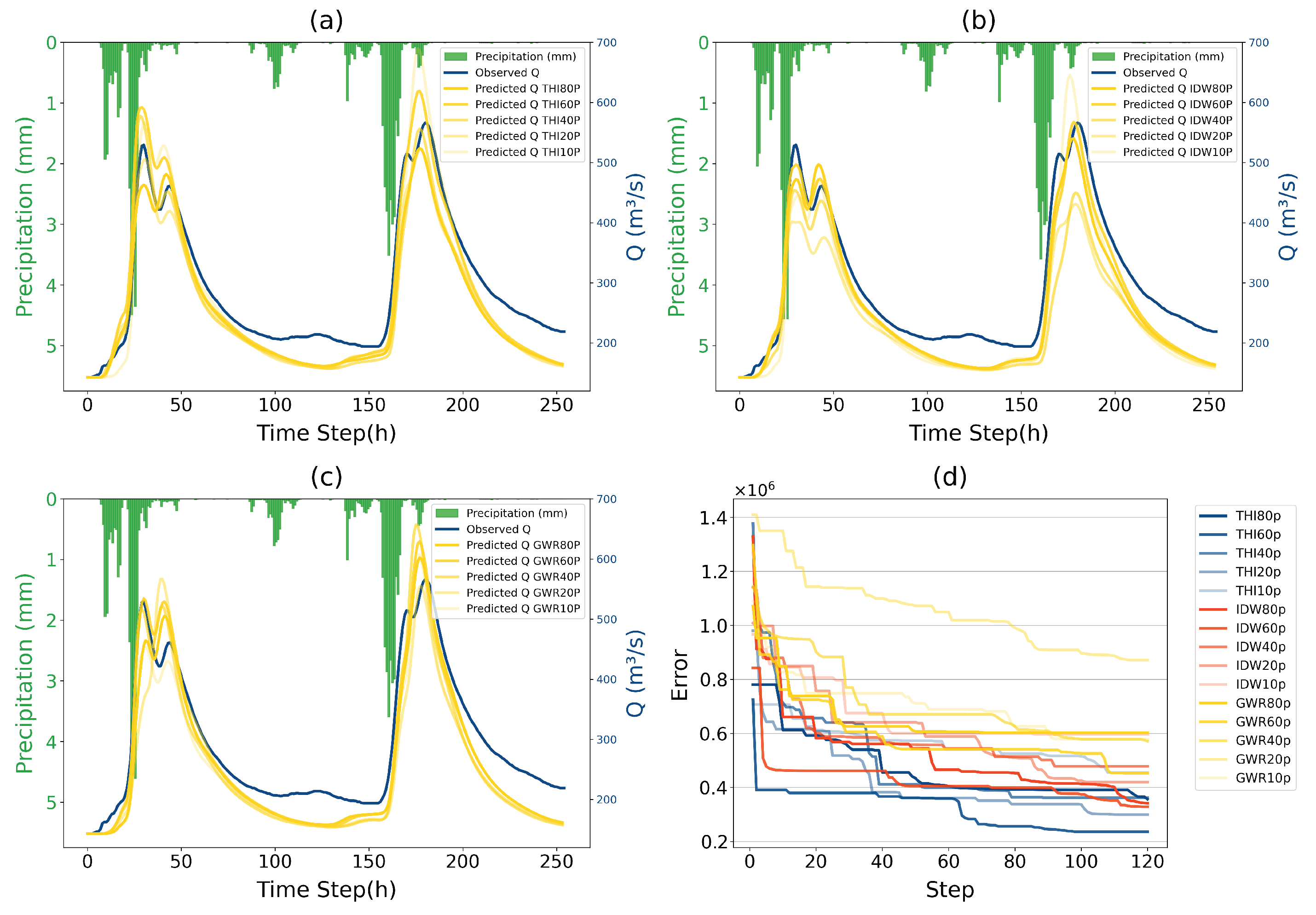
Gauges are selected from a scale of the average distance, which could be regarded as a scale of gauge density. For simplicity, use an abbreviated notation for experiment naming, e.g., “100P” represents the experiment on existing gauge density ($100\%\times \rho$), “THI80P” represents the experiment on gauges sampled by intersection with ${\displaystyle \frac{D}{0.8}}$ spacing points ($80\%\times \rho$) and use THI to interpolate distributed rainfall surfaces. Combining six gauge density conditions with three spatial interpolation methods, there are 18 scenarios in total. The model parameters are optimized only for scenarios THI100P, IDW100P and GWR100P in the same PSO settings, as the characteristics of their interpolated surface are different. The performance of the experiments THI100P, IDW100P, and GWR100P will be evaluated first, serving as the reference baseline for observing how the model’s performance changes under varying rain gauge density conditions.

The evaluators chosen to compare the model performance are Kling–Gupta Efficiency (KGE) [41], Nash–Sutcliffe Efficiency (NSE), peak relative error (PRE), and absolute peak time error (APTE). KGE and NSE evaluate the overall agreement between the predicted and observed hydrographs. While NSE focuses on how well the predictions capture the observed variability, KGE offers a more balanced evaluation by incorporating correlation, bias, and variability into the assessment and is less affected by extreme values [42]. PRE and APTE assess the model’s flood forecasting performance from the perspective of peak flow, while the former focuses on the magnitude of the peak flow, and the latter on the timing of the peak. These four evaluators together provide a comprehensive comparison of the model’s performance. Their definitions are as follows.

$$KGE=1-\sqrt{{(r-1)}^2+{(\alpha -1)}^2+{(\beta -1)}^2}$$

(6)

where r is the Pearson correlation coefficient, $\alpha$ is the ratio of the mean of simulated flows and observed flows defined as ${\displaystyle \frac{\overline{Q_s}}{\overline{Q_o}}}$, and $\beta$ is the ratio of the standard deviation of simulated flow and observed flows defined as ${\displaystyle \frac{{\delta }_s}{{\delta }_o}}$.

$$NSE=1-{\displaystyle \frac{{\sum }_{t=1}^n{(Q_{o,t}-Q_{s,t})}^2}{{\sum }_{t=1}^n{(Q_{o,t}-\overline{Q_o})}^2}}$$

(7)

where $Q_{o,t}$ is the observed flow at time t, $Q_{s,t}$ is the simulated flow at time t, $\overline{Q_o}$ is the mean of observed flows over the simulation period, n is the number of observations.

$$PRE={\displaystyle \frac{|Q_{o,max}-Q_{s,max}|}{Q_{o,max}}}$$

(8)

where $Q_{o,max}$ is the observed flow peak, and $Q_{s,max}$ is the simulated flow peak.

$$APTE=|t_{Q_{o,max}}-t_{Q_{s,max}}|$$

(9)

where $t_{Q_{o,max}}$ and $t_{Q_{s,max}}$ are flood peak occurrence time of the observed flow and simulated flow, respectively.

3. Results

3.1. Results of Parameter Optimization

As mentioned above, models using THI100P, IDW100P, and GWR100p as inputs were first subjected to parameter optimization. Figure 5 presents the results of this optimization. Subplots (a), (b), and (c) are hydrographs that represent THI100P, IDW100P, and GWR100P, respectively, showing predicted discharge (Q) for the training event 2016-11-19 using initial parameters (yellow line) and optimized parameters (red line). The predicted hydrographs from the three models align closely with the observed hydrographs. Subplot (d) depicts the change in object function error across iterations. It demonstrates that, as iterations increase, prediction errors for the training event gradually decrease and stabilize after 120 iterations, reaching a range of 3 × 10⁵ to 4 × 10⁵ for the three interpolation settings. This corresponds to the average absolute difference in the squared values of observed and predicted flows per time step between 34.367 and 39.683 (calculated from Equation (1)), which is an acceptable value. Figure 5 illustrates the effectiveness of parameter optimization, indicating that the optimized parameters can be used to further assess model performance.

3.2. Testing Performance of Models Using All Available Gauges

The models THI100P, IDW100P, and GWR100P use rainfall surfaces interpolated from all available rain gauges as inputs, serving as benchmarks for assessing model performance under varying rain gauge density conditions. Figure 6 shows hydrographs for these three models’ predictions on the 15 test events after parameter optimization, with the predicted hydrographs for THI100P, IDW100P, and GWR100P represented in red, orange, and yellow, respectively, and the observed discharge shown in blue. As seen in Figure 6, the predicted hydrographs from all three models are close to each other.

Table 2. Statistical metrics of the experiments 100 Ps.

Event	KGE	NSE	PRE (%)	APTE (h)
2013-08-21	0.971/IDW	0.947/THI	4.1/THI	2/IDW
2014-03-01	0.852/IDW	0.867/GWR	2.8/GWR	0/IDW
2014-03-26	0.884/IDW	0.914/THI	5.0/THI	0/THI
2014-06-16	0.902/IDW	0.885/IDW	6.6/IDW	0/IDW
2014-07-13	0.850/GWR	0.697/GWR	3.7/IDW	4/GWR
2014-08-11	0.905/GWR	0.825/GWR	6.2/THI	4/GWR
2015-05-27	0.921/GWR	0.858/THI	15.9/GWR	4/THI/IDW/GWR
2015-07-01	0.856/IDW	0.875/IDW	9.6/IDW	4/THI
2015-11-10	0.754/GWR	0.798/IDW	18.1/GWR	6/IDW/GWR
2016-05-04	0.907/IDW	0.858/IDW	2.7/IDW	2/THI/GWR
2016-06-14	0.924/GWR	0.860/GWR	4.4/GWR	2/IDW/GWR
2016-07-16	0.933/IDW	0.954/IDW	0.3/IDW	5/GWR
2016-09-27	0.858/GWR	0.908/GWR	2.2/IDW	1/THI/IDW
2017-03-27	0.933/THI	0.885/THI	3.5/THI	0/THI/IDW
2017-06-12	0.920/GWR	0.859/GWR	0.4/GWR	7/THI/GWR

summarizes the statistical metrics quantifying model performance, where only the best values among the three models are listed for brevity, along with the corresponding model for each value.

From Figure 6, it is evident that the predicted hydrographs for all three models closely match the key features of the observed hydrographs across the 15 test events. Statistically, 14 out of 15 events achieve KGE values above 0.85, 13 out of 15 events have NSE values exceeding 0.82; the peak relative error (PRE) is below 10% for 13 out of 15 events, and the absolute peak time error (APTE) is within 5 h for 13 out of 15 events. These results indicate that models using the existing rain gauges in this catchment yield satisfactory outcomes for flood forecasting and can be used as benchmarks for further comparison.

3.3. Testing Performance Under Rain Gauges Density Changes

The optimized parameters from the baseline scenarios THI100P, IDW100P, and GWR100P were applied to other rain gauge density scenarios, resulting in Figure 7 and Figure 8.

In Figure 7, subplots (a) to (d) display the relationship curves of four statistical metrics—KGE, NSE, PRE, and APTE—showing the average values across 15 test events as rain gauge density varies. The rainfall interpolation methods THI, IDW, and GWR are represented in red, blue, and gray, respectively. The shaded area surrounding each curve indicates the range, with the upper and lower boundaries representing the maximum and minimum metrics values in the 15 test events.

Figure 7 reflects the general findings of the experiment. Figure 8, however, provides box plots of the experimental results, offering a more detailed view of the distribution, variability, and outliers of model performance metrics across the 15 test events for each scenario. The three spatial interpolation methods—THI, IDW, and GWR—are represented in red, blue, and gray, corresponding to columns (a), (b), and (c) in the figure.

As shown in Figure 7, model performance gradually declines as rain gauge density decreases, a trend consistently observed across experiments using different interpolation methods. This is evident in the close alignment of the curves representing THI, IDW, and GWR. Specifically, as rain gauge density decreases from 100P (approximately 38 km² per rain gauge) to 10P (approximately 394 km² per rain gauge), the average values of the metrics across the 15 test events show a reduction: the KGE decreases from 0.879 to 0.816, and the NSE drops from 0.848 to 0.800 (the listed values represent the average results across the three interpolation methods).

The overall performance of the models across the 15 test events declines gradually, with global metrics such as KGE and NSE showing a change of approximately 5%. However, as seen in Figure 7 and Figure 8, the boundary ranges of the metrics expand, and the boxplots become longer as rain gauge density decreases. The boundaries of the shaded area represent the maximum and minimum values of the metrics across the test events, while the box represents the interquartile range (IQR), which contains the middle 50% of the data distribution. This suggests that the model’s performance in certain flood events has deteriorated, leading to increased dispersion. The model’s generalization ability decreases as rain gauge density declines.

For the metrics PRE and APTE, taking the THI scenario as an example, when rain gauge density decreases from 100P to 10P, the average range of PRE fluctuates between 8% and 14.7%, and the range of APTE fluctuates between 3.6 and 4.4 h. This indicates that the sensitivity of PRE and APTE to changes in rain gauge density is relatively low, suggesting that the model’s ability to predict peak flow and peak time is less affected by changes in rain gauge density.

A slight but noticeable inflection is observed from 40P (one gauge per 107 km²) to 20P (one gauge per 182 km²), where the model’s average performance experiences a relatively sharp (though not significant) decline and the range of the shadow area widens. This suggests that when the rain gauge density decreases to 20P or lower, the rain gauge network may fail to capture sufficient spatial rainfall information, leading to a decline in model performance. This finding is reflected across all four metrics. Therefore, for the Ningdu catchment, ensuring approximately one gauge per 107 km² is operational may be the minimum requirement to ensure stable flood forecasting accuracy for the model.

4. Discussion

4.1. Impact of Rain Gauge Density on the Interpolated Rainfall Surfaces

The results indicate that as rain gauge density decreases, model performance declines and the dispersion of metrics across the 15 test events increases. This is intuitive, as fewer rain gauges capture less rainfall information, leading to poorer model performance. The primary cause of the decline in model performance lies in the spatial heterogeneity of the rainfall input from different gauge density conditions. This section discusses the impact of changes in rain gauge density on the interpolated rainfall surfaces, which may offer insight into some of the patterns observed in the results.

Figure 9 visualizes the interpolated rainfall surfaces from the event 2016-11-19, which was used to optimize the model parameters.

In Figure 9, the rainfall interpolation surface generated by the THI method appears as polygonal patches, which become increasingly larger as rain gauge density decreases, resulting in a loss of distributed characteristics essential for PBDHMs. The IDW method produces a continuous rainfall surface; however, it can display “holes” that may not accurately reflect actual rainfall distribution. The GWR method generates a smoother rainfall surface, integrating local peaks into adjacent regions, and providing a more blended representation. Visually, each interpolation method produces distinctive rainfall surfaces. Figure 10 and

Table 3. Total amount of averaged rainfall in event 2016-11-19.

Rainfall (mm)	100P	80P	60P	40P	20P	10P
THI	112.953	112.192	112.217	112.157	105.038	118.824
IDW	114.536	112.828	114.693	108.381	105.226	117.084
GWR	114.586	112.225	115.177	106.024	103.367	115.625

further analyze the characteristics of the interpolated rainfall surface for the event 2016-11-19, from a statistical perspective.

Figure 10 shows bar plots of the average rainfall for event 2016-11-19 in experiments 100 Ps, calculated by summing the rainfall surface grids and dividing by the number of grids at each time step. As seen in Figure 10, the average rainfall generated by the three interpolation methods (THI, IDW, and GWR) is very similar at each time step. Table 3 further supports this observation, indicating that the total rainfall input to the model remains nearly equivalent across all three methods under the same rain gauge density conditions, with the largest difference being 6 mm in scenario 40P. This statistical similarity in total rainfall aligns with findings from Ly et al. [36], which compared THI, IDW, and four Kriging methods in a Belgium case study. This consistency in total rainfall input may help explain why the experimental results (Figure 7) remain largely consistent across interpolation scenarios and why metrics such as PRE and APTE are relatively insensitive to changes in rain gauge density, as the total rainfall differences are minimal across varying scenarios.

4.2. Parameter Optimization for Each Scenario

In the experimental settings section, the rainfall generated using all available rain gauges was used to optimize the model parameters. This setup investigates how changes in rain gauge density affect model performance after parameter optimization. From the above discussion, it was noted that each interpolation method (THI, IDW, and GWR) produces rainfall surfaces with distinct characteristics under different gauge density scenarios, leading to input uncertainty. Parameter optimization, to some extent, compensates for this variability. This section discusses the impact of gauge density changes on models that parameter optimization across the 18 scenarios (THI, IDW, and GWR, 100P to 10P).

Figure 11 presents the results of parameter optimization for each scenario under the same experimental conditions as before. Compared to the results in Figure 5, the models optimized individually for each rain gauge scenario visually perform slightly worse on training data than models optimized with all rain gauges (100 Ps), with object function values concentrating between 4 × 10⁵ and 6 × 10⁵ after 120 iterations.

Figure 12 shows line plots of the average metric values across the 15 test events, plotted against decreasing rain gauge density. The spatial interpolation methods THI, IDW, and GWR are represented by red, blue, and gray, respectively. Unlike the stable decline in model performance with decreasing gauge density seen in Figure 7, models optimized for each scenario show performance within a defined range or with fluctuations. The degree of fluctuation varies by interpolation method, with THI and GWR showing greater variability, while IDW remains comparatively steady and consistent. IDW, compared to THI and GWR (which consider only spatial locations as variables in this study), may be better suited to handle changes in rain gauge density. This also suggests that the sensitivity of model performance to changes in rain gauge density is influenced by the choice of spatial interpolation method to some extent.

Identifying interpolation methods that exhibit low sensitivity to gauge density variations is crucial for reliable flood forecasting with PBDHMs. Further investigation into advanced methods is warranted, such as coupling rain gauge observation with satellite data [43,44], integrating additional variables like elevation [37] and time [45]. Developing more automated and robust rainfall interpolation tools for use by catchment managers also remains essential. These are important directions for future research.

5. Conclusions

Flood forecasting performance in physically based distributed hydrological models (PBDHMs) is significantly influenced by rainfall input, which is related to the density of rain gauges and the chosen spatial interpolation method. A quantitative understanding of the impact of rain gauge density on PBDHMs flood forecasting performance offers insights into the expected upper and lower limits of model performance. This information can serve as a reference for rain gauge installation, flood forecasting system setup, and the selection of spatial interpolation methods in practice.

The main findings and conclusions of this study are summarized as follows:

• Using rainfall surfaces generated by interpolation from a high-density rain gauge network to calibrate model parameters results in a model with stable performance. As rain gauge density decreases, model performance declines gradually, with minimal variability; a trend consistently observed across commonly used spatial interpolation methods.
• With decreasing rain gauge density, the spatial heterogeneity of interpolated rainfall surfaces diminishes, reducing the model’s generalization capability. However, the amount of surface average rainfall remains largely unchanged, and the model’s ability to predict peak flow and peak timing is less sensitive to changes in rain gauge density.
• Parameter optimization can partially compensate for model error, with varying effectiveness depending on the characteristics of the rainfall interpolation method used. Identifying rainfall interpolation methods with low sensitivity to changes in rain gauge density may enhance the flood forecasting ability of PBDHMs.