Predicting the Dynamic of Debris Flow Based on Viscoplastic Theory and Support Vector Regression
Abstract
1. Introduction
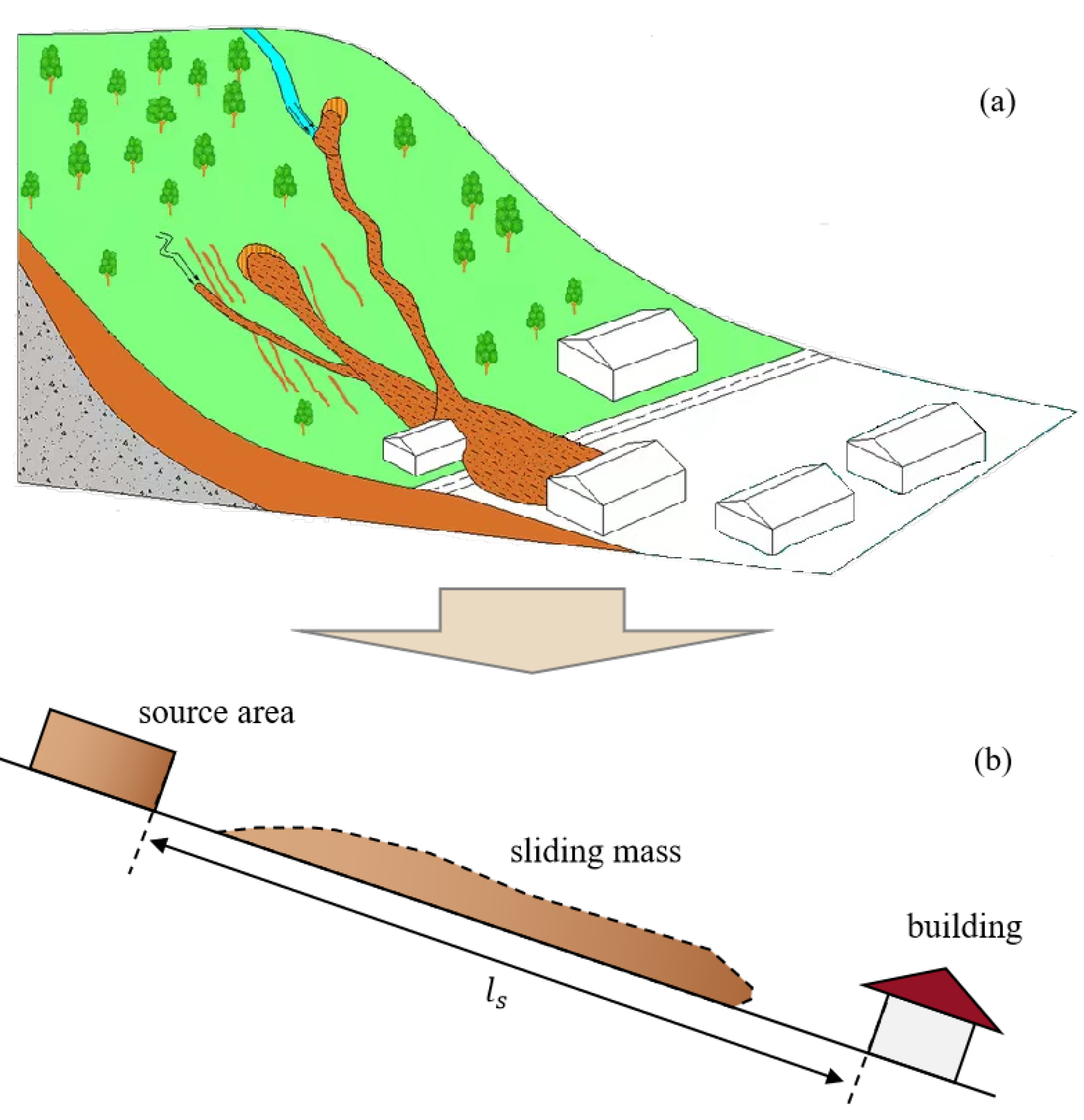
2. Simplification of the Issue
2.1. Physical Model
2.2. Material Modeling
3. Prediction Model Development
3.1. Theoretical Analysis Based on Lubrication Model and Kinematic Wave Model
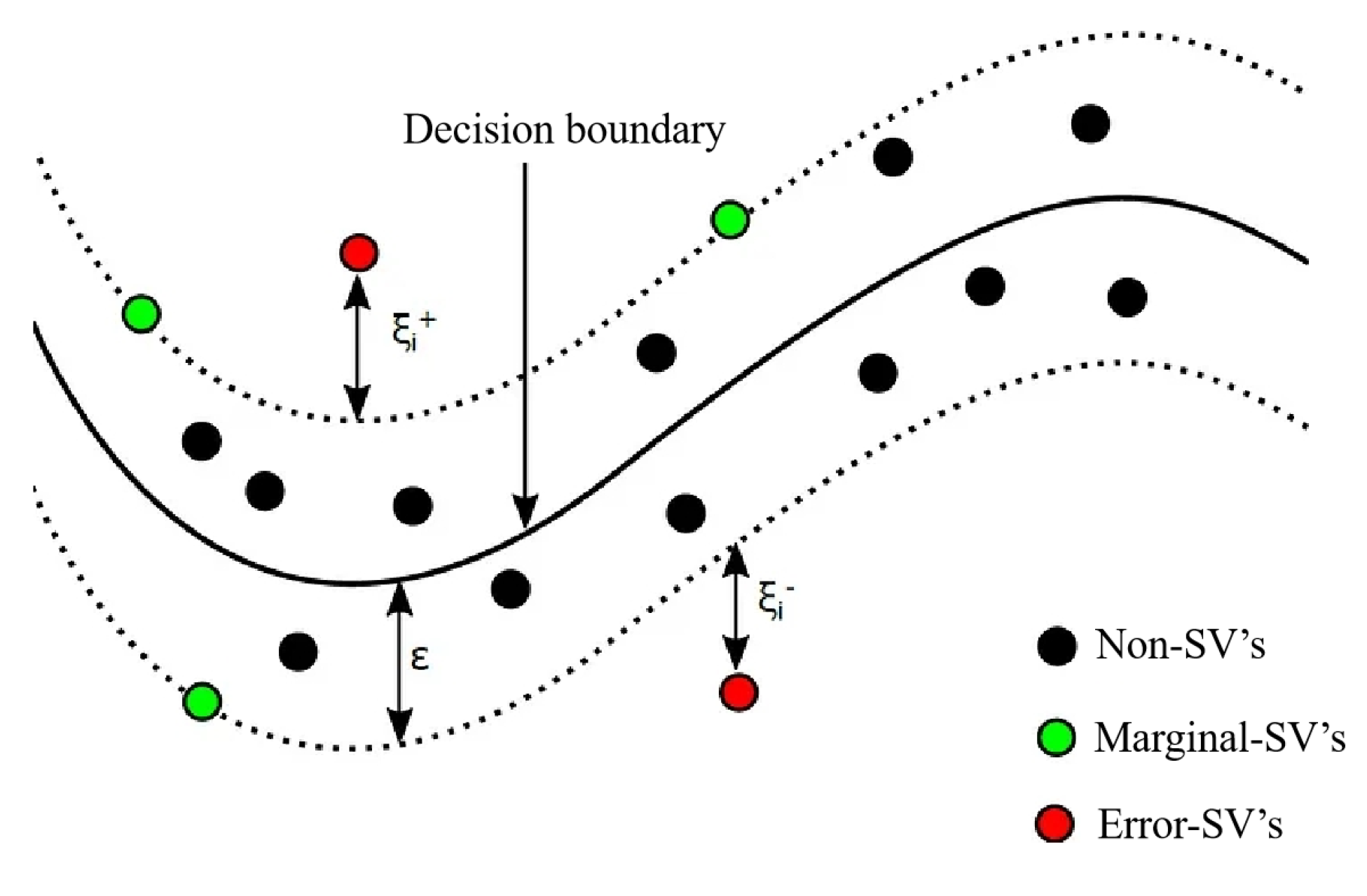
3.2. Mathematical Procedure of Data Modeling Using Support Vector Regression
4. Results
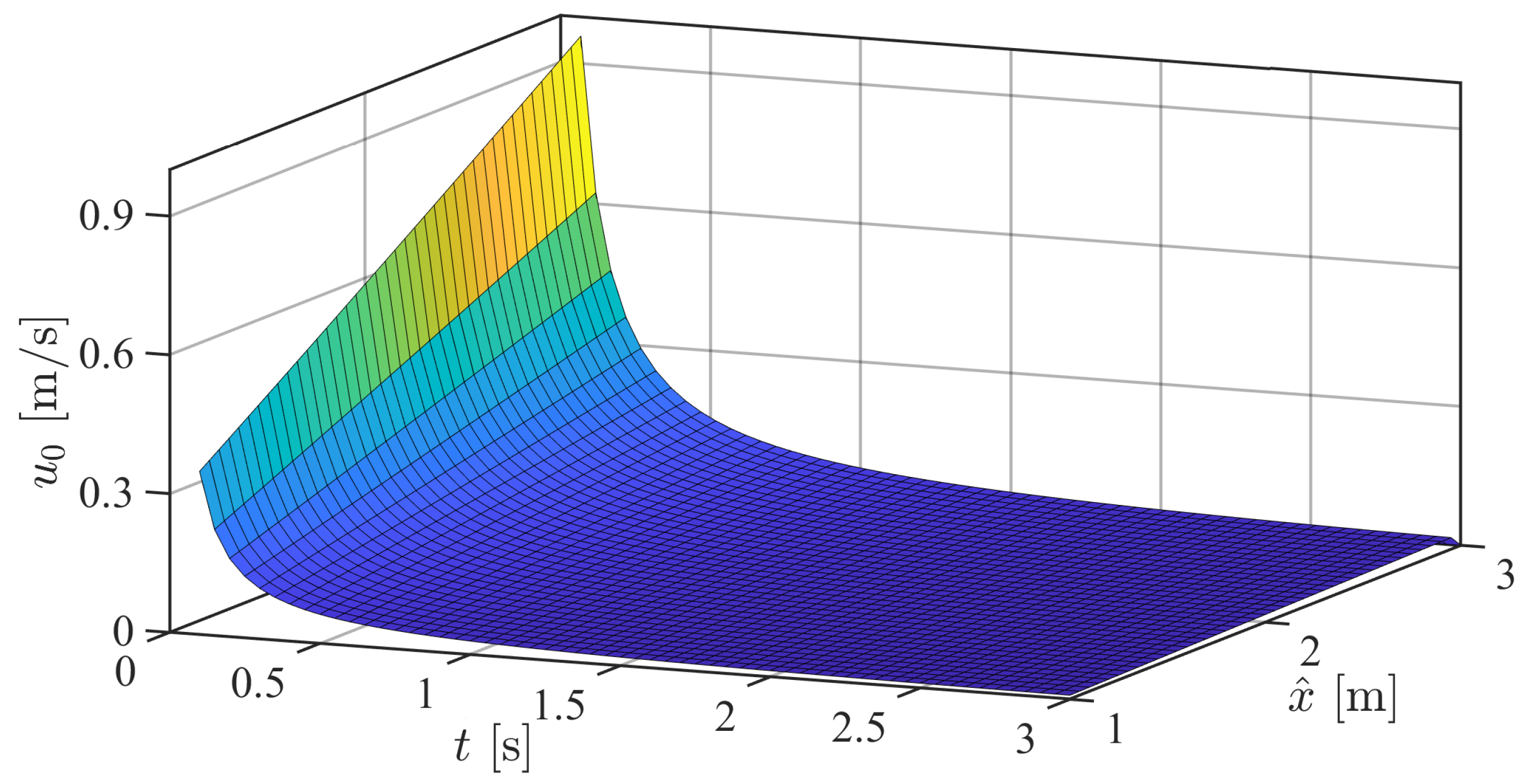
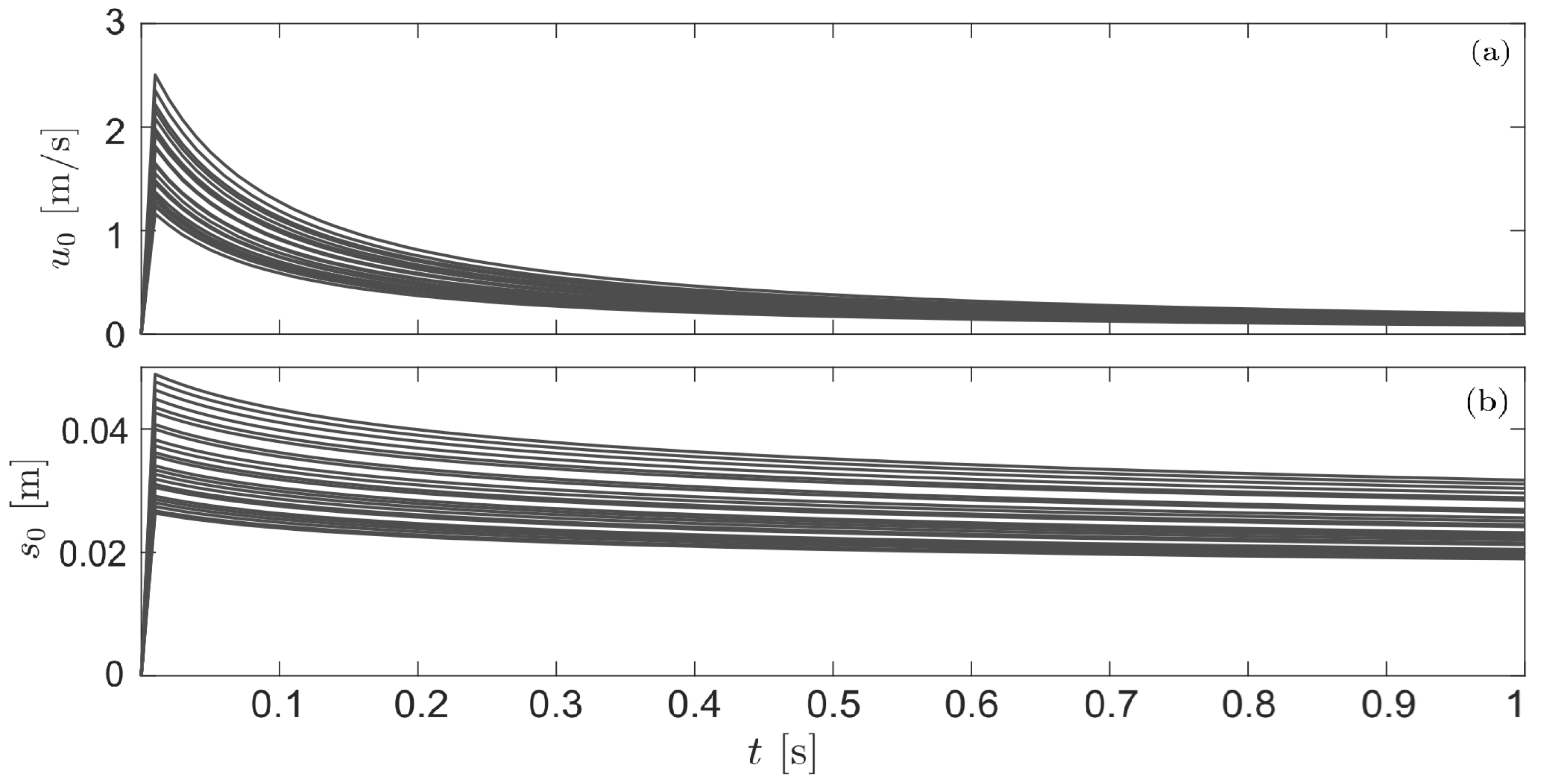
4.1. Numerical Solution of the Theoretical Model
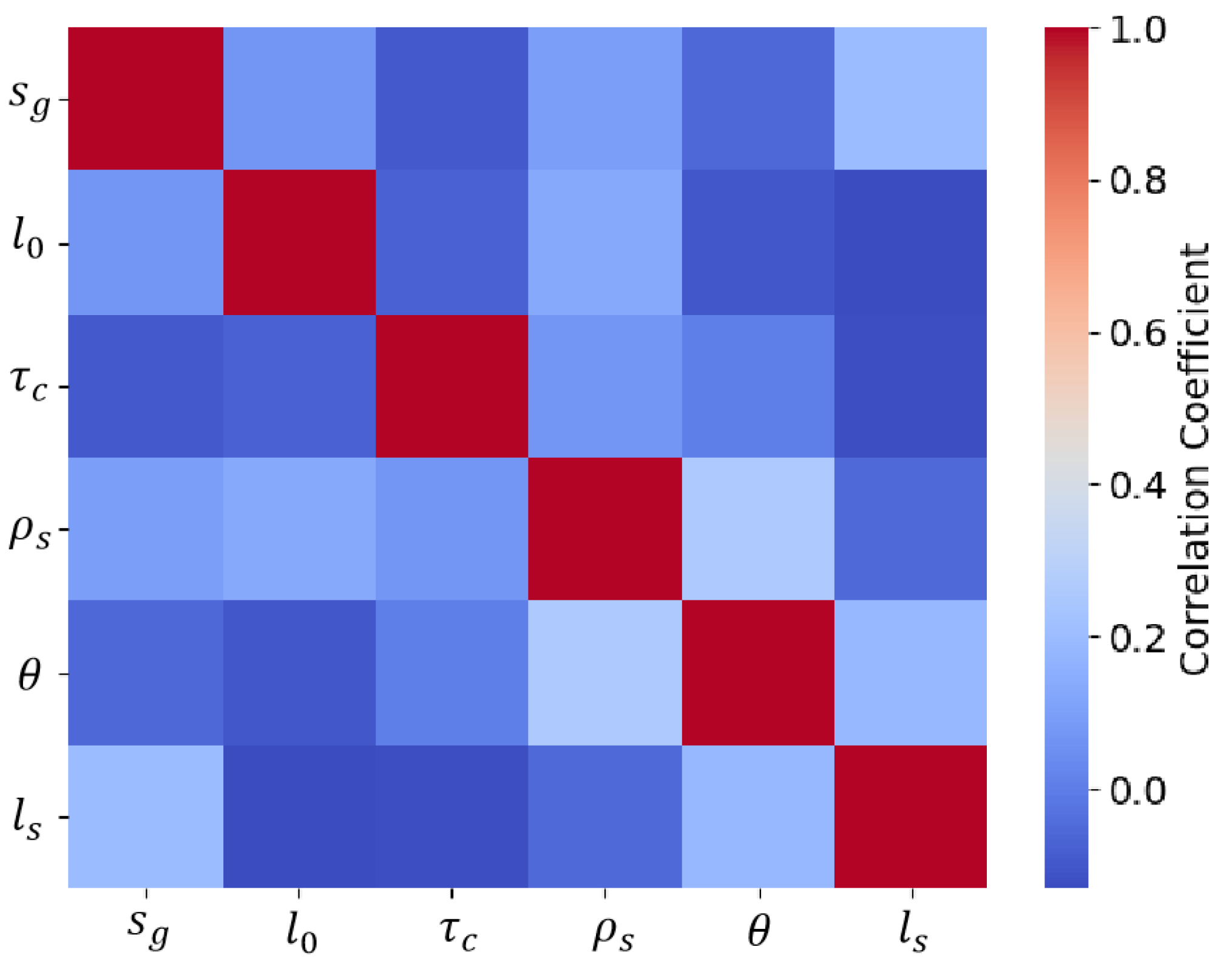
4.2. Parameters Selection
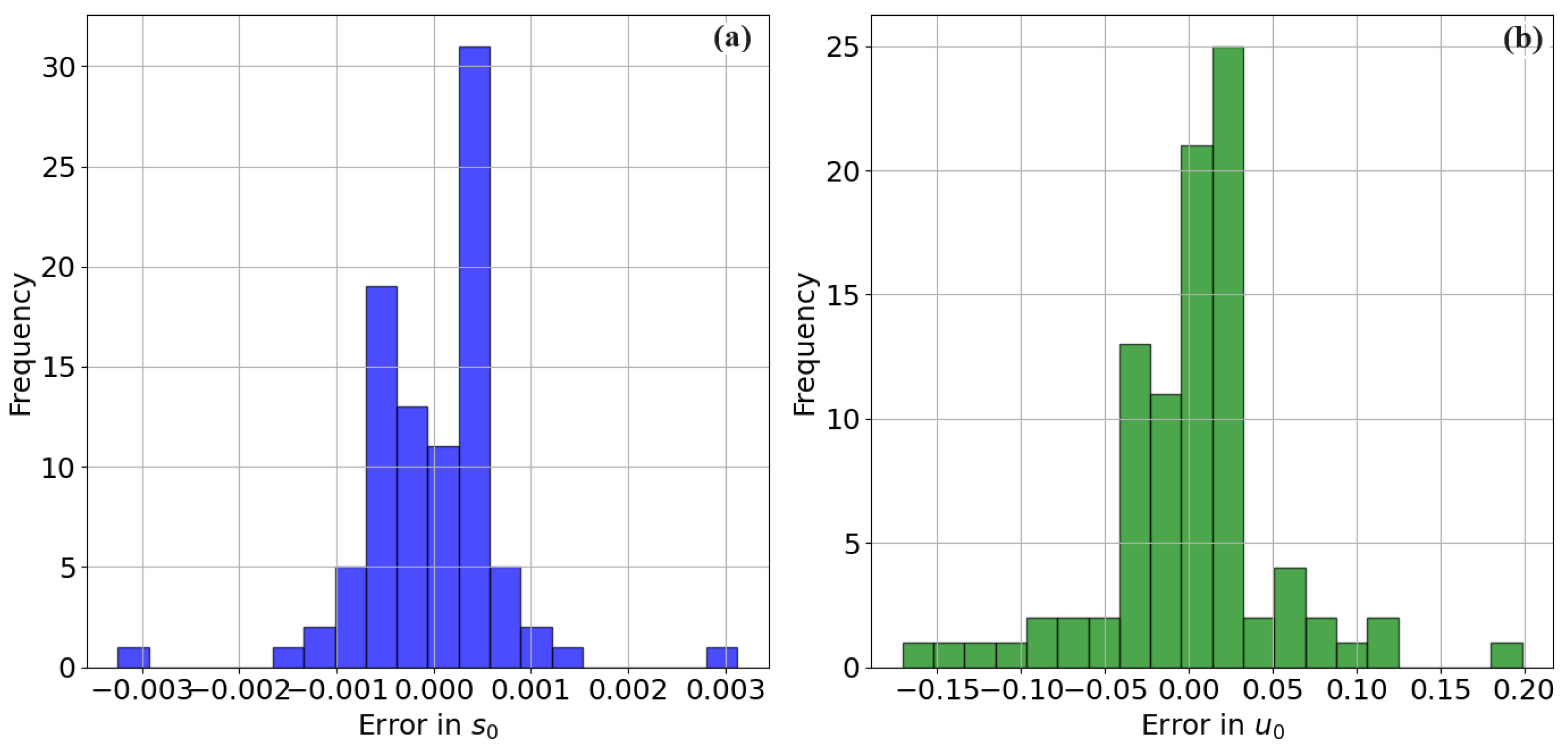
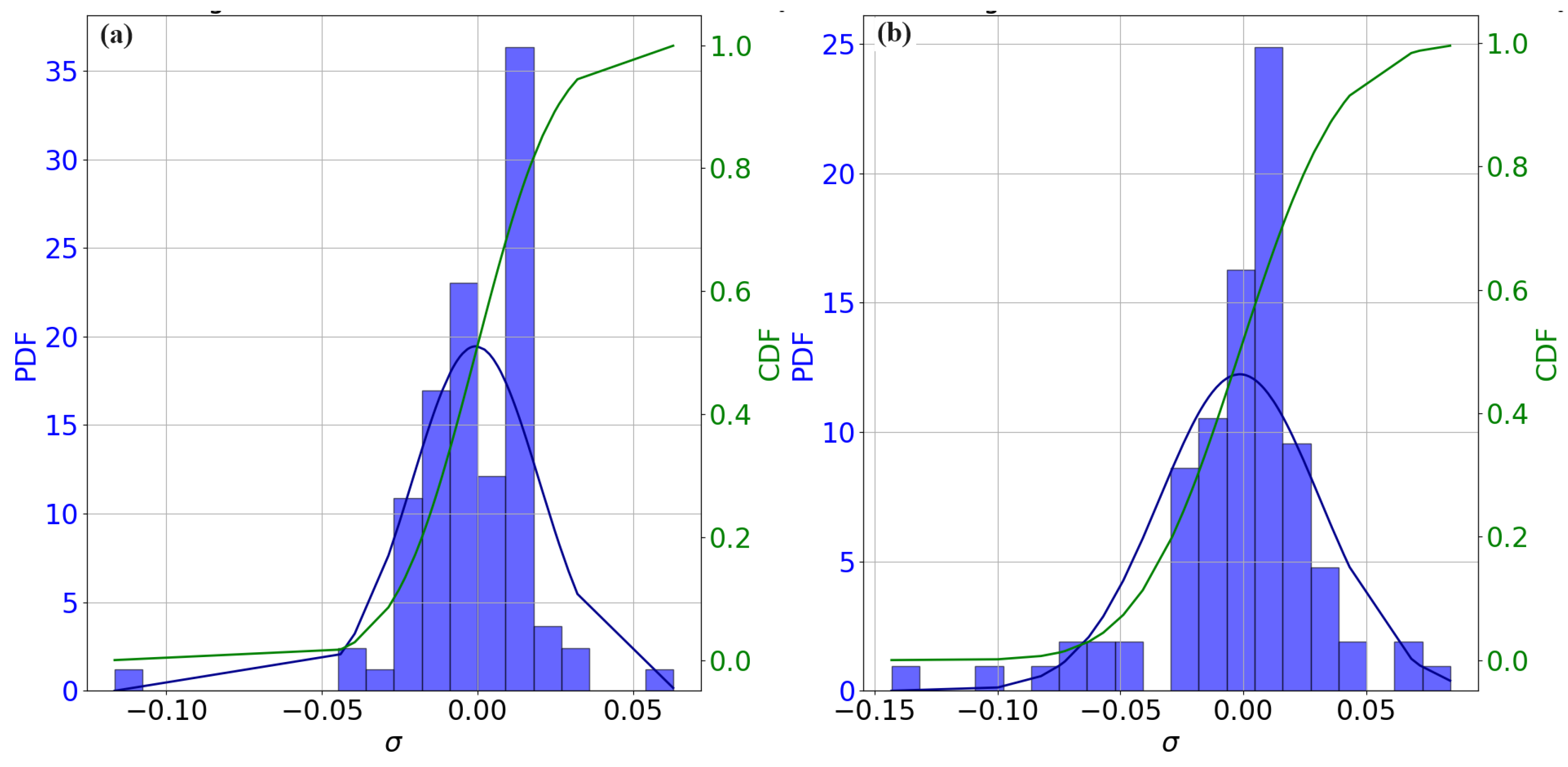
4.3. Regression Analysis Using the SVR Model
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meng, Z. Experimental study on impulse waves generated by a viscoplastic material at laboratory scale. Landslides 2018, 15, 1173–1182. [Google Scholar] [CrossRef]
- Meng, Z.; Zhang, J.; Hu, Y.; Ancey, C. Temporal Prediction of Landslide-Generated Waves Using a Theoretical-Statistical Combined Method. J. Mar. Sci. Eng. 2023, 11, 1151. [Google Scholar] [CrossRef]
- Li, Y.; Cui, Y.; Hu, X.; Lu, Z.; Guo, J.; Wang, Y.; Wang, H.; Wang, S.; Zhou, X. Glacier retreat in Eastern Himalaya drives catastrophic glacier hazard chain. Geophys. Res. Lett. 2024, 51, e2024GL108202. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Li, H.; Fan, Y.; Meng, Z.; Liu, D.; Pan, S. Optimization of Water Quantity Allocation in Multi-Source Urban Water Supply Systems Using Graph Theory. Water 2024, 17, 61. [Google Scholar] [CrossRef]
- Chen, H.; Huang, S.; Xu, Y.P.; Teegavarapu, R.S.; Guo, Y.; Nie, H.; Xie, H. Using baseflow ensembles for hydrologic hysteresis characterization in humid basins of Southeastern China. Water Resour. Res. 2024, 60, e2023WR036195. [Google Scholar] [CrossRef]
- Coussot, P.; Laigle, D.; Arattano, M.; Deganutti, A.; Marchi, L. Direct determination of rheological characteristics of debris flow. J. Hydraul. Eng. 1998, 124, 865–868. [Google Scholar] [CrossRef]
- Hutter, K.; Svendsen, B.; Rickenmann, D. Debris flow modeling: A review. Contin. Mech. Thermodyn. 1994, 8, 1–35. [Google Scholar] [CrossRef]
- Zhou, W.; Qiu, H.; Wang, L.; Pei, Y.; Tang, B.; Ma, S.; Yang, D.; Cao, M. Combining rainfall-induced shallow landslides and subsequent debris flows for hazard chain prediction. Catena 2022, 213, 106199. [Google Scholar] [CrossRef]
- Takahashi, T. Debris Flow: Mechanics, Prediction and Countermeasures; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Ma, T.; Chen, H.; Zhang, K.; Shen, L.; Sun, H. The rheological intelligent constitutive model of debris flow: A new paradigm for integrating mechanics mechanisms with data-driven approaches by combining data mapping and deep learning. Expert Syst. Appl. 2025, 126405. [Google Scholar] [CrossRef]
- Zegers, G.; Mendoza, P.A.; Garces, A.; Montserrat, S. Sensitivity and identifiability of rheological parameters in debris flow modeling. Nat. Hazards Earth Syst. Sci. 2020, 20, 1919–1930. [Google Scholar] [CrossRef]
- Petley, D.N.; Bulmer, M.H.; Murphy, W. Patterns of movement in rotational and translational landslides. Geology 2002, 30, 719–722. [Google Scholar] [CrossRef]
- Van Westen, C.J.; Castellanos, E.; Kuriakose, S.L. Spatial data for landslide susceptibility, hazard, and vulnerability assessment: An overview. Eng. Geol. 2008, 102, 112–131. [Google Scholar] [CrossRef]
- Tien Bui, D.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, logistic regression, and their ensemble. Geomorphology 2016, 231, 102–120. [Google Scholar]
- Meng, Z.; Hu, Y.; Ancey, C. Using a data driven approach to predict waves generated by gravity driven mass flows. Water 2020, 12, 600. [Google Scholar] [CrossRef]
- Cui, Y.; Li, Y.; Tang, H.; Turowski, J.M.; Yan, Y.; Bazai, N.A.; Wei, R.; Li, L. A digital-twin platform for cryospheric disaster warning. Natl. Sci. Rev. 2024, 11, nwae300. [Google Scholar] [CrossRef]
- Chmiel, M.; Walter, F.; Wenner, M.; Zhang, Z.; McArdell, B.W.; Hibert, C. Machine learning improves debris flow warning. Geophys. Res. Lett. 2021, 48, e2020GL090874. [Google Scholar] [CrossRef]
- Huang, J.; Hales, T.C.; Huang, R.; Ju, N.; Li, Q.; Huang, Y. A hybrid machine-learning model to estimate potential debris-flow volumes. Geomorphology 2020, 367, 107333. [Google Scholar] [CrossRef]
- Korup, O.; Stolle, A. Landslide prediction from machine learning. Geol. Today 2014, 30, 26–33. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S. Landslide susceptibility assessment and factor effect analysis: Backpropagation artificial neural networks and their comparison with frequency ratio and bivariate logistic regression modelling. Environ. Model. Softw. 2010, 25, 747–759. [Google Scholar] [CrossRef]
- Wang, L.J.; Guo, M.; Sawada, K.; Lin, J.; Zhang, J. A comparative study of landslide susceptibility maps using logistic regression, frequency ratio, decision tree, weights of evidence and artificial neural network. Geosci. J. 2016, 20, 117–136. [Google Scholar] [CrossRef]
- Chen, H.; Xu, B.; Qiu, H.; Huang, S.; Teegavarapu, R.S.; Xu, Y.P.; Guo, Y.; Nie, H.; Xie, H. Adaptive assessment of reservoir scheduling to hydrometeorological comprehensive dry and wet condition evolution in a multi-reservoir region of southeastern China. J. Hydrol. 2025, 648, 132392. [Google Scholar] [CrossRef]
- Huangfu, W.; Qiu, H.; Cui, P.; Yang, D.; Liu, Y.; Tang, B.; Liu, Z.; Ullah, M. Quick and automatic detection of co-seismic landslides with multi-feature deep learning model. Sci. China Earth Sci. 2024, 67, 2311–2325. [Google Scholar] [CrossRef]
- Wei, Y.; Qiu, H.; Liu, Z.; Huangfu, W.; Zhu, Y.; Liu, Y.; Yang, D.; Kamp, U. Refined and dynamic susceptibility assessment of landslides using InSAR and machine learning models. Geosci. Front. 2024, 15, 101890. [Google Scholar] [CrossRef]
- Liu, Z.; Qiu, H.; Zhu, Y.; Huangfu, W.; Ye, B.; Wei, Y.; Tang, B.; Kamp, U. Increasing irrigation-triggered landslide activity caused by intensive farming in deserts on three continents. Int. J. Appl. Earth Obs. Geoinf. 2024, 134, 104242. [Google Scholar] [CrossRef]
- Stumpf, A.; Malet, J.P.; Kerle, N.; Niethammer, U.; Rothmund, S. Image-based mapping of surface fissures for the investigation of landslide dynamics. Geomorphology 2018, 231, 102–113. [Google Scholar] [CrossRef]
- Meng, Z.; Wang, Y.; Zheng, S.; Wang, X.; Liu, D.; Zhang, J.; Shao, Y. Abnormal Monitoring Data Detection Based on Matrix Manipulation and the Cuckoo Search Algorithm. Mathematics 2024, 12, 1345. [Google Scholar] [CrossRef]
- Ancey, C.; Cochard, S. The dam-break problem for Herschel–Bulkley viscoplastic fluids down steep flumes. J. -Non-Newton. Fluid Mech. 2009, 158, 18–35. [Google Scholar] [CrossRef]
- Ancey, C.; Andreini, N.; Epely-Chauvin, G. Viscoplastic dambreak waves: Review of simple computational approaches and comparison with experiments. Adv. Water Resour. 2012, 48, 79–91. [Google Scholar] [CrossRef]
- Meng, Z.; Ancey, C. The effects of slide cohesion on impulse-wave formation. Exp. Fluids 2019, 60, 151. [Google Scholar] [CrossRef]
- Meng, Z.; Li, X.; Han, S.; Wang, X.; Meng, J.; Li, Z. The Motion and Deformation of Viscoplastic Slide while Entering a Body of Water. J. Mar. Sci. Eng. 2022, 10, 778. [Google Scholar] [CrossRef]
- Meng, Z.; Hu, J.; Zhang, J.; Zhang, L.; Yuan, Z. The Momentum Transfer Mechanism of a Landslide Intruding a Body of Water. Sustainability 2023, 15, 13940. [Google Scholar] [CrossRef]
- Suthaharan, S.; Suthaharan, S. Support vector machine. In Machine Learning Models and Algorithms for Big Data Classification: Thinking with Examples for Effective Learning; Springer Nature: Berlin, Germany, 2016; pp. 207–235. [Google Scholar]
- Pisner, D.A.; Schnyer, D.M. Support vector machine. In Machine learning; Elsevier: Amsterdam, The Netherlands, 2020; pp. 101–121. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. (TIST) 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Singh, A.; Kotiyal, V.; Sharma, S.; Nagar, J.; Lee, C.C. A machine learning approach to predict the average localization error with applications to wireless sensor networks. IEEE Access 2020, 8, 208253–208263. [Google Scholar] [CrossRef]



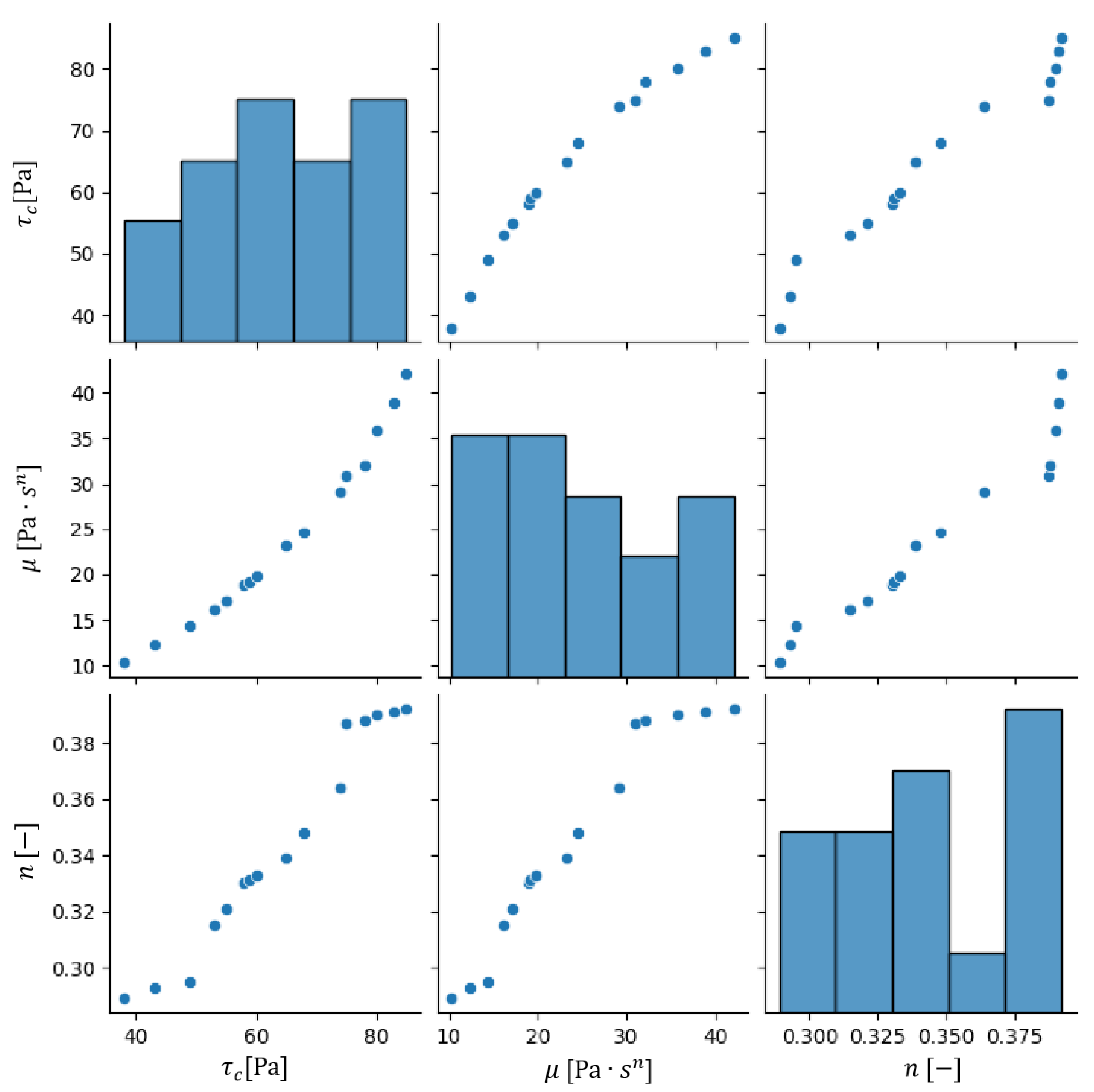


| [Pa] | [Pa · sn] | n [-] |
|---|---|---|
| 38 | 10.3 | 0.289 |
| 49 | 14.4 | 0.295 |
| 55 | 17.1 | 0.321 |
| 68 | 24.6 | 0.348 |
| 75 | 30.9 | 0.387 |
| 80 | 35.8 | 0.390 |
| 85 | 42.1 | 0.392 |
| Parameters | Value |
|---|---|
| Regularization parameter C | 0.01 |
| tolerance | 0.01 |
| Kernel function | Polynomial function |
| Type | Parameters | Symbols |
|---|---|---|
| Input parameters | yield stress of the slide material | |
| density of the slide material | ||
| depth of the material at the gate | ||
| length of the material at the source area | ||
| slope angle | ||
| distance between the gate and indicated position | ||
| depth of the slide on impact | ||
| Output parameters | depth-averaged velocity on impact |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Li, H.; Fan, Y.; Zhang, L.; Peng, S.; Huang, J.; Zhang, J.; Meng, Z. Predicting the Dynamic of Debris Flow Based on Viscoplastic Theory and Support Vector Regression. Water 2025, 17, 120. https://doi.org/10.3390/w17010120
Zhang X, Li H, Fan Y, Zhang L, Peng S, Huang J, Zhang J, Meng Z. Predicting the Dynamic of Debris Flow Based on Viscoplastic Theory and Support Vector Regression. Water. 2025; 17(1):120. https://doi.org/10.3390/w17010120
Chicago/Turabian StyleZhang, Xinhai, Hanze Li, Yazhou Fan, Lu Zhang, Shijie Peng, Jie Huang, Jinxin Zhang, and Zhenzhu Meng. 2025. "Predicting the Dynamic of Debris Flow Based on Viscoplastic Theory and Support Vector Regression" Water 17, no. 1: 120. https://doi.org/10.3390/w17010120
APA StyleZhang, X., Li, H., Fan, Y., Zhang, L., Peng, S., Huang, J., Zhang, J., & Meng, Z. (2025). Predicting the Dynamic of Debris Flow Based on Viscoplastic Theory and Support Vector Regression. Water, 17(1), 120. https://doi.org/10.3390/w17010120






