An Ecology-Oriented Single–Multi-Objective Optimal Operation Modeling and Decision-Making Method in the Case of the Ganjiang River
Abstract
1. Introduction
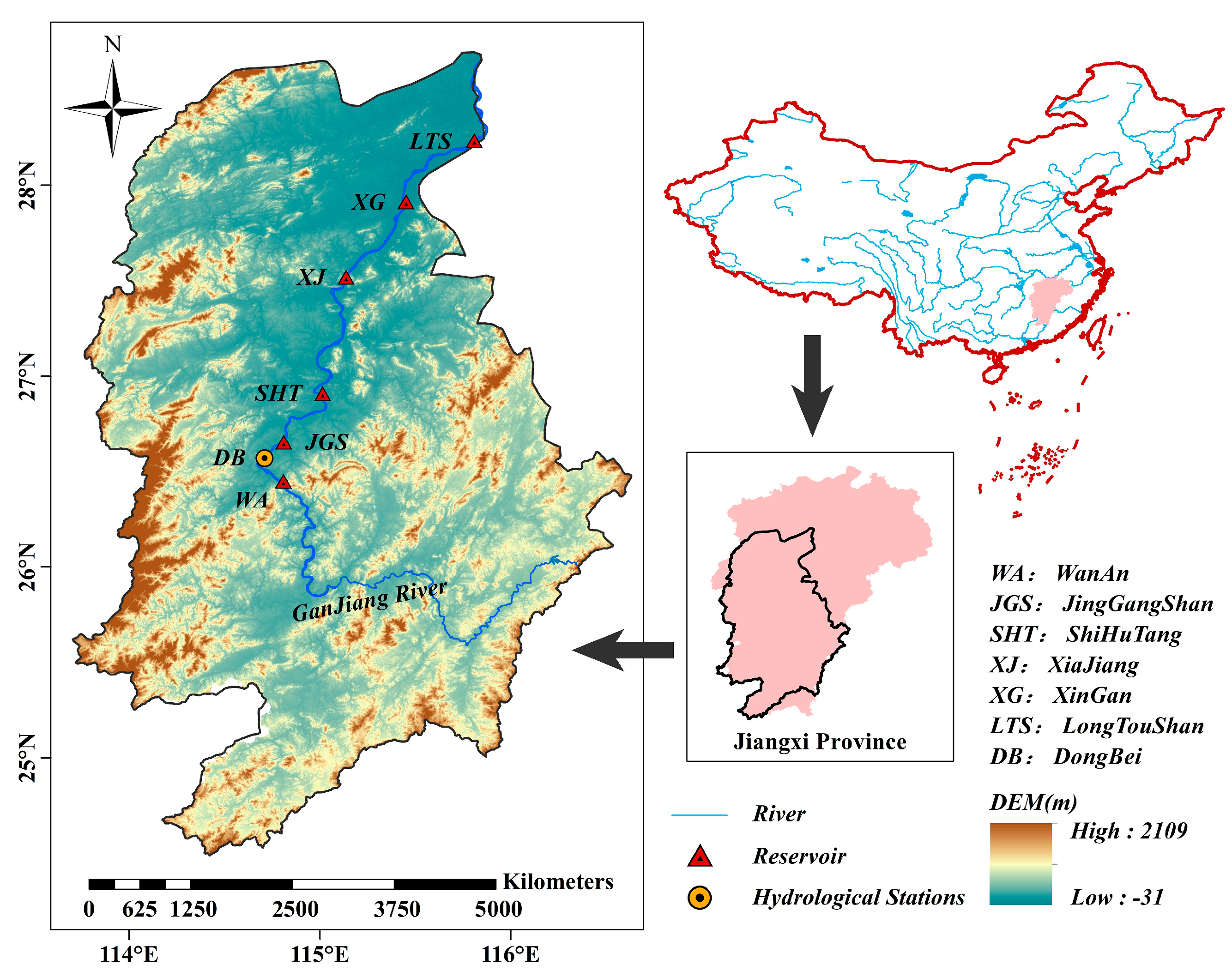
2. Research Area and Data
Study Object
3. Models and Methods
3.1. Hydrological Variation Diagnosis and Mutation Point Testing
3.1.1. Mann–Kendall Method
3.1.2. Ordered Clustering Method
3.1.3. Run Test
3.2. Ecological Guarantee Degree
3.3. Objective Function
3.4. Constraints
- (1)
- Water balance constraints:where Vt+ 1 and Vt are the initial storages at times t + 1 and t, respectively. It and represent the inflow and outflow at time t, respectively. t is the time interval.
- (2)
- Water level constraints:where and represent the minimum and maximum water levels at time t, respectively.
- (3)
- Outflow constraints:where and denote the minimum and maximum allowable outflows at time t, respectively. is determined by comprehensive downstream water use, shipping, and ecological requirements. is determined based on the downstream flood control requirements.
- (4)
- Hydropower outputs constraints:where and represent the minimum and maximum hydropower outputs at time t, respectively. In general, is the guaranteed output and is the installed capacity.
- (5)
- Other constraints:
3.5. Optimization Algorithm
- (1)
- As an optimization algorithm based on the swarm intelligence theory, DE is widely used to solve single-objective operation models. This study used the standard DE algorithm to solve Models 1 and 2.
- (2)
- The solution of multi-objective problems can be approximated from two perspectives: target transformation and obtaining a Pareto non-inferior solution set. However, the method of target transformation can only obtain the best solution from the results. It cannot analyze the transformation laws between multiple objectives from the perspective of the process, which is unfavorable for benefit analysis between multiple objectives. The NSGA-II algorithm is an efficient multi-objective problem-solving algorithm that was improved by Deb et al. in 2002 [51] and has the advantages of good convergence and high robustness. A constraint transformation is used to increase the proportion of feasible regions in the search space to improve the algorithm’s convergence speed and accuracy. Before solving the problem, convert constraints such as flow and ecological water demand into unified decision constraints (water level constraints). The non-convertible constraints are controlled by a fitness function. When the constraint is broken, a penalty function reduces the fitness value and ensures optimization efficiency. Therefore, this study uses the improved NSGA-II to solve Model 3. This improved algorithm can effectively prevent the problem of data falling into local optima during solution processing, thereby improving the efficiency and accuracy of the solution.
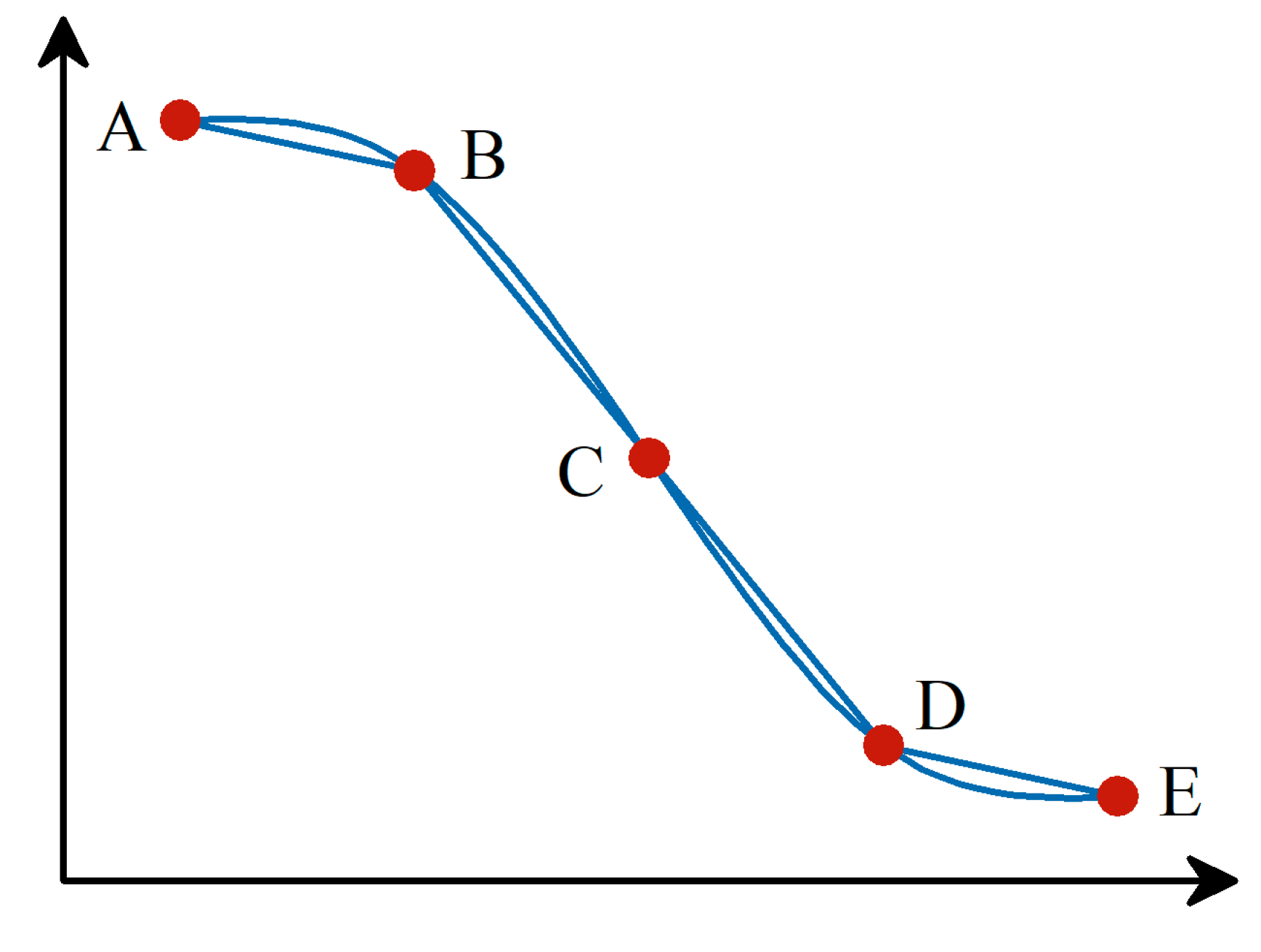
3.6. Method for Determining Inflection Points
3.7. CV-ITOPSIS
4. Results and Discussion
4.1. Result of Hydrological Variation Diagnosis
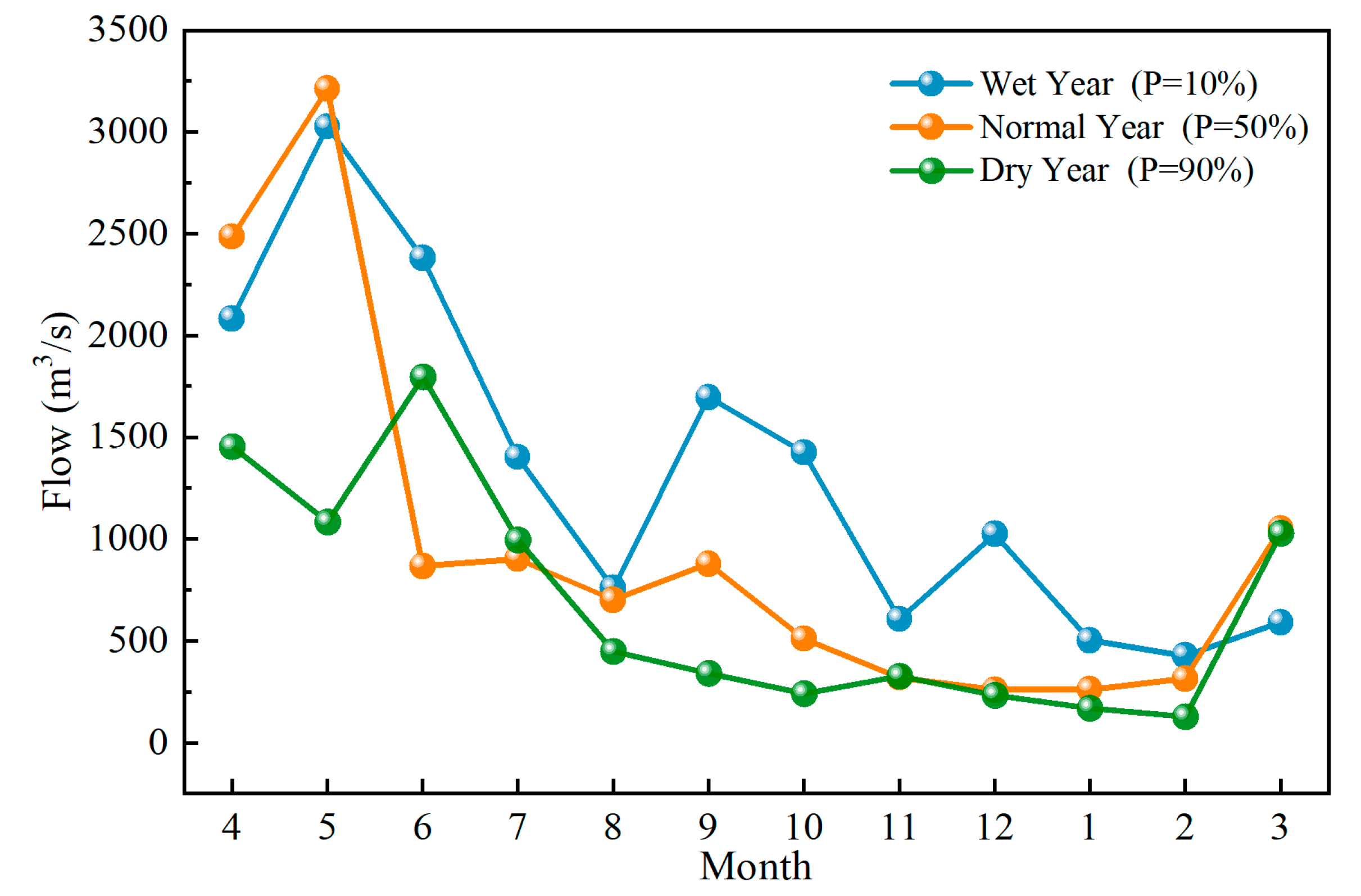
4.2. Ecological Flow
4.3. Analysis of the Impact of Ecological Objective on Operation Results
- (1)
- Because of the constraints of ecological flow, reservoirs must increase their discharge flow to maximize the ecological benefits of downstream rivers as much as possible. Therefore, Model 2 had lower water levels and higher discharge flow than Model 1, particularly during the post-flood season. The water regime in the Wan’an Basin was relatively simple, and the annual distribution of runoff was relatively concentrated. The water level dropped to the flood limit level before the flood season to meet the flood control needs. Model 1 increased the water level during the post-flood season and maintained it at the normal water storage level, minimizing the water discharge as much as possible to maximize energy generation while meeting the water usage requirements during the dry season. Model 2 sacrifices a high head to increase the discharge flow during the post-flood season and satisfy the ecological water demand of the river as much as possible.
- (2)
- Considering the need to provide normal survival and reproductive conditions for aquatic organisms in downstream river channels, this study used 80% as the standard for ecological assurance, which is the average level that meets the upper and lower limits of a suitable ecological flow. As shown in Table 2, in Model 2, the number of ecological guarantee months for each typical year increased by 2, 3, and 2 months, respectively. Assuming that the reduction in energy generation levels is roughly the same in each typical year, the annual average ecological guarantee degree in wet years increased by 3.12% compared to Model 1. In contrast, the annual average ecological guarantee degree increased by 10.09% and 13.47% in normal and dry years, respectively, which is 3–4 times higher than in wet years. The main reason for this is that, in Model 2, due to significantly lower inflow runoff during the dry season in both normal and dry years compared to the wet year, the reservoir must adopt a method of lowering the water level while increasing discharge flow during the dry season to improve ecological benefits. In Model 1, to maximize energy generation, high water levels were maintained for most of the typical years, resulting in a low level of ecological guarantee degree during the dry season in both normal and dry years. The operational results of the two models corresponded with each other, reflecting a significant increase in ecological guarantee degree during the normal and dry years of Model 2.
4.4. Result Analysis of Multi-Objective Operation
- (1)
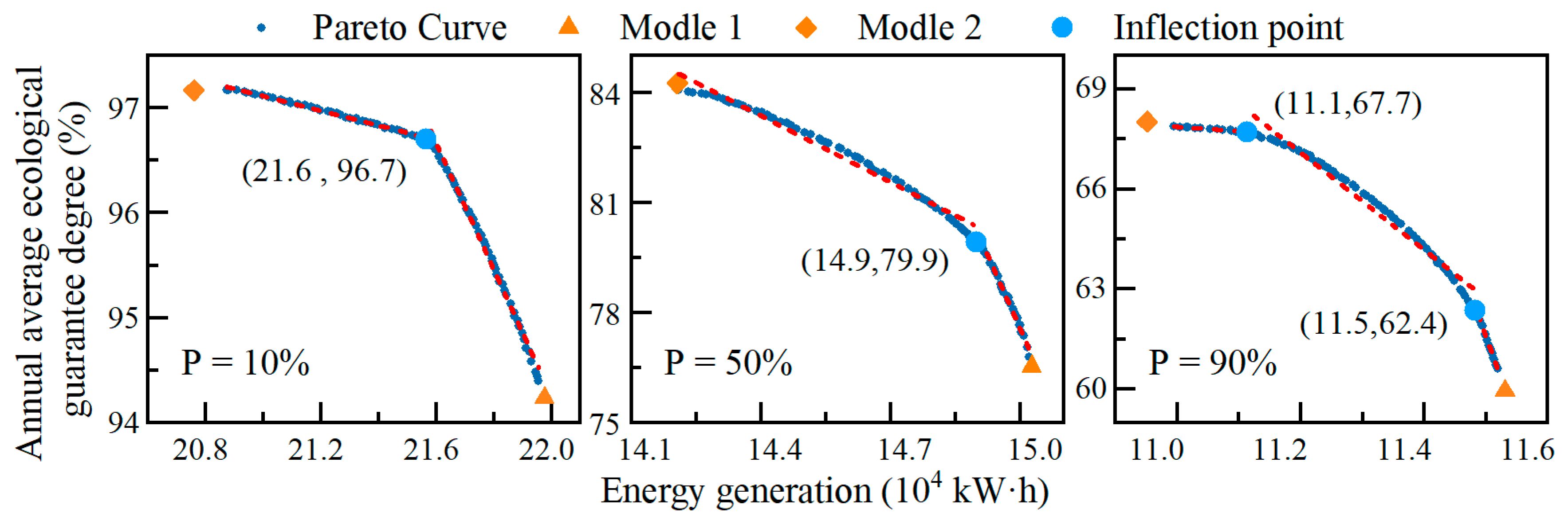
- The calculation results of Models 1 and 2 under single-objective scheduling fall near the extreme right and left points of the Pareto front curve, respectively. This confirms that the solution set of the multi-objective operation has a good degree of approximation of the real Pareto front. In multi-objective operation, the interannual variation interval widths of energy generation in the three typical wet, normal, and dry years were 11,000 kWh, 8200 kWh, and 5200 kWh, respectively. The interannual variation interval widths of ecological guarantee degree were 2.94%, 7.55%, and 7.26%, respectively. From a numerical standpoint, as the inflow decreases, both the interannual energy generation and the ecological guarantee degree decrease. However, the conversion rate between energy generation and ecology has greatly improved, exacerbating the contradiction between the two objectives.
- (2)
- The two objectives of energy generation and ecology exhibit a piecewise linear contradictory relationship in an image. This study used a non-fitting curve method to determine the approximate inflection point of the Pareto front curve. The Pareto front curve was fitted linearly after the approximate inflection point was obtained to obtain the conversion formula between the two objectives, as depicted in Table 3. The larger the slope of the piecewise straight line, the lower the efficiency of converting energy generation benefits into ecological benefits, and vice versa. Discharge flow is an important factor affecting the energy generation and ecological assurance degree, and there is a negative correlation between the discharge flow and water head. Analysis of the conversion law between the two objectives began with the discharge flow and water head. Considering a wet year as an example, the water head significantly impacted the conversion rate from energy generation to ecology before the inflection point. Increasing the water head reduced the discharge flow. A high water head positively affected the increase in energy generation. However, a low flow was unfavorable for the ecological guarantee degree of downstream river channel. Therefore, the conversion rate from energy generation to ecology was relatively low. The discharge flow significantly impacted the conversion rate from energy generation to ecology after the inflection point. The increase in discharge flow plays a crucial role in alleviating the ecological pressure on the downstream river channel, while appropriately increasing energy generation. Therefore, the conversion rate between energy generation and ecology corresponding to this piecewise straight line was relatively high.
- (3)
- The ecological objective of this study was to define the ecological flow calculated using a multiyear runoff series. As the inflow increased, the inflection point gradually shifted to the left and up, and the global conversion rate from energy generation to ecology gradually increased. In dry years with less water inflow, bearing a higher ecological water demand was necessary, resulting in an unstable relationship between energy generation and ecological objectives. Therefore, there were two inflection points. Decision-makers could use the Pareto front curves and inflection points between the piecewise straight lines to make decisions based on different inflow conditions, achieving maximum benefits. In addition, the expression of piecewise straight lines and their inflection points helped decision-makers to quantitatively describe the conversion law between two objectives, providing them with rich decision-making plans and important application value.
4.5. Multi-Attribute Decision-Making Based on CV-ITOPSIS
- (1)
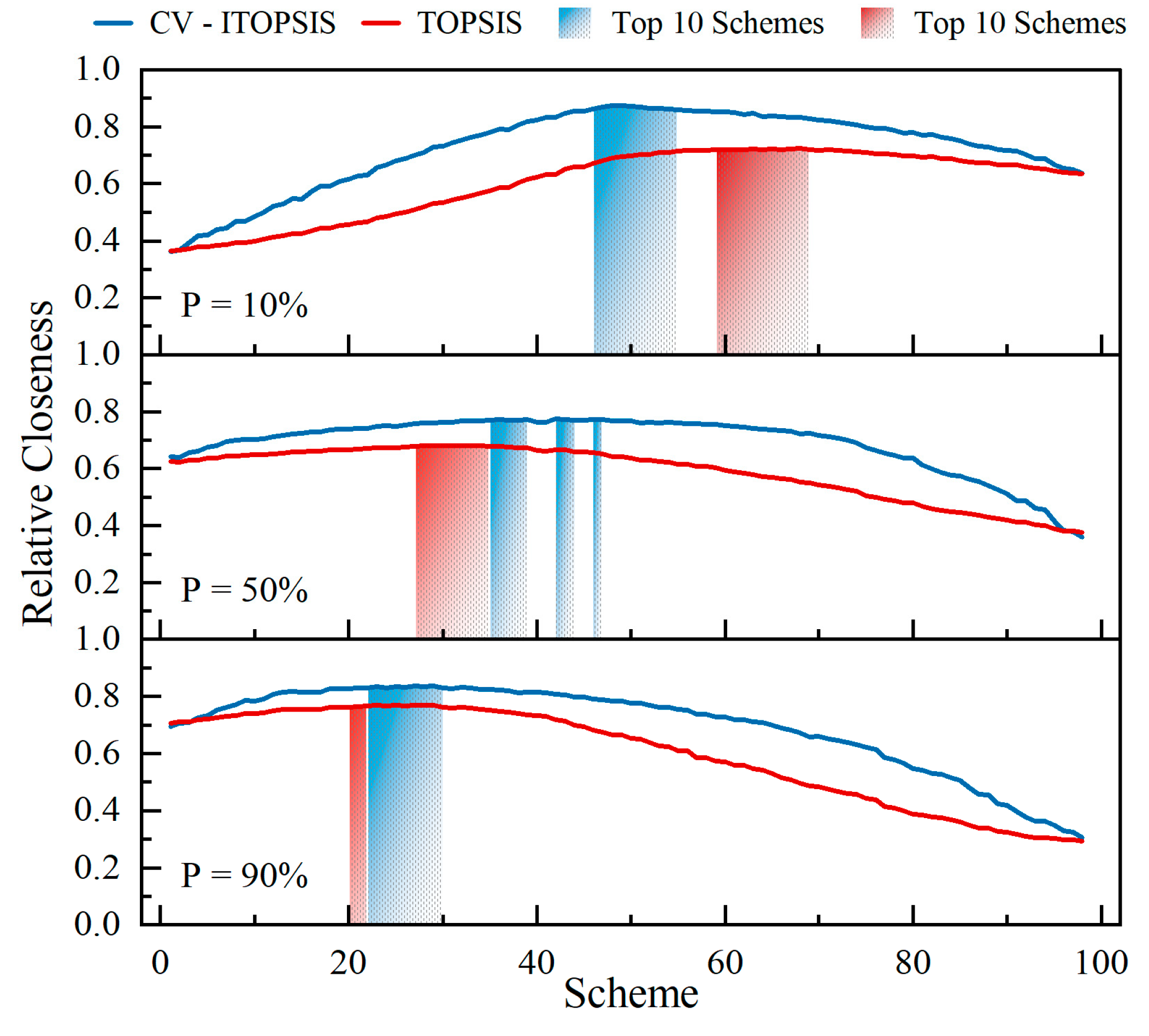
- The top ten schemes in the CV-ITOPSIS method for the three typical wet, normal, and dry years were stable around Scheme 50 and Scheme 40, and 25, respectively. In the case of sufficient incoming water, a series of schemes simultaneously consider both energy generation and ecological benefits. A series of schemes prioritized ecological benefits for normal and dry years with less incoming water. This decision aligns with the practical production requirements and reflects the applicability of the CV-ITOPSIS method. Furthermore, the optimal schemes for the three typical years correspond to or are close to the inflection point schemes of the Pareto front curve, indicating that the obtained decision schemes have reached a multi-objective equilibrium state and comply with the multi-objective conversion law.
- (2)
- In the decision results of the CV-ITOPSIS method, the decision results of the schemes before the optimal schemes were influenced by many factors, and the ranking of each scheme was closely related to the weight and degree of correlation between the evaluation system indicators. Following the optimal scheme, the relative closeness gradually decreased with an increase in energy generation, and the virtues or defect degrees of the schemes were mainly determined by the degree of ecological guarantee.
- (3)
- The optimal schemes and ranking results obtained using CV-ITOPSIS and traditional TOPSIS methods were not completely consistent. However, as can be seen from the top ten series of schemes, neither of the two decision-making methods recommends the schemes with the highest energy generation as the optimal schemes. This results from weighing the comprehensive benefits between the indicators, which reflects the rationality of applying multi-attribute decision-making methods to scheme evaluation. A correlation analysis of relative closeness under two decision-making methods was performed. Combining Table 4 and Figure 9, it can be observed that the evaluation results of the two methods show consistency in the overall trend. This indicates that the Mahalanobis distance calculation evaluation results retain TOPSIS’s good comprehensive evaluation performance while effectively weighting indicators and removing overlapping information between indicators.
5. Conclusions
- (1)
- Two methods were used to diagnose the hydrological variations in the middle and lower reaches of the Ganjiang River. The results showed no mutation points in the 59-year historical runoff sequence of Dongbei Station. Based on this, the complete runoff sequence was used to calculate the minimum ecological flow and suitable ecological flow, and the hierarchical and phased ecological flow processes were obtained. Moreover, the degree of ecological guarantee was defined to construct the single- and multi-objective scheduling models.
- (2)
- Two single-objective optimal operation models were built with one maximizing energy generation and the other maximizing ecological guarantee degree, respectively. The comparison results revealed the competitive relationship between energy generation objective and ecological objective. A non-fitting curve method was used to determine the approximate inflection point of the Pareto front curve, and the curve was fitted linearly based on the approximate inflection point to obtain a conversion formula between the objectives. The results clarify the piecewise linear contradiction between the objectives of energy generation and ecology; that is, improving energy generation benefits will inevitably reduce ecological benefits. Moreover, as the frequency of the incoming water increases, the contradiction between the two objectives intensifies. Before the approximate inflection point, the head significantly influenced the conversion rate from the energy generation to ecology, while the discharge flows is the major influencing factor after the point. The non-inferior solution set and conversion formula for energy generation and ecology were obtained from the calculation results of single- and multi-objective operation models, which provide a suitable coordination scheme for the actual operation of reservoirs and watershed management.
- (3)
- A novel multi-attribute decision-making method, CV-TOPSIS, is constructed. Compared with the traditional decision-making method, this method fully considers the correlation between indicators while considering the degree of differentiation of indicator data. Moreover, it can recommend the optimal schemes from the multi-objective non-inferior solution set. The schemes chosen by this method comprehensively coordinate the competitive and synergistic relationship between energy generation and ecological objectives for the Ganjiang River Basin’s ecological optimization operation and decision-making. The decision-making results met the actual task requirements, which improved the reliability of the reservoir operation decisions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dorber, M.; Arvesen, A.; Gernaat, D.; Verones, F. Controlling biodiversity impacts of future global hydropower reservoirs by strategic site selection. Sci. Rep. 2020, 10, 21777. [Google Scholar] [CrossRef]
- Yujun, Y.; Yanning, G.; Shanghong, Z. The impact of dams on the river connectivity of the two largest river basins in China. River Res. Appl. 2021, 38, 185–193. [Google Scholar] [CrossRef]
- Su, W.; Wang, S.; Liu, C.; Liu, X.; Chen, K.; Fan, H.; Wang, L.; Jiang, Z.; Li, B.; Hu, B. Construction and Application of a Water Quality Risk Sensitive Area Identification System in the Wudongde Reservoir. Water 2022, 14, 962. [Google Scholar] [CrossRef]
- Ma, T.; Shi, L.; Li, Z.; Wu, C.; Huang, Y.; Lu, X. Eutrophication trend analysis and forewarning model construction of water source reservoirs: Gaozhou Reservoir, China. Ecohydrology 2021, 15, e2371. [Google Scholar] [CrossRef]
- Jiang, Z.; Duan, J.; Xiao, Y.; He, S. Elite collaborative search algorithm and its application in power generation scheduling optimization of cascade reservoirs. J. Hydrol. 2022, 615, 128684. [Google Scholar] [CrossRef]
- Bradford, A. An Ecological Flow Assessment Framework: Building a Bridge to Implementation in Canada. Can. Water Resour. J. 2008, 33, 215–232. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, J.; Zhao, J.; Peng, W.; Fu, Y.; Wang, Q.; Zhang, Y. A new method for calculating the downstream ecological flow of diversion-type small hydropower stations. Ecol. Indic. 2021, 125, 107530. [Google Scholar] [CrossRef]
- Zhang, C.; Wan, Z.; Jing, Z.; Zhang, S.; Zhao, Y. Calculation of ecological water requirements of urban rivers using a hydrological model: A case study of Beiyun River. J. Clean. Prod. 2020, 262, 121368. [Google Scholar] [CrossRef]
- Ouyang, Y. A potential approach for low flow selection in water resource supply and management. J. Hydrol. 2012, 454, 56–63. [Google Scholar] [CrossRef]
- Mao, Y.; Huang, J.; Li, R.; Huang, W.; Wang, Q.; Feng, J. Optimal reservoir operation based on hydrological and hydraulic methods incorporating the multiple water replenishment process. J. Clean. Prod. 2020, 276, 124154. [Google Scholar] [CrossRef]
- Gao, C.; Hao, M.; Song, L.; Rong, W.; Shao, S.; Huang, Y.; Guo, Y.; Liu, X. Comparative study on the calculation methods of ecological base flow in a mountainous river. Front. Environ. Sci. 2022, 10, 1241. [Google Scholar] [CrossRef]
- Wang, L.; Mo, K.; Chen, Q.; Zhang, J.; Xia, J.; Lin, Y. Estimating ecological flows for fish overwintering in plain rivers using a method based on water temperature and critical water depth. Ecohydrology 2019, 12, e2098. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Q.; Zhang, J.; Xia, J.; Mo, K.; Wang, J. Incorporating fish habitat requirements of the complete life cycle into ecological flow regime estimation of rivers. Ecohydrology 2020, 13, e2204. [Google Scholar] [CrossRef]
- Yin, Z.J.; Yang, C.H.; Xu, J.J. Ecological regulation of cascade dams in the lower Jinsha river under different ecological flow constraints. J. Hydroelectr. Eng. 2013, 32, 66–70+81. [Google Scholar]
- Li, Z.; Cai, S.; Lei, X.; Wang, L. Diagnosis of Basin Eco-Hydrological Variation Based on Index Sensitivity of Similar Years: A Case Study in the Hanjiang River Basin. Water 2022, 14, 1931. [Google Scholar] [CrossRef]
- He, Z.; Wang, C.; Wang, Y.; Zhang, H.; Yin, H. An Efficient Optimization Method for Long-term Power Generation Scheduling of Hydropower Station: Improved Dynamic Programming with a Relaxation Strategy. Water Resour. Manag. 2022, 36, 1481–1497. [Google Scholar] [CrossRef]
- Zhu, D.; Mei, Y.; Xu, X.; Liu, Z.; Wu, Z.; Cai, H. Optimal operation of a parallel multireservoir system for flood control using a stagewise compensation method. Water Resour. Manag. 2021, 35, 1689–1710. [Google Scholar] [CrossRef]
- Wabela, K.; Hammani, A.; Abdelilah, T.; Tekleab, S.; El-Ayachi, M. Optimization of Irrigation Scheduling for Improved Irrigation Water Management in Bilate Watershed, Rift Valley, Ethiopia. Water 2022, 14, 3960. [Google Scholar] [CrossRef]
- Kumar, D.N.; Reddy, M.J. Ant colony optimization for multi-purpose reservoir operation. Water Resour. Manag. 2006, 20, 879–898. [Google Scholar] [CrossRef]
- Dong, Z.; Ni, X.; Chen, M.; Yao, H.; Jia, W.; Zhong, J.; Ren, L. Time-varying decision-making method for multi-objective regulation of water resources. Water Resour. Manag. 2021, 35, 3411–3430. [Google Scholar] [CrossRef]
- Dong, W.S.; Wang, H. Study for modeling and solving method of water resources optimizing allocation under considering uncertainties. Appl. Mech. Mater. 2012, 212–213, 554–559. [Google Scholar] [CrossRef]
- Zhang, X.; Luo, J.; Sun, X.; Xie, J. Optimal reservoir flood operation using a decomposition-based multi-objective evolutionary algorithm. Eng. Optim. 2018, 51, 42–62. [Google Scholar] [CrossRef]
- Bai, T.; Ji, H.-W.; Yang, W.-W.; Huang, Q.; Liu, X. Study on multi-objective optimal operation of Xiaolangdi Reservoir based on NNIA algorithm. Phys. Chem. Earth Parts A/B/C 2022, 126, 103142. [Google Scholar] [CrossRef]
- Ni, X.; Dong, Z.; Xie, W.; Jia, W.; Duan, C.; Yao, H. Research on the Multi-Objective Cooperative Competition Mechanism of Jinsha River Downstream Cascade Reservoirs during the Flood Season Based on Optimized NSGA-III. Water 2019, 11, 849. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, K.; Hu, H.; Su, L. The Cascade Reservoirs Multi-Objective Ecological Operation Optimization Considering Different Ecological Flow Demand. Water Resour. Manag. 2018, 33, 207–228. [Google Scholar] [CrossRef]
- Bai, T.; Li, L.; Yang, W.-W.; Chang, F.-J.; Huang, Q. Optimal dispatching scheme of multi-objective cascade reservoirs by parallel mechanism-optimization algorithms. J. Hydrol. 2022, 612, 128050. [Google Scholar] [CrossRef]
- Afshar, M.H.; Hajiabadi, R. A novel parallel cellular automata algorithm for multi-objective reservoir operation optimization. Water Resour. Manag. 2017, 32, 785–803. [Google Scholar] [CrossRef]
- Ai, X.; Ding, J.; Yang, B.; Guo, J.; Chen, S.; Mu, Z. Research on Multi-Objective Decision Making of Hydropower Station Group Based on CRITIC-TOPSIS Method. In Proceedings of the Applications of Decision Science in Management: Proceedings of International Conference on Decision Science and Management (ICDSM 2022), Changsha, China, 7–9 January 2022; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Wang, Q.; Zhou, J.; Huang, K.; Dai, L.; Zha, G.; Chen, L.; Qin, H. Risk assessment and decision-making based on mean-CVaR-entropy for flood control operation of large scale reservoirs. Water 2019, 11, 649. [Google Scholar] [CrossRef]
- Jia, B.; Simonovic, S.P.; Zhong, P.; Yu, Z. A multi-objective best compromise decision model for real-time flood mitigation operations of multi-reservoir system. Water Resour. Manag. 2016, 30, 3363–3387. [Google Scholar] [CrossRef]
- Dhillon, J.; Parti, S.; Kothari, D. Fuzzy decision making in multiobjective long-term scheduling of hydrothermal system. Int. J. Electr. Power Energy Syst. 2001, 23, 19–29. [Google Scholar] [CrossRef]
- Xu, H.; Ma, C.; Lian, J.; Xu, K.; Chaima, E. Urban flooding risk assessment based on an integrated k-means cluster algorithm and improved entropy weight method in the region of Haikou, China. J. Hydrol. 2018, 563, 975–986. [Google Scholar] [CrossRef]
- Chen, N.; Chen, L.; Ma, Y.; Chen, A. Regional disaster risk assessment of China based on self-organizing map: Clustering, visualization and ranking. Int. J. Disaster Risk Reduct. 2018, 33, 196–206. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, L.; Zhang, Y.; Wu, J.; Ma, Q.; Yue, L. Application of Marginal Rate of Transformation in Decision Making of Multi-Objective Reservoir Optimal Operation Scheme. Sustainability 2021, 13, 1488. [Google Scholar] [CrossRef]
- Wei, N.; Yang, F.; Lu, K.; Xie, J.; Zhang, S. A Method of Multi-Objective Optimization and Multi-Attribute Decision-Making for Huangjinxia Reservoir. Appl. Sci. 2022, 12, 6300. [Google Scholar] [CrossRef]
- Wang, Z.-X.; Wang, Y.-Y. Evaluation of the provincial competitiveness of the Chinese high-tech industry using an improved TOPSIS method. Expert Syst. Appl. 2014, 41, 2824–2831. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- He, Z.; Zhou, J.; Qin, H.; Jia, B.; Lu, C. Long-term joint scheduling of hydropower station group in the upper reaches of the Yangtze River using partition parameter adaptation differential evolution. Eng. Appl. Artif. Intell. 2019, 81, 1–13. [Google Scholar] [CrossRef]
- Bai, T.; Liu, X.; Ha, Y.-P.; Chang, J.-X.; Wu, L.-Z.; Wei, J.; Liu, J. Study on the Single-Multi-Objective Optimal Dispatch in the Middle and Lower Reaches of Yellow River for River Ecological Health. Water 2020, 12, 915. [Google Scholar] [CrossRef]
- Liu, X.; Yang, M.; Meng, X.; Wen, F.; Sun, G. Assessing the Impact of Reservoir Parameters on Runoff in the Yalong River Basin using the SWAT Model. Water 2019, 11, 643. [Google Scholar] [CrossRef]
- Du, J.; Zheng, D.; Xu, Y.; Hu, S.; Xu, C. Evaluating Functions of Reservoirs′ Storage Capacities and Locations on Daily Peak Attenuation for Ganjiang River Basin Using Xinanjiang Model. Chin. Geogr. Sci. 2016, 26, 789–802. [Google Scholar] [CrossRef]
- Richter, B.D.; Warner, A.T.; Meyer, J.L.; Lutz, K. A collaborative and adaptive process for developing environmental flow recommendations. River Res. Appl. 2006, 22, 297–318. [Google Scholar] [CrossRef]
- Huang, Y.; Huang, B.; Qin, T.; Nie, H.; Wang, J.; Li, X.; Shen, Z. Assessment of Hydrological Changes and Their Influence on the Aquatic Ecology over the last 58 Years in Ganjiang Basin, China. Sustainability 2019, 11, 4882. [Google Scholar] [CrossRef]
- Sinnathamby, S.; Douglas-Mankin, K.R.; Muche, M.E.; Hutchinson, S.L.; Anandhi, A. Ecohydrological Index, Native Fish, and Climate Trends and Relationships in the Kansas River Basin. Ecohydrology 2017, 11, 1909. [Google Scholar] [CrossRef] [PubMed]
- Feng, B.; Zhang, M.; Chen, J.; Xu, J.; Xiao, B.; Zhou, M.; Zhang, M. Reduction in the phytoplankton index of biotic integrity in riverine ecosystems driven by industrial activities, dam construction and mining: A case study in the Ganjiang River, China. Ecol. Indic. 2020, 120, 106907. [Google Scholar] [CrossRef]
- Zhu, D.; Chen, H.; Zhou, Y.; Xu, X.; Guo, S.; Chang, F.-J.; Xu, C.-Y. Exploring a multi-objective cluster-decomposition framework for optimizing flood control operation rules of cascade reservoirs in a river basin. J. Hydrol. 2022, 614, 128602. [Google Scholar] [CrossRef]
- Ali, R.; Kuriqi, A.; Abubaker, S.; Kisi, O. Long-Term Trends and Seasonality Detection of the Observed Flow in Yangtze River Using Mann-Kendall and Sen’s Innovative Trend Method. Water 2019, 11, 1855. [Google Scholar] [CrossRef]
- Li, F.-F.; Wang, Z.-Y.; Zhao, X.; Xie, E.; Qiu, J. Decomposition-ANN Methods for Long-Term Discharge Prediction Based on Fisher’s Ordered Clustering with MESA. Water Resour. Manag. 2019, 33, 3095–3110. [Google Scholar] [CrossRef]
- Chen, E.; Kelton, W. Determining simulation run length with the runs test. Simul. Model. Pract. Theory 2003, 11, 237–250. [Google Scholar] [CrossRef]
- Bai, T.; Xu, Y.; Sun, X.G.; Wei, J.; Pan, X.Y. Study on Multi—Objective Ecological Scheduling of Guanting Reservoir. Water Resour. Prot. 2023, 39, 101–108+124. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Li, T.; Tian, X. The Algorithm and application of discrete inflection point. Microcomput. Inf. 2007, 193, 248–249+254. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, Q.; Xie, Y.; Xu, P.; Du, H. Evaluation of Minimum and Suitable Ecological Flows of an Inland Basin in China Considering Hydrological Variation. Water 2023, 15, 649. [Google Scholar] [CrossRef]
- Guan, X.; Zhang, Y.; Meng, Y.; Liu, Y.; Yan, D. Study on the theories and methods of ecological flow guarantee rate index under different time scales. Sci. Total. Environ. 2021, 771, 145378. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Zhang, X.; Wan, H.; Wang, Y.; Liu, C.; Xia, J. Spatial and temporal characteristics of rainfall across Ganjiang River Basin in China. Meteorol. Atmos. Phys. 2015, 128, 167–179. [Google Scholar] [CrossRef]
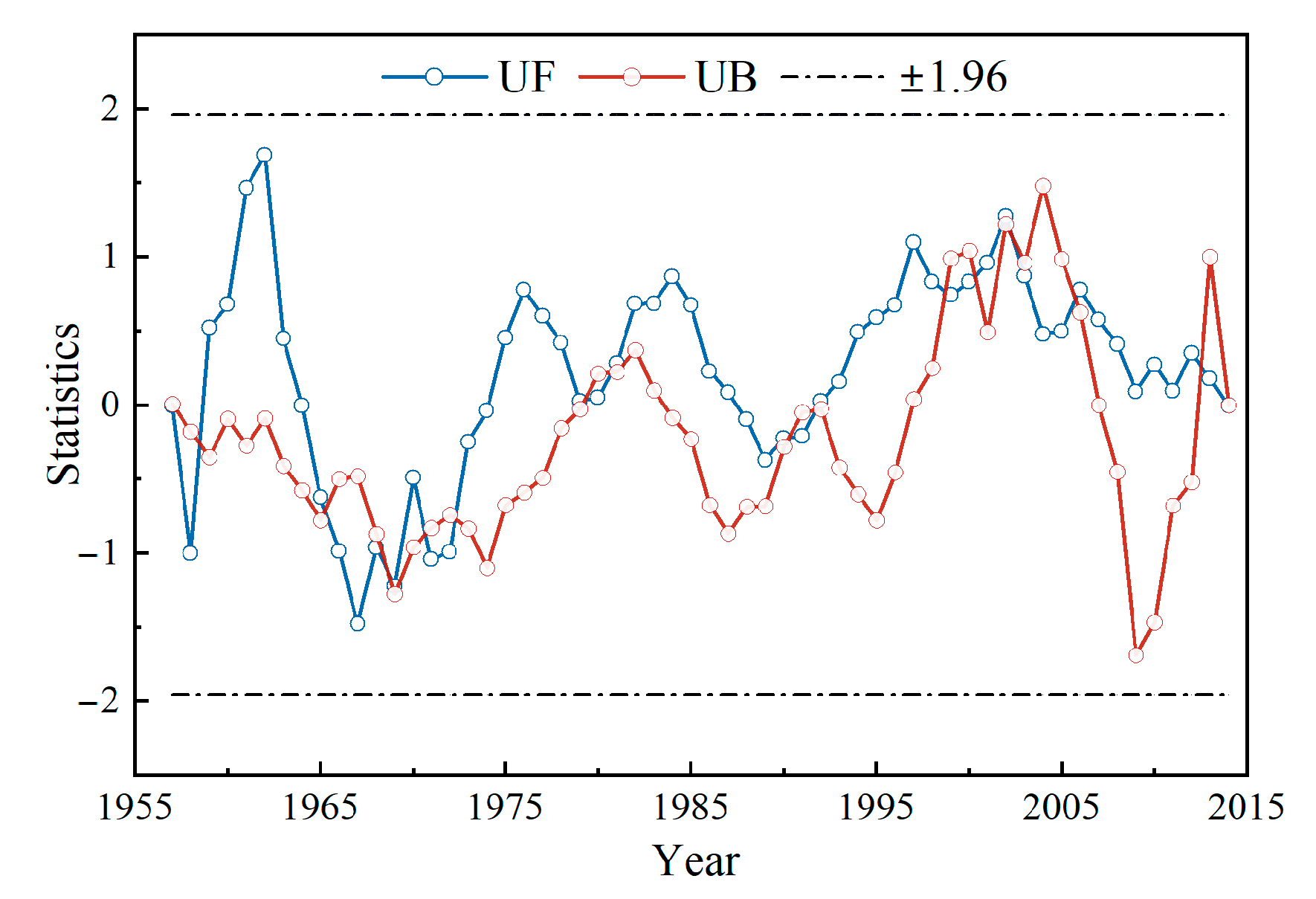
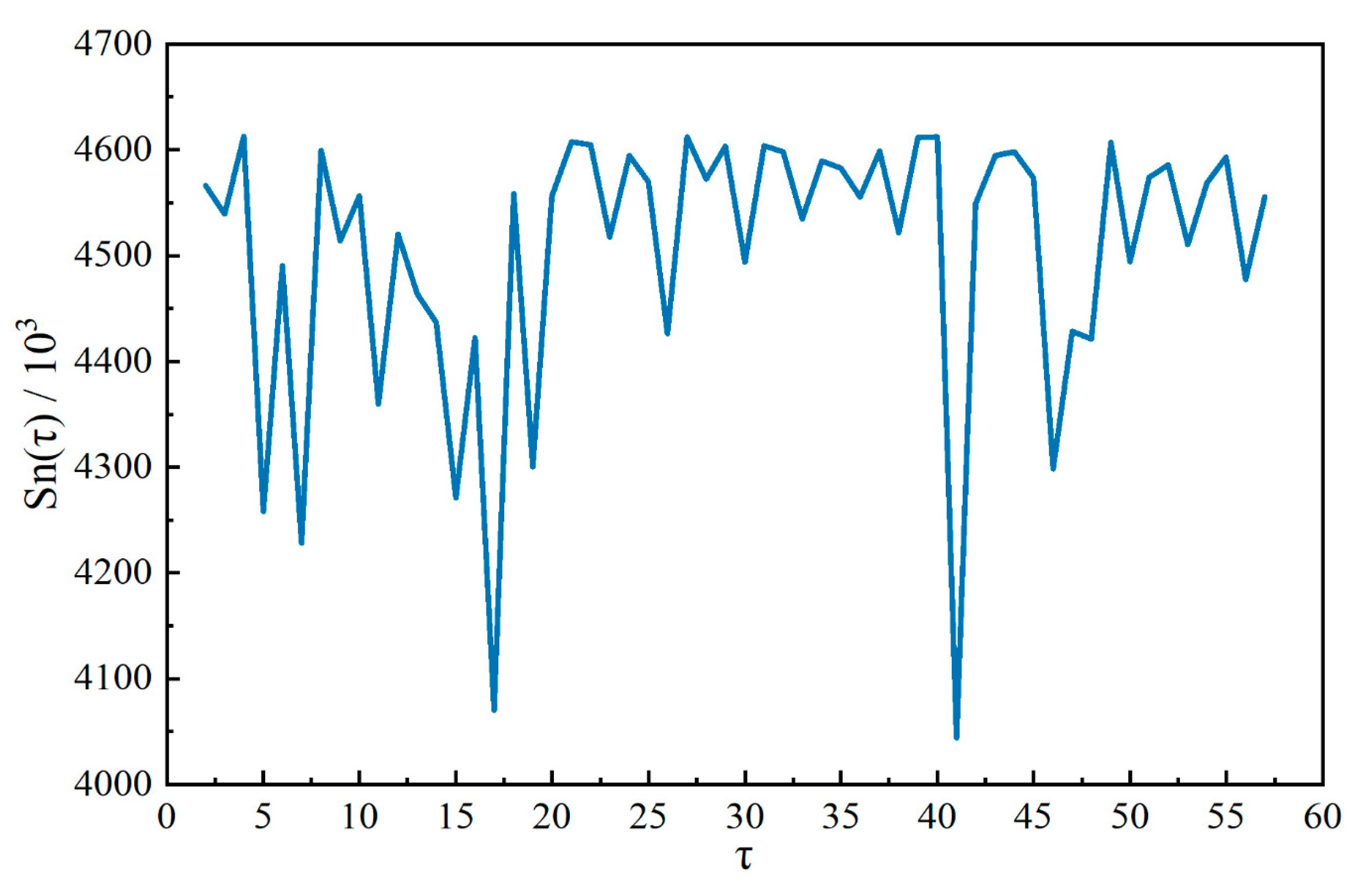
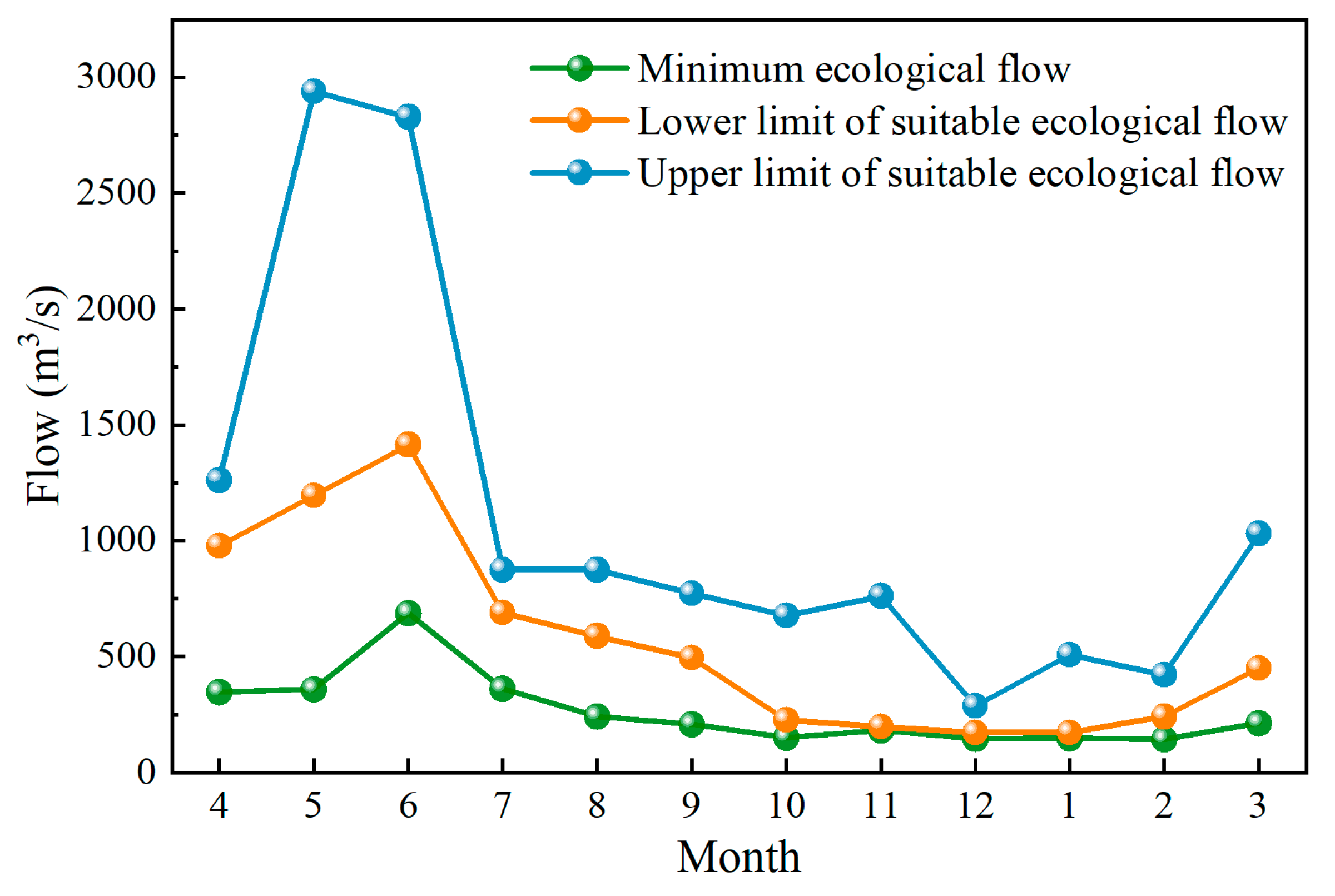
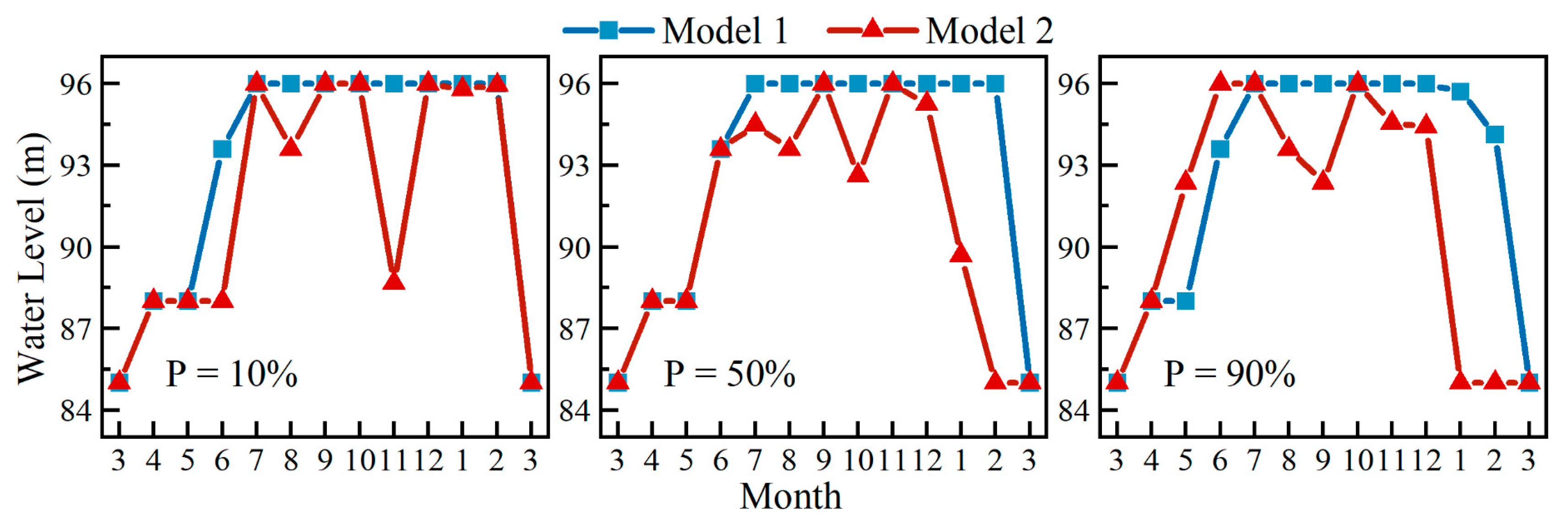
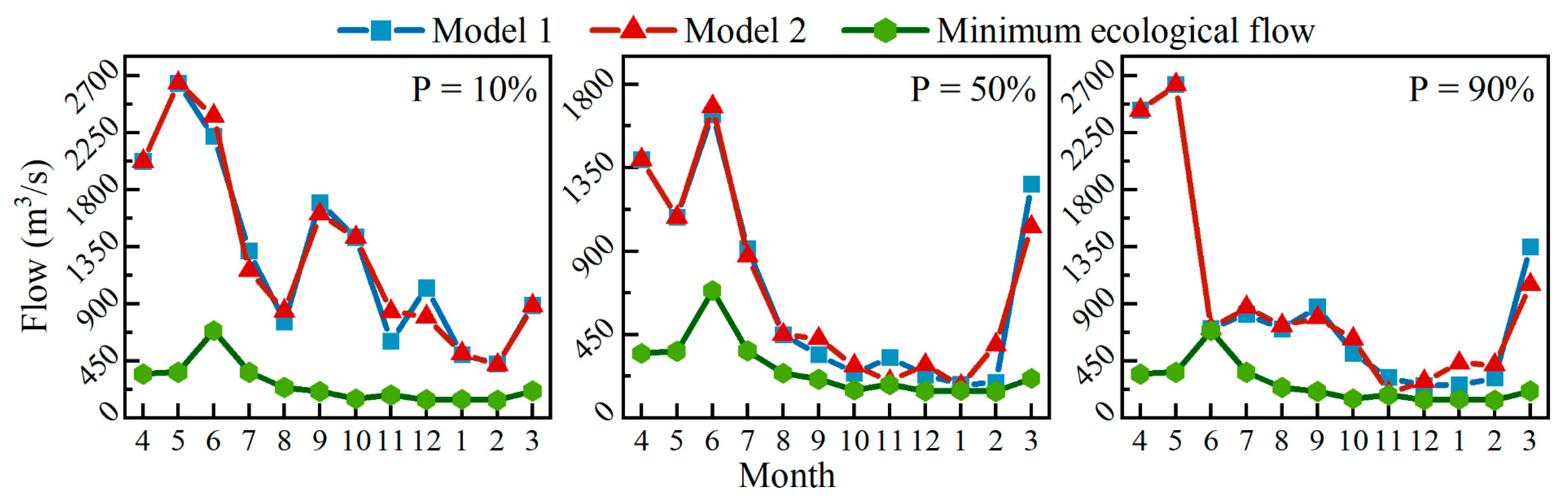
| Hydrologic Station | Mutation Point | Run Number r | Statistics Z | p Value | Significance Level | ||
|---|---|---|---|---|---|---|---|
| Dongbei Station | 1963 | 3 | 0.189 | 0.850 | 0.05 | 1.96 | Not significant |
| 1973 | 5 | 0.313 | 0.754 | 0.05 | 1.96 | Not significant | |
| 1997 | 3 | 0.189 | 0.850 | 0.05 | 1.96 | Not significant |
| Wet Year | Normal Year | Dry Year | ||||
|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 1 | Model 2 | Model 1 | Model 2 | |
| Annual energy generation/104 kW·h | 21.97 | 20.76 | 15.03 | 14.21 | 11.53 | 10.95 |
| Annual average ecological guarantee degree/% | 94.23 | 97.17 | 76.53 | 84.25 | 59.94 | 68.01 |
| Number of months of ecological guarantee | 10 | 12 | 7 | 10 | 3 | 5 |
| Frequency | Formula 1 | Inflection Point 1 | Formula 2 | Inflection Point 2 | Formula 3 |
|---|---|---|---|---|---|
| p = 10% | y = 111.81 − 0.7×x | (21.6, 96.7) | y = 227.1 − 6.04×x | --- | --- |
| p = 50% | y = 170.35 − 6.04×x | (14.9, 79.9) | y = 478.73 − 26.75×x | --- | --- |
| p = 90% | y = 81.8 − 1.27×x | (11.1, 67.7) | y = −230.38 − 14.58×x | (11.5, 62.4) | y = 653.62 − 51.49×x |
| p = 10% | p = 50% | p = 90% | |
|---|---|---|---|
| Weight of annual energy generation/ω1 | 0.633 | 0.392 | 0.280 |
| Weight of annual average ecological guarantee degree/ω2 | 0.367 | 0.608 | 0.720 |
| Correlation coefficient between objectives/ρ | −0.890 | −0.955 | −0.955 |
| Correlation coefficient of Cj sequence between methods/ρ | 0.976 | 0.885 | 0.949 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Mo, L.; Lou, S.; Zhu, Y.; Liu, T. An Ecology-Oriented Single–Multi-Objective Optimal Operation Modeling and Decision-Making Method in the Case of the Ganjiang River. Water 2024, 16, 970. https://doi.org/10.3390/w16070970
Liu Z, Mo L, Lou S, Zhu Y, Liu T. An Ecology-Oriented Single–Multi-Objective Optimal Operation Modeling and Decision-Making Method in the Case of the Ganjiang River. Water. 2024; 16(7):970. https://doi.org/10.3390/w16070970
Chicago/Turabian StyleLiu, Zixuan, Li Mo, Sijing Lou, Yuxin Zhu, and Tong Liu. 2024. "An Ecology-Oriented Single–Multi-Objective Optimal Operation Modeling and Decision-Making Method in the Case of the Ganjiang River" Water 16, no. 7: 970. https://doi.org/10.3390/w16070970
APA StyleLiu, Z., Mo, L., Lou, S., Zhu, Y., & Liu, T. (2024). An Ecology-Oriented Single–Multi-Objective Optimal Operation Modeling and Decision-Making Method in the Case of the Ganjiang River. Water, 16(7), 970. https://doi.org/10.3390/w16070970






