Historical Phosphorus Mass and Concentrations in Utah Lake: A Case Study with Implications for Nutrient Load Management in a Sorption-Dominated Shallow Lake
Abstract
1. Introduction
1.1. Study Motivation
1.2. Utah Lake Background
1.3. Phosphorous-Rich Sediments
1.4. Nutrient Mass Balance Models
1.5. Sorption
1.6. Research Overview
1.7. Hypothesis
2. Data and Methods
2.1. Data Sources and Descriptions
2.1.1. Utah Lake Volume
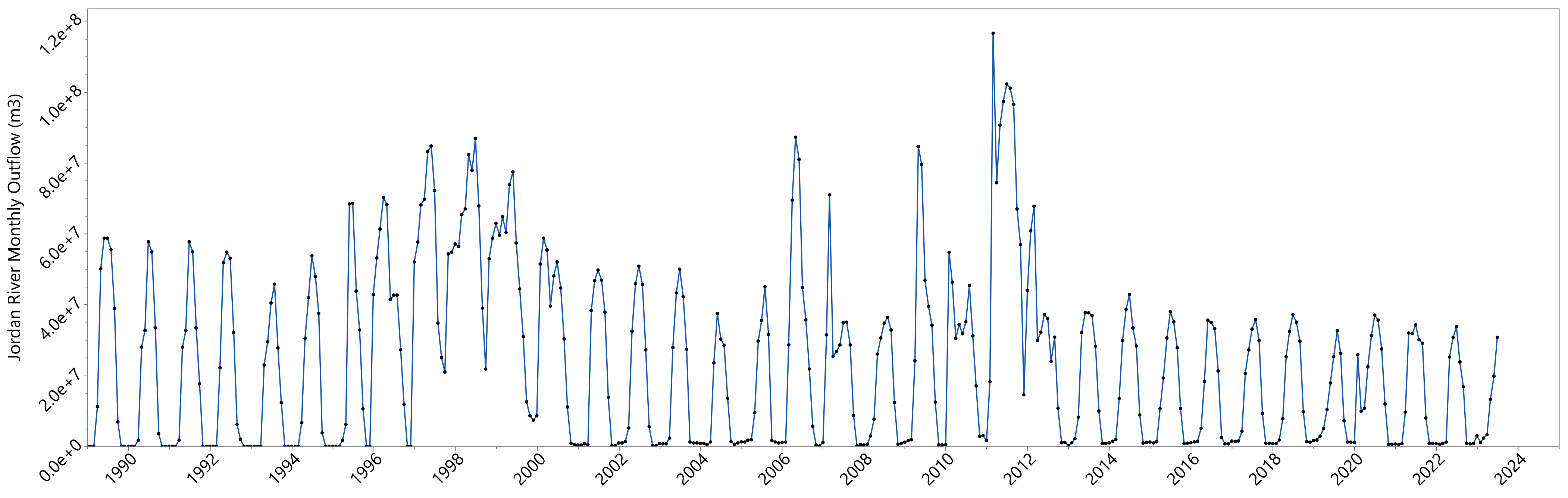
2.1.2. Jordan River Outflow
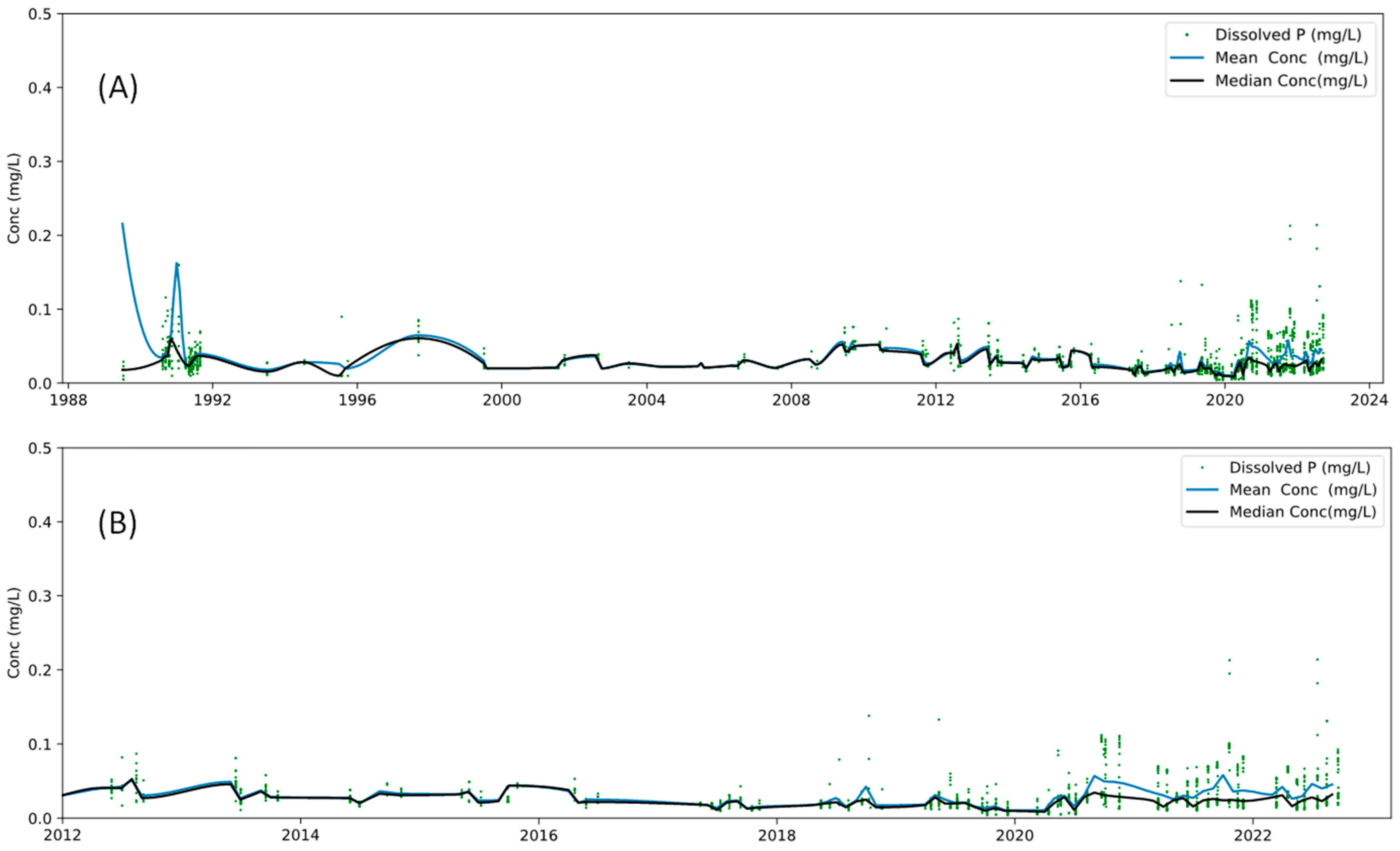
2.1.3. Phosphorus Concentrations
2.2. Analysis Methods
2.2.1. Statistical Analyses
2.2.2. Phosphorus Mass Calculations
2.2.3. Sorption Calculations
3. Results
3.1. Lake Volume Varibility
3.1.1. Volume Annual Variability
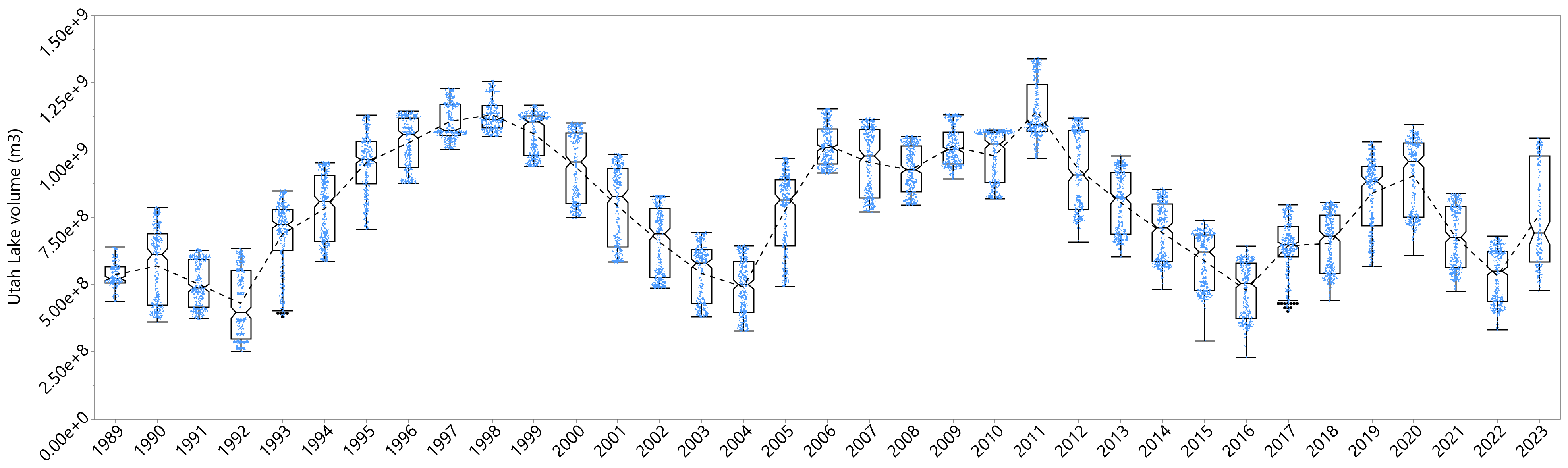

3.1.2. Volume Monthly Variability

3.2. Phosphorus Concentration Variabilty
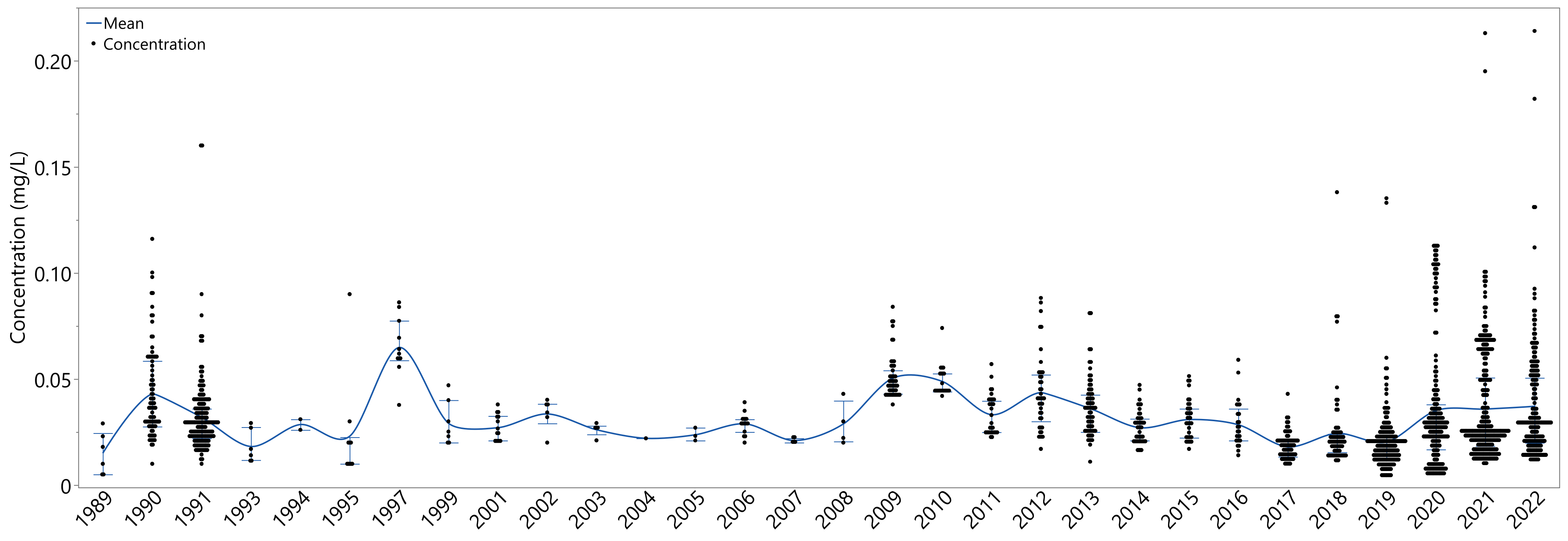
3.2.1. Phosphorus Concentration Annual Variability
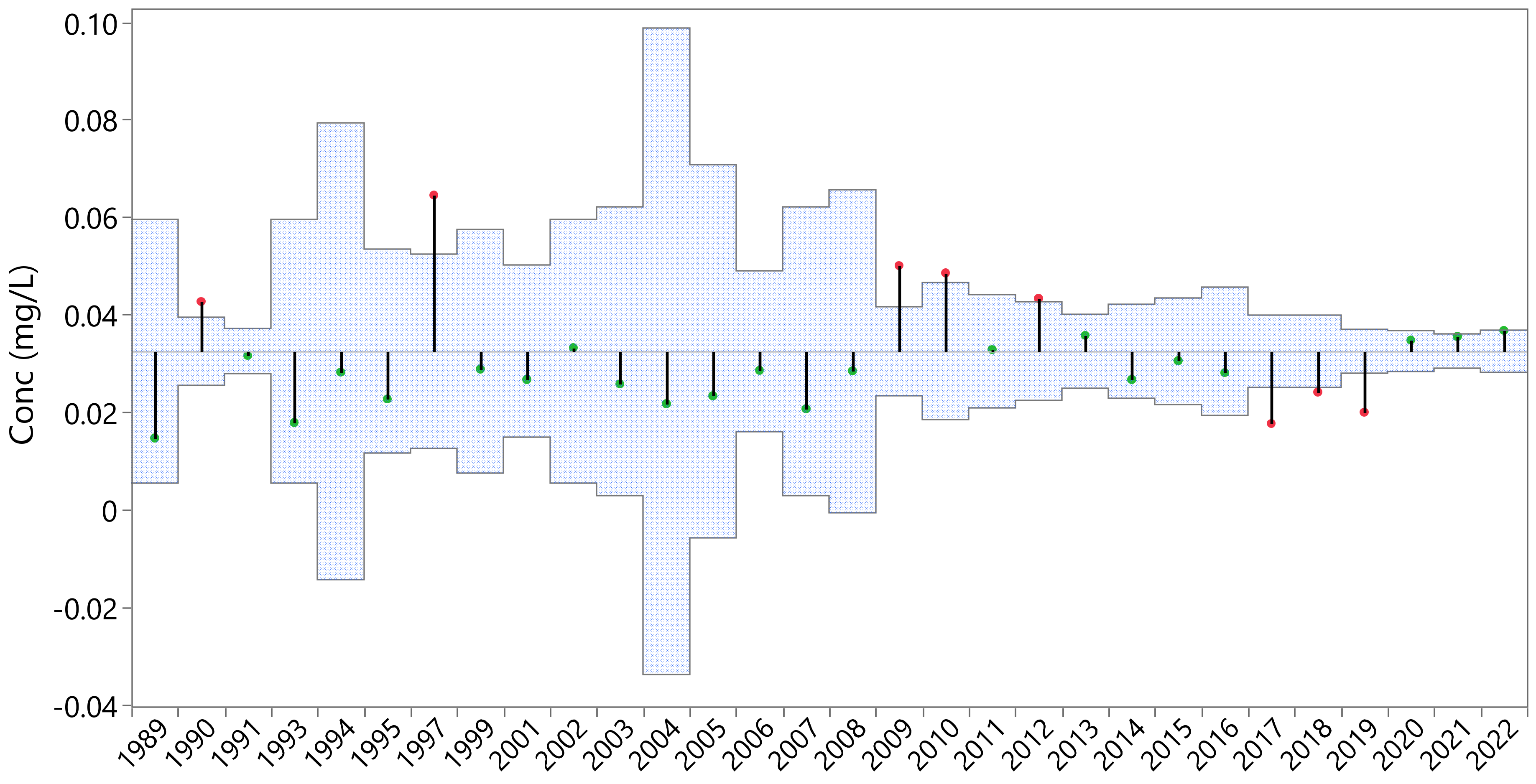
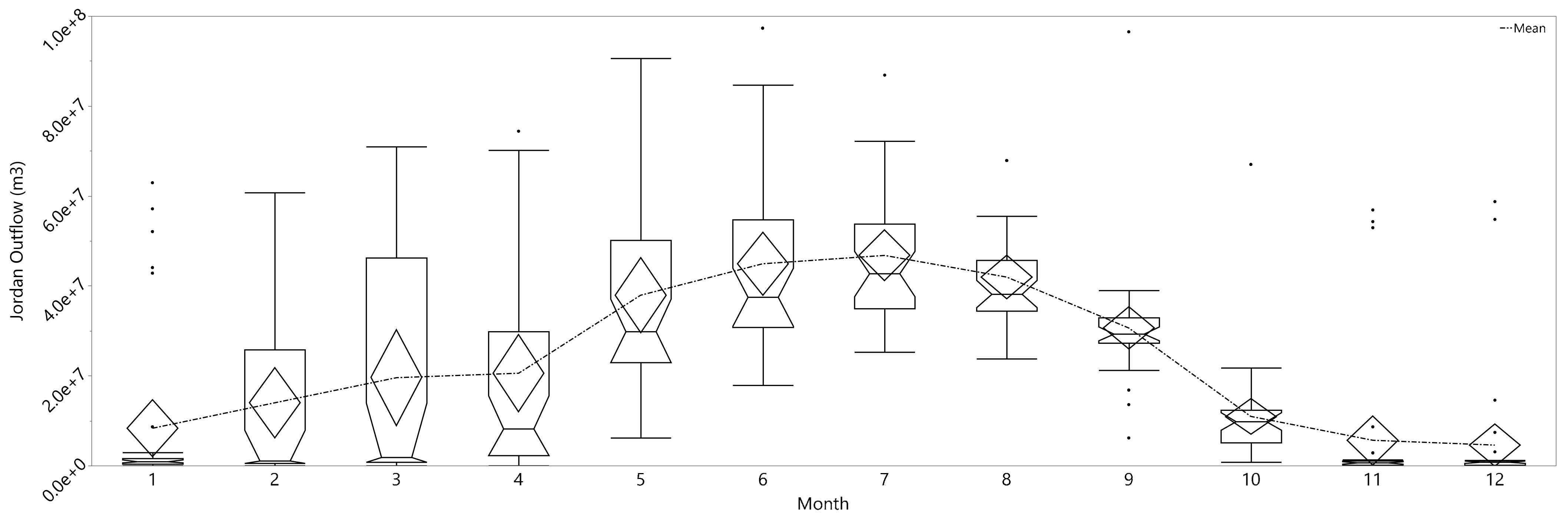
3.2.2. Phosphorus Concentration Monthly Variability
3.2.3. Phosphorus Concentration Variability by Location
3.3. Phosphorous Outflow—Jordan River

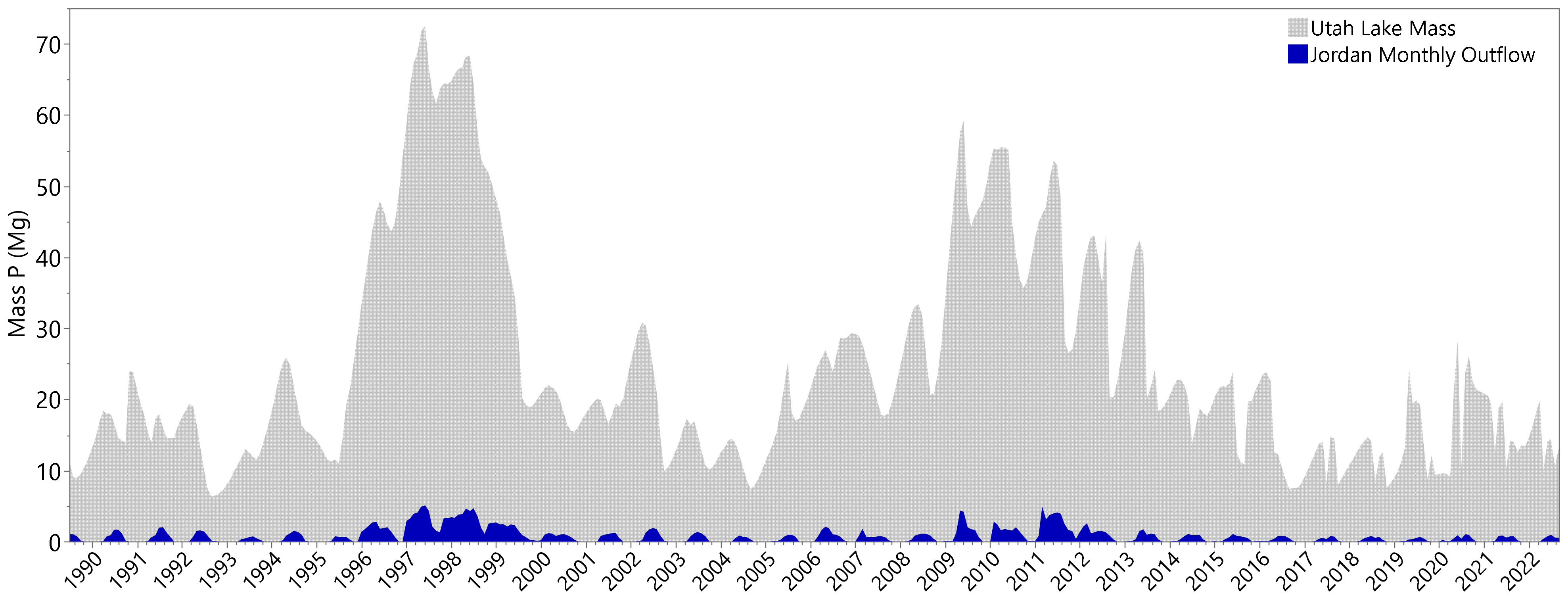

3.4. Phosphorus Mass Varibilty
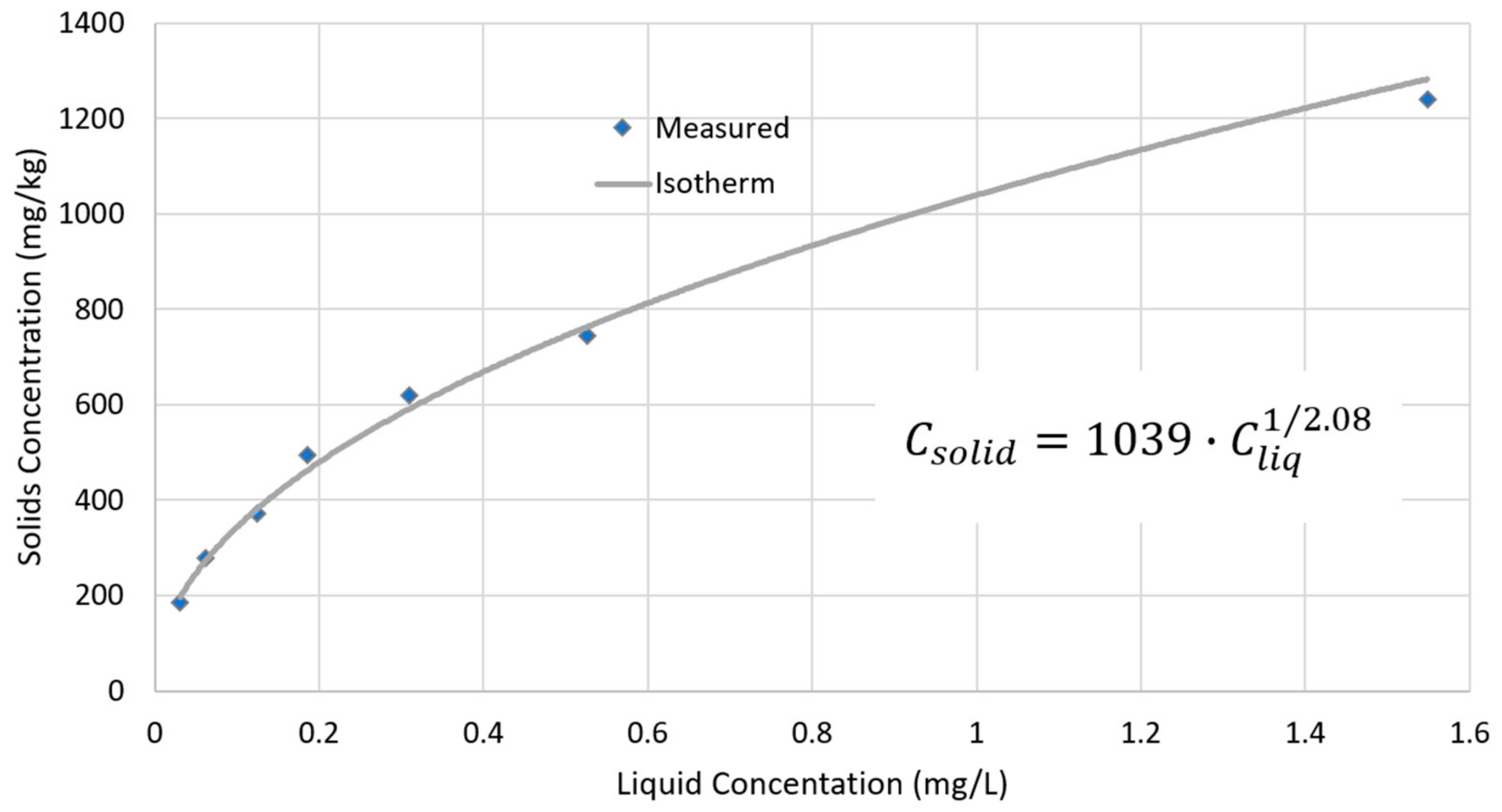
3.5. Sorption Calculations
4. Discussion
4.1. Varability
4.2. Isotherm Calculations Implications
4.3. Sorption Lines of Evidence
- Utah Lake sediments are high in P that is available for partitioning. This P is geologic in origin rather than anthropogenic. Lakebed sediments [10], surrounding lacustrine soils [11], and sediment 40 km upstream [12] all have P concentrations on the order of 1000 mg/kg, with about 40% of the P in the fractions being available to the sorption process [10]. In addition, the sediments underlying the lake are deep [27], and because of the potential for anaerobic releases, the sediments represent an essentially infinite reservoir of P.
- Utah Lake is very shallow, with a long fetch (~40 km), and strong winds. The lake does not stratify, and because of the depth, fetch, and winds, the lake’s sediments are continually mixed with the water column. We regularly measure total suspended solid concentrations on the order of 1000 mg/L and Secchi depths of a few 10s of cm. Because of this mixing with sediments, the water column can equilibrate with sediments in a sorption process.
- Utah Lake has a large population of invasive carp. These fish contribute to sediment water column mixing through bioturbation, continually stirring up the sediment through bottom feeding and by preventing the establishment of vegetation that could armor the lakebed and help isolate the sediment from the water column [13].
- Utah Lake volumes are variable, easily changing volume by a factor of 2 in any given year, and often more (Section 3.1.1). Conversely, DP concentrations in Utah Lake are relatively constant, with values ranging from about 0.02 to 0.06 mg/L but remain mostly in the 0.03 to 0.04 range (Section 3.2). With large changes in lake volume, we would expect P concentrations to be diluted in the spring after spring runoff fills the lake and then be concentrated in the late summer, as about half the lake volume is lost to evaporation. While we do see changes in water column DP, they are small and are better explained by the kinetics of sorption processes.
- An ANOM analysis of Utah Lake volume (Figure 10) and water column DP concentrations by year (Figure 12) shows that, for most years, the volume is outside of the decision boundaries and is significantly different from the mean, while the opposite is true for the concentration data—only a few years are outside the boundaries and only by a small amount. Statistically, the different annual average concentrations are not different from the population mean when nearly all the annual average yearly volumes are different from the population mean.
- Monthly changes in the mass of DP in the water column show that large changes can occur in just a month’s time (Section 3.4). When we estimate P inflows using lake mass and Jordan River mass outflows, we see that monthly mass inflows are large and switch from loads to removals in short time periods (Section 3.4). These estimated monthly mass inflows are larger in magnitude than estimated loads. More importantly, these loads are both positive and negative, switching from month to month. This can easily be explained using a sorption approach, where the sorption term is significantly larger than other P loads or sinks. This same phenomenon is difficult to explain using external loads alone.
- Using an isotherm fitted to data taken from the literature (as we do not have an isotherm for Utah Lake sediments) and an assumed value of half the literature’s Kd value, we can show the following:
- The sediment concentration at equilibrium with a water column concentration of 0.03 mg/L (the average) is consistent with measured sediment P concentrations in the fractions available for sorption.
- Because of the large sediment reservoir, it would require large P loads to cause even small changes in water column P concentrations when the system is at equilibrium. In a system without this large sediment reservoir in equilibrium with the water column, loads this large would increase water column concentrations by almost two orders of magnitude.
- In most lakes, the water column is not vertically-mixed well enough to be in equilibrium with reservoir sediments and the reservoir sediments are not enriched in P from geological sources. These two unique features, shallow waters that are well mixed with sediments enriched in geologic P, allow sorption processes to dominate water column P concentrations.
- It would require the addition of either 714 t or 346 t of P to change water column concentrations by only 0.005 mg/L for Kd values of 1039 and 500, respectively; this buffering process is supported by the constant water column concentrations observed over our 34-year study period.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- DWQ. Utah Lake Water Quality Study Stakeholder Process, Version 10—Approved May 12, 2017; Utah Department of Environmental Quality Water Quality: Salt Lake City, UT, USA, 2017; pp. 1–11.
- DWQ. Study Phases: Utah Lake Water Quality Study. Available online: https://deq.utah.gov/water-quality/study-phases-utah-lake (accessed on 6 February 2024).
- DEQ. Utah Lake Water Quality Study Phase 1 Report, Final—December 7, 2018; Utah Department of Environmental Quality: Salt Lake City, UT, USA, 2018; pp. 1–111.
- Brett, M. Quantification of nutrient inputs, sediment storage and release, and long-term recovery in Utah Lake. In Proceedings of the Utah Lake Science Panel Meeting, Salt Lake City, UT, USA, 29 June 2023. [Google Scholar]
- Brown, M.M.; Telfer, J.T.; Williams, G.P.; Miller, A.W.; Sowby, R.B.; Hales, R.C.; Tanner, K.B. Nutrient Loadings to Utah Lake from Precipitation-Related Atmospheric Deposition. Hydrology 2023, 10, 200. [Google Scholar] [CrossRef]
- Barrus, S.M.; Williams, G.P.; Miller, A.W.; Borup, M.B.; Merritt, L.B.; Richards, D.C.; Miller, T.G. Nutrient Atmospheric Deposition on Utah Lake: A Comparison of Sampling and Analytical Methods. Hydrology 2021, 8, 123. [Google Scholar] [CrossRef]
- Olsen, J.M.; Williams, G.P.; Miller, A.W.; Merritt, L. Measuring and Calculating Current Atmospheric Phosphorous and Nitrogen Loadings to Utah Lake Using Field Samples and Geostatistical Analysis. Hydrology 2018, 5, 45. [Google Scholar] [CrossRef]
- Telfer, J.T.; Brown, M.M.; Williams, G.P.; Tanner, K.B.; Miller, A.W.; Sowby, R.B.; Miller, T.G. Source Attribution of Atmospheric Dust Deposition to Utah Lake. Hydrology 2023, 10, 210. [Google Scholar] [CrossRef]
- Hogsett, M.; Li, H.; Goel, R. The Role of Internal Nutrient Cycling in a Freshwater Shallow Alkaline Lake. Environ. Eng. Sci. 2019, 36, 551–563. [Google Scholar] [CrossRef]
- Randall, M.C.; Carling, G.T.; Dastrup, D.B.; Miller, T.; Nelson, S.T.; Rey, K.A.; Hansen, N.C.; Bickmore, B.R.; Aanderud, Z.T. Sediment potentially controls in-lake phosphorus cycling and harmful cyanobacteria in shallow, eutrophic Utah Lake. PLoS ONE 2019, 14, e0212238. [Google Scholar] [CrossRef] [PubMed]
- Abu-Hmeidan, H.Y.; Williams, G.P.; Miller, A.W. Characterizing total phosphorus in current and geologic utah lake sediments: Implications for water quality management issues. Hydrology 2018, 5, 8. [Google Scholar] [CrossRef]
- Casbeer, W.; Williams, G.P.; Borup, M.B. Phosphorus Distribution in Delta Sediments: A Unique Data Set from Deer Creek Reservoir. Hydrology 2018, 5, 58. [Google Scholar] [CrossRef]
- PSOMAS. Utah Lake TMDL: Pollutant Loading Assessment & Designated Beneficial Use Impairment Assessment; PSOMAS: Salt Lake City, UT, USA, 2007. [Google Scholar]
- Hooton, L.W., Jr. Utah Lake & Jordan River Water Rights & Management Plan; The Salt Lake City Department of Public Utilities: Salt Lake City, UT, USA, 1989. [Google Scholar]
- United States Fish and Wildlife Service. Reclassification of the Endangered June Sucker to Threatened with a Section 4(d) Rule; Final Rule; Fish and Wildlife Service: West Valley City, UT, USA, 2021; pp. 192–212.
- URMCC. Utah Reclamation Mitigation and Conservation Commission—Utah Lake Wetland Preserve. Available online: https://www.mitigationcommission.gov/wetlands/wetlands_ulwp.html (accessed on 10 November 2023).
- Zanazzi, A.; Wang, W.; Peterson, H.; Emerman, S.H. Using Stable Isotopes to Determine the Water Balance of Utah Lake (Utah, USA). Hydrology 2020, 7, 88. [Google Scholar] [CrossRef]
- State of Utah Division of Water Quality. Text of the Final TBPEL Rule (R317-1-3.3); Division of Water Quality: Salt Lake City, UT, USA, 2015.
- Clark, D.L.; Kirby, S.M.; Oviatt, C.G. Geologic Map of the Rush Valley 30′ × 60′ Quadrangle, Tooele, Utah, and Salt Lake Counties, Utah; Utah Geological Survey: Salt Lake City, UT, USA, 2023.
- Constenius, K.N.; Clark, D.L.; King, J.K.; Ehler, J.B. Interim Geologic Map of the Provo 30′ × 60′ Quadrangle, Utah, Wasatch, and Salt Lake Counties, Utah; Utah Geological Survey: Salt Lake City, UT, USA, 2011.
- Pampeyan, E.H. Geological Map of the Lynndyl 30′ × 60′ Quadrangle, West-Central Utah; Utah Geological Survey: Salt Lake City, UT, USA, 2005.
- Witkind, I.J.; Weiss, M.P. Geologic Map of the Nephi 30′ × 60′ Quadrangle, Carbon, Emery, Juab, Sanpete, Utah, and Wasatch Counties, Utah; U.S. Geological Survey: Denver, CO, USA, 1991.
- Rupke, A. Today’s (And Tomorrow’s?) Phosphate. Surv. Notes 2015, 47, 6–7. [Google Scholar]
- Jewell, P.W.; Silberling, N.J.; Nichols, K.M. Geochemistry of the Mississippian Delle Phosphatic Event, Eastern Great Basin, U.S.A. J. Sediment. Res. 2000, 70, 1222–1233. [Google Scholar] [CrossRef][Green Version]
- Hiatt, E.E.; Budd, D.A. Sedimentary phosphate formation in warm shallow waters: New insights into the paleoceanography of the Permian Phosphoria Sea from analysis of phosphate oxygen isotopes. Sediment. Geol. 2001, 145, 119–133. [Google Scholar] [CrossRef]
- Maughan, E.K. Phosphoria Formation (Permian) and Its Resource Significance in the Western Interior, U.S.A. Pangea Glob. Environ. Resour. 1994, Memoir 17, 479–495. [Google Scholar]
- Hintze, L.F.; Kowallis, B.J. Geologic History of Utah: A Field Guide to Utah’s Rocks, Special Publications 9th ed.; Department of Geological Sciences, Brigham Young University: Provo, UT, USA, 2009. [Google Scholar]
- Vollenweider, R.A. Possibilities and limits of elementary models concerning budget of substances in lakes. Arch. Hydrobiol. 1969, 66, 1. [Google Scholar]
- Mueller, D.K. Mass Balance Model Estimation Of Phosphorus Concentrations In Reservoirs 1. JAWRA J. Am. Water Resour. Assoc. 1982, 18, 377–382. [Google Scholar] [CrossRef]
- Vollenweider, R.A. Input-output models: With special reference to the phosphorus loading concept in limnology. Schweiz. Z. Hydrol. 1975, 37, 53–84. [Google Scholar] [CrossRef]
- Jones, J.R.; Bachmann, R.W. Prediction of Phosphorus and Chlorophyll Levels in Lakes. Water Pollut. Control Fed. 1976, 48, 2176–2182. [Google Scholar]
- Bryhn, A.C.; Håkanson, L. A Comparison of Predictive Phosphorus Load-Concentration Models for Lakes. Ecosystems 2007, 10, 1084–1099. [Google Scholar] [CrossRef][Green Version]
- Chapra, S.C. Total Phosphorus Model for the Great Lakes. J. Environ. Eng. Div. 1977, 103, 147–161. [Google Scholar] [CrossRef]
- Chapra, S.C. Surface Water-Quality Modeling; Waveland Press, Inc.: Long Grove, IL, USA, 2008. [Google Scholar]
- Chapra, S.C.; Dolan, D.M. Great Lakes total phosphorus revisited: 2. Mass balance modeling. J. Gt. Lakes Res. 2012, 38, 741–754. [Google Scholar] [CrossRef]
- Dillon, P.J.; Rigler, F.H. A Test of a Simple Nutrient Budget Model Predicting the Phosphorus Concentration in Lake Water. J. Fish. Res. Board Can. 1974, 31, 1771–1778. [Google Scholar] [CrossRef]
- Boynton, W.R.; Garber, J.H.; Summers, R.; Kemp, W.M. Inputs, Transformations, and Transport of Nitrogen and Phosphorus in Chesapeake Bay and Selected Tributaries. Estuaries 1995, 18, 285–314. [Google Scholar] [CrossRef]
- Anagnostou, E.; Gianni, A.; Zacharias, I. Ecological modeling and eutrophication—A review. Nat. Resour. Model. 2017, 30, e12130. [Google Scholar] [CrossRef]
- Bhagowati, B.; Ahamad, K.U. A review on lake eutrophication dynamics and recent developments in lake modeling. Ecohydrol. Hydrobiol. 2019, 19, 155–166. [Google Scholar] [CrossRef]
- Klump, J.V.; Edgington, D.N.; Sager, P.E.; Robertson, A. Sedimentary phosphorus cycling and a phosphorus mass balance for the Green Bay (Lake Michigan) ecosystem. Can. J. Fish. Aquat. Sci. 1997, 54, 10–26. [Google Scholar] [CrossRef]
- Van Heyst, A.; Sinclair, A.; Jamieson, R. Application of phosphorus loading models to understand drivers of eutrophication in a complex rural lake-watershed system. J. Environ. Manag. 2022, 302, 114010. [Google Scholar] [CrossRef] [PubMed]
- Noges, P. Water and nutrient mass balance of the partly meromictic temperate Lake Verevi. In Lake Verevi, Estonia—A Highly Stratified Hypertrophic Lake; Springer: Dordrecht, The Netherlands, 2005; pp. 21–31. [Google Scholar] [CrossRef]
- Havens, K.E.; James, R.T. The Phosphorus Mass Balance of Lake Okeechobee, Florida: Implications for Eutrophication Management. Lake Reserv. Manag. 2005, 21, 139–148. [Google Scholar] [CrossRef]
- Pollman, C.D.; James, R.T. A simple model of internal loading of phosphorus in Lake Okeechobee. Lake Reserv. Manag. 2011, 27, 15–27. [Google Scholar] [CrossRef]
- Kelderman, P.; Wei, Z.; Maessen, M. Water and mass budgets for estimating phosphorus sediment–water exchange in Lake Taihu (China P. R.). Hydrobiologia 2005, 544, 167–175. [Google Scholar] [CrossRef]
- Søndergaard, M.; Bjerring, R.; Jeppesen, E. Persistent internal phosphorus loading during summer in shallow eutrophic lakes. Hydrobiologia 2013, 710, 95–107. [Google Scholar] [CrossRef]
- van der Salm, C.; Kros, J.; de Vries, W. Evaluation of different approaches to describe the sorption and desorption of phosphorus in soils on experimental data. Sci. Total Environ. 2016, 571, 292–306. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Appan, A.; Gulliver, J.S. Modeling of phosphorus dynamics in aquatic sediments: I—Model development. Water Res. 2003, 37, 3928–3938. [Google Scholar] [CrossRef] [PubMed]
- Spears, B.; Carvalho, L.; Paterson, D. Phosphorus partitioning in a shallow lake: Implications for water quality management. Water Environ. J. 2007, 21, 47–53. [Google Scholar] [CrossRef]
- Fetter, C.W. Applied Hydrogeology, 4th ed.; Waveland Press, Inc.: Long Grove, IL, USA, 2001. [Google Scholar]
- United States Bureau of Reclamation. Historic Data|Water Operations|UC Region|Bureau of Reclamation. Available online: https://www.usbr.gov/rsvrWater/HistoricalApp.html (accessed on 23 October 2023).
- DWR. Document Listing for Folder: DSYS059REPORT. Available online: https://www.waterrights.utah.gov/cgi-bin/docview.exe?Folder=DSYS059REPORT&Key=Sort%20by%20Date (accessed on 23 October 2023).
- DWQ. Databases & Information. Available online: https://deq.utah.gov/water-quality/databases-and-information (accessed on 23 October 2023).
- Kramer, C.Y. Extension of multiple range tests to group means with unequal numbers of replications. Biometrics 1956, 12, 307–310. [Google Scholar] [CrossRef]
- Tukey, J.W. The problem of multiple comparisons. In Multiple Comparisons; Chapman and Hall: Boca Raton, FL, USA, 1953. [Google Scholar]
- McKinney, W. Data structures for statistical computing in python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 51–56. [Google Scholar]
- Sparks, D.L. Environmental Soil Chemistry, 3rd ed.; Academic Press: San Diego, CA, USA, 2003. [Google Scholar]
- Brezonik, P.L.; Arnold, W.A. Water Chemistry: An Introduction to the Chemistry of Natural and Engineered Aquatic Systems; Oxford University Press, Inc.: New York City, NY, USA, 2011; p. 782. [Google Scholar]
- Tanner, K.B.; Cardall, A.C.; Williams, G.P. A Spatial Long-Term Trend Analysis of Estimated Chlorophyll-a Concentrations in Utah Lake Using Earth Observation Data. Remote Sens. 2022, 14, 3664. [Google Scholar] [CrossRef]
- Cardall, A.C.; Hales, R.C.; Tanner, K.B.; Williams, G.P.; Markert, K.N. LASSO (L1) Regularization for Development of Sparse Remote-Sensing Models with Applications in Optically Complex Waters Using GEE Tools. Remote Sens. 2023, 15, 1670. [Google Scholar] [CrossRef]
- Sposito, G. The Surface Chemistry of Soils; Oxford University Press: Oxford, UK, 1984. [Google Scholar]






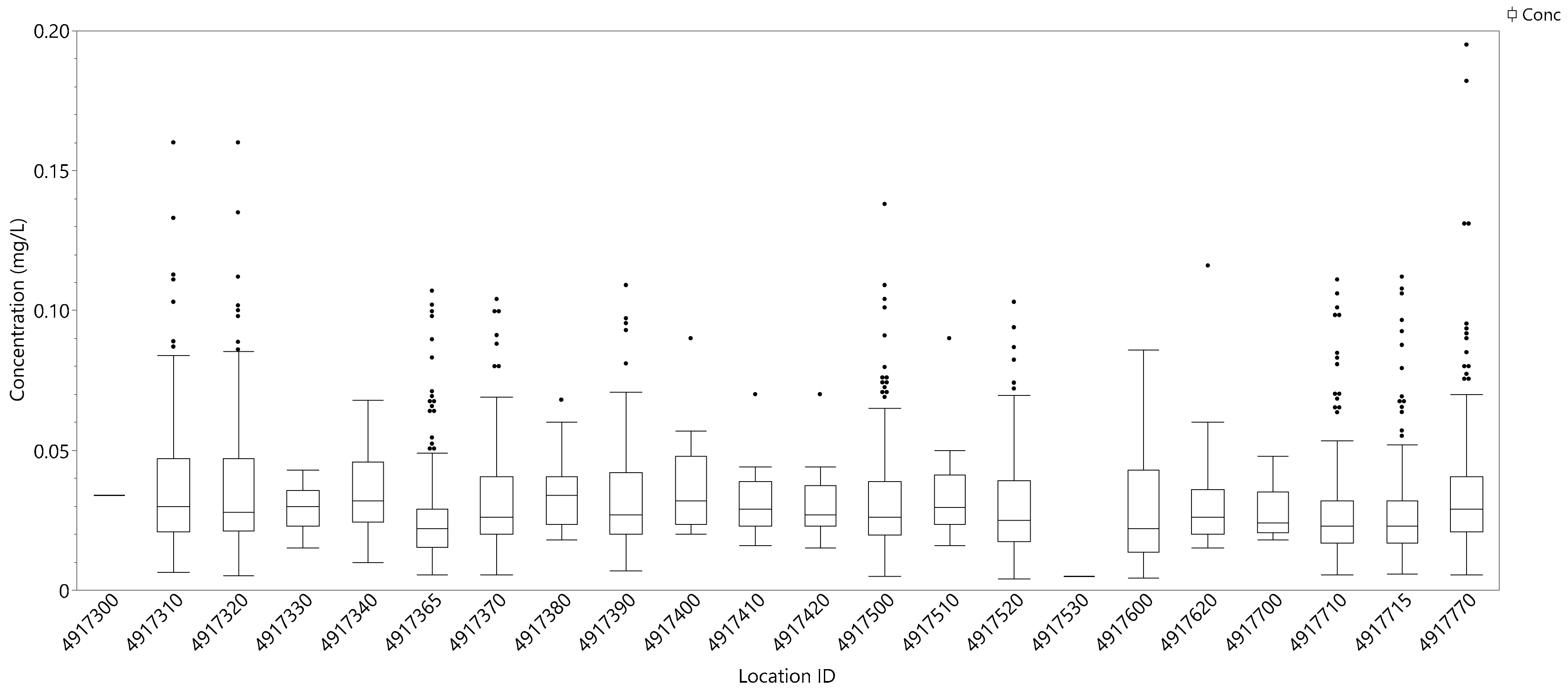
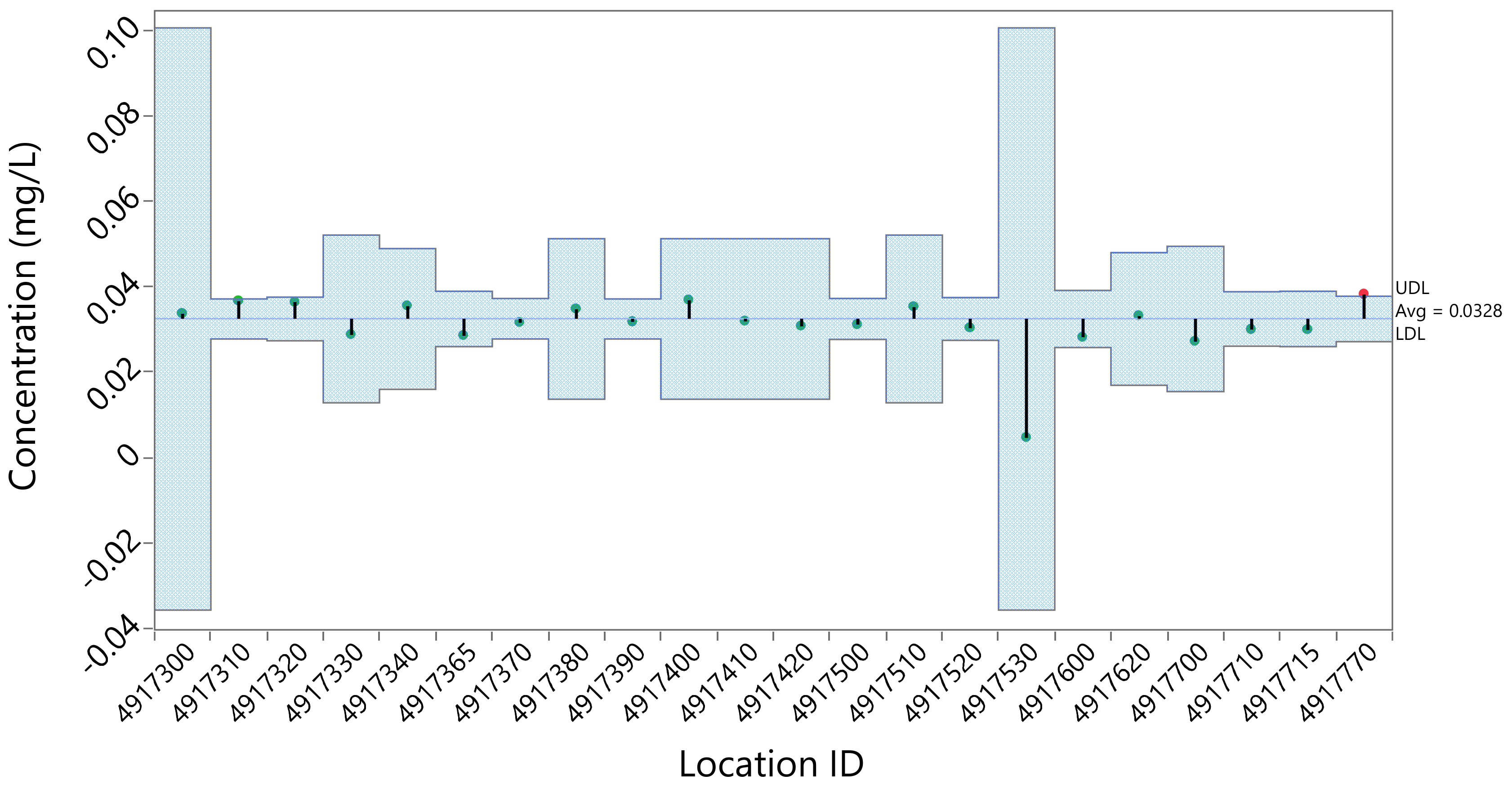

| Location ID | Location Name |
|---|---|
| 4917770 | Utah Lake Outside Entrance to Provo Bay |
| 4917380 | Utah Lake 0.5 mi S of American Fork Boat Harbor #14 |
| 4917310 | Utah Lake 0.5 mi W of Geneva Discharge #15-A |
| 4917320 | Utah Lake 0.5 mi W of Geneva Discharge #15-A Replicate Of 4917310 |
| 4917530 | Utah Lake 0.7 mi East of Pelican Point |
| 4917370 | Utah Lake 1 mi East of Pelican Point |
| 4917710 | Utah Lake 1 mi NE of Lincoln Point #03 |
| 4917410 | Utah Lake 1 mi NE of Pelican Point #10 |
| 4917420 | Utah Lake 1 mi SE of Pelican Point #09 |
| 4917390 | Utah Lake 1 mi West of Provo Boat Harbor |
| 4917715 | Utah Lake 1 mile Southeast of Bird Island |
| 4917400 | Utah Lake 1.5 mi NW of Provo Boat Harbor #16 |
| 4917520 | Utah Lake 2 mi E of Saratoga Springs #12 |
| 4917365 | Utah Lake 2 miles West of Vineyard |
| 4917700 | Utah Lake 2.5 mi NE of Lincoln Point #02 |
| 4917500 | Utah Lake 3 mi W/NW of Lincoln Beach |
| 4917300 | Utah Lake 300 ft Offshore from Geneva Steel |
| 4917510 | Utah Lake 4 mi E of Saratoga Springs #11 |
| 4917330 | Utah Lake 5mi N/NW Of Lincoln Beach/1 mi Offshore |
| 4917620 | Utah Lake Goshen Bay Midway Off Main Point On East Shore |
| 4917600 | Utah Lake Goshen Bay Southwest End |
| 4917340 | Utah Lake W of Provo Boat Harbor/6 mi N Of Lincoln Beach #08 |
| Year | Connecting Letter | Mean | Year | Connecting Letter | Mean | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1997 | A | 0.065 | 2008 | A | B | C | D | E | F | G | 0.029 | ||||||
| 2009 | A | B | 0.050 | 1994 | A | B | C | D | E | F | G | 0.029 | |||||
| 2010 | A | B | C | D | 0.049 | 2016 | C | D | E | F | G | 0.028 | |||||
| 2012 | A | B | C | D | E | 0.044 | 2001 | B | C | D | E | F | G | 0.027 | |||
| 1990 | A | B | C | 0.043 | 2014 | E | F | G | 0.027 | ||||||||
| 2022 | C | D | E | 0.037 | 2003 | A | B | C | D | E | F | G | 0.026 | ||||
| 2013 | B | C | D | E | F | 0.036 | 2018 | F | G | 0.024 | |||||||
| 2021 | C | D | E | 0.036 | 2005 | A | B | C | D | E | F | G | 0.024 | ||||
| 2020 | C | D | E | 0.035 | 1995 | B | C | D | E | F | G | 0.023 | |||||
| 2002 | A | B | C | D | E | F | G | 0.034 | 2004 | A | B | C | D | E | F | G | 0.022 |
| 2011 | B | C | D | E | F | G | 0.033 | 2007 | B | C | D | E | F | G | 0.021 | ||
| 1991 | D | E | F | 0.032 | 2019 | G | 0.020 | ||||||||||
| 2015 | C | D | E | F | G | 0.031 | 1993 | B | C | D | E | F | G | 0.018 | |||
| 1999 | A | B | C | D | E | F | G | 0.029 | 2017 | G | 0.018 | ||||||
| 2006 | B | C | D | E | F | G | 0.029 | 1989 | C | D | E | F | G | 0.015 | |||
| Month | Connected Letters | Mean | |||||
|---|---|---|---|---|---|---|---|
| 1 | A | 0.059 | |||||
| 10 | B | 0.039 | |||||
| 9 | B | C | 0.038 | ||||
| 11 | B | C | D | E | 0.036 | ||
| 8 | B | C | E | 0.035 | |||
| 6 | C | D | E | F | 0.032 | ||
| 7 | D | F | 0.029 | ||||
| 3 | D | E | F | 0.028 | |||
| 4 | D | F | 0.028 | ||||
| 5 | F | 0.027 | |||||
| 12 | D | E | F | 0.025 | |||
| Cliq (mg/L) | Csolid (mg/kg) | Psolid (mg) | Pliq (mg) | Ptot (mg) | Padded (mg) |
|---|---|---|---|---|---|
| 0.020 | 158.41 | 28.51 | 0.060 | 28.57 | −6.17 |
| 0.025 | 176.35 | 31.74 | 0.075 | 31.82 | −2.92 |
| 0.030 | 192.51 | 34.65 | 0.090 | 34.74 | 0.00 |
| 0.035 | 207.32 | 37.32 | 0.105 | 37.42 | 2.68 |
| 0.040 | 221.07 | 39.79 | 0.120 | 39.91 | 5.17 |
| 0.045 | 233.95 | 42.11 | 0.135 | 42.25 | 7.50 |
| 0.050 | 246.11 | 44.30 | 0.150 | 44.45 | 9.71 |
| 0.055 | 257.65 | 46.38 | 0.165 | 46.54 | 11.80 |
| 0.060 | 268.65 | 48.36 | 0.180 | 48.54 | 13.80 |
| 0.065 | 279.19 | 50.25 | 0.195 | 50.45 | 15.71 |
| 0.070 | 289.32 | 52.08 | 0.210 | 52.29 | 17.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taggart, J.B.; Ryan, R.L.; Williams, G.P.; Miller, A.W.; Valek, R.A.; Tanner, K.B.; Cardall, A.C. Historical Phosphorus Mass and Concentrations in Utah Lake: A Case Study with Implications for Nutrient Load Management in a Sorption-Dominated Shallow Lake. Water 2024, 16, 933. https://doi.org/10.3390/w16070933
Taggart JB, Ryan RL, Williams GP, Miller AW, Valek RA, Tanner KB, Cardall AC. Historical Phosphorus Mass and Concentrations in Utah Lake: A Case Study with Implications for Nutrient Load Management in a Sorption-Dominated Shallow Lake. Water. 2024; 16(7):933. https://doi.org/10.3390/w16070933
Chicago/Turabian StyleTaggart, Jacob B., Rebecca L. Ryan, Gustavious P. Williams, A. Woodruff Miller, Rachel A. Valek, Kaylee B. Tanner, and Anna C. Cardall. 2024. "Historical Phosphorus Mass and Concentrations in Utah Lake: A Case Study with Implications for Nutrient Load Management in a Sorption-Dominated Shallow Lake" Water 16, no. 7: 933. https://doi.org/10.3390/w16070933
APA StyleTaggart, J. B., Ryan, R. L., Williams, G. P., Miller, A. W., Valek, R. A., Tanner, K. B., & Cardall, A. C. (2024). Historical Phosphorus Mass and Concentrations in Utah Lake: A Case Study with Implications for Nutrient Load Management in a Sorption-Dominated Shallow Lake. Water, 16(7), 933. https://doi.org/10.3390/w16070933







