Applying Recurrent Neural Networks and Blocked Cross-Validation to Model Conventional Drinking Water Treatment Processes
Abstract
1. Introduction
2. Methodology
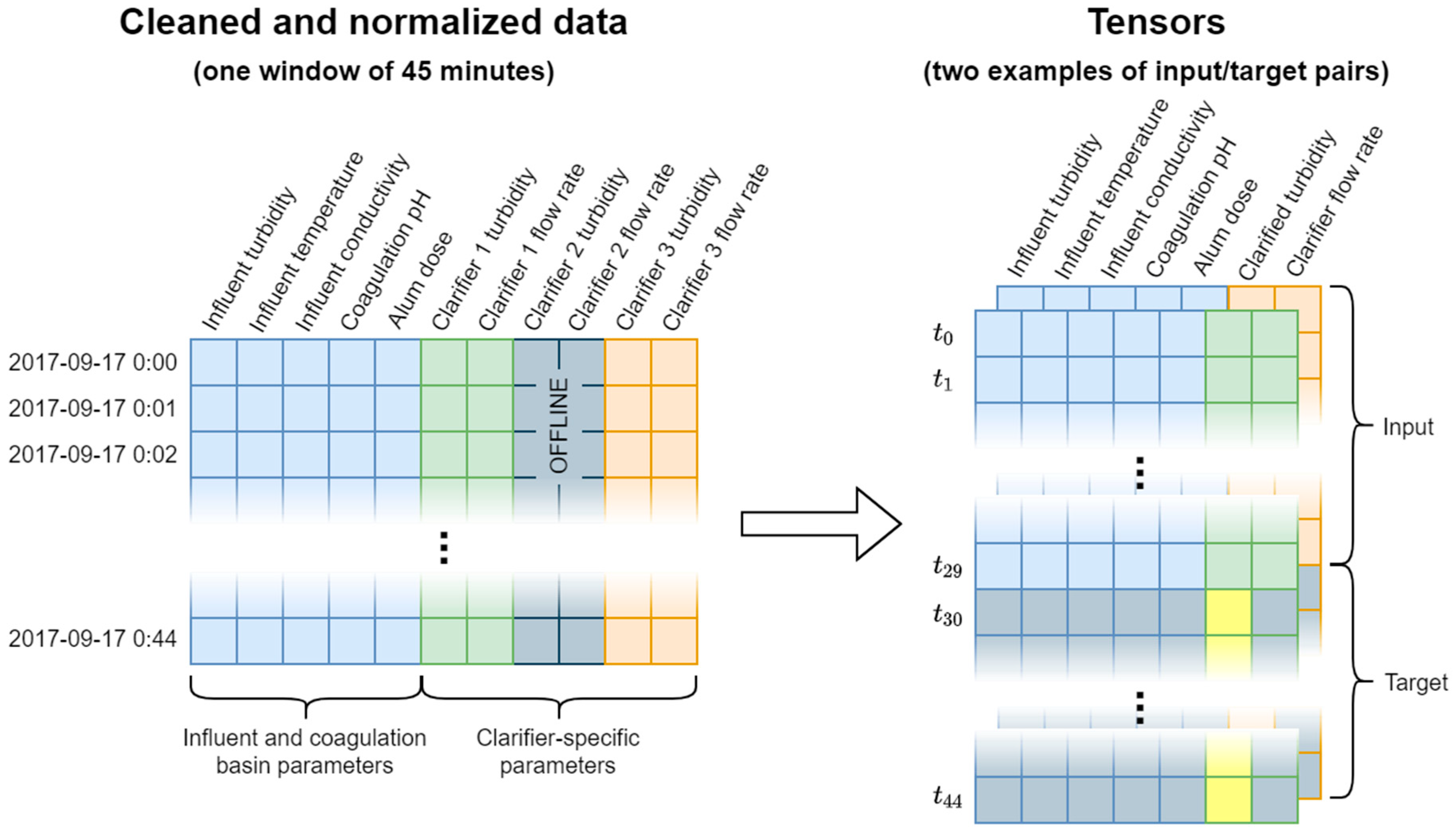
2.1. Data Analysis and Preprocessing
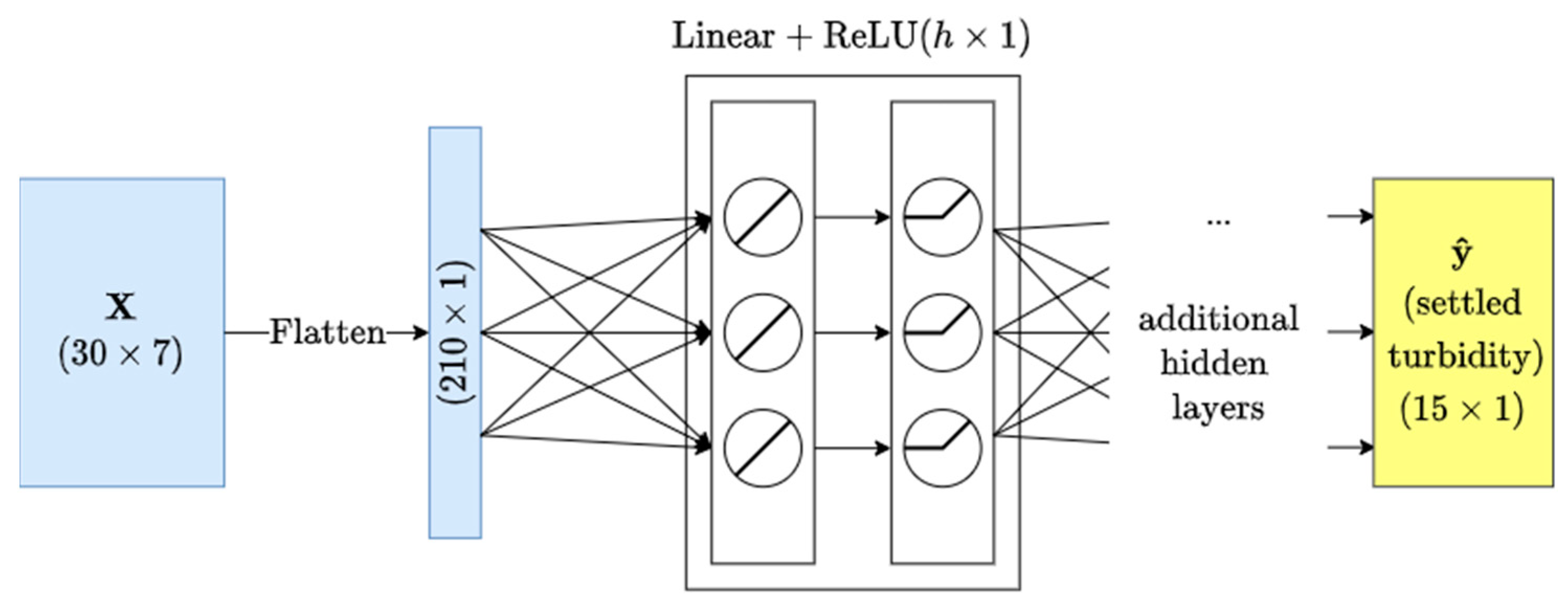
2.2. Implementation
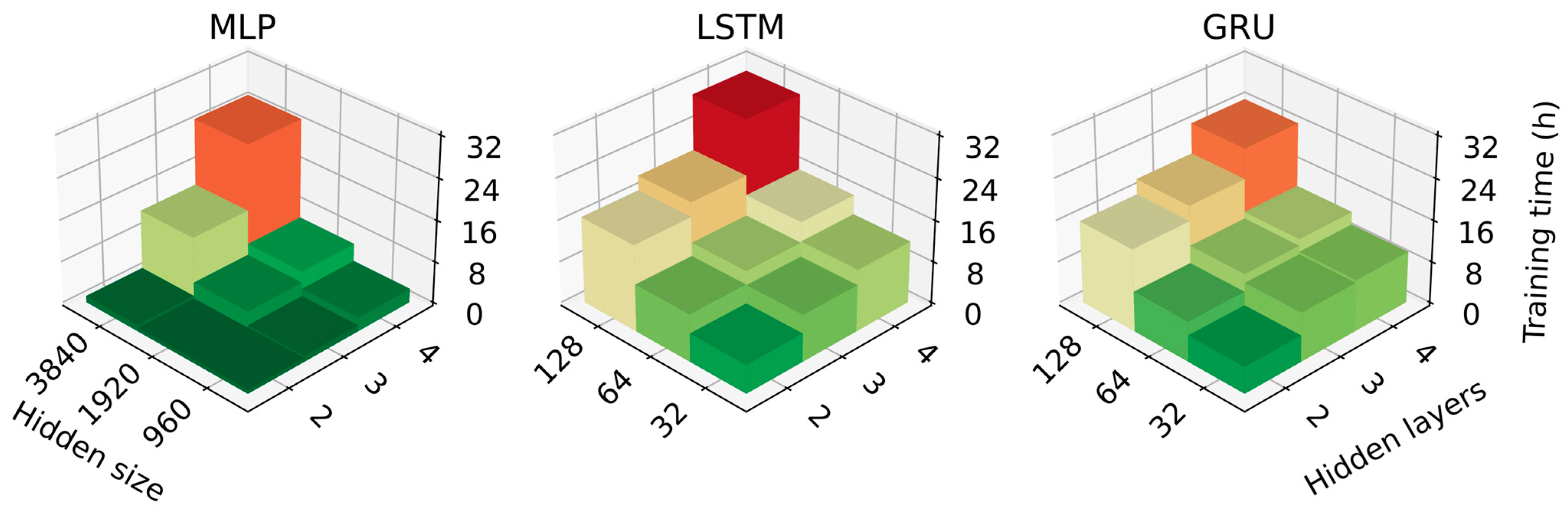
2.3. Model Selection
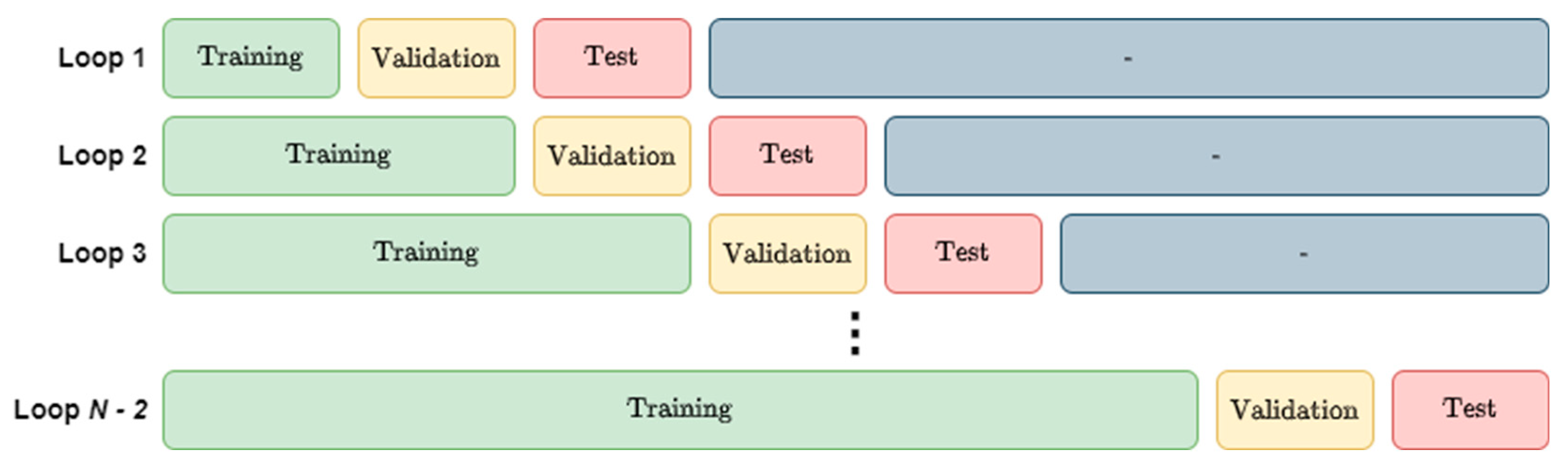
2.4. Training and Testing
3. Results
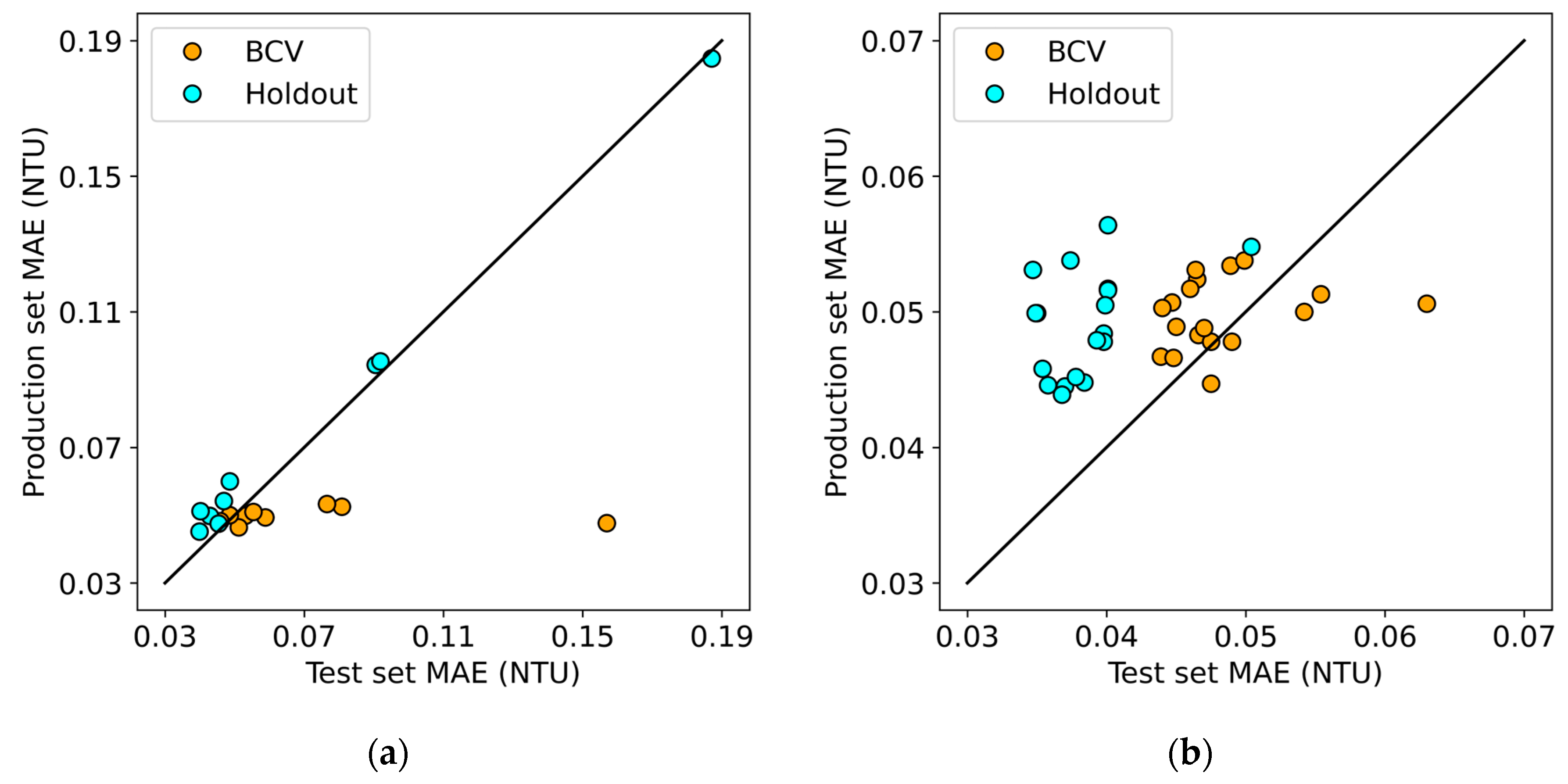
3.1. Model Performance
3.2. Cross-Validation Methods
4. Discussion
4.1. Key Findings
4.2. Limitations and Future Work
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Desjardins, C.; Koudjonou, B.; Desjardins, R. Laboratory study of ballasted flocculation. Water Res. 2002, 36, 744–754. [Google Scholar] [CrossRef]
- Ratnaweera, H.; Fettig, J. State of the Art of Online Monitoring and Control of the Coagulation Process. Water 2015, 7, 6574–6597. [Google Scholar] [CrossRef]
- Van Benschoten, J.E.; Jensen, J.N.; Rahman, M.A. Effects of Temperature and pH on Residual Aluminum in Alkaline-Treated Waters. J. Environ. Eng. 1994, 120, 543–559. [Google Scholar] [CrossRef]
- ASTM International. ASTM International. ASTM D2035-19: Standard Practice for Coagulation-Flocculation Jar Test of Water. In Book of Standards; ASTM International: West Conshohocken, PA, USA, 2019; Volume 11.02. [Google Scholar]
- Adgar, A.; Cox, C.S.; Jones, C.A. Enhancement of coagulation control using the streaming current detector. Bioprocess Biosyst. Eng. 2005, 27, 349–357. [Google Scholar] [CrossRef] [PubMed]
- Sibiya, S.M. Evaluation of the Streaming Current Detector (SCD) for Coagulation Control. Procedia Eng. 2014, 70, 1211–1220. [Google Scholar] [CrossRef]
- Edzwald, J.; Kaminski, G.S. A practical method for water plants to select coagulant dosing. J. New Engl. Water Work. Assoc. 2009, 123, 15–31. [Google Scholar]
- Jackson, P.J.; Tomlinson, E.J. Automatic Coagulation Control–Evaluation of Strategies and Techniques. Water Supply 1986, 4, 55–67. [Google Scholar]
- Robinson, W.A. Climate change and extreme weather: A review focusing on the continental United States. J. Air Waste Manag. Assoc. 2021, 71, 1186–1209. [Google Scholar] [CrossRef]
- Bladon, K.D.; Emelko, M.B.; Silins, U.; Stone, M. Wildfire and the future of water supply. Environ. Sci. Technol. 2014, 48, 8936–8943. [Google Scholar] [CrossRef]
- Slavik, I.; Uhl, W. A new data analysis approach to address climate change challenges in drinking water supply. In Proceedings of the IWA DIGITAL World Water Congress, Copenhagen, Denmark, 24 May – 4 June 2021. [Google Scholar]
- Gómez-Martínez, G.; Galiano, L.; Rubio, T.; Prado-López, C.; Redolat, D.; Paradinas Blázquez, C.; Gaitán, E.; Pedro-Monzonís, M.; Ferriz-Sánchez, S.; Añó Soto, M.; et al. Effects of Climate Change on Water Quality in the Jucar River Basin (Spain). Water 2021, 13, 2424. [Google Scholar] [CrossRef]
- Lee, J.M.; Ahn, J.; Kim, Y.D.; Kang, B. Effect of climate change on long-term river geometric variation in Andong Dam watershed, Korea. J. Water Clim. Chang. 2021, 12, 741–758. [Google Scholar] [CrossRef]
- Baxter, C.W.; Stanley, S.J.; Zhang, Q.; Smith, D.W. Developing artificial neural network models of water treatment processes: A guide for utilities. J. Environ. Eng. Sci. 2002, 1, 201–211. [Google Scholar] [CrossRef]
- Griffiths, K.A.; Andrews, R.C. The application of artificial neural networks for the optimization of coagulant dosage. Water Supply 2011, 11, 605–611. [Google Scholar] [CrossRef]
- Santos, F.C.R.d.; Librantz, A.F.H.; Dias, C.G.; Rodrigues, S.G. Intelligent system for improving dosage control. Acta Sci. Technol. 2017, 39, 33. [Google Scholar] [CrossRef]
- Jayaweera, C.D.; Aziz, N. Development and comparison of Extreme Learning machine and multi-layer perceptron neural network models for predicting optimum coagulant dosage for water treatment. J. Phys. Conf. Ser. 2018, 1123, 012032. [Google Scholar] [CrossRef]
- Fan, K.; Xu, Y. Intelligent control system for flocculation of water supply. J. Phys. Conf. Ser. 2021, 1939, 012064. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Kaufman, S.; Rosset, S.; Perlich, C.; Stitelman, O. Leakage in data mining. ACM Trans. Knowl. Discov. Data 2012, 6, 1–21. [Google Scholar] [CrossRef]
- Snijders, T.A.B. On Cross-Validation for Predictor Evaluation in Time Series. In Proceedings of the On Model Uncertainty and its Statistical Implications, Groningen, The Netherlands, 25–26 September 1986; pp. 56–69. [Google Scholar]
- Bergmeir, C.; Benítez, J.M. On the use of cross-validation for time series predictor evaluation. Inf. Sci. 2012, 191, 192–213. [Google Scholar] [CrossRef]
- Meteorological Service of Canada. Canadian Climate Normals 1981–2010 Station Data: Montreal/Pierre Elliott Trudeau Intl A; Meteorological Service of Canada: Dorval, QC, Canada, 2023. [Google Scholar]
- Veolia Water Technologies. ACTIFLO® HCS. Available online: https://www.veoliawatertechnologies.com/en/solutions/technologies/actiflo-hcs (accessed on 16 May 2023).
- Ministère de l’Environnement de la Lutte Contre les Changements Climatiques de la Faune et des Parcs. Banque de Données sur la Qualité du Milieu Aquatique. 2002. Available online: https://www.environnement.gouv.qc.ca/eau/atlas/documents/conv/ZGIESL/2002/Haut-St-Laurent_et_Grand_Montreal_2000-2002.xlsx (accessed on 26 March 2024).
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; Van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation. arXiv 2014, arXiv:1406.1078. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. In Proceedings of the NIPS 2014 Deep Learning and Representation Learning Workshop, Montreal, Quebec, Canada, 12–13 December 2014. arXiv 2014, arXiv:1412:3555. [Google Scholar] [CrossRef]
- Williams, R.J.; Zipser, D. A Learning Algorithm for Continually Running Fully Recurrent Neural Networks. Neural Comput. 1989, 1, 270–280. [Google Scholar] [CrossRef]
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Zhang, K.; Achari, G.; Li, H.; Zargar, A.; Sadiq, R. Machine learning approaches to predict coagulant dosage in water treatment plants. Int. J. Syst. Assur. Eng. Manag. 2013, 4, 205–214. [Google Scholar] [CrossRef]
- Godo-Pla, L.; Emiliano, P.; Valero, F.; Poch, M.; Sin, G.; Monclús, H. Predicting the oxidant demand in full-scale drinking water treatment using an artificial neural network: Uncertainty and sensitivity analysis. Process Saf. Environ. Prot. 2019, 125, 317–327. [Google Scholar] [CrossRef]
- Wang, D.; Wu, J.; Deng, L.; Li, Z.; Wang, Y. A real-time optimization control method for coagulation process during drinking water treatment. Nonlinear Dyn. 2021, 105, 3271–3283. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]



| MAE (NTU) | MLP | LSTM | GRU |
|---|---|---|---|
| Range (best–worst) | 0.046–0.157 | 0.046–0.063 | 0.044–0.054 |
| Mean | 0.070 | 0.050 | 0.047 |
| Median | 0.055 | 0.049 | 0.045 |
| Standard deviation | 0.033 | 0.005 | 0.003 |
| MAE (NTU) | MLP | LSTM | GRU |
|---|---|---|---|
| Range (best–worst) | 0.040–0.187 | 0.035–0.050 | 0.035–0.040 |
| Mean | 0.070 | 0.040 | 0.037 |
| Median | 0.047 | 0.040 | 0.037 |
| Standard deviation | 0.046 | 0.004 | 0.002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jakovljevic, A.; Charlin, L.; Barbeau, B. Applying Recurrent Neural Networks and Blocked Cross-Validation to Model Conventional Drinking Water Treatment Processes. Water 2024, 16, 1042. https://doi.org/10.3390/w16071042
Jakovljevic A, Charlin L, Barbeau B. Applying Recurrent Neural Networks and Blocked Cross-Validation to Model Conventional Drinking Water Treatment Processes. Water. 2024; 16(7):1042. https://doi.org/10.3390/w16071042
Chicago/Turabian StyleJakovljevic, Aleksandar, Laurent Charlin, and Benoit Barbeau. 2024. "Applying Recurrent Neural Networks and Blocked Cross-Validation to Model Conventional Drinking Water Treatment Processes" Water 16, no. 7: 1042. https://doi.org/10.3390/w16071042
APA StyleJakovljevic, A., Charlin, L., & Barbeau, B. (2024). Applying Recurrent Neural Networks and Blocked Cross-Validation to Model Conventional Drinking Water Treatment Processes. Water, 16(7), 1042. https://doi.org/10.3390/w16071042








