Reducing Water Conveyance Footprint through an Advanced Optimization Framework
Abstract
1. Introduction
- A nonlinear chaotic honey badger algorithm, i.e., NCHBA, incorporating a nonlinear control parameter and a chaotic map to strike a balance between exploration and exploitation, is proposed. The efficiency of NCHBA is validated by solving a high-dimensional pump scheduling problem.
- A new multi-objective variant of NCHBA is proposed, and its performance is assessed using four ZDT benchmark functions.
- The proposed multi-objective algorithm is utilized to optimize the pump scheduling program of a large WDS to minimize the energy consumption and footprint of pumping stations, quality risk, and nodal pressure. The optimal compromise solution is determined through the TOPSIS method.
2. Materials and Methods
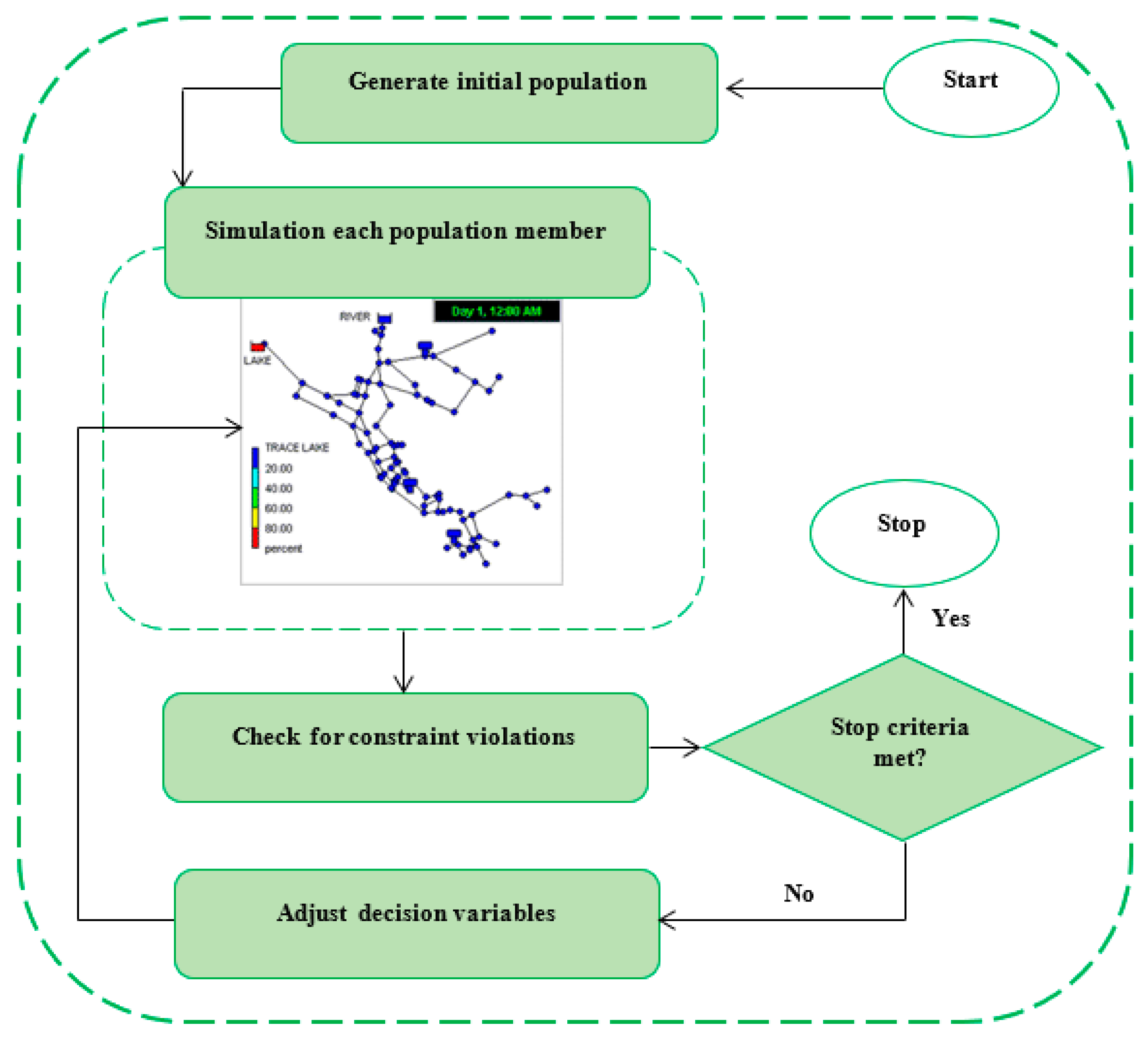
2.1. Optimization Process and Problem Formulation
2.1.1. Objective Functions
2.1.2. Constraints
2.2. Optimization Model
2.2.1. Honey Badger Algorithm
2.2.2. Improved Honey Badger Algorithm
- Utilizing the chaotic maps instead of random numbers.
- Utilizing a nonlinear parameter to create a good balance between the exploitation and exploration phases.
2.2.3. Multi-Objective NCHBA
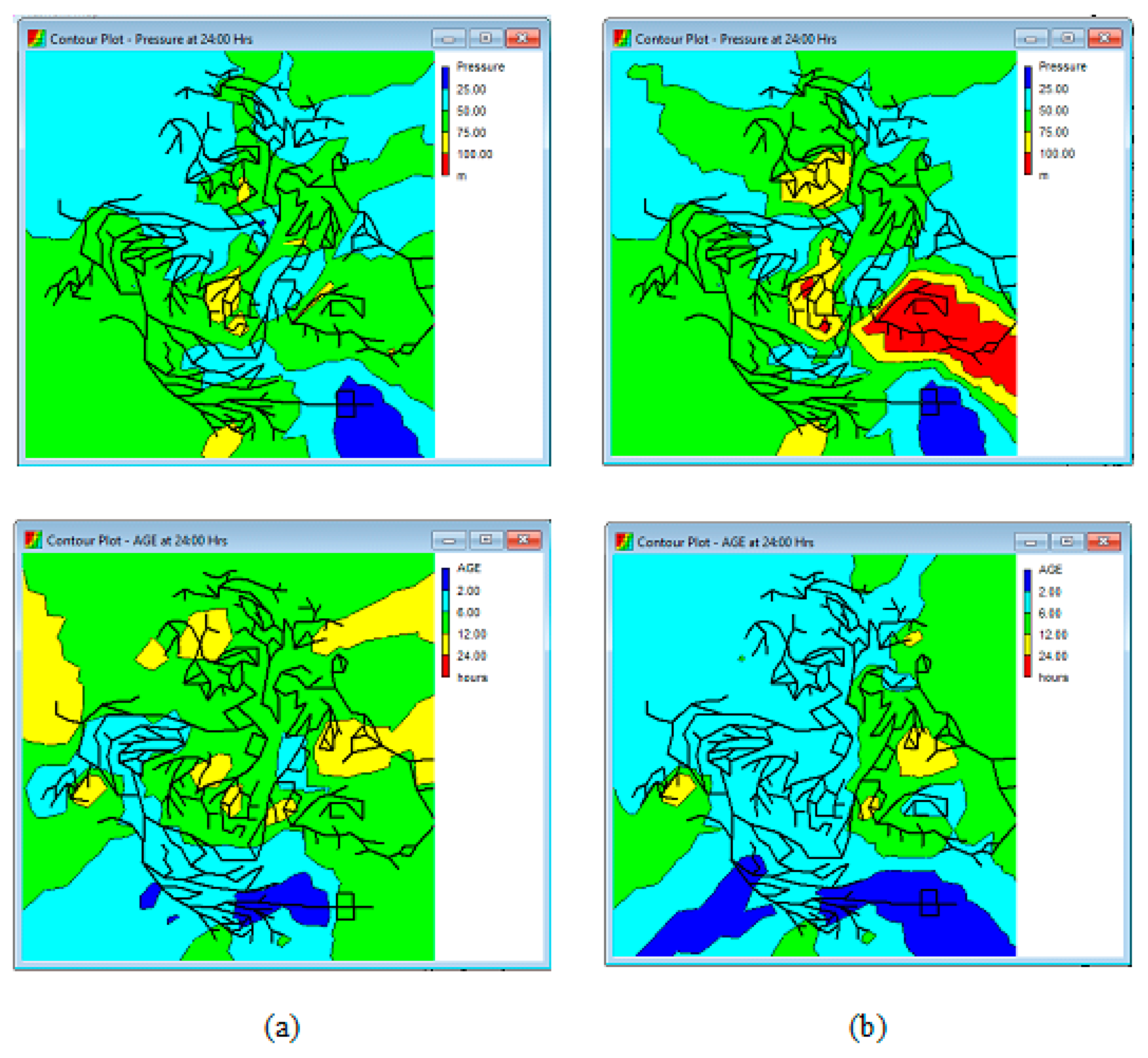
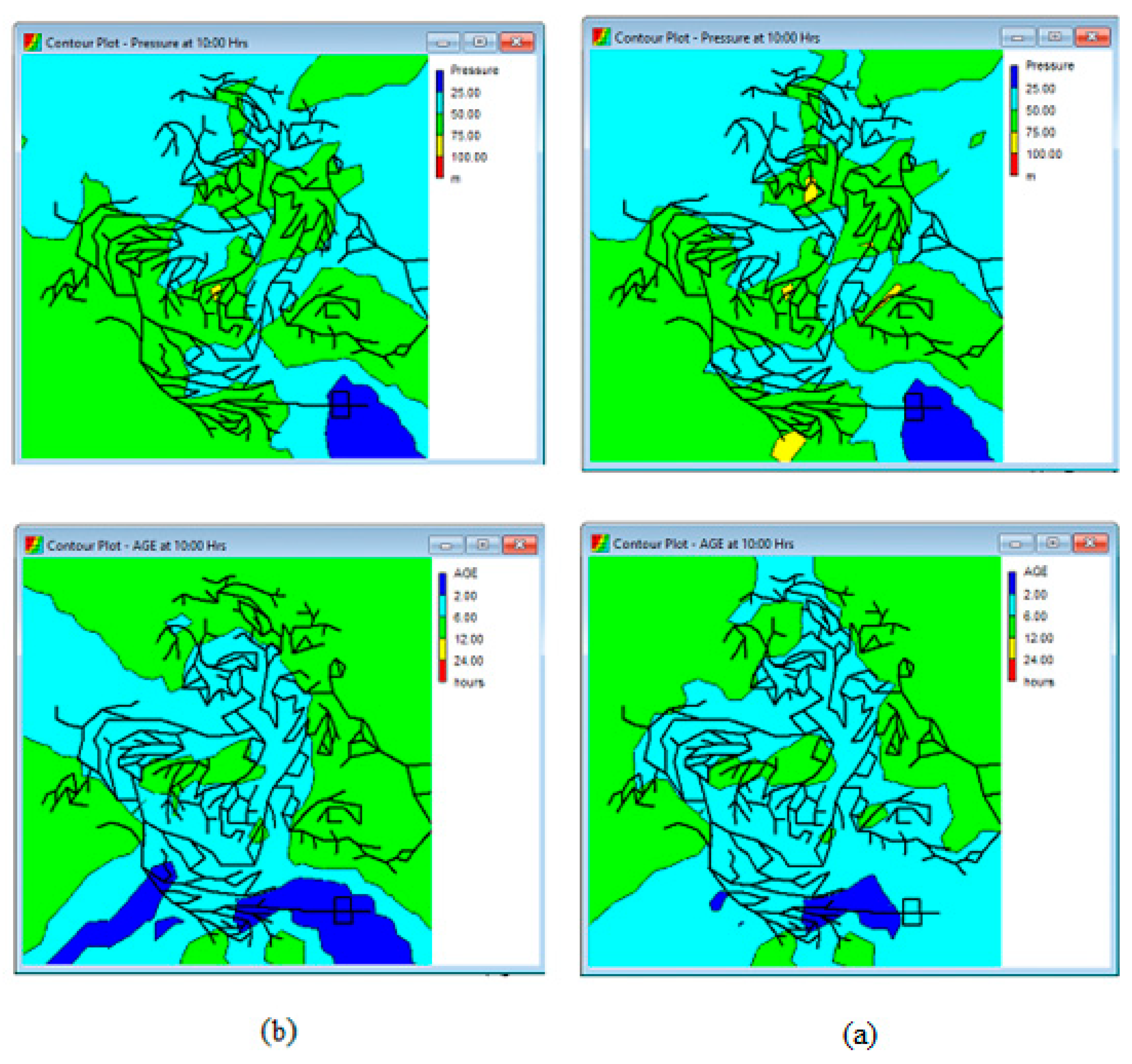
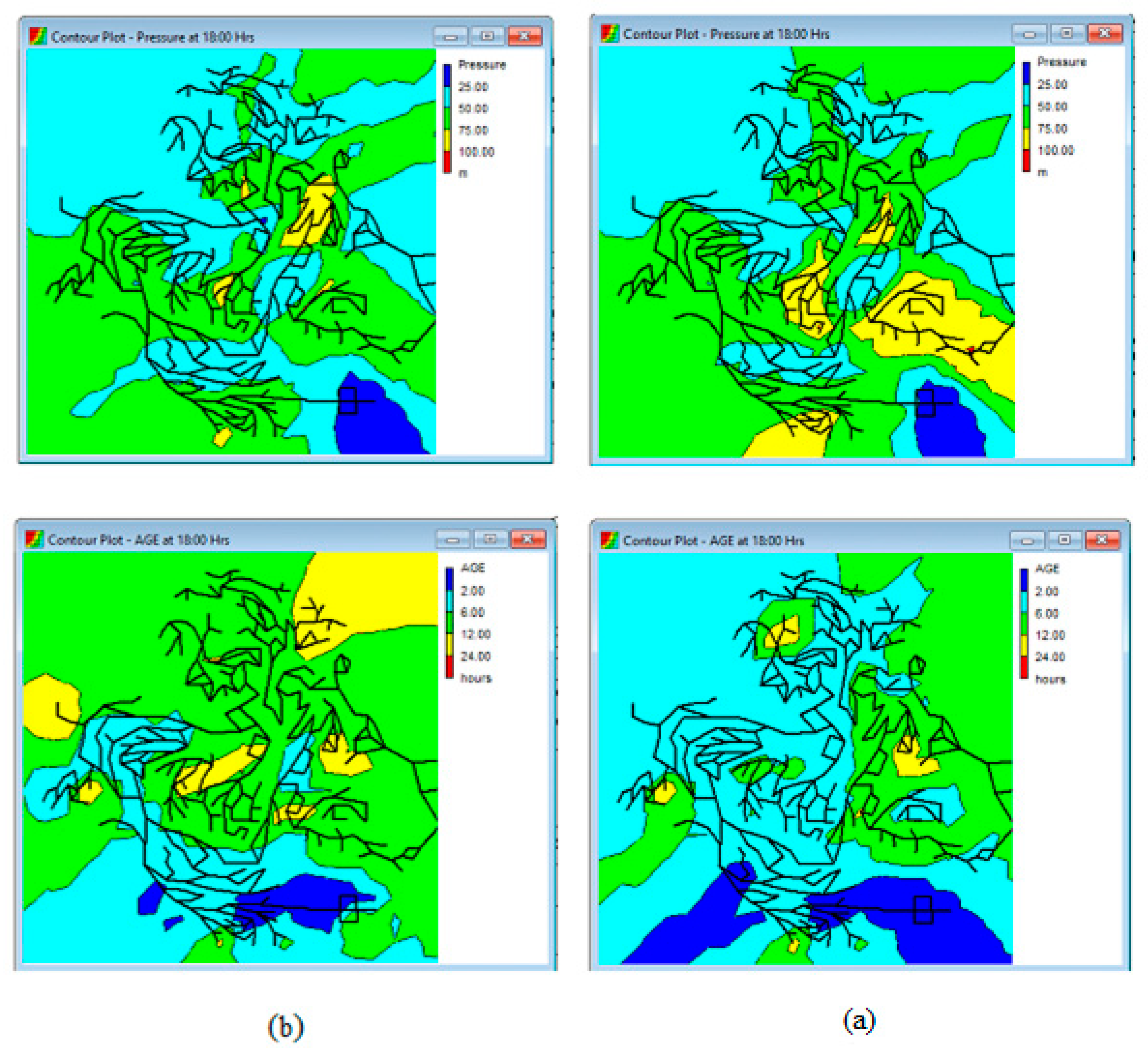
3. Results and Implementation
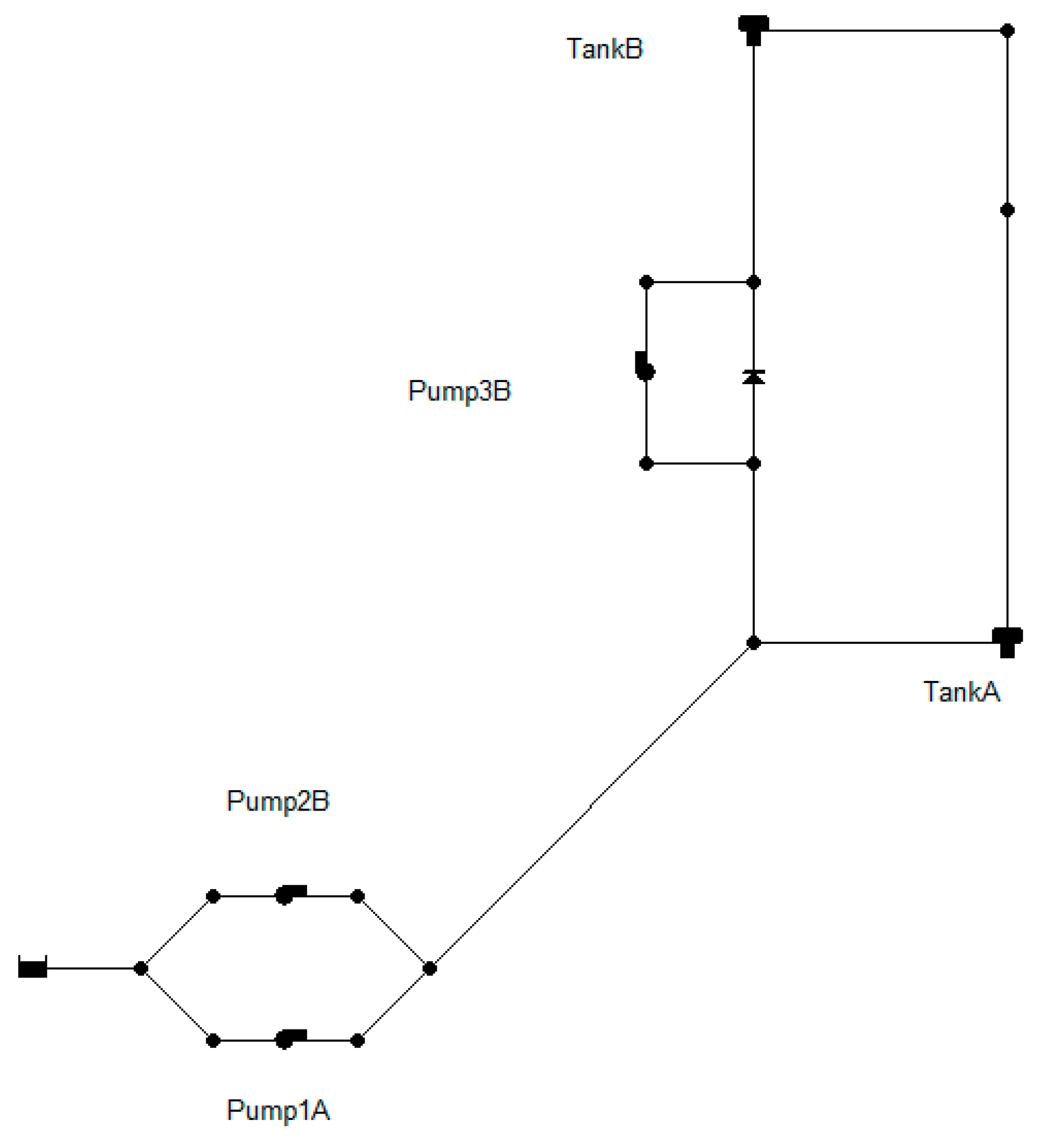
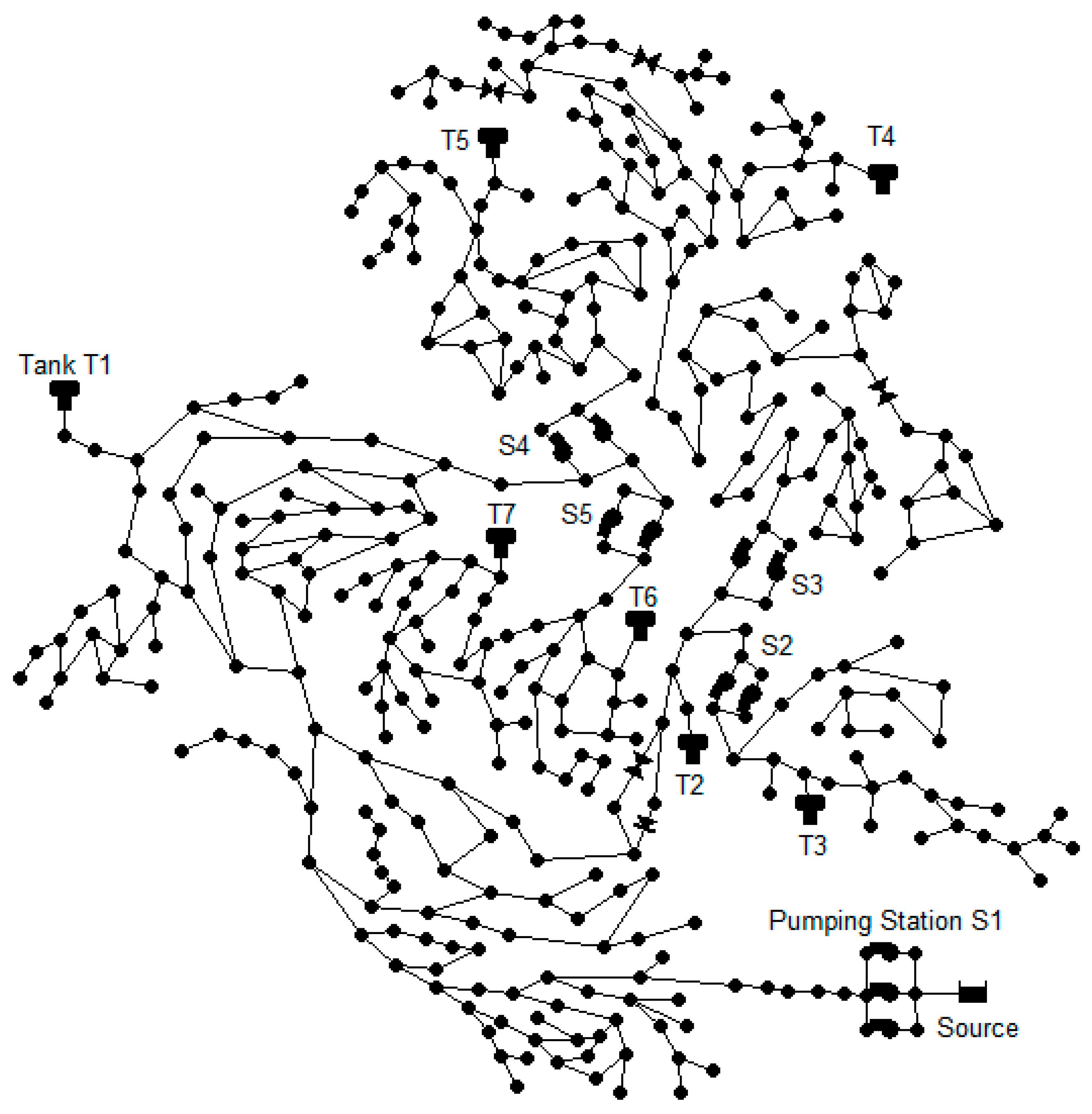
3.1. Model Validation
3.2. Single Objective NCHBA for Energy Optimization
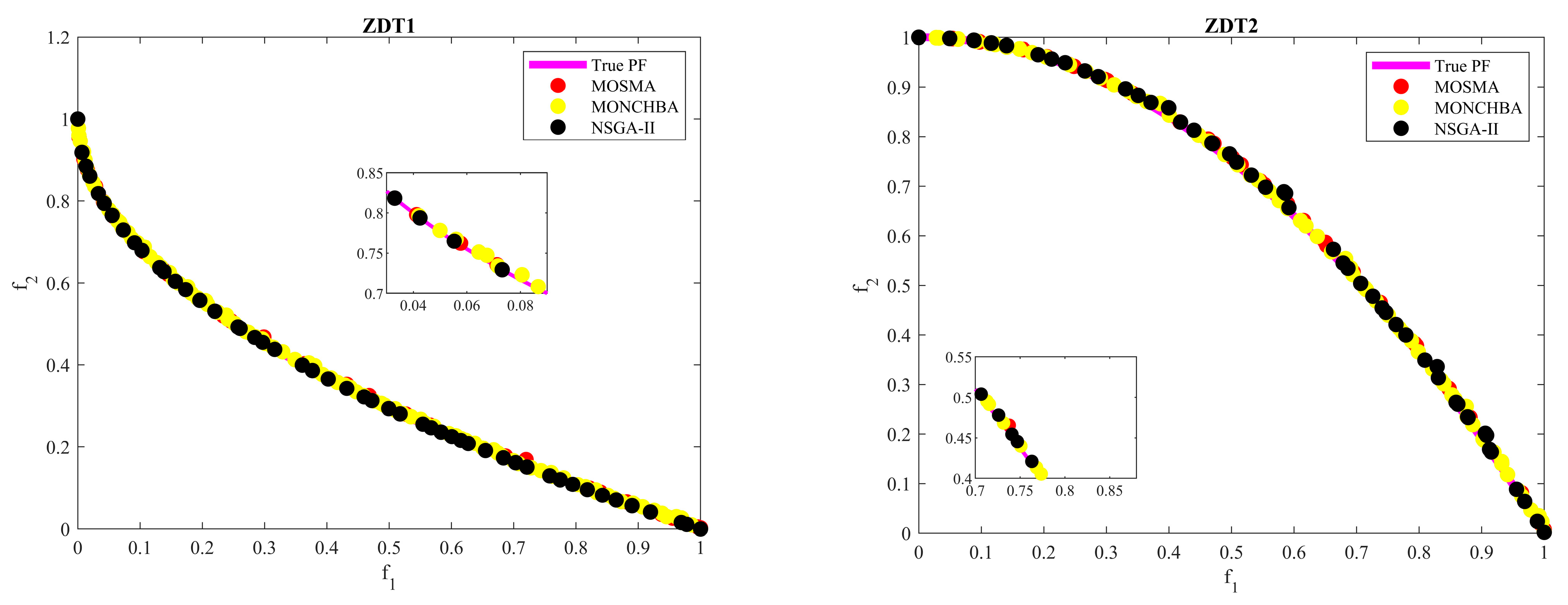
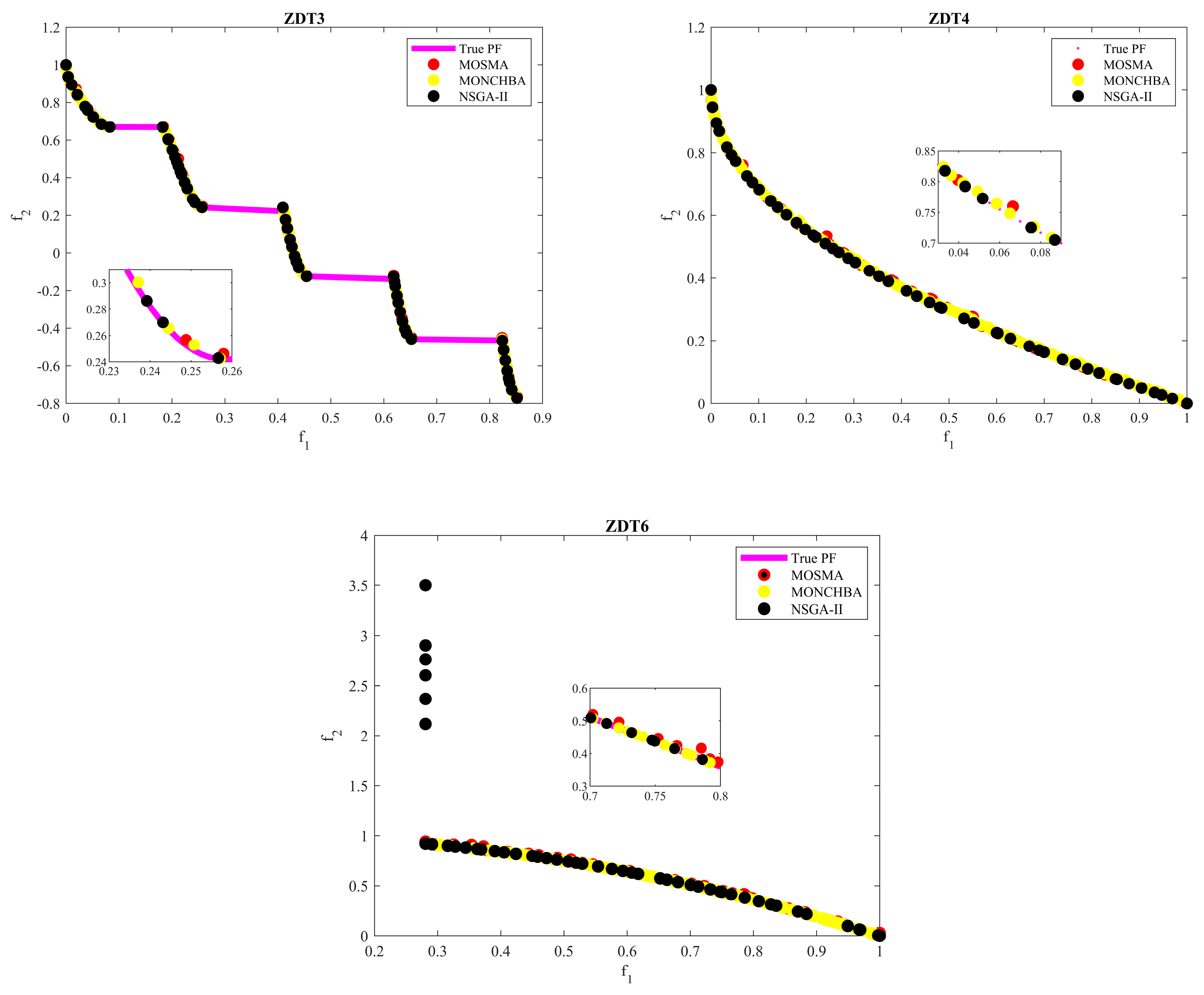
3.3. Multi-Objective NCHBA for Benchmark Problems
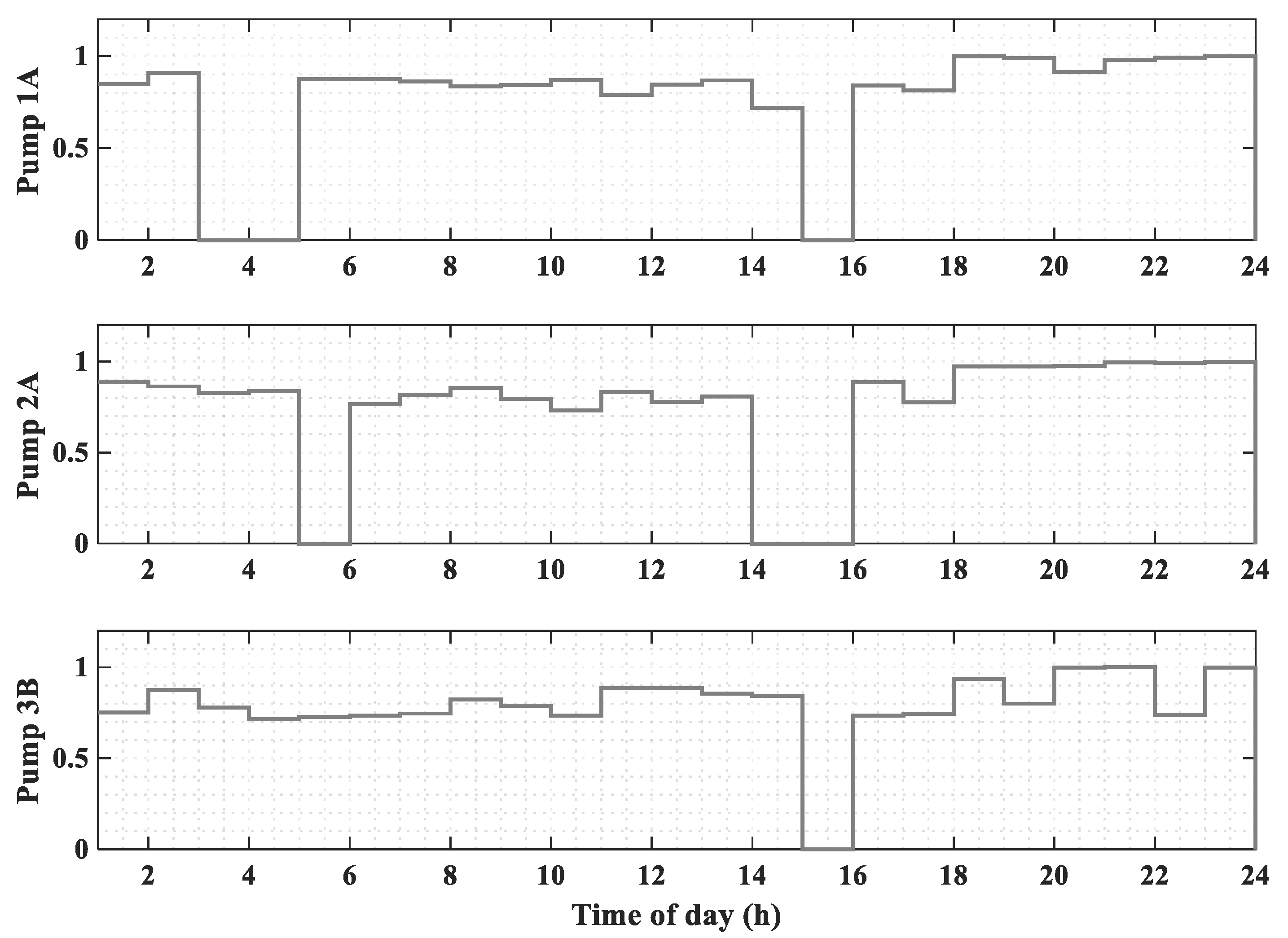
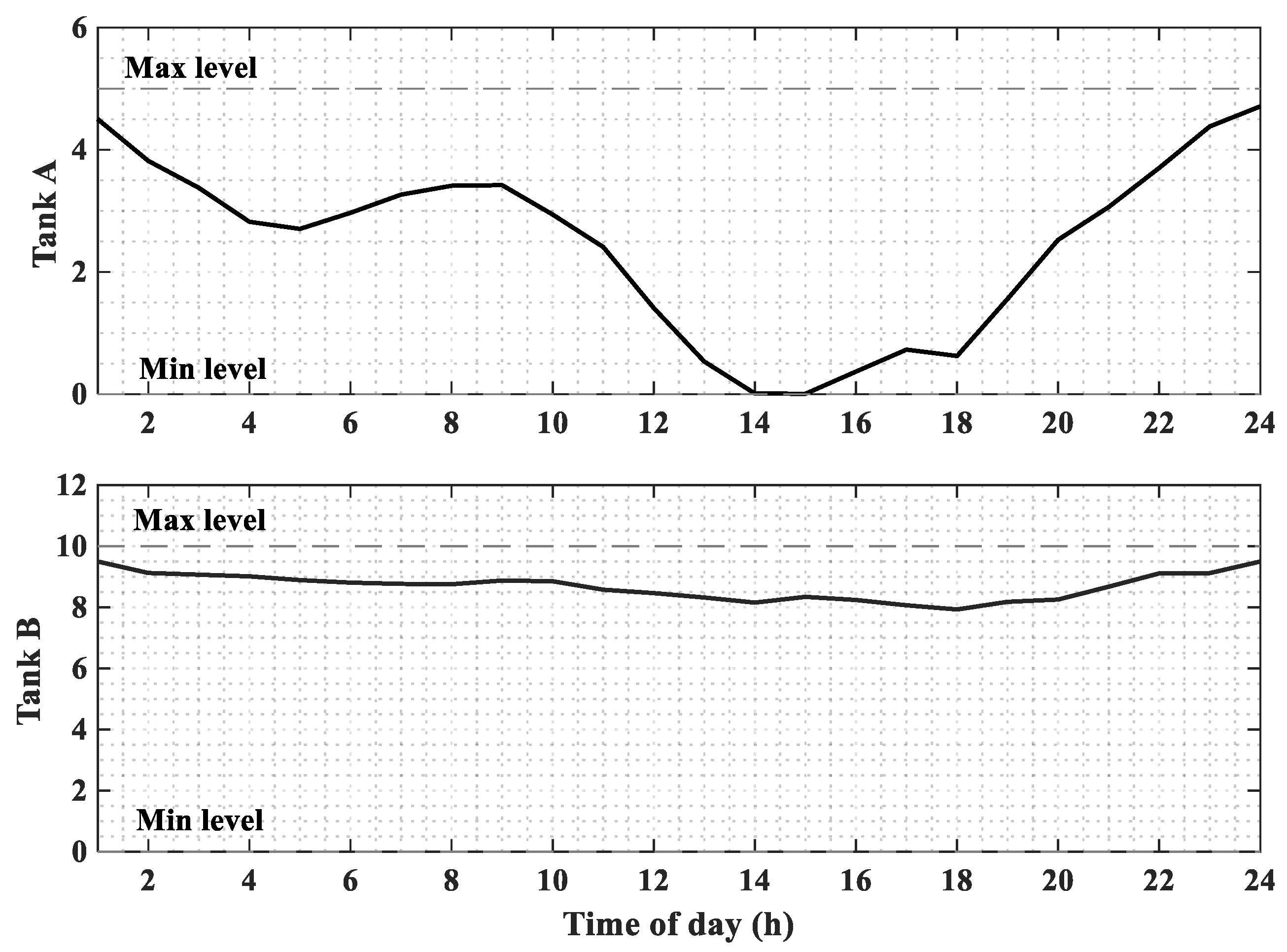
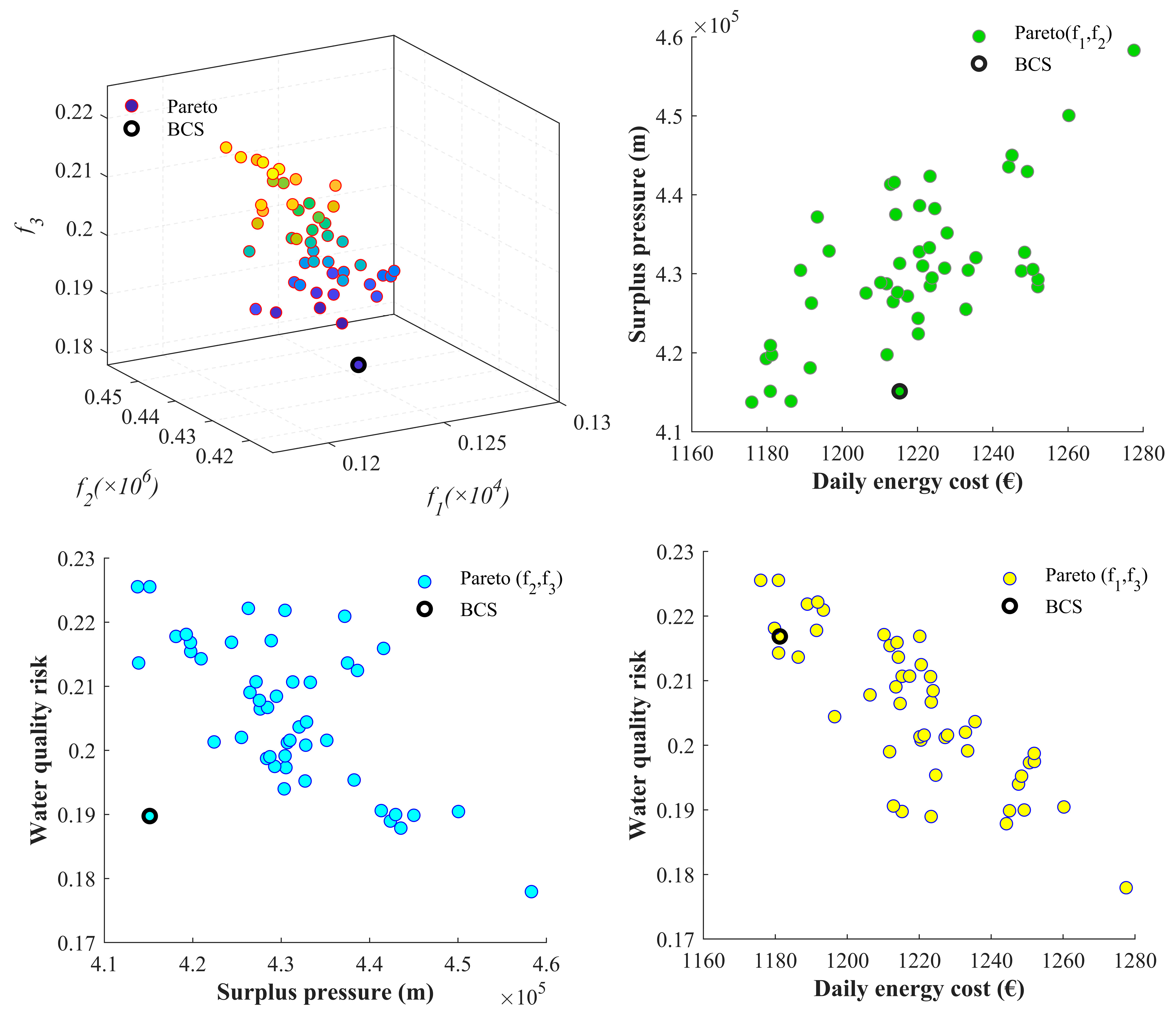
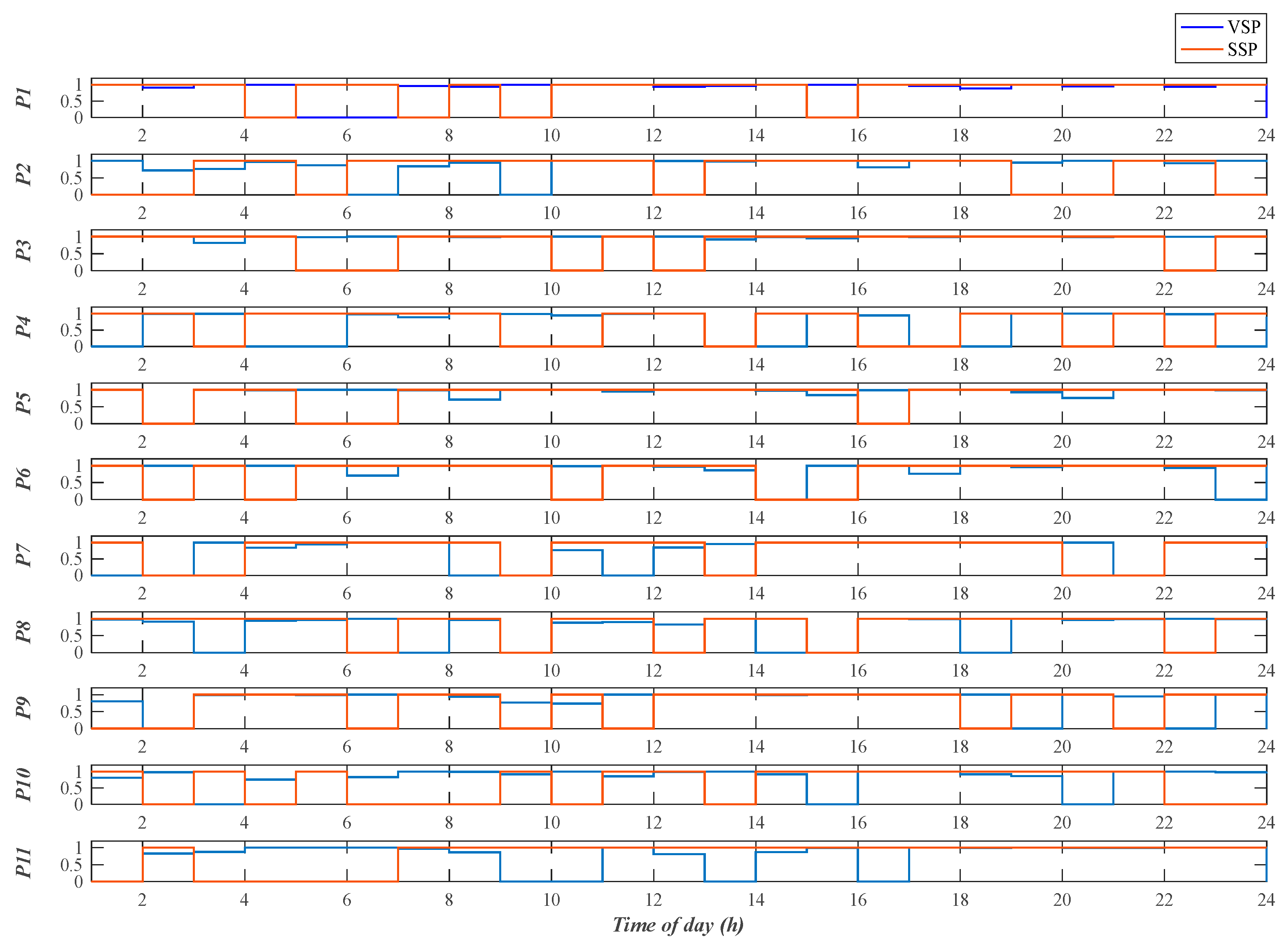
3.4. Multi-Objective NCHBA for Energy Optimization
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Notation and List of Acronyms
| Flow rate between nodes i and j | DMA | District mater area | |
| Number of pipes meeting at node j | FSP | Fixed-speed pump | |
| Nodal demand at node j | VSP | Variable-speed pump | |
| GA | Genetic Algorithm | ||
| Head added by pumps in pipe j | LP | Linear programming | |
| Number of pipes included in loop i | NLP | Nonlinear programming | |
| Head loss between node i and j | DP | Dynamic programming | |
| Pipe length | ACO | Ant Colony Optimization | |
| Pipe diameter | DA | Dragonfly Algorithm | |
| C | Hazen–Williams coefficient | NSGA-II | Non-Dominated Sorting Genetic Algorithm |
| Flow through pump during each time step t in pump n | HBA | Honey badger algorithm | |
| Total dynamic head during each time step t in pump n | WDS | Water distribution system | |
| Electricity tariff at time t (USD/kWh) | PDSM | Pressure-driven simulation method | |
| Status of pump n as being off or on at time t | RUN | Runge–Kutta Optimization Algorithm | |
| Length of a time interval t | NDS | Non-dominated sorting | |
| Efficiency of pump n during each time step t | CD | Crowding distance | |
| Peak discharge through the pump n | SMA | Slim Mould Algorithm | |
| ED | Demand charge (USD/kW) | AO | Aquila Optimizer |
| Pressure at node i in time t | HGA | Hunger Games search | |
| Minimum required pressure at node i | EA | Evolutionary algorithm | |
| Required demand for node i at time t | IGD NCHBA | Inverted generation distance Nonlinear chaotic honey badger algorithm | |
| Available discharge node i at time t | |||
| FA | Firefly algorithm |
Appendix A
Appendix A.1. EPANET Hydraulic Simulation Model
- Continuity at node j (j = 1 to N – 1)
- Conservation of energy for loop i (i = 1 to NL)
Appendix A.2. Modeling Variable-Speed Pumps
Appendix B
Developed Algorithm
| Algorithm A1. The pseudo code of NCHBA |
| Step 1: Initialize parameters (i.e., N, , , C) Step 2: Generate random solutions Step 3: Evaluate the fitness of each search agent using objective function and save best solution ) while do Update the decreasing factor using (18). Generate Chaotic number. Calculate using Equation (24). for to do Calculate the intensity using Equation (17). if then Update the position using Equation (22). Else Update the position using Equation (23). end if Evaluate new position and assign to . if then Set and . end if if then Set and . end if end for end while Stop criteria satisfied. Return . |
References
- Ang, W.K.; Jowitt, P.W. Some new insights on informational entropy for water distribution networks. Eng. Optim. 2005, 37, 277–289. [Google Scholar] [CrossRef]
- Latifi, M.; Farahi Moghadam, K.; Naeeni, S.T. Pressure and energy management in water distribution networks through optimal use of Pump-As-Turbines along with pressure-reducing valves. J. Water Resour. Plan. Manag. 2021, 147, 04021039. [Google Scholar] [CrossRef]
- Gheisi, A.; Naser, G. Multistate reliability of water-distribution systems: Comparison of surrogate measures. J. Water Resour. Plan. Manag. 2015, 141, 04015018. [Google Scholar] [CrossRef]
- Van Zyl, J.E.; Savic, D.A.; Walters, G.A. Operational optimization of water distribution systems using a hybrid genetic algorithm. J. Water Resour. Plan. Manag. 2004, 130, 160–170. [Google Scholar] [CrossRef]
- Jowitt, P.W.; Germanopoulos, G. Optimal pump scheduling in water-supply networks. J. Water Resour. Plan. Manag. 1992, 118, 406–422. [Google Scholar] [CrossRef]
- Ormsbee, L.E.; Walski, T.M.; Chase, D.V.; Sharp, W.W. Methodology for improving pump operation efficiency. J. Water Resour. Plan. Manag. 1989, 115, 148–164. [Google Scholar] [CrossRef]
- Chase, D.V.; Ormsbee, L.E. Computer-Generated Pumping Schedules for Satisfying Operational Objectives. J. Am. Water Work. Assoc. 1993, 85, 54–61. [Google Scholar] [CrossRef]
- Lansey, K.E.; Awumah, K. Optimal pump operations considering pump switches. J. Water Resour. Plan. Manag. 1994, 120, 17–35. [Google Scholar] [CrossRef]
- Nitivattananon, V.; Sadowski, E.C.; Quimpo, R.G. Optimization of water supply system operation. J. Water Resour. Plan. Manag. 1996, 122, 374–384. [Google Scholar] [CrossRef]
- Pasha, M.F.; Lansey, K. Strategies to develop warm solutions for real-time pump scheduling for water distribution systems. Water Resour. Manag. 2014, 28, 3975–3987. [Google Scholar] [CrossRef]
- Afshar, M.H.; Rajabpour, R. Application of local and global particle swarm optimization algorithms to optimal design and operation of irrigation pumping systems. Irrig. Drain. J. Int. Comm. Irrig. Drain. 2009, 58, 321–331. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Riasi, A.; Kandi, A. Selection optimization of variable speed pump as turbine (PAT) for energy recovery and pressure management. Energy Convers. Manag. 2021, 227, 113586. [Google Scholar] [CrossRef]
- Soltani, M.; Nabat, M.H.; Razmi, A.R.; Dusseault, M.B.; Nathwani, J. A comparative study between ORC and Kalina based waste heat recovery cycles applied to a green compressed air energy storage (CAES) system. Energy Convers. Manag. 2020, 222, 113203. [Google Scholar] [CrossRef]
- Li, M.; Zhao, L.; Zhang, C.; Liu, Y.; Fu, Q. Optimization of agricultural resources in water-energy-food nexus in complex environment: A perspective on multienergy coordination. Energy Convers. Manag. 2022, 258, 115537. [Google Scholar] [CrossRef]
- Barbarelli, S.; Amelio, M.; Florio, G. Experimental activity at test rig validating correlations to select pumps running as turbines in microhydro plants. Energy Convers. Manag. 2017, 149, 781–797. [Google Scholar] [CrossRef]
- Lydon, T.; Coughlan, P.; McNabola, A. Pressure management and energy recovery in water distribution networks: Development of design and selection methodologies using three pump-as-turbine case studies. Renew. Energy 2017, 114, 1038–1050. [Google Scholar] [CrossRef]
- Moazeni, F.; Khazaei, J. Optimal operation of water-energy microgrids; a mixed integer linear programming formulation. J. Clean. Prod. 2020, 275, 122776. [Google Scholar] [CrossRef]
- Moazeni, F.; Khazaei, J.; Mendes, J.P.P. Maximizing energy efficiency of islanded micro water-energy nexus using co-optimization of water demand and energy consumption. Appl. Energy 2020, 266, 114863. [Google Scholar] [CrossRef]
- Bagirov, A.M.; Barton, A.F.; Mala-Jetmarova, H.; Al Nuaimat, A.; Ahmed, S.T.; Sultanova, N.; Yearwood, J. An algorithm for minimization of pumping costs in water distribution systems using a novel approach to pump scheduling. Math. Comput. Model. 2013, 57, 873–886. [Google Scholar] [CrossRef]
- López-Ibáñez, M. Operational Optimisation of Water Distribution Networks. Ph.D. Thesis, Edinburgh Napier University, Edinburgh, UK, 2009. [Google Scholar]
- Jafari-Asl, J.; Azizyan, G.; Monfared, S.A.H.; Rashki, M.; Andrade-Campos, A.G. An enhanced binary dragonfly algorithm based on a V-shaped transfer function for optimization of pump scheduling program in water supply systems (case study of Iran). Eng. Fail. Anal. 2021, 123, 105323. [Google Scholar] [CrossRef]
- Farmani, R.; Walters, G.A.; Savic, D.A. Trade-off between total cost and reliability for Anytown water distribution network. J. Water Resour. Plan. Manag. 2005, 131, 161–171. [Google Scholar] [CrossRef]
- Abiodun, F.T.; Ismail, F.S. Pump scheduling optimization model for water supply system using AWGA. In Proceedings of the 2013 IEEE Symposium on Computers & Informatics (ISCI), Langkawi, Malaysia, 7–9 April 2013; pp. 12–17. [Google Scholar]
- Kurek, W.; Ostfeld, A. Multi-objective optimization of water quality, pumps operation, and storage sizing of water distribution systems. J. Environ. Manag. 2013, 115, 189–197. [Google Scholar] [CrossRef]
- Makaremi, Y.; Haghighi, A.; Ghafouri, H.R. Optimization of pump scheduling program in water supply systems using a self-adaptive NSGA-II; a review of theory to real application. Water Resour. Manag. 2017, 31, 1283–1304. [Google Scholar] [CrossRef]
- Price, E.; Ostfeld, A. Optimal pump scheduling in water distribution systems using graph theory under hydraulic and chlorine constraints. J. Water Resour. Plan. Manag. 2016, 142, 04016037. [Google Scholar] [CrossRef]
- Mala-Jetmarova, H.; Barton, A.; Bagirov, A. Exploration of the trade-offs between water quality and pumping costs in optimal operation of regional multiquality water distribution systems. J. Water Resour. Plan. Manag. 2015, 141, 04014077. [Google Scholar] [CrossRef]
- Castro-Gama, M.; Pan, Q.; Lanfranchi, E.A.; Jonoski, A.; Solomatine, D.P. Pump scheduling for a large water distribution network. Milan, Italy. Procedia Eng. 2017, 186, 436–443. [Google Scholar] [CrossRef]
- Yan, P.; Zhang, Z.; Lei, X.; Hou, Q.; Wang, H. A multi-objective optimal control model of cascade pumping stations considering both cost and safety. J. Clean. Prod. 2022, 345, 131171. [Google Scholar] [CrossRef]
- Guo, S.; Song, G.; Li, M.; Zhao, X.; He, Y.; Kurban, A.; Ji, W.; Wang, J. Multi-objective bi-level quantity regulation scheduling method for electric-thermal integrated energy system considering thermal and hydraulic transient characteristics. Energy Convers. Manag. 2022, 253, 115147. [Google Scholar] [CrossRef]
- Jafari-Asl, J.; Seghier, M.E.A.B.; Ohadi, S.; van Gelder, P. Efficient method using Whale Optimization Algorithm for reliability-based design optimization of labyrinth spillway. Appl. Soft Comput. 2021, 101, 107036. [Google Scholar] [CrossRef]
- Rad, M.J.G.; Ohadi, S.; Jafari-Asl, J.; Vatani, A.; Ahmadabadi, S.A.; Correia, J.A. GNDO-SVR: An efficient surrogate modeling approach for reliability-based design optimization of concrete dams. Structures 2022, 35, 722–733. [Google Scholar] [CrossRef]
- Rahmanshahi, M.; Jafari-Asl, J.; Fathi-Moghadam, M.; Ohadi, S.; Mirjalili, S. Metaheuristic learning algorithms for accurate prediction of hydraulic performance of porous embankment weirs. Appl. Soft Comput. 2024, 151, 111150. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET 2: User’s Manual; U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2000. [Google Scholar]
- Coelho, B. Energy Efficiency of Water Supply Systems Using Optimisation Techniques and Micro-Hydroturbines. Ph.D. Thesis, Universidade de Aveiro, Aveiro, Portugal, 2016. [Google Scholar]
- Shokoohi, M.; Tabesh, M.; Nazif, S.; Dini, M. Water quality based multi-objective optimal design of water distribution systems. Water Resour. Manag. 2017, 31, 93–108. [Google Scholar] [CrossRef]
- Wagner, J.M.; Shamir, U.; Marks, D.H. Water distribution reliability: Simulation methods. J. Water Resour. Plan. Manag. 1988, 114, 276–294. [Google Scholar] [CrossRef]
- Dehkordi, A.A.; Sadiq, A.S.; Mirjalili, S.; Ghafoor, K.Z. Nonlinear-based chaotic harris hawks optimizer: Algorithm and internet of vehicles application. Appl. Soft Comput. 2021, 109, 107574. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Houssein, E.H.; Çelik, E.; Mahdy, M.A.; Ghoniem, R.M. Self-adaptive Equilibrium Optimizer for solving global, combinatorial, engineering, and Multi-Objective problems. Expert Syst. Appl. 2022, 195, 116552. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-Qaness, M.A.; Gandomi, A.H. Aquila optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, H.; Heidari, A.A.; Gandomi, A.H. Hunger games search: Visions, conception, implementation, deep analysis, perspectives, and towards performance shifts. Expert Syst. Appl. 2021, 177, 114864. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Heidari, A.A.; Gandomi, A.H.; Chu, X.; Chen, H. RUN beyond the metaphor: An efficient optimization algorithm based on Runge Kutta method. Expert Syst. Appl. 2021, 181, 115079. [Google Scholar] [CrossRef]
- Bagirov, A.; Ahmed, S.; Barton, A.; Mala-Jetmarova, H.; Al Nuaimat, A.; Sultanova, N. Comparison of metaheuristic algorithms for pump operation optimization. In Proceedings of the 14th Water Distribution Systems Analysis Conference 2012, Adelaide, SA, Australia, 24–27 September 2012; pp. 886–896. [Google Scholar]
- López-Ibáñez, M.; Prasad, T.D.; Paechter, B. Representations and evolutionary operators for the scheduling of pump operations in water distribution networks. Evol. Comput. 2011, 19, 429–467. [Google Scholar] [CrossRef]
- Hashemi, S.S.; Tabesh, M.; Ataeekia, B. Ant-colony optimization of pumping schedule to minimize the energy cost using variable-speed pumps in water distribution networks. Urban Water J. 2014, 11, 335–347. [Google Scholar] [CrossRef]
- Li, L.L.; Ren, X.Y.; Tseng, M.L.; Wu, D.S.; Lim, M.K. Performance evaluation of solar hybrid combined cooling, heating and power systems: A multi-objective arithmetic optimization algorithm. Energy Convers. Manag. 2022, 258, 115541. [Google Scholar] [CrossRef]
- Mellal, M.A.; Zio, E.; Pecht, M. Multi-objective reliability and cost optimization of fuel cell vehicle system with fuzzy feasibility. Inf. Sci. 2023, 640, 119112. [Google Scholar] [CrossRef]


| Chebyshev | Circle | Gauss-Mouse | Iterative | Logistic | Sine | Singer | Sinusoidal | Tent | HBA | |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| F2 | 4.02 × 10−298 | 9.50 × 10−271 | 1.48 × 10−322 | 4.70 × 10−290 | 1.20 × 10−291 | 1.62 × 10−300 | 1.40 × 10275 | 1.17 × 10−247 | 3.70 × 10−273 | 4.18 × 10−169 |
| F3 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.30 × 10−250 |
| F4 | 4.55 × 10−295 | 2.12 × 10−271 | 2.09 × 10−320 | 3.49 × 10−291 | 3.35 × 10−296 | 1.50 × 10−299 | 3.80 × 10−276 | 2.89 × 10−244 | 7.26 × 10−265 | 5.32 × 10−143 |
| F5 | −3.10 | −3.32 | −3.17 | −3.20 | −3.32 | −3.32 | −3.20 | −3.32 | −2.91 | −3.13 |
| F6 | −1.02 × 10 | −1.02 × 10 | −4.82 × 10 | −1.02 × 10 | −1.02 × 10 | −1.01 × 10 | −1.02 × 10 | −1.02 × 10 | −8.75 | −1.02 × 10 |
| F7 | 8.75 × 10−5 | 1.04 × 10−5 | 6.12 × 10−6 | 1.48 × 10−4 | 3.63 × 10−5 | 8.62 × 10−5 | 7.72 × 10−5 | 3.07 × 10−5 | 1.44 × 10−5 | 6.47 × 10−5 |
| F8 | 3.90 × 10−1 | 3.90 × 10−1 | 3.90 × 10−1 | 3.90 × 10−1 | 3.90 × 10−1 | 3.90 × 10−1 | 3.90 × 10−1 | 3.90 × 10−1 | 3.90 × 10−1 | 3.90 × 10−1 |
| F9 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| F10 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 |
| F11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| F12 | −1.04 × 10 | −1.04 × 10 | −1.73 | −1.04 × 10 | −1.04 × 10 | −1.04 × 10 | −1.04 × 10 | −1.04 × 10 | −1.02 × 10 | −1.04 × 10 |
| F13 | −1.05 × 10 | −1.05 × 10 | −1.05 × 10 | −1.05 × 10 | −1.05 × 10 | −1.05 × 10 | −1.05 × 10 | −1.05 × 10 | −1.05 × 10 | −1.05 × 10 |
| Best | 0.00 | 0.00 | 4.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Algorithm | Parameter |
|---|---|
| AO | |
| HGA | |
| Run | |
| SMA | = [2 0] |
| HBA | |
| NCHBA | C (Nonlinear control parameter) |
| No. Run | AO | HGA | Run | SMA | HBA | NCHBA |
|---|---|---|---|---|---|---|
| 1 | 360.627 | 310.873 | 299.894 | 300.080 | 281.745 | 261.891 |
| 2 | 361.164 | 303.752 | 300.279 | 300.087 | 301.290 | 249.798 |
| 3 | 360.191 | 301.465 | 301.207 | 299.416 | 284.834 | 266.977 |
| 5 | 350.543 | 306.884 | 291.234 | 297.725 | 300.661 | 259.558 |
| 6 | 359.868 | 298.520 | 295.697 | 299.458 | 316.968 | 260.232 |
| 7 | 359.938 | 302.123 | 290.906 | 284.270 | 295.006 | 259.945 |
| 8 | 380.171 | 308.970 | 304.920 | 299.252 | 308.427 | 263.015 |
| 9 | 358.250 | 299.807 | 290.167 | 299.743 | 300.812 | 260.346 |
| 10 | 361.700 | 310.898 | 308.929 | 300.279 | 324.785 | 264.362 |
| Average | 361.384 | 304.810 | 298.137 | 297.812 | 301.614 | 260.680 |
| Min | 350.543 | 298.52 | 290.167 | 284.27 | 281.745 | 249.798 |
| Max | 380.171 | 310.898 | 308.929 | 300.279 | 324.785 | 266.977 |
| Std | 7.801 | 4.737 | 6.605 | 5.134 | 13.878 | 4.752 |
| Algorithm | Variables | Reference | Optimal Cost ($/day) |
|---|---|---|---|
| GA | Tank level controls (on/off) | [4] | 344.19 |
| Hybrid GA | 344.19 | ||
| EA | Tank level controls | [47] | 337.2 |
| ABC | Tank level controls | [46] | 363.85 |
| FF | 361.72 | ||
| PSO | 363.44 | ||
| ACO | Pump on/off | [48] | 388.04 |
| Pump speed | 349.43 | ||
| BDA | Pump on/off | [21] | 325.23 |
| NCHBA | Pump speed | Current study | 249.79 |
| IGD | SP | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Average | St.d | Best | Worst | Average | St.d | Best | Worst | ||
| ZDT1 | MONCHBA | 4.63 × 10−3 | 1.95 × 10−4 | 4.43 × 10−3 | 4.93 × 10−3 | 5.85 × 10−3 | 3.51 × 10−3 | 5.50 × 10−3 | 6.39 × 10−3 |
| NSGA-II | 6.23 × 10−2 | 7.39 × 10−2 | 2.97 × 10−1 | 1.97 × 10 | 6.23 × 10−2 | 4.51 × 10−2 | 9.47 × 10−3 | 1.09 × 10−1 | |
| MOSMA | 1.21 × 10−2 | 7.52 × 10−2 | 1.48 × 10−2 | 3.33 × 10−2 | 1.21 × 10−2 | 4.75 × 10−2 | 8.96 × 10−3 | 1.62 × 10−2 | |
| ZDT2 | MONCHBA | 4.54 × 10−3 | 2.58 × 10−4 | 4.32 × 10−3 | 4.96 × 10−3 | 5.23 × 10−3 | 3.95 × 10−4 | 4.92 × 10−3 | 5.98 × 10−3 |
| NSGA-II | 1.05 | 6.33 × 10−1 | 8.45 × 10−3 | 1.61 | 2.46 × 10−2 | 1.49 × 10−2 | 4.65 × 10−2 | 1.23 × 10−2 | |
| MOSMA | 2.98 × 10−1 | 2.90 × 10−1 | 2.46 × 10−2 | 7.72 × 10−1 | 1.21 × 10−2 | 4.75 × 10−2 | 8.96 × 10−3 | 1.62 × 10−2 | |
| ZDT3 | MONCHBA | 6.12 × 10−3 | 1.24 × 10−3 | 4.68 × 10−3 | 7.11 × 10−3 | 6.28 × 10−3 | 8.63 × 10−4 | 5.60 × 10−3 | 7.31 × 10−3 |
| NSGA-II | 7.68 × 10−2 | 1.18 × 10−1 | 8.72 × 10−3 | 2.86 × 10−1 | 1.21 × 10−1 | 1.75 × 10−1 | 2.34 × 10−2 | 4.32 × 10−1 | |
| MOSMA | 6.05 × 10−2 | 1.72 × 10−2 | 8.76 × 10−2 | 4.13 × 10−2 | 3.35 × 10−2 | 4.25 × 10−2 | 1.91 × 10−2 | 4.65 × 10−2 | |
| ZDT4 | MONCHBA | 4.80 × 10−3 | 2.70 × 10−4 | 4.47 × 10−3 | 5.22 × 10−3 | 5.87 × 10−3 | 5.49 × 10−3 | 5.18 × 10−3 | 6.36 × 10−3 |
| NSGA-II | 3.71 | 2.33 | 7.77 × 10−1 | 6.45 | 6.50 × 10−1 | 3.73 × 10−1 | 1.90 × 10−1 | 1.08 | |
| MOSMA | 4.75 × 10 | 2.43 × 10 | 1.94 × 10 | 7.45 × 10 | 2.64 | 1.12 × 10−2 | 1.23 × 10−1 | 5.15 | |
| ZDT6 | MONCHBA | 3.33 × 10−3 | 4.37 × 10−4 | 2.69 × 10−3 | 3.82 × 10−3 | 5.05 × 10−3 | 4.34 × 10−4 | 4.60 × 10−3 | 5.73 × 10−3 |
| NSGA-II | 5.69 × 10−2 | 2.02 × 10−2 | 3.55 × 10−2 | 8.47 × 10−2 | 5.99 × 10−2 | 4.75 × 10−2 | 1.34 × 10−1 | 2.28 × 10−2 | |
| MOSMA | 5.16 × 10−1 | 1.14 | 3.89 × 10−3 | 2.55 | 8.72 × 10−2 | 3.33 × 10−1 | 1.86 × 10−2 | 2.22 × 10−1 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jafari-Asl, J.; Hashemi Monfared, S.A.; Abolfathi, S. Reducing Water Conveyance Footprint through an Advanced Optimization Framework. Water 2024, 16, 874. https://doi.org/10.3390/w16060874
Jafari-Asl J, Hashemi Monfared SA, Abolfathi S. Reducing Water Conveyance Footprint through an Advanced Optimization Framework. Water. 2024; 16(6):874. https://doi.org/10.3390/w16060874
Chicago/Turabian StyleJafari-Asl, Jafar, Seyed Arman Hashemi Monfared, and Soroush Abolfathi. 2024. "Reducing Water Conveyance Footprint through an Advanced Optimization Framework" Water 16, no. 6: 874. https://doi.org/10.3390/w16060874
APA StyleJafari-Asl, J., Hashemi Monfared, S. A., & Abolfathi, S. (2024). Reducing Water Conveyance Footprint through an Advanced Optimization Framework. Water, 16(6), 874. https://doi.org/10.3390/w16060874








