Stability of Expansive Soil Slopes under Wetting–Drying Cycles Based on the Discrete Element Method
Abstract
1. Introduction
2. Discrete Element Model of Expansive Soil Slopes
2.1. Basic Discrete Element Model
2.2. Discrete Element Simulation Method of Crack Evolution
2.3. Principle and Method of Discrete Element Slope Stability Calculation
3. Discrete Element Simulation of Expansive Soil Slopes Cracks in Wetting–Drying Cycle
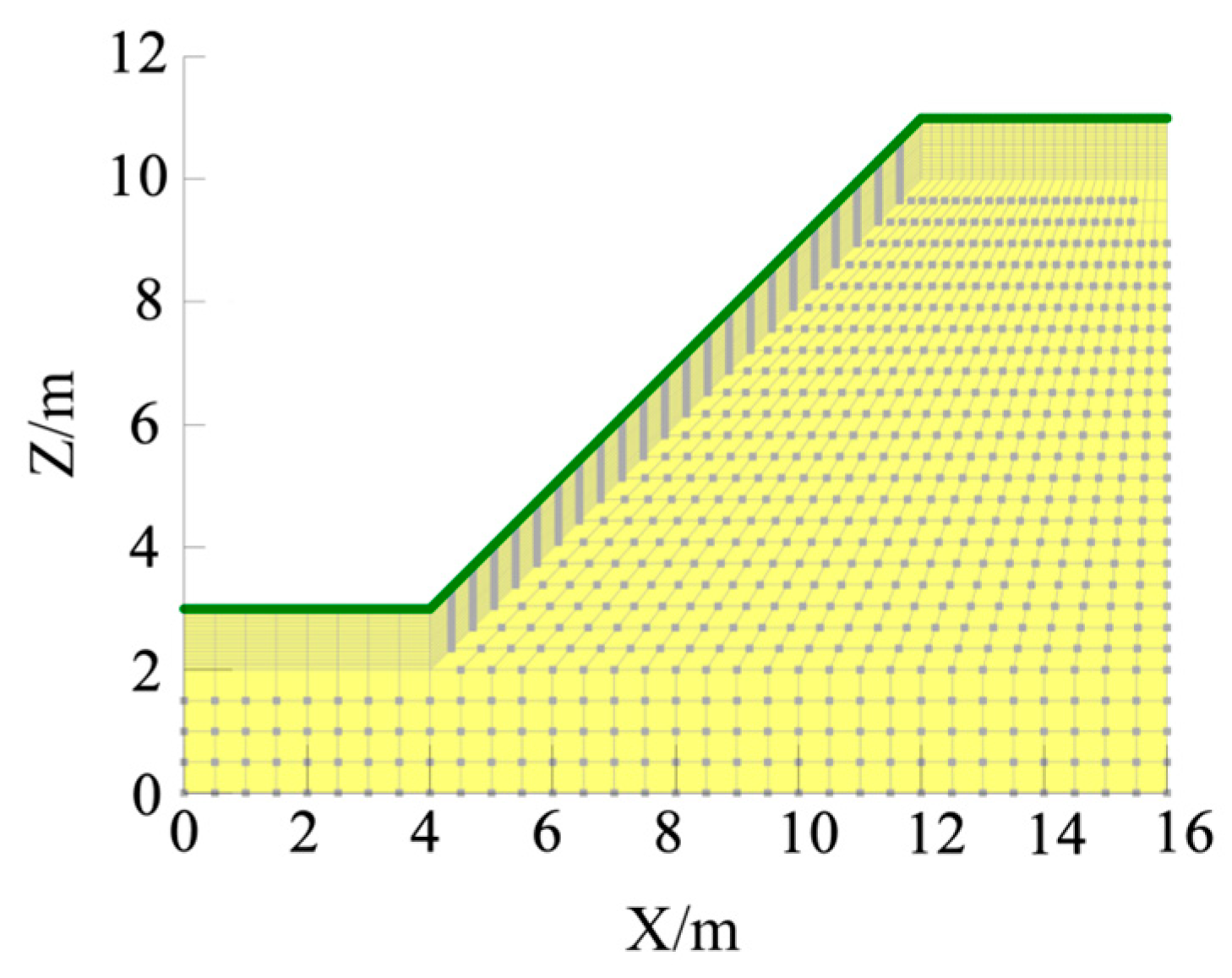
3.1. Initial Model Establishment
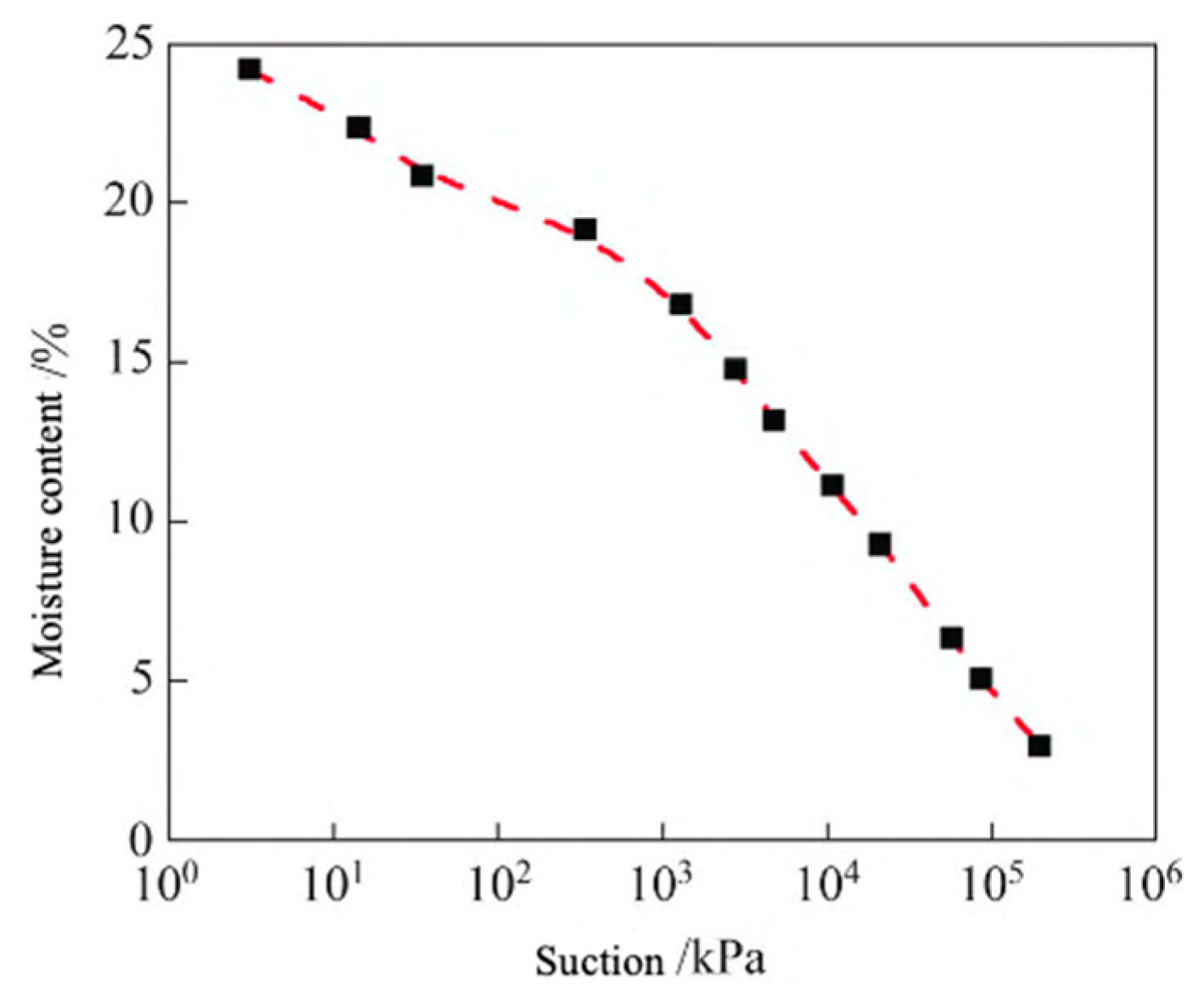
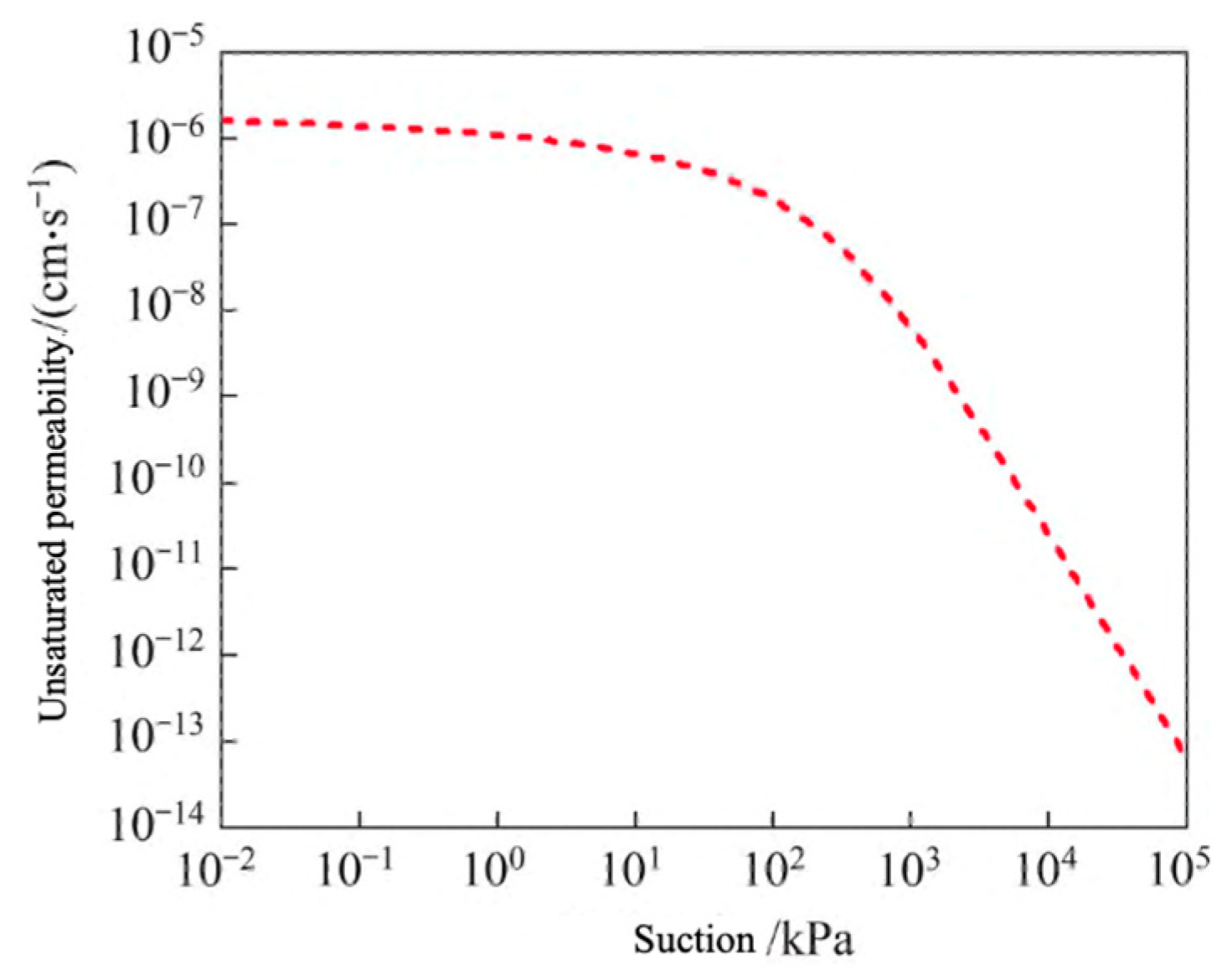
3.2. Material Setting and Parameter Determination
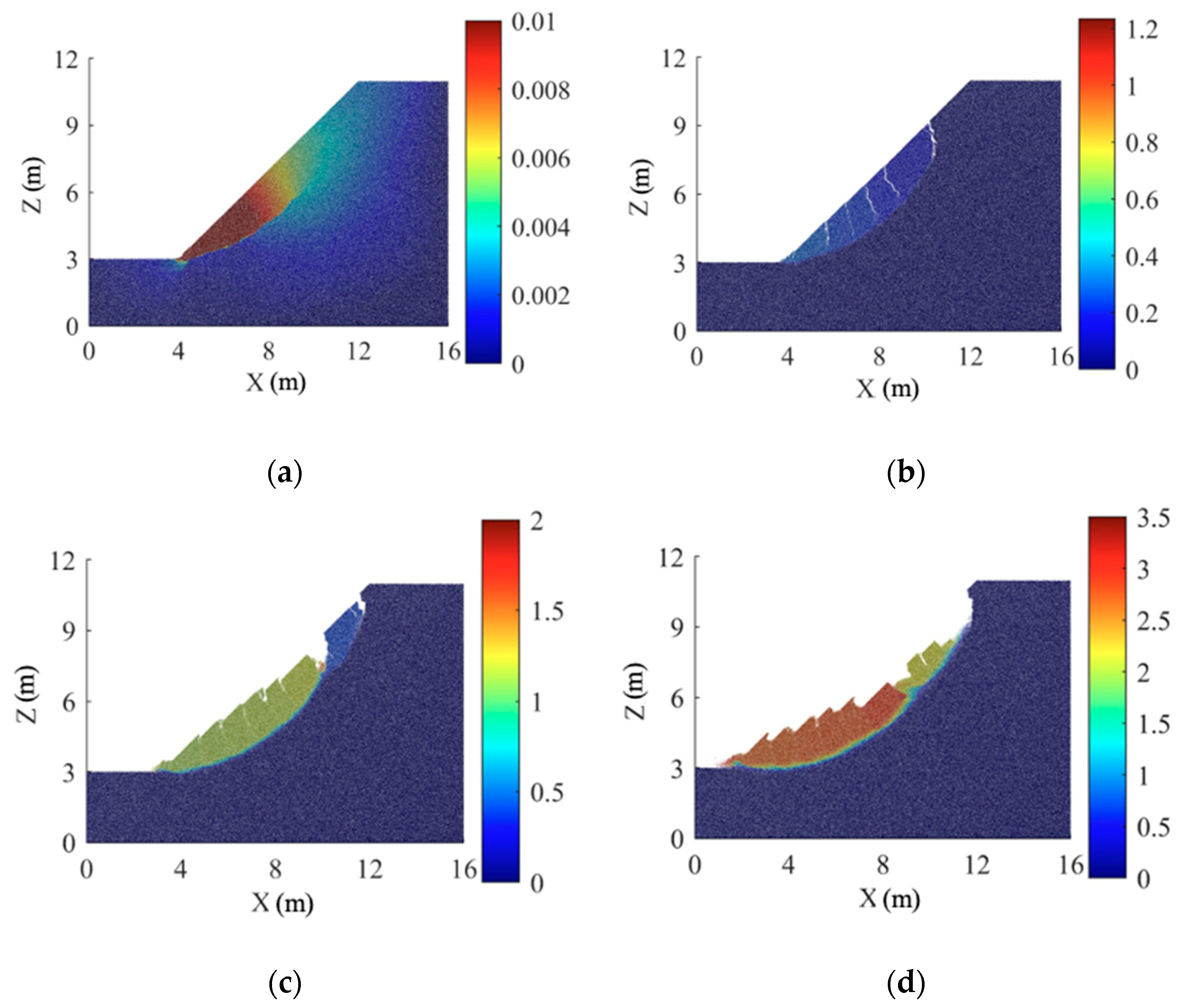
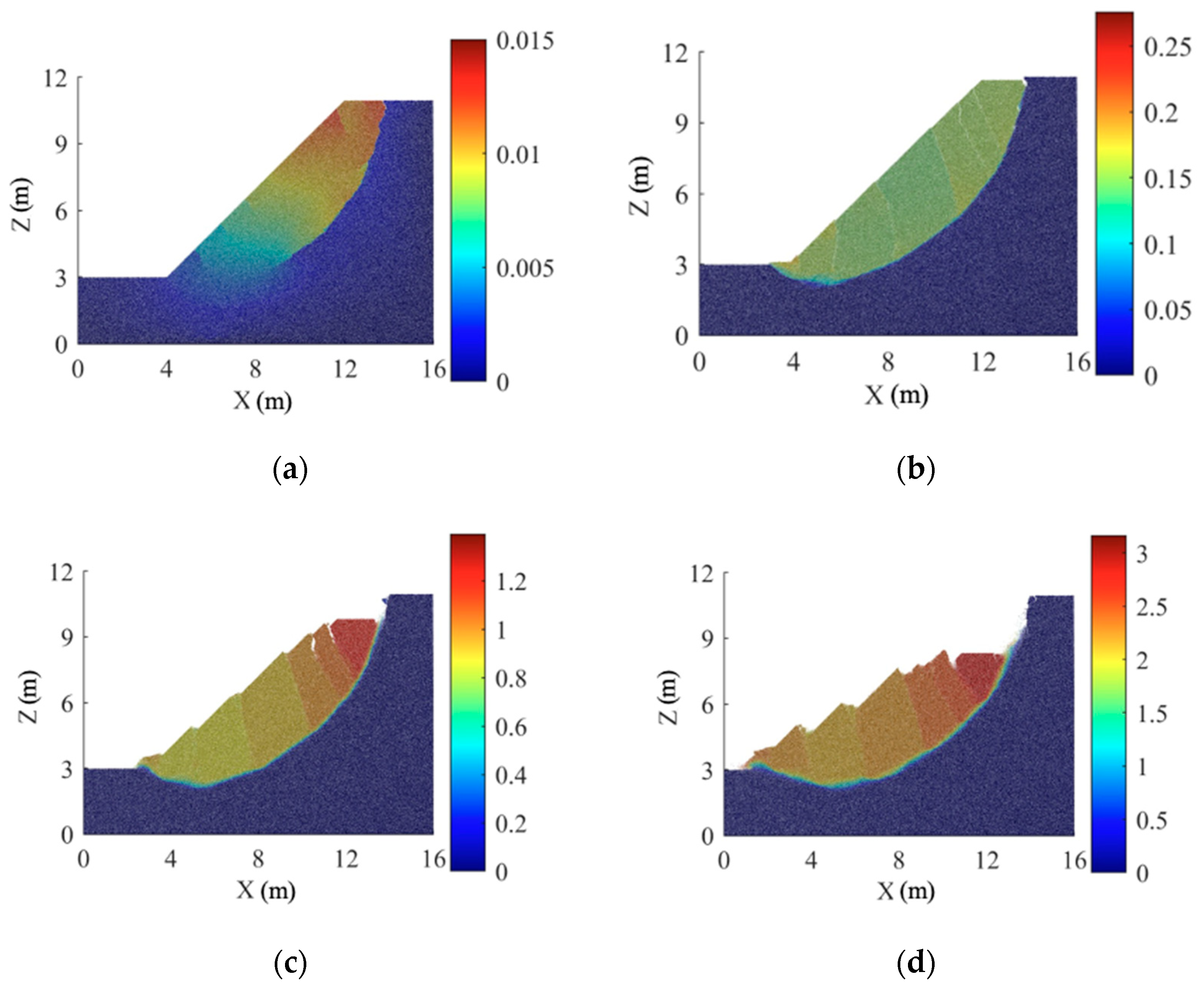
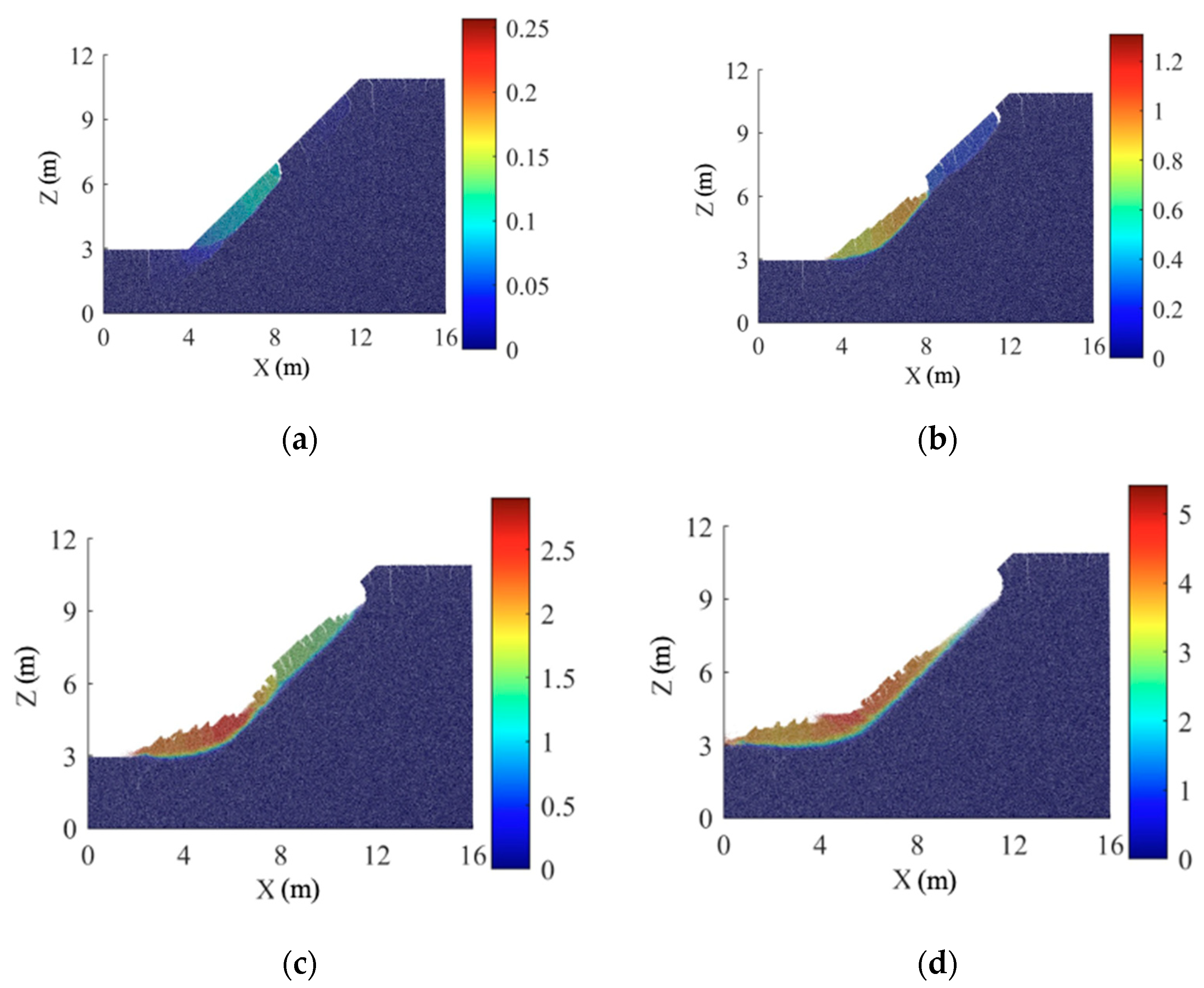
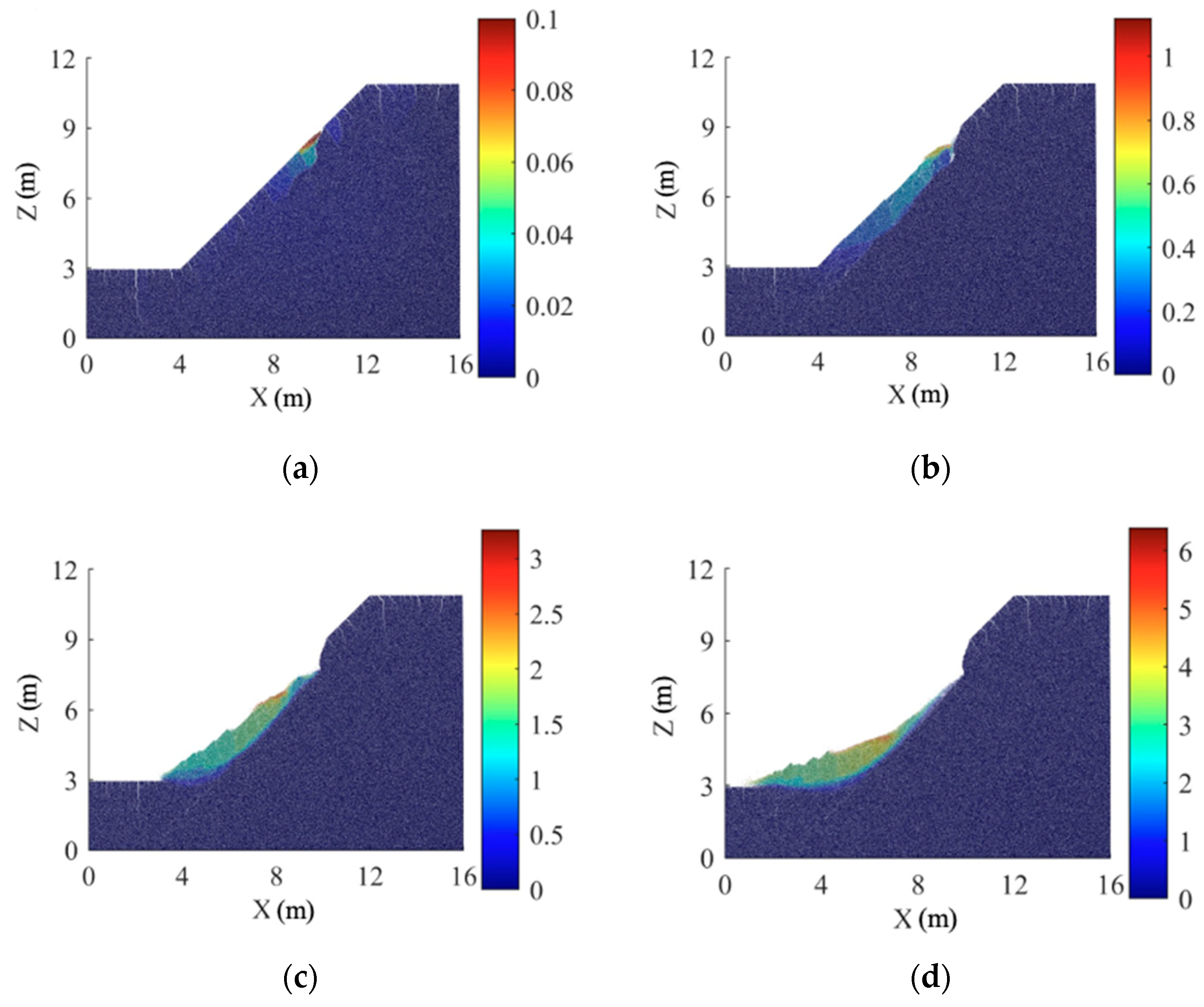
3.3. The Effects of Crack on the Stability of Expansive Soil Slopes
4. Results Analysis
4.1. Failure Model
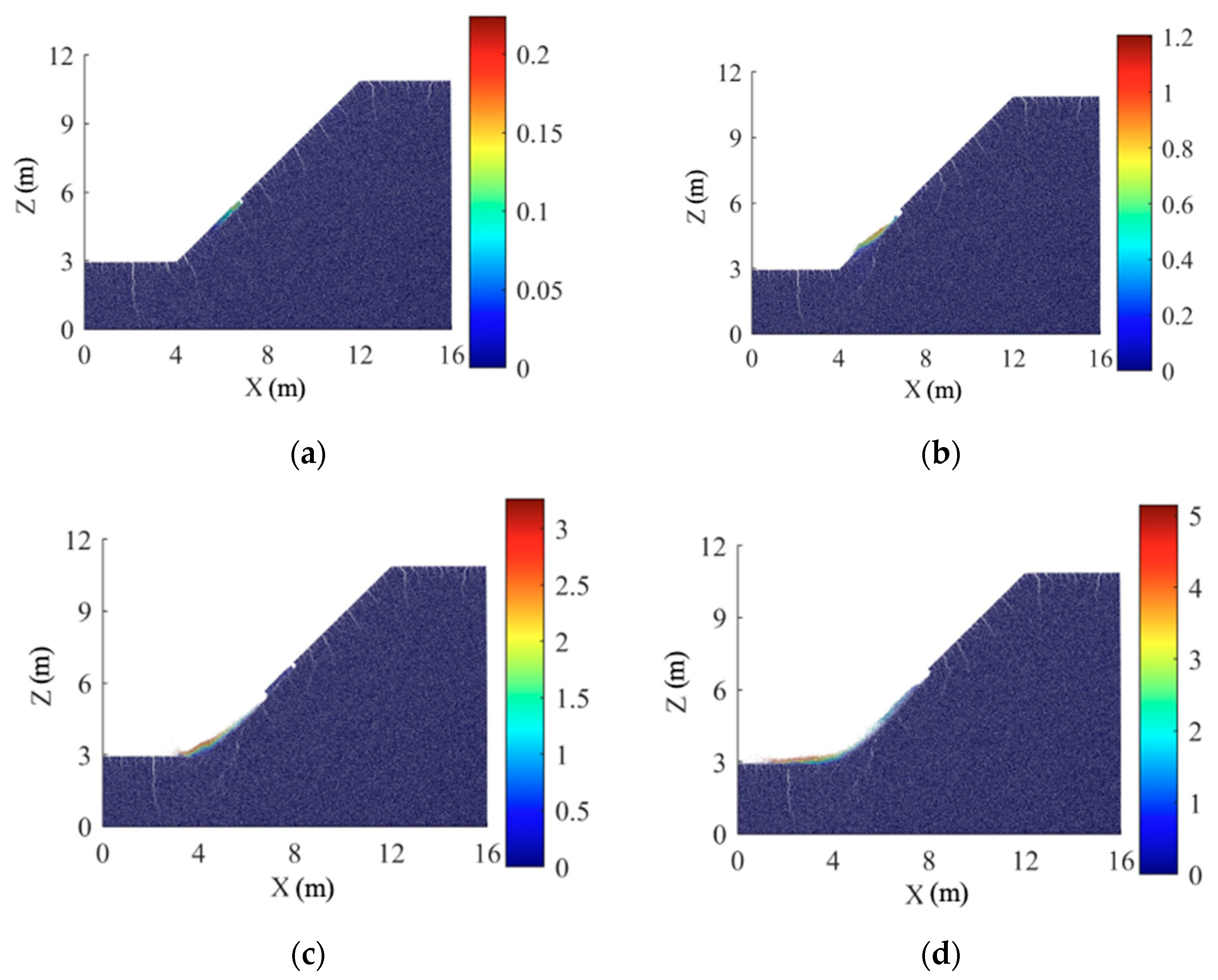
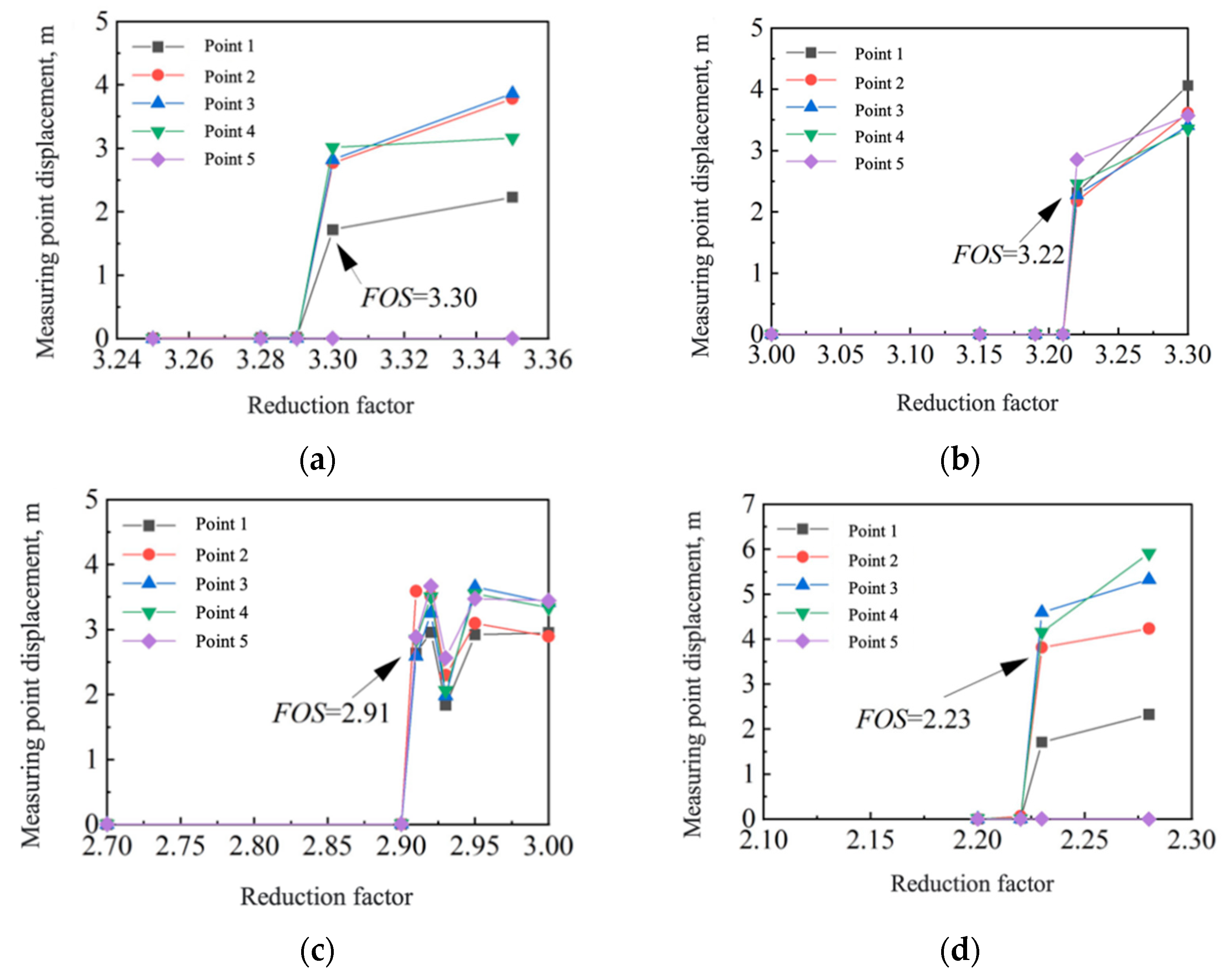
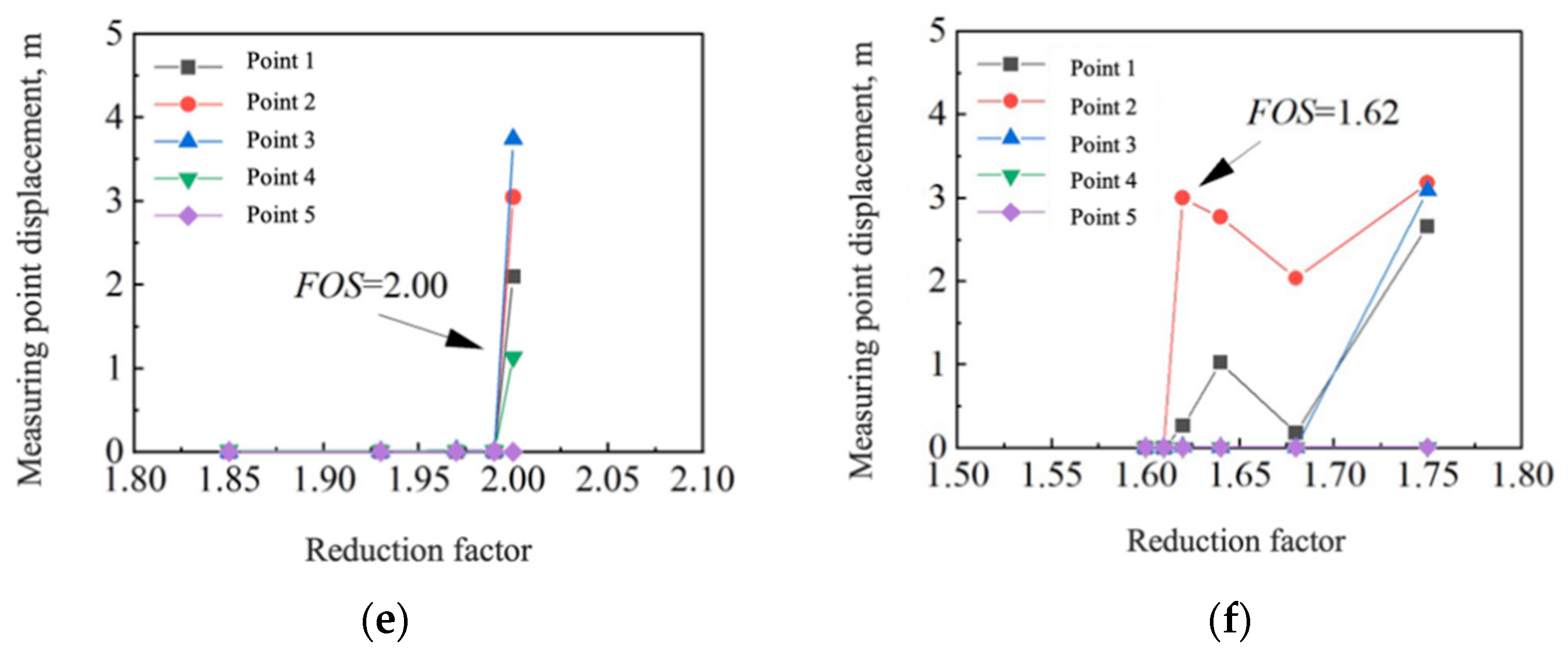
4.2. Slope Stability
4.3. Comparison between the Limit Equilibrium Method and the Finite Element Method
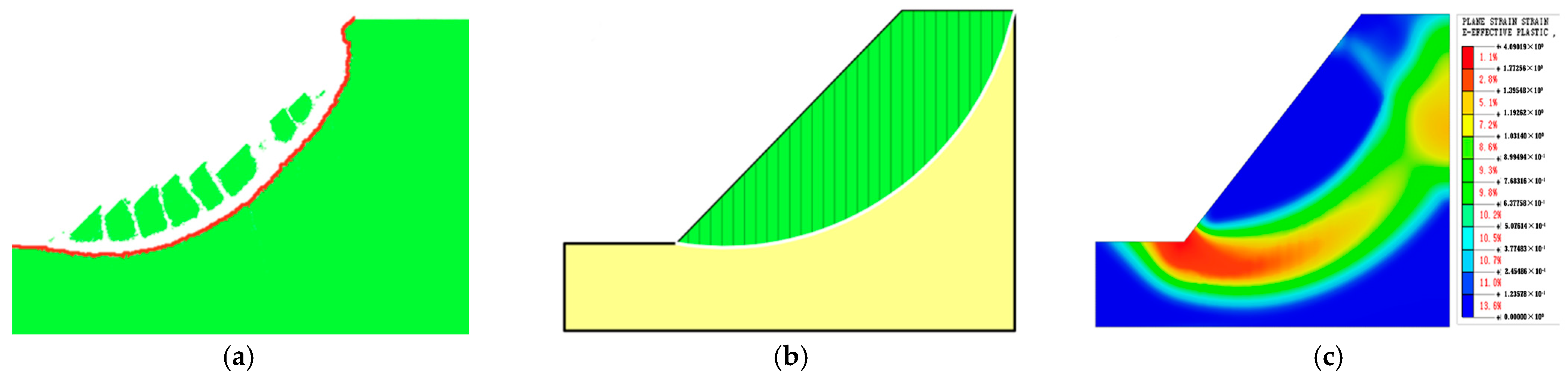
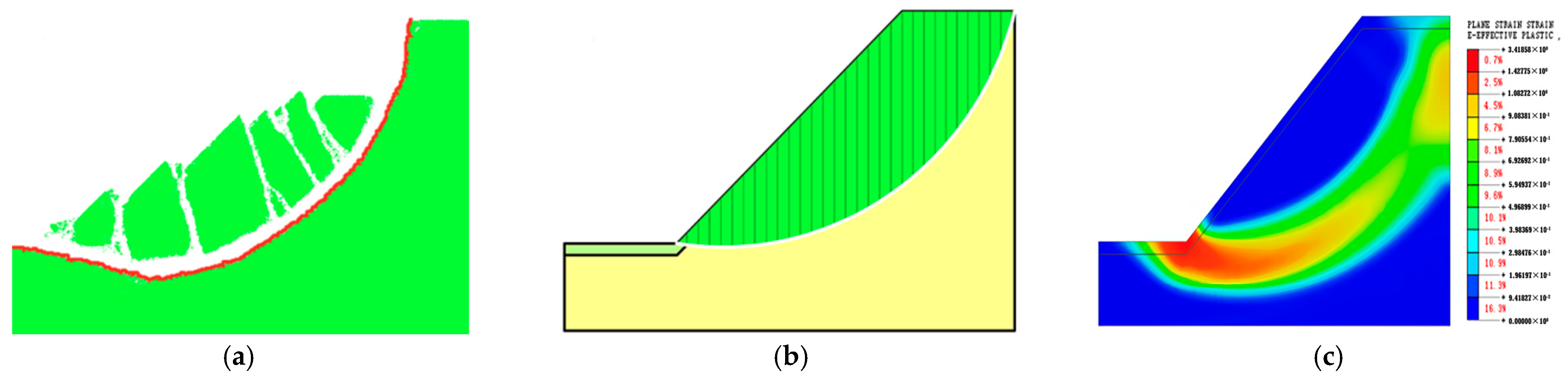
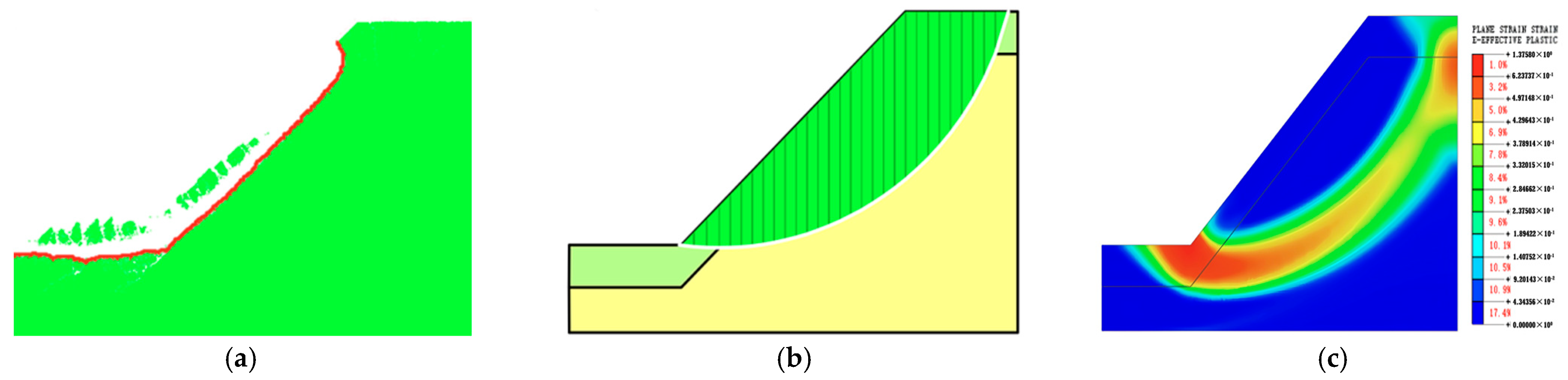
4.3.1. The Slope Failure Pattern
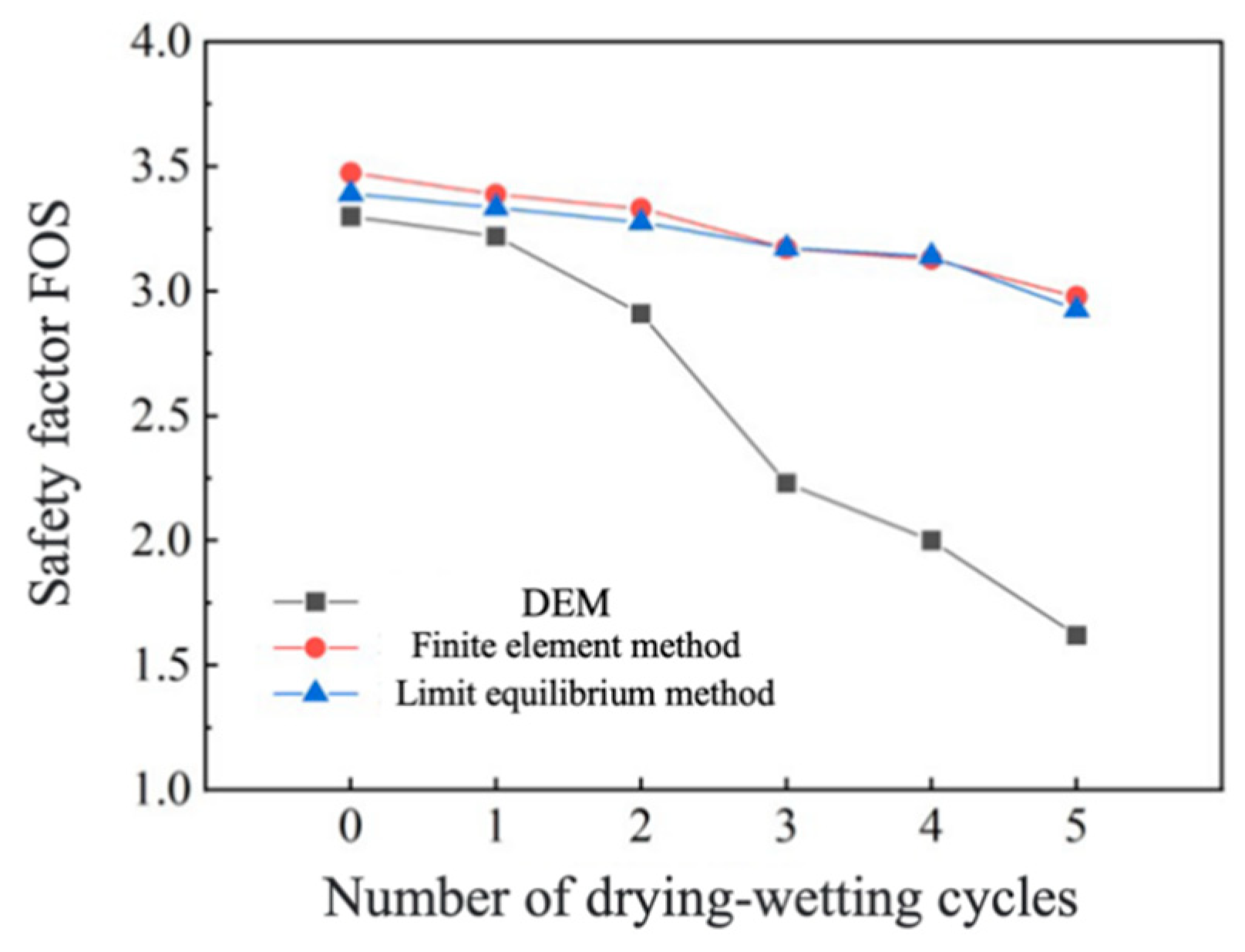
4.3.2. The Slope Safety Factor
5. Conclusions
- The slope stability can be obtained by the discrete element strength reduction method. Compared with the calculation results of the limit equilibrium method and finite element method, a much lower stability was computed in the DEM considering the crack evolutions in the expansive soil slopes, and the effectiveness of the discrete element strength reduction method is verified.
- The safety factor of an expansive soil slope, calculated by the discrete element strength reduction method, gradually decreases with an increase in the number of wetting–drying cycles. The decrease rate of the slope safety factor increases gradually when the number of wetting–drying cycles is between 0 and 3. However, during three to five wetting–drying cycles, the reduction rate of the slope safety factor gradually decreases and tends to stabilize. The trend in variation in the safety factor, as calculated by the DEM, differs significantly from that of the limit equilibrium method and the finite element method. As the number of wetting–drying cycles increases, the calculation results of the discrete element method are much smaller than those of the other two methods.
- Following 0–2 wetting–drying cycles, the discrete element slope reaches a critical state, presenting a deep arc-shaped sliding surface. The sliding surface initially develops at the foot of the slope without wetting–drying cycles, and after 1–2 wetting–drying cycles, it begins with the expansion and contraction cracks at the top of the slope. After 3–5 wetting–drying cycles, the discrete element slope reaches a critical state of shallow sliding. As the number of wetting–drying cycles increases, the volume of shallow sliding soil gradually decreases, and the depth of the sliding surface decreases accordingly. There is a significant discrepancy between the sliding surface calculated using the DEM and the results obtained from the limit equilibrium method and the finite element method.
- The study put emphasis on the evolution of cracks in the stability analysis of expansive soil slopes. Important factors were considered: not only the reduction in soil strength but also the presence, number, depth, and distribution of cracks. These factors greatly influence the stability of expansive soil slopes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
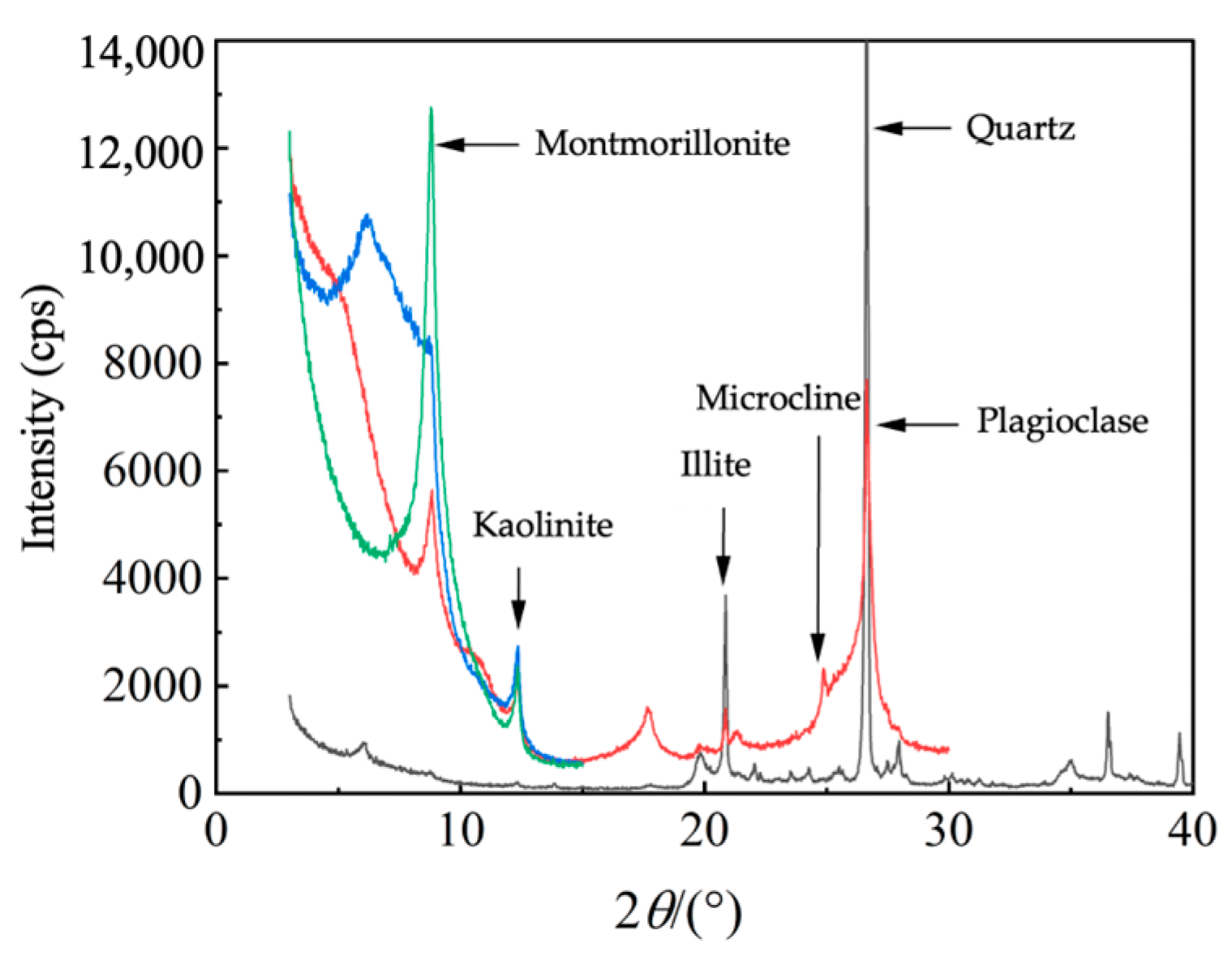
| Description of Sample | Quartz | Plagioclase | Microcline | Total Amount of Clay Minerals |
|---|---|---|---|---|
| Nanyang expansive soil | 61% | 8% | 5% | 26% |
| Description of Sample | Relative Content of Clay Minerals | Ratio of Mixed-Layer | ||||||
|---|---|---|---|---|---|---|---|---|
| S | I/S | It | Kao | C | C/S | I/S | C/S | |
| Nanyang expansive soil | - | 93 | 5 | 2 | - | - | 40 | - |
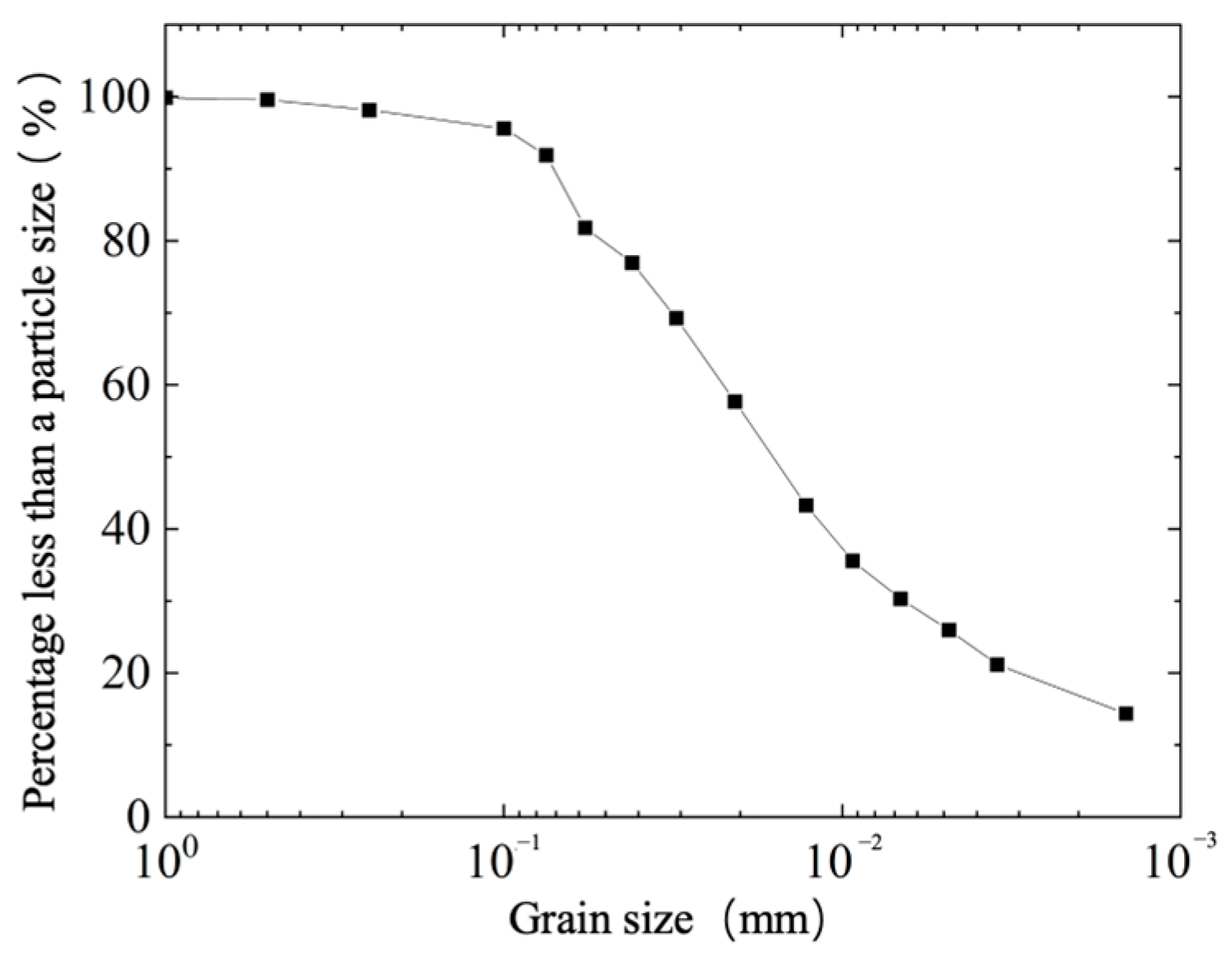
References
- Leng, T.; Tang, C.S.; Xu, D.; Li, Y.S.; Zhang, Y.; Wang, J.; Shi, B. Advance on the Engineering Geological Characteristics of Expansive Soil. J. Eng. Geol. 2018, 26, 112–128. [Google Scholar] [CrossRef]
- Tiwari, N.; Satyam, N. Coupling Effect of Pond Ash and Polypropylene Fiber on Strength and Durability of Expansive Soil Subgrades: An Integrated Experimental and Machine Learning Approach. Rock Mech. Geotech 2021, 13, 1101–1112. [Google Scholar] [CrossRef]
- Tang, C.S.; Shi, B.; Liu, C. Study on Desiccation Cracking Behavior of Expansive Soil. J. Eng. Geol. 2012, 20, 663–673. [Google Scholar] [CrossRef]
- Cao, L.; Wang, Z.J.; Zhang, Z.H. Experimental Research of the Cracking Process of Expansive Soil under Rainfall Infiltration and Evaporation. Chin. J. Rock Mech. Eng. 2016, 35, 413–421. [Google Scholar] [CrossRef]
- Xu, B.; Yin, Z.Z.; Liu, S.L. Experimental Study of Factors Influencing Expansive Soil Strength. Rock Soil Mech. 2011, 32, 44–50. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, S.; Weng, L.; Wang, L.; Li, Z.; Xu, L. Fractal Analysis of Cracking in a Clayey Soil under Freeze–Thaw Cycles. Eng. Geol. 2016, 208, 93–99. [Google Scholar] [CrossRef]
- Khan, M.S.; Hossain, S.; Ahmed, A.; Faysal, M. Investigation of a Shallow Slope Failure on Expansive Clay in Texas. Eng. Geol. 2016, 219, 118–129. [Google Scholar] [CrossRef]
- Xie, C.R.; Ni, P.P.; Xu, M.J.; Mei, G.X.; Zhao, Y.L. Combined Measure of Geometry Optimization and Vegetation for Expansive Soil Slopes. Comput. Geotech. 2020, 123, 103588. [Google Scholar] [CrossRef]
- Zhang, J.M.; Luo, Y.; Zhou, Z.; Chong, L.; Victor, C.; Zhang, Y.F. Effects of Preferential Flow Induced by Desiccation Cracks on Slope Stability. Eng. Geol. 2021, 288, 106164. [Google Scholar] [CrossRef]
- Wang, G.L.; Chen, S.S.; Xu, G.M. Centrifuge Model Test on Stability of Expansive Soil Slope under Alternation between Drying and Wetting. Hydro-Sci. Eng. 2005, 2005, 6–10. [Google Scholar] [CrossRef]
- Chen, S.S.; Zheng, C.F.; Wan, G.L. Researches on Long-Term Strength Deformation Characteristics and Stability of Expansive Soil Slopes. Chin. J. Geotech. Eng. 2007, 29, 795–799. [Google Scholar] [CrossRef]
- Cui, W.; Zhang, Z.G.; Yan, S.W. Cyclic Behavior of Expansive Soils and Its Application in Slope Stability Analysis. J. Water Resour. Archit. Eng. 2010, 8, 4. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Liu, J.Q.; Yang, D.S.; Yuan, J.Q. Model Test Study of Expansive Rock Slope under Different Types of Precipitation. Rock Soil Mech. 2016, 37, 3401–3409. [Google Scholar] [CrossRef]
- Cai, Z.Y.; Chen, H.; Huang, Y.H.; Zhang, C. Failure Mechanism of Canal Slopes of Expansive Soils Considering Action of Wetting-Drying Cycles. Chin. J. Geotech. Eng. 2019, 41, 1977–1982. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, J.M.; Zhi, Z.; Victor, C.; Shen, J. Evolution Law of Critical Moisture Content of Soil Cracking under Rainfall-Evaporation Conditions. Rock Soil Mech. 2020, 41, 2592–2600. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, J.M.; Ning, F.L.; Luo, Y.; Wang, J.L. Temporal and Spatial Characteristics of Moisture Migration and Instability Mechanism of Cracked Soil Slope under Rainfall Infiltration. Traffic Transp. Eng. 2020, 20, 107–119. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, J.; Wang, L.; Xu, Y. Model Test on the Dynamic Characteristics of Crack Formation in Expansive Soil Slopes under Alternate Drying and Wetting. Acta Geotech. 2022, 18, 2097–2115. [Google Scholar] [CrossRef]
- Zhang, J.M.; Luo, Y.; Zhou, Q.; Victor, C.; Yuan, C.; Wang, S.F. Evolution Law of Cracks Based on Full-Scale Model Test of Slope. J. Cent. South Univ. 2021, 51, 1037–1048. [Google Scholar] [CrossRef]
- Yao, Z.; Chen, Z.H.; Fang, X.F.; Huang, X.F. Elastoplastic Damage Seepage-Consolidation Coupled Model of Unsaturated Intact Loess and Its Application. Rock Soil Mech. 2019, 40, 216–226. [Google Scholar] [CrossRef]
- Jin, Y.F.; Yin, Z.Y.; Yuan, W.H. Simulating Retrogressive Slope Failure Using Two Different Smoothed Particle Finite Element Methods: A Comparative Study. Eng. Geol. 2020, 279, 105870. [Google Scholar] [CrossRef]
- Shen, J.; Karakus, M. Three-Dimensional Numerical Analysis for Rock Slope Stability Using Shear Strength Reduction Method. Can. Geotech. J. 2014, 51, 164–172. [Google Scholar] [CrossRef]
- Qu, C.X.; Wang, G.; Feng, K.; Xia, Z.D. Large Deformation Analysis of Slope Failure Using Material Point Method with Cross-Correlated Random Fields. J. Zhejiang Univ. Sci. A 2021, 22, 856–869. [Google Scholar] [CrossRef]
- Feng, K.; Huang, D.; Wang, G. Two-Layeer Material Point Method for Modeling Soil-Water Interaction in Unsaturated Soils and Rainfall-Induced Slope Failure. Acta Geotech. 2021, 16, 2529–2551. [Google Scholar] [CrossRef]
- Feng, K.; Wang, G.; Huang, D.; Jin, F. Material Point Method for Large-Deformation Modeling of Coseismic Landslide and Liquefaction-Induced Dam Failure. Soil Dyn. Earthq. Eng. 2021, 150, 106907. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, D.; Liu, F.; Zheng, H. Modeling the Entire Progressive Failure Process of Rock Slopes Using a Strength-Based Criterion. Comput. Geotech. 2020, 126, 103726. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, H.Z.; Hu, W.J. Impact of Wetting-Drying Cycle Effects on Stability of Expansive Soil Slopes. Chin. J. Geotech. Eng. 2013, 35, 152–156. [Google Scholar]
- Zhou, J.; Wang, J.Q.; Zeng, Y.; Jia, M.C. Slope Safety Factor by Methods of Particle Flow Code Strength Reduction and Gravity Increase. Rock Soil Mech. 2009, 30, 1549–1554. [Google Scholar] [CrossRef]
- Liao, J.W. Slope Stability Analysis of Silty Clay Particle Flow Based on Strength Reduction Method; Chongqing University: Chongqing, China, 2014. [Google Scholar]
- Song, K.; Wu, S.G.; Zhang, S.P. Progressive Failure Analysis of Accumulation Slope Based on Discrete Element Strength Reduction Method; Springer: Singapore, 2018; pp. 873–881. [Google Scholar]
- Ma, X. Numerical Simulation of Desiccation Cracking in the Cross Section of Clay Soil; Wuhan University: Wuhan, China, 2018. [Google Scholar]
- Chen, X.; Jing, X.; Li, X.; Chen, J.; Ma, Q.; Liu, X. Slope Crack Propagation Law and Numerical Simulation of Expansive Soil under Wetting–Drying Cycles. Sustainability 2023, 15, 5655. [Google Scholar] [CrossRef]
- Liu, C.; David, D.P.; Gu, K.; Shi, B. Mechanism of Formation of Wiggly Compaction Bands in Porous Sandstone: 2. Numerical Simulation Using Discrete Element Method. J. Geophys. Res. Solid Earth 2015, 120, 8153–8168. [Google Scholar] [CrossRef]
- Gianvito, S.; Fan, X.M.; Xu, Q.; Liu, C.; Chaojun, O.Y.; Guillem, D.; Fan, Y.; Dai, L.X. Some Considerations on the Use of Numerical Methods to Simulate Past Landslides and Possible New Failures: The Case of the Recent Xinmo Landslide (Sichuan, China). Landslides 2018, 15, 1359–1375. [Google Scholar] [CrossRef]
- Qin, Y.; Liu, C.; Zhang, X.Y.; Wang, X.G.; Deng, S. A Three-Dimensional Discrete Element Model of Triaxial Tests Based on a New Flexible Membrane Boundary. Sci. Rep. 2021, 11, 4753. [Google Scholar] [CrossRef] [PubMed]
- Luo, H.; Xing, A.; Jin, K.; Xu, S.M.; Zhuang, Y. Discrete Element Modeling of the Nayong Rock Avalanche, Guizhou, China Constrained by Dynamic Parameters from Seismic Signal Inversion. Rock Mech. Rock Eng. 2021, 54, 1629–1645. [Google Scholar] [CrossRef]
- Xue, Y.; Zhou, J.; Liu, C.; Far, M.S.; Zhang, J. Rock Fragmentation Induced by a TBM Disc-Cutter Considering the Effects of Joints: A Numerical Simulation by DEM. Comput. Geotech. 2021, 136, 104230. [Google Scholar] [CrossRef]
- Liu, C. Discrete Element Analysis of Geological and Geotechnical Engineering Matrix; Science Press: Beijing, China, 2019. [Google Scholar]
- Yin, Z.Z.; Wei, J.; Yuan, J.P.; Cao, X.S. Mechanism of Slope Slide of Expansive Soil and Reinforcement for the Slope. J. Hydraul. Eng. 2010, 41, 1–6. [Google Scholar] [CrossRef]
- Yin, Z.Z.; Yuan, J.P.; Wei, J.; Cao, X.S.; Liu, H.Q.; Xu, B. Influences of Cracks on Slope Stability of Expansive Soil. Chin. J. Geotech. Eng. 2012, 34, 2155–2161. [Google Scholar]
- Zeng, Y. Microscopic Mechanics of Soil Failure and PFC Numerical Simulation; Tongji University: Shanghai, China, 2006. [Google Scholar]
- Zhan, L.T.; Ng Charles, W.W.; Fredlund Del, G. Field Study of Rainfall Infiltration into a Grassed Unsaturated Expansive Soil Slope. Can. Geotech. J. 2007, 44, 392–408. [Google Scholar] [CrossRef]
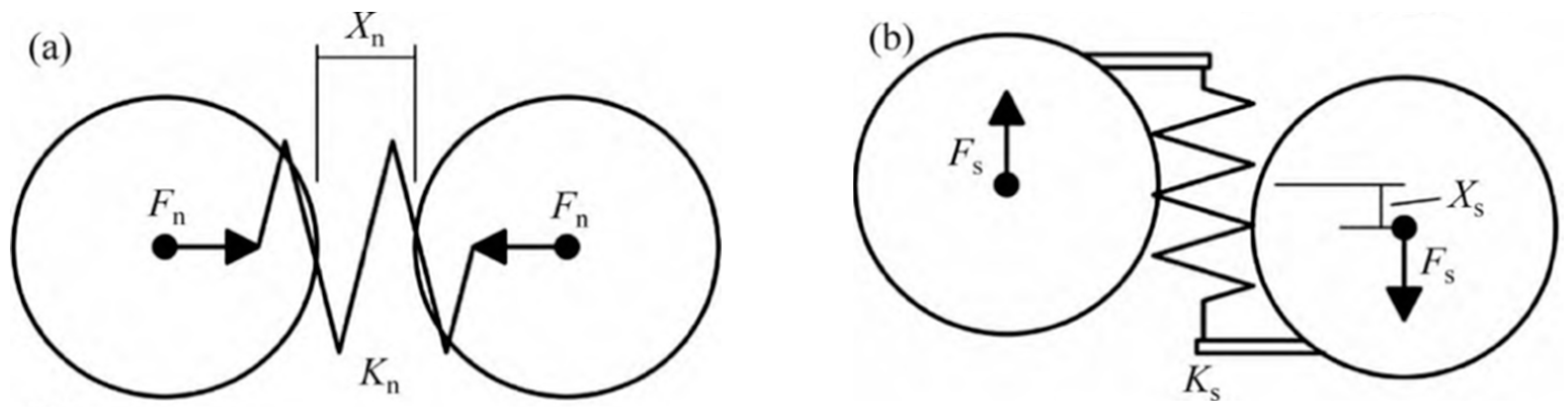
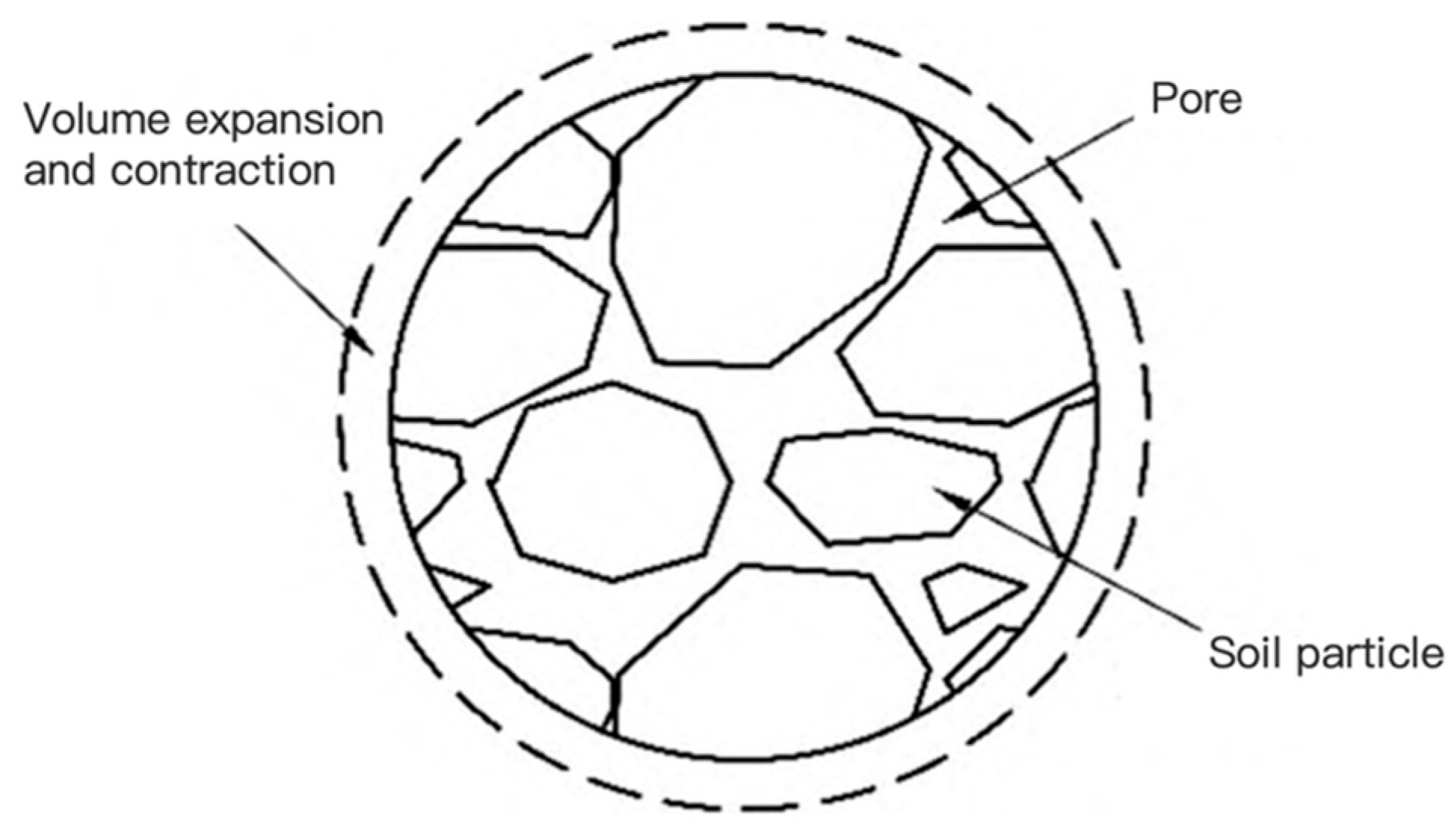
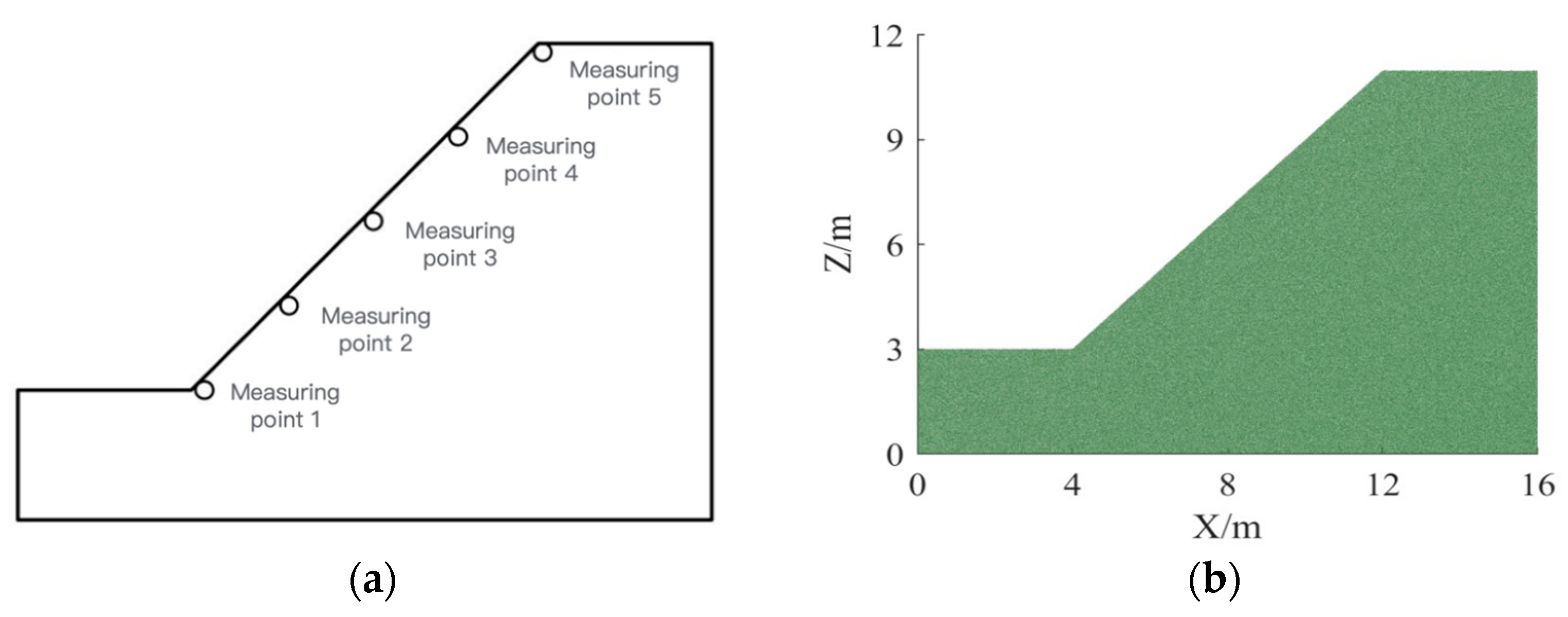



| Properties | Values |
|---|---|
| Specific gravity | 2.74 |
| Liquid limit | 47.4 |
| Plastic limit | 25.3 |
| Plasticity index | 22.1 |
| Undisturbed soil dry density | 1.60 |
| Undisturbed soil moisture content (w/) | 20.0 |
| Free swelling rate ) | 52.0 |
| Density | Young’s Modulus E/(Mpa) | Poisson Ratio v | Tensile Strength /(kpa) | Compressive Strength /(kpa) | |
|---|---|---|---|---|---|
| 1.92 | 12.0 | 0.3 | 107.38 | 192.26 | 0.4006 |
| Time of Wetting–Drying Cycle | /(kPa) | /(kPa) | /mm | /N | |
|---|---|---|---|---|---|
| 0 | 673.83 | 116.18 | 0.1220 | 55.90 | 0.1772 |
| 1 | 34.98 | 0.1910 | |||
| 2 | 26.27 | 0.1761 | |||
| 3 | 25.19 | 0.1472 | |||
| 4 | 24.51 | 0.1462 | |||
| 5 | 22.61 | 0.1457 |
| Time of Wetting–Drying Cycle | Depth of Crack Zone/mm |
|---|---|
| 0 | 0 |
| 1 | 450 |
| 2 | 800 |
| 3 | 1450 |
| 4 | 1600 |
| 5 | 1900 |
| Time of Wetting-Drying Cycle | Slope Safety Factor |
|---|---|
| 0 | 3.30 |
| 1 | 3.22 |
| 2 | 2.91 |
| 3 | 2.23 |
| 4 | 2.00 |
| 5 | 1.62 |
| 1 | 3.30 |
| Time of Wetting-Drying Cycle | DEM | Limit Equilibrium Method | The Finite Element Method |
|---|---|---|---|
| 0 | 3.30 | 3.385 | 3.475 |
| 1 | 3.22 | 3.340 | 3.388 |
| 2 | 2.91 | 3.275 | 3.331 |
| 3 | 2.23 | 3.174 | 3.172 |
| 4 | 2.00 | 3.140 | 3.128 |
| 5 | 1.62 | 2.926 | 2.978 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wang, Y.; Jin, F. Stability of Expansive Soil Slopes under Wetting–Drying Cycles Based on the Discrete Element Method. Water 2024, 16, 861. https://doi.org/10.3390/w16060861
Wang H, Wang Y, Jin F. Stability of Expansive Soil Slopes under Wetting–Drying Cycles Based on the Discrete Element Method. Water. 2024; 16(6):861. https://doi.org/10.3390/w16060861
Chicago/Turabian StyleWang, Hao, Yejiao Wang, and Fujie Jin. 2024. "Stability of Expansive Soil Slopes under Wetting–Drying Cycles Based on the Discrete Element Method" Water 16, no. 6: 861. https://doi.org/10.3390/w16060861
APA StyleWang, H., Wang, Y., & Jin, F. (2024). Stability of Expansive Soil Slopes under Wetting–Drying Cycles Based on the Discrete Element Method. Water, 16(6), 861. https://doi.org/10.3390/w16060861





