Abstract
In this study, we attempt to experimentally investigate the flow turbulence structure in a partly vegetated channel. To achieve the objective of this study, we conducted extensive measurements of flow velocities within and outside the vegetated area, where the flow is fully developed. The experiments were conducted in a very large channel at the Coastal Engineering Laboratory of the Department of Civil, Environmental, Building Engineering and Chemistry at the Polytechnic University of Bari, Italy. The instantaneous three flow velocity components were accurately measured using a 3D-Acoustic Doppler Velocimeter (ADV)-Vectrino system at high frequency. Flow behaviors through the vegetated area, at the interface, and in the unobstructed area were analyzed via time-averaged velocities, turbulence intensity, correlation properties, spectral analysis, and vortex identification. Experimental results showed the development of three distinct characteristic flow zones: (i) a vegetated area of low streamwise velocity, high turbulence intensities, dominant inward interactions, and more intense power spectrum, (ii) a shear layer zone of increasing streamwise velocity, more enhanced transverse flow motion, exponential decrease in turbulence intensities, and frequent ejection and/or outward interaction events, and (iii) a free-stream zone of higher and almost constant streamwise velocity, lower turbulence intensities, frequent sweep and/or inward interaction events, and less intense streamwise power spectrum. The results brought further insights into the flow behaviors in these characteristic flow zones. The extensive and detailed measured data can provide a basis for improving and calibrating numerical simulations of partly vegetated channels.
Keywords:
partly vegetated channels; ADV; velocities; turbulence; skewness; kurtosis; spectral analysis 1. Introduction
Natural watercourses, i.e., rivers, streams, wetlands, and estuaries, often have distinct vegetated and unvegetated parts, which influence flow characteristics [1,2,3,4]. The presence of vegetation in waterways can have various impacts on the aquatic environment and flow dynamic processes. Vegetation acts as an obstacle in the flow, causing increased friction and flow resistance which results in reduced flow velocities, increased flow depth, and altered flow patterns [5,6,7,8]. Moreover, vegetation plays an important role in stabilizing riverbanks and preventing erosion [9,10], improving water quality by acting as a natural filter [11], regulating water temperature [12], influencing sediment transport [13,14], providing important habitats for various aquatic organisms [15], and affecting flow structure and turbulence which in turn impact the transport processes and diffusion of dissolved species [16,17].
Turbulent flows in bare channels without any obstacles are indeed very complex. They exhibit intricate and chaotic behaviors, making them difficult to understand and analyze. In turbulent flows, the fluid particles move randomly and irregularly, with swirling, eddying in different directions and scales, and mixing between layers. Flow interactions with natural, such as vegetation, or artificial obstacles lead to the development of even more complex hydrodynamic structures, which require further studies to fully understand [8]. The nonlinear nature of the equations governing fluid motion in open channels, the presence of a wide range of turbulence length and time scales, and flow interactions between structures of different sizes contribute all of them to the complexity of turbulent flow problems. Turbulent flows in vegetated channels often require advanced measurement instruments, mathematical theories, and computational techniques for analysis and modeling.
In vegetated channels, several properties need to be defined to understand the hydrodynamic flow structures, including flow regime, velocity distribution, vortical structures, turbulence intensities, shear stresses, mixing and dispersion, roughness, vegetation properties, and vegetative drag. Many previous studies have extensively investigated flow dynamics in open channels and their interactions with vegetation canopies [1,2,3,4,14,16,17,18,19,20,21]. Various approaches, ranging from statistical methods to numerical models, were proposed in the literature to study and understand turbulent flows in vegetated channels. Based on a laboratory experimental study using a Laser Doppler velocimetry (LDV) probe and an analytical approach, Yang et al. [22] proposed an innovative model to estimate, simply, the bed shear stress in both emergent vegetated and bare channels with smooth beds. The authors stated that the effective bed friction velocity in an emergent canopy, which was considered almost neglected in many previous studies, is greater than or equal to the bare channel value. This important result is useful, above all, for the study of benthic processes, such as sediment transport in vegetated channels. Ben Meftah and Mossa [6] proposed a theoretical model for the flow velocity structure within an infinite square array of emergent, vertical, rigid cylinders uniformly distributed along a channel bottom. This model also led to an innovative predictor of the bulk drag coefficient of the cylinder arrays. The model was supported by measurements of the flow velocity field within the emergent cylinder arrays, using a 3D Acoustic Doppler Velocimeter. The flow dispersion process by vortical structures around emergent vegetation stems was theoretically described and experimentally verified in White and Nepf [23]. A vortex-trapping dispersion phenomenon, due to the entrainment in the unsteady recirculation zone in the vicinity of each cylinder, in addition to advection through the random flow velocity field created by the random distribution of the wake velocity defect are fundamental mechanisms of longitudinal dispersion within a random array of emergent vegetation in open channels.
Elzahry et al. [24] experimentally tried to evaluate the effect of rigid aquatic unilateral and bilateral bank weeds on vertical velocity distribution and channel bed morphology. Considering three vegetation densities of 0.0013, 0.0028, and 0.013, whether in a movable (sandy sediment with a median grain size of 0.65 mm) or fixed bed, the authors measured various vertical profiles at different transversal positions from the vegetated banks as well as along the channel centerline upstream, in the middle distance, and downstream of the vegetated area. The measured flow velocity results were combined with the scouring process, leading to several empirical equations to evaluate and understand the impact of bank vegetation density on flow dynamics and channel bed morphology. Ben Meftah et al. [1] and Ben Meftah and Mossa [2] conducted flow velocity measurements, using high-frequency ADV, in a very large partly emergent vegetated channel with different contraction ratios (defined as the ratio of the vegetated area width to the width of the unvegetated area), focusing on flow hydrodynamic structures inside and outside the vegetated area. In addition to analyzing the effect of the contraction ratio on flow patterns and determining the vegetation drag coefficient, the authors proposed some practical approaches to predict the transversal velocity profile at the flow–vegetation interface. More details on partly vegetated flow dynamics can also be found in White and Nepf [5,25].
Vegetation drags cause flow separation and the formation of vortex/eddies structures around individual vegetation stems and at the interface between the vegetated and unvegetated zones. Arora et al. [4] examined the flow structure behaviors at the flow–vegetation interface in a partly vegetated channel. The flow turbulence properties were statistically analyzed, such as the transverse flux, turbulent kinetic energy, probability density function, and anisotropy. Results demonstrated higher turbulence intensity occurring at the interface. A transversal flow from the vegetated to the unvegetated area also occurred at the interface. Anisotropy analysis showed that a one-dimensional turbulence is dominant in a partly vegetated channel. Zhang et al. [26] studied the effect of vegetation density on flow turbulence characteristics and Reynolds shear stress in a partly vegetated channel. A series of experiments were carried out in a rectangular channel of 30 m length (facilitates the generation of gradual varied flow), 1.3 m width, and 0.8 m depth. To be closer to reality, the authors employed natural reed of 7 mm mean diameter, along an area of 4 m length and 0.65 m width, to simulate emergent vegetation. Three vegetation densities of 54, 108, and 202 stems/m2 were considered and compared with the case of bare channel condition. The flow velocities were measured in several channel cross-sections using an ADV. The results demonstrated that vegetation forces the water flowing from vegetated areas to unvegetated areas, with an intensity that increases as the vegetation density increases. Zhang et al. [26] also claimed that compared to bare channels, partially vegetation areas in open channels may reduce both relative turbulence intensities and Reynolds shear stresses. This reduction in flow turbulence properties was found disproportional to the vegetation density. The authors affirmed the existence of an optimal vegetation density for reducing relative turbulence intensity and Reynolds shear stress, which provides important guidance for the practice of river ecological restoration and soil erosion control.
Knowing flow turbulence behavior in vegetated channels is important in various applications, such as ecological studies, sediment transport analysis, and hydraulic modeling. This study aims to increase understanding of the main structures associated with flow turbulence in a partly vegetated channel, including velocity distributions, turbulence intensities, skewness/kurtosis, correlation properties, and spectrum analysis. Very extensive measurements of the flow velocities, using high-frequency ADV-Vectrino, were carried out inside and outside the vegetation canopy, at the center of the experimental area where flow is fully developed [1,2]. The flow velocities were measured along the transversal (y-axis) and vertical (z-axis) directions with a displacement step of 2 cm. The goal of these in-depth measurements is to obtain clearer details of the flow features into and out of the vegetation canopy. The results can also help to accurately predict flow discharges [3] in the different cross-section areas. These experimental results would allow for more accurate and effective planning and management of natural watercourses with the presence of vegetation.
2. Experimental Setup and Model Design
To have further details on the hydrodynamic flow structures in partially vegetated channels, a physical model was realized in a very large channel (Figure 1) at the Coastal Engineering Laboratory (L.I.C.) of the Department of Civil, Environmental, Building Engineering, and Chemistry at the Polytechnic University of Bari, Italy. The channel consisted of base and lateral walls made of glass. The channel was 15 m long, 4 m large, and 0.4 m deep. In a closed hydraulic circuit, the water was pumped from a large steel tank downstream to another upstream, using a Flygt centrifugal electric pump with a maximum discharge of 100 L/s. To create a smooth flow transition from the upstream tank to the flume, a set of stilling grids was installed in the upstream tank to dampen inlet turbulence. A side-channel spillway of adjustable height was also installed in the upstream tank to maintain constant flow-head condition. Any overflow water was discharged via a pipe into the downstream tank. Two electromagnetic flowmeters mounted on the channel’s hydraulic circuit were used to measure the pumped and overflow water discharges with a relative uncertainty of ±0.5%. The net total discharge of the channel was determined as the difference between these two discharges. The channel was equipped with an upstream and a downstream vertically moving gate to define both the depth and the mean velocity of the flow (Figure 2).

Figure 1.
Image of the laboratory channel.
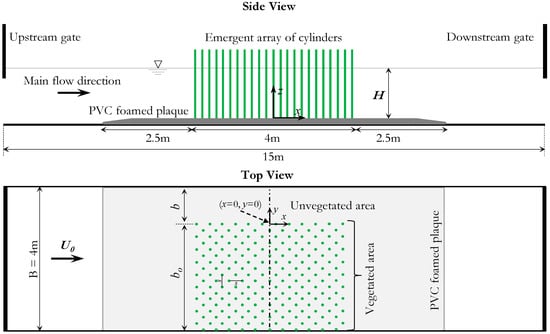
Figure 2.
General sketch of the partly vegetated channel.
Vegetation is a fundamental component of most natural and artificial aquatic environments. Many aquatic plants such as bamboo (subfamily Bambusoideae), reed (Phragmites australis), as well as many trees which typically can tolerate several weeks of flooding, e.g., the red maple (Acer rubrum), river birch (Betula nigra), hackberry (Celtis occidentalis), sweetgum (Liquidambar styraciflua), tupelo or black gum (Nyssa sylvatica), are characterized by trunks (stems) or a complete body of cylindrical shape. To artificially simulate such a type of vegetation, in this study, we used arrays of vertical, rigid, circular, and threaded steel cylinders. The cylinder height, h, was 23.5 cm, and its diameter, d, was 6 mm. The cylinders were inserted into a bottom of PVC foamed plaque 9.0 m long, 4.0 m wide, and 0.02 m thick. The array of cylinders was partially mounted in a lateral part of the channel, forming the experimental area of 4 m length and bo width. A lateral region immediately adjacent to the left (concerning the main flow direction) channel side, of width b, was left for free flow circulation (see Figure 2). In this study, the measurements were carried out with bo = 2.985 m and b = 1.015 m. Four experimental configurations with different flow depths were investigated. The 2.5 m extension of the PVC foamed, both upstream and downstream of the experimental area with arrays of cylinders, helped to minimize flow disturbance. The cylinders were arranged in a uniform staggered array. The longitudinal and transversal space between two adjacent in-lined cylinders was s = 7.5 cm, giving rise to a density, N, of 355.56 cylinders/m2 and a volume solid fraction of the cylinders φ = 0.010.
The origin of the longitudinal x-axis (x = 0) was taken at the mid-distance of the experimental area, while that of the transversal y-axis (y = 0) was taken at the interface between the vegetated and unvegetated areas. The vertical z-axis had its origin at the channel bottom (see Figure 2). Based on previous studies [1,2], the interface boundary shear layer will be fully developed at x = 0. At x = 0, we conducted extensive measurements of the three flow velocity components (u, v, w) at different positions, moving transversally and vertically 2 cm by 2 cm, where u, v, and w are the streamwise, spanwise and vertical velocity components in x-, y-, and z-direction, respectively. Since the flow within the canopy was turbulent and highly heterogeneous at the scale of the individual cylinder, some transverse velocity profiles were also taken with a displacement of 1 cm, rather than 2 cm.
The three flow velocity components were accurately measured using an Acoustic Doppler Velocimeter (ADV)-Vectrino, manufactured by Nortek with a relative uncertainty of ±1%. Using the ADV-Vectrino, a velocity range of ±0.30 m/s, a vertical extension of sampling volume of 7 mm, a sampling rate of 180 Hz, and a time of acquisition of 2 min were established. The acquired data were filtered, and the bad samples (SNR < 15 and correlation coefficient <70%) were removed.
Table 1 illustrates the experimental conditions and some characteristic parameters of this study, where T is the water temperature, H is the flow depth, U0 is the main channel velocity without vegetation presence, U1 is the mean velocity of the vegetated area, obtained as the spatial and time-averaged velocities within the vegetation canopy, U2 is the flow velocity in the free stream zone in the unvegetated area, defined as the spatial and time-averaged velocity along the transversal distance, where the time-averaged streamwise velocity, U(y), reaches almost a constant value. Figure 3 shows a descriptive scheme of the experimental area with the different flow zones. Re0 = U0H/ν is the Reynolds number based on flow depth, Red = U1d/ν is the Reynolds number based on cylinder diameter, and ν is the water kinematic viscosity. For all configurations, the main channel discharge was 100 L/s.

Table 1.
Experimental conditions and some characteristic parameters of this study.
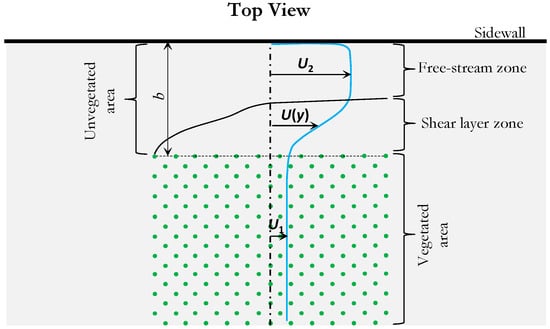
Figure 3.
Descriptive scheme of the experimental area with the different flow zones.
3. Results and Discussion
3.1. Mean Flow and Turbulence Characteristics
Figure 4 shows transversal profiles of the normalized streamwise velocity U/U0 obtained at different vertical positions z/H, varying from 0.02 to 0.68. It is worth mentioning here that due to the probe’s downlooking ADV configuration, approximately the uppermost 7 cm of the flow could not be sampled. In Figure 4, the transversal coordinate y is normalized by the width b of the unvegetated area (see Figure 2 and Figure 3), and the data refer to the C1H22 configuration. Figure 4a displays the U/U0 profiles within the vegetation canopy. It is important to mention that, in Figure 4a, given the difficulty of moving the ADV laterally due to the small gap between the cylinders, the measurements at each y/b position were obtained at the center between four neighboring cylinders, at x = 0, as shown by the dot-dashed line in Figure 2 and Figure 3. Figure 4a highlights that U/U0 at the different y/b positions has a value of the order 0.66, determined as the average of all these velocities and indicated by U1/U0 in Table 1. The spatial and temporal average velocity U1/U0 is considered as the representative mean flow velocity in the vegetated area [1,2,5,25]. Normally, the flow within a vegetation canopy is highly complex, where separation and alteration phenomena occur around stems, forming a wake region at low velocities near the stems [1,6,25]. Moving away from the wake region, the flow velocity undergoes greater values. This implies that, for the C1H22 configuration, a velocity U1/U0 = 0.66 could represent the highest value achievable within the vegetation canopy. Figure 4a exhibits that, due to the drag forces from the cylinder arrays, the main flow velocity magnitude within emergent cylinders decreases by more than 34% compared to the main channel velocity U0.
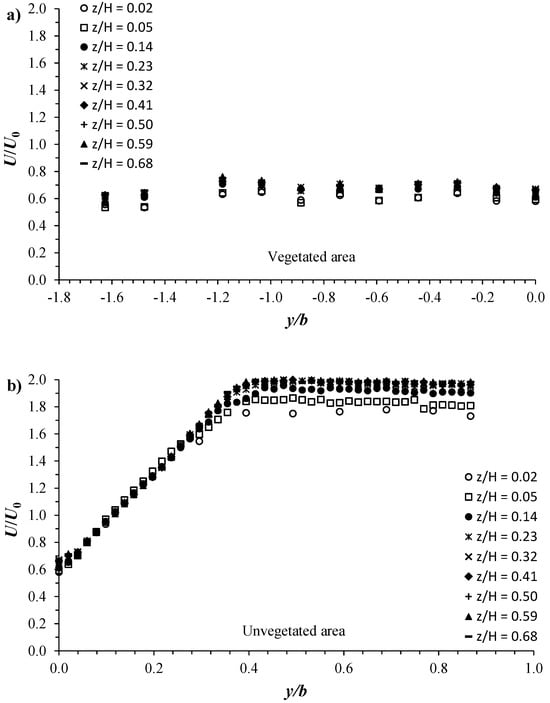
Figure 4.
Transversal streamwise velocity distribution at different vertical positions z/H for the C1H22 configuration (a) in the vegetated area, (b) in the unvegetated area.
Figure 4b shows the transversal profiles of U/U0 in the unvegetated area. Since there are no obstacles in the area without vegetation that prevent the movement of the ADV, we have taken very extensive velocity measurements along the y-direction, displacing with a constant step (Δy/b) of 0.02 from the interface (y = 0) toward the channel wall. Figure 4b shows that, from y/b = 0, U/U0 starts to gradually increase in a curvature manner, of upward concavity, up to y/b = 0.04. From y/b = 0.04 up to 0.28, U/U0 persists to increase almost linearly, collapsing into a single profile for all the vertical positions z/H. From y/b = 0.28 up to almost 0.43, a slight shift appears between the different velocity profiles, and U/U0 continues to increase in a curvature fashion of downward concavity. This hyperbolic distribution of U/U0, from y/b = 0 up to 0.43, characterizes the flow shear layer zone, as shown qualitatively in Figure 3. From y/b = 0.43 going towards the channel wall, U/U0 reaches a maximum value which remains almost constant for each vertical position z/H as y/b varies. This channel flow sector is defined as the free-stream zone with characteristic velocity U2, determined by averaging all measured velocities along this zone (Figure 3). In this flow zone, Figure 4b shows more significant shifts between the different velocity profiles, which are more pronounced with the profiles obtained near the channel bed at z/h = 0.02 to 0.14. The shift level decreases with the increase in z/H. Figure 4 highlights that the streamwise velocity in the free-stream zone is almost three times greater than that in the vegetated area.
To better understand the flow behavior across the partly vegetated channel, in Figure 5, we plot some vertical profiles of U/U0 at four representative transversal locations: (i) y/b = −0.74, in the vegetated area, (ii) y/b = 0, at the interface between the vegetated and unvegetated areas, (iii) y/b = 0.20, in the shear layer zone, and (iv) y/b = 0.49, in the free-stream zone. In the vegetated area and at the interface (y/b = −0.74 and 0), the vertical profiles of U/U0 show comparable trends and values, with a slight decrease in U/U0 at the interface. This slight decrease in U/U0 at the interface can be explained by a slight increase in transversal flow motion, which will be analyzed below. Figure 5 shows that within the emergent vegetated area (y/b ≤ 0), the vertical velocity profiles exhibit an almost null gradient of U/U0 over z/H > 0.05, making the bottom surface boundary layer compressed toward the bed. These results are in good agreement with the findings reported in Ben Meftah and Mossa [6] and Yang et al. [22]. In the shear layer (y/b = 0.20), the streamwise velocity, along the water column, behaves similarly to that in the vegetated zone. Beyond z/H > 0.05, U/U0 also has a null vertical gradient, leading to a downward compression of the bed boundary layer. In the free-stream zone (y/b = 0.49), the vertical profile of U/U0 appears similar to a classical profile in a bare (without vegetation or bedforms) smooth channel, where the velocity typically follows a logarithmic distribution. At y/b = 0.49, U/U0 increases logarithmically until nearly z/H = 0.23 and then flattens upwards. This indicates that in the free-stream zone, the bottom boundary layer is pushed up against the bed, in contrast to what is observed in the vegetated and shear layer zones.
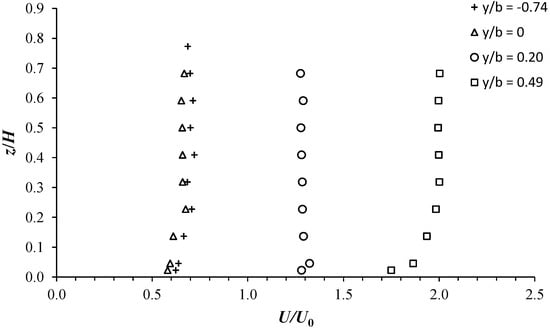
Figure 5.
Vertical profiles of U/U0 at some transversal locations, y/b, representing the different flow zones, for the C1H22 configuration.
In Figure 6, we plot the normalized streamwise velocity U/U0 versus y/b. The data refer to the four configurations C1H12, C1H15, C1H18, and C1H22, obtained at the flow mid-depth z/H = 0.5. Unlike Figure 4a, in Figure 6, we also consider additional data measured in the vegetated area from y/b = 0 to y/b = −0.15, as shown by the enlarged region at the top left of Figure 6. Along this distance, flow velocities at very close lateral positions were recorded by moving the ADV probe with a step of 1 cm (Δy/b ≈ 0.01). To allow the ADV to move laterally within the vegetated area, at the end of each configuration, we specifically removed some cylinders from the row at x = 0, as shown by the descriptive sketch in Figure 6. The similarity between the velocity profiles of the different configurations illustrated in Figure 6 confirms almost the same flow behaviors already analyzed with C1H22, as shown in Figure 4. In the different configurations, the three characteristic flow zones appear, with similar relative velocity distribution. The data of U/U0 illustrated in Figure 6 show more dispersion over the lateral distance from y/b = 0 to −0.15. This data scattering reflects the local effect of cylinders on the flow velocity distribution, due to the development of wake structures in which small-scale shedding vortices (on the order of the cylinder diameter) and intermittent fluid acceleration/deceleration occur [6,23]. Contrary to what was observed with C1H22 (Figure 4) and in previous studies [1,2,5,25], Figure 6 shows that in the free-stream zone, U/U0 is not always constant, but undergoes a slight gradual decrease as y/b increases. This is well pronounced with C1H12 and C1H15 as the flow depth decreases. This important finding requires further analysis, carrying out additional experiments, and will be addressed separately in future work.
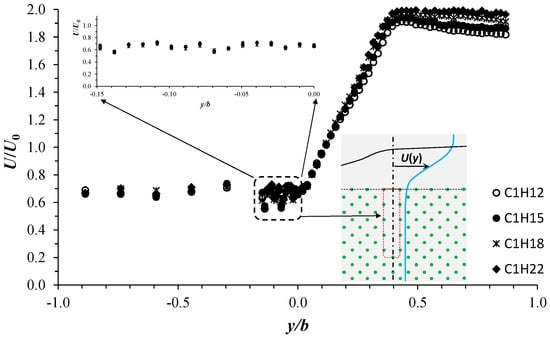
Figure 6.
Transversal profiles of U/U0 at z/H = 0.5, for the four configurations analyzed.
Following the same procedure explained previously in Section 3, Figure 7 displays the normalized spanwise velocity distribution V/U0 of the C1H22 configuration plotted against y/b in both the vegetated and unvegetated areas. Inside the vegetated area, Figure 7a shows that V/U0 attains its smallest values at y/b = −1.6, ranging between 0.02 and 0.04 with the different z/H positions. Going towards the vegetation edge, V/U0 increases polynomially, reaching its maximum at the interface (y/B = 0) with the most profiles. In the unvegetated area, very close to the interface, at y/b = 0.02, a slight sharp decrease in V/U0 occurs. Along the width of the shear layer zone, from y/b = 0.02, V/U0 appears to slightly increase in an almost linear fashion as y/b increases. After reaching its maximum magnitude at the edge of the shear layer zone, in the free-stream zone, V/U0 begins to gradually decrease as one approaches the channel wall. In the vegetated area, Figure 7a shows that V/U0 reaches a maximum magnitude near the channel bed at z/H = 0.02, decreasing with increasing z/H. This behavior is reversed in the shear layer zone, as shown in Figure 7b, where V/U0 is of minimum magnitude near the bed at z/H = 0.02, increasing with increasing z/H.
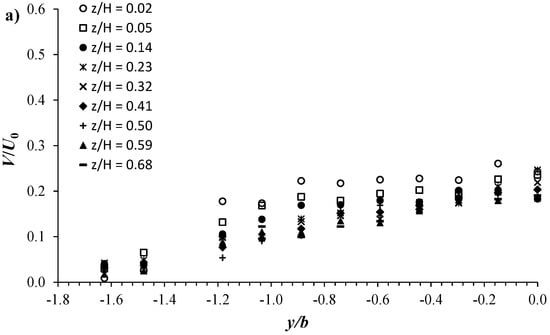
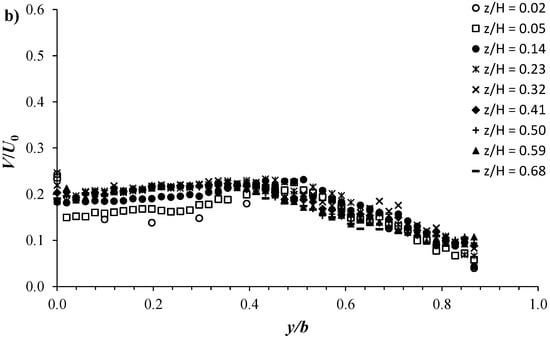
Figure 7.
V/U0 plotted versus y/b at different vertical positions z/H for the C1H22 configuration in the (a) vegetated area and (b) unvegetated area.
Figure 8 illustrates the vertical V/U0 profiles for the C1H22 configuration at four representative transversal positions: within the vegetated area (y/b = −0.74), at the interface between the vegetated and unvegetated areas (y/b = 0), in the shear layer zone (y/b = 0.20), and the free-stream zone (y/b = 0.49). Figure 8 indicates the reversible vertical trend of V/U0 between the vegetated and shear layer zones. At y/b = −0.74 (in the vegetated area), V/U0 shows a value of the order of 0.22 at z/H = 0.02 with an almost decreasing trend as z/H increases (dotted profile), reaching minimal values of O(0.12) for z/H > 0.5. In the shear layer zone (y/b = 0.20), V/U0 shows a value of O(0.14) at z/H = 0.02, increases significantly to a value of O(0.21) at z/H = 0.23, and then remains almost constant with a value of O(22) for z/H > 0.23. At the interface (y/b = 0) and in the free-stream zone (y/b = 0.49), V/U0 behaves almost similarly with comparable values, showing a maximum value around z/H = 0.20 and then decreases as z/H increases. This reverse velocity trend along the vertical between the different flow zones could be explained by the presence of downward flow (due to the obstruction by vegetation) and upward flow (in the shear layer) processes, leading to the development of clockwise and counterclockwise vortex cells along the cross-section of the partially vegetated channel.
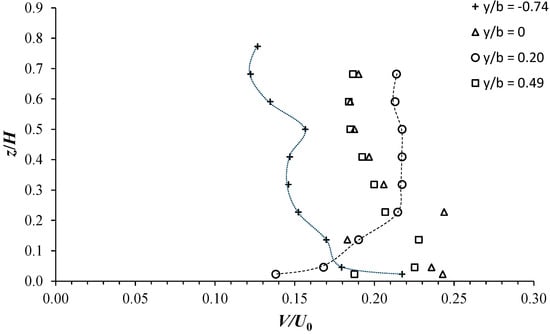
Figure 8.
Vertical profiles of V/U0 at different transversal positions y/b, for the C1H22 configuration.
Figure 9 shows the normalized vertical velocity W/U0 plotted against y/b. The data refer to the configurations C1H12, C1H15, C1H18, and C1H22 obtained at z/H = 0.5. Figure 9 highlights that the vertical velocity component is almost null in most of the different flow zones. The collapse of the transversal profiles of the different configurations into a single profile indicates a complete similarity of the W/U0 distribution as a function of y/b. With the different profiles, illustrated in Figure 9, W/U0 shows a slight V-shape decrease between the shear layer and free-stream zones. W/U0 attains a minimum of O(−0.02) at almost y/b = 0.40, position of the shear layer edge. Despite the small magnitudes of W/U0, in the vegetated area (y/b ≤ 0), most of the W/U0 values are negative, confirming the downward flow process in this region. Along almost half the width of the shear layer, W/U0 exhibits positive values where upward flow occurs; going further toward the channel wall, it becomes negative and then positive again. The alternation of W/U0 between positive and negative values confirms the development of flow vortex structures.
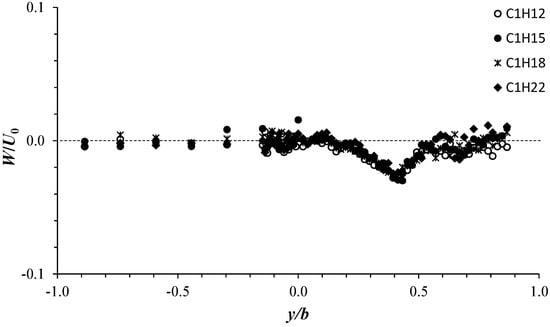
Figure 9.
Transversal profiles of W/U0 at z/H = 0.5 for the four configurations C1H12 to C1H22.
To better understand and predict the impact of vegetation on the flow properties, in Figure 10, we plot the streamwise relative-turbulence intensity U′/U versus the transversal coordinate y/b at various vertical positions z/H for the C1H22 configuration. Herein, U′ (=⟨u′2⟩1/2) is the root mean square of the streamwise velocity fluctuations, u′ is the instantaneous velocity fluctuation, and the bracket indicates the time average. Figure 10a highlights that within the vegetation canopies, U′/U randomly varies with the variation of y/b between values of order 0.2 and 0.45. U′/U shows maximum values further inside the vegetation area at y/b = −1.8 and −1.6, resulting in an almost decreasing trend going towards the interface. From a value of O(0.3) at the interface (y/b = 0), Figure 10b shows that U′/U undergoes a sharp decrease of almost 50% only up to y/b = 0.06. From y/b = 0.06, U′/U decreases monotonically in the shear layer until almost y/b = 0.40. In the free-stream zone, for each vertical position z/H, U′/U shows the smallest intensities which remain almost constant as y/b varies. In the unvegetated area, Figure 10b depicts that U′/U is maximum near the channel bottom (z/H = 0.02), resulting in a decreasing trend with the increase in z/H up to 0.32 and then, an increasing tendency going towards the free-surface flow. This is clearly shown in Figure 11 by the vertical U′/U profiles at y/b = 0.20 and 0.49. In both the shear layer and free-stream zones, the vertical distribution of turbulence U′/U is similar to that obtained in smooth and rough bare channels [27,28]. Figure 11 also highlights, as indicated by the profiles at y/b = −0.74 and 0, the significant effect of cylinder arrays in inducing a further flow perturbation that increases the intensity of turbulence, enhancing mixing and diffusion processes within the vegetated area [18].
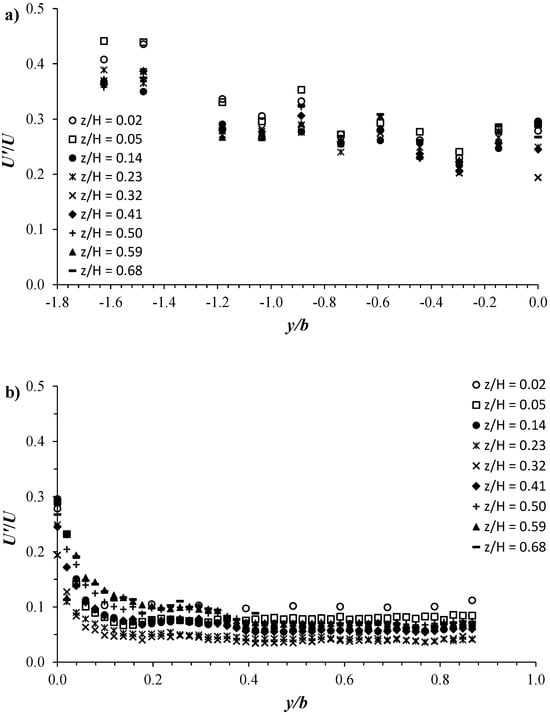
Figure 10.
Transversal profiles of the relative turbulence intensity U′/U at different vertical positions z/H = 0.5 for the C1H22 configuration in the (a) vegetated area and (b) unvegetated area.
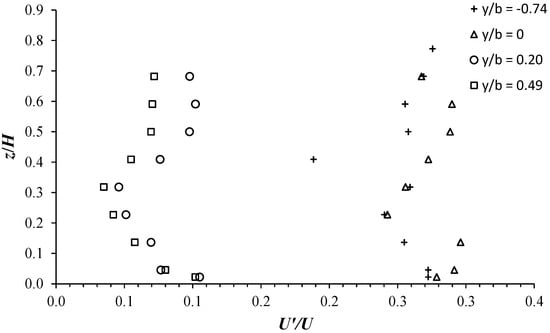
Figure 11.
Vertical profiles of U′/U at different transversal locations for the C1H22 configuration.
In open channel flows, a free surface may be deformed by fluid motions [29,30,31,32], causing significant effects on turbulence structure. Despite the large width of the laboratory channel used for experiments of the present study, we did not observe any surface deformation in the different flow zones. Therefore, the velocity-interface interaction effect is negligible in this study case.
Figure 12 displays the transversal distribution of the flow turbulence intensities V′/U and W′/U at the vertical position z/H = 0.5 for the four configurations C1H12, C1H15, C1H18, and C1H22. Here, V′ (=⟨V′2⟩1/2) and W′ (=⟨W′2⟩1/2) are the root mean square of the spanwise and vertical velocity fluctuations u′ and W′, respectively. It is worth pointing out that in Figure 12, we plot more additional data recorded close to the interface, from y/b = −0.15 to 0, with a lateral step of y/b = 0.01, as clearly explained in Figure 6. Both the spanwise, V′/U, and vertical, W′/U, turbulence intensities have the same tendency of U′/U, as shown in Figure 10. In the vegetated area, V′/U and W′/U show the largest values with notable data dispersion, which is more pronounced along y/b = 0 to −0.15, reflecting the relative effect of proximity to individual stems. In the unvegetated area, the profiles of the turbulence intensities V′/U and W′/U collapse into a single profile, showing an almost harmonic decline trend starting from a maximum magnitude obtained at the interface (y/b = 0). In both the vegetated and unvegetated areas, V′/U shows an intensity comparable to U′/U, while a significant reduction in W′/U can be seen.
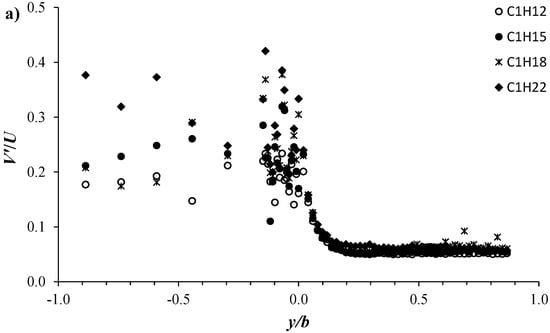
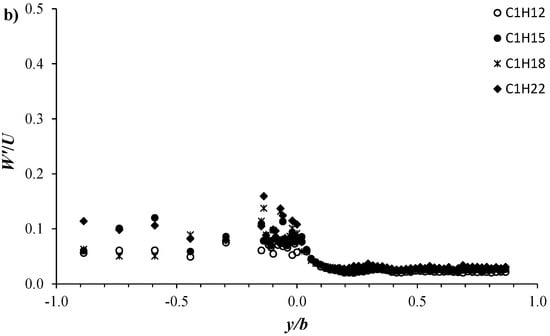
Figure 12.
Transversal profiles of (a) V′/U and (b) W′/U at z/H = 0.5 for the four configurations C1H12 to C1H22.
Figure 13 displays the transversal profiles of the time-averaged turbulent kinetic energy, k = 0.5(U′2 + V′2 + W′2), normalized by the streamwise velocity U at the vertical position z/H = 0.5 for the four configurations C1H12, C1H15, C1H18, and C1H22. The k-profiles in the different flow zones show a trend almost similar to that of the turbulence intensities. In the vegetated zone, k/U experiences scattered values ranging between 0.02 and 0.12. A maximum of k/U is reached at the interface (y/b = 0). Along the shear layer zone, k/U undergoes a rapid decrease up to y/b = 0.20, reaching an almost constant value of the order of 0.005, which also remains invariant along the free-stream zone.
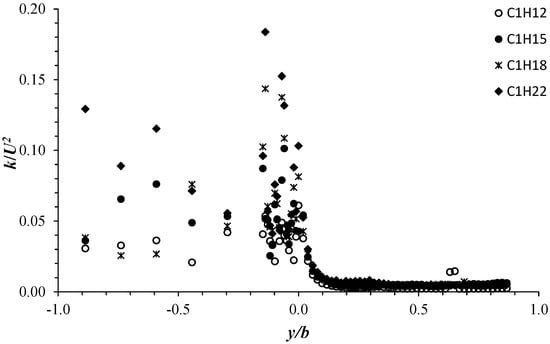
Figure 13.
Transversal profiles of k/U at z/H = 0.5 for the four configurations C1H12 to C1H22.
3.2. Skewness and Kurtosis Factors
To gain further useful information on flow dynamics in the partly vegetated channel, the skewness and kurtosis factors distribution within the vegetated and unvegetated areas were also analyzed. Skewness and kurtosis are important parameters for describing turbulence, such as the turbulent bursting phenomenon. In addition, they are used to ensure the quality of turbulence measurements, indicating the asymmetry, tailedness, or peakedness of a dataset. The bursting phenomenon can be assessed according to the skewness factors, providing information on the flow exchange between vegetated and unvegetated areas [33]. Figure 14 shows the transversal distribution of the skewness and kurtosis factors for the streamwise and spanwise velocity components obtained at mid-depth flow (z/H = 0.5) for the four configurations C1H12, C1H15, C1H18, and C1H22. Herein, we denote by Su and Sv the skewness factors of the streamwise and spanwise velocity components, respectively, while by Ku and Kv, the kurtosis factors. The skewness and kurtosis factors are defined as follows:
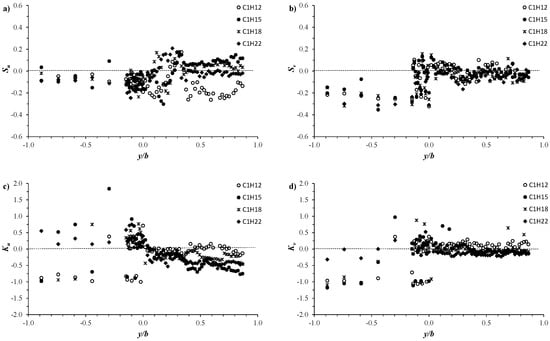
Figure 14.
Transversal profiles of the skewness factor: (a) Su for the streamwise velocity component, (b) Sv for the spanwise velocity component, and kurtosis factor: (c) Ku for the streamwise velocity component, (d) Kv for the spanwise velocity component.
For bursting phenomenon, four types of turbulence events can be classified according to the sign of the skewness factors Su and Sv: (i) outward interaction (Su > 0, and Sv > 0), (ii) ejection (Su < 0, and Sv > 0), (iii) inward interaction (Su < 0, and Sv < 0), and (iv) sweep (Su > 0, and Sv < 0). Figure 14a,b show that, in the vegetated area, both Su and Sv have negative values, indicating the dominance of inward interaction contribution from bursting events. For most data, the absolute magnitude of Sv appears three times larger than that of Su, which is O(0.1). The dominance of this countergradient-type (inward interaction) motion indicates the inward transversal momentum fluxes of low streamwise momentum flow. Around the interface and in the shear layer zone, there is a dominance of outward interactions in addition to ejection contributions, indicating inward transversal momentum fluxes of high/low streamwise momentum flows. In the free-stream zone, Su and Sv show the smallest values, except those for the C1H12 configuration. Su has positive values with the C1H15 and C1H18 configurations and negative values with C1H12 and C1H22, while most of the Sv values are almost negative with the four configurations. This implies that sweeps and inward interactions are mainly bursting events in the free-stream zone, indicating inward transversal momentum fluxes of high/low streamwise momentum flows.
Figure 14c,d display the kurtosis factors Ku and Kv plotted versus the relative positions y/b. Since the presence of cylinder arrays introduce locally very high velocity fluctuation, in the vegetated area, both Ku and Kv show the highest values. Ku alternates between negative values of O(−1) and positive values of O(0.5), while the most Kv values are negative and are O(−1). In the unvegetated area, Ku and Kv are significantly reduced. The most Ku values appear negative, ranging between −0.2 and 0 in the shear layer zone, while they decrease more in the free-stream zone up to values of the order of −0.7.
Figure 14 shows that the Ku and Kv data cover a range around zero, and the excess kurtosis (=Ku/v − 3) is always negative in both the vegetated and unvegetated areas. This implies that the velocity fluctuations have small outliers and an approximately symmetric distribution, reflecting the good quality of the measured data, as shown in Figure 15. In Figure 15, we plot the frequency of the normalized streamwise velocity fluctuation u′/U′ obtained at the vertical position z/H = 0.32 with the C1H22 configuration. The frequency profiles illustrated in Figure 15 represent the different flow zones (see Figure 3): the vegetated area at y/b = −0.89, interface at y/b = 0, shear layer zone at y/b = 0.20, and free-stream zone at y/b = 0.69. Data refer to C1H22 configuration at the vertical position z/H = 0.32. Figure 15 highlights that the u′/U′ values are distributed according to a Gauss law with mean zero, affirming the high quality of acquired data in the different flow zones.
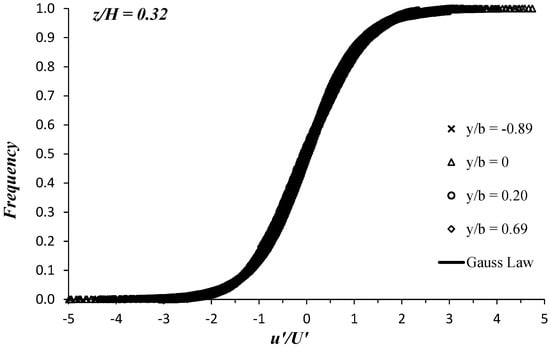
Figure 15.
Gaussian frequency distribution of the streamwise velocity fluctuation in the vegetated area (y/b = −0.89), interface (y/b = 0), shear layer zone (y/b = 0.20), and free-stream zone (y/b = 0.69). Data refer to the C1H22 configuration at the vertical position z/H = 0.32.
3.3. Power Spectral Density Analysis
Figure 16 presents the power spectral density, PSD, of the instantaneous streamwise and spanwise velocities at four transverse locations representative of the different flow zones: (i) in the vegetated area (y/b = −0.89), (ii) at the interface (y/b = 0), (iii) in the shear layer zone (y/b = 0.20), and (iv) in the free-stream zone (y/b = 0.69). The data were obtained at the vertical location z/H = 0.32 with the C1H22 configuration. In Figure 16, we indicate with the solid lines the power spectra of the streamwise velocity, while with the dashed lines, that of the spanwise velocity. The PSD reflects the turbulence kinetic energy of flow eddies at different frequency, f, values. Figure 16 shows almost comparable values of the PSD in the vegetated area (y/b = −0.89) and at the interface (y/b = 0). For a cylinder with a diameter of 6 mm and a Reynolds number Red = 510 (Table 1), the Strouhal number (St = fL/U1) is approximately constant at 0.21 [6,34], where L is a characteristic length of the vortex size. In the vegetated area (y/b ≤ 0), previous studies (e.g., [6,30]) found that L is close to the diameter of the individual vegetation stem. Therefore, and considering L = 6 mm, the shedding frequency, in the vegetated area, falls at an approximate value of O(2.6 Hz). For the present study, the characteristic eddy length-scale was simply calculated as the integral time scale times the local time-averaged velocity, where the time scale is computed integrating the autocorrelation of the measured instantaneous flow velocities. In the vegetated area, as an example, the normalized integral length scale Lx/d, in the x-direction, is O(1), while in the unvegetated area, it is O(10 to 14). The frequency order (2.6 Hz) corresponds to the scaling subrange, characterized by the largest vortex sizes, also known as the energy-containing production range. The production range is often characterized by a −3/2 spectral slope [6], as in the case of SPDs, with a frequency between 2 and 7 Hz, obtained at y/b = −0.89 and 0. Within the vegetation canopy (y/b ≤ 0), Figure 16 shows that the PSD experiences a peak at a frequency of 2.9 Hz, reflecting the influence of O(d)-scale von Karman vortices, shedding from the cylinders due to Kelvin Helmholtz instability. For y/b ≤ 0, the PSD exhibits a Kolmogorov slope of −5/3 with a frequency ranging almost between 7 and 20 Hz. In the vegetated area, the PSD shows comparable values for both the streamwise and spanwise velocity components.
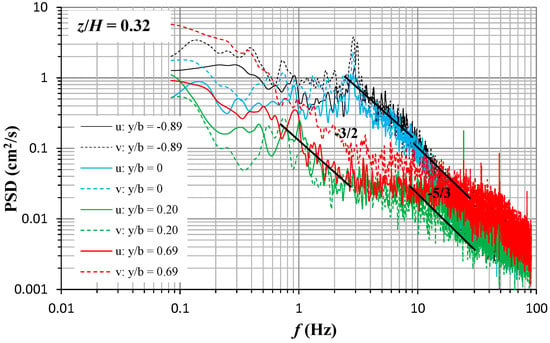
Figure 16.
Power spectral density of the streamwise and spanwise velocities at four transverse representative locations: in the vegetated area (y/b = −0.89), at the interface (y/b = 0), in the sheer layer zone (y/b = 0.20), and in the free-stream zone (y/b = 0.69). The solid line represents the spectra of streamwise velocity, while the dashed line represents that of the spanwise velocity. Data refer to the C1H22 configuration at z/H = 0.32.
At y/b = 0.20 and 0.69, the PSD expresses lower values than the vegetated area in a frequency range below 10 Hz. The PSD exhibits a driving (production) range with a frequency ranging between almost 0.6 and 3 Hz. At 3 < f < 7 Hz, a less steep slope of the PDS occurs, followed by an inertial range with a −5/3 slope, appearing in a frequency range between 7 and 30 Hz. Figure 16 shows that the PSD of the streamwise and spanwise velocities are comparable in the shear layer zone (y/b = 0.20), while, in the free-stream zone, the PSD of the spanwise velocity component exhibits greater values. This implies that, in the free-stream zone, the spanwise velocity undergoes a greater intensity of fluctuation than the streamwise velocity components, as also confirmed by a variation of U′/U and V′/U around 0.03 and 0.05, respectively.
3.4. Vortex Identification
The interaction between the emergent vegetated and the free-stream regions creates a sharp velocity gradient resulting in the development of vertical and lateral mixing-layers controlling mass and momentum exchange [35]. According to Unigarro Villota et al. [35], the mixing-layer width is found to be larger in the transversal direction than in the vertical one, and inversely proportional to the vegetation density. The authors also emphasized the evolution of downward and upward flows respectively in the vegetated and non-vegetated regions, which is in good agreement with the results of this study discussed in Section 3.1. The downwelling and upwelling flows give rise to the development of vortex structure in the vertical cross-plane (y-z). To confirm the presence of vortical structures in the cross-plane (y-z), we applied the well-known vortex identification method Q-criterion [36]. The Q-criterion is derived directly from the velocity gradient tensor analysis and calculated using the detailed measured velocity data obtained in the unvegetated area (y/b ≥ 0). In the vegetated area, the available data are not sufficient to calculate the Q-criterion, due to the difficulty of moving the ADV with a step at the scale of the diameter of vegetation stems. The Q-criterion is defined as the difference between the vorticity magnitude, Ω, and the magnitude of the strain rate, Sv, resulting as Qcr = 0.5(|Ω|2 − |Sv|2) = −0.5[(∂V/∂y)2 + [(∂W/∂z)2] − (∂V/∂z)(∂W/∂y).
Figure 17 shows the values of the Q-criterion for the C1H22 configuration at different vertical positions z/H. The positive values of Qcr indicate the predominance of the vorticity compared to the strain rate and therefore the existence of a vortex, while the negative ones indicate a predominance of the velocity strain rate. Despite the predominance of velocity strain rate at most positions along the vertical plane (y-z), Qcr experiences positive values at several positions, indicating the development of vortex structure through the unvegetated area. Figure 17 indicates that Qcr undergoes more positive values at the vertical positions of z/H ≤ 50. This implies that most vortices occur in the flow mid-depth, near the bottom of the channel.
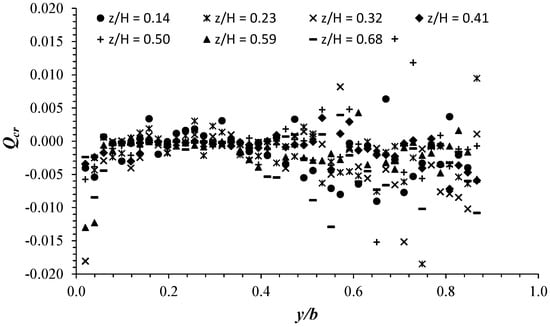
Figure 17.
Distribution of the Qcr values in the cross-plane (y-z) at the unvegetated area at x = 0.
4. Conclusions
The transverse velocity distributions across the partly vegetated channel revealed the existence of three characteristic flow zones: (i) a vegetated zone, characterized by lower U-velocity, due to high drag from the cylinder arrays, (ii) a shear layer zone, along which the U-velocity increases hyperbolically up to a maximum value, and (iii) a free-stream zone of maximum and homogeneous velocity.
The vertical profiles of the streamwise velocity at the different flow zones highlighted that, in the vegetated and shear layer zones, U/U0 shows constant magnitude along the water column and has a null gradient, making the bottom surface boundary layer compressed toward the bed. In the free-stream zone, U/U0 follows a logarithmic distribution similar to that typically obtained in a smooth/rough bare open channel flow (without vegetation or bottom shape), pushing the bottom boundary layer upwards against the channel bed.
The experimental results showed a significant transversal flow diversion toward the unvegetated area, caused by the additional flow resistance by the cylinder arrays. This results in an increase in V/U0 in the vegetated and shear layer zones, going towards the channel wall, while there is a decrease in the free-stream zone. The vertical profile of V/U0 showed a reversible tendency between the different flow zones. V/U0 has a decreasing profile from the bed towards the flow-free surface in the vegetated area, an increasing profile in the shear layer zone, and a decreasing profile in the free-stream zone from a maximum reached at a location close to the bed.
The different flow zones in the partly vegetated channel are characterized by negligible vertical velocity components, and the flow is mostly governed by the longitudinal and transversal components. Despite its tiny magnitude, W/U0 had ascending and descending flow zones, leading to the development of vortical structures.
In the vegetated area, the transversal distribution of the three turbulence intensities U′/U, V′/U, and W′/U were influenced by the relative proximity to individual stems, showing the largest values. In the unvegetated area, however, they decreased exponentially in the shear layer, going from the interface (y/b = 0) towards the channel wall, reaching almost constant minimum values along the free-flow zone. In the unvegetated area, the vertical distribution of the streamwise turbulence intensities is similar to that obtained in smooth/rough bare open channels. In both the vegetated and unvegetated areas, U′/U and V′/U are of comparable intensities, while a significant reduction in W′/U was observed.
Results showed that the inward interactions are mainly bursting events in the vegetated area. At the interface and in the shear layer zone, ejection actions and outward interactions are more reproducible, while sweeps and inward interactions are the most bursting events in the free-stream zone. In both the vegetated and unvegetated areas, the Ku and Kv data cover a range around zero, and the excess kurtosis of the streamwise and spanwise velocity components is always negative, implying small outliers and an approximately symmetric distribution of velocity fluctuations reflecting the good quality of the measured data.
The power spectral density analysis conducted in the different characteristic flow zones indicated a notable difference between the vegetated and non-vegetated areas with the lowest frequency range, while in the highest frequency range, the spectra are very similar to each other. The velocity spectrum exhibits a −3/2 slope in the scaling subrange with a frequency between 2 and 7 Hz and in the vegetated area, showing higher values. In the unvegetated area, the SPD exhibits the same slope (−3/2) in a frequency ranging between 0.6 and 3 Hz. For both the vegetated and unvegetated flow regions, the SPD obeys a Kolmogorov −5/3 law at a frequency ranging almost between 7 and 30 Hz.
The detailed velocity fields are analyzed through the application of the Q-criterion vortex identification method. The Qcr analysis confirms the development of vortex structures in the unvegetated area, where detailed data were acquired. Most vortices occur at z/H ≤ 50 near the boundaries of the channel bottom.
In summary, the results of the present study will provide a valuable reference for numerical modeling and management of partly vegetated channels. Further testing scenarios and detailed turbulence analysis are also planned for future studies, including more specific flow conditions by varying the width of vegetated/unvegetated areas. Furthermore, it is recommended to consider any field observations with different vegetation properties and under different meteorological conditions to obtain a more complete description of the hydrodynamic process.
Author Contributions
M.B.M. and D.A.B. designed and performed the experiments—methodology, formal analysis—study design—writing—original draft preparation, D.D.P. and M.M. contributed suggestions—discussions and reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to copyright protection.
Acknowledgments
This study was carried out at the Coastal Engineering Laboratory of the Department of Civil, Environmental, Building Engineering and Chemistry at the Polytechnic University of Bari, Italy.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Ben Meftah, M.; De Serio, F.; Mossa, M. Hydrodynamic behavior in the outer shear layer of partly obstructed open channels. Phys. Fluids 2014, 26, 065102. [Google Scholar] [CrossRef]
- Ben Meftah, M.; Mossa, M. Partially obstructed channel: Contraction ratio effect on the flow hydrodynamic structure and prediction of the transversal mean velocity profile. J. Hydrol. 2016, 542, 87–100. [Google Scholar] [CrossRef]
- Ben Meftah, M.; Mossa, M. Discharge prediction in partly vegetated channel flows: Adaptation of IDCM method with a curved interface and large-scale roughness elements. J. Hydrol. 2023, 616, 128805. [Google Scholar] [CrossRef]
- Arora, S.; Patel, H.K.; Srinivasulu, G.; Kumar, B. Turbulent characteristics at interface of partly vegetated alluvial channel. Int. J. Civ. Eng. 2023, 22, 75–85. [Google Scholar] [CrossRef]
- White, B.L.; Nepf, H.M. Shear instability and coherent structures in shallow flow adjacent to a porous layer. J. Fluid Mech. 2007, 593, 1–32. [Google Scholar] [CrossRef]
- Ben Meftah, M.; Mossa, M. Prediction of channel flow characteristics through square arrays of emergent cylinders. Phys. Fluids 2013, 25, 045102. [Google Scholar] [CrossRef]
- Hamidifar, H.; Omid, M.H.; Keshavarzi, A. Longitudinal dispersion in waterways with vegetated floodplain. Ecol. Eng. 2015, 84, 398–407. [Google Scholar] [CrossRef]
- Ben Meftah, M. Flow hydrodynamic in open channels: A constantly evolving topic. Water 2023, 14, 4120. [Google Scholar] [CrossRef]
- Tisserant, M.; Bourgeois, B.; González, E.; Evette, A.; Poulin, M. Controlling erosion while fostering plant biodiversity: A comparison of riverbank stabilization techniques. Ecol. Eng. 2021, 172, 106387. [Google Scholar] [CrossRef]
- Li, Q.; Wang, L.; Ma, X.; Nie, R. Experimental study of the effects of riverbank vegetation conditions on riverbank erosion processes. Environ. Fluid Mech. 2023, 23, 621–632. [Google Scholar] [CrossRef]
- Peng, B.; Shi, B.; Wang, Y.P.; Li, J.; Zhang, X.; Liu, X.; Mo, L.; Shen, A.; Ding, Y. Establishment and application of ecological health evaluation system for urban and rural rivers in Yangtze Estuary. Anthr. Coasts 2023, 6, 9. [Google Scholar] [CrossRef]
- Garner, G.; Malcolm, I.A.; Sadler, J.P.; Hannah, D.M. The role of riparian vegetation density, channel orientation and water velocity in determining river temperature dynamics. J. Hydrol. 2017, 553, 471–485. [Google Scholar] [CrossRef]
- Huai, W.; Yang, L.; Guo, Y. Analytical solution of suspended sediment concentration profile: Relevance of dispersive flow term invegetated channels. Water Resour. Res. 2020, 56, e2019WR027012. [Google Scholar] [CrossRef]
- Wang, M.; Mi, S.; Avital, E.; Li, N.; Chen, Y.; Williams, J. A study on the influence of submergence ratio on the transport of suspended sediment in a partially vegetated channel flow. Water Resour. Res. 2023, 59, e2022WR032876. [Google Scholar] [CrossRef]
- Massicotte, P.; Bertolo, A.; Brodeur, P.; Hudon, C.; Mingelbier, M.; Magnan, P. Influence of the aquatic vegetation landscape on larval fish abundance. J. Great Lakes Res. 2015, 41, 873–880. [Google Scholar] [CrossRef]
- Penna, N.; Coscarella, F.; D’Ippolito, A.; Gaudio, R. Bed roughness effects on the turbulence characteristics of flows through emergent rigid vegetation. Water 2020, 12, 2401. [Google Scholar] [CrossRef]
- Lou, S.; Wang, H.; Liu, H.; Zhong, G.; Radnaeva, L.D.; Nikitina, E.; Ma, G.; Liu, S. Laboratory study of the effects of flexible vegetation on solute diffusion in unidirectional flow. Environ. Sci. Eur. 2021, 33, 80. [Google Scholar] [CrossRef]
- Huai, W.; Xue, W.; Qian, Z. Large-eddy simulation of turbulent rectangular open-channel flow with an emergent rigid vegetation patch. Adv. Water Resour. 2015, 80, 30–42. [Google Scholar] [CrossRef]
- Nezu, I.; Onitsuka, K. Turbulent structures in partly vegetated open-channel flows with LDA and PIV measurements. J. Hydraul. Res. 2001, 39, 629–642. [Google Scholar] [CrossRef]
- Rahimi, H.; Fael, C.M.S.; Taborda, C.S.B.; Yuan, S.; Tang, X.; Singh, P.K.; Fardoost, E.; Santos, C.A.V. Numerical modelling of turbulence kinetic energy in open channel flows with mixed-layer vegetation. Water 2023, 15, 2544. [Google Scholar] [CrossRef]
- Wang, S.; Zhuo, J.; Jia, L.; Deng, L.; Wang, H.; Han, Y. Simulation of pollutant diffusion in vegetation open channel based on LBM-CA method. Environ. Sci. Pollut. Res. 2023, 30, 71252–71269. [Google Scholar] [CrossRef]
- Yang, J.Q.; Kerger, F.; Nepf, H.M. Estimation of the bed shear stress in vegetated and bare channels with smooth beds. Water Resour. Res. 2015, 51, 3647–3663. [Google Scholar] [CrossRef]
- White, B.L.; Nepf, H.M. Scalar transport in random cylinder arrays at moderate Reynolds number. J. Fluid Mech. 2003, 487, 43–79. [Google Scholar] [CrossRef]
- Elzahry, E.F.M.; Eltoukhy, M.A.R.; Abdelmoaty, M.S.; Eraky, O.M.; Shaaban, I.G. Effect of rigid aquatic bank weeds on flow velocities and bed morphology. Water 2023, 15, 3173. [Google Scholar] [CrossRef]
- White, B.L.; Nepf, H.M. A vortex-based model of velocity and shear stress in a partially vegetated shallow channel. Water Resour. Res. 2008, 44, W01412. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Z.; Dai, L.; Xu, W. Influence of vegetation on turbulence characteristics and Reynolds shear stress in partly vegetated channel. J. Fluids Eng. 2015, 137, 061201. [Google Scholar] [CrossRef]
- Blinco, P.H.; Partheniades, E. Turbulence characteristics in free surface flows over smooth and rough boundaries. J. Hydraul. Res. 1971, 9, 43–71. [Google Scholar] [CrossRef]
- Wang, J.J.; Dong, Z.N. Open-channel turbulent flow over non-uniform gravel beds. Appl. Sci. Res. 1996, 56, 243–254. [Google Scholar] [CrossRef]
- Brocchini, M.; Peregrine, D.H. The dynamics of strong turbulence at free surfaces. Part 1. Description. J. Fluid Mech. 2001, 449, 225–254. [Google Scholar] [CrossRef]
- Brocchini, M.; Peregrine, D.H. The dynamics of strong turbulence at free surfaces. Part 2. Free-surface boundary conditions. J. Fluid Mech. 2001, 449, 255–290. [Google Scholar] [CrossRef]
- Wacławczyk, M.; Wacławczyk, T. A priori study for the modelling of velocity–interface correlations in the stratified air-water flows. Int. J. Heat Fluid Flow 2015, 52, 40–49. [Google Scholar] [CrossRef]
- Smolentsev, S.; Miraghaie, R. Study of a free surface in open-channel water flows in the regime from weak to strong turbulence. Int. J. Multiph. Flows 2005, 31, 921–939. [Google Scholar] [CrossRef]
- Huang, T.; He, M.; Hong, K.; Lin, Y.; Jiao, P. Effect of rigid vegetation arrangement on the mixed layer of curved channel flow. J. Mar. Sci. Eng. 2023, 11, 213. [Google Scholar] [CrossRef]
- Huai, W.X.; Zhang, J.; Wang, W.J.; Katul, G.G. Turbulence structure in open channel flow with partially covered artificial emergent vegetation. J. Hydrol. 2019, 573, 180–193. [Google Scholar] [CrossRef]
- Unigarro Villota, S.; Ghisalberti, M.; Philip, J.; Branson, P. Characterizing the three-dimensional flow in partially vegetated channels. Water Resour. Res. 2023, 59, e2022WR032570. [Google Scholar] [CrossRef]
- Zhan, J.M.; Li, Y.T.; Wai, W.H.O.; Hu, W.Q. Comparison between the Q criterion and Rortex in the application of an in-stream structure. Phys. Fluids 2019, 31, 121701. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).