A Generalization of the Drainage Capacity in Data-Scarce Urban Areas: An Improved Equivalent Infiltration Method
Abstract
1. Introduction
2. Materials and Methods
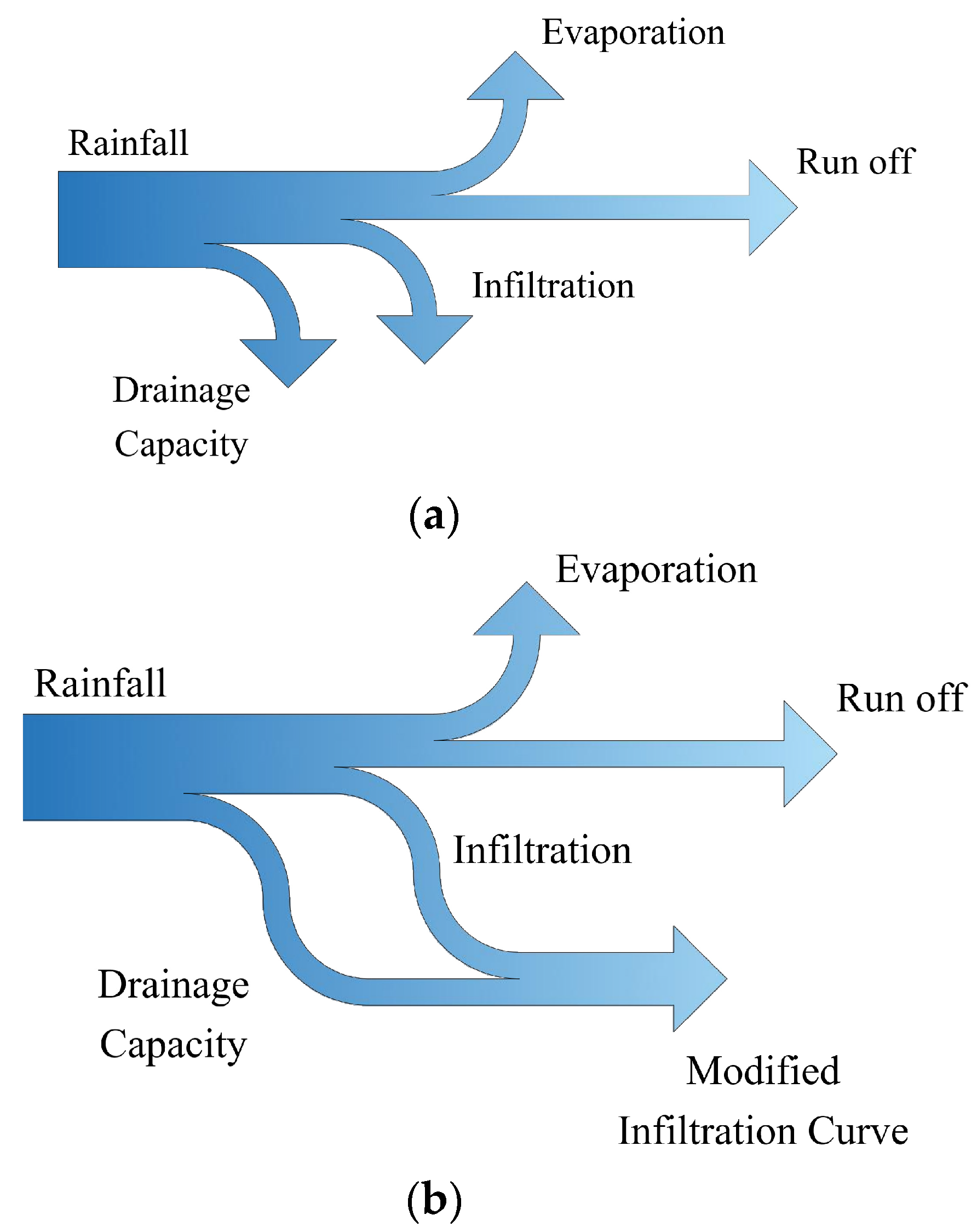
2.1. Principle of the MEI
2.2. Evaluation Indicators
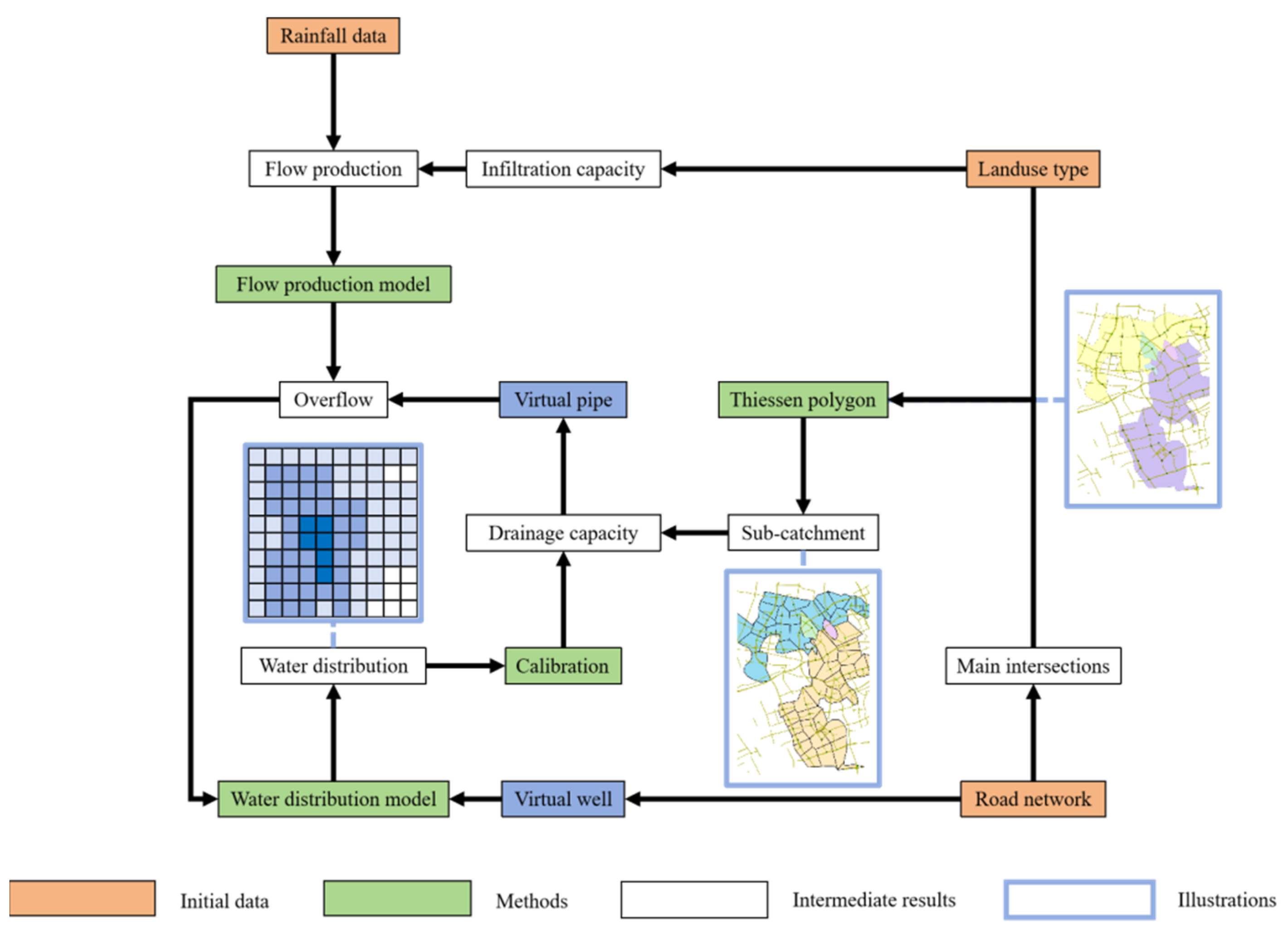
2.3. Preprocessing of Data
3. Case Study
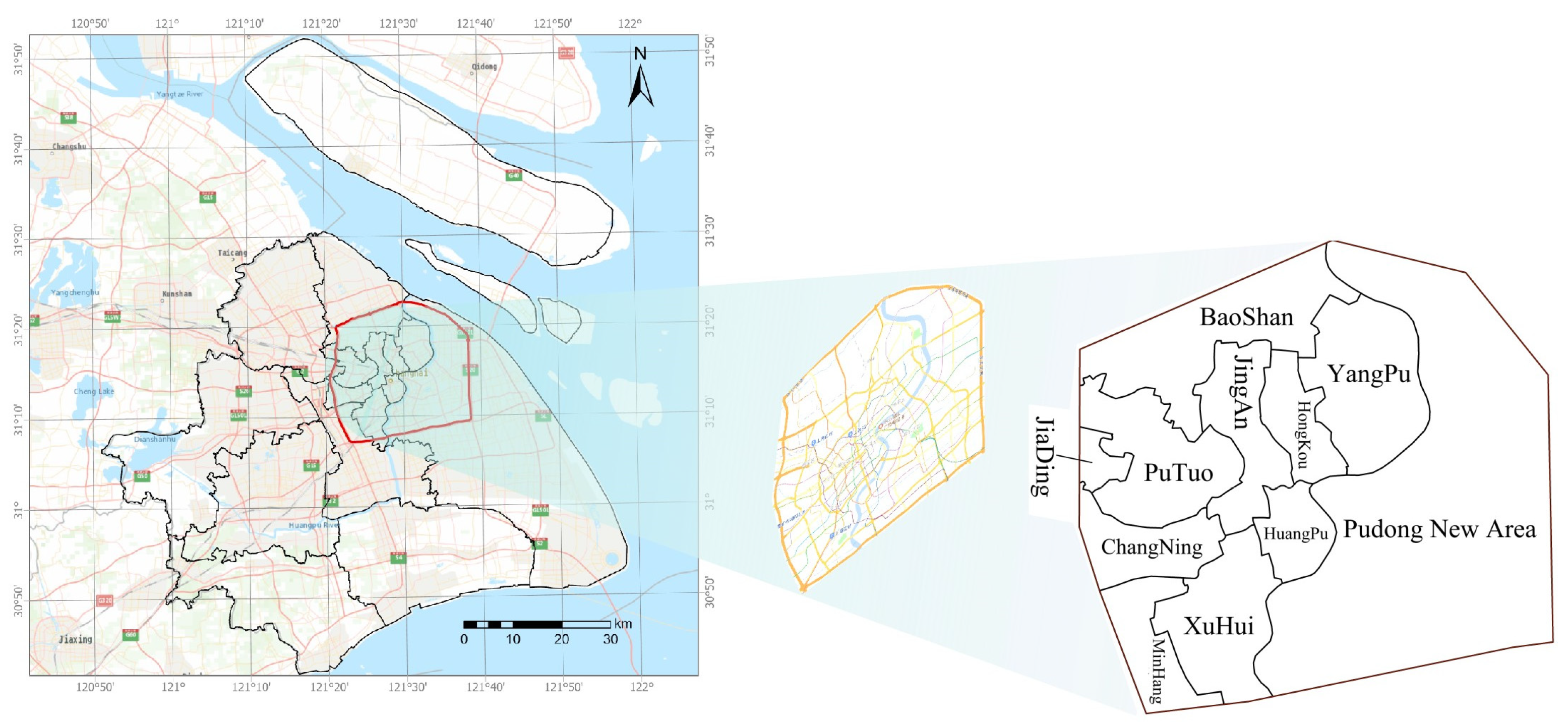
Research Site
4. Results and Discussion
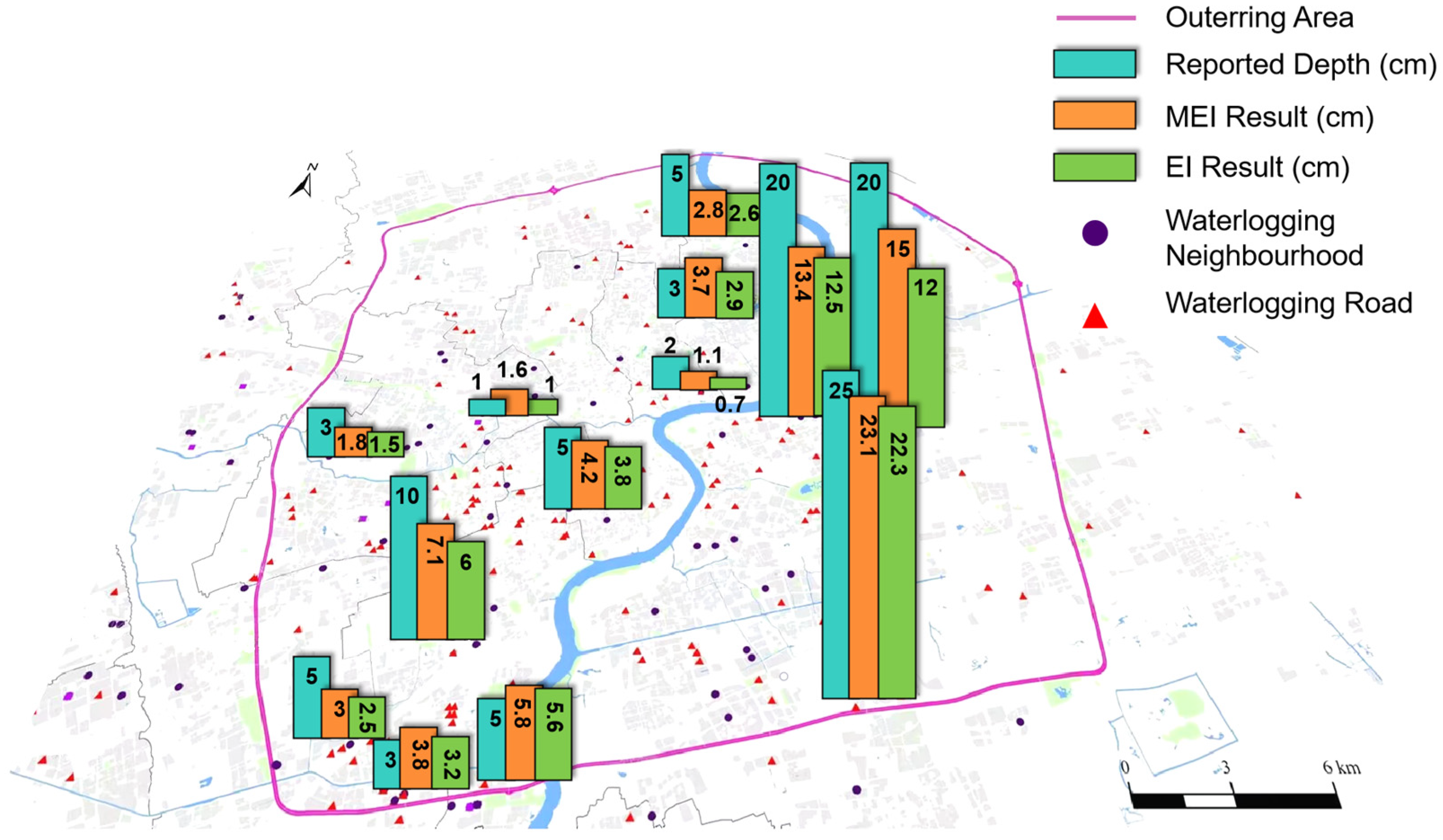
4.1. Model Validation
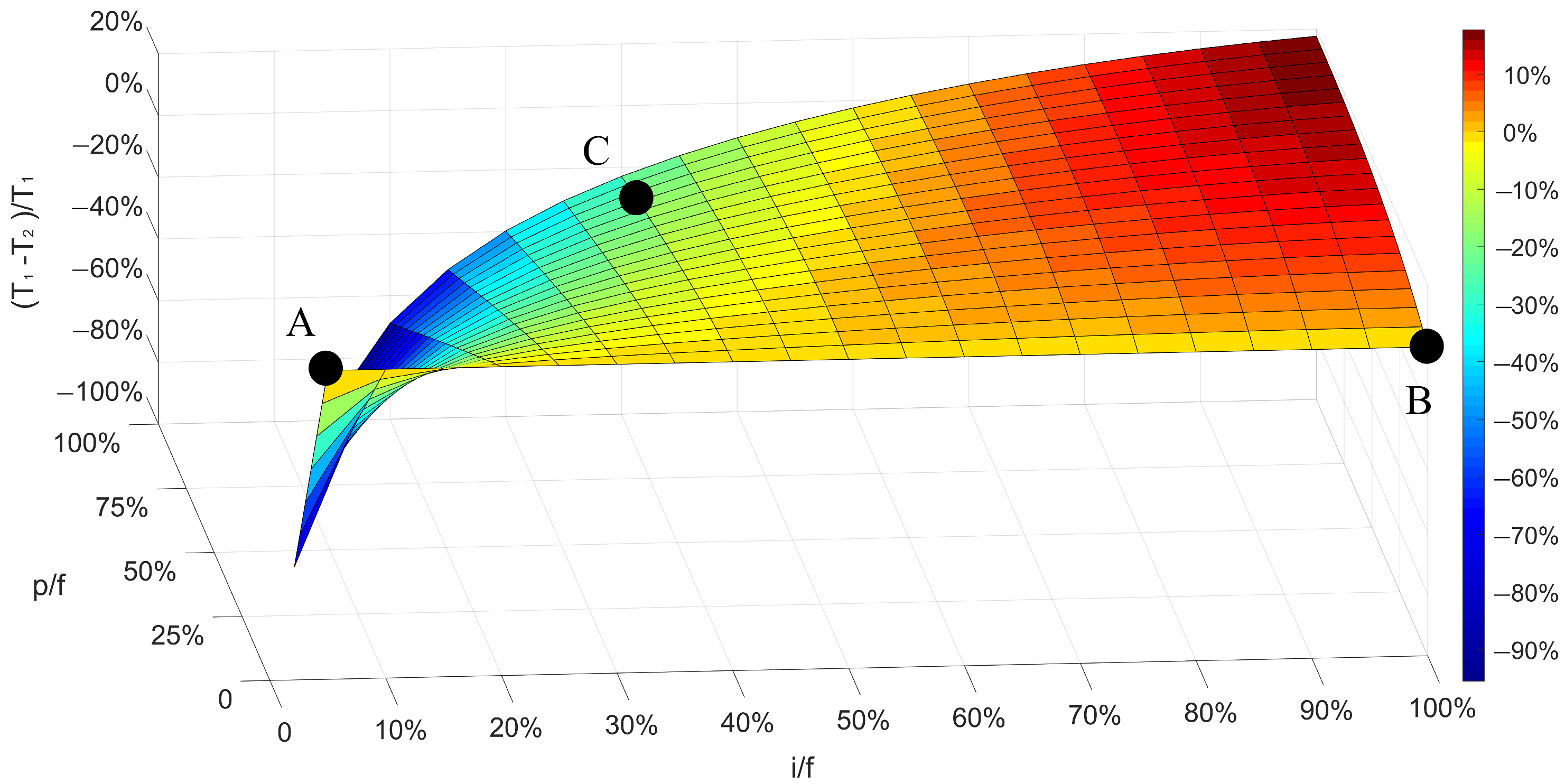
4.2. Comparison of EI and MEI
4.3. Effect of Spatial Distribution of Virtual Well
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.; Dutta, D.; Kim, S.J.E.M. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Bernet, D.B.; Prasuhn, V.; Weingartner, R. Surface water floods in Switzerland: What insurance claim records tell us about the damage in space and time. Nat. Hazards Earth Syst. Sci. 2017, 17, 1659–1682. [Google Scholar] [CrossRef]
- Moncoulon, D.; Veysseire, M.; Naulin, J.P.; Wang, Z.X.; Tinard, P.; Desarthe, J.; Déqué, M. Modelling the evolution of the financial impacts of flood and storm surge between 2015 and 2050 in France. Int. J. Saf. Secur. Eng. 2016, 6, 141–149. [Google Scholar] [CrossRef][Green Version]
- Chen, P.; Wang, Z.; Zeng, Z.; Chen, X. Assessing influence of future urbanization on hydrological process in typical river basin. J. Hydroelectr. Eng. 2020, 39, 69–77. (In Chinese) [Google Scholar] [CrossRef]
- Mignot, E.; Li, X.; Dewals, B. Experimental modelling of urban flooding: A review. J. Hydrol. 2019, 568, 334–342. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, Z.; Guo, G.; Zhang, H.; Tarolli, P. Explicit the urban waterlogging spatial variation and its driving factors: The stepwise cluster analysis model and hierarchical partitioning analysis approach. Sci. Total Environ. 2021, 763, 143041. [Google Scholar] [CrossRef]
- Xia, J.; Zhang, Y.; Liang, C.; Liu, J. Review on urban storm water models. Eng. J. Wuhan Univ. 2018, 51, 95–105. [Google Scholar] [CrossRef]
- Armson, D.; Stringer, P.; Ennos, A.R. The effect of street trees and amenity grass on urban surface water runoff in Manchester, UK. Urban For. Urban Green. 2013, 12, 282–286. [Google Scholar] [CrossRef]
- Skotnicki, M.; Sowiński, M. The influence of depression storage on runoff from impervious surface of urban catchment. Urban Water J. 2015, 12, 207–218. [Google Scholar] [CrossRef]
- Li, S.; Wang, Z.; Lai, C.; Wu, X.; Chen, X.; Lin, G.; Zhao, J. Hydrological effect simulation of LID-underground integrated pipe corridors in Yangmei River Basin. Water Resour. Prot. 2022, 38, 68–75. [Google Scholar] [CrossRef]
- Niu, Y. Rainwater Pipe Network and Waterlogging Risk Assessment of Airport Traffic Area Based on SWMM and MIKE Model. J. Munic. Technol. 2022, 40, 242–245. (In Chinese) [Google Scholar] [CrossRef]
- Qiu, R.; Cao, J.; Zhang, X. Parameter Selection of Pollutant Module in SWMM Model Based on the Study of Non-Point Source Pollutants in Old Residential Areas. China Munic. Eng. 2022, 4, 51–54. (In Chinese) [Google Scholar] [CrossRef]
- Szeląg, B.; Suligowski, R.; De Paola, F.; Siwicki, P.; Majerek, D.; Łagód, G. Influence of urban catchment characteristics and rainfall origins on the phenomenon of stormwater flooding: Case study. Environ. Model. Softw. 2022, 150, 105335. [Google Scholar] [CrossRef]
- Guo, K.; Guan, M.; Yu, D. Urban surface water flood modelling–a comprehensive review of current models and future challenges. Hydrol. Earth Syst. Sci. 2021, 25, 2843–2860. [Google Scholar] [CrossRef]
- Kratt, C.B.; Woo, D.K.; Johnson, K.N.; Haagsma, M.; Kumar, P.; Selker, J.; Tyler, S. Field trials to detect drainage pipe networks using thermal and RGB data from unmanned aircraft. Agric. Water Manag. 2020, 229, 105895. [Google Scholar] [CrossRef]
- Okwori, E.; Pericault, Y.; Ugarelli, R.; Viklander, M.; Hedström, A. Data-driven asset management in urban water pipe networks: A proposed conceptual framework. J. Hydroinform. 2021, 23, 1014–1029. [Google Scholar] [CrossRef]
- Sitzenfrei, R.; Möderl, M.; Rauch, W. Assessing the impact of transitions from centralised to decentralised water solutions on existing infrastructures–Integrated city-scale analysis with VIBe. Water Res. 2013, 47, 7251–7263. [Google Scholar] [CrossRef]
- Tscheikner-Gratl, F.; Caradot, N.; Cherqui, F.; Leitão, J.P.; Ahmadi, M.; Langeveld, J.G.; Clemens, F. Sewer asset management–state of the art and research needs. Urban Water J. 2019, 16, 662–675. [Google Scholar] [CrossRef]
- Mohammadiun, S.; Yazdi, J.; Hager, J.; Salehi Neyshabouri, S.A.A.; Sadiq, R.; Hewage, K.; Alavi Gharahbagh, A. Effects of bottleneck blockage on the resilience of an urban stormwater drainage system. Hydrol. Sci. J. 2020, 65, 281–295. [Google Scholar] [CrossRef]
- Barton, N.A.; Hallett, S.H.; Jude, S.R. The challenges of predicting pipe failures in clean water networks: A view from current practice. Water Supply 2022, 22, 527–541. [Google Scholar] [CrossRef]
- Chang, X.; Xu, Z.; Zhao, G.; Du, L. Urban rainfall-runoff simulations and assessment of low impact development facilities using swmm model—A case study of qinghe catchment in beijing. J. Hydroelectr. Eng. 2016, 35, 84–93. [Google Scholar]
- Ma, M.; Li, J.; Deng, C. Analysis of urban waterlogging and pollution load based on swmm model. J. Hydroelectr. Eng. 2017, 36, 62–72. (In Chinese) [Google Scholar] [CrossRef]
- Wu, L.; Tajima, Y.; Sanuki, H.; Shibuo, Y.; Furumai, H. A novel approach for determining integrated water discharge from the ground surface to trunk sewer networks for fast prediction of urban floods. J. Flood Risk Manag. 2022, 15, e12773. [Google Scholar] [CrossRef]
- Wang, H.; Hu, Y.; Guo, Y.; Wu, Z.; Yan, D. Urban flood forecasting based on the coupling of numerical weather model and stormwater model: A case study of Zhengzhou city. J. Hydrol. Reg. Stud. 2022, 39, 100985. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Huang, Q.; Xia, J.; Li, J.; Liu, D.; Tan, Q. Performance assessment of sponge city infrastructure on stormwater outflows using isochrone and SWMM models. J. Hydrol. 2021, 597, 126151. [Google Scholar] [CrossRef]
- Shrestha, A.; Mascaro, G.; Garcia, M. Effects of stormwater infrastructure data completeness and model resolution on urban flood modeling. J. Hydrol. 2022, 607, 127498. [Google Scholar] [CrossRef]
- Liang, Q.; Smith, L.; Xia, X. New prospects for computational hydraulics by leveraging high-performance heterogeneous computing techniques. J. Hydrodyn. 2016, 28, 977–985. [Google Scholar] [CrossRef]
- Dasallas, L.; An, H.; Lee, S. Developing synthetic sewer pipe system for data-scarce domains in application for urban flood modeling. Hydrol. Res. 2023, 54, 1387–1406. [Google Scholar] [CrossRef]
- Xu, H.; Wang, Y.; Fu, X.; Wang, D.; Luan, Q. Urban Flood Modeling and Risk Assessment with Limited Observation Data: The Beijing Future Science City of China. Int. J. Environ. Res. Public Health 2023, 20, 4640. [Google Scholar] [CrossRef]
- Petersson, L.; Ten Veldhuis, M.C.; Verhoeven, G.; Kapelan, Z.; Maholi, I.; Winsemius, H.C. Community mapping supports comprehensive urban flood modeling for flood risk management in a data-scarce environment. Front. Earth Sci. 2020, 8, 304. [Google Scholar] [CrossRef]
- Yu, D.; Yin, J.; Liu, M. Validating city-scale surface water flood modelling using crowd-sourced data. Environ. Res. Lett. 2016, 11, 124011. [Google Scholar] [CrossRef]
- Environment Agency. Updated Flood Map for Surface Water-national Scale Surface Water Flood Mapping Methodology; Environment Agency: Bristol, UK, 2013.
- Chen, A.; Djordjević, S.; Fowler, H.; Burton, A.; Walsh, C.; Harvey, H.; Hall, J.; Dawson, R.; Wood, G. Pluvial flood modelling of the South East London Resilience Zone in the Community Resilience to Extreme Weather (CREW) Project. In Proceedings of the Flood and Coastal Risk Management Conference, Telford, UK, 4–6 January 2009. [Google Scholar]
- Chang, T.; Wang, C.; Chen, A.S. A novel approach to model dynamic flow interactions between storm sewer system and overland surface for different land covers in urban areas. J. Hydrol. 2015, 524, 662–679. [Google Scholar] [CrossRef]
- Leandro, J.; Chen, A.S.; Djordjević, S.; Savić, D.A. Comparison of 1D/1D and 1D/2D coupled (sewer/surface) hydraulic models for urban flood simulation. J. Hydraul. Eng. 2009, 135, 495–504. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, A.S.; Fu, G.; Djordjević, S.; Zhang, C.; Savić, D.A. An integrated framework for high-resolution urban flood modelling considering multiple information sources and urban features. Environ. Modell. Softw. 2018, 107, 85–95. [Google Scholar] [CrossRef]
- Hou, J.; Wang, R.; Li, G.; Li, G. High-performance numerical model for high-resolution urban rainfall-runoff process based on dynamic wave method. J. Hydroelectr. Eng. 2018, 37, 40–49. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, K.; Lu, M.; Huang, J. Analysis on Drainage Capacity of an Urban Road in Shanghai Based on SWMM Model. Urban Rds. Brdgs. Flood Contr. 2020, 146–149. (In Chinese) [Google Scholar] [CrossRef]
- Mair, M.; Zischg, J.; Rauch, W.; Sitzenfrei, R. Where to Find Water Pipes and Sewers?—On the Correlation of Infrastructure Networks in the Urban Environment. Water 2017, 9, 146. [Google Scholar] [CrossRef]
- Chang, J.; Liu, M.; Xu, S.; Hou, L.; Wang, H.; Ballo, S. Temporal-spatial distribution and first flush effect of urban stormwater runoff pollution in Shanghai City. Geogr. Res. 2006, 25, 994–1002. (In Chinese) [Google Scholar]
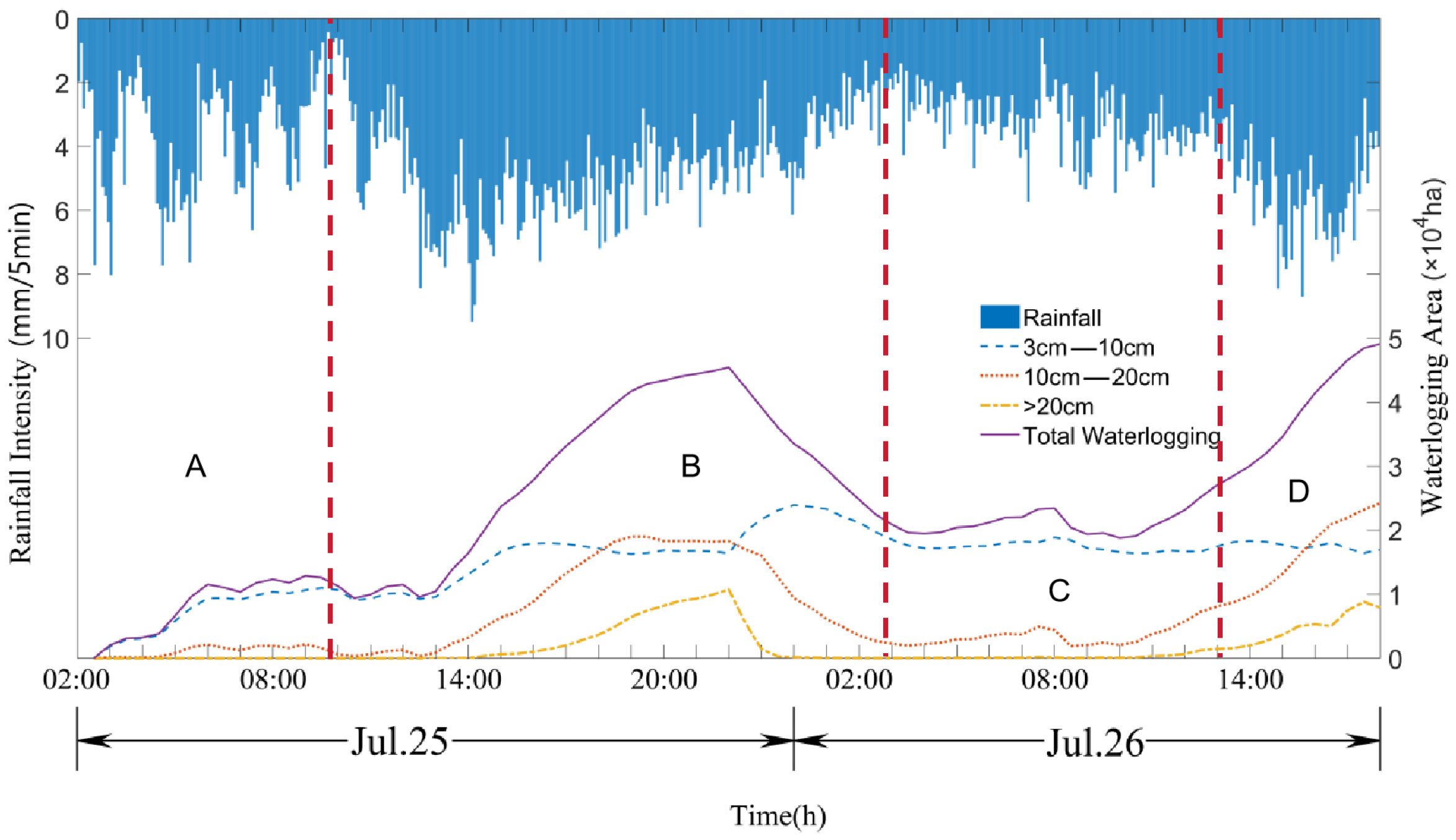
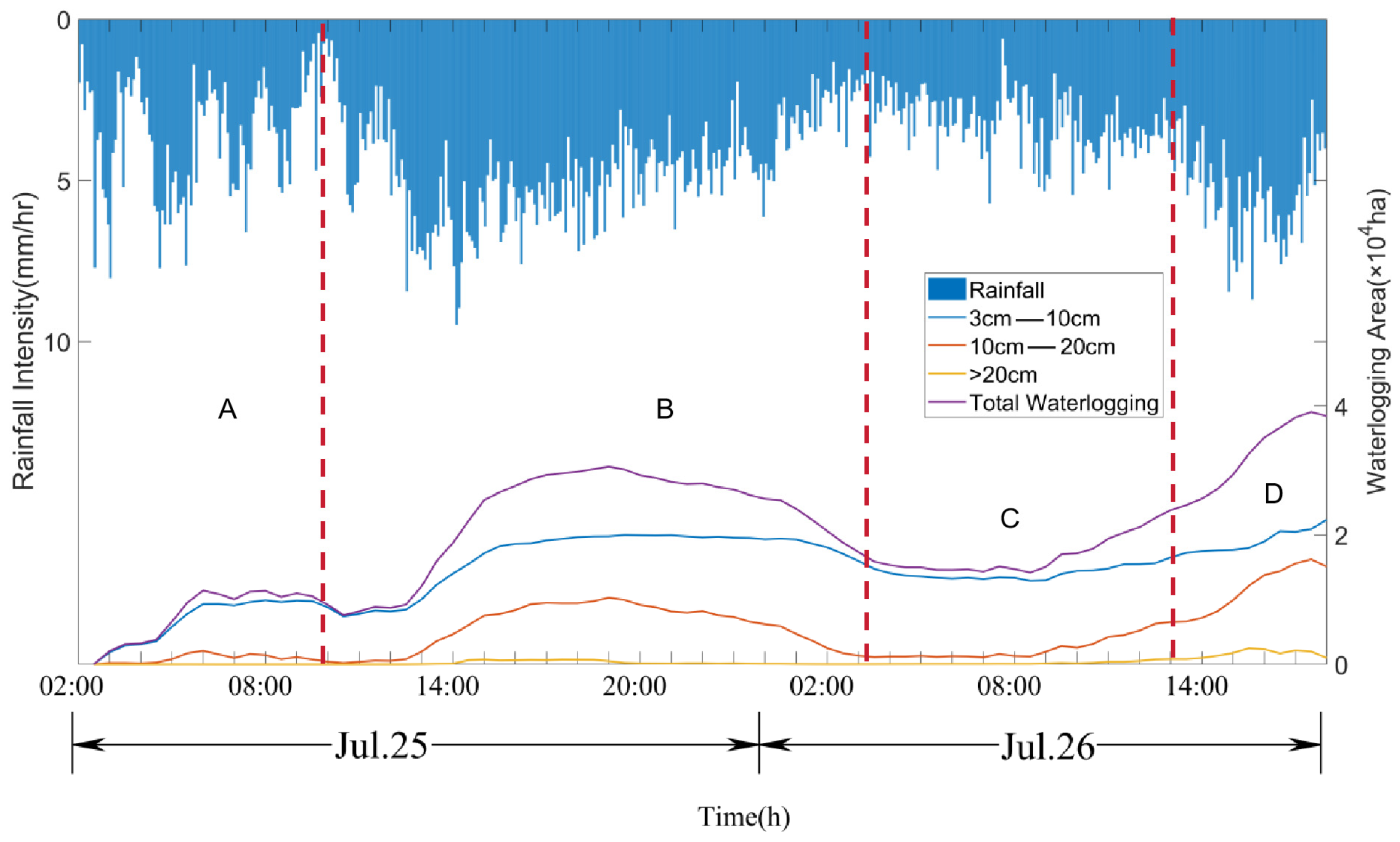
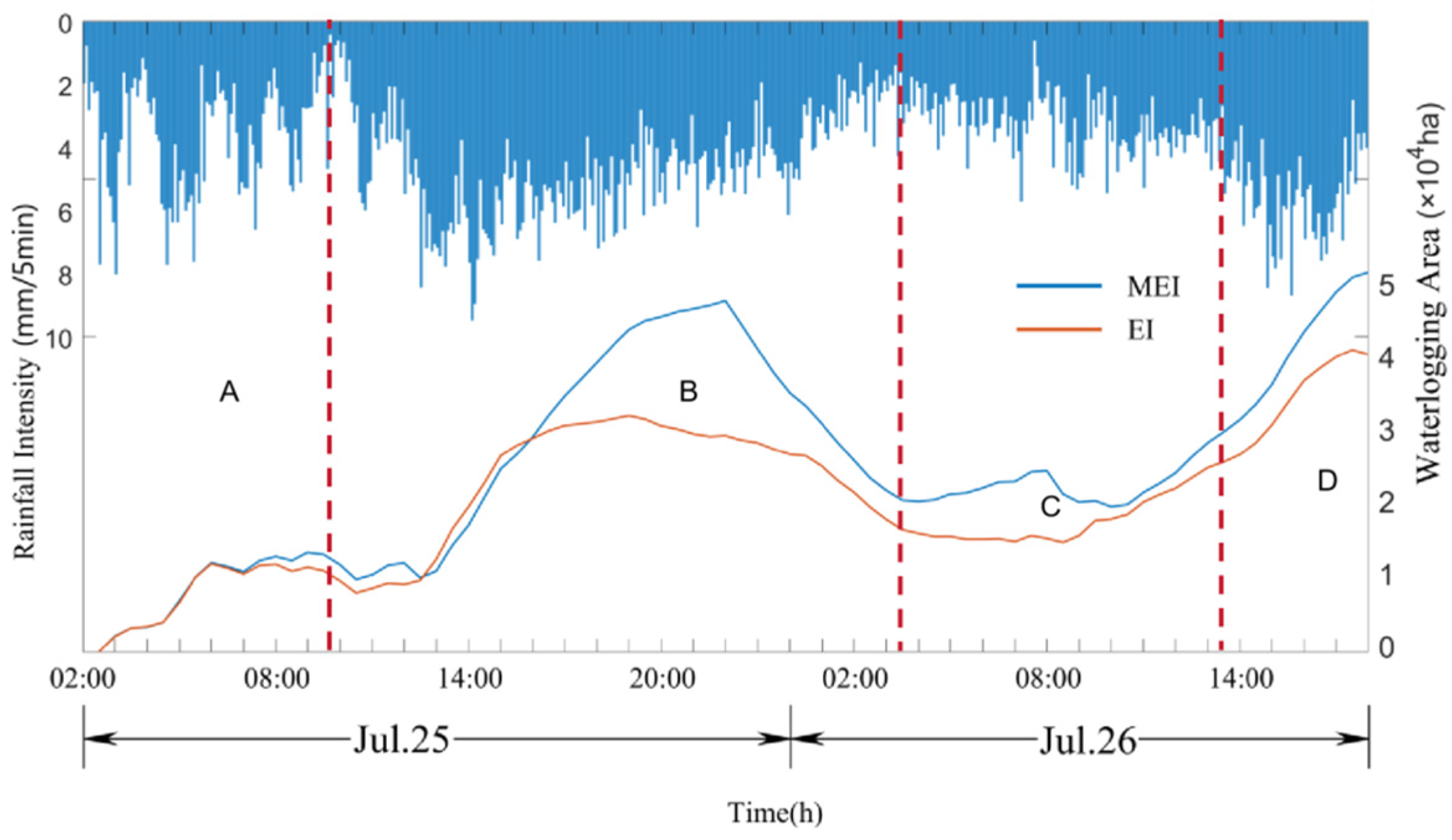

| Name | Description | Values |
|---|---|---|
| D-Imperv | Impermeable depression storage | 1.905 mm |
| D-Perv | Water storage in permeable depressions | 3.81 mm |
| MaxRate | Maximum infiltration rate | 76.2 mm/h |
| MinRate | Minimum infiltration rate | 2.54 mm/h |
| Decay | Attenuation factor | 6 |
| No. | Reporting Depth (cm) | Average Depth (cm) | Relative Error (%) |
|---|---|---|---|
| (I) | 5 | 2.8 | 44 |
| (II) | 5 | 3 | 40 |
| (III) | 20 | 15 | 25 |
| (IV) | 5 | 5.8 | 16 |
| (V) | 10 | 7.1 | 29 |
| (VI) | 2 | 1.1 | 45 |
| (VII) | 3 | 3.7 | 23 |
| (VIII) | 1 | 1.6 | 60 |
| (IX) | 3 | 3.8 | 27 |
| (X) | 3 | 1.8 | 40 |
| (XI) | 20 | 13.4 | 33 |
| (XII) | 25 | 23.1 | 10 |
| (XIII) | 5 | 4.2 | 22 |
| Average Relative error | 31.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zheng, M.; Gao, J.; Wang, X.; Zhang, H.; Jiang, S. A Generalization of the Drainage Capacity in Data-Scarce Urban Areas: An Improved Equivalent Infiltration Method. Water 2024, 16, 589. https://doi.org/10.3390/w16040589
Liu J, Zheng M, Gao J, Wang X, Zhang H, Jiang S. A Generalization of the Drainage Capacity in Data-Scarce Urban Areas: An Improved Equivalent Infiltration Method. Water. 2024; 16(4):589. https://doi.org/10.3390/w16040589
Chicago/Turabian StyleLiu, Junbing, Maohui Zheng, Jinwei Gao, Xinshu Wang, Hu Zhang, and Simin Jiang. 2024. "A Generalization of the Drainage Capacity in Data-Scarce Urban Areas: An Improved Equivalent Infiltration Method" Water 16, no. 4: 589. https://doi.org/10.3390/w16040589
APA StyleLiu, J., Zheng, M., Gao, J., Wang, X., Zhang, H., & Jiang, S. (2024). A Generalization of the Drainage Capacity in Data-Scarce Urban Areas: An Improved Equivalent Infiltration Method. Water, 16(4), 589. https://doi.org/10.3390/w16040589







