A Unified Spatial-Pressure Sensitivity Partitioning and Leakage Detection Method within a Deep Learning Framework

Abstract

This study introduces an innovative approach for leak detection in water distribution systems (WDSs), integrating three-order embedding, k-means clustering, and long short-term memory (LSTM) networks, with pressure-sensitive analysis techniques. This comprehensive methodology segments the network into distinct partitions, utilizes simulated leak events to train the deep learning networks, and establishes a sophisticated model for accurately identifying leak partitions. This approach generates a leak dataset by adjusting water demands, which could effectively pinpoint the leaks in a specific partition by leveraging both the pressure sensitivity and spatial coordinates of nodes, allowing for the elimination of the need for manual work and precise identification of leaks in targeted areas. Through the analysis of two case studies, the model demonstrates its ability to effectively pinpoint potential leak partitions, significantly enhancing operational efficiency and reliability in managing the complex problems of urban water resource management. This approach not only optimizes leak detection but also paves the way for advanced, data-driven strategies in WDSs, ensuring sustainable and secure water distribution in urban settings.

1. Introduction

The efficient management of water distribution systems (WDSs) is a cornerstone of urban infrastructure, fundamental to public health, economic stability, and environmental sustainability. However, the management of these vast and complex networks poses significant challenges, particularly in leak detection and network partitioning [1]. Hydraulic modeling has emerged as a pivotal tool, simulating the dynamic behaviors of WDSs to predict, analyze, and optimize their performance [2]. Developing hydraulic models of WDSs is a vital step in the information era, providing comprehensive insights into the components of nodes and links. The nodes include junctions, reservoirs, towers, and tanks. Hydraulic models have traditionally provided insights into network flow dynamics, aiding in the prediction of system behavior under various operational scenarios [3,4]. However, these models could not analyze leak detection, and network partitioning is often hampered by the complexity of WDSs [5]. There is a growing recognition of the need to enhance these models with more sophisticated analytical methods.

Partitioning a WDS into district-metered areas (DMAs) has become an important tool for water utilities to improve leakage control, water quality monitoring, and valve system operability [6,7]. DMAs are created by closing selected boundary pipes to separate the network into individual pressure zones that can be continuously monitored. Developing optimal DMA boundaries is a complex optimization problem that considers competing objectives, such as minimizing the number of boundary pipes while maintaining adequate system pressures and water quality [8,9]. A variety of methods have been proposed for the DMA partitioning problem. Perelman presented a clustering method based on network flow directions to identify DMAs [10]. Zheng et al. decomposed a network graph into subnetworks and then used an evolutionary algorithm to optimize boundary pipes [6]. More recently, community detection techniques from complex network analysis have shown promise for finding inherent clusters in water distribution topologies [11,12]. Community detection, for instance, uses modularity to evaluate the effectiveness of division between network pressure differences using graph theory. Ciaponi et al. introduced a practical DMA design method combining modularity containing minimum pressure and pipe size constraints [13]. They applied the Tabu search to determine near-optimal boundaries after partitioning a WDS using community detection. This hybrid approach allows leveraging the strengths of both graph partitioning techniques and multi-objective optimizations, which produced a high-quality solution meeting operational requirements in a case study. Perelman et al. worked on detecting leaks and ensuring the integrity of water networks in transient modeling, which leverages the K-nearest neighbors modularity for classifying transient pressure data parallels. These contribute to the efficient and accurate identification of leakages, reducing water loss and enhancing the efficiency of water distribution systems [14]. Zhang et al. developed an integrated framework using multiscale community detection and multi-objective optimization for water network partitioning, which introduced random walk-based modularity to overcome the limitations of traditional modularity metrics in identifying partitions [15]. The extended modularity integrates nodal pressure information to partition the network according to both topology and hydraulic conditions. Then, boundaries are further optimized by minimizing the number of boundary links and maximizing pressure uniformity using the BORG evolutionary algorithm. A real WDS demonstrated that their approach can effectively decompose the network into zones with balanced pressures. While these methods provide an effective integrated approach to WDS partitioning, they do have some limitations. Specifically, pressure sensitivities are used to partition, but the spatial status of nodes—their locations and connectivity—which should always be accessible or reliable, are not simultaneously considered [16].

Recent advances in network embedding and deep learning provide alternative data-driven techniques to address these weaknesses. Network embedding methods such as Deepwalk, Graph Sample and AggreGatE (GraphSAGE), Node to Vector (N2V), and large-scale information network embedding (LINE) [17,18] can encode topological and attribute information from massive networks in a low-dimensional representation that preserves structural relationships. Deep learning graph partitioning models can then detect patterns and cluster these embeddings to partition the network in a scalable unsupervised fashion without relying on hydraulic simulations [18,19,20]. Specifically, LINE explicitly captures first-order and second-order proximities between nodes in the network through optimized objective functions. The resulting node embeddings summarize not only node attributes but also connectivity patterns and community structure. Then, some cluster models such as k-means could automatically learn features from the graph embeddings to group nodes into clusters for pressure or water quality detection objectives [21,22]. In the cluster models, network nodes are grouped in a partition based on certain properties or behaviors. In the LINE model, nodes within the same partition have similar embeddings with each other compared to nodes in a different partition, which is useful for understanding the structure and hydraulic dynamics of networks.

After partitioning, effective leakage detection is critical for water utilities to reduce non-revenue water loss and ensure adequate water supply. However, locating pipe leaks in complex pipe networks poses significant challenges. Conventional acoustic sounding and logging surveys are time-consuming and lack efficiency at the city-wide system level due to their reliance on labor-intensive procedures. Further, acoustic methods may not always accurately detect issues in complex network structures, requiring multiple surveys and interpretations. Logging survey methods may require massive leakage data as references that are scarce and difficult to obtain. Data-driven approaches using hydraulic models have shown promise for leakage detection. For example, Wu et al. developed a pressure-dependent leakage detection (PDLD) methodology integrating leak simulation within hydraulic model calibration [23]. However, the methodology’s performance suffers from computational complexity when applied to multiple partitioning networks, which have exponentially expanding solution search spaces, though it can successfully identify leakage. To enhance the scalability of calibration methods, Zhang et al. proposed a leakage zone identification framework using multiclass support vector machines (SVM) [24]. The approach divides the network into zones using k-means clustering. Leakage simulation data train the SVM classifier model to predict leak events from nodal pressure sensitivity, which demonstrated effectiveness in a real case study. However, the method has some limitations. Manual intervention is required to select the optimal hyperparameters of the model and to re-train it when there are some changes in the network topology. Inaccuracy may arise in pressure-sensitivity-based leak detection if the actual pressure readings are in a state of instability over a period.

Deep learning provides an intriguing technology pathway to overcome these challenges through highly flexible neural network architectures. Deep learning includes deep brief networks (DBNs), convolutional neural networks (CNNs), and recurrent neural networks (RNNs), which have been widely applied in numerous areas. Deep neural networks can learn abstract representations and patterns in massive, high-dimensional datasets like sensor measurements in complex urban environments [25]. Deep learning leakage detection frameworks can capitalize on physics knowledge while adapting models to operational data distributions. For instance, Guo et al. developed a vision-based CNN for image recognition of leak acoustic signals [26]. Basnet et al. explored the efficacy of supervised machine learning models, specifically multilayer perceptron (MLP) and CNN for leak detection in each node of WDSs. They emphasized the models’ capability to address the complexities inherent in real-world leak characteristics, which marks a significant advancement in recognizing leaks without the need for leak data collection through labor-intensive methods [27]. However, topological networks often comprise hundreds or even thousands of nodes, making it impractical to determine the pressure states of all of them. This limitation can diminish the accuracy of leak detection. To address this issue, it is advisable to focus on detecting specific leakage zones that contain a subset of nodes. Concentrating on such integrated frameworks provides a promising direction for efficient, robust, and scalable leak detection across entire WDSs.

Therefore, in this study, we propose a partition and leak detection method with a deep learning framework using embedding and pressure sensitivity. Our contributions include the following: (1) a three-order embedding method is presented based on LINE, (2) a WDS partition method is presented with integrated k-means clustering and graph embedding, and (3) a deep learning framework is applied to analyze pressure sensitivity for leakage detection. This model’s novelties include the following: (1) the ability to locate leaks in a specific leakage partition containing a subset of nodes; (2) generating a leak dataset by increasing water demands, which obviates the need for manual data collection; (3) considering pressure sensitivity and topology simultaneously, allowing for more accurate identification of leak locations.

The rest of this paper is organized as follows: Section 2 illustrates the methodology of the partition and leak detection model. Section 3 focuses on case studies for this method, and compares the results with those of another model. We present the advantages and weaknesses of this method in Section 4. Finally, in Section 5, the conclusions are drawn.

2. Methods

2.1. Pressure Sensitivity Matrix

Pressure sensitivity analysis is an essential component, primarily focusing on understanding how changes in pressure affect water flow and network stability. Pressure sensitivity could be expressed as Equation (1)

$$\Delta p_i^j=|p_i^j-p_i|$$

(1)

where $\Delta p_i^j$ is the absolute difference in values of pressure between abnormal and normal at node i, with node j regarded as a leakage point; $p_i^j$ is abnormal pressure, as node j is regarded as a leakage point; $p_i$ is normal pressure.

Leakage can cause sudden changes in water demand and pressure at the nodes of a pipe network, especially in the case of pipe bursts. In the pipe network topology model, the occurrence of leakage can be simulated by increasing the leakage demand. To obtain the pressure sensitivity of each node, an extended period simulation (EPS) is conducted. Firstly, one node is assigned a leakage demand $q_l$. Subsequently, the hydraulic model is executed to compute pressure variations at both normal and abnormal conditions in all nodes to simulate the leakage event using Equation (1). Finally, an N × N pressure sensitivity matrix can be obtained, as expressed by Equation (2).

$$\left[\begin{array}{ccc}\begin{array}{c}\begin{array}{cc}\Delta p_1^1& \Delta p_2^1\end{array}\\ \begin{array}{cc}\Delta p_1^2& \Delta p_2^2\end{array}\end{array}& \cdots & \begin{array}{c}\Delta p_N^1\\ \Delta p_N^2\end{array}\\ ⋮& \ddots & ⋮\\ \begin{array}{cc}\Delta p_1^N& \Delta p_2^N\end{array}& \cdots & \Delta p_N^N\end{array}\right]$$

(2)

where $N$ is the number of nodes in a WDS.

Due to the great variation in water base demands across various nodes, the pressure sensitivity can differ by orders of magnitude [28]. Thus, standardization should be implemented. The average values of the pressure differences are set to zero, and the standard deviation is scaled to one after applying the standardization process, which can be expressed as Equation (3) [29].

$$\Delta {p^{\prime }}_i^j=\frac{\Delta p_i^j-\Delta {\overline{p}}^j}{S_j}$$

(3)

where $\Delta {p^{\prime }}_i^j$ is the standardization pressure sensitivity of node i, as the leakage appeared in node j; $\Delta {\overline{p}}^j$ is the average value of pressure sensitivity, as node j is regarded as a leakage node, which is expressed as $\Delta {\overline{p}}^j=\frac{1}{N}{\sum }_{i=1}^N\Delta p_i^j$; $S_j$ is the standard deviation of pressure sensitivity of all nodes as node j is experiencing leakage, which is expressed as:

$$S_j=\sqrt{\frac{1}{N}{\sum }_{i=1}^N{\left(\Delta p_i^j-\Delta {\overline{p}}^j\right)}^2}$$

(4)

Furthermore, the standardized values are normalized to a 0 to 1 real-valued range across all nodes. This normalization transformation shifts and scales the distribution of standardized pressure sensitivity to span from 0 to 1, thereby balancing the data contribution and range across all network nodes for the subsequent analysis. The normalization process converts the standardized values using Equation (5), as follows:

$$\Delta {p^{″}}_i^j=\frac{\Delta {p^{\prime }}_i^j-\max (\Delta {p^{\prime }}^j)}{\max \left(\Delta {p^{\prime }}^j\right)-\min (\Delta {p^{\prime }}^j)}$$

(5)

where $\Delta {p^{″}}_i^j$ is the normalization pressure sensitivity of node I, as the leakage appeared in node j; $\max \left(\Delta {p^{\prime }}^j\right)\mathrm{and} \min (\Delta {p^{\prime }}^j)$ are determined from the bounds of the standardized dataset.

Through standardization and normalization, the pressure differences are transformed to have a mean of zero and a standard deviation of one with the same orders of magnitude. This allows the data to be analyzed on a common, normalized scale regardless of the raw data distribution across nodes.

2.2. Improvement Using Three-Order Embedding

There are numerous water demand nodes in a WDS. Detecting leakage at each node would require installing a large number of SCADA sensors, significantly increasing costs. Additionally, processing massive data would consume considerable time, and storing it would require extensive storage space in the server. Dividing the network into zones, detecting only the leak node’s partition, and then further localizing the leakage within that area, can significantly reduce costs and computational efforts. The most effective method for partitioning a network through clustering algorithms involves considering the interconnections between nodes in the graph and integrating the characteristics of adjacent nodes to reflect their spatial topological relationships. Embedding using LINE could serve as a pivotal method for transforming complex network structures into a more interpretable, low-dimensional space. This process is crucial for mapping the extensive and intricate networks of pipes and nodes within a WDS. By embedding these elements into a vector space, it becomes possible to analyze relationships and interactions within a WDS more effectively, such as the clustering in terms of water pressure sensitivity.

In this study, we improve the LINE model via a three-order proximity objective function to apply to the partitioning of WDSs. During the LINE model step, random embeddings could be generated for each node in the WDS. Then, three-order proximity objection functions are applied to optimize the embeddings.

The first-order proximity objective function uses Kullback–Leibler divergence to optimize the embeddings via a direct hydraulic relationship between two connected nodes [30]. Given two nodes i and j with an edge between them, their embeddings are u_i = [u₁, u₂,…, u_k] and v_j = [v₁, v₂,…, v_k]. The objective function can be formulated as Equation (6), which adjusts the embeddings of the nodes so that directly connected nodes are close to each other. For instance, for three nodes A, B, and C in WDSs, node A is directly connected to node B, and node B is directly connected to node C. The direct hydraulic relationship between node A and node B would be analyzed, focusing on the weights of the pipe connecting them, obtaining $J_1^{\mathrm{A},\mathrm{B}}$. Node B is directly connected to node B, and the hydraulic relationship with node C would be analyzed in a similar way, obtaining $J_1^{\mathrm{B},\mathrm{C}}$. Finally, $J_1^{\mathrm{A},\mathrm{B}}$ and $J_1^{\mathrm{B},\mathrm{C}}$ would be added to accurately represent the overall hydraulic interactions between directly connected nodes in the WDS.

$$J_1=-{\sum }_{\left(i,j\right)\in E}{\omega }_{ij}log\sigma \left(u_i^T{v}_j\right)$$

(6)

where $J_1$ is the value of the first-order proximity objective function and ${\omega }_{ij}$ is the weight of the edge between nodes i and j. If i is directly connected with j, the value is ${\omega }_{ij}$. If there is no direct connection between them, the value is zero. $\sigma \left(x\right)=\frac{1}{1+e^{-x}}$ is the sigmoid function.

For the weight of the edge between two nodes, the average of pressure sensitivities is solved, expressed as Equation (7).

$${\omega }_{ij}=\frac{\left|\Delta p_i^i-\Delta p_j^j\right|}{2}$$

(7)

Second-order proximity focuses on preserving the neighborhood structure, which shares the connections of nodes, even if they are not directly connected. The objective function aims to preserve the context of nodes, where the context is defined by the node’s neighborhood expressed as Equation (8). For instance, taking nodes A, B, and C again, node A and node C are not directly connected, but both have a direct connection to node B. Second-order proximity analyzes this indirect relationship by examining the similarity in their connections through B. This could involve assessing how a change in pressure at node B affects both A and C, or how A and C might have similar pressure profiles due to their shared connection with B, despite no direct pipe between them.

$$J_2=-{\sum }_{\left(i,j\right)\in E}{\omega }_{ij}logp\left(u_i{|v}_j\right)$$

(8)

where $J_2$ is the value of the second-order proximity objective function and $p\left(u_i{|v}_j\right)$ is the ratio of ${\omega }_{ij}$ and the out-degree in node i. The details of this objective function can be found in reference [17].

Third-order proximity focuses on the spatial distribution of nodes. The network is divided into different partitions. Some outliers might exist in each partition, especially in complex networks, which would give rise to partition discontinuity [1]. To ensure node connectivity in each partition, connectivity optimization for all nodes should be determined, as expressed in Equation (9).

$$J_3=-{\sum }_{(i,j)\in E}{d}_{ij}^2{X}_i{X}_j^{T}log\sigma (-u_i^T{v}_j)$$

(9)

where $J_3$ is the value of the third-order proximity objective function; d_ij is the distance between node i and j; $X_i$ represents the spatial coordinates of node i, encapsulated by the vector [x_i, y_i, z_i]; x_i, and y_i are the horizontal coordinates within a two-dimensional plane, reflecting the geographical positioning of the node; and z_i represents the elevation data at the location of node i.

To effectively embed nodes with three orders, this model separately preserves the three-order proximity functions during optimization. Firstly, the topological network is preprocessed to convert it to an adjacency matrix, establishing a structured representation for subsequent operations. Secondly, the dimensionality of the embeddings is determined, and embeddings are generated randomly. Higher dimensions capture more information but take longer to train. Thirdly, the first-, second-, and third-order proximity are calculated using Equations (6)–(9). Fourthly, the stochastic gradient descent algorithm is employed to minimize the first-order proximity function. Following the optimization of the first-order proximity, the second- and third-order proximities are minimized in sequence, employing a similar approach. This ensures that not just direct connections but also neighborhood similarities and spatial distribution relationships are accurately reflected in the embeddings. Fifth, the embeddings are updated to reflect the minimized proximity functions, gradually improving the representation of the network’s structure in the low-dimensional space. Sixth, a maximum epoch is set and steps 3–5 are repeated until the model converges or the predefined maximum number of epochs is reached, ensuring the optimization process is thorough yet bounded.

For each node, we concatenate the embeddings obtained from these three functions, thereby capturing the comprehensive relational dynamics within the network. The flow chart of the partition method is illustrated in Figure 1a.

2.3. Network Partition

Partitioning a network in WDSs is key for efficient management and operation, as it enables more precise leak detection, reduces response time for repairs, and enhances system reliability and safety by isolating problems to prevent widespread impact. By integrating the pressure sensitivity matrix with the LINE embedding and clustered topological network, we can simulate various scenarios, such as pipe bursts or leakages, and predict their impact on the network. The k-means algorithm is introduced for dividing a network into different leakage partitions. This clustering method groups nodes into K number of clusters, where each point belongs to the cluster with the nearest mean value. Initially, cluster centers are chosen randomly. Each node in the network is then assigned to the nearest cluster center based on Euclidean distance, which is calculated using Equation (10).

$$D={\sum }_{i=1}^N\sqrt{{\left(\Delta p_i^{″}-\Delta p_j^{″}\right)}^2}$$

(10)

where D is the distance between two nodes, i and j.

The centroid of each cluster is recalculated after all nodes have been assigned. The mean position of all the points in each cluster is solved. It involves calculating the average of all the dimensions for the points in each cluster. The equation for the new centroid for a cluster is given by Equation (11).

$$C_k=\frac{{\sum }_{j=1}^N\Delta {p^{″}}_i^j}{N}$$

(11)

where $C_k$ is the centroid of the kth partition.

This recalculated centroid then becomes the new center for the respective cluster in the next iteration and the process repeats until the centroids stabilize, ensuring the network is divided into distinct and optimized leakage partitions. Finally, pressure sensors would be installed at the nodes nearest to each centroid within the partitions.

2.4. Leak Detection

To locate the areas with leakage nodes, pressure sensitivity can be used for analysis. After partitioning, a pressure sensor is installed at the point nearest to center in each zone. The Monte Carlo simulation is employed to stochastically generate instances of leak events via increasing the demand of nodes, where each event is solved through the EPS process. For the specific implementation steps, the Monte Carlo method is first utilized to randomly select one or two nodes and assign random leakage demands to them in each partition, respectively. If there are K partitions in the pipe network, and leakage occurs at nodes in the kth partition, the pressure at the sensor points might change. The hydraulic model is executed to compute pressure variations for both normal and abnormal conditions at each sensor for every leakage event. The pressure sensitivity of the sensor can be calculated using Equation (1). Subsequently, the Monte Carlo process is repeated for the next leakage event until all events have been simulated. The number of leakage events is $C_N^2+C_N^1$, where N is the number of nodes. Finally, the inputs of training samples are composed and expressed as Equation (12). Meanwhile, the outputs of training samples are the labels of partitions.

$$P={\left[\begin{array}{ccc}\Delta {p^{″}}_1^1& \cdots & \Delta {p^{″}}_K^1\\ ⋮& \ddots & ⋮\\ \Delta {p^{″}}_1^L& \cdots & \Delta {p^{″}}_K^L\end{array}\right]}_{L\times K}$$

(12)

where P is the array of input data in LSTM and L is the number of leakage events ${L=C}_N^2+C_N^1$;

RNN models are a type of recursive neural network that processes sequential inputs and are among the most crucial algorithms in deep learning. Long short-term memory (LSTM) networks, the most popular RNN models, are capable of learning long-term dependencies. In the context of leak detection, an LSTM has the ability to handle complex, non-linear relationships in data, which can lead to more accurate detection of leaks under varying conditions. Additionally, LSTMs can adapt to changes in the network’s behavior over time, maintaining effectiveness even as the system leaks.

Therefore, this study established a three-layer LSTM model for leak detection [31,32]. For the input layer, the preprocessed dataset serves as the input variable. The second layer is the LSTM layer shown in Figure 1b. The LSTM has three gates. The first is a forget gate with a sigmoid activation function $\sigma$, producing numbers between 0 and 1. A value of 1 retains the last cell state, while 0 forgets it. The second is the input gate, updating the cell state using hyperbolic tangent and sigmoid activation functions. The third is the output gate, where the tangent activation function is used. Finally, the output layer is connected to a fully connected layer, which serves as the third layer. The output layer consists of M neuron cells indicating the partition of leaks. Both models employ the Softmax activation function [33] in their output layers. In addition, the cross-entropy loss function is used during the backpropagation to refine the classification accuracy between the model’s predicted and the actual partition labels, expressed as Equation (13). This loss function quantifies the difference between the predicted probability distributions and the actual labels across the dataset. The main advantage of using cross-entropy is its ability to handle probabilities in a way that penalizes incorrect classifications more severely, guiding the model towards more accurate predictions. This optimization process is crucial for enhancing the model’s ability to accurately distinguish between the presence of leaks and their absence in WDSs, by minimizing the prediction error [34,35].

$$L=-{\sum }_{l=1}^L{\sum }_{k=1}^K{y}_k\log \left(p_k\right)$$

(13)

where $y_k$ is an indicator of whether class k is the correct leak partition. If correct, the $y_k$ is one, or zero. The $p_k$ is the predicted probability that a leak appears in partition k.

The framework of this state-of-the-art model is illustrated in Figure 1c.

3. Case Studies

Two cases, A and B, are used to verify this methodology. The Open Water Analytics (OWA) toolbox is employed for hydraulic calculations [36], which is an EPANET classlib of MATLAB developed by the KIOS Research Center for Intelligent Systems and Networks, University of Cyprus.

3.1. Network A

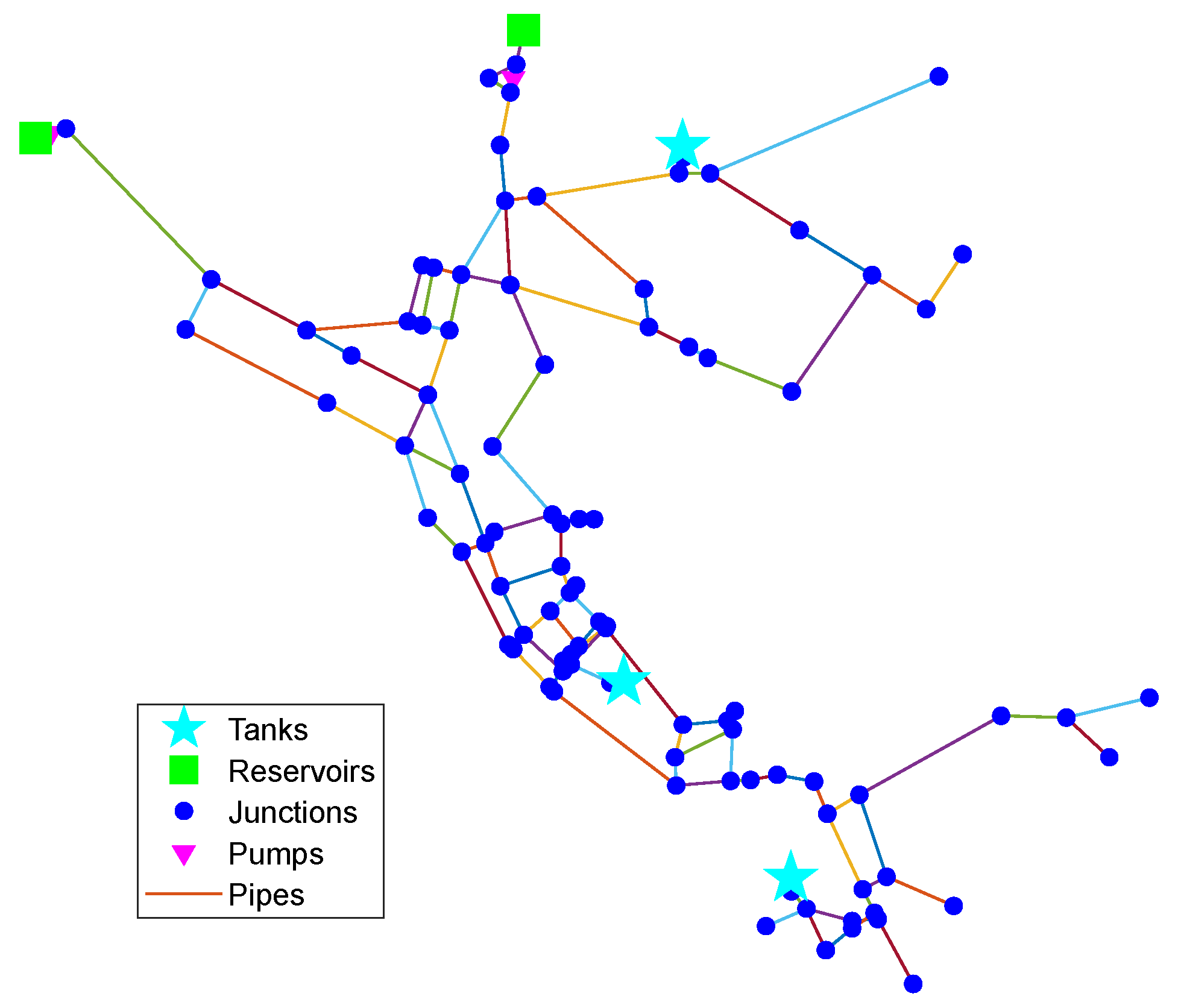
Network A has 92 junctions, 117 pipes, two pumps, two reservoirs, and three tanks, as shown in Figure 2 [19,37]. The average water demand is 2450.03 m³/h. The time interval of hydraulic calculation is set to one hour during the EPS process via the EPANET OWA toolbox. The maximum time of EPS is set to 24 h.

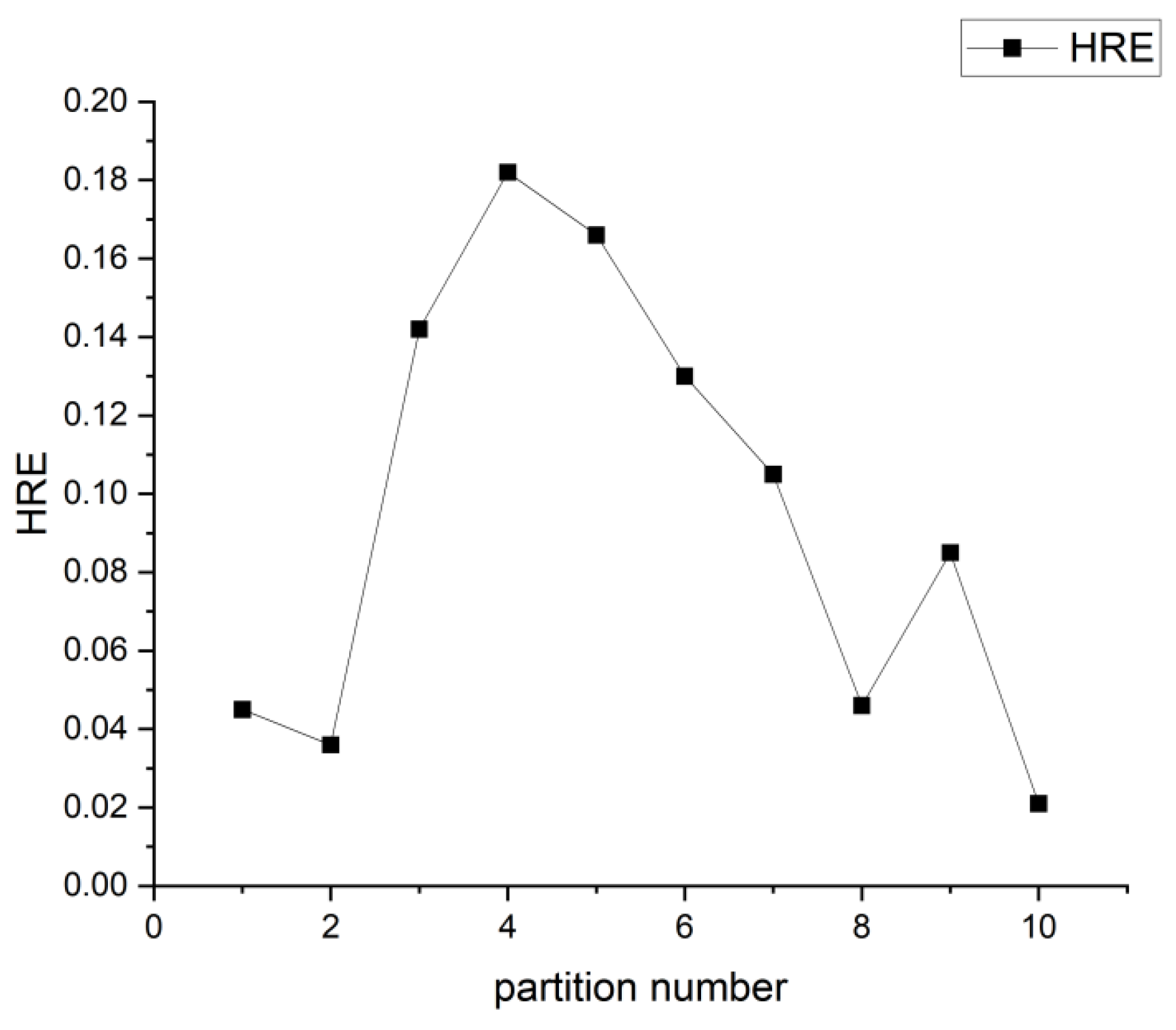
Firstly, the network partition is processed. In order to select an effective number of partitions, the hydraulic reliability estimation (HRE) method is employed as the objective function [38], which represents the probability of leakage occurring. The water demands are set as an independent variable in HRE, where water demands are randomly allocated to the nodes of the WDS following a normal distribution. Then, coefficients including 0.1, 0.2, 0.4, 0.6, 0.8, and 1.0 are multiplied with the demands to represent five different scenarios. The details can be found in the Supplementary Materials. In the process of partitioning, the three-order embedding model is used. The embedding length is determined for enhancing calculating efficiency and removing outliers. The embedding lengths ranging from 2 to 6 are tested, as illustrated in Table S3, where the number of partitions is set at ten, clustered by the k-means algorithm. When the length is three, the number of outliers is seven, and stability is maintained with the increase in the length. Thus, the embedding length is set to three, where the dimension of pressure sensitivity would be reduced (92 to 3). Then, the k-means algorithm is applied to cluster the nodes to different partitions. The network is divided into different partitions ranging from 2 to 10. Valves would be installed in the boundary pipes after partitioning. The states of valves (open or closed) are selected to obtain the best HRE solution. An exhaustive search method is employed to identify the optimal states of the boundary valves for the best HRE outcome. The exhaustive search method involves systematically evaluating all possible combinations of valve states to identify the configuration that obtains the highest HRE. The HRE solutions are solved, as illustrated in Figure 3. Five partitions yield the largest HRE, which indicates that the leakage will occur with a lower probability. There are 13 valves installed in the boundary pipes of the network, as shown in Figure 4. The pipe indexes are 19, 39, 57, 59, 63, 64, 73, 89, 102, 103, 106, 112, and 113. The states of these valves are [0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1], where 0 represents closed and 1 is open.

The best strategy of partition is shown in Figure 4. The nearest center node would be regarded as the sensor for each partition. The sensors’ indexes are 12, 24, 46, 66, and 79.

After that, the EPS is conducted to calculate the normal pressures at the locations of five sensors. Following this, a leakage equivalent to 3% of demand is introduced at one or two specific nodes, and the EPS is conducted once more to calculate the abnormal pressures at the sensors. The number of $3(C_{92}^2+C_{92}^1)$ = 12,834 potential leak events would be generated, leveraging combinations of leaks at different nodes. For each event, both the normal and abnormal pressures at each sensor are calculated over a 24 h period using Equation (1). Finally, the samples are integrated according to Equation (12), forming samples where the inputs comprise the pressure sensitivities detected by sensors, and the outputs denote the partition labels indicative of leak presence. The output employs a one-hop structure with the Softmax activation function, consisting of five neurons, each representing a different partition, such as [0, 0, 0, 0, 0] and [1, 0, 1, 0, 0], indicating no leak and leaks in the first and third partitions, respectively.

As the datasets are composed, the LSTM model is applied to detect the leaks. The dataset is divided into a training set and a testing set. The proportion of the two sets is 4:1. After the model training is completed, the test data are input into the trained model to determine the leakage partition numbers. These are then compared with the leakage area labels to calculate the leak detection rate. The leak detection rate is formulated as Equation (14). The results of leak locations in the five test datasets are shown in

Table 1. The results of leakage detection rates for network A.

Times	Leak Detection Rate %
1	94.57
2	95.65
3	92.39
4	94.57
5	93.48
Average	94.13

.

$$LDR=\frac{N_{correct}}{N_{correct}+N_{incorrect}}\times 100\%$$

(14)

where $N_{correct}$ is the number of leakage nodes correctly identified by the partition label; $N_{incorrect}$ is the number of leakage nodes that the partition label failed to detect correctly.

The leakage detection rate reaches its maximum at 95.65%, and the lowest detection rate is 92.39%. The detection rates in different time periods all exceed 90%, indicating a relatively high performance. The standard deviation could be solved. There is a small standard deviation of only 1.24 in the five tests. Thus, the model is stable and reliable, with minimal fluctuation in its ability to predict water leakage scenarios in five different test samples. Therefore, it can effectively detect leaks in network A.

3.2. Network B

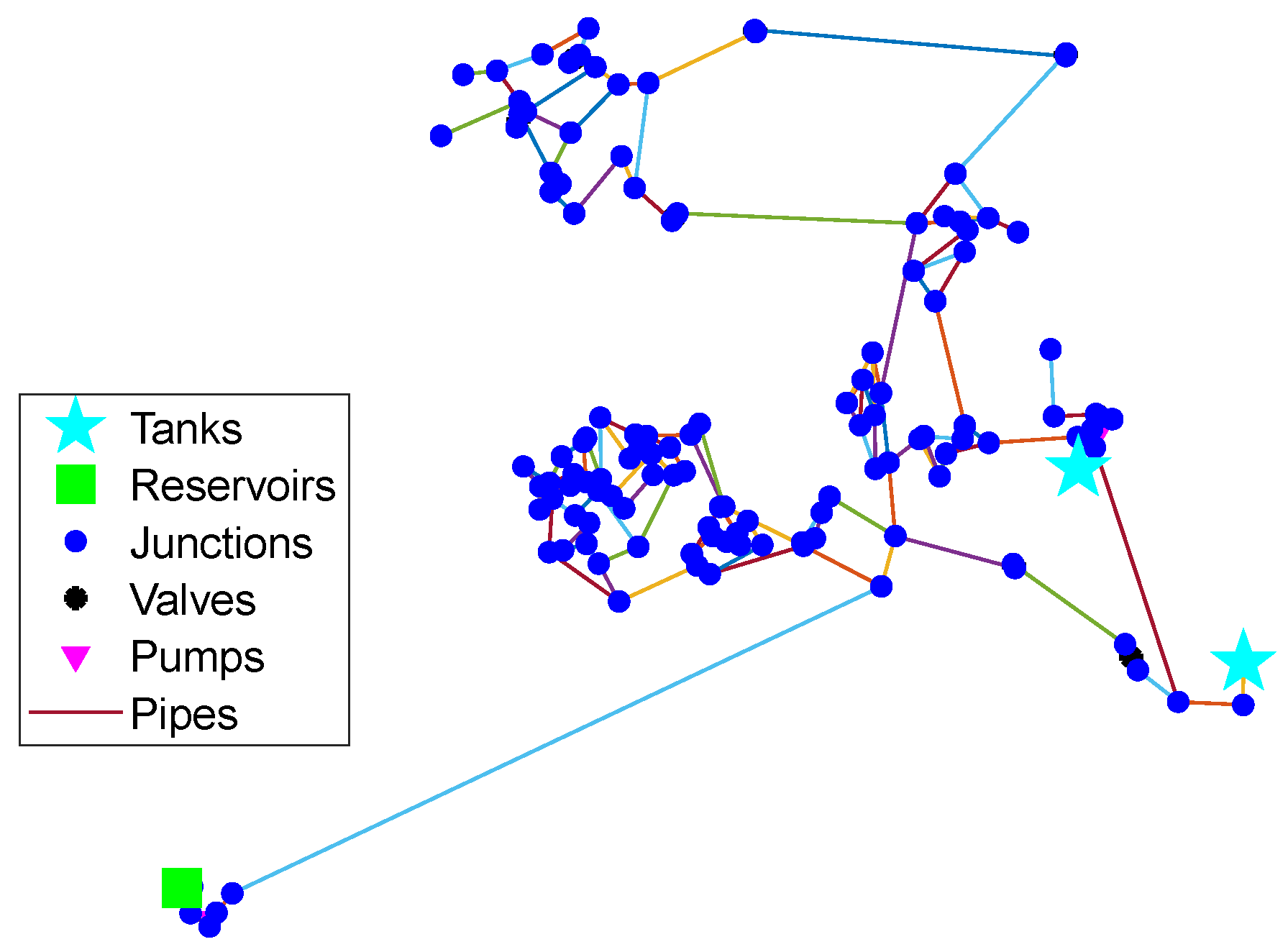
Network B has 126 junctions, 168 pipes, two pumps, one reservoir, and two tanks [39], as shown in Figure 5. The average water demand is 211.81 m³/h. The maximum time of EPS is set to 24 h.

The network partition is processed. The embedding lengths ranging from 2 to 6 are tested, as illustrated in Table S4. The k-means algorithm is used to cluster the node into ten partitions. The length of embedding is set to three, having an optimized number of outliers, where the dimension of pressure sensitivity would be reduced (126 to 3). Then, the k-means algorithm is applied to cluster the nodes to different partitions. The network is divided into different partitions ranging from 2 to 10. Valves would be installed in the boundary pipes after partitioning. The states of valves are selected to obtain the best HRE solution with an exhaustive search. The HREs are solved, as illustrated in Figure 6. Four partitions exhibit the largest HRE, which indicates that the leakage will occur with a lower probability. There are five valves in the network and the boundary pipe indexes are 1, 36, 42, 46, and 170. The states of these valves are [1, 0, 0, 1, 1].

The best strategy of partition is shown in Figure 7. The nearest center nodes would be regarded as the sensors for each partition. The sensors’ indexes are 5, 43, 62, and 110. The details can be found in the Supplementary Materials.

The 3% leakage demands are added to the nodes. The normal and abnormal pressures are solved by the EPS process. Then, the number of $3(C_{126}^2+C_{126}^1)$ = 24,003 leakage events are generated. After the EPS process, the pressure sensitivities are solved. Then, the samples are imported to the LSTM model. The dataset is divided into a training set and a testing set with a proportion of 4:1. The average values of the leak detection rate for the partitions are calculated, as shown in

Table 2. The results of leakage detection rates for network B.

Times	Leak Detection Rate %
1	87.30
2	91.27
3	89.68
4	88.10
5	90.08
Average	89.29

.

The leakage detection rate reaches its maximum at 91.27%, and the lowest detection rate is 87.30%. The detection rates in different time periods all exceed 85%, indicating a relatively high performance. Meanwhile, there is a small standard deviation of 1.59 in the five tests. So, the model is also stable and reliable, with minimal fluctuation in its ability to predict water leakage scenarios in five different test samples. Our results demonstrate that this model is effective at predicting leaks.

3.3. Comparison

To prove the efficiency and reliability of the method for leak detection in this study, a multiple support vector machine (M-SVM) approach could be adopted in the abovementioned two cases. The pressure sensitivities of sensors are used directly as input data for the M-SVM models, with details provided in reference [24]. The inputs are the water pressure sensitivity matrix, and the outputs are the leak partition labels. Finally, we evaluate the efficiency and reliability of the proposed model for leakage detection on the simulated validation dataset using standard classification metrics, including leak detection rates, accuracy, precision, recall, and F1 score. The equations are expressed as follows:

$$\mathrm{ACC}=\frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{TN}+\mathrm{FP}+\mathrm{FN}}$$

(15)

$$\mathrm{PREC}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}$$

(16)

$$\mathrm{REC}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}$$

(17)

$$\mathrm{F}=\frac{2\times \mathrm{PREC}\times \mathrm{REC}}{\mathrm{PREC}+\mathrm{REC}}$$

(18)

where ACC, PREC, REC, and F are the accuracy, precision, recall, and F1 score of leak detection, respectively. TP is the true positive where the model correctly identified leakage partitions, TN is the true negative that correctly identified no leakage partitions, FP is the false positive that incorrectly identified leakage partitions, and FN is the false negative that failed to identify an actual leakage partition.

The results of these evaluations are shown in

Table 3. The comparison of the models in the two cases.

Model (Network A)	Average Leak Detection Rate %	Accuracy %	Precision %	Recall %	F1 Score %
M-SVM	91.30	96.52	91.03	91.67	91.19
This study	94.13	97.83	94.64	94.80	94.55
Model (Network B)	Average Leak Detection Rate %	Accuracy %	Precision %	Recall %	F1 Score %
M-SVM	86.51	93.25	86.20	87.02	86.45
This study	89.29	94.84	90.18	90.37	90.24

. In cases A and B, the leak detection rates, accuracy, precision, recall, and F1 score of this study surpass those of M-SVM. With its enhanced accuracy and precision, the model demonstrates an ability to detect leaks with a reduced number of FPs, facilitating more efficient management for leakage. The high recall indicates fewer FNs, confirming the model’s reliability without missing leakage incidents. Moreover, higher F1 scores imply that it is capable of performing consistently under a variety of pressure sensitivities. Additionally, a higher average leak detection rate indicates the model is effective in detecting leakages. Therefore, the model can efficiently process data and provide reliability for leakage detection.

4. Discussion

As we embark on an in-depth analysis of the innovative leak detection method employed in WDSs, the integration of LSTM with k-means clustering represents a significant advancement in addressing the complexity of leak patterns. The progressive strides and the inherent limitations of this advanced method offer a balanced perspective on its implications in the field of water resource management.

Based on the aforementioned method, a degree of progress can be achieved, as follows:

(1)

The approach offers a significant advantage by leveraging the k-means clustering analysis model with three-order embedding to create distinct pressure sensitivity partitions. This method enables an effective division of a WDS into distinct areas, facilitating precise leak localization within specific partitions containing subsets of nodes without outliers. The three-order embedding enriches the topological graph representation, enhancing k-means clustering’s ability to differentiate areas based on pressure sensitivity and nodes’ locations and connectivity attributes. Additionally, this technique automates leak dataset generation by adjusting water demands, thereby eliminating the need for manual data collection and overcoming the challenge of insufficient leakage data. This ensures a more accurate and focused leak detection strategy, outperforming traditional methods like M-SVM by enabling separate subsets of nodes of each partition for more effective leak identification and location.

(2)

The advantage of using LSTM networks within a deep learning framework for leak detection in WDSs lies in their ability to accurately localize the labels of leakage partitions. This precise localization minimizes water losses. When leaks are accurately identified, it reduces the amount of water wasted, leading to cost savings and enhancing the overall safety of the WDS.

Despite these advancements, the method faces certain limitations.

(1)

The training intensity of deep learning frameworks, especially LSTM networks, poses a challenge in terms of resource requirements and scalability. While the method is effective in specific contexts, such as cases A and B, adapting it to larger or more complex network systems may present scalability challenges.

(2)

The three-order embedding is optimized sequentially, step by step. A more efficient optimization method that can simultaneously optimize all three functions should be developed, which could enhance the overall performance and speed of the system.

(3)

While LSTM networks have the capacity to process and analyze time-series data, currently only the average pressure is considered. This approach might not leverage the potential of LSTM to utilize historical data. Incorporating time-series data more comprehensively could lead to more accurate and informed decision-making, enhancing the system’s ability to predict and localize leaks with greater precision.

Therefore, this approach marks a significant step forward in leak detection technology, but addressing its limitations is essential for broader application and effectiveness in diverse WDSs.

5. Conclusions

This paper innovatively combines three-order embedding, k-means clustering, and long short-term memory (LSTM) networks with pressure sensitivity, spatial data, and connectivity for efficient partitioning and leak detection in water distribution systems (WDSs). Through detailed analysis and its successful application in two case studies, the method achieved an impressive average leak detection rate of up to 85%. Compared to other models, this research highlights the potential of our approach to improve the efficiency and reliability of WDSs, representing a significant step forward in the field of WDS monitoring and maintenance.

However, certain limitations exist. Future efforts will concentrate on resolving the challenges related to objective function optimization, historical data series processing to assess WDS resilience, and further refining and integrating this method into comprehensive water management strategies.