Abstract
The development of human society over the past century has led to an explosion in population numbers and a migration of settlements to river valleys, which have become increasingly exposed to the risk of flooding. In this context, the scientific community has begun to work on identifying mathematical and spatial models that can help to identify areas at risk as quickly as possible. The present article is one that follows this objective, proposing an automatic model that can be implemented in ArcGIS and that aims to identify only areas at risk of flooding using a single file, the DEM. The novelty of this article and the usefulness of the method are given precisely by the fact that it is possible to quickly find out which areas may be exposed to flooding, i.e., water accumulations, only based on relief, which is extremely useful for local authorities. The analysis was conducted on all hierarchy orders, according to the Horton–Strahler classification system, for the entire Romanian territory. The results consist of a polygonal vector layer in shapefile format, containing an attribute table with all the initial, intermediary, and final calculations in separate numeric fields. Each parameter was normalized in order to obtain the final morphometric flood vulnerability score. Postprocessing these results involved applying a Principal Component Analysis to identify weights for the components that encompass all morphometric parameters. Each drainage basin reveals a dimensionless morphometric flood vulnerability score value that is comparable with all other basins in Romania.
1. Introduction
In recent history, climate changes have led to different changes in several types of climatic phenomena, correlating to the genesis and manifestation of extreme hydrological events, such as floods. During the last 50 years, there have been recordings of increased frequency, intensity, and magnitude of floods [1,2,3]. For this particular reason, many states have started to implement new and modern monitoring systems as part of flood protection programs and also allocate funds for studies that address damage mitigation through the use of mathematical, geospatial models that can accurately predict and identify areas affected by potential floods [4,5,6]. The increase in frequency of flood occurrence can also be correlated with urban and rural expansion, with special attention given to flood-prone areas. It has been roughly estimated that a quarter of the World’s population lives at a maximum distance of 10–15 km from riverbanks [7,8]. Other human-induced reasons for increased exposure to flood risk correspond to hydro-technical constructions in the floodplain areas, such as oversized bridges, roads, or other communication structures constructed along river valleys, the partial or complete covering of embankments, river regularization [1,9], and also changes in land use [10].
While extreme precipitation events are not uncommon in Mediterranean regions, the year 2023 witnessed a particularly exceptional series of storm occurrences, including the formation of tropical storm Daniel over the Mediterranean Sea. These storms generated extreme amounts of precipitation, with 750 mm recorded in Greece within a 24 h period and over 400 mm in Libya’s northeastern region within the same time interval. These rainfall records are unprecedented for these nations, emphasizing the unusual nature of these events [11]. To effectively analyze the propagation of these large-scale floods, it is crucial to consider the entire drainage basin as it provides the most comprehensive hydrological context for flood quantification.
In Europe, Romania is known as a country with large floods that can have devastating consequences, and the more recent examples have increased in frequency. In the XX and XXI centuries, there have been 8 years with major floods that registered significant material damage [12,13,14]. During the last 20 years, there have been several catastrophic floods in at least five large drainage basins in the eastern and southern parts of the country [15,16,17,18,19,20,21]. The specific events that took place between 2005–2006, 2008, 2010, and 2013 have been the worst floods of the last 100 years, causing damages totaling millions of euros and interrupting regional economic activities in the corresponding areas for extended periods of time [17,18,22,23].
In Romania, the human settlements located in the mountainous areas are some of the most exposed to flood risk. The reasoning behind this is mostly related to the physical geographical context and the characteristics of the drainage basins, such as slope and other morphometric parameters, land use/land cover, soil texture, etc. Furthermore, in the mountainous areas, the on-site housing distribution pattern has changed during the last 5 decades, with their location migrating more and more towards the floodplain area of the major rivers. Out of all of Romania’s major river basins, two of the most exposed are Siret and Prut. They have registered some of the worst floods in the last 100 years on many mountainous tributaries [17,23,24]. Floods have caused major financial losses and human casualties in these basins, which raises the issue of developing and improving flood forecasting methodologies adapted for the local context and particularities and based on previously recorded floods, as well as on the morphometric parameters of included drainage basins.
The current study aims to describe a newly developed automated model for comparative analysis of flood vulnerability for drainage basins based on morphometric criteria. This has been achieved according to the drainage basin hierarchy classification system, which was introduced by Horton (1932–1945) [25,26] and modified by Strahler (1952–1964) [27,28,29,30]. The model has been applied to the entire surface of Romania. It calculates morphometric values for each analyzed parameter in a dimensionless form.
The model has been developed in ArcGIS/ArcMap software (version 10.8), using the model builder module. During recent decades, there have been dozens of variants of hydrological analysis models, with drainage basin level approaches, which intended to provide better and more relevant results for the on-site context: Storm Water Management Model (SWMM) [31], Precipitation-Runoff Modeling System (PRMS) [32], National Weather Service (NWS) River Forecast System [33], Streamflow Synthesis and Reservoir Regulation (SSARR) [34], Systeme Hydrologique Europeen (SHE) [35,36], TOPMODEL [37], Institute of Hydrology Distributed Model (IHDM) [38], etc. [39].
The novelty of this article is given by the implementation of a model that was developed in the model builder interface and that can be integrated and optimized into an ArcGIS tool, calculating the morphometric flood vulnerability score for drainage basins of a specific Horton–Strahler hierarchic order, resulting in the creation of a file that indicates, based on morphometric factors extracted from DEM, the susceptibility of basins to flooding. Secondly, this tool is completely automated, requiring no intervention from the user, except for inputting an elevation model, and choosing the threshold value and which river order should the model run for. Thirdly, the tool does not take into account only one parameter but eight morphometric parameters, which it calculates on its own, from a single layer. Furthermore, several types of potential errors that may occur while running the model have been accounted for, and solutions for their mitigations have been implemented directly into the model. In addition, the final result is a unitary vector file, with a detailed, comprehensive attribute table, which is easily interpretable. These types of files can be the basis for other flood simulation models, but they can also be a useful basis for local authorities when planning the expansion of the built-up area of settlements, as well as when allowing the construction of new homes. The model can be applied both at large and small scales, it being suitable for all types of areas, depending on different resolutions of digital terrain models. Lastly, the model has been run and has provided results for the entire country at all available drainage basin hierarchical orders, according to the Horton–Strahler classification system. The vast majority of previous studies on this topic have only addressed specific case studies, in the form of smaller drainage basins, and not a centralized geospatial situation of the entirety of Romania. This model has been applied to basins throughout Romania, and the result is a novelty for the country; it is the only applied model that results in the identification of flood-prone areas based on morphometric considerations for the entire country.
This article is divided into three chapters: methodology, results, and discussion. The methodology chapter presents the databases used and the software involved in the analysis model, the analysis steps and how the working layers are calibrated and corrected, as well as the PCA analysis. The results chapter presents the results obtained in tabular and cartographic format. The last chapter, the discussion chapter, deals with the results obtained in terms of their quality and the advantages and disadvantages of applying this model at different orders of scale, based on the Horton–Strahler hierarchy system.
2. Materials and Methods
Romania is a medium-sized country in southeastern Europe; it exhibits remarkable topographical diversity, with the Carpathian Mountains and Subcarpathian region dominating the central area, encompassing the Transylvanian Depression (Figure 1).
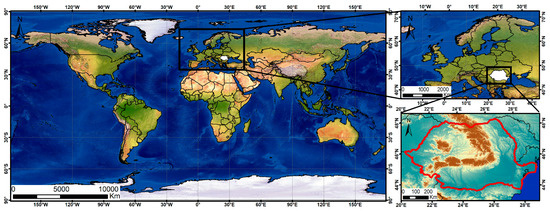
Figure 1.
Geographic location of the study area.
These mountain ranges are encircled by a semi-circular configuration of plateaus and plains that gradually descend from the mountainous core. Further enhancing this intricate topography is the Dobrogea Plateau, which borders the Black Sea. The elevation range spans from sea level to 2544 m, with an average value of 398 m. Romania’s climate lies within a region of interaction among five major pressure centers influencing Europe: the Azores, East-European, and Scandinavian Highs and the Mediterranean and Icelandic Lows. The interplay between these pressure systems and the underlying topography plays a crucial role in shaping the country’s regional climate conditions, which fall into four climate groups according to the Köppen–Geiger climate classification system: dry (Bsk), temperate (Cfa, Cfb), continental (Dfa, Dfb), and polar (ET) [40]. Mean multiannual temperatures range from below 0 °C in the high mountains to over 11 °C in the southern and southeastern regions. Annual precipitation averages 631 mm, with values ranging from 277 mm to 1246 mm and a standard deviation of 149 mm [41]. Precipitation generally declines eastward, with the lowest averages (below 350 mm) observed in the Dobrogea Plateau and Danube Delta. Elevation plays a significant role in precipitation patterns, with mountainous regions receiving over 700 mm annually. Rainfall distribution is uneven throughout the year, with June being the wettest month (85 mm average) and February the driest (33 mm average) [42].
Hydrographically, Romania is predominantly part of the Danube River basin, with 98% of the country’s territory drained by tributary basins, with the exception of rivers in the southeastern part of the country that flow directly into the Black Sea. At the country level, 15 major river basins are identified, including the Danube Valley and the Black Sea. The characteristic runoff regimes are rainfall–snowmelt, with the exception of the southeastern part of the country where only rainfall-based runoff is typical [43].
Floods are most often caused by torrential rainfall, and one of the most important climatic parameters relevant for flood analysis is rainfall erosivity. While compared to the global average of 2190 MJ mm ha−1 h−1 yr−1, the rainfall erosivity values in Romania are generally low; the mean rainfall erosivity in Romania is 785 MJ mm ha−1 h−1 yr−1, which is above the EU average of 722 MJ mm ha−1 h−1 yr−1. Therefore, the need for this type of study, especially in the context of climate change and more intense weather patterns, is confirmed. The maximum rainfall erosivity in Romania is 1150 MJ mm ha−1 h−1 yr−1, while the minimum rainfall erosivity is 462 MJ mm ha−1 h−1 yr−1. The territories most exposed to rainfall erosion are the Carpathians, the Subcarpathians, and the Moldavian Plateau [42,44,45].
The current study is aimed at developing a methodological tool that allows the quantification and relative comparison of similarly hierarchized drainage basins, according to several morphometric parameters. This entire study focuses on providing a comprehensive description of the methodological aspects related to the model that has been developed alongside the corresponding results. This study specifically addresses the issue of vulnerability and a specific kind of vulnerability, i.e., in the form of morphometric flood vulnerability. Vulnerability was analyzed in order to identify which areas will generate more potential damage at all scales, from a morphometric perspective, in case of flood occurrence.
There are several types of software that work with geospatial layers and have the option of connecting functions and layers into automated methodological flows, such as QGIS or SNAP; but, for the purpose of this study, the preferred piece of software used was ArcGIS/ArcMap software (version 10.8), with the included model builder geoprocessing interface. There are multiple reasons for choosing to use this program as the main software for the model. Firstly, ESRI, Redlands, CA, USA (the company that produces the software) is the market leader in the field of geospatial analysis using proprietary software; therefore, the functions are widely adopted and understood, and their long existence in the field has given them an advantage in terms of algorithms, efficiency, and diverse functions. Secondly, this is the main software preferred by many companies across the world that deal with geospatial data, considering their complete software package; therefore, tools, such as those developed in the current paper, can be easily reproduced and applied all around the globe. Thirdly, this is arguably the industry standard, which is universally accepted in the commercial and academic worlds, and compatibility between file types and layers is maximized. Lastly, model builder is a very mature interface that allows for fine control over functions, formulas, and files in the GIS environment.
The model requires as input a single geospatial layer, in the form of a DEM (digital elevation model), it is not layer dependent and does not require a specific type of elevation layer (it can be radar, LiDAR, interpolated from contour lines, etc.). For the purpose of this paper, considering the fact that this study addressed the entire area of Romania, FABDEM v1.2 was the chosen layer for running the model [46]. FABDEM (Forest and Buildings removed Copernicus DEM) is a processed layer from ESA’s Copernicus program (derived from the COPDEM layer), which was chosen due to the fact that the forests and buildings of the raw layer were filtered out, and it is an elevation model that has received improvements with hydrological applications in mind. Furthermore, previous studies on floods have proven the suitability of the FABDEM layer for hydrological analysis in large-scale areas [47,48,49,50,51,52]. In addition, FABDEM has global coverage, thereby facilitating the replicability of the current results in other areas as well.
Due to the fact that across the globe, the administrative limits only occasionally overlap the hydrologic/basinal limits, the study area was significantly larger than the country’s administrative borders. Firstly, the model was run for the 16 major drainage basins that overlap Romania’s territory and they were analyzed individually at all the possible Horton–Strahler hierarchical orders. In order to segment the analysis on the 16 major drainage basins, vector layers with watershed limits were used, based on the HydroSHEDS layers, from the HydroBASINS database [53]. Considering the fact that this database was originally published in 2013 [54], the polygon layers required some spatial corrections, in isolated cases, due to the differences in accuracy and fidelity of the elevation layers used when generating the original polygons and in the current study.
In order to correctly associate the absolute cartographic scale to the elevation layer used, there have been two approaches taken into consideration. Firstly, the specialized literature in this field was researched and analyzed, regarding the correspondence between certain types of freely available large-scale elevation layers, and several representative correlations were identified. SRTM data, which have similar spatial resolution values with FABDEM data, were found to best correlate to DEMS derived from topographic maps at a 1:100,000 scale [55]. Other studies confirm the compatibility of similar elevation layers (ASTER and SRTM) of 1:80,000 and 1:100,000 [56] or only for the 1:100,000 scale [57].
Secondly, in order to minimize errors and ensure the correctness of extraction of the river network, according to the Horton–Strahler classification system, manual tests were performed on topographic maps. This process required using topographic maps at a 1:100,000 scale and consisted of manually digitizing the hydrographic network, followed by applying a threshold value in the flow accumulation function. By running tests with different threshold values, a recommended threshold range was eventually identified for this specific use case; it was used for automatically extracting the entire river network as accurately as possible from the FABDEM layer in order for it to be as close as possible to the river network manually digitized from the topographic maps.
2.1. Morphometric Parameters
There are numerous factors/parameters that influence the occurrence and manifestation of floods, and several previous studies have combined as many as possible in order to try to identify the most vulnerable areas that are prone to flooding [58,59,60,61]. This current study has applied some of the most relevant parameters for flood analysis, that could be calculated automatically in the model builder. These morphometric parameters are dimensionless in nature, meaning they do not have any measuring units attributed to them, but the minimum–maximum values range successfully depicts the relative comparison between different drainage basins in any hierarchy order.
2.1.1. Elongation Ratio
This parameter represents the ratio between the diameter of the circle with the same area as the basin and the maximum length of the basin, which was measured in a parallel direction to the axis of the main river. It was first formulated by Schumm in 1956 [62] and has been a parameter used ever since in hydrological and morphometrical analysis.
The values that are generated using this parameter are inversely proportional to the actual shape of the drainage basins for which it is calculated using the values in the attribute table [53]. Therefore, on the range of values that are generated for each drainage basin, on the lower side there are values corresponding to more elongated basins, correlating to a higher flood vulnerability, while on the higher side, there are basins that are less vulnerable to floods, from the perspective of this particular parameter [63].
2.1.2. Circularity Ratio
The circularity ratio was developed in 1953 [64], and then it was re-analyzed and taken into account for basinal analysis by Strahler [30]. The purpose of this parameter is to assess the overall shape of a drainage basin, and it consists of the ratio between the surface of the basin itself and the area of the circle that has the same length as the perimeter of the same basin.
This ratio is directly proportional to the susceptibility to flooding [59]. The highest values of the circularity ratio correlate to a basin shape that resembles, as much as possible, the shape of a perfect circle, while the lowest values correspond to a longer basin shape. The shape is directly tied to the flood hydrograph and the way in which all the tributaries concentrate (simultaneously or successively, when the ratio is higher or lower, respectively) [63].
2.1.3. Relief Ratio
The relief ratio was also first formulated by Schumm in 1956 [62], and it is defined as the ratio between the difference between the maximum and minimum elevation values in the drainage basin and the length of that basin. For obvious reasons, it is strongly correlated to the main river’s longitudinal profile, corresponding to the given basin.
It correlates to a direct proportionality to the flood vulnerability, with high values associated to high vulnerability and vice versa [59]. The greater the altitudinal values and the landscape, the more potential energy it holds to transport the runoff water through the basin itself. Basins with higher relief ratios will have shorter times for runoff delay, as well as taller flood hydrographs and higher water velocities.
2.1.4. Drainage Density
Drainage density was first conceived as a quantifiable parameter by Horton in 1932 [25]. He stated that this represents the ratio between the sum of all river lengths in a given drainage basin and its total surface area.
It is also a parameter that is directly proportional to flood vulnerability [53]. High values of drainage density emphasize the existence of a longer, cumulated river length value per surface unit, indicating a denser hydrographic network, which can implicitly carry greater flow rates during floods, thereby corresponding to higher flood vulnerability values.
2.1.5. Roughness Number
Also introduced by Schumm in 1956 [62], the roughness number is defined as the product between the absolute altitudinal range in a drainage basin and the drainage density.
Higher values of this parameter correspond to the existence of small river valleys, but with defining steep slopes that favor concentrated runoff and the occurrence of floods; therefore, there is a direct proportionality between the value of the roughness number and vulnerability to flood [59].
2.1.6. Topographic Wetness Index
Conceived by Beven and Kirkby in 1979 [37], the topographic wetness index (also known as the compound topographic index or “CTI”) was developed as part of the TOPMODEL runoff model. Several researchers have modified the base version of the index in more recent research [65,66,67,68,69,70,71,72,73,74].
This index is also directly proportional to flood vulnerability; therefore, the greater the TWI value, the higher the vulnerability. According to Qin et al., 2011 [71], TWI allows for delineating a certain portion of the drainage basin, which is potentially exposed to floods, by filtering all areas over a certain value.
2.1.7. Hypsometric Integral
This is another dimensionless parameter that is generated through the ratio between two subtractions: the minimum altitude subtracted from the average altitude and the minimum altitude subtracted from the maximum altitude.
Similarly, to the elongation ratio, this parameter is inversely proportional, meaning that the lowest values correspond to high flood vulnerability.
2.1.8. Slope Value
Slope value is an obvious morphometric parameter from a hydrological perspective, considering it influences runoff, flow rate velocity, water stagnation, etc. Like most parameters addressed previously, this also poses a relation of direct proportionality [59]. Declivity affects floods both by the speed with which the water from neighboring slopes flows into the riverbed and the speed of the tributaries that meet at confluence points.
2.2. Model Builder Analysis
There are 5 main stages of the model, during which there are functions running with specific purposes, as shown in Figure 2.
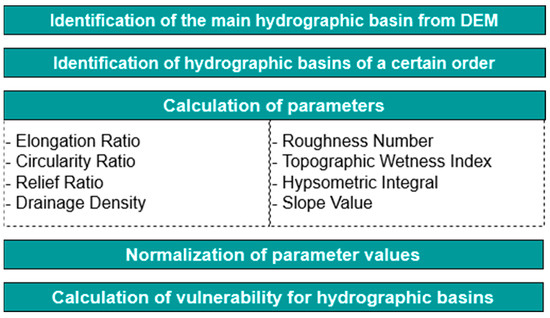
Figure 2.
Main stages of the model.
The first stage is a sum of functions that extracts the large drainage basin from the DEM (the DEM does not have to be previously cropped to the exact limit of the watershed). Afterwards, the model extracts all sub-basins included in the larger drainage basin, which were created during the previous stage, according to a specific Horton–Strahler order, and had to be input by the user when first running the model. Arguably the most important stage is the third one, when all the basic morphometric indicators are extracted from the DEM, and then each of the 8 parameters is also calculated. The fourth stage refers to normalizing each value of each parameter in order for them to be relatively comparable. Lastly, the final geo-formula is run, adding up all the parameters, in order to depict a final morphometric flood vulnerability score.
There are a total of 206 functions used in the model, and, out of all of these, 40 unique tools have been used throughout the entire model. Proportionally speaking, there are 31 tools related to raster file formats (15%), 12 tools used for vector calculations (6%), 10 tools for conversions (5%), and 153 tools related to attribute table calculations (74%). In total, the model generates 59 individual vector files and 36 raster format files (Figure 2). These are mostly intermediate files, considering the final result consists of only one vector file in .shp (shapefile) format, containing an attribute table that encompasses all the calculated parameters.
The entire model has been broken down in detail, in the following five figures (Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7), in order to fully describe each main stage of the analysis.
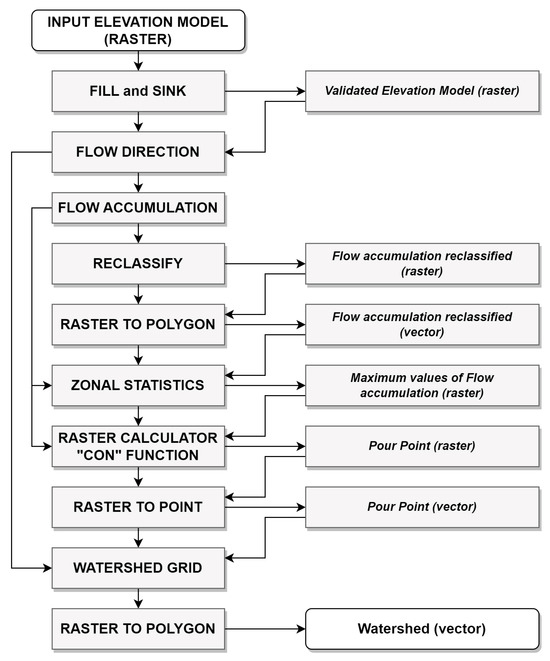
Figure 3.
First major stage of the model.
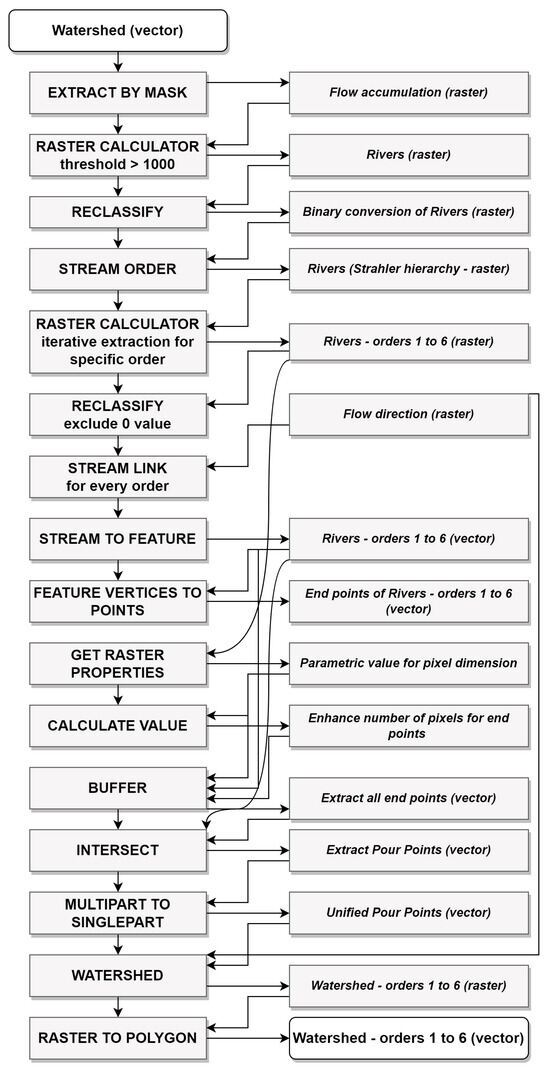
Figure 4.
Second major stage of the model.
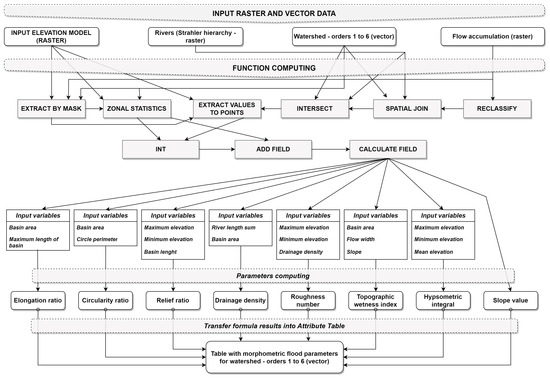
Figure 5.
Third major stage of the model.
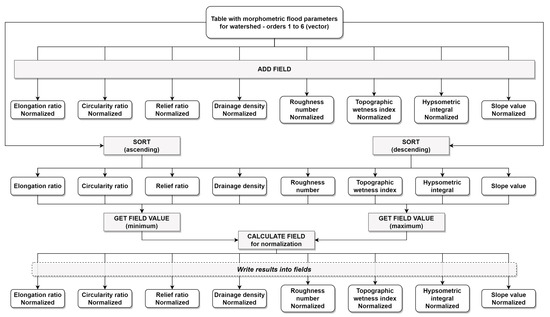
Figure 6.
Fourth major stage of the model.
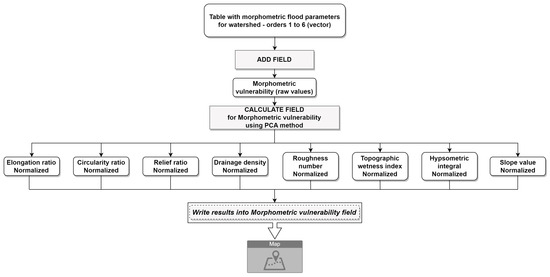
Figure 7.
Last major stage of the model.
2.2.1. Preconditions Required before Running the Model
In order for the model to run appropriately, there are a few prerequisites that must be addressed, regarding technical conditions. Firstly, while virtually any type of DEM can be used, the name of the file itself should be “srtm”, and the file extension should be “.tiff”. This is due to the fact that during intermediate raster functions, in order to ensure that no errors occur related to default file names, the original input file should have a very specific name. Furthermore, the generation method of the input elevation model is not relevant (radar, lidar, generating from contour lines, etc.); however, the file should have a projected coordinate system and not a geographic coordinate system, due to the way the model addresses measuring units. Geographic coordinate systems use degrees, minutes, and seconds for measuring distances, which does not correctly integrate into certain functions that use measuring units corresponding to projected coordinate systems. The model has been configured to function completely into the “C://” partition of the computer it runs on into a folder named “ModelBuilder”, which should be created by the user. Although it might be seen as a limitation, this ensures that there are no errors occurring due to differences in partition configuration on other computers. Finally, for obvious space constraint reasons, there should be sufficient storage space available before running the model, depending on the total area being analyzed, as well as the spatial resolution of the layer.
During the first major stage, the model extracts the main drainage basin that encompasses all the smaller drainage basins within it. It does this by running a series of functions that allow generating flow direction, flow accumulation, and the identification of the pour point, and then generating the watershed in raster format, and then subsequently converting it to a vector file (Figure 3).
The second stage identifies the smaller drainage basins within the watershed extracted during the first stage, according to the Horton–Strahler hierarchy number, for an order that was chosen by the user, during the initial input of the tool. This is achieved by generating the river network, according to a threshold value, from the flow accumulation raster, followed by generating the Horton–Strahler classification raster, using the stream order function, followed by extracting the pour points from the confluences of the initially specified order value. These pour points become input for the watershed function once again, in order to extract the drainage basins included in the initial, larger basin, corresponding to the specified Horton–Strahler order (Figure 4).
The third stage is the most technically involved, due to the fact that it requires the extraction of the general initial morphometric values for each drainage basin from which it generates the 8 aforementioned parameter absolute values (Figure 5). This stage uses 2 types of functions. Firstly, there are tools that operate at a geospatial level, such as Zonal statistics, or Extract values to points, which convert the spatial information into table-form data. Secondly, there are numerous field- and table-related tools that turn all the theoretical formulas of each morphometric parameter into a concrete value. Some of these most common tools are Add Field or Calculate Field. Additionally, the “Delete Field” function was used repeatedly in order to provide a clean, final result, with no redundant fields, and this also avoids errors due to names already in existence from previous steps. This stage also includes the use of some other error-avoiding tools, applied, as discussed in more detail, further along in this chapter.
The fourth stage (Figure 6) is a consecutive row of functions with the sole purpose of normalizing the values of each parameter so that they range from 0 to 1 and are comparable in a subsequent table field formula. This normalization process was undergone in order to equitably add the value from each of the 8 parameters through a simple addition process and provide a quick comparative perspective straight from the model itself. This does not portray the maximum accuracy possible in this generated form, but users can choose afterward whether they want to calculate proportional weights for each parameter by applying any statistical method for weight identification (AHP, PCA, etc.). In order to mitigate errors, two parameters required an extra tool in the form of the “Collect value” function, which allows the model to completely run without interruption. The final result of this stage consists of 8 new fields that correspond to each parameter, with normalized values for each drainage basin.
The final stage is the addition of the previous 8 normalized fields, corresponding to each parameter in a regular, non-weighted sum (Figure 7). Each drainage basin has a final morphometric vulnerability flood score, which ranges from 0 to 1.
2.2.2. Threshold
The threshold value (used in the flow accumulation function) is crucial when talking about Horton–Strahler classifications, because it is a very dependent parameter to other cartographic aspects (such as spatial resolution or general map scale) and could be easily overlooked. However, it is arguably the most important parameter when generating the river network (via a combination of flow accumulation and stream order functions in ArcGIS/ArcMap 10.8). By setting lower or higher values, the sizes of the rivers (and their corresponding drainage basins) can be significantly altered, and the entire analysis can become irrelevant and difficult to compare to same-scale mapping products.
Previous studies have revealed that certain threshold values correlate to specific digital elevation models. For example, similar elevation layers, such as SRTM data (available at a spatial resolution of 30 × 30 m) correspond to a cartographic scale of 1:80,000 and 1:100,000 [56], or only for the 1:100,000 scale [57].
The elevation model used in this study has the same spatial resolution, thereby correlating to the same absolute scale. In order to achieve this degree of correlation, multiple maps at a 1:100,000 scale were tested to reveal which threshold value interval would correspond to the river network on the maps, if extracted from the FABDEM raster. By comparing manually digitized rivers from topographic maps at a scale of 1:100,000 and the rivers generated in ArcGIS 10.8, for this specific scale, from the FABDEM 1.2 layer, it was revealed that the threshold values required a numerical range between 950 and 1000. For an easier standardization process and replication purposes, the threshold value used in this study for the flow accumulation function was 1000.
2.2.3. Error Addressing
During the creation of the model, numerous successive runs were undergone at each development stage in order to verify the correctness and precision of each function across a large elevation raster file. Several errors were observed to be introduced that were derived from the elevation model or from function limitations in ArcGIS/ArcMap 10.8. Therefore, several situation-dependent steps were undergone in order to mitigate or eliminate these issues.
Under specific morphometric conditions, the rivers of two neighboring watersheds would join together at a very acute angle and sometimes flow parallel over very small distances, considering the native pixel pattern of a raster layer. Just before the confluence, the rivers would “virtually flow” in parallel and generate neighboring pixel rows, which would combine into a 2-pixel thick alignment of pixels. This would introduce confusion into the algorithm, which would not generate two separate watersheds but solely one watershed, which would not be hydrologically correct. The chosen solution was to automatically generate a very small, proportional buffer area at the output (corresponding to the “pour points”) of each drainage basin, which is derived from the pixel size of the input elevation model. This buffer area was intersected with the river network, thereby generating new pour points at a distance of 5 pixels upstream of the original confluence point, which was found to be statistically insignificant. This subtracts a small area from each watershed, but it is a very similar area (counted in no. of pixels) from each basin, and these basins are all from the same Horton–Strahler hierarchy order; therefore, they are comparable in absolute area size, and this subtracted area is proportional to all drainage basins, thereby resolving this error.
On some occasions, if the minimum altitude value was equal to the maximum altitude value (perfectly flat areas), the model stopped running while generating the hypsometric integral; however, these cases were observed only in small, erroneously generated polygons. In order to mitigate this, a supplementary “IF statement” function was added, which would add 1 m to the maximum height value so that the equation could properly run and not stop the entire model from completing the task. These basins can easily be identified at the end of the processing stage by introducing a new field in the attribute table with an “IF statement” for the cases where the minimum and the maximum values are the same.
For a couple of functions, during the final normalization stage, after applying the “Get Field value” tool, the model occasionally generated several polygons with a 0 value (which would be perfectly correct from a hydrological perspective). However, when feeding these output values as preconditions into the “Calculate Field” function, the software interprets the zero value as false, thereby stopping the model from running until completion. To mitigate this, a few “Collect Value” tools were added before the “Calculate Field” tools, which allows the model to transfer the values, including 0 (“zero”), into a temporary table, thereby allowing the model to run properly.
After completely running the model for all hierarchical orders, there were several basins that depicted geometric anomalies in the sense that their polygonal shape was perfectly straight on at least one side. This situation was mostly visible at the lowest value orders. Subsequent manual observations on the elevation model concluded that these erroneous polygons were attributed to the fidelity of the elevation model in areas where slope values were almost 0 (flat fields, or mainly wide riverbeds). These were caused either by imperfections of the elevation model or straight levees built in flood-prone areas. Depending on each case, these were manually corrected or completely removed, and the parameters were regenerated in order to comply with the new morphometric values of each parameter and ensure a correct normalization process.
This model was run on all 14 major drainage basins that flow in Romania and cover the entirety of its surface. This process was performed for all possible Horton–Strahler hierarchy orders, adding up to a total of 6 orders all across the country when run from the FABDEM elevation model. The final shapefiles containing a hierarchical order were united into a single shapefile, using the Merge function, to properly consolidate all the parameters calculated for each sub-basin for that particular order. This process was repeated for each hierarchical order to consolidate the basins for all of Romania.
2.3. PCA (Principal Component Analysis)
In order to identify how each parameter impacts the final vulnerability score, further statistical analysis was required. This is most commonly performed by attributing weights to each parameter, and some of the most used techniques are PCA (Principal Component Analysis) or AHP (Analytical Hierarchy Process). In previous studies [75], it was proven that, although they can deliver comparable results, the PCA method can have a technical advantage by eliminating the presumed structure and human-driven score ranking process. Therefore, for the purpose of identifying the different weights in the final vulnerability score, the preferred method used in the current study was the PCA method, which was similarly used in other hydrologic studies [61] and was applied for all 6 hierarchical orders. This would provide proportional weights by generating a number of principal components, which would minimize any potential errors introduced by erroneous human input.
The main result of the model consists of a vector layer in shapefile format, with an attribute table that contains all the final parameters, calculated for each drainage basin, for that particular hierarchical order. The parameters are contained in this table both in raw form and also in normalized values. Additionally, spatial information that correlates to each drainage basin, which is primarily used to calculate the 8 morphometric parameters, is also kept in the final table (such as minimum, maximum, and mean altitudes, perimeter, area, basin length, etc.). In order to depict an immediate vulnerability score, the model calculates this risk based on a direct sum of all 8 parameters, after which it creates another field, where it normalizes this vulnerability score. In order to calculate a more representative, weighted sum, the Principal Component Analysis was applied. The PCA was not performed as part of the model but following the model results. Depending on the use case or requirements, any other appropriate statistical analysis could be performed on the dataset, but for the current study, PCA was conducted.
After generating the entire table with normalized parameters, as well as a final, dimensionless value of the vulnerability value for each sub-basin from each hierarchical order, the attribute table for each of the 6 shapefile layers was subjected to a Principal Component Analysis in JASP software (version 0.18.1.0) [76] in order to better emphasize the differences between each variable in the final formula, thereby calculating the weights. For each of the 6 hierarchical orders, the PCA was applied, using an orthogonal varimax rotation and eigenvalues above 0 (in order to analyze all variables, adding up to a total of 100% weights), generating 8 principal components. Choosing an eigenvalue over 1 would generate only 3 principal components, accounting for only 81.7% of the total variance. Therefore, in order to fully integrate all parameters and account for the entirety of the dataset, the eigenvalue was set to 0. By doing this, 8 principal components were generated, integrating all 8 parameters.
Generating the final dimensionless vulnerability score and comparing drainage basins required creating a geo-formula that assigns weights. Two types of weights were applied. First, each principal component (out of a total of 8) received a weight derived from the rotated solution table, corresponding to the orthogonal-varimax analysis (Table 1). Second, inside each principal component, each of the 8 parameters was assigned a weight based on the component loadings table, adding up to 100% of all the variables analyzed.

Table 1.
Weight values for principal components for each Horton–Strahler hierarchy order.
3. Results
The first attempt to run the model was on the entire Danube drainage basin, but this was not successfully completed due to a few factors. First, the number of computational resources required to run the model for larger files is significantly higher in order to generate results in reasonable amounts of time (even days, in some cases). Furthermore, if ArcMap is used, the software interface is not optimized; therefore it does not access all resources of a PC even if it has sufficient computational power. Storage space was another issue, considering that almost 170 GB in intermediate files were generated, and the model had stopped running only after partly being able to run. Due to the lack of optimization on the software side and a large initial elevation file, the time required to only partly run was 8 days; therefore, temporal constraints are also a potential issue when dealing with extremely large areas. Lastly, file type limitations were reached, i.e., an intermediate polygon vector in .shp (shapefile) format cannot surpass 2 GB, and the model would have required .shp files larger than 2 GB, thereby not being able to complete the full model workflow. This should be mitigated by changing file types in multiple functions, but these changes would require adapting the entire model, which would be the subject of a future version of this model, considering the large amount of time put into developing the model itself.
The second, successful attempt required running the model separately on all 14 major watersheds in Romania for all Horton–Strahler orders. Additionally, smaller basins located next to the borders required separate application of the model and subsequent merging. All the resulting shapefile layers were merged into six final shapefiles with complete coverage for the entire country. In total, for all six hierarchical orders, the model generated over 90,000 drainage basins (Table 2).

Table 2.
Statistics of resulting layers for drainage basins of all 6 Horton–Strahler orders.
When compared to the raw hypsometry on a country-wide analysis, the flood vulnerability values do not fully correlate with altitude values, which is to be expected, despite the morphometric dependency on the terrain. For verification purposes, several basins were sampled and their parameters and final morphometric flood vulnerability score were manually calculated, and there were no erroneous values found that were generated by the model.
The results of the first order add up to over 70,000 drainage basins (Figure 8). Both for the first-order basins and for all other orders, the watershed divides were not cut using the clip tool using the country border layer but selected and extracted out of all the generated basins via the select-by-location tool without losing any surface area. This ensures that the morphometric relevance remains unaltered from the original form it had when all the parameters were calculated.
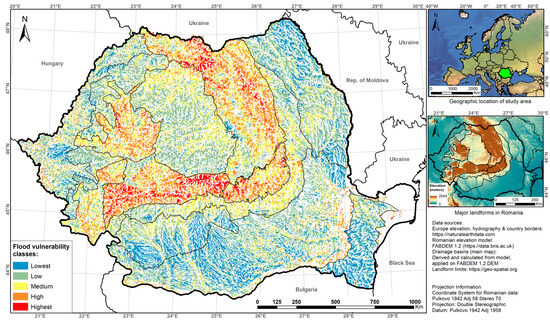
Figure 8.
Morphometric flood vulnerability score mapped for the 1st-order drainage basins.
The number of basins of the second order adds up to 16,000 individual basins, and their number continues to reduce the greater the hierarchy order is (Table 2). There are flat areas that already correspond to great floodplains, such as the Danube River floodplain, which are extremely flat (especially on the elevation models); they do not generate accurately drawn basins and were eliminated from the final results. This is why the area known as “The Great Brăila Island” has little coverage, especially on the lower value classification orders (Figure 8, Figure 9 and Figure 10). The same is true for the entire Danube Delta, and this should be relevant, considering the fact that floods that occur in these areas are never associated with small drainage basins but cover vast areas due to the high flow rates of the Danube or its major local tributaries.
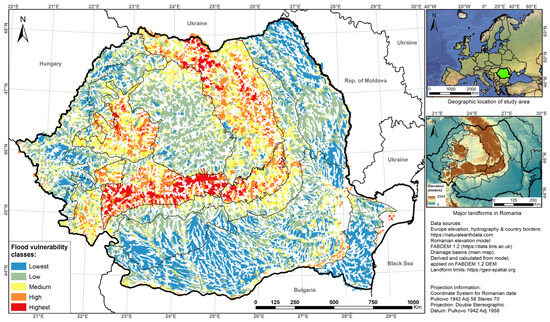
Figure 9.
Morphometric flood vulnerability score mapped for the 2nd-order drainage basins.
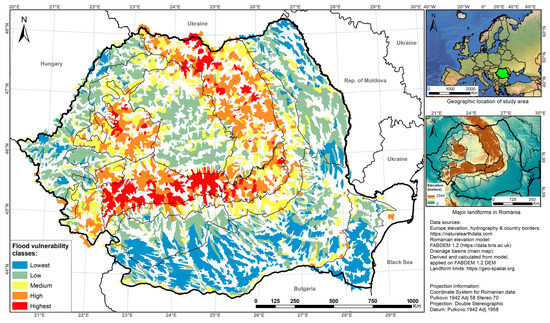
Figure 10.
Morphometric flood vulnerability score mapped for the 3rd-order drainage basins.
It is important to mention the fact that the larger order watersheds do not necessarily correlate to the drainage basins of the biggest Romanian river basins, considering that the shape of these basins is not dictated by the confluence of same-order tributaries, but the fact is that they flow into a larger river despite its Horton–Strahler number (Figure 11, Figure 12 and Figure 13).
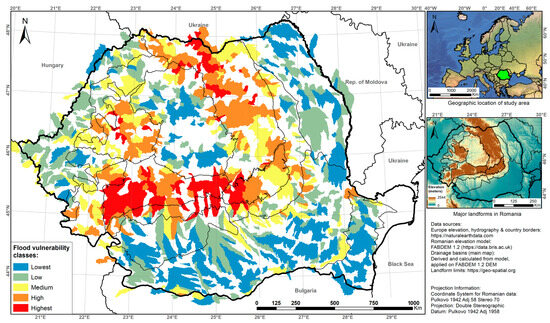
Figure 11.
Morphometric flood vulnerability score mapped for the 4th-order drainage basins.
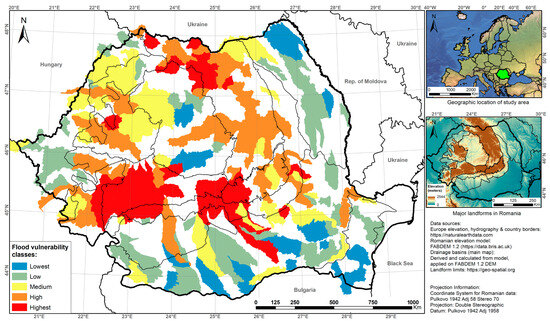
Figure 12.
Morphometric flood vulnerability score mapped for the 5th-order drainage basins.
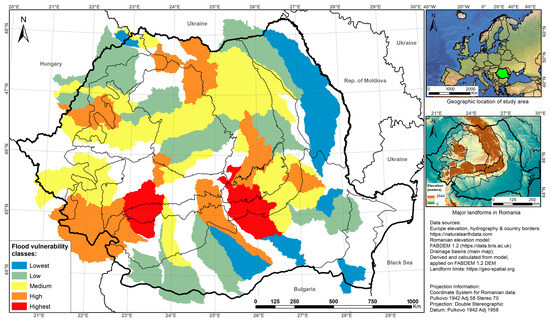
Figure 13.
Morphometric flood vulnerability score mapped for the 6th-order drainage basins.
3.1. Validation
For such large-scale studies, validation is also a critical part of ensuring that the methodology is relevant and appropriate and does not introduce any anomalies in the final results.
Considering the parameter dependency on each type of landform (mountainous, hilly, plateau, or plains), the final distribution of classes is rational and also well distributed among the transitional areas between major landforms. This is valid for almost all orders, except for the largest one, where drainage basins frequently cross multiple landforms, and they do not fall into a single landform-specific category. However, general altimetry and slope value distribution reveal that basins located in steeper and higher relief energy areas are the basins corresponding to the highest scores of morphometric vulnerability.
3.2. Historic Floods Validation
Despite not taking into account all flood-related parameters (such as vegetation, interception, synoptic context, rainfall distribution, etc.), the morphometric vulnerability score generated by the model strongly correlates with numerous instances of historic floods, which have had a great impact both in form of great damages and also in casualties. Scientific literature in the field of hydrological risk has revealed certain rivers in Romania that tend to generate repeated significant floods and have implicitly been the subject of multiple studies. Some of the most susceptible areas to flooding are mountain areas, and among the most exposed drainage basins, there are a few notable examples, such as Siret (located mainly in the Oriental Carpathian Mountain range), where numerous flood events have taken place between 2005–2006, 2008, and 2010 [20,77,78,79,80,81,82]. Other regions with similar examples that correlate to basins with high morphometric flood vulnerability scores are Iza, Viseu, Somes, and Mures, which are frequently affected by floods [83,84,85]. In the Meridional Carpathian Mountains, drainage basins that generate repeated floods have been studied in the area of the Olt, Jiu, Timis, or Vedea Rivers [86,87,88,89,90,91,92,93].
3.3. Spatial Validation
Unfortunately, country-wide, freely available historic flood databases are inaccessible or nonexistent despite the numerous floods that have been recorded almost on a yearly basis.
However, a very relevant source of geospatial flood data, useful for validation purposes, originates from the Romanian Waters National Administration (RoWater). According to the RoWater EPRI Reports (Preliminary Evaluation for Flood Risk), which encompass all areas with historic floods in Romania, most major historic floods have been centralized, and they correlate well with basins identified through the current study as having a higher degree of flood vulnerability. It is difficult to fully correlate exact flood sectors from EPRI Reports to drainage basins generated by the model due to the fact that major rivers have flood risk areas that correspond almost to their entire length. Furthermore, this difficulty is emphasized by the fact that neighboring drainage basins contribute differently to certain sectors of a floodplain, and it is very complicated to precisely state which basin contributes to a flood-prone sector most out of tens or hundreds of basins with different vulnerability scores. However, empirical and expert knowledge suggests that, by proximity principles and flow path directions, numerous major rivers that have had historical floods source their floodwaters in drainage basins with high vulnerability scores, such as Siret, Moldova, Olt, Mures, Arges, Dambovita, Prahova, Jiu, Vedea, Teleorman, Somes, and Trotus.
All across Romania, from a historical perspective, major floods have corresponded mostly to the floodplains of major rivers and some smaller-sized rivers. The medium, high, and highest vulnerability scores are located in the vicinity of these aforementioned floodplains, especially on the lower orders of hierarchy and in regions that neighbor landforms of higher elevation (which act as the source areas for floodwater concentration). The medium class is mostly present in two main areas: in the near vicinity of higher altitude areas and along the floodplains of major rivers in hilly regions, which acts as a hybrid validation for the location of numerous historical flood areas in the hilly and plateau areas. In addition, the lowest scores for morphometric flood vulnerability also correlate to the areas with no significant historical floods, confirming the distribution of the lowest values.
For validation purposes, it is relevant to state the fact that the smallest basins (first and second orders) do not generate floods by themselves, as recorded in RoWater data, but correlate to the upstream region of floodwater formation and accumulation, which eventually ends up flowing into the larger drainage basins located downstream. At this point, for the fourth, fifth, and even sixth orders of hierarchy, the floodplains of these corresponding rivers generate floods, as shown in the EPRI reports.
To conclude, validation is not only relevant for the results of this study, applied to the entirety of Romania, but rather for the model itself, which has proven to generate valid results, with comprehensive parameters, that do correlate to real-world flood-prone areas.
4. Discussion
The model created for the purpose of this study managed to provide drainage basins with morphometric flood vulnerability scores for all relevant Horton–Strahler hierarchical orders. The values could be compared across the country for all six orders that resulted from the analysis. Several differences in score distribution have been observed and taken into account for the purpose of this study.
The orders with the lowest Horton–Strahler value have proven to be relevant only for depicting the extremely local flood manifestation when a flood event occurs, but these are highly isolated scenarios, due to the fact that common floods are generated by rainfall that extends well beyond the 1.7 km2 average drainage basin area, corresponding to this first order. Furthermore, their reduced area correlates to a higher probability of encompassing only steeper areas with greater relief energy, which obviously generates very high morphometric flood vulnerability scores but does not necessarily explain the vulnerability of the entire neighboring region, which would also be affected by the same flood event. This situation stays partly valid for the second hierarchical order, considering that, despite being approximately four–five times larger in areas of the first-order basins, basins averaging 8 km2 do not encompass rainfall events fully in their watershed divide perimeters in order to be completely relevant for local rainfall analysis. However, there is a clear distinction of the vulnerability score in basins located at the very edge of the major river courses, where the first-order basins tend to depict higher vulnerability, while the scores average out over the larger basin areas and portray more realistic values. These basins correlate with the more flood-prone areas, especially when discussing major floods that take place on the main tributary river they flow into. Results from the second order retain this tendency only partly in basins that are more sparsely distributed along the major river valleys, filtering out the smaller exceptions from the previous, smaller order.
The major difference between the first and second-order basins is the middle vulnerability class, which relates to basins with morphometric indices that tend to average out over slightly larger average areas. This means that the second and fourth class of vulnerability scores from the second-order basins will encompass more basins that are better differentiated in terms of morphometric flood vulnerability.
Therefore, the first two Horton–Strahler orders do not reveal the individual flood vulnerability scores as accurately as larger orders, due to their very small nature.
The following two intermediate orders (three and four) are the most relevant for floods that occur at local levels, with average areas ranging from 37 to 167 km2. These areas are not large enough to correlate to floods that could affect entire regions but can certainly be associated with local rivers that generate floods with increased damage and even potential casualties.
The last two orders addressed in the analysis (five and six) provide morphometric flood vulnerability scores within a more regional context. Their larger average surface areas (772 and 3506 km2, respectively) are associated with more devastating floods generated by torrential rainfall; they are correlated to a more regional perspective. These are usually the basin sizes that summertime torrent floods take place in. At these higher orders or hierarchies, the vulnerability scores for drainage basins located at the edge of the main river valleys can not be addressed, considering the difference in scale/spatial resolution fidelity. Basically, for the fifth- and sixth-order basins, there are not any smaller basins neighboring the main river valley.
The smaller basins that correspond to the first and second order almost always correlate to the torrential basins. Technically, this is the source area of the concentration of torrential rainfall and not necessarily the area where floodwater induces damages and casualties in the floodplain areas. The floodwaters mostly form and originate in these lower-order basins from which they meet and increase in volume in the next, larger hierarchical orders. Here, the water concentrates into the floodplain sections, where most damages and casualties are generated. As mentioned in the validation section, the lower-order drainage basins do not generate floods, as recorded in the historical hydrological registries, but rather identify the first stage of upstream floodwater formation, which eventually concentrates in the floodplains located downstream, as depicted in the EPRI historical floods map, thereby correlating to the fourth, fifth, and even sixth orders of hierarchy.
Despite these differences between all the Horton–Strahler orders, a main distribution aspect is obvious, which consists of the consistency of the location for the extreme classes of morphometric vulnerability scores (the highest and the lowest classes). This acts as a technical means of cross-validation between the morphometric flood vulnerability scores of all six orders.
The results emphasize the fact that the areas with the most morphometrically vulnerable drainage basins generally correspond to the mountainous region. This is valid and evident for almost all hierarchy orders. This general region is the one where most drainage basins are located, which have a maximum vulnerability class, according to our findings. This has been applicable in multiple studies that have identified the same highest elevation areas as flood-prone in more specific case studies.
Small-sized river basins, with a surface area of up to 1000 km2, are the most exposed to floods in Romania. These basins are predominantly located in the mountainous region, where the relief is characterized by narrow and deep valleys with steep slopes. In the event of heavy rainfall, these valleys can quickly fill up with water, leading to local flooding [94,95,96]. This acts as partial validation for the current findings, regarding the spatial distribution of the most vulnerable regions as depicted by the maps of all six hierarchical orders.
This is also supported by other scientific studies conducted in Romania, as well as by field observations. For example, a study conducted by the National Administration of Water Resources (ANAR) in 2023 identified 526 areas with potentially significant flood risk (APSFR) in Romania [97]. Of these, 344 (i.e., 65%) are located in the mountainous region. Field observations have also confirmed this. In recent years, Romania has been affected by a series of major floods, which have mainly occurred in mountainous areas [18,20,23].
Various studies have shown that the mountainous region is most exposed to flash floods in a short period of time, due to the relief configuration. Mountainous areas can quickly concentrate large amounts of water, which are then transported with increased velocities into the river valleys, occupying most or the entire floodplain. In the event of heavy rainfall, these can lead to local floods that can have serious consequences, both for the environment and for the population [98].
In addition, larger river basins are more prone to more complex floods in the valleys of major rivers such as the Siret, Prut, Mureș, Olt, Jiu, etc. These floods can be caused by heavy rainfall, melting snow or ice, as well as by other factors, such as hydro-technical constructions or climate change [86,87,88,89,90,91,92,93,99].
Flood risk analysis on river basins has normally been carried out in Romania in smaller areas, and other drainage-basin-based flood analyses at the scale of the current study were not carried out at the national level. This is due to the fact that Romania is a large country with complex relief, and the analyses are carried out on case studies. Some of the most intensively studied areas are those in eastern Romania. Here, it has been found, as in the current study, that the Moldavian Plateau, but also the Subcarpathian region, is more exposed to the risk of flooding; therefore, the drainage basins pose a higher susceptibility to flash floods/floods occurrence [17,100]. In the analysis of the susceptibility of river basins by physiographic classification, there are a number of studies carried out at the national level that focus on the eastern or central part [17,94,101].
4.1. Advantages
The model exhibits several obvious advantages, when run, both from a technical perspective and also from a pragmatic standpoint. Some of the most relevant advantages are as follows:
- There is only one required input layer, which is in the form of a digital elevation model (DEM), and other geospatial layers are not required at all.
- The means through which the elevation layer was generated are not relevant. An elevation layer can be used despite being generated via radar techniques (i.e., SRTM), lidar, or interpolation from topographic contour lines, etc.
- There are several elevation layers in raster format that have global coverage (SRTM, FABDEM, etc.); therefore, this model can be used virtually for any region on Earth, while also being free to download and use.
- The model can be applied in areas where datasets used for flood analysis are scarce or completely non-existent. Furthermore, administrative borders are irrelevant, especially in cases where one country has data, while the neighboring country does not.
- The elevation raster does not require preprocessing or any spatial filtering processes applied to it for the model to run properly. There are several functions embedded in the model that include steps involving layer preparations (i.e., fill sink).
- The input elevation file does not have to be in the exact shape of a drainage basin. The model extracts the main drainage basin automatically. The only requirement for the user is to make sure that the input file does not crop the drainage basin so that the model results are complete and comprehensive.
- The spatial resolution of the model is irrelevant, and this is an advantage in the sense that, for very large drainage basins, elevation models can be used with a coarser spatial resolution (i.e., the 90 × 90 m version of SRTM).
- If the input layer has significant fidelity, the model can be run on any landform type. It provides very accurate results on most mountainous and hilly regions, but it can provide very good results even on flatter plains if the elevation model is sufficiently accurate.
- Minimum GIS knowledge is required from the user in order to simply run the model.
- The model can be run on any computer with ArcMap software installed, although it does help to run the model on a more powerful computer, due to reasons related to time of processing. In addition, there are no complex extensions or plug-ins that are required to be installed, other than the base software.
- While still depending on the configuration of the computer it is run on, as well as the input file size, the execution speed of the model is significantly fast.
- The result is simple, comprehensive, unitary, and in a standard vector format (.shp), with a simple attribute table and easily interpretable. Additionally, the table can be exported and further analyzed in commonly available software, such as Microsoft Excel or LibreOffice.
- Most errors that could occur due to certain technical aspects are already addressed and mitigated in the model, as described in greater detail in the previous Section 2.
- On future iterations, the model can be expanded and improved and can be configured to add potentially more parameters.
- For further analysis and validation purposes, the model retains all the important, initial parameters, such as minimum, average, and maximum altitudes, basin area, perimeter, etc.
- The values for all eight parameters are normalized right within the model itself, saving time and providing more appropriate comparison capabilities.
4.2. Disadvantages and Limitations
- The model is input-dependent, meaning that despite the fact that the model can generate accurately drawn basins (along with the corresponding morphometric parameters) in areas with flat fields when using high-fidelity elevation data, it can still generate results with poor accuracy both from a spatial and attribute perspective. In order to ensure a greater degree of accuracy, the model must be hydrologically prepared/corrected, to avoid certain flow-related issues, at pixel level.
- Furthermore, for these flat areas, there can be occasional issues, even when using hydrologically correct elevation models. Therefore, it requires filtering and post-processing the polygons in the final resulting shapefile if the model was run in very flat areas (such as fields, or very wide river valleys) due to the fact that it can generate error-free results, but the shape of some small basins is either very elongated or very geometric, which is caused by imperfections in the elevation model. This probably would not be an issue if the model was run using a theoretically perfect elevation model (which does not exist). Lastly, this issue is mostly valid for lower hierarchical order basins.
- The final, normalized values for the morphometric flood vulnerability score can be larger at higher Horton–Strahler order values. This implies the fact that the average values are calculated for much larger surface areas at greater hierarchy orders; therefore, this averages out the parameter values more, meaning there are less extreme scores, which are canceled by calculating the averages. This means that comparing different hierarchy orders can be difficult but still relevant when comparing general areas for scores of similar vulnerability classes.
- Specific regions with a higher degree of hydro-technical constructions may pose problems in the sense that dams, levees, or even wider bridges, which would not disappear during a “sink fill” function, can stop the model during its run or isolate upstream regions. In this particular case, the high fidelity of an elevation model can be a drawback instead of an advantage. However, this can be mitigated by editing the elevation model itself and introducing a “virtual spillway” through where the river course would flow (Figure 14).
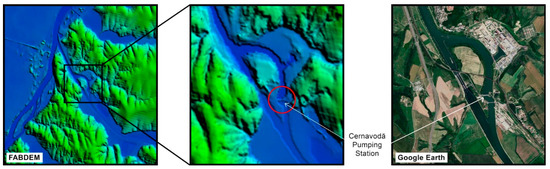
Figure 14.
Example of a man-made construction interfering with flow functions (pumping station).
- In certain countries or study areas, some rivers drain directly into the sea/ocean. This exoreic character can manifest from very low hierarchical orders, thereby requiring several runs of the model for very small areas (low execution efficiency), but there is no workaround, considering this is the field reality, which has to be addressed as it is.
- The watershed polygon datasets can also be a drawback due to the inaccuracy of the watershed divide for certain elevation models. For the current study, the HydroATLAS [52] dataset was used (level 5) in order to identify, extract, and run the model for all drainage basins in Romania; however, some issues were encountered. In some cases, not even the 5 km buffer area (used to extract the FABDEM) was enough to encompass the watershed divide offset in the HydroATLAS datasets; therefore, manual corrections of specific regions in several watersheds were performed in order for the model to fully cover all the country’s watersheds.
- There was an attempt to run the model on the entirety of the Danube drainage basin, but certain technical limitations were hit. When running the model on extremely large areas, file format limitations can be reached, such as the 2 GB space limit, which is associated with shapefile layers. Therefore, the model will not be complete in its entirety when hitting these limits.
5. Conclusions
In the context of climate change, floods are very dynamic phenomena, which also increase in frequency and intensity all around the globe. In the current analysis, a geospatial model was created to provide a morphometric flood vulnerability score that can compare drainage basins for any Horton–Strahler hierarchy order automatically. The model functions in five main stages: extraction of the main drainage basin, extraction of a specific order of drainage basins, calculation of parameter values, normalization of each parameter, and calculation and normalization of normalized morphometric flood vulnerability score.
The model that was developed for the purpose of this study was applied to all drainage basins in Romania (ranging from major basins to smaller, exoreic basins) and generated detailed polygons (both in terms of geometry and the attributes table) for six hierarchy orders, cumulating over 90,000 drainage basins.
There are several advantages in regards to using this model. Some of the most important ones are as follows: ease of use; very fast processing time, relative to the number of tools integrated into the model; compatibility with most elevation models; error mitigation steps, which are introduced automatically in multiple processing stages; and a comprehensive and easy to use final vector file, etc.
The model can be adapted in terms of parameter calculation, depending on the specific use case, and the final result, consisting of a shapefile vector layer with a comprehensive attribute table, can be further post-processed as it provides all intermediate relevant parameters, facilitating any potential supplementary manual verification procedures or formula validations. The final result also provides an easy table-form numerical database that can further be included in statistical analysis through different types of methods (PCA, AHP, or any other means of parameter weight identification).
While using the FABDEM elevation model as input for the entire area of Romania, it was found that the first two Horton–Strahler orders act as areas with torrential character, where the floodwaters form, while the following orders correspond to the actual basins that contain floodplains, which are vulnerable from a morphometric perspective.
The relevance of the model consists of the short time it requires to perform the analysis on all basin orders. This implies the fact that for smaller basins (lower hierarchy numbers) it is useful for national water basin administrations in different regions. Therefore, drainage basins located in a certain area can be ranked based on morphometric vulnerability, while not being dependent on the type of area (it can be administrative, hydrographic, landform, etc.).
Consequently, for the larger basins (higher hierarchy numbers), the model can be very useful for governmental institutions that manage resources, such as funds, projects, grants, or even intervention measures, for different regions based on their vulnerability to floods. For this reason, the dimensionless character of the model output can easily compare basins from any hierarchy order, according to any limit. This implies that, in regional management plans or pre-emergency situations, decisions and funds can be allocated accordingly.
Author Contributions
Conceptualization, C.C.S. and A.E.; methodology, C.C.S. and A.E.; software, C.C.S. and A.E.; validation, C.C.S., A.E. and M.I.; formal analysis, A.E. and L.N.; investigation, C.C.S. and L.N.; resources, C.C.S., A.E., M.I. and L.N.; data curation, A.E. and C.C.S.; writing—original draft preparation, C.C.S., A.E., M.I. and L.N.; writing—review and editing, C.C.S., A.E. and M.I.; visualization, A.E. and C.C.S.; supervision, A.E.; project administration, A.E.; funding acquisition, A.E. All the authors of this study contributed equally to the current article. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a grant of the “Alexandru Ioan Cuza” University of Iasi, within the Research Grants program, Grant UAIC, code GI-UAIC-2021-02.
Data Availability Statement
Data are contained within the article.
Acknowledgments
This work was supported by a grant of the “Alexandru Ioan Cuza” University of Iasi, within the Research Grants program, Grant UAIC, code GI-UAIC-2021-02. Acknowledgment is given by L.N., A.E. and M.I. to the infrastructure support from the Operational Program Competitiveness 2014–2020, Axis 1, under POC/448/1/1 Research infrastructure projects for public R&D institutions/Sections F 2018, through the Research Center with Integrated Techniques for Atmospheric Aerosol Investigations in Romania (RECENT AIR) project, under grant agreement MySMIS no. 127324. Acknowledgment is also given to the Department of Geography, Faculty of Geography & Geology, “Alexandru Ioan Cuza” University of Iasi (Internal Research Program no. 1/2021).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Slater, L.; Villarini, G.; Archfield, S.; Faulkner, D.; Lamb, R.; Khouakhi, A.; Yin, J. Global changes in 20-year, 50-year, and 100-year river floods. Geophys. Res. Lett. 2021, 48, e2020GL091824. [Google Scholar] [CrossRef]
- Mangini, W.; Viglione, A.; Hall, J.; Hundecha, Y.; Ceola, S.; Montanari, A.; Rogger, M.; Salinas, J.L.; Borzì, I.; Parajka, J. Detection of trends in magnitude and frequency of flood peaks across Europe. Hydrol. Sci. J. 2018, 63, 493–512. [Google Scholar] [CrossRef]
- Tabari, H. Climate change impact on flood and extreme precipitation increases with water availability. Sci. Rep. 2020, 10, 13768. [Google Scholar] [CrossRef]
- Garcin, M.; Desprats, J.F.; Fontaine, M.; Pedreros, R.; Attanayake, N.; Fernando, S.; Siriwardana, C.H.E.R.; De Silva, U.; Poisson, B. Integrated approach for coastalhazards and risks in Sri Lanka. Nat. Hazards Earth Syst. Sci. 2008, 8, 577–586. [Google Scholar] [CrossRef]
- Wipulanusat, W.; Nakrod, S.; Prabnarong, P. Multi-hazard risk assessment using GIS and RS applications: A case study of Pak Phanang Basin Walailak. J. Sci. Technol. 2011, 6, 109–125. Available online: https://wjst.wu.ac.th/index.php/wjst/article/view/76 (accessed on 12 September 2023).
- Chelariu, O.E.; Minea, I.; Iațu, C. Geo-hazards assessment and land suitability estimation for spatial planning using multi-criteria analysis. Heliyon 2023, 9, e18159. [Google Scholar] [CrossRef]
- Small, C.; Cohen, J. Continental physiography, climate, and the global distribution of human population. Curr. Anthropol. 2004, 45, 269–277. [Google Scholar] [CrossRef]
- Kalyanapu, A.J.; Judi, D.R.; McPherson, T.N.; Burian, S.J. Monte Carlo-based flood modelling framework for estimating probability weighted flood risk. J. Flash Flood Risk Manag. 2021, 5, 37–48. [Google Scholar] [CrossRef]
- Green, C.H.; Parker, D.J.; Tunstall, S.M. Assessment of Flood Control and Management Options; Thematic Review IV.4 Prepared as an Input to the World Commission on Dams; WCD: Cape Town, South Africa, 2000; Available online: http://www.dams.org (accessed on 12 September 2023).
- Rusu, A.; Ursu, A.; Stoleriu, C.C.; Groza, O.; Niacșu, L.; Sfîcă, L.; Minea, I.; Stoleriu, O.M. Structural Changes in the Romanian Economy Reflected through Corine Land Cover Datasets. Remote Sens. 2020, 12, 1323. [Google Scholar] [CrossRef]
- World Meteorological Organization. Available online: https://public.wmo.int/en/media/news/storm-daniel-leads-extreme-rain-and-floods-mediterranean-heavy-loss-of-life-libya (accessed on 3 October 2023).
- Bîrsan, M.V.; Zaharia, L.; Chendeș, V.; Brănescu, E. Recent trends in streamflow in Romania (1976–2005). Rom. Rep. Physics. 2012, 64, 275–280. [Google Scholar]
- Chendeș, V.; Corbuș, C.; Petreș, N. Characteristics of April 2005 flood event and affected areas in the Timis-Bega Plain (Romania) analysed by hydrologic, hydraulic and GIS methods. In Proceedings of the 15th International Multidisciplinary Scientific GeoConference, SGEM2015, Water Resources. Forest, Marine and Ocean Ecosystems, Albena, Bulgaria, 18–24 June 2015; Conference Proceedings. Volume 1, pp. 121–128. [Google Scholar]
- Pollner, J.; Kryspin-Watson, J.; Nieuwejaar, S. Disaster Risk Management and Climate Change Adaptation in Europe and Central Asia; Report World Bank; World Bank: Washington, DC, USA, 2008; 54p. [Google Scholar]
- Barredo, J.I. Major flood disasters in Europe: 1950–2005. Nat. Hazards 2007, 42, 125–148. [Google Scholar] [CrossRef]
- Cîmpianu, C.I.; Mihu-Pintilie, A.; Stoleriu, C.C.; Urzică, A.; Huţanu, E. Managing Flood Hazard in a Complex Cross-Border Region Using Sentinel-1 SAR and Sentinel-2 Optical Data: A Case Study from Prut River Basin (NE Romania). Remote Sens. 2021, 13, 4934. [Google Scholar] [CrossRef]
- Iosub, M.; Minea, I.; Chelariu, O.E.; Ursu, A. Assessment of flash flood susceptibility potential in Moldavian Plain (Romania). J. Flash Flood Risk Manag. 2020, 13, e12588. [Google Scholar] [CrossRef]
- Romanescu, G.; Nistor, I. The effect of the July 2005 catastrophic inundations in the Siret River’s Lower Watershed, Romania. Nat. Hazards 2011, 57, 345–368. [Google Scholar] [CrossRef]
- Tirnovan, A.; Covaci, O.; Gazda, M.R.; Barsan, N.; Enea, A. Flood vulnerability reduction. Case study: Tazlău river basin, downstream of its confluence with Tazlău Sărat. Present Environ. Sustain. Dev. 2021, 15, 189–198. [Google Scholar] [CrossRef]
- Romanescu, G.; Stoleriu, C. Causes and effects of the catastrophic flooding on the Siret River (Romania) in July–August 2008. Nat. Hazards 2013, 69, 1351–1367. [Google Scholar] [CrossRef]
- Romanescu, G.; Stoleriu, C. An inter-basin backwater overflow (the Buhai Brook and the Ezer reservoir on the Jijia River, Romania). Hydrol. Process. 2013, 28, 3118–3131. [Google Scholar] [CrossRef]
- Ministerul Mediului și Pădurilor. Romania’s Fifth National Communication on Climate Change under the United Nations Framework Convention on Climate Change 2010; Report; Grue and Hornstrup: Holstebro, Denmark, 2010; 188p. [Google Scholar]
- Romanescu, G.; Cimpianu, C.I.; Mihu-Pintilie, A.; Stoleriu, C.C. Historic flood events in NE Romania (post-1990). J. Maps 2017, 13, 787–798. [Google Scholar] [CrossRef]
- Ionita, M.; Nagavciuc, V. Extreme Floods in the Eastern Part of Europe: Large-Scale Drivers and Associated Impacts. Water 2021, 13, 1122. [Google Scholar] [CrossRef]
- Horton, R.E. Drainage basin characteristics. Trans. Am. Geophys. Union 1932, 13, 350–361. [Google Scholar] [CrossRef]
- Horton, R.E. Erosional development of streams and their drainage basins-hydrophysical approach to quantitative morphology. Geol. Soc. Am. Bull. 1945, 56, 275–370. [Google Scholar] [CrossRef]
- Strahler, A.N. Hypsometric (area-altitude) analysis of erosional topography. Bull. Geol. Soc. Am. 1952, 63, 1117–1142. [Google Scholar] [CrossRef]
- Strahler, A.N. Quantitative analysis of watershed geomorphology. Trans. Am. Geophy. Union 1957, 38, 913–920. [Google Scholar] [CrossRef]
- Strahler, A.N. Dimensional analysis applied to fluvially eroded landforms. Geol. Soc. Am. Bull. 1958, 69, 279–300. [Google Scholar] [CrossRef]
- Strahler, A.N. Quantitative geomorphology of drainage basin and channel networks. In Handbook of Applied Hydrology; Chow, V.T., Ed.; McGraw Hill Book: New York, NY, USA, 1964; pp. 4–76. [Google Scholar]
- Metcalf & Eddy, Inc. Storm Water Management Model; Final Report; I. Environmental Protection Agency: Washington, DC, USA, 1971; Volume I. [Google Scholar]
- Leavesley, G.H.; Lichty, R.W.; Troutman, B.M.; Saindon, L.G. Precipitation-Runoff Modeling System—User’s Manual; Water-Resources Investigations Report; US Department of the Interior: Washington, DC, USA, 1983; pp. 83–4238. [Google Scholar]
- Burnash, R.J.C.; Ferral, R.L.; McGuire, R.A. A Generalised Stream Flow Simulation System—Conceptual Modelling for Digital Computers; US Department of Commerce, National Weather Service and State of California, Department of Water Resources: Washington, DC, USA, 1973.
- Rockwood, D.M. Application of Stream-Flow Synthesis and Reservoir Regulation-“SSARR”-Program to the Lower Mekong River; US Army Corps of Engineers: Washington, DC, USA, 1968; pp. 329–344. [Google Scholar]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An introduction to the European Hydrological System—Systeme HydrologiqueEuropeen, “SHE”, 1: History and philosophy of physically-based, distributed modelling system. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmossen, J. An introduction to the European Hydrological System—Systeme HydrologiqueEuropeen, "SHE", 2: Structure of a physically-based, distributed modeling system. J. Hydrol. 1986, 87, 61–77. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrolog. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Morris, E.M. Modelling the flow of mass and energy within a snowpack for hydrological forecasting. Ann. Glaciol. 1980, 4, 198–203. [Google Scholar] [CrossRef][Green Version]
- Singh, V.P.; Fevert, D.K. Watershed Models; Taylor & Francis: New York, NY, USA, 2006. [Google Scholar]
- Cheval, S.; Bulai, A.; Croitoru, A.E.; Dorondel, Ș.; Micu, D.; Mihăilă, D.; Sfîcă, L.; Tișcovschi, A. Climate change perception in Romania. Theor. Appl. Climatol. 2022, 149, 253–272. [Google Scholar] [CrossRef]
- Dumitrescu, A.; Birsan, M.V. ROCADA: A gridded daily climatic dataset over Romania (1961–2013) for nine meteorological variables. Nat. Hazards 2015, 78, 1045–1063. [Google Scholar] [CrossRef]
- Patriche, C.V. Applying RUSLE for soil erosion estimation in Romania under current and future climate scenarios. Geoderma Reg. 2023, 34, e00687. [Google Scholar] [CrossRef]
- Birsan, M.V.; Zaharia, L.; Chendes, V.; Branescu, E. Seasonal trends in Romanian streamflow. Hydrol. Process. 2014, 28, 4496–4505. [Google Scholar] [CrossRef]
- Panagos, P.; Ballabio, C.; Borrelli, P.; Meusburger, K.; Klik, A.; Rousseva, S.; Tadić, M.P.; Michaelides, S.; Hrabalíková, M.; Olsen, P.; et al. Rainfall erosivity in Europe. Sci. Total Environ. 2015, 511, 801–814. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K.; Yu, B.; Klik, A.; Lim, K.J.; Yang, J.E.; Ni, J.; Miao, C.; Chattopadhyay, N.; et al. Global rainfall erosivity assessment based on high-temporal resolution rainfall records. Sci. Rep. 2017, 7, 4175. [Google Scholar] [CrossRef]
- Hawker, L.; Uhe, P.; Neal, J. FABDEM Updates—FABDEM V1-2. GeoMorphometry, Iasi, Romania, 10–14 July 2023; pp. 1–4. Available online: https://data.bris.ac.uk/data/dataset/25wfy0f9ukoge2gs7a5mqpq2j7. (accessed on 3 October 2023). [CrossRef]
- Bhardwaj, A. Assessment of FABDEM on the Different Types of Topographic Regions in India Using Differential GPS Data. Eng. Proc. 2022, 27, 79. [Google Scholar] [CrossRef]
- Seeger, K.; Minderhoud, P.S.; Peffeköver, A.; Vogel, A.; Brückner, H.; Kraas, F.; Oo, N.W.; Brill, D. Assessing land elevation in the Ayeyarwady Delta (Myanmar) and its relevance for studying sea level rise and delta flooding. Hydrol. Earth Syst. Sci. 2023, 27, 2257–2281. [Google Scholar] [CrossRef]
- Marsh, C.B.; Harder, P.; Pomeroy, J.W. Validation of FABDEM, a global bare-earth elevation model, against UAV-lidar derived elevation in a complex forested mountain catchment. Environ. Res. Commun. 2023, 5, 031009. [Google Scholar] [CrossRef]
- Borgohain, A.; Khajuria, V.; Garg, V.; Koti, S.R.; Bhardwaj, A. Comparison of Geomorphological Parameters Detected Using MERIT and FABDEM Products. Environ. Sci. Proc. 2023, 25, 59. [Google Scholar] [CrossRef]
- Muench, R.; Cherrington, E.; Griffin, R.; Mamane, B. Assessment of Open Access Global Elevation Model Errors Impact on Flood Extents in Southern Niger. Front. Environ. Sci. 2022, 10, 880840. [Google Scholar] [CrossRef]
- Loli, M.; Kefalas, G.; Dafis, S.; Mitoulis, S.A.; Schmidt, F. Bridge-specific flood risk assessment of transport networks using GIS and remotely sensed data. Sci. Total Environ. 2022, 850, 157976. [Google Scholar] [CrossRef]
- HydroSHEDS. Available online: https://www.hydrosheds.org (accessed on 13 July 2023).
- Lehner, B.; Grill, G. Global river hydrography and network routing: Baseline data and new approaches to study the world’s large river systems. Hydrol. Process. 2013, 27, 2171–2186. [Google Scholar] [CrossRef]
- Oliveira, P.T.S.; Rodrigues, D.B.B.; Sobrinho, T.A.; Panachuki, E.; Wendland, E. Use of SRTM data to calculate the (R)USLE topographic factor. Acta Scientiarum. Technol. 2013, 35, 507–513. [Google Scholar] [CrossRef]
- Reginato, V.D.S.C. Altimetry Quality of SRTM and ASTER GDEM Products for Areas with Different Reliefs. J. Geogr. Inf. Syst. 2019, 11, 683–714. [Google Scholar] [CrossRef]
- De Oliveira, C.G.; Paradella, W.R. An Assessment of the Altimetric Information Derived from Spaceborne SAR (RADARSAT-1, SRTM3) and Optical (ASTER) Data for Cartographic Application in the Amazon Region. Sensors 2008, 8, 3819–3829. [Google Scholar] [CrossRef]
- Rawat, A.; Bisht, M.P.S.; Sundriyal, Y.P.; Banerjee, S.; Singh, V. Assessment of soil erosion, flood risk and groundwater potential of Dhanari watershed using remote sensing and geographic information system, district Uttarkashi, Uttarakhand, India. Appl. Water Sci. 2021, 11, 119. [Google Scholar] [CrossRef]
- Obeidat, M.; Awawdeh, M.; Al-Hantouli, F. Morphometric analysis and prioritisation of watersheds for flood risk management in Wadi Easal Basin (WEB), Jordan, using geospatial technologies. J. Flash Flood Risk Manag. 2021, 14, e12711. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Kushwaha, D.P.; Kisi, O.; Salih, S.Q.; Al-Ansari, N.; Yaseen, Z.M. The Implementation of a Hybrid Model for Hilly Sub-Watershed Prioritization Using Morphometric Variables: Case Study in India. Water 2019, 11, 1138. [Google Scholar] [CrossRef]
- Arefin, R.; Mohir, M.M.I.; Alam, J. Watershed prioritization for soil and water conservation aspect using GIS and remote sensing: PCA-based approach at northern elevated tract Bangladesh. Appl. Water Sci. 2020, 10, 91. [Google Scholar] [CrossRef]
- Schumm, S.A. The evolution of drainage systems and slopes in badlands at Perth Amboi, New Jersey. Geol. Sac. Am. Bull. 1956, 67, 597–646. [Google Scholar] [CrossRef]
- Zavoianu, I. Morphometry of Drainage Basins; Elsevier: Amsterdam, The Netherlands, 1985. [Google Scholar]
- Miller, V.C. A Quantitative Geomorphologic Study of Drainage Basin Characteristics in the Clinch Mountain Area. Virginia and Tennessee; Department of Geology; Technical Report, No. 3; Contract N6 ONR; Columbia University: New York, NY, USA, 1953; pp. 271–300. [Google Scholar]
- Hjerdt, K.; McDonnell, J.; Seibert, J.; Rodhe, A. A new topographic index to quantify downslope controls on local drainage. Water Resour. Res. 2004, 40, W05602. [Google Scholar] [CrossRef]
- Sörensen, R.; Zinko, U.; Seibert, J. On the calculation of the topographic wetness index: Evaluation of different methods based on field observations. Hydrol. Earth Syst. Sci. 2006, 10, 101–112. [Google Scholar] [CrossRef]
- Grabs, T.; Seibert, J.; Bishop, K.; Laudon, H. Modeling spatial patterns of saturated areas: A comparison of the topographic wetness index and a dynamic distributed model. J. Hydrol. 2009, 373, 15–23. [Google Scholar] [CrossRef]
- Kopecký, M.; Čížková, Š. Using topographic wetness index in vegetation ecology: Does the algorithm matter? Appl. Veg. Sci. 2010, 13, 450–459. [Google Scholar] [CrossRef]
- Nguyen, T.T.M.; Wilson, J.P. Sensitivity of quasi-dynamic topographic wetness index to choice of DEM resolution, flow routing algorithm, and soil variability. In Proceedings of the Ninth International Symposium on Spatial Accuracy Assessment in Natural Resources and the Environmental Sciences (Accuracy 2010), Leicester, UK, 20–23 July 2010; pp. 205–208. [Google Scholar]
- Pei, T.; Qin, C.Z.; Zhu, A.; Yang, L.; Luo, M.; Li, B.; Zhou, C. Mapping soil organic matter using the topographic wetness index: A comparative study based on different flow-direction algorithms and kriging methods. Ecol. Indic. 2010, 10, 610–619. [Google Scholar] [CrossRef]
- Qin, C.Z.; Zhu, A.X.; Pei, T.; Li, B.L.; Scholten, T.; Behrens, T.; Zhou, C.H. An approach to computing topographic wetness index based on maximum downslope gradient. Precis. Agric. 2011, 12, 32–43. [Google Scholar] [CrossRef]
- Ruhoff, A.L.; Castro, N.M.R.; Risso, A. Numerical modelling of the topographic wetness index: An analysis at different scales. Int. J. Geosci. 2011, 2, 476–483. [Google Scholar] [CrossRef]
- Lewis, G.; Holden, N.M. A comparison of grid-based computation methods of topographic wetness index derived from digital elevation model data. Biosyst. Eng. Res. Rev. 2012, 17, 103–106. [Google Scholar]
- Yong, B.; Ren, L.L.; Hong, Y.; Gourley, J.J.; Chen, X.; Zhang, Y.J.; Yang, X.L.; Zhang, Z.X.; Wang, W.G. A novel multiple flow direction algorithm for computing the topographic wetness index. Hydrol. Res. 2012, 43, 135–145. [Google Scholar] [CrossRef]
- Kurek, K.A.; Heijman, W.; van Ophem, J.; Gędek, S.; Strojny, J. Measuring local competitiveness: Comparing and integrating two methods PCA and AHP. Qual. Quant. 2022, 56, 1371–1389. [Google Scholar] [CrossRef]
- JASP. Available online: https://jasp-stats.org (accessed on 3 October 2023).
- Romanescu, G.; Mihu-Pintilie, A.; Stoleriu, C.C.; Carboni, D.; Paveluc, L.E.; Cimpianu, C.I. A Comparative Analysis of Exceptional Flood Events in the Context of Heavy Rains in the Summer of 2010: Siret Basin (NE Romania) Case Study. Water 2018, 10, 216. [Google Scholar] [CrossRef]
- Arseni, M.; Rosu, A.; Calmuc, M.; Calmuc, V.A.; Iticescu, C.; Georgescu, L.P. Development of Flood Risk and Hazard Maps for the Lower Course of the Siret River, Romania. Sustainability 2020, 12, 6588. [Google Scholar] [CrossRef]
- Popa, M.C.; Simion, A.G.; Peptenatu, D.; Dima, C.; Draghici, C.C.; Florescu, M.S.; Dobrea, C.R.; Diaconu, D.C. Spatial assessment of flash-flood vulnerability in the Moldova river catchment (N Romania) using the FFPI. J. Flash Flood Risk Manag. 2020, 13, e12624. [Google Scholar] [CrossRef]
- Cojoc, G.M.; Romanescu, G.; Tirnovan, A. Exceptional floods on a developed river: Case study for the Bistrita River from the Eastern Carpathians (Romania). Nat. Hazards. 2015, 77, 1421–1451. [Google Scholar] [CrossRef]
- Adam, B.O.; Nacu, S. Flood events in bacău county during 2005–2019. Air Water Compon. Environ. 2020, 12, 59. [Google Scholar]
- Ţîncu, R.; Zêzere, J.L.; Lazar, G. Identification of elements exposed to flood hazard in a section of Trotus River, Romania. Geomat. Nat. Hazards Risk 2018, 9, 950–969. [Google Scholar] [CrossRef]
- Serban, G.; Rândasu-Beuran, S.I.; Rosu, I.; Nacu, S.; Sabau, D.; Nitoaia, A. Exceptional floods in small basins in North-Western Romania and the induced effects-Bârsau River, Maramures county. Forum Geogr. 2016, 15, 25. [Google Scholar] [CrossRef]
- Ştecz, Ş.; Nacu, S. Analysis of the flood produced on the Tisa River during 09-10.12. 2010. Sci. Bull. Ser. D Min. Miner. Process. Non-Ferr. Metall. Geol. Environ. Eng. 2012, 26, 115. [Google Scholar]
- Grecu, F.; Zaharia, L.; Ioana-Toroimac, G.; Armaș, I. Floods and Flash-Floods Related to River Channel Dynamics. In Landform Dynamics and Evolution in Romania; Radoane, M., Vespremeanu-Stroe, A., Eds.; Springer Geography; Springer: Cham, Switzerland, 2017; pp. 821–844. [Google Scholar] [CrossRef]
- Szopos, N.M.; Czellecz, B. High water level observations along the upper course of the Olt River (Romania) from a hydrological modelling aspect. Acta Geogr. Debrecina Landsc. Environ. Ser. 2017, 11, 10–19. [Google Scholar] [CrossRef]
- Irimescu, A.; Mihailescu, D.; Stancalie, G. Sentinel data for flood disaster monitoring and assessment: Case studies in Romania. In Proceedings of the FLOODrisk 2020—4th European Conference on Flood Risk Management, Online, 21–25 June 2021; Budapest University of Technology and Economics: Budapest, Hungary, 2021. [Google Scholar] [CrossRef]
- Ionuş, O.; Licurici, M.; Pătroescu, M.; Boengiu, S. Assessment of flood-prone stripes within the Danube drainage area in the South-West Oltenia Development Region, Romania. Nat. Hazards 2015, 75, 69–88. [Google Scholar] [CrossRef]
- Ionuş, O.; Dobre, M.; Ciocan, E. Assessing flood magnitude and frequency. Case study: 2013 spring floods on the Jiu River, Filiaşi-Craiova sector (South-West Romania). Ann. Univ. Craiova. Ser. Geography. S. Geogr. 2014, 16, 20. [Google Scholar]
- Teleteu, C.E.; Branescu, E.; Berghezan, A.; Emilia, B. Assessment of the floods potential in Jiu River catchment. Aerul Si Apa. Compon. Ale Mediu. 2014, 32–39. [Google Scholar]
- Giurea, A.A.; Comănescu, L.; Dobre, R.; Nedelea, A.; Mirea, I.A. Flood risk identification using multicriteria spatial analysis. Case study: Gilort River between Bălcești and Bolbocești. Res. Sq. 2022. [Google Scholar] [CrossRef]
- Ignea, F.S.; Birou, A.F. Comparative study of the flash flood waves from the summer and autumn of 2014 on Bârzava River In the Gataia-Partos sector. Aerul Si Apa. Compon. Ale Mediu. 2015, 508–515. [Google Scholar]
- Toma, F.M.; Minoniu, A.S. Comparative analysis of the floods frequence on Teleorman and Galben Rivers. Aerul Si Apa. Compon. Ale Mediu. 2012, 511–518. [Google Scholar]
- Bilaşco, Ş. Implementarea GIS în Modelarea Viiturilor de Versant; Casa Cărţii de Ştiinţă: Cluj-Napoca, Romania, 2008. [Google Scholar]
- Zaharia, L.; Costache, R.; Prăvălie, R.; Ioana-Toroimac, G. Mapping flood and flooding potential indices: A methodological approach to identifying areas susceptible to flood and flooding risk. Case study: The Prahova catchment (Romania). Front. Earth Sci. 2017, 11, 229–247. [Google Scholar] [CrossRef]
- Ilinca, V. Using morphometrics to distinguish between debris flow, debris flood and flood (Southern Carpathians, Romania). Catena 2021, 197, 104982. [Google Scholar] [CrossRef]
- Planul de Management al Riscului la Inundatii A.B.A Crișuri. Ciclul II de Implementare a Directivei Inundații 2007/60/CE. Available online: https://sgg.gov.ro/1/wp-content/uploads/2023/09/PMRI_Ciclul-II_ABA-Crisuri.pdf (accessed on 25 July 2023).
- Chelariu, O.E.; Iațu, C.; Minea, I. A GIS-Based Model for Flood Shelter Locations and Pedestrian Evacuation Scenarios in a Rural Mountain Catchment in Romania. Water 2022, 14, 3074. [Google Scholar] [CrossRef]
- Albano, R.; Samela, C.; Crăciun, I.; Manfreda, S.; Adamowski, J.; Sole, A.; Sivertun, Å.; Ozunu, A. Large Scale Flood Risk Mapping in Data Scarce Environments: An Application for Romania. Water 2020, 12, 1834. [Google Scholar] [CrossRef]
- Albulescu, A.C.; Minea, I.; Boicu, D.; Larion, D. Comparative Multi-Criteria Assessment of Hydrological Vulnerability—Case Study: Drainage Basins in the Northeast Region of Romania. Water 2022, 14, 1302. [Google Scholar] [CrossRef]
- Enea, A.; Stoleriu, C.; Romanescu, G. GIS techniques used in the analysis of the morphometrical parameters of the Red Lake drainage basin. Lucr. Semin. Geogr. Dimitrie Cantemir 2011, 31, 39–48. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).