Study on a Geomorphic Indicator for Evaluating Sediment Transport Capacity in Mountainous Rivers
Abstract
1. Introduction
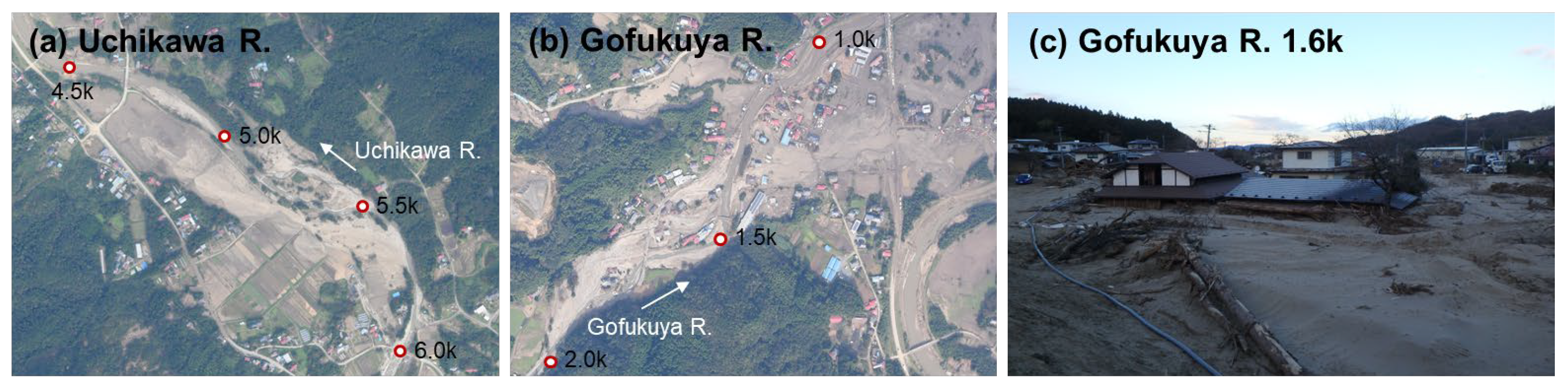
2. Overview of Target River Basins and Disasters
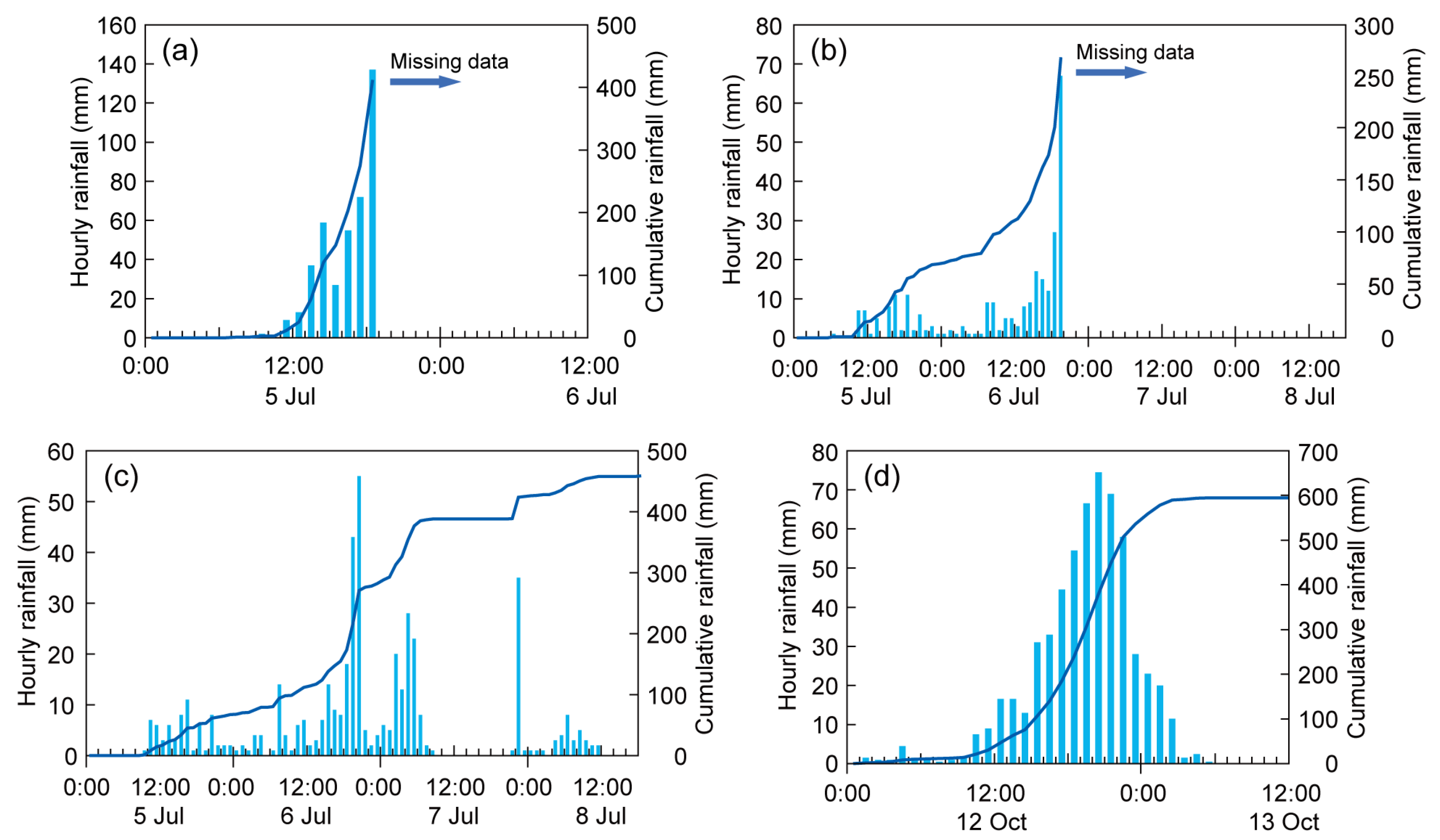
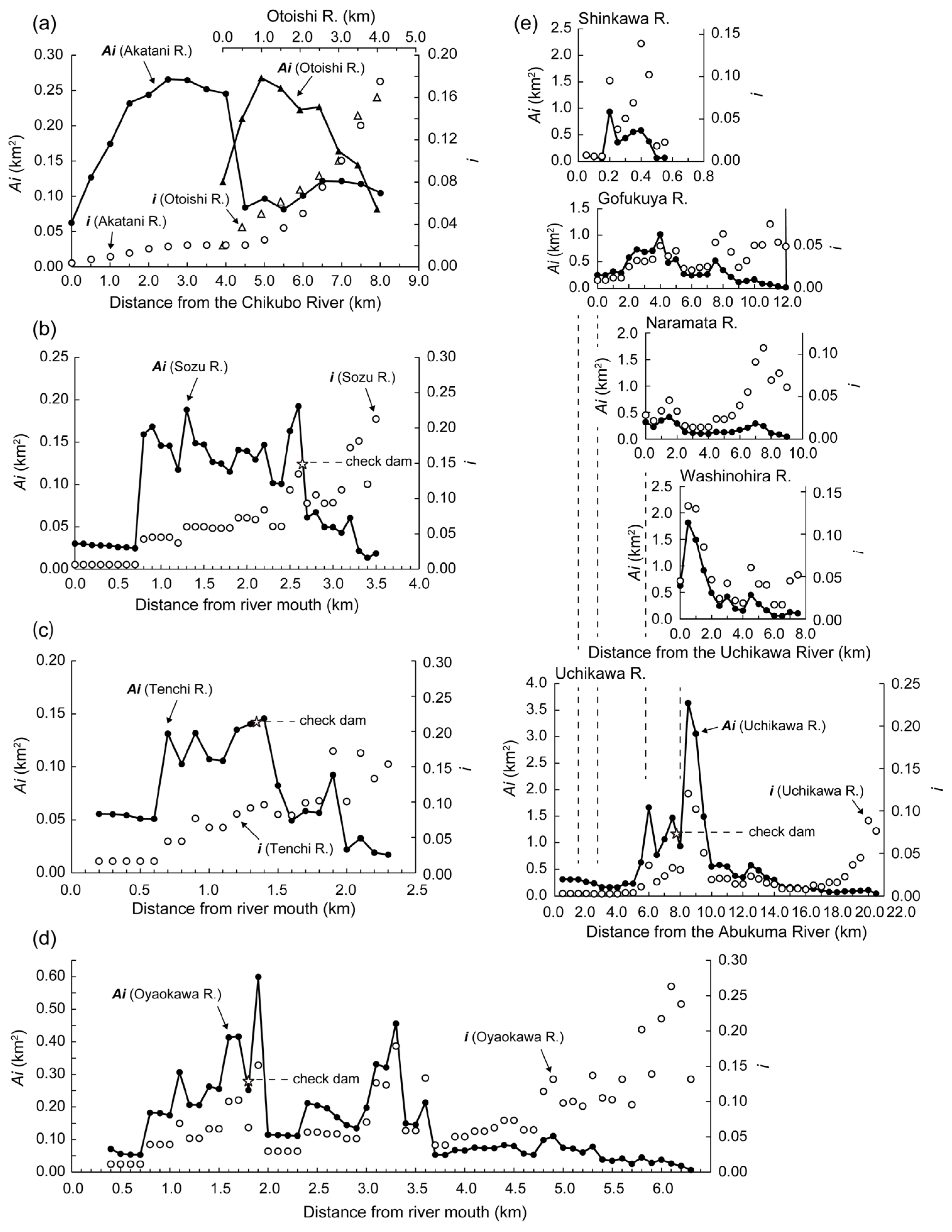
3. Derivation of an Indicator for Identifying Hazardous Areas
4. Relationship Between Sediment Behavior and the Longitudinal Distribution of
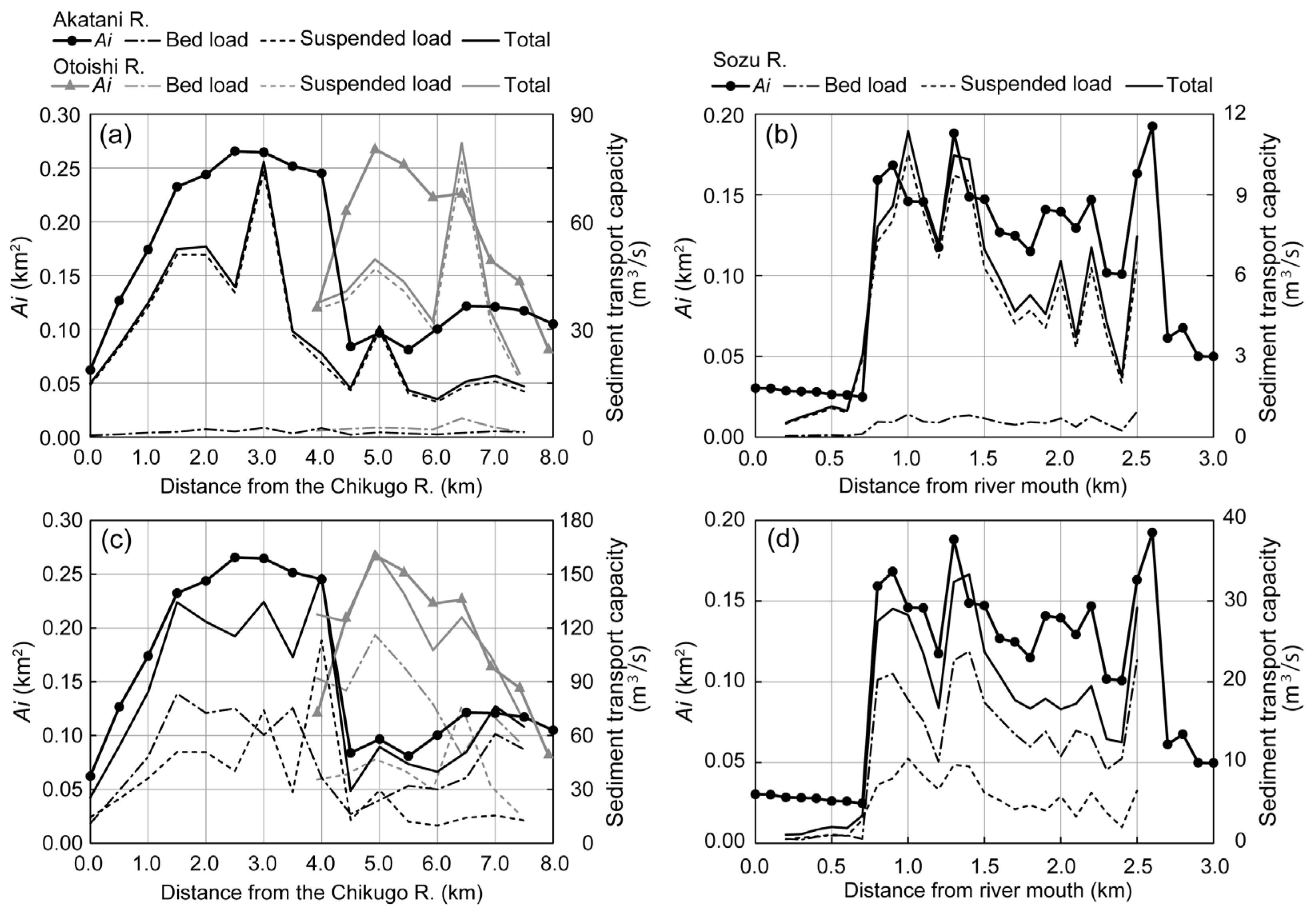
5. Longitudinal Profiles of Sediment Transport Capacity and the Geomorphic Indicator
5.1. Hydrodynamic Evaluation of Sediment Transport Capacity
5.2. Relationship Between Sediment Transport Capacity and the Geomorphic Indicator
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Takahashi, Y.; Sakaguchi, Y. Rivers in Japan. Kagaku 1976, 46, 488–499. (In Japanese) [Google Scholar]
- Yoshikawa, T. Geomorphology of Tectonically Active and Intensely Denuded Regions. Geog. Rev. Jpn. Ser. A 1984, 57, 691–702. (In Japanese) [Google Scholar] [CrossRef]
- Oya, M.; Nakayama, M.; Takagi, I. Studies on the Geomorphological Features of the Fluvial Plains in Japan Focusing the Distribution, Geomorphological Land Classification and Its Application. Geog. Rev. Jpn. Ser. B 1988, 61, 35–49. [Google Scholar] [CrossRef]
- Ohmori, H.; Shimazu, H. Distribution of Hazard Types in a Drainage Basin and Its Relation to Geomorphological Setting. Geomorphology 1994, 10, 95–106. [Google Scholar] [CrossRef]
- Ohmori, H. Geomorphological Characteristics of Longitudinal Profiles of the Rivers in Japan, Taiwan and New Zealand. Trans. Jpn. Geomorphol. Union 1997, 18, 349–364. [Google Scholar]
- Oguchi, T.; Saito, K.; Kadomura, H.; Grossman, M. Fluvial Geomorphology and Paleohydrology in Japan. Geomorphology 2001, 39, 3–19. [Google Scholar] [CrossRef]
- Sediment Disaster Prevention Act. Available online: https://laws.e-gov.go.jp/law/412AC0000000057/ (accessed on 4 July 2024). (In Japanese)
- Uchida, T.; Nishimoto, H.; Osanai, N.; Shimizu, T. Countermeasures for Sediment-related Disasters in Japan Using Hazard Maps. Int. J. Eros. Control Eng. 2009, 2, 46–53. [Google Scholar] [CrossRef]
- Osanai, N.; Shimizu, T.; Kuramoto, K.; Kojima, S.; Noro, T. Japanese Early-warning for Debris Flows and Slope Failures Using Rainfall Indices with Radial Basis Function Network. Landslides 2010, 7, 325–338. [Google Scholar] [CrossRef]
- Kanbara, J.; Imamori, N. Outline of Measures for Sediment Disaster by the Sabo Department of MLIT, Japan. Landslides 2020, 17, 2503–2513. [Google Scholar]
- Furuichi, T.; Osanai, N.; Hayashi, S.; Izumi, N.; Kyuka, T.; Shiono, Y.; Miyazaki, T.; Hayakawa, T.; Nagano, N.; Matsuoka, N. Disastrous Sediment Discharge due to Typhoon-Induced Heavy Rainfall over Fossil Periglacial Catchments in Western Tokachi, Hokkaido, Northern Japan. Landslides 2018, 15, 1645–1655. [Google Scholar] [CrossRef]
- Hashimoto, A.; Oshikawa, H.; Komatsu, T. Characteristics of the 2017 Flood Disaster in Northern Kyushu and Learned Lessons. J. Jpn. Soc. Civ. Eng. B1 2018, 74, I_1087–I_1092. (In Japanese) [Google Scholar] [CrossRef] [PubMed]
- Goto, H.; Kumahara, Y.; Uchiyama, S.; Iwasa, Y.; Yamanaka, T.; Motoyoshi, R.; Takeuchi, S.; Murata, S.; Nakata, T. Distribution and Characteristics of Slope Movements in the Southern Part of Hiroshima Prefecture Caused by the Heavy Rain in Western Japan in July 2018. J. Disaster Res. 2019, 14, 894–902. [Google Scholar] [CrossRef]
- Mori, S.; Ono, K. Landslide Disasters in Ehime Prefecture Resulting from the July 2018 Heavy Rain Event in Japan. Soils Found. 2019, 59, 2396–2409. [Google Scholar] [CrossRef]
- Ohara, M.; Nagumo, N. Mortality by Age Group and Municipality in the July 2018 Torrential Rainfall. J. Disaster Res. 2019, 14, 912–921. [Google Scholar] [CrossRef]
- Hashimoto, R.; Tsuchida, T.; Moriwaki, T.; Kano, S. Hiroshima Prefecture Geo-disasters due to Western Japan Torrential Rainfall in July 2018. Soils Found. 2020, 60, 283–299. [Google Scholar] [CrossRef]
- Moriguchi, S.; Matsugi, H.; Ochiai, T.; Yoshikawa, S.; Inagaki, H.; Ueno, S.; Suzuki, M.; Tobita, Y.; Chida, T.; Takahashi, K.; et al. Survey Report on Damage Caused by 2019 Typhoon Hagibis in Marumori Town, Miyagi Prefecture, Japan. Soils Found. 2021, 61, 586–599. [Google Scholar] [CrossRef]
- Rickenmann, D.; Zimmermann, M. The 1987 Debris Flows in Switzerland: Documentation and Analysis. Geomorphology 1993, 8, 175–189. [Google Scholar] [CrossRef]
- van Steijn, H. Debris-flow Magnitude—Frequency Relationships for Mountainous Regions of Central and Northwest Europe. Geomorphology 1996, 15, 259–273. [Google Scholar] [CrossRef]
- Rickenmann, D. Empirical Relationships for Debris Flows. Nat. Hazards 1999, 19, 47–77. [Google Scholar] [CrossRef]
- Iverson, R.M.; Reid, M.E.; Iverson, N.R.; LaHusen, R.G.; Logan, M.; Mann, J.E.; Brien, D.L. Acute Sensitivity of Landslide Rates to Initial Soil Porosity. Science 2000, 290, 513–516. [Google Scholar] [CrossRef] [PubMed]
- Marchi, L.; D’Agostino, V. Estimation of Debris-flow Magnitude in the Eastern Italian Alps. Earth Surf. Process. Landf. 2004, 29, 207–220. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, X.; Su, P.; Kong, Y.; Liu, J. A Scaling Distribution for Grain Composition of Debris Flow. Geomorphology 2013, 192, 30–42. [Google Scholar]
- Theule, J.I.; Liébault, F.; Laigle, D.; Loye, A.; Jaboyedoff, M. Channel Scour and Fill by Debris Flows and Bedload Transport. Geomorphology 2015, 243, 92–105. [Google Scholar] [CrossRef]
- Takebayashi, H.; Fujita, M. Numerical Simulation of a Debris Flow on the Basis of a Two-dimensional Continuum Body Model. Geosciences 2020, 10, 45. [Google Scholar] [CrossRef]
- Scorpio, V.; Cavalli, M.; Steger, S.; Crema, S.; Marra, F.; Zaramella, M.; Borga, M.; Marchi, L.; Comiti, F. Storm Characteristics Dictate Sediment Dynamics and Geomorphic Changes in Mountain Channels: A Case Study in the Italian Alps. Geomorphology 2022, 403, 108173. [Google Scholar] [CrossRef]
- Pudasaini, S.P.; Krautblatter, M. The Mechanics of Landslide Mobility with Erosion. Nat. Commun. 2021, 12, 6793. [Google Scholar] [CrossRef]
- Tal, M.; Paola, C. Dynamic Single-Thread Channels Maintained by the Interaction of Flow and Vegetation. Geology 2007, 35, 347–350. [Google Scholar] [CrossRef]
- Egozi, R.; Ashmore, P. Experimental Analysis of Braided Channel Pattern Response to Increased Discharge. J. Geophys. Res. Earth Surf. 2009, 114, F02012. [Google Scholar] [CrossRef]
- Kleinhans, M.G.; van den Berg, J.H. River Channel and Bar Patterns Explained and Predicted by an Empirical and a Physics-based Method. Earth Surf. Process. Landf. 2010, 36, 721–738. [Google Scholar] [CrossRef]
- Asahi, K.; Shimizu, Y.; Nelson, J.; Parker, G. Numerical Simulation of River Meandering with Self-evolving Banks. J. Geophys. Res. Earth Surf. 2013, 118, 2208–2229. [Google Scholar] [CrossRef]
- Wickert, A.D.; Martin, J.M.; Tal, M.; Kim, W.; Sheets, B.; Paola, C. River Channel Lateral Mobility: Metrics, Time Scales, and Controls. J. Geophys. Res. Earth Surf. 2013, 118, 396–412. [Google Scholar] [CrossRef]
- Okitsu, T.; Iwasaki, T.; Kyuka, T.; Shimizu, Y. The Role of Large-Scale Bedforms in Driftwood Storage Mechanism in Rivers. Water 2021, 13, 811. [Google Scholar] [CrossRef]
- Rachelly, C.; Vetsch, D.F.; Boes, R.M.; Weitbrecht, V. Sediment Supply Control on Morphodynamic Processes in Gravel-Bed River Widenings. Earth Surf. Process. Landf. 2022, 47, 3415–3434. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Egashira, S.; Nagumo, N. Method to Predict Sediment Runoff Resulting from Landslides and Debris Flows. In Scour and Erosion IX, Proceedings of the 9th International Conference on Scour and Erosion (ICSE 2018), Taipei, Taiwan, 5–8 November 2018; CRC Press/Balkema: Leiden, The Netherlands, 2019; Volume 9, pp. 683–688. [Google Scholar]
- Harada, D.; Egashira, S.; Kakinuma, D.; Nagumo, N.; Ito, H. Characteristics of Flood Flow with a Large Amount of Sediment in the Gofukuya River in the Typhoon No.19, 2019. Adv. River Eng. 2020, 26, 609–614. (In Japanese) [Google Scholar]
- Kyuka, T.; Okabe, K.; Shimizu, Y.; Yamaguchi, S.; Hasegawa, K.; Shinjo, K. Dominating Factors Influencing Rapid Meander Shift and Levee Breaches Caused by a Record-Breaking Flood in the Otofuke River, Japan. J. Hydro-Environ. Res. 2020, 31, 76–89. [Google Scholar] [CrossRef]
- Shogaki, T.; Tsusue, A.; Yano, S.; Ksama, K. Evaluation of Driftwood Generation in the Northern Kyushu Heavy Rain in 2017 by Logistic Regression. In Proceedings of the 22nd IAHR-APD Congress, Sapporo, Japan, 14–17 September 2020. [Google Scholar]
- Harada, D.; Egashira, S. Method to Evaluate Large-Wood Behavior in Terms of the Convection Equation Associated with Sediment Erosion and Deposition. Earth Surf. Dyn. 2023, 11, 1183–1197. [Google Scholar] [CrossRef]
- Nagumo, N.; Egashira, S. Flood Hazard Analysis and Locations of Damaged Houses Based on Land Classification in the Akatani River Basin Following Torrential Rainfall in Northern Kyushu. J. Geogr. (Chigaku Zasshi) 2017, 128, 835–854. (In Japanese) [Google Scholar] [CrossRef]
- Nagumo, N.; Egashira, S. Research on Sediment Transport Processes in Mountainous Rivers Based on Geomorphic Analysis. Geogr. Rev. Jpn. Ser. A 2021, 94, 64–81. (In Japanese) [Google Scholar]
- Fujita, M.; Yamanoi, K. Integrated Simulation of Landslide and Flood on a Heavy Rainfall Event in Akadani River Basin, Asakura City. Investigation Report on the Northern Kyushu Torrential Rainfall Disaster in 2017. Disaster Prev. Res. Inst. Kyoto Univ. 2018, 68–71. Available online: https://repository.kulib.kyoto-u.ac.jp/dspace/handle/2433/232513?locale=en (accessed on 4 July 2024). (In Japanese).
- Egashira, S.; Harada, D.; Nagumo, N.; Yamazaki, Y.; Yorozuya, A. A Method to Predict Fine Sediment Runoff Focusing on Debris Cones Resulting from Landslides and Debris Flows–Sediment Hazards Occurred at Akadani Drainage Basin in July, 2017. J. Jpn. Soc. Civ. Eng. B1 2018, 74, I_925–I_930. (In Japanese) [Google Scholar] [CrossRef]
- Damage Situation of Northern Kyushu Torrential Rainfall in July 2017. Available online: https://www.bousai.go.jp/fusuigai/kyusyu_hinan/pdf/dai1kai/siryo2.pdf (accessed on 4 July 2024). (In Japanese).
- Detailed Distribution Map of Landslides Caused by the July 2018 Heavy Rainfall in Hiroshima Prefecture (Version 2: Final Report). Available online: https://www.ajg.or.jp/disaster/files/201807_report008.pdf (accessed on 4 July 2024). (In Japanese).
- Information on Typhoon No. 19 in 2019. Available online: https://www.gsi.go.jp/BOUSAI/R1.taihuu19gou.html (accessed on 4 July 2024). (In Japanese).
- Verification of Evacuation Responses in Saka Town During the Heavy Rainfall Disaster in July 2018 and Recommendations for Supporting Appropriate Future Evacuation Actions. Available online: https://www.bousai.go.jp/fusuigai/suigai_dosyaworking/pdf/sakamachiteigen.pdf (accessed on 4 July 2024). (In Japanese).
- Kure City Disaster Record on Heavy Rainfall Disaster in July 2018. Available online: https://www.city.kure.lg.jp/uploaded/attachment/52026.pdf (accessed on 4 July 2024). (In Japanese).
- Heavy Rain, Strong Winds, and High Waves Caused by Typhoon No. 19 in 2019. Available online: https://www.data.jma.go.jp/sendai/data/saigai/siryou/T1919touhoku.pdf (accessed on 4 July 2024). (In Japanese).
- Yano, S.; Shogaki, T.; Yato, S.; Tsusue, A.; Wu, Y.; Kasama, K. Development of Logistic Regression Model for Slope Failure and Estimation of Driftwoods Generation in Marumori Town due to the East Japan Typhoon 2019. J. Jpn. Soc. Civ. Eng. B1 2020, 76, 253–263. (In Japanese) [Google Scholar] [CrossRef] [PubMed]
- Marumori Town Record of East Japan Typhoon Disaster. 2019. Available online: https://cccc.backshelf.jp/bookview/?filseq=10099&user=guest (accessed on 4 July 2024). (In Japanese).
- Meyer-Peter, E.; Müller, R. Formulas for Bed-Load Transport. In Proceedings of the 2nd IAHR World Congress, Stockholm, Sweden, 7–9 June 1948. [Google Scholar]
- Bagnold, R.A. An Approach to the Sediment Transport Problem from General Physics. In Geological Survey Professional Paper; Government Printing Office: Washington, DC, USA, 1966; Volume 422–I, pp. 1–37. [Google Scholar]
- Ashida, K.; Michiue, M. Study on Hydraulic Resistance and Bed-load Transport Rate in Alluvial Streams. Proc. Jpn. Soc. Civ. Eng. 1972, 206, 59–69. (In Japanese) [Google Scholar] [CrossRef]
- Brown, C.B. Sediment Transportation. In Engineering Hydraulics; Rouse, H., Ed.; John Wiley and Sons: New York, NY, USA, 1950; pp. 769–857. [Google Scholar]
- Shinohara, K.; Tsubaki, T. On the Characteristics of Sand Waves Formed upon the Beds of the Open Channels and Rivers. Rep. Res. Inst. Appl. Mech. Kyushu Univ. 1959, 7, 15–45. [Google Scholar] [CrossRef]
- van Rijn, L.C. Sediment Transport, Part I: Bed Load Transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef]
- Egashira, S.; Miyamoto, K.; Ito, T. Bed-load Rate in View of Two Phase Flow Dynamics. Proc. Hydr. Eng. 1997, 41, 789–794. (In Japanese) [Google Scholar] [CrossRef]
- Rouse, H. Modern Conceptions of the Mechanics of Fluid Turbulence. Trans. ASCE 1937, 102, 463–505. [Google Scholar] [CrossRef]
- Lane, E.W.; Kalinske, A.A. Engineering Calculations of Suspended Sediment. Trans. Am. Geophys. Union 1941, 22, 603–607. [Google Scholar]
- Ashida, K.; Michiue, M. Study on the Suspended Sediment (1): Concentration of the Suspended Sediment near the Bed Surface. Disaster Prev. Res. Inst. Annu. 1970, 13B, 233–242. (In Japanese) [Google Scholar]
- Itakura, T.; Kishi, T. Open Channel Flow with Suspended Sediments. J. Hydraul. Div. 1980, 106, 1325–1343. [Google Scholar] [CrossRef]
- Ashida, K.; Fujita, M. Mechanism of Particle Suspension in an Open Channel. Proc. Jpn. Soc. Civ. Eng. 1986, 375, 79–88. (In Japanese) [Google Scholar] [CrossRef] [PubMed][Green Version]
- van Rijn, L.C. Mathematical Modeling of Suspended Sediment in Nonuniform Flows. J. Hydraul. Eng. 1986, 112, 433–455. [Google Scholar] [CrossRef]
- Garcia, M.; Parker, G. Entrainment of Bed Sediment into Suspension. J. Hydraul. Eng. 1991, 117, 414–435. [Google Scholar] [CrossRef]
- Harada, D.; Egashira, S.; Ahmed, T.S.; Ito, H. Entrainment of Bed Sediment Composed of Very Fine Material. Earth Surf. Process. Landf. 2022, 47, 3051–3061. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagumo, N.; Harada, D.; Egashira, S. Study on a Geomorphic Indicator for Evaluating Sediment Transport Capacity in Mountainous Rivers. Water 2024, 16, 3688. https://doi.org/10.3390/w16243688
Nagumo N, Harada D, Egashira S. Study on a Geomorphic Indicator for Evaluating Sediment Transport Capacity in Mountainous Rivers. Water. 2024; 16(24):3688. https://doi.org/10.3390/w16243688
Chicago/Turabian StyleNagumo, Naoko, Daisuke Harada, and Shinji Egashira. 2024. "Study on a Geomorphic Indicator for Evaluating Sediment Transport Capacity in Mountainous Rivers" Water 16, no. 24: 3688. https://doi.org/10.3390/w16243688
APA StyleNagumo, N., Harada, D., & Egashira, S. (2024). Study on a Geomorphic Indicator for Evaluating Sediment Transport Capacity in Mountainous Rivers. Water, 16(24), 3688. https://doi.org/10.3390/w16243688






