Modeling Complex Interactions Between Acid–Rock Reactions and Fracture Propagation in Heterogeneous Layered Formations
Abstract
1. Introduction
2. Model Description
2.1. Characterization of Rock Heterogeneity
2.2. Equations of Fluid Flow and Acid Transport
2.3. Equations of Mechanical Deformation and Crack Propagation
3. Numerical Methods
4. Simulation Results
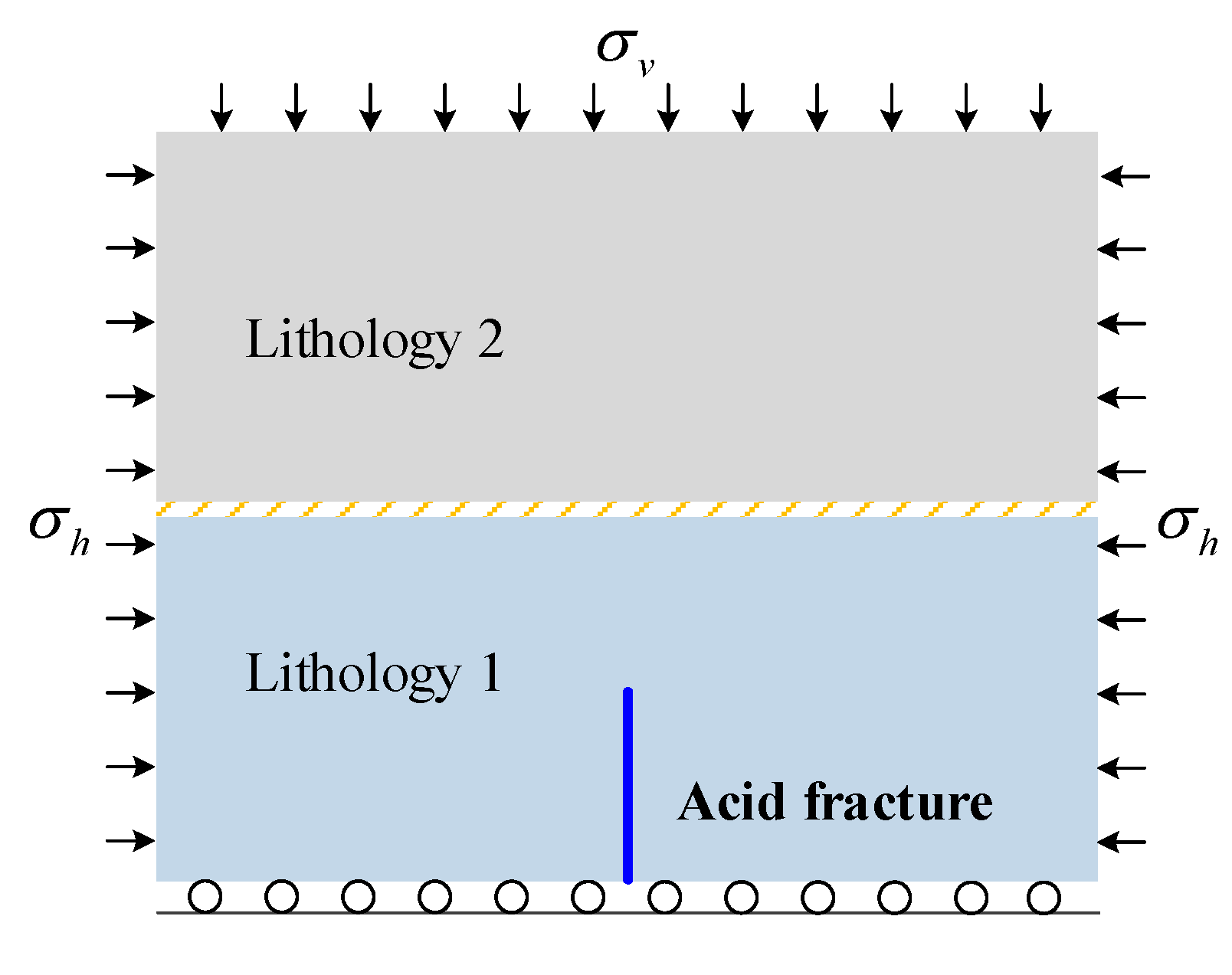
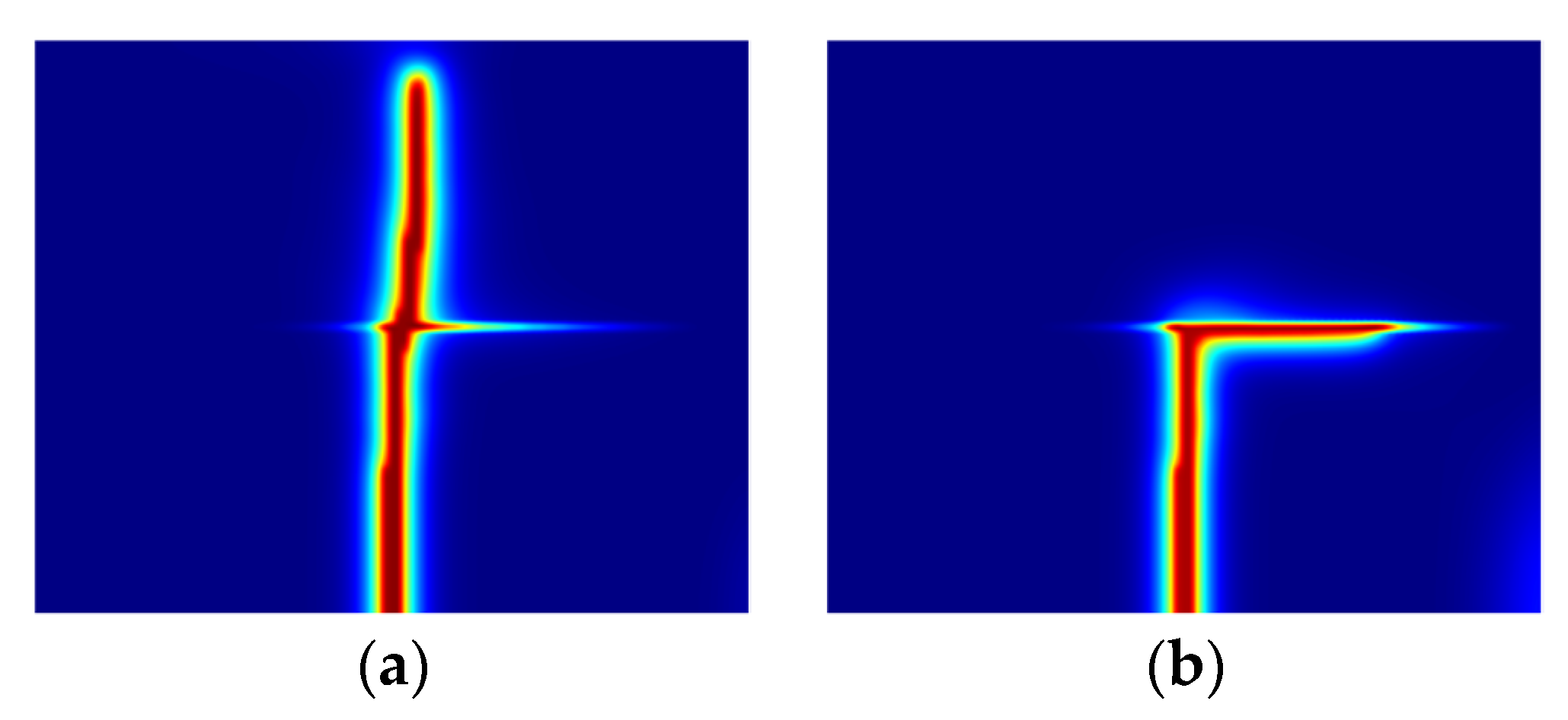
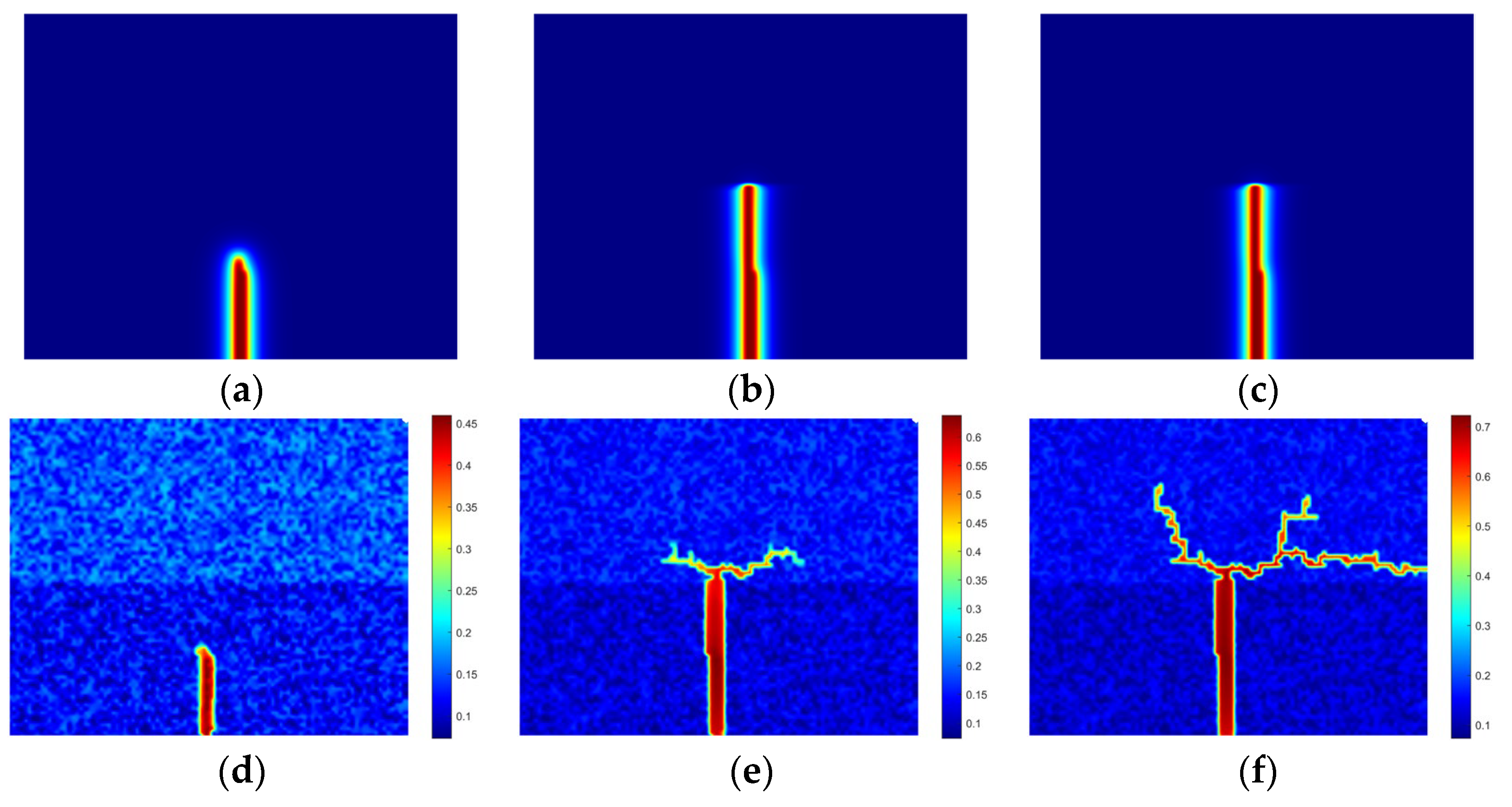
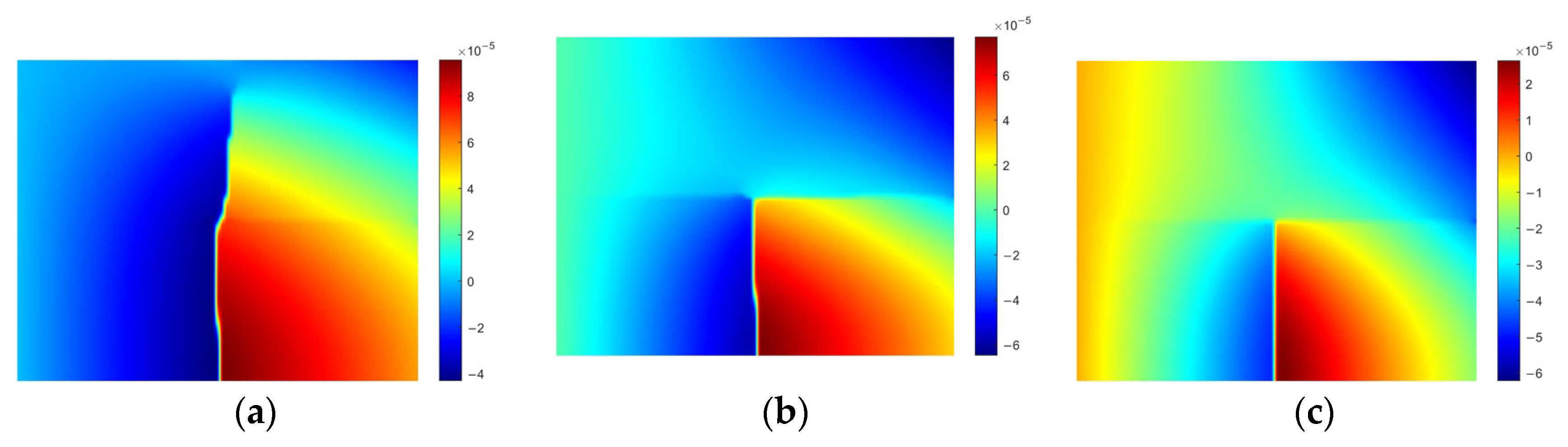
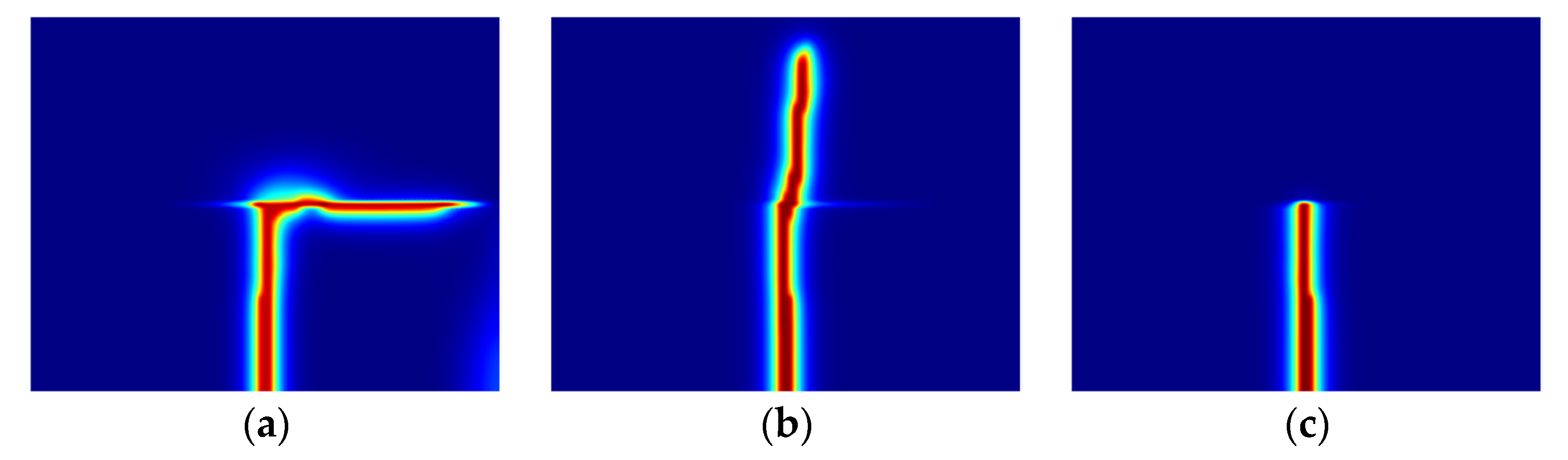
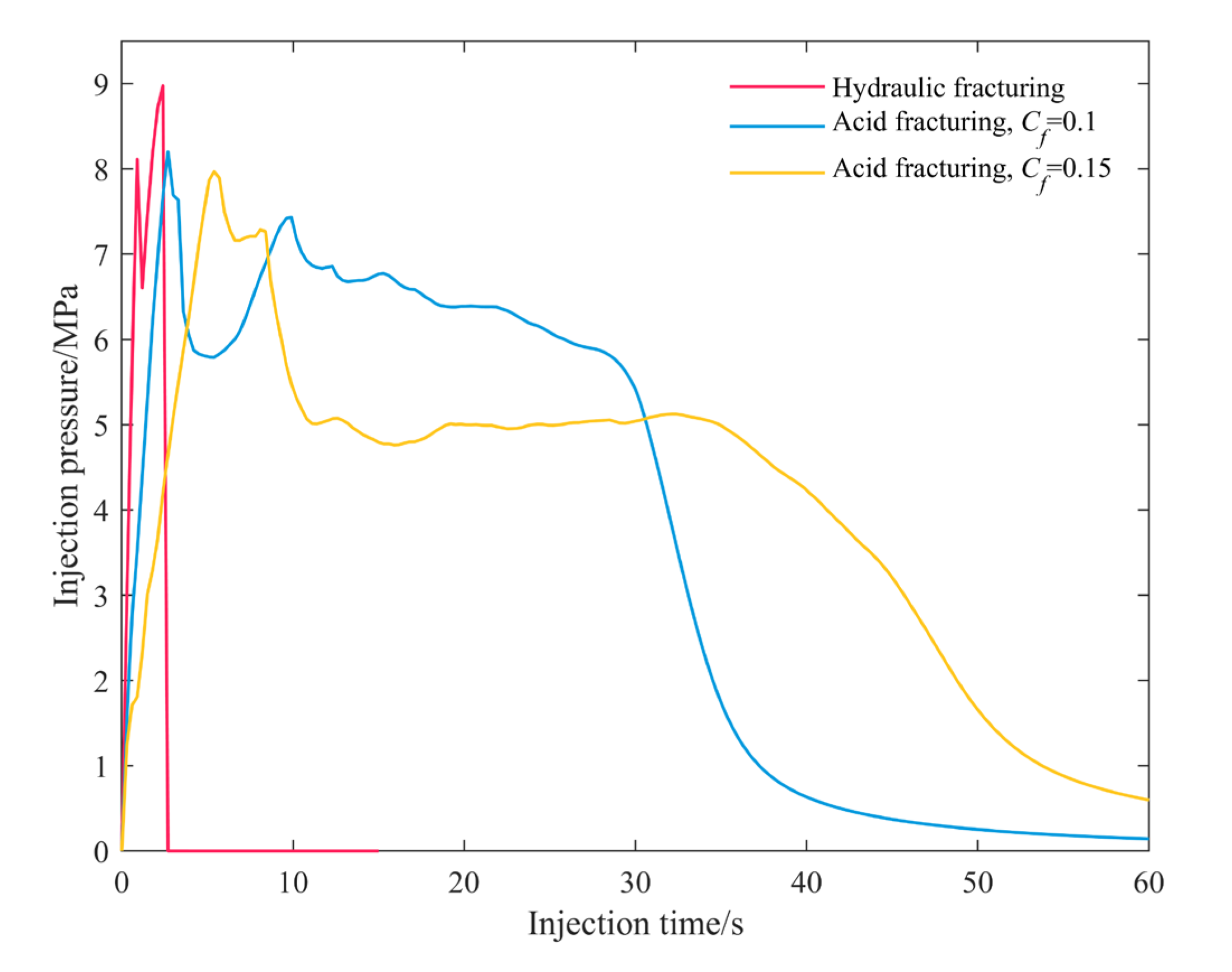
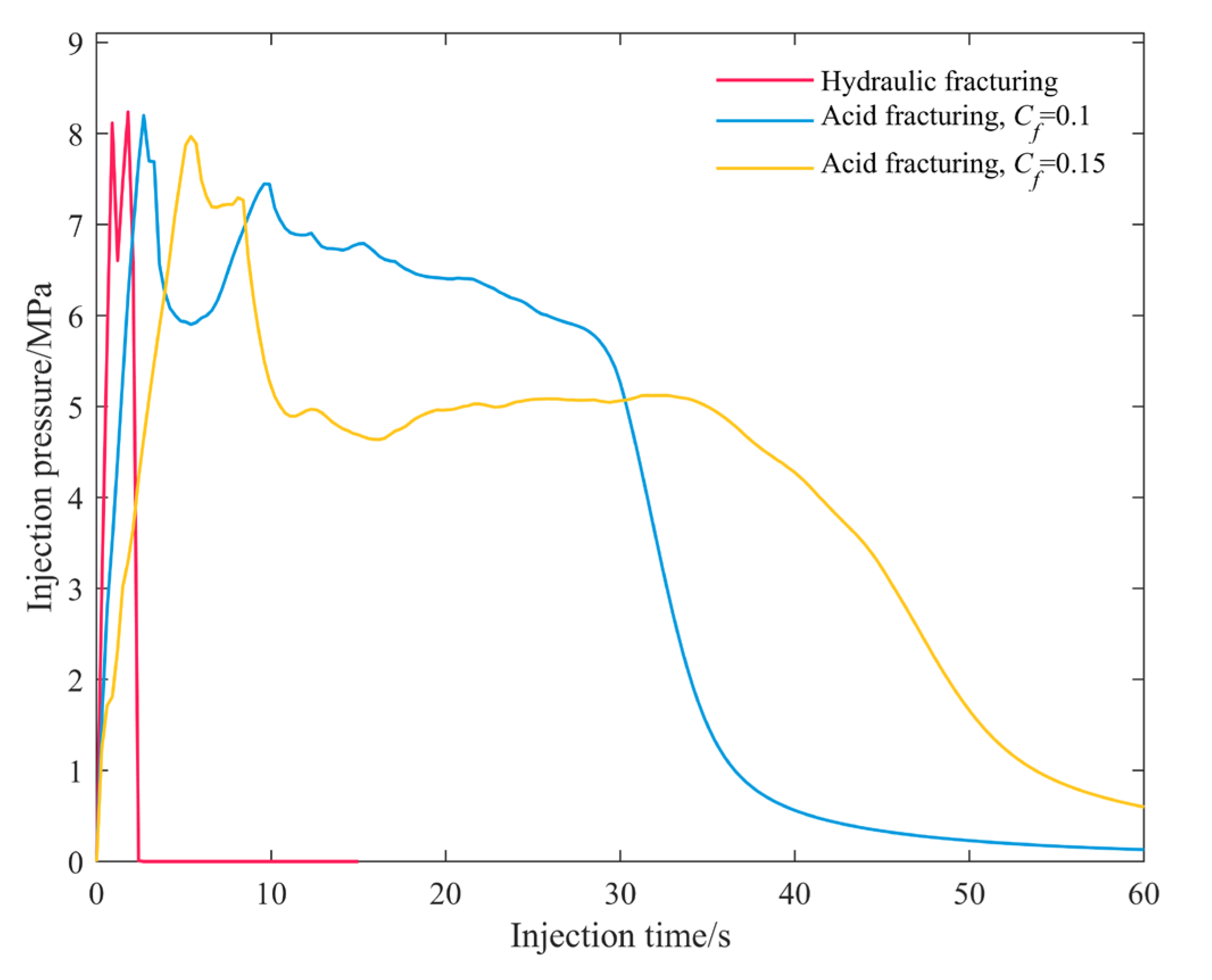
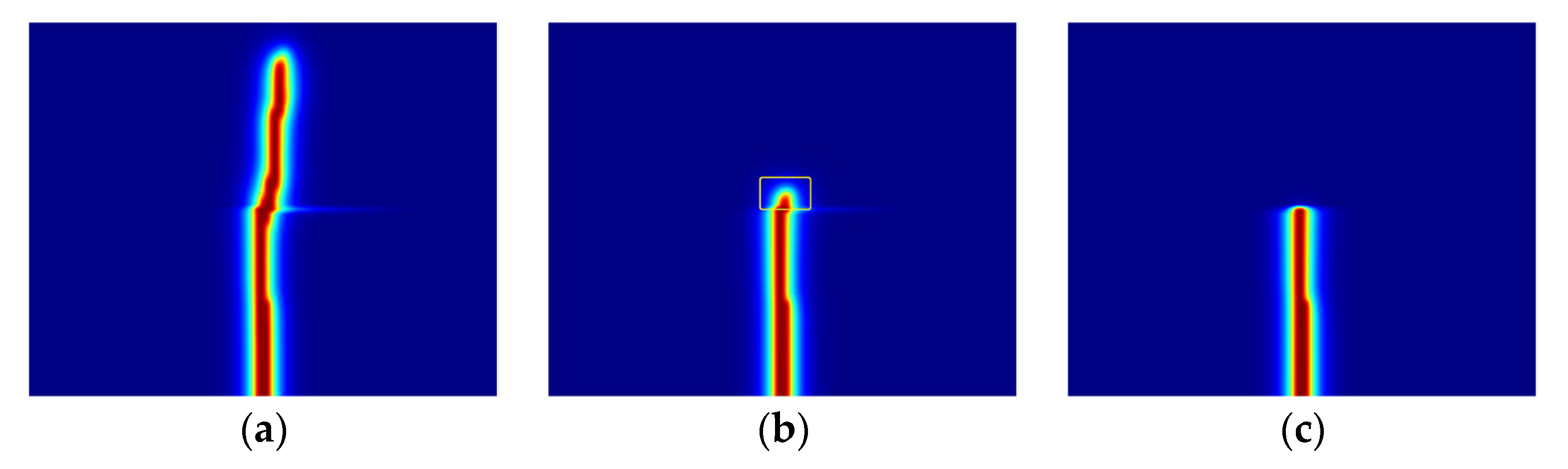
4.1. Hydraulic Fracturing in Layered Reservoirs
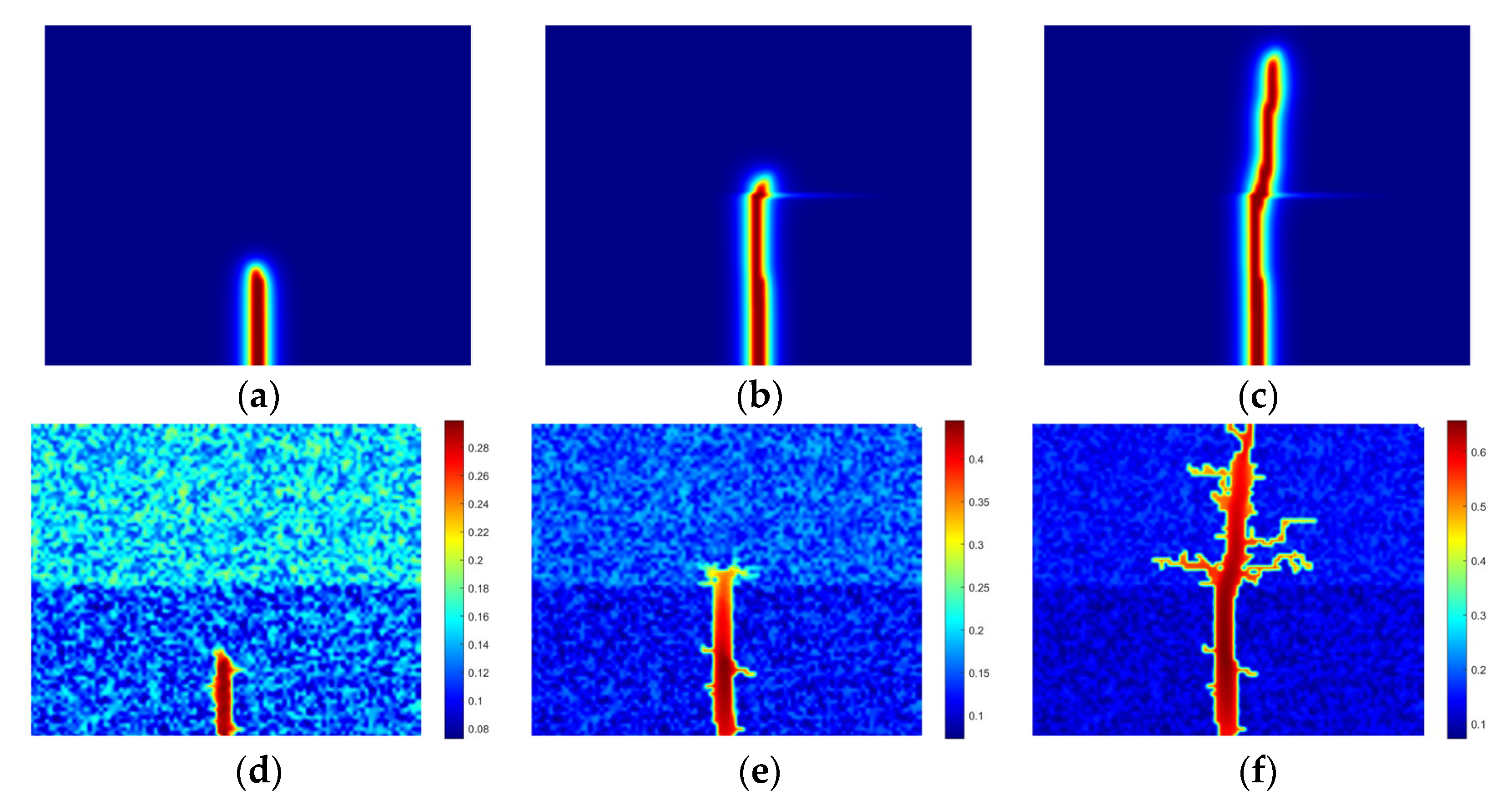
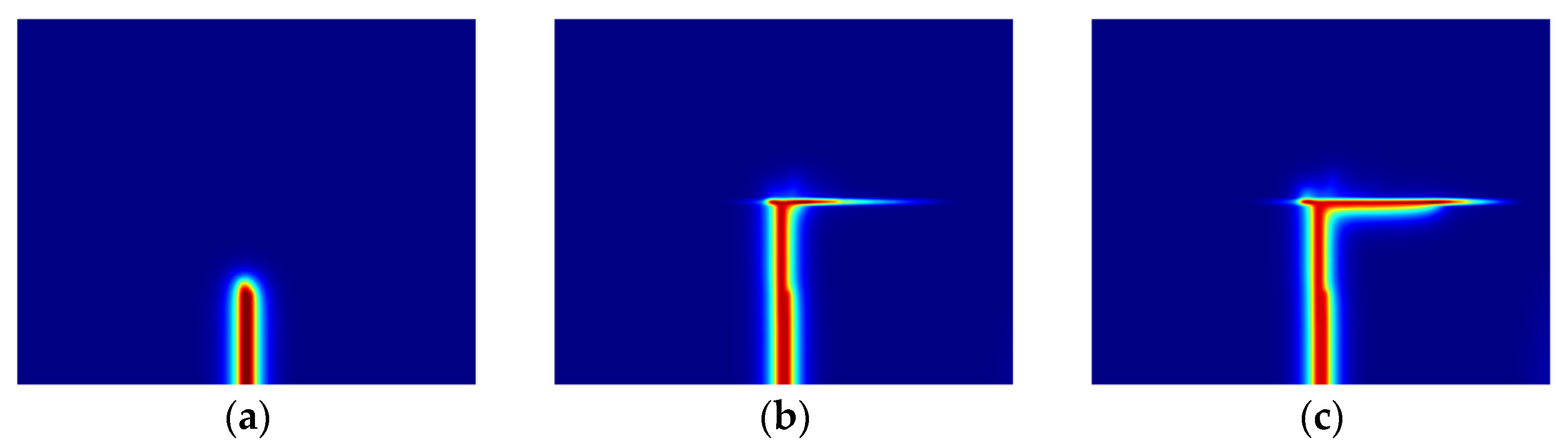
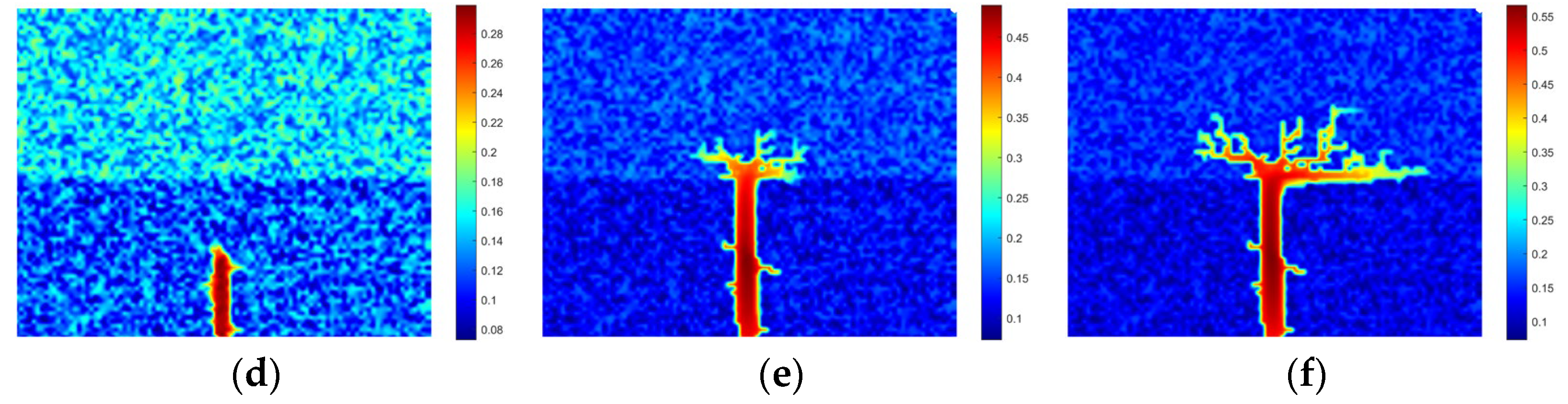
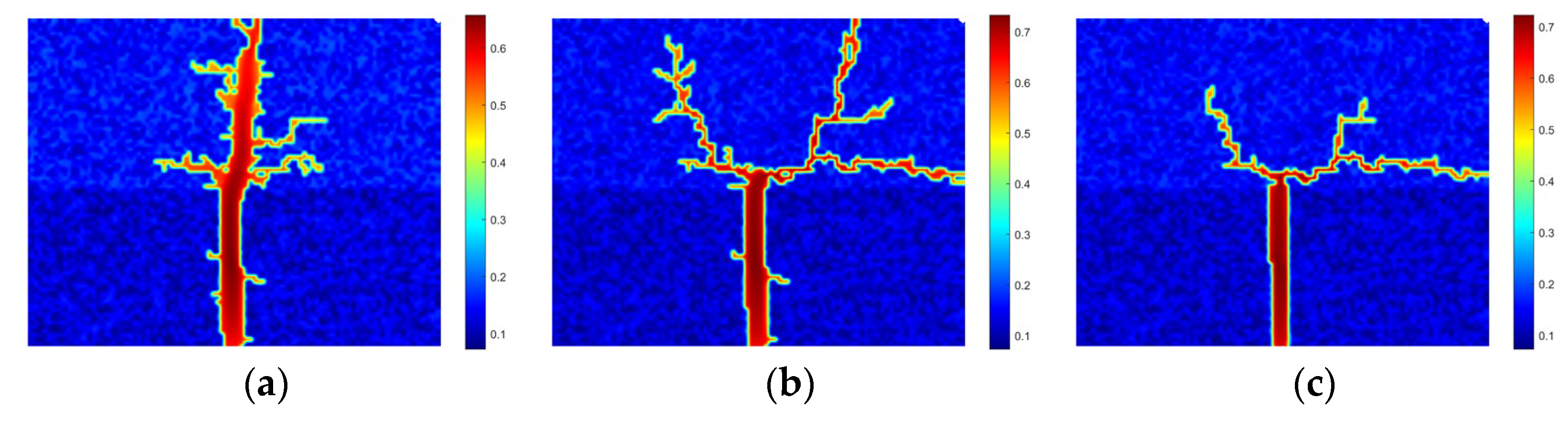
4.2. Propagation Modes of Acid Fracture in Layered Reservoir
4.3. Effect of Acid Concentration
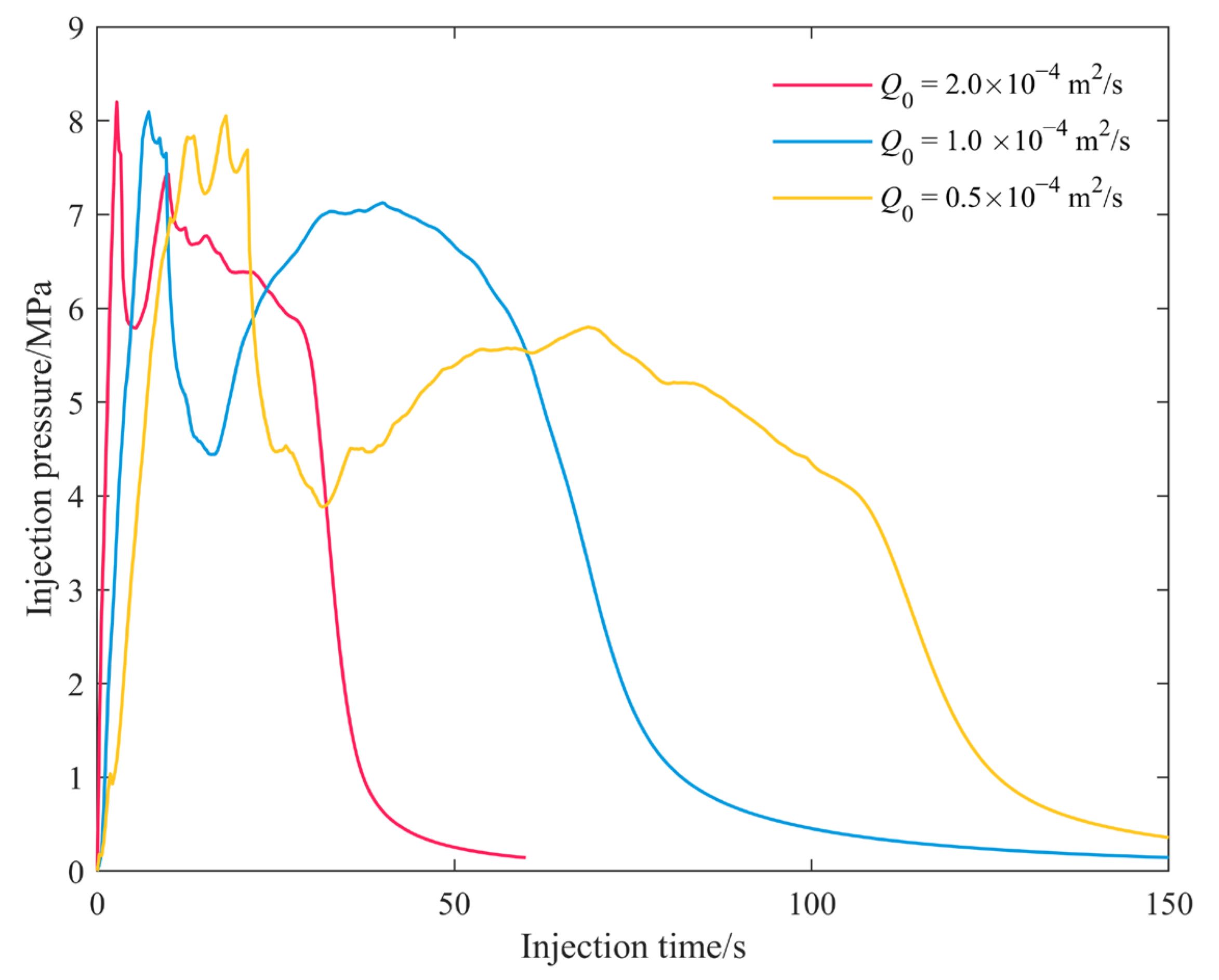
4.4. Effect of Injection Rate
5. Conclusions
- (1)
- Three distinct propagation modes of acid fractures are identified: crossing, diversion, and arresting, each influenced by treatment parameters and geological conditions.
- (2)
- Increasing acid concentration initially facilitates fracture crossing by reducing peak pressure for initiation. However, excessive wormhole formation at higher concentrations leads to fracture arresting, underscoring the need for balanced acid concentration to optimize propagation.
- (3)
- The injection rate significantly affects fracture propagation, with moderate rates promoting optimal crossing by balancing pressure accumulation and dissipation. This highlights the importance of optimizing injection rates to control fracture behavior effectively.
- (4)
- Stress conditions and interface properties critically influence fracture propagation, with mechanical stress differences affecting hydraulic fractures more than acid fractures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Hou, B.; Wang, D.; Jia, Z. Features of Fracture Height Propagation in Cross-Layer Fracturing of Shale Oil Reservoirs. Pet. Explor. Dev. 2021, 48, 469–479. [Google Scholar] [CrossRef]
- Zeng, Q.; Bo, L.; Li, Q.; Sun, J.; Yao, J. Numerical Investigation of Hydraulic Fracture Propagation Interacting with Bedding Planes. Eng. Fract. Mech. 2023, 291, 109575. [Google Scholar] [CrossRef]
- Zheng, H.; Pu, C.; Sun, C. Numerical Investigation on the Hydraulic Fracture Propagation Based on Combined Finite-Discrete Element Method. J. Struct. Geol. 2020, 130, 103926. [Google Scholar] [CrossRef]
- Yang, X.; Chang, C.; Cheng, Q.; Xie, W.; Hu, H.; Li, Y.; Huang, Y.; Peng, Y. The Influence of Rock and Natural Weak Plane Properties on the Vertical Propagation of Hydraulic Fractures. Processes 2024, 12, 2477. [Google Scholar] [CrossRef]
- Zhang, B.; Guo, T.; Chen, M.; Wang, J.; Cao, J.; Wang, H.; Qu, Z. Effect of Bedding Planes and Property Contrast between Layers on the Propagation Mechanism of Hydraulic Fracture Height in Shale Reservoirs. Comput. Geotech. 2024, 175, 106715. [Google Scholar] [CrossRef]
- Guo, J.; Luo, B.; Lu, C.; Lai, J.; Ren, J. Numerical Investigation of Hydraulic Fracture Propagation in a Layered Reservoir Using the Cohesive Zone Method. Eng. Fract. Mech. 2017, 186, 195–207. [Google Scholar] [CrossRef]
- Yang, L.; Sheng, X.; Zhang, B.; Yu, H.; Wang, X.; Wang, P.; Mei, J. Propagation Behavior of Hydraulic Fractures in Shale under Triaxial Compression Considering the Influence of Sandstone Layers. Gas Sci. Eng. 2023, 110, 204895. [Google Scholar] [CrossRef]
- Tan, P.; Chen, Z.-W.; Huang, L.-K.; Zhao, Q.; Shao, S.-R. Evaluation of the Combined Influence of Geological Layer Property and In-Situ Stresses on Fracture Height Growth for Layered Formations. Pet. Sci. 2024, 21, 3222–3236. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, D.; Xu, H.; Zhao, T.; Hou, W. Effect of Interlayer Mechanical Properties on Initiation and Propagation of Hydraulic Fracturing in Laminated Coal Reservoirs. J. Pet. Sci. Eng. 2022, 208, 109381. [Google Scholar] [CrossRef]
- Wang, F.; Liu, W.; Deng, J.; Xu, K.; Xing, C.; Yan, K. Hydraulic Fracture Propagation Research in Layered Rocks Based on 3D FEM Modeling and Laboratory Experiments. Geoenergy Sci. Eng. 2024, 234, 212670. [Google Scholar] [CrossRef]
- He, J.-C.; Zhang, K.-S.; Liu, H.-B.; Tang, M.-R.; Zheng, X.-L.; Zhang, G.-Q. Laboratory Investigation on Hydraulic Fracture Propagation in Sandstone-Mudstone-Shale Layers. Pet. Sci. 2022, 19, 1664–1673. [Google Scholar] [CrossRef]
- Huang, C.-H.; Zhu, H.-Y.; Wang, J.-D.; Han, J.; Zhou, G.-Q.; Tang, X.-H. A FEM-DFN Model for the Interaction and Propagation of Multi-Cluster Fractures during Variable Fluid-Viscosity Injection in Layered Shale Oil Reservoir. Pet. Sci. 2022, 19, 2796–2809. [Google Scholar] [CrossRef]
- Lyu, J.; Hou, B.; Zhou, T. Fracture Propagation Behavior via Multi-Cluster Fracturing in Sandstone-Shale Interbedded Reservoirs. Geoenergy Sci. Eng. 2024, 243, 213356. [Google Scholar] [CrossRef]
- Zeng, Q.; Yao, J.; Shao, J. An Extended Finite Element Solution for Hydraulic Fracturing with Thermo-Hydro-Elastic–Plastic Coupling. Comput. Methods Appl. Mech. Eng. 2020, 364, 112967. [Google Scholar] [CrossRef]
- Zeng, Q.; Bo, L.; Liu, W.; Huang, Z.; Yao, J. An Investigation of Hydraulic Fracture Propagation in Multi-Layered Formation via the Phase Field Method. Comput. Geotech. 2023, 156, 105258. [Google Scholar] [CrossRef]
- Yi, L.-P.; Li, X.-G.; Yang, Z.-Z.; Yang, C.-X. Phase Field Modeling of Hydraulic Fracturing in Porous Media Formation with Natural Fracture. Eng. Fract. Mech. 2020, 236, 107206. [Google Scholar] [CrossRef]
- Qin, M.; Yang, D.; Jia, Y.; Zhou, Y. Peridynamics Modeling of Hydraulic Fracture Interaction with Natural Fractures in Fractured Rock Mass. Eng. Fract. Mech. 2024, 307, 110299. [Google Scholar] [CrossRef]
- Mao, S.; Wu, K.; Moridis, G. Integrated Simulation of Three-Dimensional Hydraulic Fracture Propagation and Lagrangian Proppant Transport in Multilayered Reservoirs. Comput. Methods Appl. Mech. Eng. 2023, 410, 116037. [Google Scholar] [CrossRef]
- Aimene, Y.; Hammerquist, C.; Ouenes, A. Anisotropic Damage Mechanics for Asymmetric Hydraulic Fracture Height Propagation in a Layered Unconventional Gas Reservoir. J. Nat. Gas Sci. Eng. 2019, 67, 1–13. [Google Scholar] [CrossRef]
- Li, H.; Kang, T.; Zhang, R.; Zhang, X.; Liang, X.; Zhu, W.; Zhang, B. Numerical Study of the Effects of Loading Parameters on High-Energy Gas Fracture Propagation in Layered Rocks with Peridynamics. Eng. Fract. Mech. 2024, 310, 110516. [Google Scholar] [CrossRef]
- Ni, T.; Fan, X.; Zhang, J.; Zaccariotto, M.; Galvanetto, U.; Schrefler, B. A Peridynamic-Enhanced Finite Element Method for Thermo–Hydro–Mechanical Coupled Problems in Saturated Porous Media Involving Cracks. Comput. Methods Appl. Mech. Eng. 2023, 417, 116376. [Google Scholar] [CrossRef]
- Xu, H.; Cheng, J.; Zhao, Z.; Lin, T.; Liu, G.; Chen, S. Coupled Thermo-Hydro-Mechanical-Chemical Modeling on Acid Fracturing in Carbonatite Geothermal Reservoirs Containing a Heterogeneous Fracture. Renew. Energy 2021, 172, 145–157. [Google Scholar] [CrossRef]
- Kong, X.; Shi, X.; Xie, G. Numerical Characterization of Acid Fracture Wall Etching Morphology and Experimental Investigation on Sensitivity Factors in Carbonate Reservoirs. Geoenergy Sci. Eng. 2024, 237, 212762. [Google Scholar] [CrossRef]
- Gou, B.; Zhang, J.; Wang, K.; Xu, K.; Xiao, B.; Zeng, J.; Guo, J. Effect of Acid Viscosity on Conductivity during Online Acid-Fracturing in Ultra-Deep Carbonate Reservoir. Geoenergy Sci. Eng. 2024, 243, 213381. [Google Scholar] [CrossRef]
- Zhu, T.; Wei, X.; Zhang, Z. Numerical Simulation of Hydraulic-Mechanical-Chemical Field Coupled Acid Fracturing in Complex Carbonate Reservoir. Comput. Geotech. 2023, 156, 105277. [Google Scholar] [CrossRef]
- Zeng, Q.; Li, T.; Liu, P.; Bo, L.; Yao, C.; Yao, J. A Phase Field Framework to Model Acid Fracture Propagation with Hydro-Mechano-Reactive Flow Coupling. Comput. Geotech. 2024, 174, 106658. [Google Scholar] [CrossRef]
- Zhao, J.J.; Shen, W.Q.; Shao, J.F.; Liu, Z.B.; Vu, M.N. A Constitutive Model for Anisotropic Clay-Rich Rocks Considering Micro-Structural Composition. Int. J. Rock Mech. Min. Sci. 2022, 151, 105029. [Google Scholar] [CrossRef]
- Yu, Z.; Shao, J.; Sun, Y.; Wang, M.; Vu, M.; Plua, C. Numerical Analysis of Hydro-Thermal Fracturing in Saturated Rocks by Considering Material Anisotropy and Micro-Structural Heterogeneity. Int. J. Rock Mech. Min. Sci. 2023, 170, 105457. [Google Scholar] [CrossRef]
- Giraud, A.; Huynh, Q.V.; Hoxha, D.; Kondo, D. Application of Results on Eshelby Tensor to the Determination of Effective Poroelastic Properties of Anisotropic Rocks-like Composites. Int. J. Solids Struct. 2007, 44, 3756–3772. [Google Scholar] [CrossRef]
- Panga, M.K.R.; Ziauddin, M.; Balakotaiah, V. Two-Scale Continuum Model for Simulation of Wormholes in Carbonate Acidization. AIChE J. 2005, 51, 3231–3248. [Google Scholar] [CrossRef]
- Lee, S.; Wheeler, M.F.; Wick, T. Pressure and Fluid-Driven Fracture Propagation in Porous Media Using an Adaptive Finite Element Phase Field Model. Comput. Methods Appl. Mech. Eng. 2016, 305, 111–132. [Google Scholar] [CrossRef]
- Palchik, V.; Hatzor, Y.H. Crack Damage Stress as a Composite Function of Porosity and Elastic Matrix Stiffness in Dolomites and Limestones. Eng. Geol. 2002, 63, 233–245. [Google Scholar] [CrossRef]
- Croizé, D.; Bjørlykke, K.; Jahren, J.; Renard, F. Experimental Mechanical and Chemical Compaction of Carbonate Sand. J. Geophys. Res. 2010, 115, B11204. [Google Scholar] [CrossRef]
- Wojtacki, K.; Lewandowska, J.; Gouze, P.; Lipkowski, A. Numerical Computations of Rock Dissolution and Geomechanical Effects for CO2 Geological Storage. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 482–506. [Google Scholar] [CrossRef]
- Borden, M.J.; Verhoosel, C.V.; Scott, M.A.; Hughes, T.J.R.; Landis, C.M. A Phase-Field Description of Dynamic Brittle Fracture. Comput. Methods Appl. Mech. Eng. 2012, 217–220, 77–95. [Google Scholar] [CrossRef]






| Parameter | Notation | Magnitude | Unit |
|---|---|---|---|
| Domain length | L | 0.5 | m |
| Domain height | H | 0.4 | m |
| Height of layer 1 | L1 | 0.195 | m |
| Height of layer 2 | L2 | 0.195 | m |
| Height of interface | L12 | 0.01 | m |
| Length of initial hydraulic fracture | lhf | 0.1 | m |
| Characteristic length parameter | l0 | 0.01 | – |
| Mean porosity of layer 1 | fp1 | 0.12 | – |
| Mean porosity of layer 2 | fp2 | 0.15 | – |
| Elastic modulus of solid matrix in layer 1 | Em1 | 25 | GPa |
| Elastic modulus of solid matrix in layer 2 | Em2 | 32 | GPa |
| Elastic modulus of interface | Emf | 5 | GPa |
| Elastic modulus of mineral inclusion | Ei | 98 | GPa |
| Volume ratio of mineral inclusion | fi | 0.4 | – |
| Critical fracture energy of layer 1 | Gc1 | 50 | Pa·m |
| Critical fracture energy of layer 2 | Gc2 | 120 | Pa·m |
| Critical fracture energy of interface | Gcf | 2 | Pa·m |
| Primary vertical stress | σv | 7 | MPa |
| Minimum horizontal stress | σh | 5 | MPa |
| Matrix permeability | kr | 1.0 × 10−15 | m2 |
| Fracture permeability | kr | 1.0 × 10−8 | m2 |
| Injection rate | Q0 | 2.0 × 10−4 | m2/s |
| Fluid viscosity | μ | 1.0 × 10−3 | Pa·s |
| Parameter | Notation | Magnitude | Unit |
|---|---|---|---|
| Acid concentration | Cf0 | 0.15 | – |
| Injection rate | Q0 | 2.0 × 10−4 | m2/s |
| Acid reaction rate | ks | 2.0 × 10−3 | m/s |
| Molecular diffusion coefficient | Dm | 3.6 × 10−9 | m2/s |
| Asymptotic Sherwood number | Sh∞ | 3.66 | – |
| Constants | αos, λX, λT | 0.5 | – |
| Initial average permeability | kr | 1.0 × 10−15 | m2 |
| Specific surface area | α0 | 5.0 × 103 | m−1 |
| Pore diameter | d0 | 1.0 × 10−5 | m |
| Pore broadening parameter | β | 1 | – |
| Chemical degradation coefficient | r | 5 | – |
| Rock density | ρs | 2.71 × 103 | kg/m3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Q.; Li, T.; Zhou, T.; Bo, L.; Liu, S.; Li, X.; Yao, J. Modeling Complex Interactions Between Acid–Rock Reactions and Fracture Propagation in Heterogeneous Layered Formations. Water 2024, 16, 3586. https://doi.org/10.3390/w16243586
Zeng Q, Li T, Zhou T, Bo L, Liu S, Li X, Yao J. Modeling Complex Interactions Between Acid–Rock Reactions and Fracture Propagation in Heterogeneous Layered Formations. Water. 2024; 16(24):3586. https://doi.org/10.3390/w16243586
Chicago/Turabian StyleZeng, Qingdong, Taixu Li, Tong Zhou, Long Bo, Shumin Liu, Xuelong Li, and Jun Yao. 2024. "Modeling Complex Interactions Between Acid–Rock Reactions and Fracture Propagation in Heterogeneous Layered Formations" Water 16, no. 24: 3586. https://doi.org/10.3390/w16243586
APA StyleZeng, Q., Li, T., Zhou, T., Bo, L., Liu, S., Li, X., & Yao, J. (2024). Modeling Complex Interactions Between Acid–Rock Reactions and Fracture Propagation in Heterogeneous Layered Formations. Water, 16(24), 3586. https://doi.org/10.3390/w16243586






