Monthly Runoff Prediction Based on Stochastic Weighted Averaging-Improved Stacking Ensemble Model
Abstract
1. Introduction
2. Methodology
2.1. Deep Learning Models
2.1.1. Long Short-Term Memory (LSTM)
2.1.2. Gated Recurrent Unit (GRU)
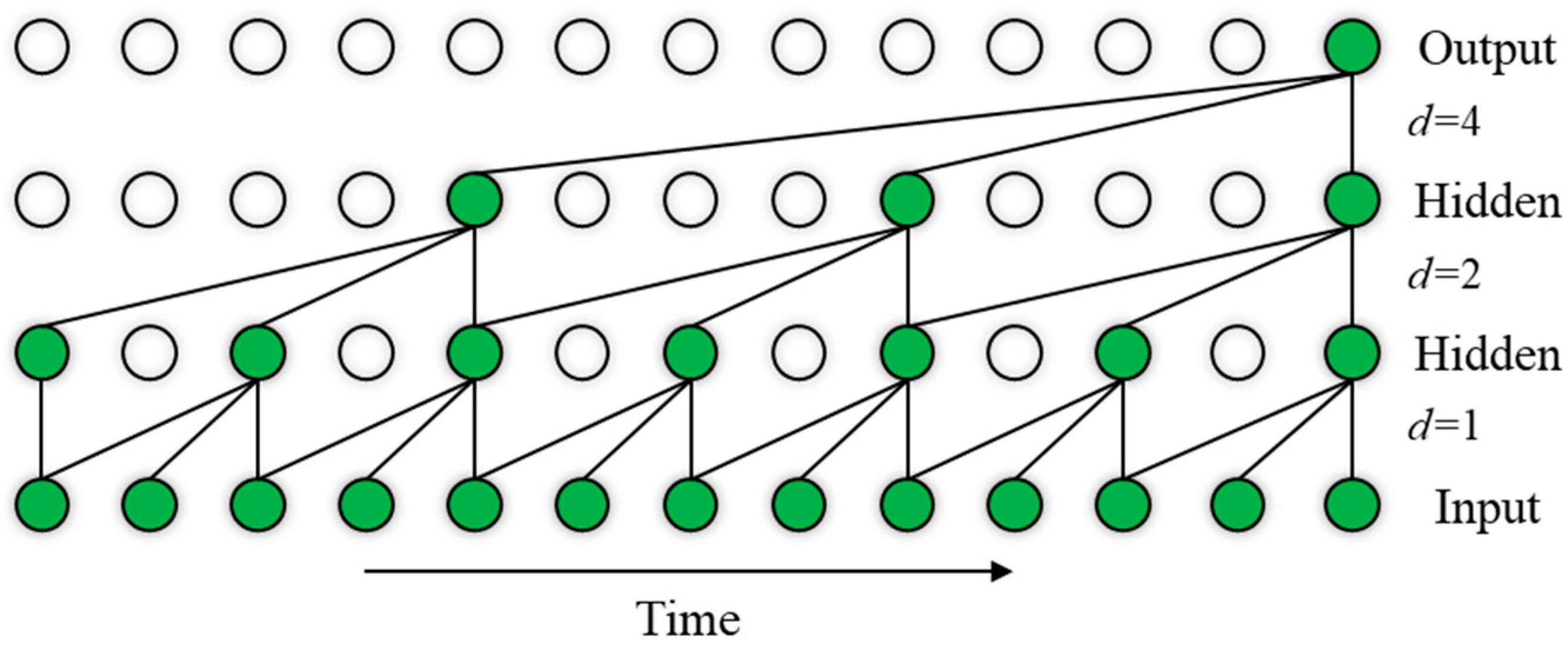
2.1.3. Temporal Convolutional Network (TCN)
2.1.4. Light Gradient Boosting Machine (LightGBM)
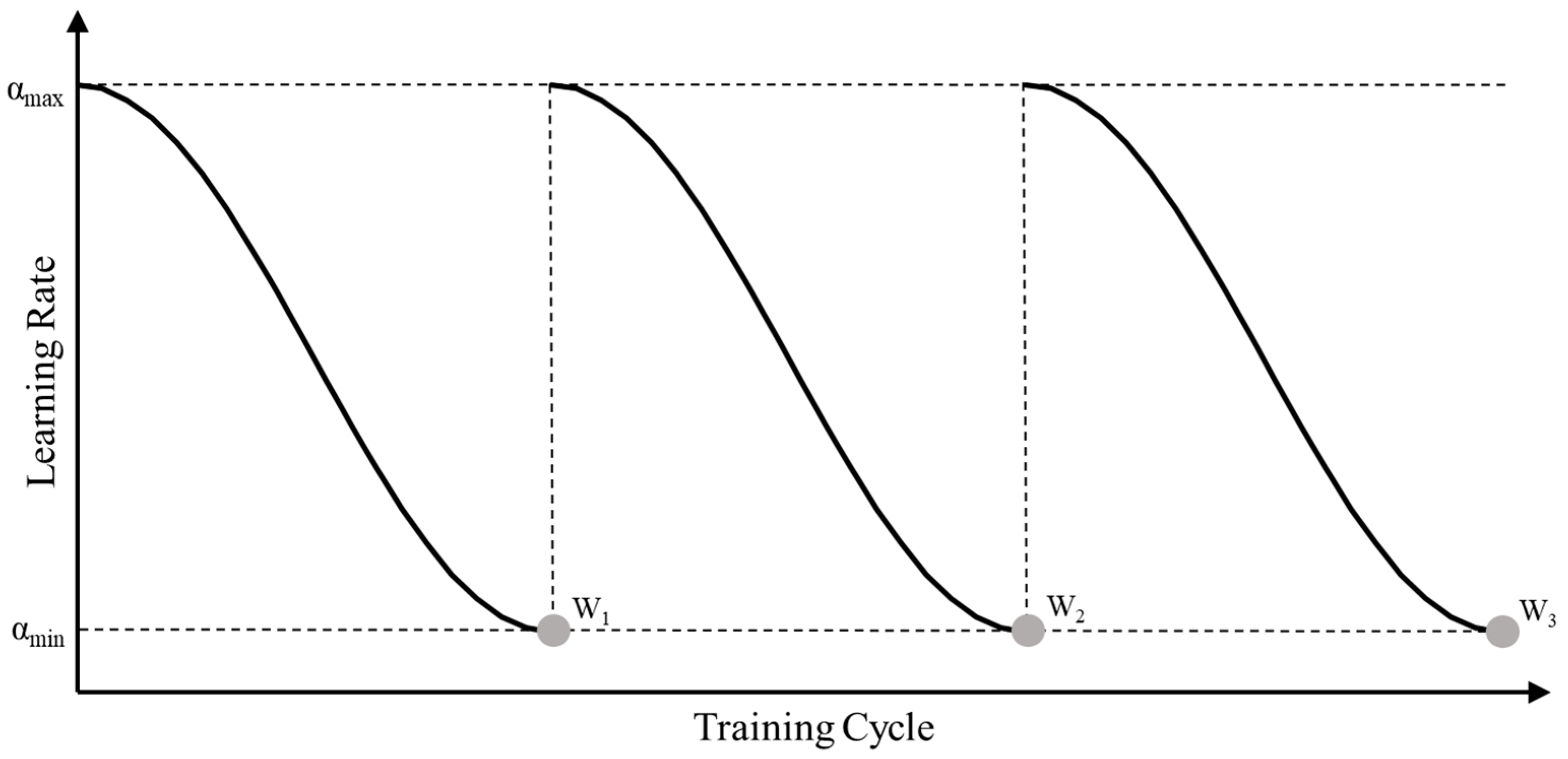
2.2. Stochastic Weighted Average (SWA)
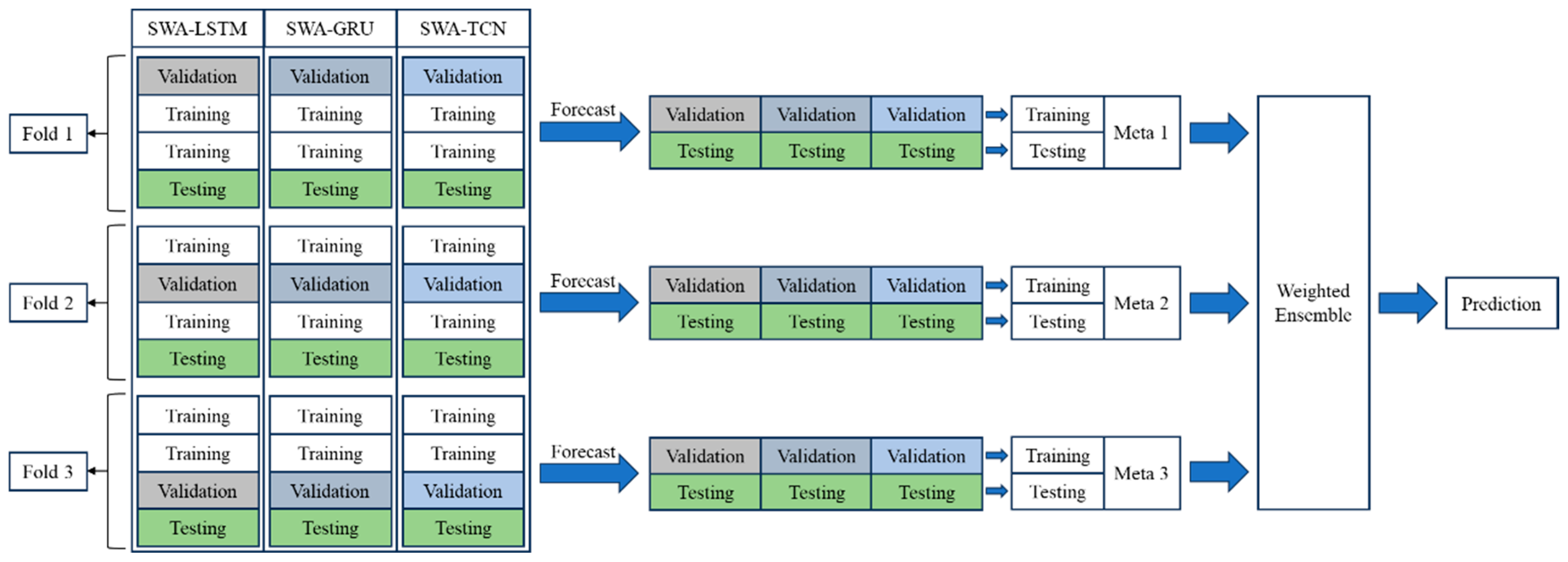
2.3. The Proposed SWA–FWWS Model for Monthly Runoff Prediction
- (1)
- Set hyper-parameters for the SWA. This includes determining the upper and lower bounds of the learning rate and when using the SWA algorithm, the total training cycles , the starting cycle for ensembling , the learning rate adjustment period , and the number of cycles . The hyper-parameters should satisfy .
- (2)
- Perform single-model ensembles for multiple deep learning models using SWA. Each deep learning model begins training with the maximum learning rate . When the training cycle reaches , the learning rate is adjusted to the cosine annealing schedule. During each model’s training process, the model parameters are recorded and averaged each time the learning rate reduces to . These averaged parameters are used as the final parameters for an SWA-ensembled base model.
- (3)
- Use K-fold cross-validation to process the original data. The original runoff data and other feature data are divided into a training set and a test set. The training set is then divided into k copies on average using K-fold cross-validation, with one of these copies selected as the sub-validation set. The remaining copies are used as the sub-training set, resulting in k groups of different sub-training sets and sub-validation sets. The ratio of each sub-training set and sub-validation set in the same group to the original training set is , with no overlap between the sets.
- (4)
- Train and predict with the SWA-ensembled base models. For each fold, the SWA-ensembled base models obtained from step (2) are trained on the K-fold cross-validation sub-training sets and used to predict the sub-validation and test sets. Each base model is trained and predicted k times, independently, to generate the sub-validation and test set predictions for each fold.
- (5)
- Train and predict with the meta models in the FWWS method. The prediction results of the sub-validation set and test set of multiple basic models on each fold are horizontally spliced and used as the training set and test set of the meta model. After training, the meta model is used to predict its training and test sets. A total of k meta models are trained, yielding k sets of predictions for both the training and test sets.
- (6)
- Construct the multi-scale ensemble model based on SWA and Fold-Wise Weighted Stacking. According to the root mean square error (RMSE) of the prediction results of k meta models on their training sets, the weights were assigned to each meta model by Equation (13), and the multi-scale ensemble model based on SWA and Fold-Wise Weighted Stacking was constructed.
2.4. Evaluation Metrics
3. Case Study
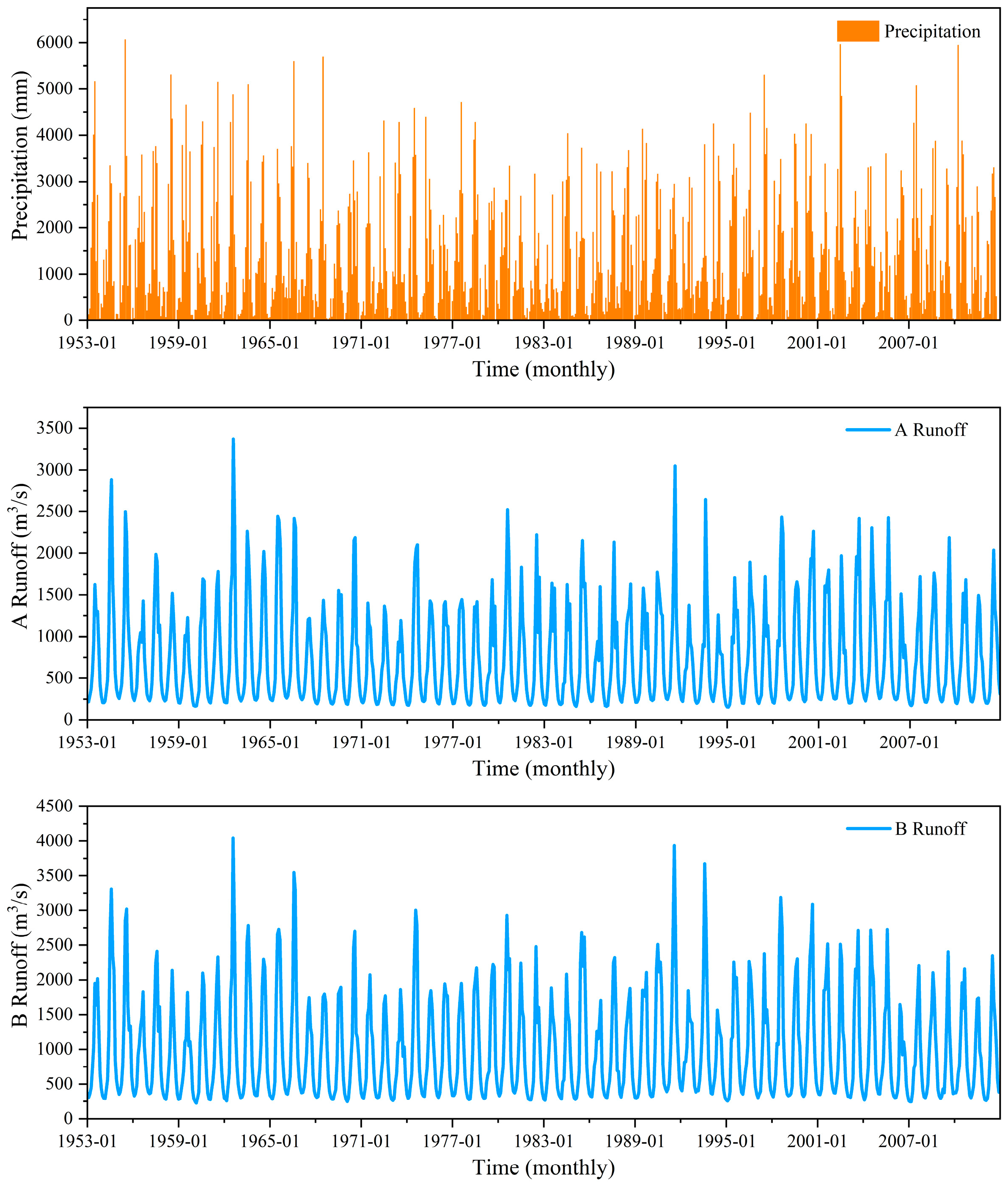
3.1. Study Data
3.2. Data Preprocessing
3.3. Comparative Experiment Design
- (1)
- The SWA-ensembled deep learning models (SWA–LSTM, SWA–GRU, SWA–TCN) were compared with their respective non-ensembled base models (LSTM, GRU, TCN) to demonstrate the optimization performance of the SWA method on these three models.
- (2)
- To ensure consistency in the structure of the base and meta models across ensemble models, trained LSTM, GRU, and TCN models were chosen as the base models for all ensemble models, and LightGBM is selected as the meta model. The proposed FWWS model is compared with the novel Blending model and the traditional Stacking model.
- (3)
- To further improve the prediction performance of the FWWS model regarding runoff in the river, the trained SWA–LSTM, SWA–GRU, and SWA–TCN models were used as base models in the FWWS framework, forming the SWA–FWWS model for monthly runoff prediction. By comparing it with other ensemble models, the superiority of the proposed SWA–FWWS model is demonstrated from multiple aspects.
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qin, P.; Xu, H.; Liu, M.; Du, L.; Xiao, C.; Liu, L.; Tarroja, B. Climate change impacts on Three Gorges Reservoir impoundment and hydropower generation. J. Hydrol. 2020, 580, 123922. [Google Scholar] [CrossRef]
- Evsukoff, A.-G.; Cataldi, M.; de Lima, B.-S.-L.-P. A multi-model approach for long-term runoff modeling using rainfall forecasts. Expert Syst. Appl. 2012, 39, 4938–4946. [Google Scholar] [CrossRef]
- Zolfaghari, M.; Golabi, M.-R. Modeling and predicting the electricity production in hydropower using conjunction of wavelet transform, long short-term memory and random forest models. Renew. Energy 2021, 170, 1367–1381. [Google Scholar] [CrossRef]
- Liu, Z.; Mo, L.; Lou, S.; Zhu, Y.; Liu, T. An Ecology-Oriented Single-Multi-Objective Optimal Operation Modeling and Decision-Making Method in the Case of the Ganjiang River. Water 2024, 16, 970. [Google Scholar] [CrossRef]
- Worthington, T.-A.; Brewer, S.-K.; Vieux, B.; Kennen, J. The accuracy of ecological flow metrics derived using a physics-based distributed rainfall—Runoff model in the Great Plains, USA. Ecohydrology 2019, 12, 2090. [Google Scholar] [CrossRef]
- Tian, Y.; Zhao, Y.; Son, S.; Luo, J.; Oh, S.; Wang, Y. A Deep-Learning Ensemble Method to Detect Atmospheric Rivers and Its Application to Projected Changes in Precipitation Regime. J. Geophys. Res. Atmos. 2023, 128, 037041. [Google Scholar] [CrossRef]
- Cloke, H.-L.; Pappenberger, F. Ensemble flood forecasting: A review. J. Hydrol. 2009, 375, 613–626. [Google Scholar] [CrossRef]
- Chen, C.; Jiang, J.; Liao, Z.; Zhou, Y.; Wang, H.; Pei, Q. A short-term flood prediction based on spatial deep learning network: A case study for Xi County, China. J. Hydrol. 2022, 607, 127535. [Google Scholar] [CrossRef]
- Man, Y.; Yang, Q.; Shao, J.; Wang, G.; Bai, L.; Xue, Y. Enhanced LSTM Model for Daily Runoff Prediction in the Upper Huai River Basin, China. Engineering 2023, 24, 229–238. [Google Scholar] [CrossRef]
- Sengul, S.; Ispirli, M.-N. Predicting Snowmelt Runoff at the Source of the Mountainous Euphrates River Basin in Turkey for Water Supply and Flood Control Issues Using HEC-HMS Modeling. Water 2022, 14, 284. [Google Scholar] [CrossRef]
- Brown, C.-M.; Lund, J.-R.; Cai, X.; Reed, P.-M.; Zagona, E.-A.; Ostfeld, A.; Hall, J.; Characklis, G.-W.; Yu, W.; Brekke, L. The future of water resources systems analysis: Toward a scientific framework for sustainable water management. Water Resour. Res. 2015, 51, 6110–6124. [Google Scholar] [CrossRef]
- Zang, S.; Li, Z.; Zhang, K.; Yao, C.; Liu, Z.; Wang, J.; Huang, Y.; Wang, S. Improving the flood prediction capability of the Xin’anjiang model by formulating a new physics-based routing framework and a key routing parameter estimation method. J. Hydrol. 2021, 603, 126867. [Google Scholar] [CrossRef]
- Yu, W.; Nakakita, E.; Kim, S.; Yamaguchi, K. Improvement of rainfall and flood forecasts by blending ensemble NWP rainfall with radar prediction considering orographic rainfall. J. Hydrol. 2015, 531, 494–507. [Google Scholar] [CrossRef]
- Avila, L.; Silveira, R.; Campos, A.; Rogiski, N.; Freitas, C.; Aver, C.; Fan, F. Seasonal Streamflow Forecast in the Tocantins River Basin, Brazil: An Evaluation of ECMWF-SEAS5 with Multiple Conceptual Hydrological Models. Water 2023, 15, 1695. [Google Scholar] [CrossRef]
- Li, Y.; Wei, J.; Sun, Q.; Huang, C. Research on Coupling Knowledge Embedding and Data-Driven Deep Learning Models for Runoff Prediction. Water 2024, 16, 2130. [Google Scholar] [CrossRef]
- Sheng, Z.; Wen, S.; Feng, Z.; Gong, J.; Shi, K.; Guo, Z.; Yang, Y.; Huang, T. A Survey on Data-Driven Runoff Forecasting Models Based on Neural Networks. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 7, 1083–1097. [Google Scholar] [CrossRef]
- Feng, Z.; Niu, W.; Tang, Z.; Jiang, Z.; Xu, Y.; Liu, Y.; Zhang, H. Monthly runoff time series prediction by variational mode decomposition and support vector machine based on quantum-behaved particle swarm optimization. J. Hydrol. 2020, 583, 124627. [Google Scholar] [CrossRef]
- Wang, W.; Xu, D.; Chau, K.; Chen, S. Improved annual rainfall-runoff forecasting using PSO-SVM model based on EEMD. J. Hydroinform. 2013, 15, 1377–1390. [Google Scholar] [CrossRef]
- Dong, J.; Wang, Z.; Wu, J.; Cui, X.; Pei, R. A Novel Runoff Prediction Model Based on Support Vector Machine and Gate Recurrent unit with Secondary Mode Decomposition. Water Resour. Manag. 2024, 38, 1655–1674. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, Q.; Li, N.; Zhai, Y.; Teng, W.; Liu, S.; Ying, G. Runoff time series prediction based on hybrid models of two-stage signal decomposition methods and LSTM for the Pearl River in China. Hydrol. Res. 2023, 54, 1505–1521. [Google Scholar] [CrossRef]
- Sun, N.; Zhang, S.; Peng, T.; Zhang, N.; Zhou, J.; Zhang, H. Multi-Variables-Driven Model Based on Random Forest and Gaussian Process Regression for Monthly Streamflow Forecasting. Water 2022, 14, 1828. [Google Scholar] [CrossRef]
- Woodson, D.; Rajagopalan, B.; Zagona, E. Long-Lead Forecasting of Runoff Season Flows in the Colorado River Basin Using a Random Forest Approach. J. Water Res. Plan. Manag. 2024, 150, 6167. [Google Scholar] [CrossRef]
- Chen, S.-J.; Wei, Q.; Zhu, Y.-M.; Ma, G.-W.; Han, X.-Y.; Wang, L. Medium- and long-term runoff forecasting based on a random forest regression model. Water Supply 2020, 20, 3658–3664. [Google Scholar]
- Wu, J.; Wang, Z.; Dong, J.; Cui, X.; Tao, S.; Chen, X. Robust Runoff Prediction with Explainable Artificial Intelligence and Meteorological Variables from Deep Learning Ensemble Model. Water Resour. Res. 2023, 59, 035676. [Google Scholar] [CrossRef]
- Contreras, P.; Orellana-Alvear, J.; Munoz, P.; Bendix, J.; Celleri, R. Influence of Random Forest Hyperparameterization on Short-Term Runoff Forecasting in an Andean Mountain Catchment. Atmosphere 2021, 12, 238. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, H.; Fang, H. Component-Based Reconstruction Prediction of Runoff at Multi-time Scales in the Source Area of the Yellow River Based on the ARMA Model. Water Resour. Manag. 2022, 36, 433–448. [Google Scholar] [CrossRef]
- Khazaeiathar, M.; Hadizadeh, R.; Attar, N.-F.; Schmalz, B. Daily Streamflow Time Series Modeling by Using a Periodic Autoregressive Model (ARMA) Based on Fuzzy Clustering. Water 2022, 14, 3932. [Google Scholar] [CrossRef]
- Chai, Q.; Zhang, S.; Tian, Q.; Yang, C.; Guo, L. Daily Runoff Prediction Based on FA-LSTM Model. Water 2024, 16, 2216. [Google Scholar] [CrossRef]
- Gao, S.; Huang, Y.; Zhang, S.; Han, J.; Wang, G.; Zhang, M.; Lin, Q. Short-term runoff prediction with GRU and LSTM networks without requiring time step optimization during sample generation. J. Hydrol. 2020, 589, 125188. [Google Scholar] [CrossRef]
- Shrestha, S.-G.; Pradhanang, S.-M. Performance of LSTM over SWAT in Rainfall-Runoff Modeling in a Small, Forested Watershed: A Case Study of Cork Brook, RI. Water 2023, 15, 4194. [Google Scholar] [CrossRef]
- Li, P.; Zhang, J.; Krebs, P. Prediction of Flow Based on a CNN-LSTM Combined Deep Learning Approach. Water 2022, 14, 993. [Google Scholar] [CrossRef]
- Frame, J.-M.; Kratzert, F.; Klotz, D.; Gauch, M.; Shalev, G.; Gilon, O.; Qualls, L.-M.; Gupta, H.; Nearing, G.-S. Deep learning rainfall-runoff predictions of extreme events. Hydrol. Earth Syst. Sc. 2022, 26, 3377–3392. [Google Scholar] [CrossRef]
- Samantaray, S.; Das, S.-S.; Sahoo, A.; Satapathy, D.-P. Monthly runoff prediction at Baitarani river basin by support vector machine based on Salp swarm algorithm. Ain Shams Eng. J. 2022, 13, 101732. [Google Scholar] [CrossRef]
- Chen, X.; Huang, J.; Wang, S.; Zhou, G.; Gao, H.; Liu, M.; Yuan, Y.; Zheng, L.; Li, Q.; Qi, H. A New Rainfall-Runoff Model Using Improved LSTM with Attentive Long and Short Lag-Time. Water 2022, 14, 697. [Google Scholar] [CrossRef]
- Li, J.; Qian, K.; Liu, Y.; Yan, W.; Yang, X.; Luo, G.; Ma, X. LSTM-Based Model for Predicting Inland River Runoff in Arid Region: A Case Study on Yarkant River, Northwest China. Water 2022, 14, 1745. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, X. Applying a Multi-Model Ensemble Method for Long-Term Runoff Prediction under Climate Change Scenarios for the Yellow River Basin, China. Water 2018, 10, 301. [Google Scholar] [CrossRef]
- Arsenault, R.; Gatien, P.; Renaud, B.; Brissette, F.; Martel, J. A comparative analysis of 9 multi-model averaging approaches in hydrological continuous streamflow simulation. J. Hydrol. 2015, 529, 754–767. [Google Scholar] [CrossRef]
- Liu, S.; Qin, H.; Liu, G.; Xu, Y.; Zhu, X.; Qi, X. Runoff Forecasting of Machine Learning Model Based on Selective Ensemble. Water Resour. Manag. 2023, 37, 4459–4473. [Google Scholar] [CrossRef]
- Yao, J.; Zhang, X.; Luo, W.; Liu, C.; Ren, L. Applications of Stacking/Blending ensemble learning approaches for evaluating flash flood susceptibility. Int. J. Appl. Earth Obs. 2022, 112, 102932. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Batelaan, O.; Fadaee, M.; Hinkelmann, R. Ensemble machine learning paradigms in hydrology: A review. J. Hydrol. 2021, 598, 126266. [Google Scholar] [CrossRef]
- Leng, Z.; Chen, L.; Yang, B.; Li, S.; Yi, B. An extreme forecast index-driven runoff prediction approach using stacking ensemble learning. Geomat. Nat. Haz Risk 2024, 15, 2353144. [Google Scholar] [CrossRef]
- Xie, Y.; Sun, W.; Ren, M.; Chen, S.; Huang, Z.; Pan, X. Stacking ensemble learning models for daily runoff prediction using 1D and 2D CNNs. Expert Syst. Appl. 2023, 217, 119469. [Google Scholar] [CrossRef]
- Deb, D.; Arunachalam, V.; Raju, K.-S. Daily reservoir inflow prediction using stacking ensemble of machine learning algorithms. J. Hydroinform. 2024, 26, 972–997. [Google Scholar] [CrossRef]
- Mohammed, A.; Kora, R. A comprehensive review on ensemble deep learning: Opportunities and challenges. J. King Saud. Univ-Com. 2023, 35, 757–774. [Google Scholar] [CrossRef]
- Dong, F.; Javed, A.; Saber, A.; Neumann, A.; Arnillas, C.-A.; Kaltenecker, G.; Arhonditsis, G. A flow-weighted ensemble strategy to assess the impacts of climate change on watershed hydrology. J. Hydrol. 2021, 594, 125898. [Google Scholar] [CrossRef]
- Yao, Z.; Wang, Z.; Wang, D.; Wu, J.; Chen, L. An ensemble CNN-LSTM and GRU adaptive weighting model based improved sparrow search algorithm for predicting runoff using historical meteorological and runoff data as input. J. Hydrol. 2023, 625, 129977. [Google Scholar] [CrossRef]
- Liu, S.; Xu, J.; Zhao, J.; Xie, X.; Zhang, W. Efficiency enhancement of a process-based rainfall—Runoff model using a new modified AdaBoost.RT technique. Appl. Soft Comput. 2014, 23, 521–529. [Google Scholar] [CrossRef]
- Lu, M.; Hou, Q.; Qin, S.; Zhou, L.; Hua, D.; Wang, X.; Cheng, L. A Stacking Ensemble Model of Various Machine Learning Models for Daily Runoff Forecasting. Water 2023, 15, 1265. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- He, S.; Sang, X.; Yin, J.; Zheng, Y.; Chen, H. Short-term Runoff Prediction Optimization Method Based on BGRU-BP and BLSTM-BP Neural Networks. Water Resour. Manag. 2023, 37, 747–768. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.-Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Hewage, P.; Behera, A.; Trovati, M.; Pereira, E.; Ghahremani, M.; Palmieri, F.; Liu, Y. Temporal convolutional neural (TCN) network for an effective weather forecasting using time-series data from the local weather station. Soft Comput. 2020, 24, 16453–16482. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, K.; Huang, Y.; Zhu, Y.; Chen, B. Parallel spatio-temporal attention-based TCN for multivariate time series prediction. Neural Comput. Appl. 2023, 35, 13109–13118. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; p. 30. [Google Scholar]
- Izmailov, P.; Podoprikhin, D.; Garipov, T.; Vetrov, D.; Wilson, A.-G. Averaging Weights Leads to Wider Optima and Better Generalization. arXiv 2018, arXiv:1803.05407. [Google Scholar]
- Shen, Q.; Mo, L.; Liu, G.; Zhou, J.; Zhang, Y.; Ren, P. Short-Term Load Forecasting Based on Multi-Scale Ensemble Deep Learning Neural Network. IEEE Access 2023, 11, 111963–111975. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, C.; Lei, X.; Yuan, Y.; Adnan, R.-M. Monthly runoff forecasting based on LSTM-ALO model. Stoch. Environ. Res. Risk Assess. 2018, 32, 2199–2212. [Google Scholar] [CrossRef]



| Study Objects | Models | Hyper-Parameters |
|---|---|---|
| A | LSTM | num_layers = 2, learning_rate = 0.006, num_epochs = 400, hidden_size = 10 |
| GRU | num_layers = 2, learning_rate = 0.006, num_epochs = 400, hidden_size = 6 | |
| TCN | kernel_size = 3, learning_rate = 0.006, num_epochs = 400, num_channels = [10,11] | |
| SWA–LSTM (LSTM) | Same as LSTM | |
| SWA–GRU (GRU) | Same as GRU | |
| SWA–TCN (TCN) | Same as TCN | |
| LightGBM (Stacking) | min_data_in_leaf = 1, learning_rate = 0.03, max_depth = 5, num_epochs = 102 | |
| LightGBM (Blending) | min_data_in_leaf = 20, learning_rate = 0.1, max_depth = -1, num_epochs = 53 | |
| LightGBM (FWWS) | min_data_in_leaf = 1; 6; 25, learning_rate = 0.03; 0.02; 0.03, max_depth = 5; 4; 4, num_epochs = 174; 193; 183 | |
| LightGBM (SWA–FWWS) | min_data_in_leaf = 24; 4; 30, learning_rate = 0.008; 0.008; 0.008, max_depth = 2; 2; 2, num_epochs = 316; 479; 790 | |
| B | LSTM | num_layers = 2, learning_rate = 0.006, num_epochs = 400, hidden_size = 18 |
| GRU | num_layers = 2, learning_rate = 0.006, num_epochs = 400, hidden_size = 14 | |
| TCN | kernel_size = 3, learning_rate = 0.006, num_epochs = 400, num_channels = [12,13] | |
| SWA–LSTM (LSTM) | Same as LSTM | |
| SWA–GRU (GRU) | Same as GRU | |
| SWA–TCN (TCN) | Same as TCN | |
| LightGBM (Stacking) | min_data_in_leaf = 5, learning_rate = 0.009, max_depth = 3, num_epochs = 46 | |
| LightGBM (Blending) | min_data_in_leaf = 8, learning_rate = 0.09, max_depth = 3, num_epochs = 75 | |
| LightGBM (FWWS) | min_data_in_leaf = 5; 8; 7, learning_rate = 0.058; 0.07; 0.03, max_depth = 3; 4; 3, num_epochs = 157; 53; 168 | |
| LightGBM (SWA–FWWS) | min_data_in_leaf = 1; 8; 20, learning_rate = 0.01; 0.05; 0.01, max_depth = 2; 2; −1, num_epochs = 473; 108; 277 |
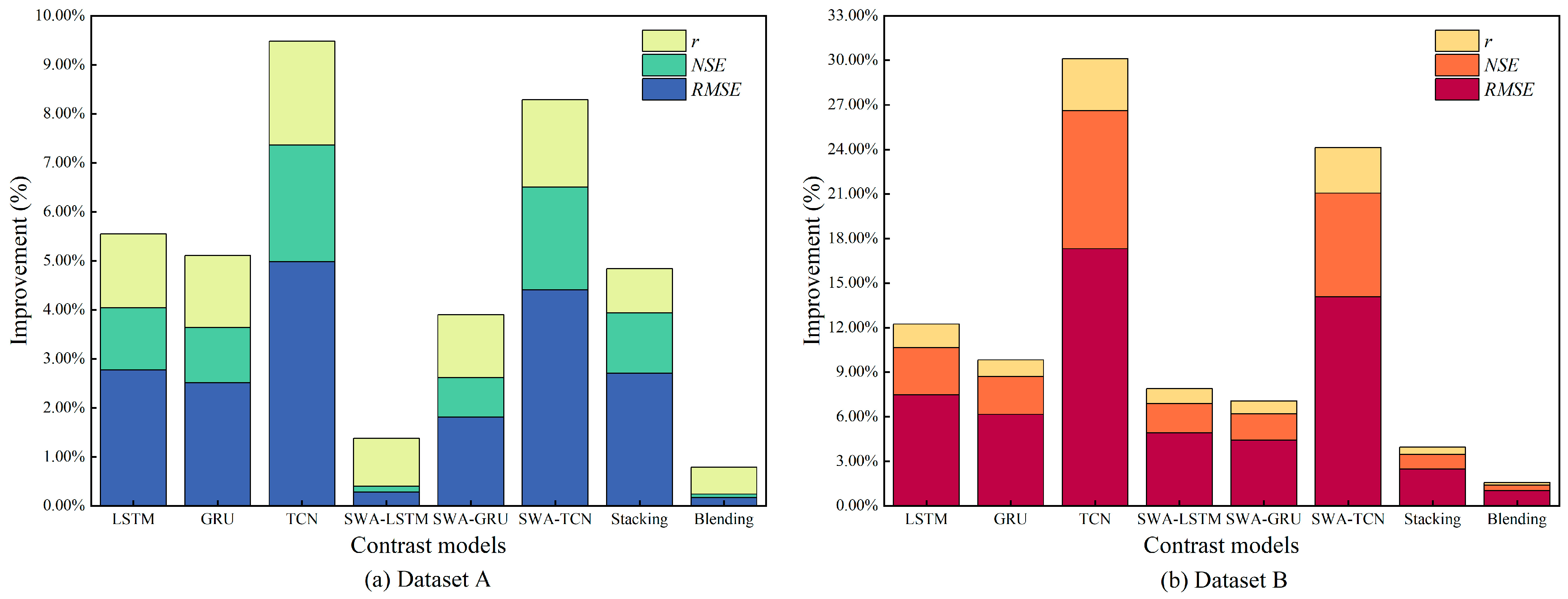
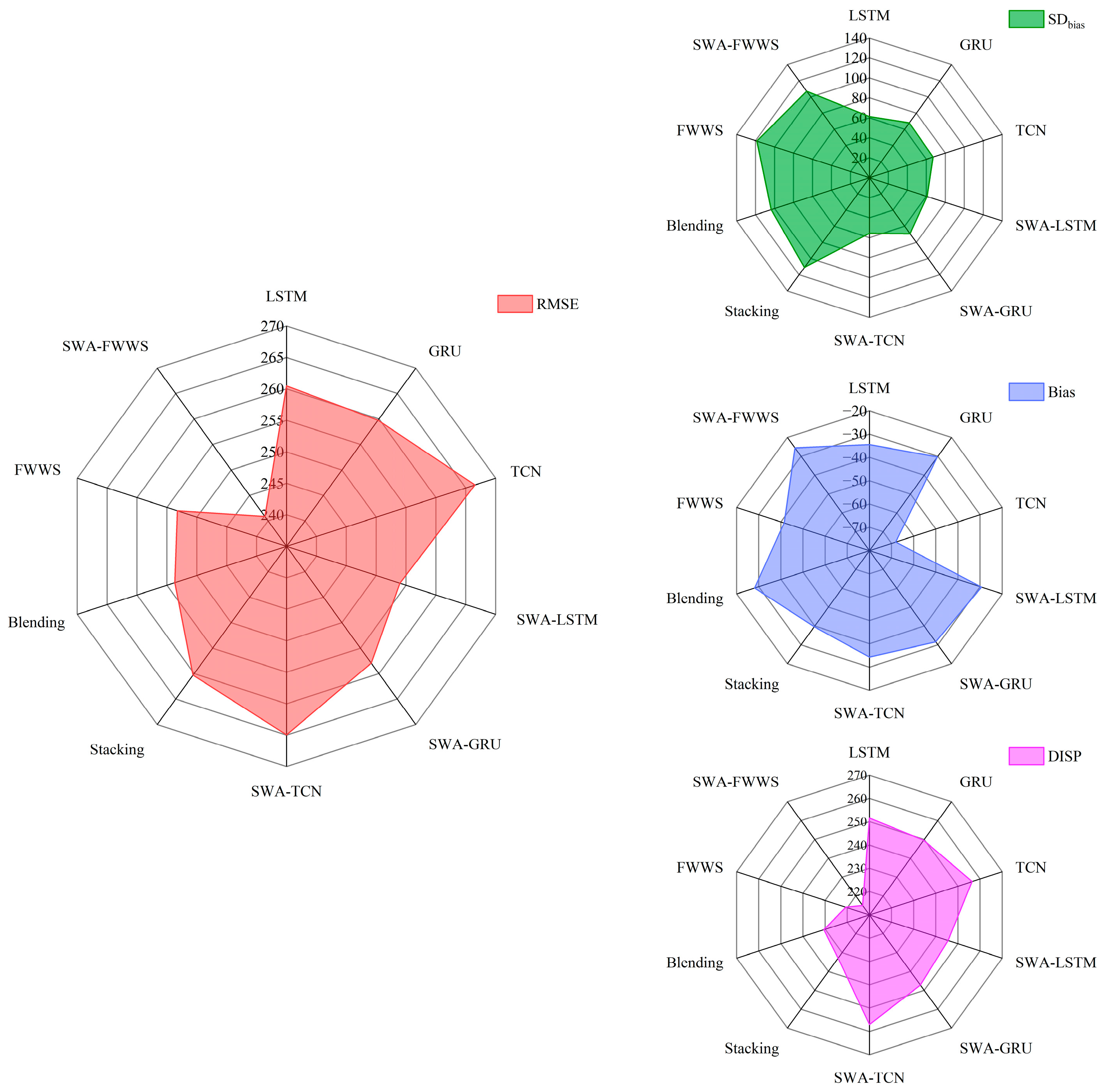
| Models | RMSE (m3/s) | NSE | r |
|---|---|---|---|
| LSTM | 260.4761 | 0.8114 | 0.9026 |
| GRU | 259.7689 | 0.8125 | 0.9029 |
| TCN | 266.5296 | 0.8026 | 0.8972 |
| SWA–LSTM | 253.9630 | 0.8207 | 0.9073 |
| SWA–GRU | 257.9381 | 0.8151 | 0.9046 |
| SWA–TCN | 264.9530 | 0.8049 | 0.9001 |
| Stacking | 260.3061 | 0.8117 | 0.9080 |
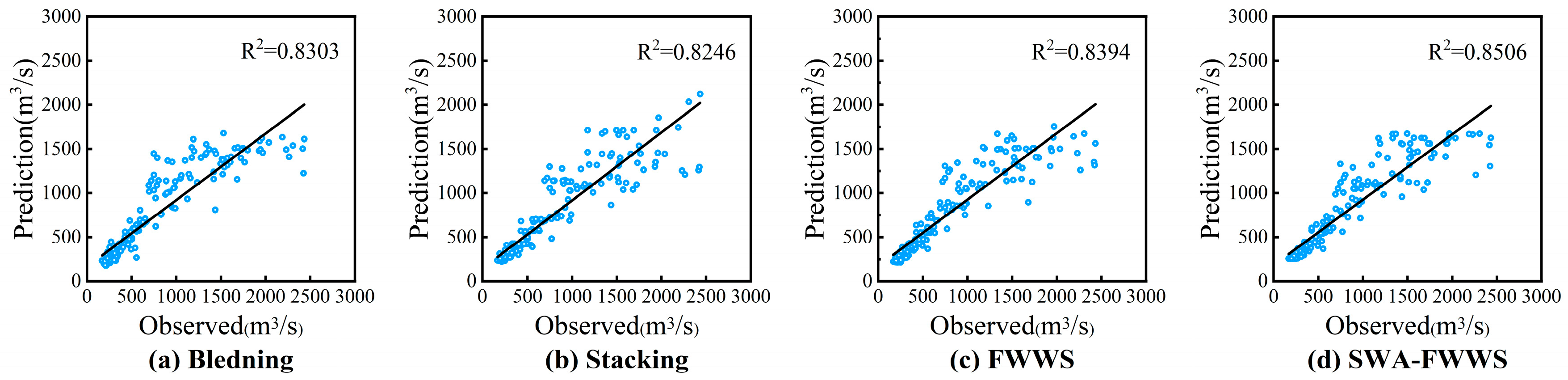
| Blending | 253.6829 | 0.8211 | 0.9112 |
| FWWS | 253.2615 | 0.8217 | 0.9162 |
| SWA–FWWS | 240.8563 | 0.8388 | 0.9223 |
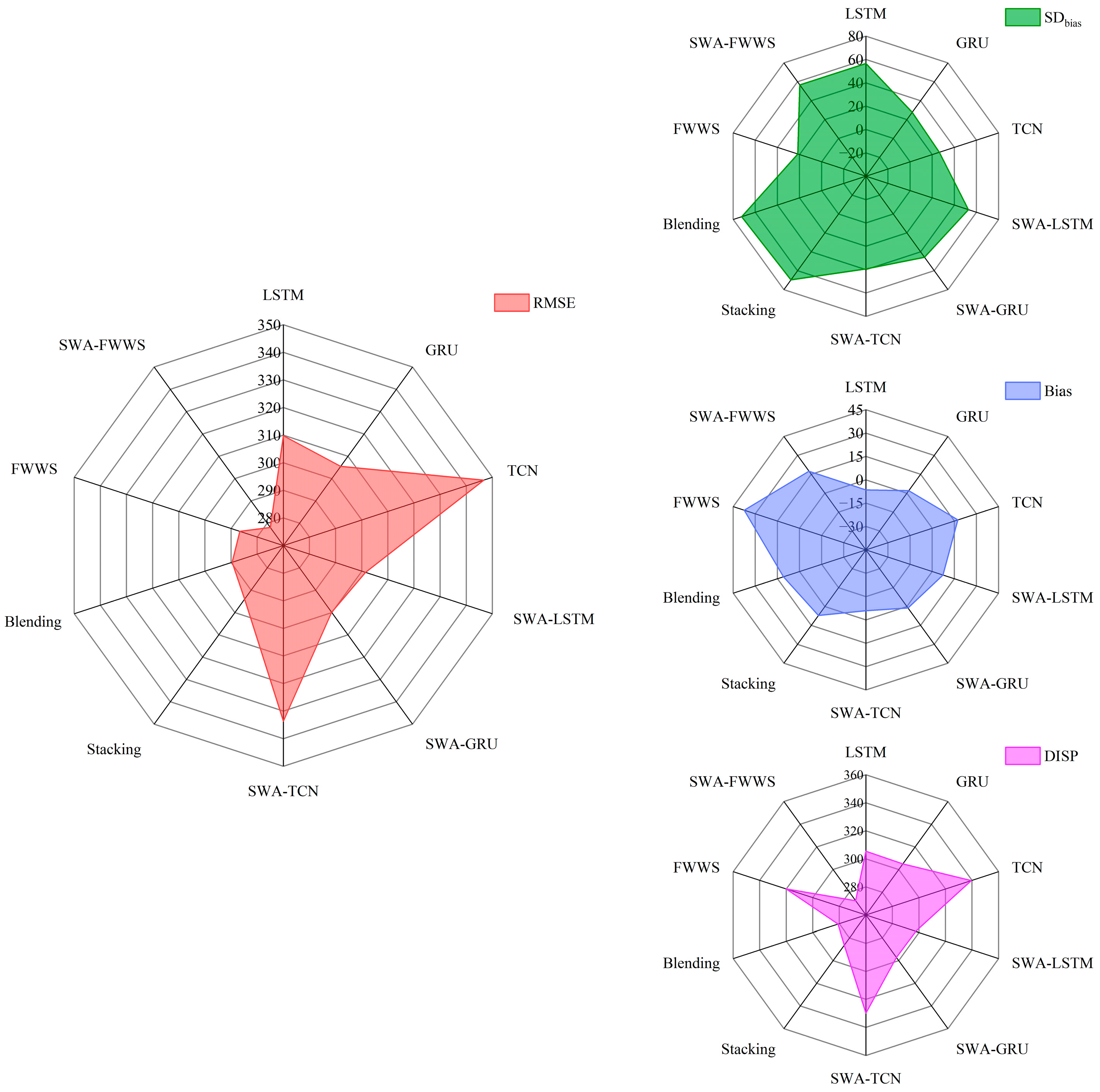
| Models | RMSE (m3/s) | NSE | r |
|---|---|---|---|
| LSTM | 309.7994 | 0.8186 | 0.9050 |
| GRU | 305.4442 | 0.8236 | 0.9091 |
| TCN | 346.6903 | 0.7728 | 0.8883 |
| SWA–LSTM | 301.4458 | 0.8282 | 0.9103 |
| SWA–GRU | 299.8995 | 0.8300 | 0.9114 |
| SWA–TCN | 333.6082 | 0.7896 | 0.8919 |
| Stacking | 293.9659 | 0.8366 | 0.9148 |
| Blending | 289.5780 | 0.8415 | 0.9176 |
| FWWS | 286.6497 | 0.8447 | 0.9193 |
| SWA–FWWS | 278.0754 | 0.8538 | 0.9243 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, K.; Sun, X.; Chen, K.; Mo, L.; Xiao, W.; Liu, S. Monthly Runoff Prediction Based on Stochastic Weighted Averaging-Improved Stacking Ensemble Model. Water 2024, 16, 3580. https://doi.org/10.3390/w16243580
Fu K, Sun X, Chen K, Mo L, Xiao W, Liu S. Monthly Runoff Prediction Based on Stochastic Weighted Averaging-Improved Stacking Ensemble Model. Water. 2024; 16(24):3580. https://doi.org/10.3390/w16243580
Chicago/Turabian StyleFu, Kaixiang, Xutong Sun, Kai Chen, Li Mo, Wenjing Xiao, and Shuangquan Liu. 2024. "Monthly Runoff Prediction Based on Stochastic Weighted Averaging-Improved Stacking Ensemble Model" Water 16, no. 24: 3580. https://doi.org/10.3390/w16243580
APA StyleFu, K., Sun, X., Chen, K., Mo, L., Xiao, W., & Liu, S. (2024). Monthly Runoff Prediction Based on Stochastic Weighted Averaging-Improved Stacking Ensemble Model. Water, 16(24), 3580. https://doi.org/10.3390/w16243580






