Flood Control Optimization Scheduling of Cascade Reservoirs in the Middle Reaches of the Gan River Based on ECDE Algorithm
Abstract
1. Introduction
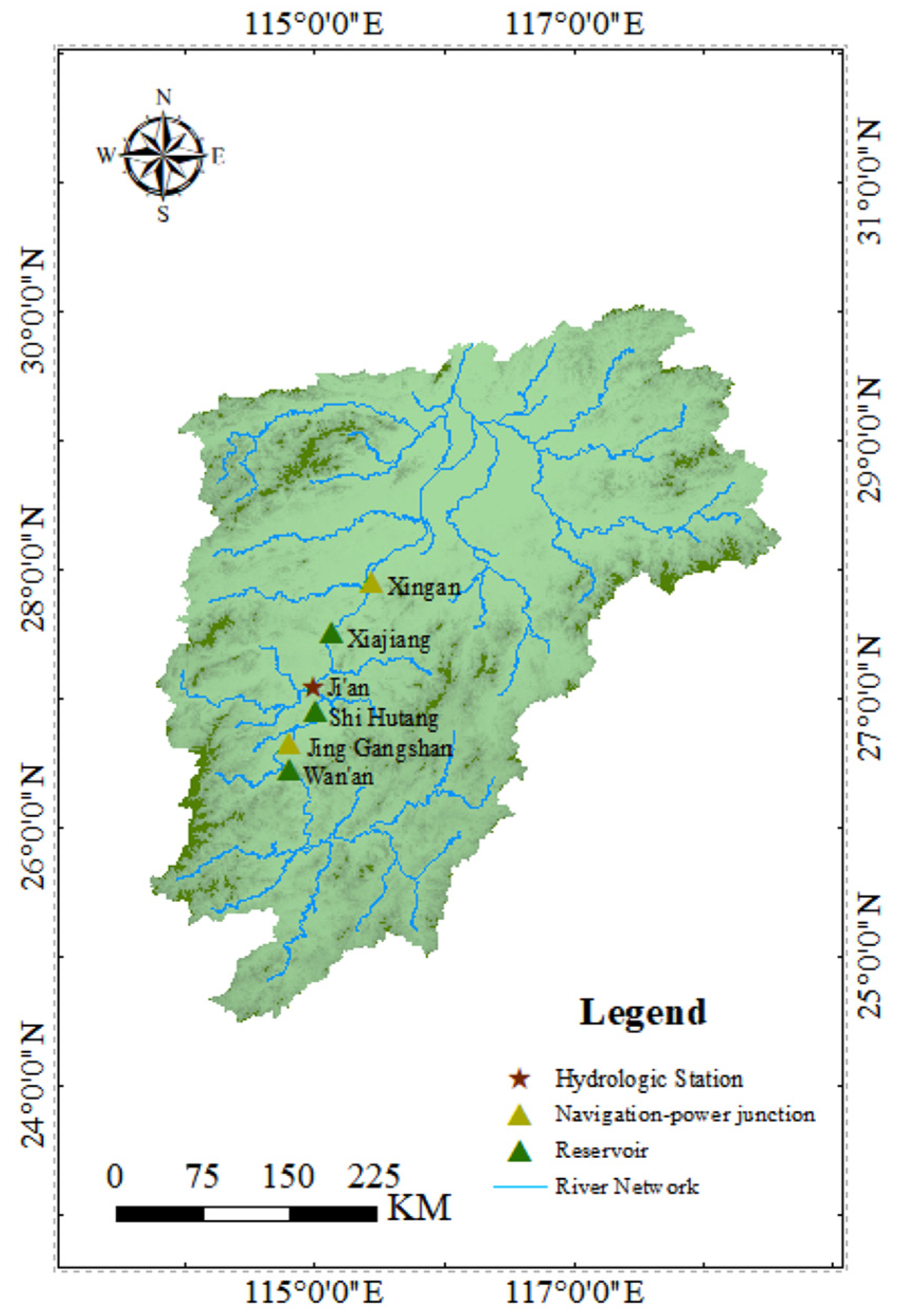
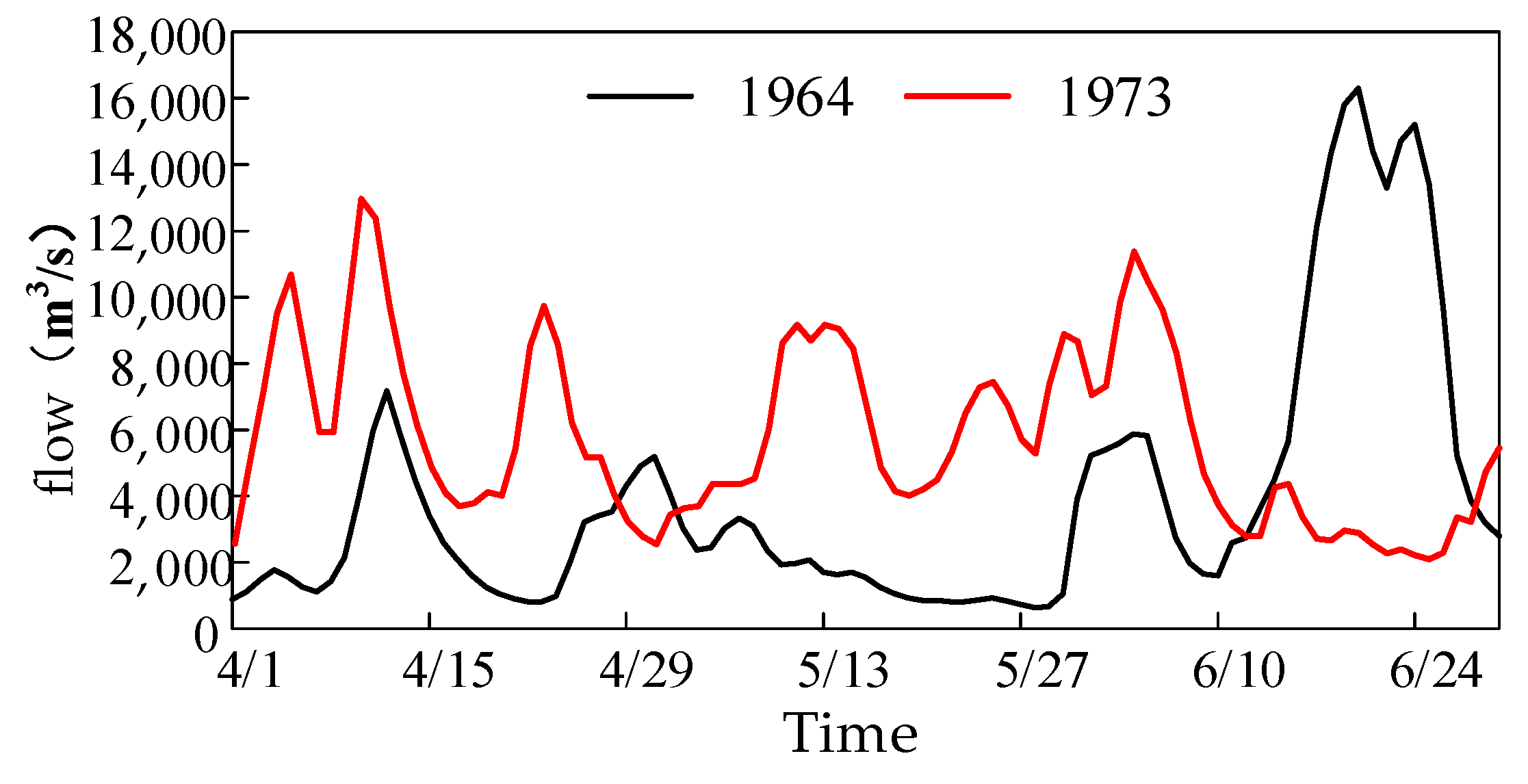
2. Research Area and Data
3. Optimization and Operation Model for Flood Control of Cascade Reservoirs in the Middle Reaches of Ganjiang River
3.1. Objective Function
3.2. Constraints
- Water balance constraint.
- Water level upper and lower bound constraint.
- Water level variation constraint.
- Flood control point discharge constraint.
- Outflow constraint.where represents the serial number of reservoir, with w, s, and x from upstream to downstream, representing Wan’an Reservoir, Shihutang Reservoir, and Xiajiang Reservoir, respectively. and , respectively, represent initial and final storage of the m-th reservoir at period . , , and , respectively, represent the inflow, outflow, and local inflow of the m-th reservoir at period . and , respectively, represent the water level and maximum water level variation of the m-th reservoir at period . and , respectively, represent the lowest water level and highest water level of the m-th reservoir at period . and , respectively, represent the minimum outflow and maximum outflow of the m-th reservoir at period . In addition, the Muskingum method was used to calculate the river flood routing; detailed information can be found in the literature [31,32,33].
4. The Details of ECDE
4.1. Classical Differential Evolution Algorithm
4.2. Adaptive Differential Mutation and Elite Conservative Strategy
4.2.1. Elite Conservative Strategy
4.2.2. Adaptive Differential Mutation Strategy
- “rand/2”:
- “current-to-rand/1”:
- “current-to-rand/2”:
- “current-to-pbest/1”:where is the number of population generations; is the -th solution or individual in the -th generation population of differential evolution; is the -th mutated individual generated by the -th generation parent through the mutation strategy; is the individual with the best performance in the fitness evaluation index of the -th generation population; is randomly selected from the top individuals with better fitness evaluation in the -th generation population, where the control parameter is a random number that obeys a uniform distribution within the range of . is the individual randomly selected from the -th generation population and the external archive set after mixing; in the random selection process, the index numbers , , ~ of the individuals are required to be different, in which the index numbers ~ of the individuals represent randomly selected in the range of .
4.3. Crossover and Selection
5. Numerical Experiment
6. Case Study
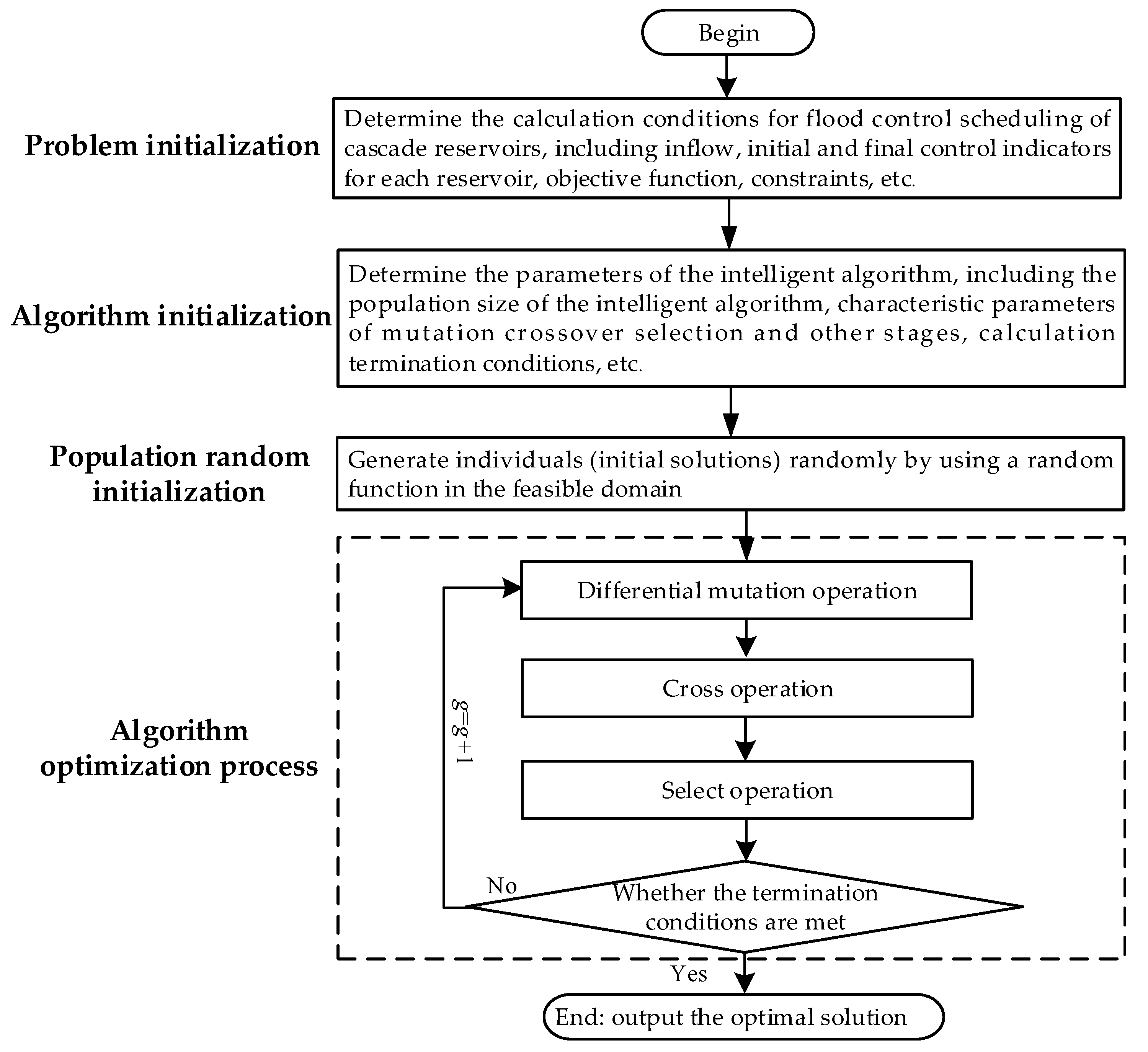
6.1. Steps of DE Solving the Flood Control Scheduling Problem of Cascade Reservoirs
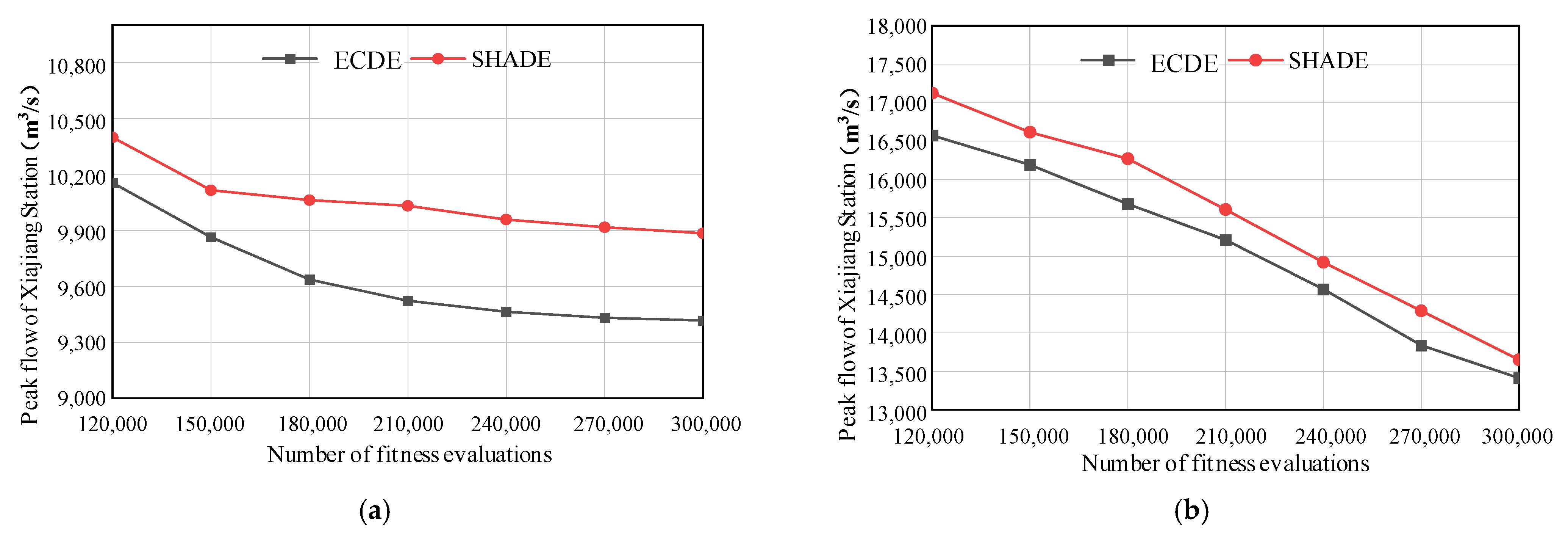
6.2. Case Study 1: Comparison of Different Algorithms
6.3. Case Study 2: Multi-Objective Flood Control Optimization Scheduling of Cascade Reservoirs
7. Discussion
8. Conclusions
- (1)
- To address the premature convergence of the greedy differential mutation in the differential evolution algorithm, an elite population conservative strategy and a general population adaptive differential mutation strategy were proposed. This strengthened individual diversity in population evolution, leading to the development of ECDE.
- (2)
- Numerical experiments with 10 test functions showed that the ECDE stably converged to the optimum for seven functions and performed the best among SHADE, SaDE, DE, GA, and PSO in terms of convergence accuracy and stability.
- (3)
- In the engineering case study of the single-objective flood-control scheduling of cascade reservoirs, only ECDE, SHADE, and GA found feasible solutions, with ECDE performing optimally in terms of the mean, standard deviation, and range of results.
- (4)
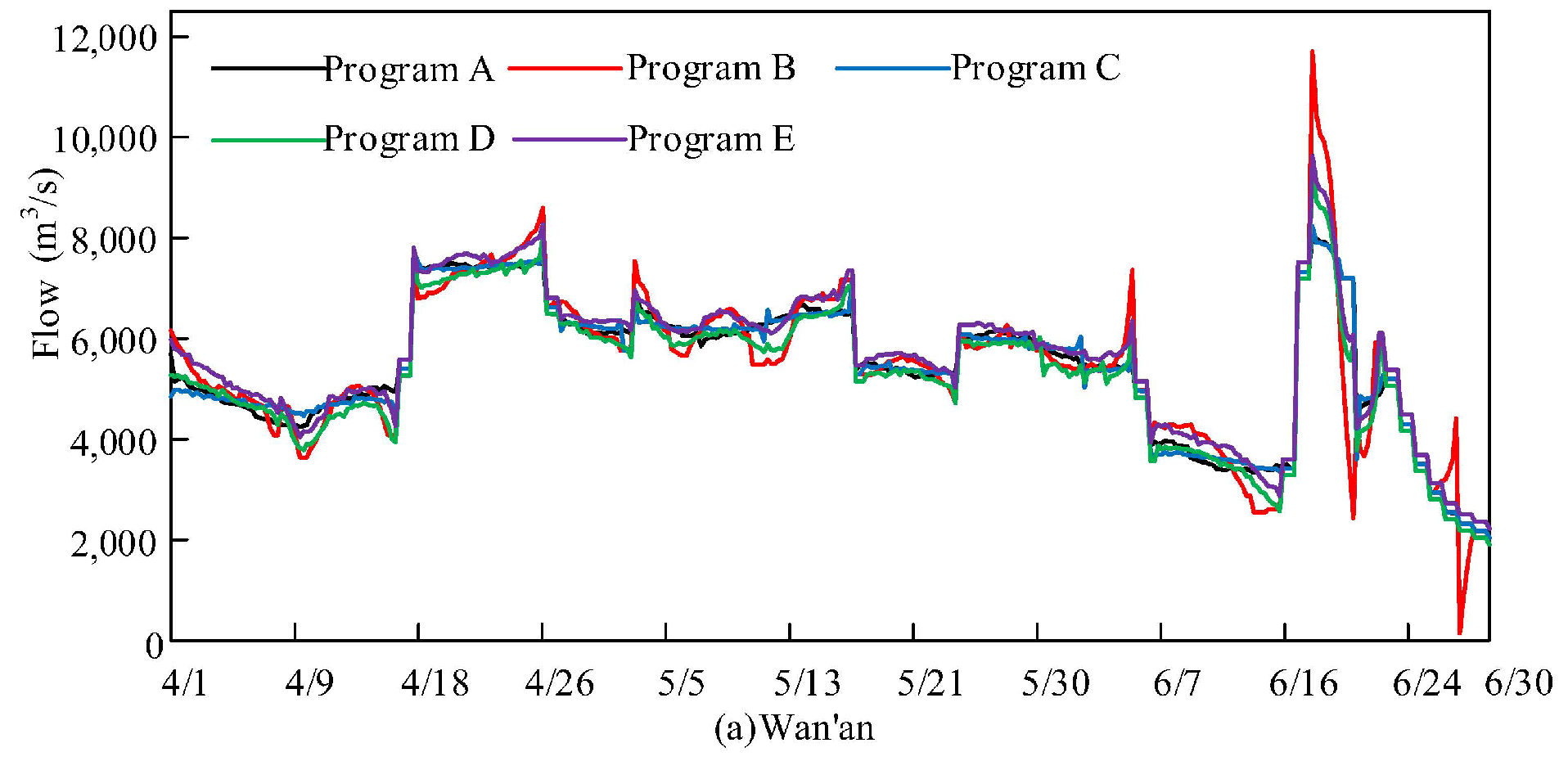
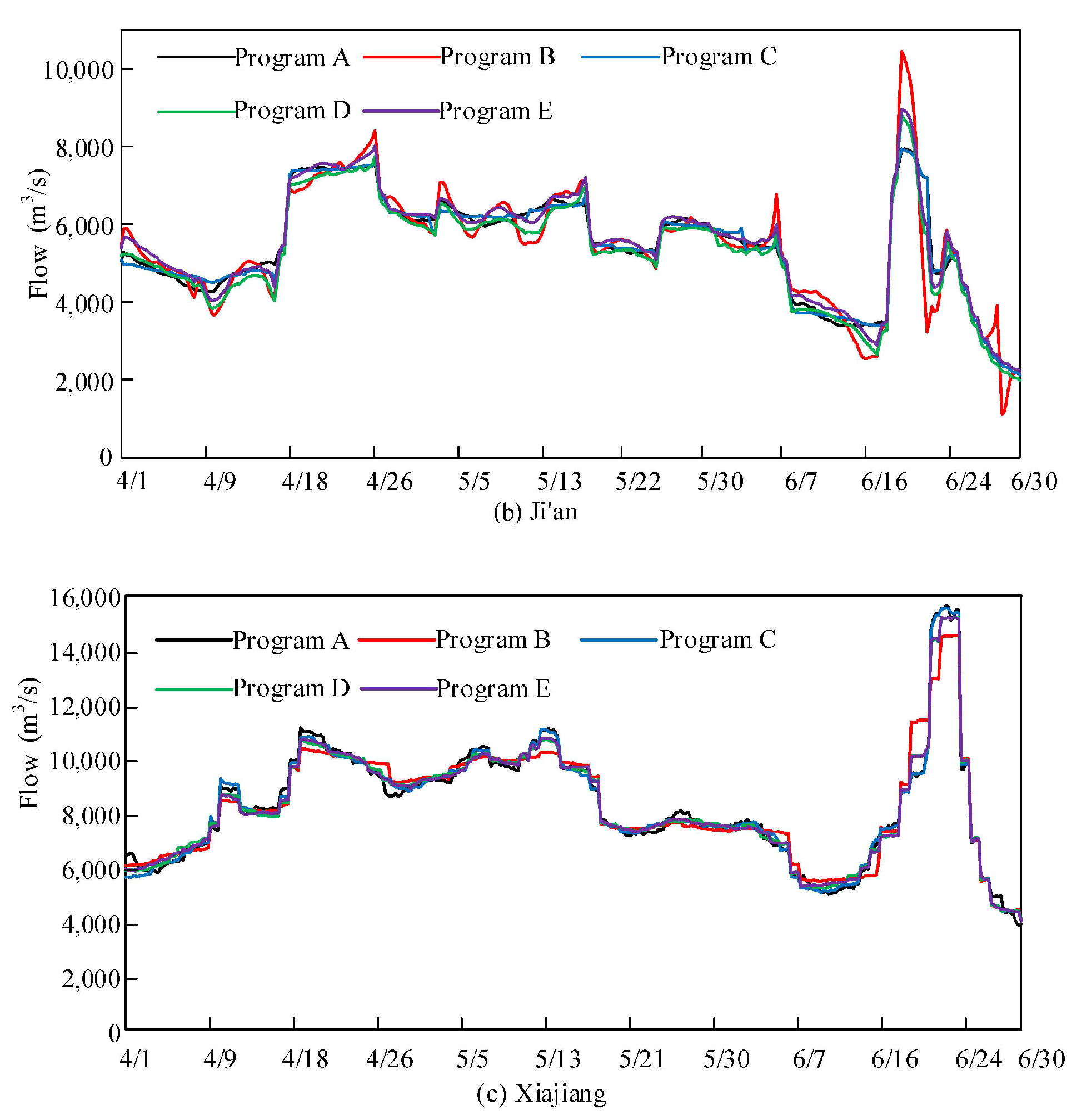
- Using ECDE for the multi-objective flood control optimization of cascade reservoirs revealed that in multi-objective optimization, weight settings should follow upstream priority or equilibrium programs; downstream priority programs lead to poor upstream flood control performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mohanavelu, A.; Soundharajan, B.S.; Kisi, O. Modeling Multi-Objective Pareto-Optimal Reservoir Operation Policies Using State-of-the-Art Modeling Techniques. Water Resour. Manag. 2022, 36, 3107–3128. [Google Scholar] [CrossRef]
- He, Z.; Wang, C.; Wang, Y.; Wei, B.; Zhou, J.; Zhang, H.; Qin, H. Dynamic Programming with Successive Approximation and Relaxation Strategy for Long-Term Joint Power Generation Scheduling of Large-Scale Hydropower Station Group. Energy 2021, 222, 119960. [Google Scholar] [CrossRef]
- Wang, W.; Jia, B.; Simonovic, S.P.; Wu, S.; Fan, Z.; Ren, L. Comparison of Representative Heuristic Algorithms for Multi-Objective Reservoir Optimal Operation. Water Resour. Manag. 2021, 35, 2741–2762. [Google Scholar] [CrossRef]
- Moeini, R.; Soltani-nezhad, M.; Daei, M. Constrained Gravitational Search Algorithm for Large Scale Reservoir Operation Optimization Problem. Eng. Appl. Artif. Intell. 2017, 62, 222–233. [Google Scholar] [CrossRef]
- Foued, B.A.; Sameh, M. Application of Goal Programming in a Multi-Objective Reservoir Operation Model in Tunisia. Eur. J. Oper. Res. 2001, 133, 352–361. [Google Scholar] [CrossRef]
- Sharifi, M.R.; Akbarifard, S.; Madadi, M.R.; Akbarifard, H.; Qaderi, K. Comprehensive Assessment of 20 State-of-the-Art Multi-Objective Meta-Heuristic Algorithms for Multi-Reservoir System Operation. J. Hydrol. 2022, 613, 128469. [Google Scholar] [CrossRef]
- Hu, M.; Huang, G.H.; Sun, W.; Li, Y.; Ding, X.; An, C.; Zhang, X.; Li, T. Multi-Objective Ecological Reservoir Operation Based on Water Quality Response Models and Improved Genetic Algorithm: A Case Study in Three Gorges Reservoir, China. Eng. Appl. Artif. Intell. 2014, 36, 332–346. [Google Scholar] [CrossRef]
- Kong, Y.; Mei, Y.; Wang, X.; Ben, Y. Solution Selection from a Pareto Optimal Set of Multi-Objective Reservoir Operation via Clustering Operation Processes and Objective Values. Water 2021, 13, 1046. [Google Scholar] [CrossRef]
- Xueshan, A.; Jie, D.; Baiyin, Y.; Jiajun, G.; Senlin, C.; Zhengyu, M. Research on Multi-Objective Decision Making of Hydropower Station Group Based on CRITIC-TOPSIS Method. Smart Innov. Syst. Technol. 2023, 260, 95–107. [Google Scholar] [CrossRef]
- Needham, J.T.; Watkins Jr, D.W.; Lund, J.R.; Nanda, S.K. Linear Programming for Flood Control in the Iowa and Des Moines Rivers. J. Water Resour. Plan. Manag. 2000, 126, 118–127. [Google Scholar] [CrossRef]
- Chen, J.; Qi, X.; Qiu, G.; Chen, L. Improved Progressive Optimality Algorithm and Its Application to Determination of Optimal Release Trajectory of Long-Term Power Generation Operation of Cascade Reservoirs. Adv. Water Resour. 2022, 166, 104253. [Google Scholar] [CrossRef]
- Fayaed, S.S.; Fiyadh, S.S.; Khai, W.J.; Ahmed, A.N.; Afan, H.A.; Ibrahim, R.K.; Fai, C.M.; Koting, S.; Mohd, N.S.; Binti Jaafar, W.Z.; et al. Improving Dam and Reservoir Operation Rules Using Stochastic Dynamic Programming and Artificial Neural Network Integration Model. Sustainability 2019, 11, 5367. [Google Scholar] [CrossRef]
- Feng, Z.; Niu, W.; Cheng, C.; Wu, X. Peak Operation of Hydropower System with Parallel Technique and Progressive Optimality Algorithm. Int. J. Electr. Power Energy Syst. 2018, 94, 267–275. [Google Scholar] [CrossRef]
- Bai, T.; Wu, L.; Chang, J.X.; Huang, Q. Multi-Objective Optimal Operation Model of Cascade Reservoirs and Its Application on Water and Sediment Regulation. Water Resour. Manag. 2015, 29, 2751–2770. [Google Scholar] [CrossRef]
- Marcelino, C.G.; Leite, G.M.C.; Delgado, C.A.D.M.; de Oliveira, L.B.; Wanner, E.F.; Jiménez-Fernández, S.; Salcedo-Sanz, S. An Efficient Multi-Objective Evolutionary Approach for Solving the Operation of Multi-Reservoir System Scheduling in Hydro-Power Plants. Expert. Syst. Appl. 2021, 185, 115638. [Google Scholar] [CrossRef]
- Chen, H.T.; Wang, W.C.; Chen, X.N.; Qiu, L. Multi-Objective Reservoir Operation Using Particle Swarm Optimization with Adaptive Random Inertia Weights. Water Sci. Eng. 2020, 13, 136–144. [Google Scholar] [CrossRef]
- Mansouri, M.; Safavi, H.R.; Rezaei, F. An Improved MOPSO Algorithm for Multi-Objective Optimization of Reservoir Operation under Climate Change. Environ. Monit. Assess. 2022, 194, 261. [Google Scholar] [CrossRef]
- Kumar, V.; Sharma, K.V.; Yadav, S.M.; Deshmukh, A. Self-Adaptive Metaheuristic Optimization Technique for Multi-Objective Reservoir Operation. Aqua Water Infrastruct. Ecosyst. Soc. 2023, 72, 1582–1606. [Google Scholar] [CrossRef]
- Dash, S.S.; Sahoo, B.; Raghuwanshi, N.S. An Adaptive Multi-Objective Reservoir Operation Scheme for Improved Supply-Demand Management. J. Hydrol. 2022, 615, 128718. [Google Scholar] [CrossRef]
- Yu, X.; Xu, Y.P.; Gu, H.; Guo, Y. Multi-Objective Robust Optimization of Reservoir Operation for Real-Time Flood Control under Forecasting Uncertainty. J. Hydrol. 2023, 620, 129421. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Qin, H.; Zhou, J.Z.; Wang, G.Q.; Zhang, Y.C. Multi-Objective Optimization of Reservoir Flood Dispatch Based on Multi-Objective Differential Evolution Algorithm. Shuili Xuebao/J. Hydraul. Eng. 2009, 40, 513–519. [Google Scholar]
- He, Z.; Zhou, J.; Qin, H.; Jia, B.; Lu, C. Long-Term Joint Scheduling of Hydropower Station Group in the Upper Reaches of the Yangtze River Using Partition Parameter Adaptation Differential Evolution. Eng. Appl. Artif. Intell. 2019, 81, 1–13. [Google Scholar] [CrossRef]
- Bilal; Pant, M.; Rani, D. Large Scale Reservoir Operation through Integrated Meta-Heuristic Approach. Memet. Comput. 2021, 13, 359–382. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Kheyrandish, A.; Jamei, M.; Gharabaghi, B. Optimizing Operating Rules for Multi-Reservoir Hydropower Generation Systems: An Adaptive Hybrid Differential Evolution Algorithm. Renew. Energy 2021, 167, 774–790. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, Z.; Zhang, Q. Differential Evolution With Composite Trial Vector Generation Strategies and Control Parameters. IEEE Trans. Evol. Comput. 2011, 15, 55–66. [Google Scholar] [CrossRef]
- Brest, J.; Greiner, S.; Boskovic, B.; Mernik, M.; Zumer, V. Self-Adapting Control Parameters in Differential Evolution: A Comparative Study on Numerical Benchmark Problems. IEEE Trans. Evol. Comput. 2006, 10, 646–657. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive Differential Evolution With Optional External Archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A. Success-History Based Parameter Adaptation for Differential Evolution. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 71–78. [Google Scholar]
- Zha, G.; Zhou, J.Z.; Yang, X.; Fang, W.; Dai, L.; Wang, Q.N.; Ding, X.L. Modeling and Solving of Joint Flood Control Operation of Large-Scale Reservoirs: A Case Study in the Middle and Upper Yangtze River in China. Water 2021, 13, 41. [Google Scholar] [CrossRef]
- Okkan, U.; Kirdemir, U. Locally Tuned Hybridized Particle Swarm Optimization for the Calibration of the Nonlinear Muskingum Flood Routing Model. J. Water Clim. Change 2020, 11, 343–358. [Google Scholar] [CrossRef]
- Akbari, R.; Hessami-Kermani, M.R. A New Method for Dividing Flood Period in the Variable-Parameter Muskingum Models. Hydrol. Res. 2022, 53, 241–257. [Google Scholar] [CrossRef]
- Niazkar, M.; Zakwan, M. Chapter 24—Parameter Estimation of a New Four-Parameter Muskingum Flood Routing Model. In Computers in Earth and Environmental Sciences; Pourghasemi, H.R., Ed.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 337–349. ISBN 978-0-323-89861-4. [Google Scholar]
- Gong, W.; Fialho, Á.; Cai, Z.; Li, H. Adaptive Strategy Selection in Differential Evolution for Numerical Optimization: An Empirical Study. Inf. Sci. 2011, 181, 5364–5386. [Google Scholar] [CrossRef]
- Qin, A.K.; Suganthan, P.N. Self-Adaptive Differential Evolution Algorithm for Numerical Optimization. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005; IEEE CEC 2005. Proceedings. Volume 2. [Google Scholar]
- Wang, Y.; Liu, Z.-Z.; Li, J.; Li, H.-X.; Wang, J. On the Selection of Solutions for Mutation in Differential Evolution. Front. Comput. Sci. 2018, 12, 297–315. [Google Scholar] [CrossRef]
- Piotrowski, A.P.; Napiorkowski, J.J. Step-by-Step Improvement of JADE and SHADE-Based Algorithms: Success or Failure? Swarm Evol. Comput. 2018, 43, 88–108. [Google Scholar] [CrossRef]
- Li, S.; He, Z.; Huang, W.; Wei, B.; Yan, F.; Fu, J.; Xiong, B. Study on the Constraint Handling Method for High-Dimensional Optimization of Cascade Reservoirs. J. Clean. Prod. 2024, 449, 141784. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Y.; Song, S.; Li, Y.; Hu, H.; Feng, J.; Xu, S.; Yang, K. Multi-Objective Operation-Decision-Making-Risk Propagation Analysis for Cascade Reservoirs Affected by Future Streamflow Process Variations. J. Hydrol. 2023, 620, 129518. [Google Scholar] [CrossRef]
- He, Z.; Zhou, J.; Qin, H.; Jia, B.; Feng, K. A Fast Water Level Optimal Control Method Based on Two Stage Analysis for Long Term Power Generation Scheduling of Hydropower Station. Energy 2020, 210, 118531. [Google Scholar] [CrossRef]


| Hydraulic Engineering | Control Basin Area (km2) | Normal Storage Level (m) | Stagnant Water Level (m) | Flood Limit (m) | High Water Mark for Flood Control (m) | Total Capacity (×108 m3) |
|---|---|---|---|---|---|---|
| Wan’an | 36,900 | 96 | 85 | 85 | 93.6 | 22.1 |
| Shihutang | 43,770 | 56.5 | 56.2 | 56.5 | 56.5 | 7.43 |
| Xiajiang | 62,710 | 46 | 44 | 45 | 49 | 11.87 |
| Benchmark Function | Name | Domain | Optimal Value |
|---|---|---|---|
| Sphere | 0 | ||
| Schwefel (2.2) | 0 | ||
| Schwefel (1.2) | 0 | ||
| Rosenbrock | 0 | ||
| Step | 0 | ||
| Quartic | 0 | ||
| Schwefel (2.26) | −418.9829×D | ||
| Rastrigin | 0 | ||
| Ackley | 0 | ||
| Griewank | 0 |
| ECDE | SHADE | SaDE | DE | GA | PSO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimum Value | Number of Successes | Optimum Value | Number of Successes | Optimum Value | Number of Successes | Optimum Value | Number of Successes | Optimum Value | Number of Successes | Optimum Value | Number of Successes | |
| Average Value | Standard Deviation | Average Value | Standard Deviation | Average Value | Standard Deviation | Average Value | Standard Deviation | Average Value | Standard Deviation | Average Value | Standard Deviation | |
| f1 | 0.00 | 100 | 0.00 | 100 | 0.00 | 100 | 3.97 × 10−1 | 0 | 7.68 × 10−6 | 0 | 4.58 × 10−5 | 0 |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.40 × 10−1 | 1.24 × 10−1 | 3.00 × 103 | 4.58 × 103 | 1.14 × 10−4 | 6.27 × 10−5 | |
| f2 | 0.00 | 100 | 1.11 × 10−85 | 0 | 5.56 × 10−62 | 0 | 6.27 × 10−1 | 0 | 6.00 × 101 | 0 | 2.03 × 10−5 | 0 |
| 0.00 | 0.00 | 6.52 × 10−82 | 1.06 × 10−81 | 6.11 × 10−59 | 8.99 × 10−59 | 8.85 × 10−1 | 1.55 × 10−1 | 9.30 × 101 | 1.84 × 101 | 4.21 × 10−5 | 2.12 × 10−5 | |
| f3 | 0.00 | 100 | 0.00 | 100 | 0.00 | 100 | 5.47 × 103 | 0 | 8.55 × 108 | 0 | 3.98 × 10−4 | 0 |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 8.42 × 103 | 1.80 × 103 | 5.74 × 109 | 5.37 × 109 | 1.90 × 10−3 | 2.69 × 10−3 | |
| f4 | 1.19 × 10−21 | 0 | 0.00 | 10 | 1.05 × 10−12 | 0 | 1.41 × 104 | 0 | 4.37 × 102 | 0 | 1.66 × 102 | 0 |
| 2.83 × 10−19 | 5.42 × 10−19 | 1.39 | 1.90 | 1.51 × 101 | 2.46 × 101 | 2.35 × 104 | 6.81 × 103 | 4.79 × 102 | 2.33 × 101 | 1.62 × 103 | 3.02 × 103 | |
| f5 | 0.00 | 100 | 1.00 | 0 | 2.40 × 101 | 0 | 4.00 | 0 | 8.00 | 0 | 0 | 7 |
| 0.00 | 0.00 | 4.55 | 3.42 | 1.58 × 102 | 1.57 × 102 | 5.80 | 1.33 | 4.02 × 103 | 6.63 × 103 | 2.68 × 101 | 7.78 × 101 | |
| f6 | 0.00 | 100 | 0.00 | 100 | 0.00 | 100 | 2.72 × 10−3 | 0 | 3.23 × 10−5 | 0 | 1.74 × 10−9 | 0 |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.71 × 10−3 | 1.58 × 10−3 | 1.79 × 101 | 3.72 × 101 | 1.99 × 10−5 | 4.86 × 10−5 | |
| f7 | −4.18 × 104 | 100 | −4.18 × 104 | 0 | −3.56 × 104 | 0 | −1.87 × 104 | 100 | −3.01 × 104 | 0 | −3.02 × 104 | 0 |
| −4.18 × 104 | 6.90 × 10−12 | −4.18 × 104 | 4.50 × 10−13 | −3.37 × 104 | 9.98 × 102 | −1.76 × 104 | 4.49 × 102 | −2.92 × 104 | 5.72 × 102 | −2.82 × 104 | 1.16 × 103 | |
| f8 | 0.00 | 100 | 0.00 | 35 | 1.41 × 102 | 0 | 8.82 × 102 | 0 | 1.18 × 103 | 0 | 6.96 × 101 | 0 |
| 0.00 | 0.00 | 1.59 × 10−15 | 1.24 × 10−15 | 1.88 × 102 | 2.99 × 101 | 8.86 × 102 | 2.33 × 101 | 1.24 × 103 | 5.63 × 101 | 2.71 × 102 | 1.37 × 102 | |
| f9 | −3.11 × 10−15 | 0 | 1.83 × 10−14 | 0 | 1.64 | 0 | 1.56 × 10−1 | 0 | 2.06 × 101 | 0 | 6.04 × 10−4 | 0 |
| −3.11 × 10−15 | 0.00 | 1.05 | 5.64 × 10−1 | 2.47 | 5.99 × 10−1 | 2.11 × 10−1 | 3.34 × 10−2 | 2.06 × 101 | 1.93 × 10−2 | 1.83 × 10−3 | 1.38 × 10−3 | |
| f10 | 0.00 | 100 | 0.00 | 41 | 2.22 × 10−16 | 54 | 2.08 × 10−1 | 0 | 1.32 × 10−2 | 0 | 5.48 × 10−7 | 0 |
| 0.00 | 0.00 | 2.58 × 10−3 | 6.00 × 10−3 | 2.31 × 10−2 | 5.36 × 10−2 | 2.77 × 10−1 | 4.23 × 10−2 | 9.01 × 101 | 4.03 × 101 | 2.71 × 10−3 | 4.85 × 10−3 | |
| Historical Floods | Evaluation Index | ECDE | SHADE | SaDE | DE | GA | PSO | |
|---|---|---|---|---|---|---|---|---|
| 1964 | Peak flow of Xiajiang Station (m3/s) | Optimal solution | 13,338.18 | 13,389.61 | 15,652.26 | 20,596.06 | 13,575.43 | 18,990.64 |
| Average solution | 13,402.71 | 13,537.3 | 17,675.99 | 22,156.19 | 13,794.24 | 20,742.34 | ||
| Worst solution | 13,473.90 | 13,811.53 | 21,596.29 | 23,678.73 | 14,067.28 | 24,260.76 | ||
| Range | 135.72 | 421.91 | 5944.02 | 3082.67 | 491.85 | 5270.12 | ||
| Standard deviation | 47.15 | 194.18 | 2116.75 | 1282.47 | 191.81 | 1974.99 | ||
| Number of infeasible solutions | 0 | 0 | 41 | 50 | 0 | 50 | ||
| Average peak shaving rate | 17.80% | 16.90% | 0.00% | 0.00% | 15.37% | 0.00% | ||
| Average calculation time (min) | 8 | 8 | 8 | 11 | 55 | 9 | ||
| 1973 | Peak flow of Xiajiang Station (m3/s) | Optimal solution | 9327.44 | 9710.3 | 10,194.67 | 16,659.36 | 10,782.66 | 15,338.56 |
| Average solution | 9465.06 | 9902.18 | 11,246.98 | 17,846.62 | 10,988.65 | 17,137.19 | ||
| Worst solution | 9782.11 | 10,204.53 | 12,618.27 | 19,510.16 | 11,205.52 | 18,843.46 | ||
| Range | 454.67 | 494.23 | 2423.6 | 2850.81 | 422.85 | 3504.9 | ||
| Standard deviation | 171.39 | 179.8 | 859.52 | 1210.09 | 202.23 | 1394.73 | ||
| Number of infeasible solutions | 0 | 0 | 0 | 50 | 0 | 50 | ||
| Average peak shaving rate | 27.20% | 23.80% | 13.48% | 0.00% | 15.47% | 0.00% | ||
| Average calculation time (min) | 9 | 9 | 9 | 12 | 58 | 10 | ||
| Design Flood | Program No. | Weight | Peak Flow (m3/s) | ||||
|---|---|---|---|---|---|---|---|
| Wan’an | Ji’an | Xiajiang | Wan’an | Ji’an | Xiajiang | ||
| 1983 | Program A | 0.7 | 0.2 | 0.1 | 8032.715 | 7947.918 | 15,642.610 |
| Program B | 0.1 | 0.2 | 0.7 | 11,699.310 | 10,450.330 | 14,540.650 | |
| Program C | 0.2 | 0.7 | 0.1 | 8238.190 | 7938.804 | 15,542.910 | |
| Program D | 0.4 | 0.3 | 0.3 | 8875.509 | 8499.476 | 15,207.370 | |
| Program E | 0.3 | 0.3 | 0.4 | 9445.197 | 8874.220 | 15,206.170 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Cao, L.; Xin, X.; Wei, B.; Wen, T.; Wang, C.; Fu, J.; Xiong, B. Flood Control Optimization Scheduling of Cascade Reservoirs in the Middle Reaches of the Gan River Based on ECDE Algorithm. Water 2024, 16, 3576. https://doi.org/10.3390/w16243576
He Z, Cao L, Xin X, Wei B, Wen T, Wang C, Fu J, Xiong B. Flood Control Optimization Scheduling of Cascade Reservoirs in the Middle Reaches of the Gan River Based on ECDE Algorithm. Water. 2024; 16(24):3576. https://doi.org/10.3390/w16243576
Chicago/Turabian StyleHe, Zhongzheng, Lei Cao, Xiuyu Xin, Bowen Wei, Tianfu Wen, Chao Wang, Jisi Fu, and Bin Xiong. 2024. "Flood Control Optimization Scheduling of Cascade Reservoirs in the Middle Reaches of the Gan River Based on ECDE Algorithm" Water 16, no. 24: 3576. https://doi.org/10.3390/w16243576
APA StyleHe, Z., Cao, L., Xin, X., Wei, B., Wen, T., Wang, C., Fu, J., & Xiong, B. (2024). Flood Control Optimization Scheduling of Cascade Reservoirs in the Middle Reaches of the Gan River Based on ECDE Algorithm. Water, 16(24), 3576. https://doi.org/10.3390/w16243576






