VARS and HDMR Sensitivity Analysis of Groundwater Flow Modeling through an Alluvial Aquifer Subject to Tidal Effects
Abstract
1. Introduction
2. Materials and Methods
2.1. Methodological Framework
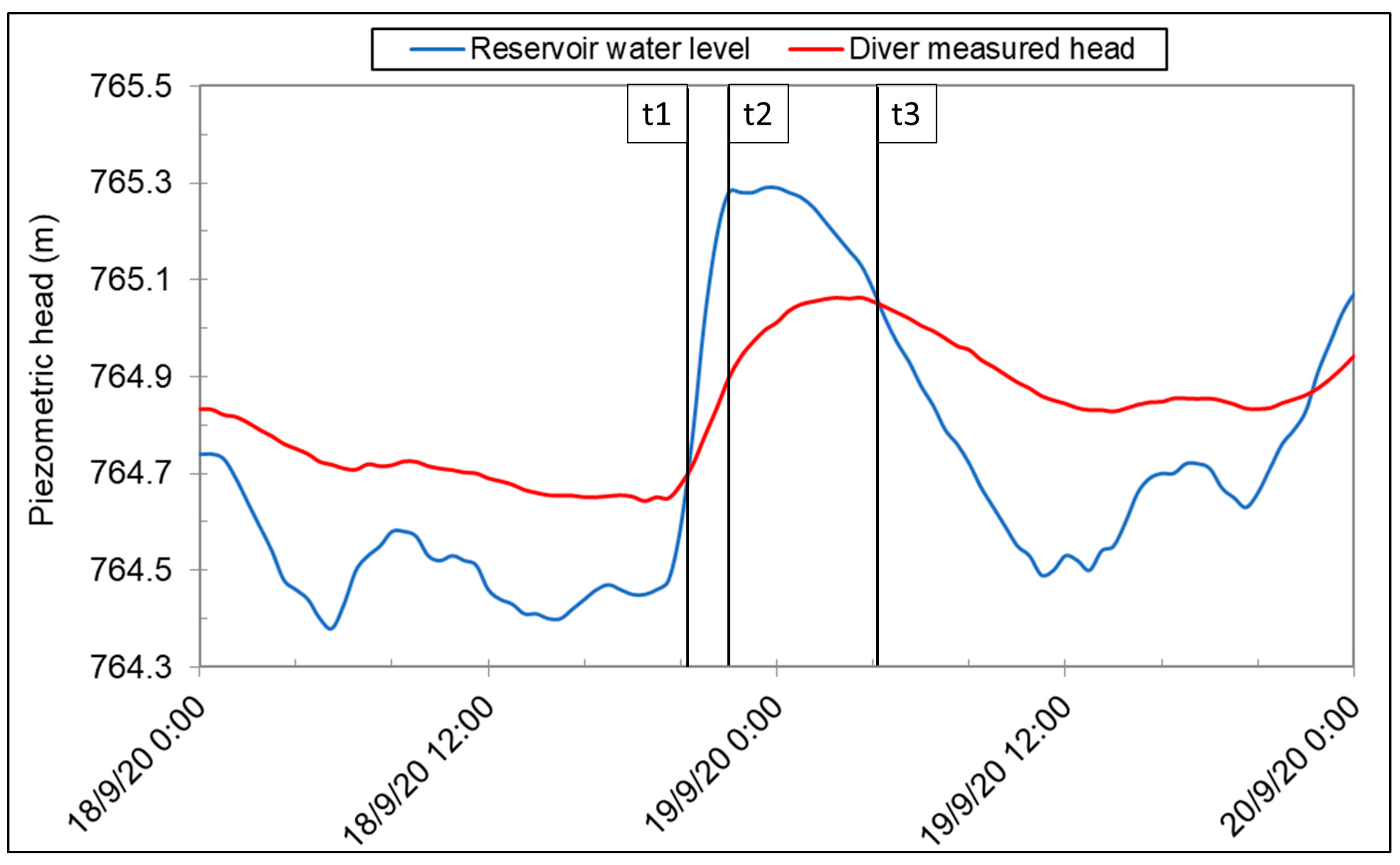
2.2. Site Description
2.3. Conceptual Model
2.4. Numerical Groundwater Flow Model
2.5. Global Sensitivity Methods
2.5.1. Graphical Methods
2.5.2. Sobol Method
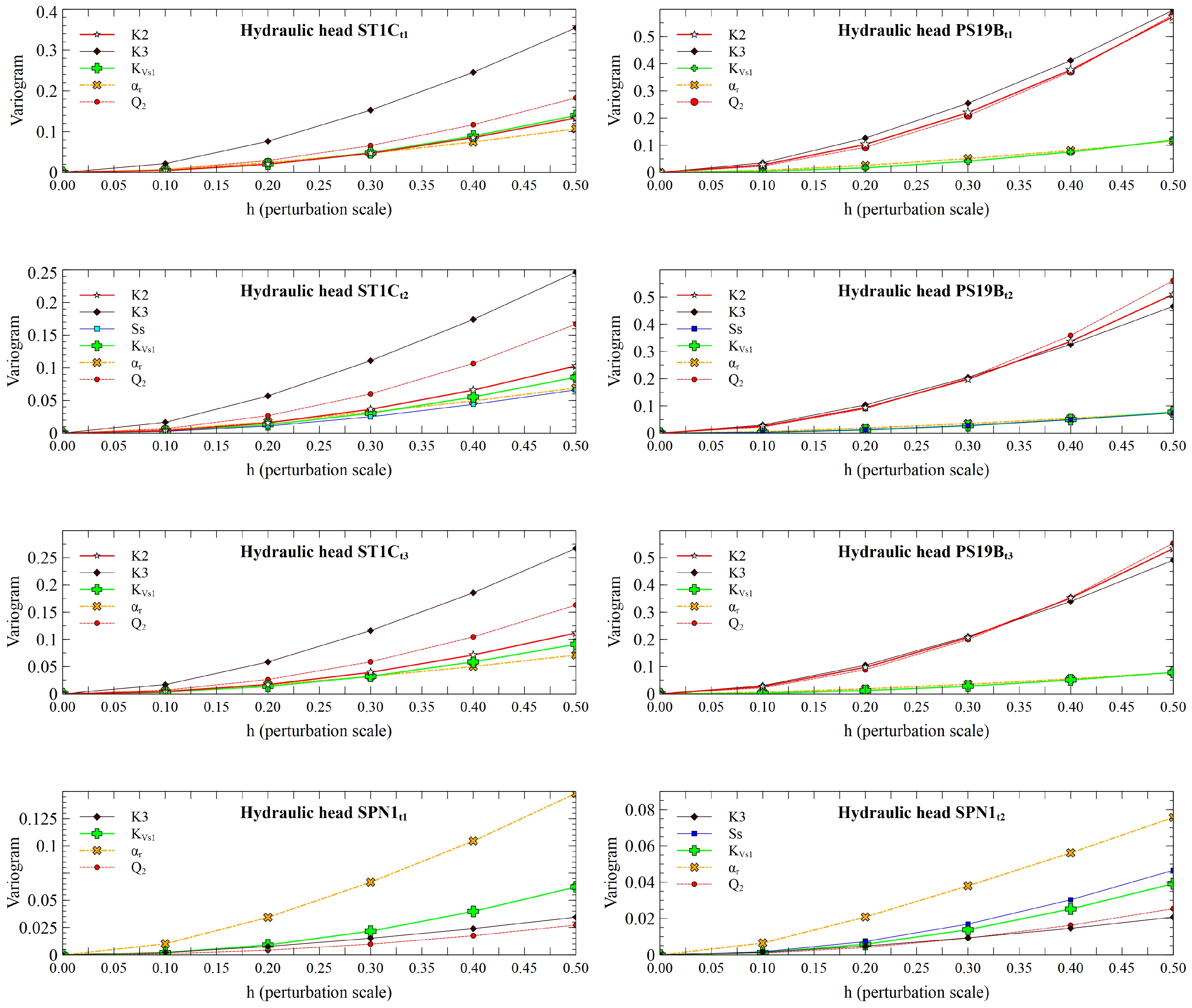
2.5.3. Variogram Analysis of Response Surfaces
2.6. Inputs and Outputs
- is the number of monitoring wells.
- is the number of measured piezometric heads in the -th well.
- is the total number of measured piezometric heads in all the wells.
- is the standard deviation of the measured piezometric heads in the -th well.
- , and are the mean absolute error, the root mean squared error, and the Nash–Sutcliffe index for the -the well.
- is the standard deviation of the measured piezometric heads in all wells.
2.7. Global Sensitivity Simulation Runs
2.8. Software
3. Results and Discussion
3.1. Groundwater Flow Model Results
3.2. GSA Results for the Groundwater Flow Model of the Gállego Alluvial Aquifer
3.2.1. Graphical Results
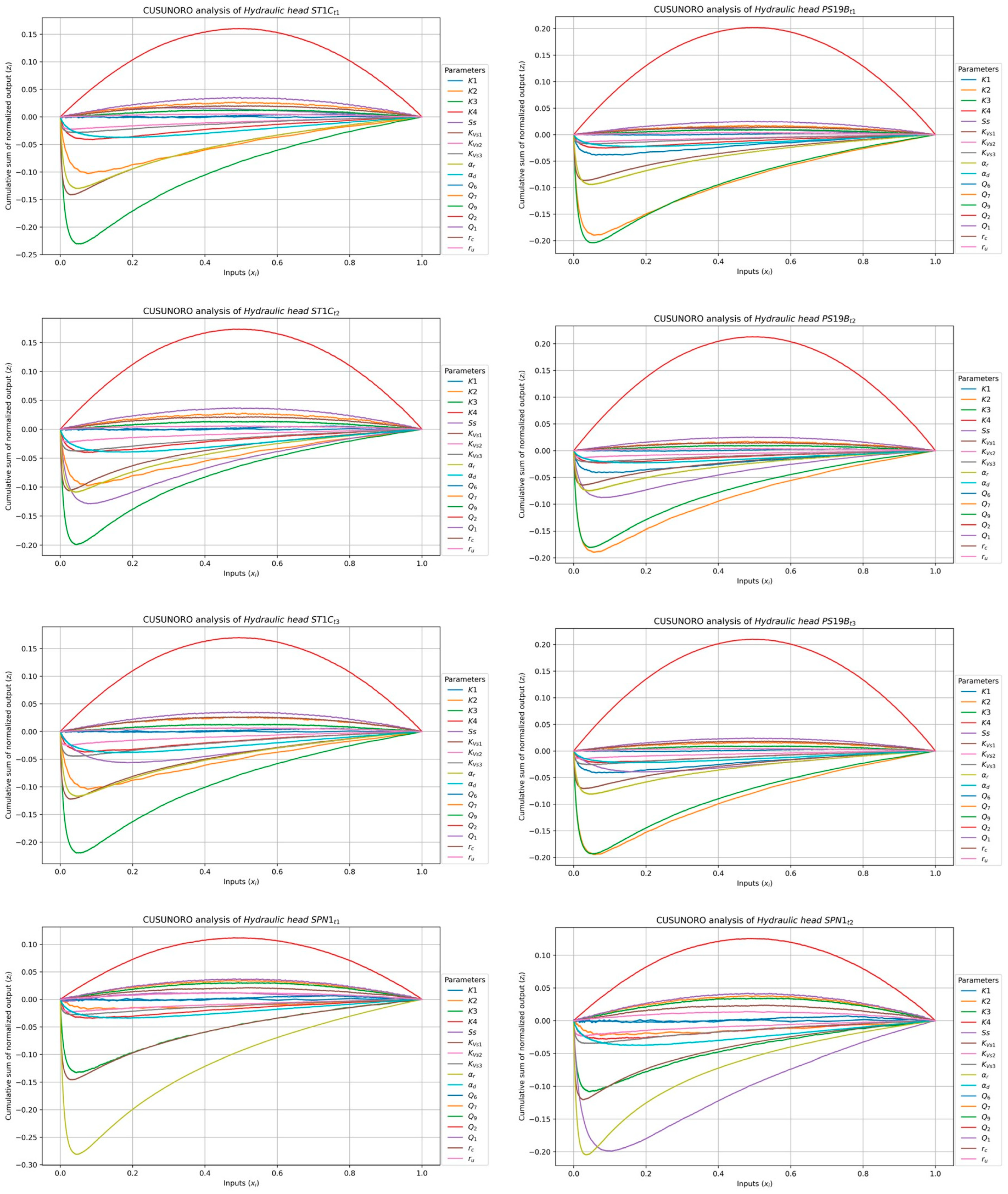
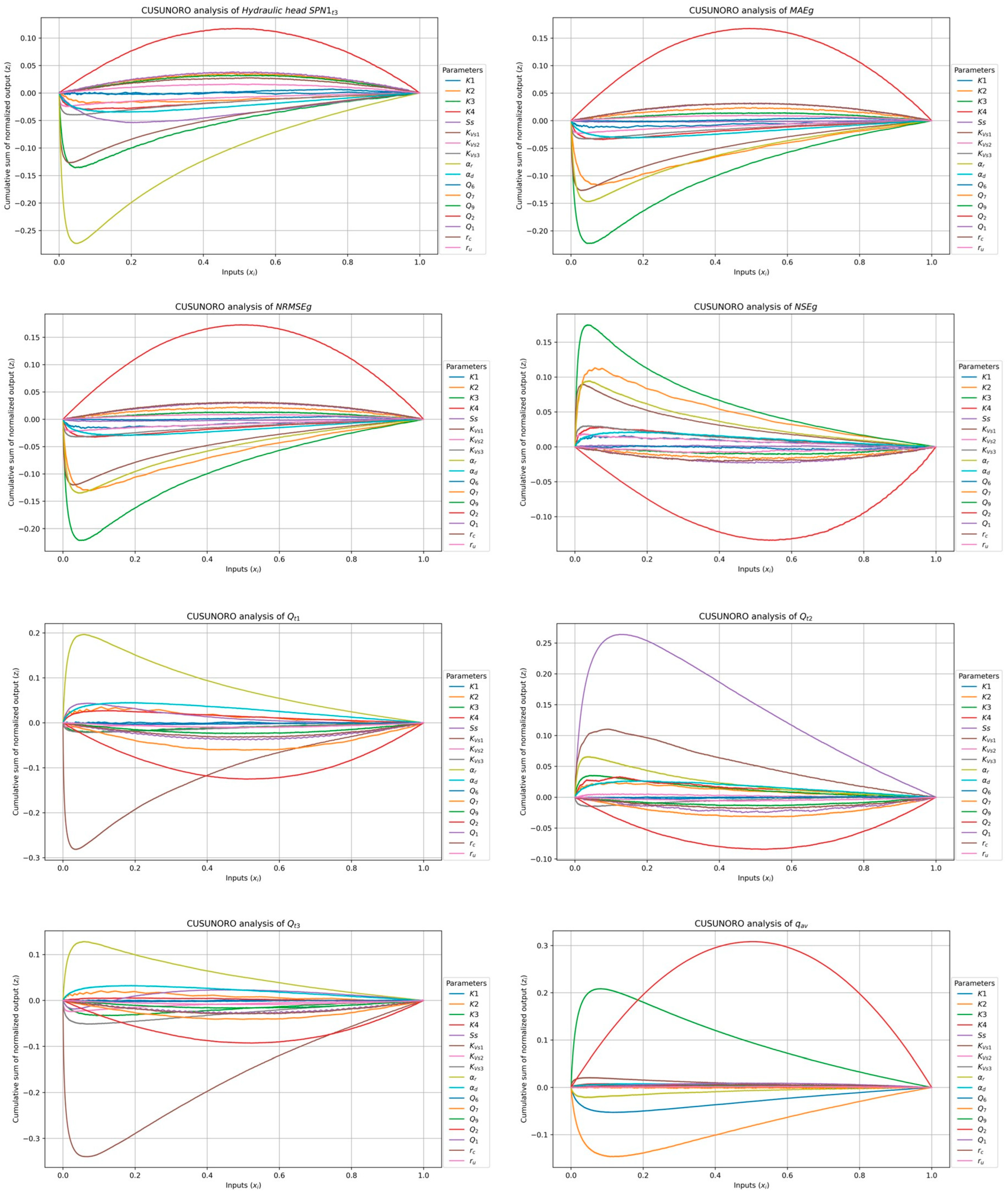
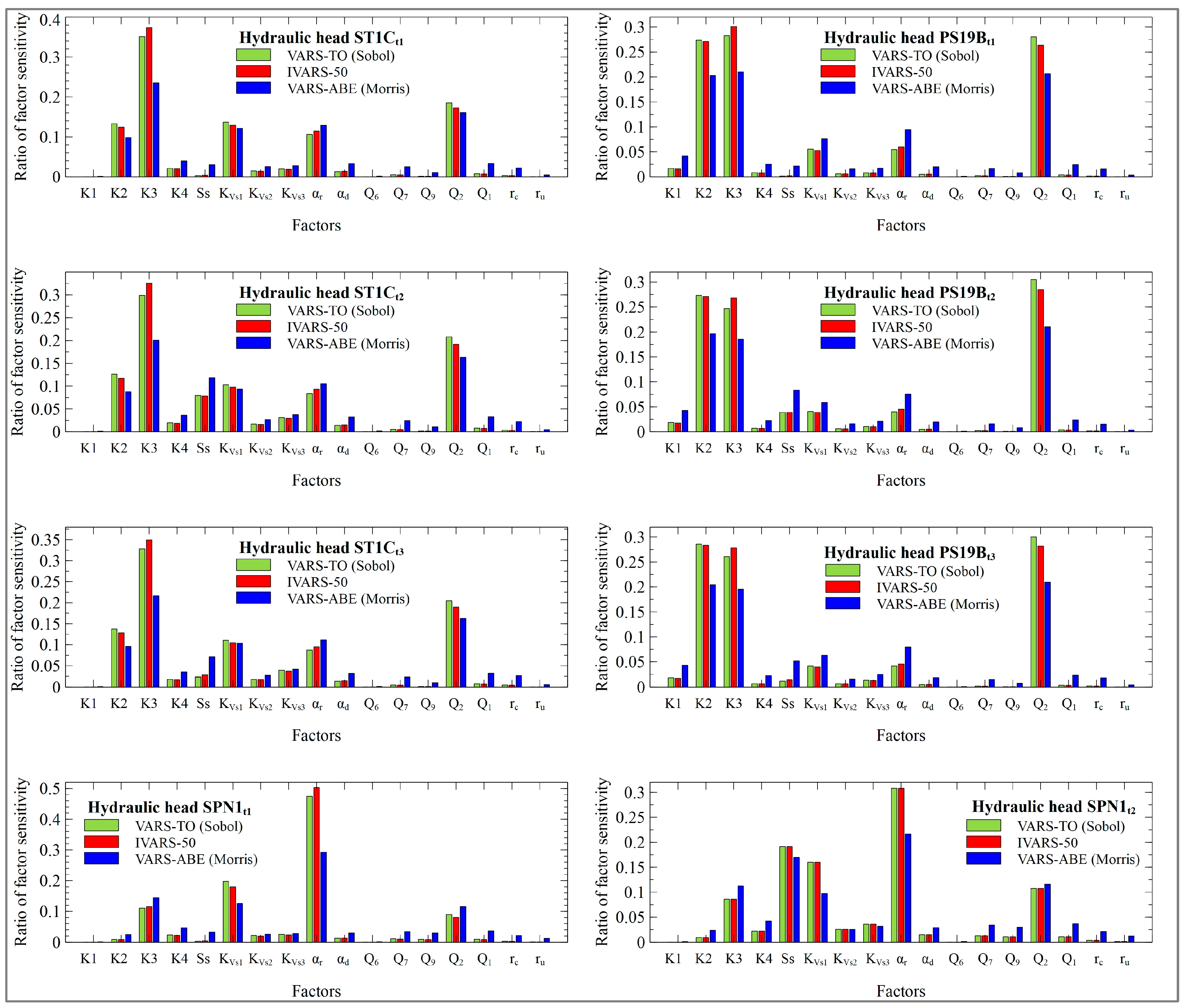
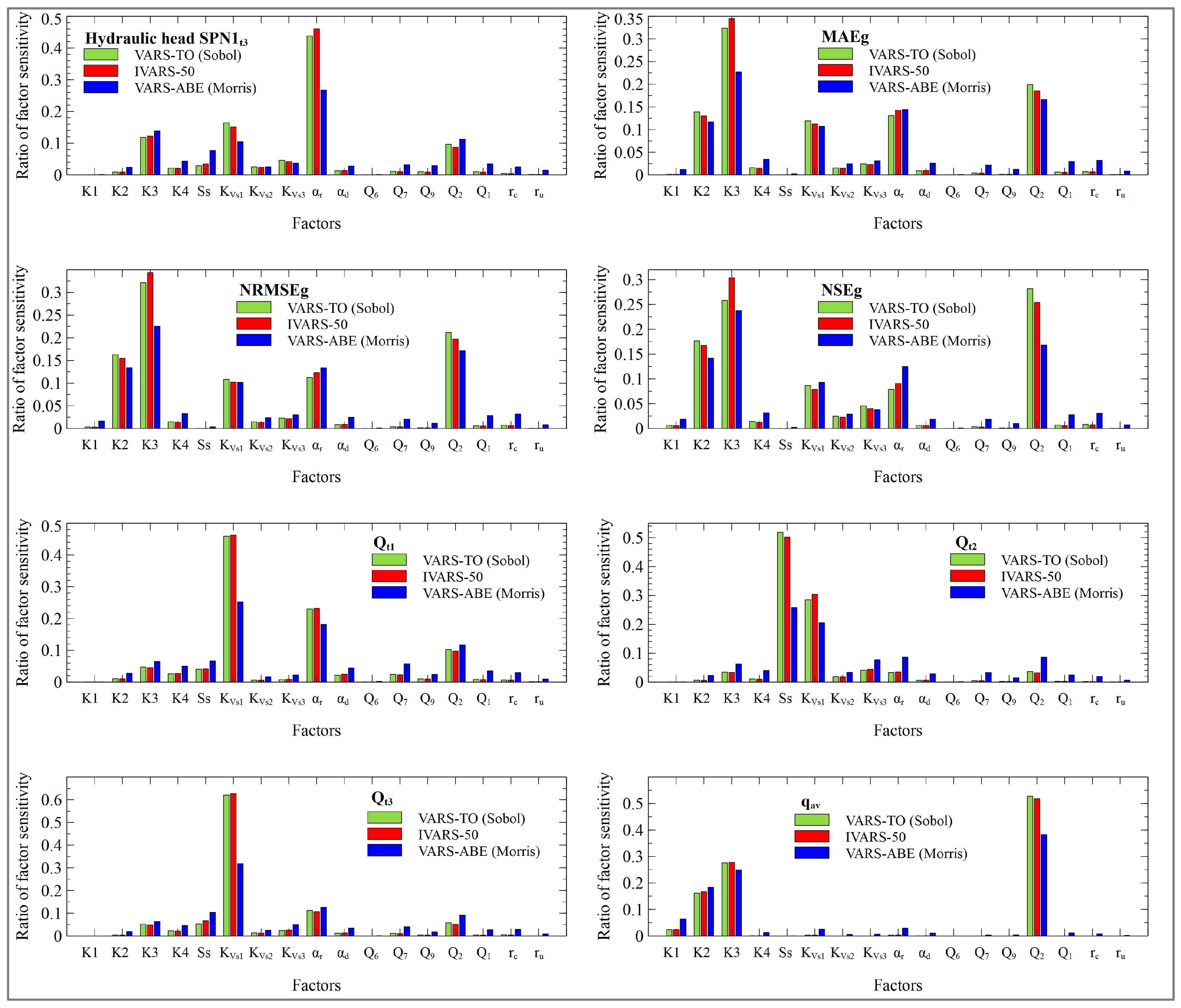
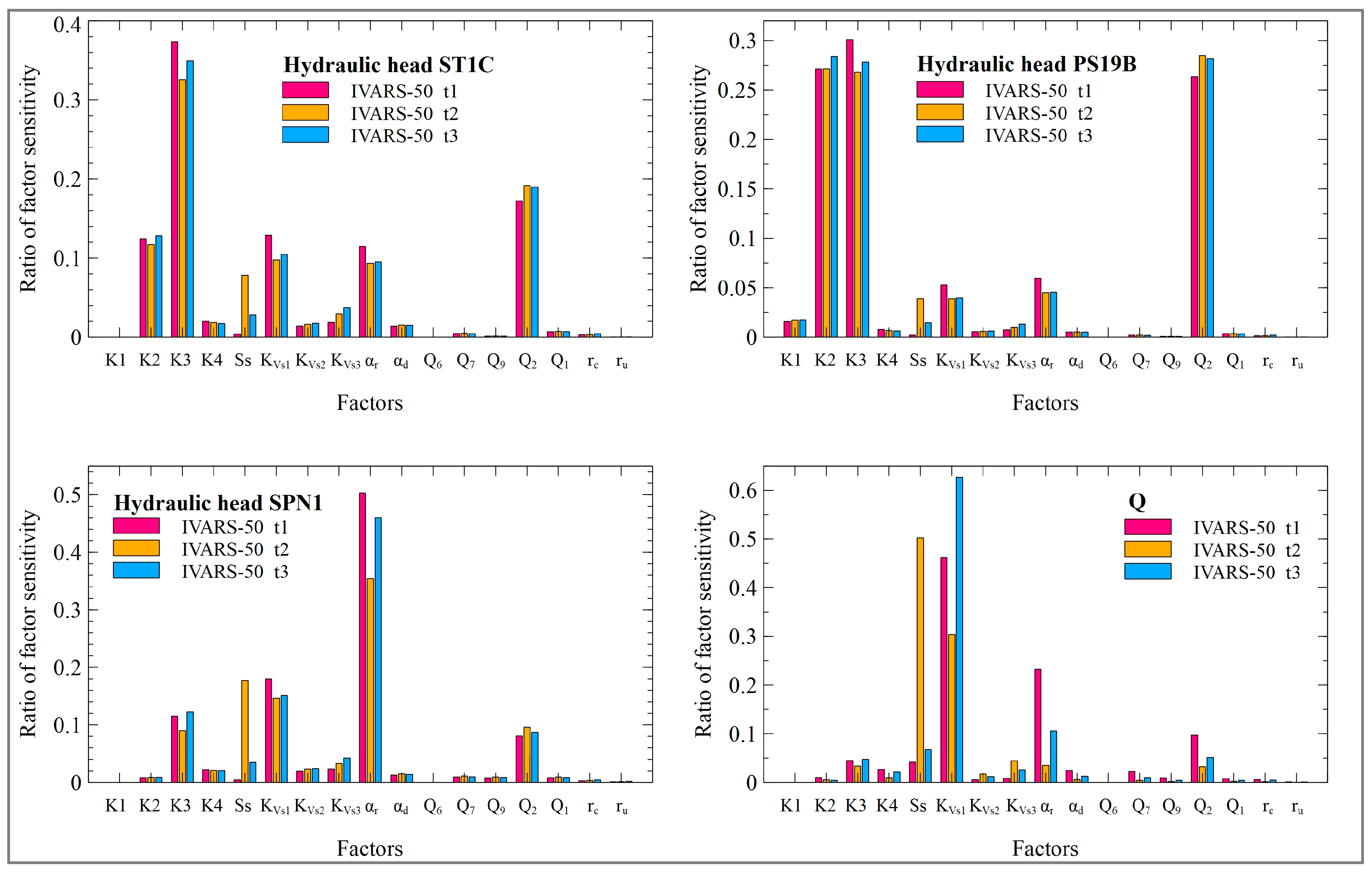
3.2.2. VARS Results
3.2.3. HDMR Results and Analysis of Interactions for the Sobol Sequence
3.2.4. HDMR Results for the VARS Runs by Using the Halton Sequence
3.3. Input Parameter Rankings
4. Conclusions
- All GSA methods agree to identify the most influential parameters which for most of the outputs are the hydraulic conductivities of the zones closest to the landfill, the vertical hydraulic conductivity of the most permeable zones of the aquitard, and the boundary inflow coming from the landfill (Q2).
- The sensitivity indexes of the computed heads in monitoring wells and aquifer/reservoir fluxes with respect to specific storage SS change with time. The sensitivity indexes of the calibration metrics are similar. MAEg is less prone to model result outliers. The average groundwater Darcy velocity is most sensitive to Q2.
- Graphical and HDMR methods identify parameter interactions for the aquifer/reservoir flux when the reservoir level is high. The interaction occurs between specific storage and aquitard conductivity.
- VARS and HDMR parameter rankings are similar for the most influential parameters. However, there are discrepancies for the less relevant parameters.
- Stable VARS results are achieved with a relatively small number of simulations.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cvetkovic, V.; Soltani, S.; Vigouroux, G. Global Sensitivity Analysis of Groundwater Transport. J. Hydrol. 2015, 531, 142–148. [Google Scholar] [CrossRef]
- Bordbar, M.; Neshat, A.; Javadi, S. A New Hybrid Framework for Optimization and Modification of Groundwater Vulnerability in Coastal Aquifer. Environ. Sci. Pollut. Res. 2019, 26, 21808–21827. [Google Scholar] [CrossRef] [PubMed]
- Balakrishnan, S.; Roy, A.; Ierapetritou, M.G.; Flach, G.P.; Georgopoulos, P.G. A Comparative Assessment of Efficient Uncertainty Analysis Techniques for Environmental Fate and Transport Models: Application to the FACT Model. J. Hydrol. 2005, 307, 204–218. [Google Scholar] [CrossRef]
- Dai, H.; Chen, X.; Ye, M.; Song, X.; Zachara, J.M. A Geostatistics-Informed Hierarchical Sensitivity Analysis Method for Complex Groundwater Flow and Transport Modeling. Water Resour. Res. 2017, 53, 4327–4343. [Google Scholar] [CrossRef]
- Bianchi Janetti, E.; Guadagnini, L.; Riva, M.; Guadagnini, A. Global Sensitivity Analyses of Multiple Conceptual Models with Uncertain Parameters Driving Groundwater Flow in a Regional-Scale Sedimentary Aquifer. J. Hydrol. 2019, 574, 544–556. [Google Scholar] [CrossRef]
- Maples, S.R.; Foglia, L.; Fogg, G.E.; Maxwell, R.M. Sensitivity of Hydrologic and Geologic Parameters on Recharge Processes in a Highly Heterogeneous, Semi-Confined Aquifer System. Hydrol. Earth Syst. Sci. 2020, 24, 2437–2456. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, F.; Yin, S.; Wallace, C.D.; Soltanian, M.R.; Dai, Z.; Ritzi, R.W.; Ma, Z.; Zhan, C.; Lü, X. Application of Upscaling Methods for Fluid Flow and Mass Transport in Multi-Scale Heterogeneous Media: A Critical Review. Appl. Energy 2021, 303, 117603. [Google Scholar] [CrossRef]
- Carrera, J.; Saaltink, M.W.; Soler-Sagarra, J.; Wang, J.; Valhondo, C. Reactive Transport: A Review of Basic Concepts with Emphasis on Biochemical Processes. Energies 2022, 15, 925. [Google Scholar] [CrossRef]
- He, X.; Jiang, L.; Moulton, J.D. A Stochastic Dimension Reduction Multiscale Finite Element Method for Groundwater Flow Problems in Heterogeneous Random Porous Media. J. Hydrol. 2013, 478, 77–88. [Google Scholar] [CrossRef]
- Tansar, H.; Duan, H.-F.; Mark, O. Global Sensitivity Analysis of Bioretention Cell Design for Stormwater System: A Comparison of VARS Framework and Sobol Method. J. Hydrol. 2023, 617, 128895. [Google Scholar] [CrossRef]
- Greskowiak, J.; Prommer, H.; Liu, C.; Post, V.; Ma, R.; Zheng, C.; Zachara, J. Comparison of Parameter Sensitivities between a Laboratory and Field-Scale Model of Uranium Transport in a Dual Domain, Distributed Rate Reactive System. Water Resour. Res. 2010, 46, W09509. [Google Scholar] [CrossRef]
- Abdelaziz, R.; Merkel, B.J. Sensitivity Analysis of Transport Modeling in a Fractured Gneiss Aquifer. J. Afr. Earth Sci. 2015, 103, 121–127. [Google Scholar] [CrossRef]
- Samper, J.; Naves, A.; Montenegro, L.; Mon, A. Reactive Transport Modelling of the Long-Term Interactions of Corrosion Products and Compacted Bentonite in a HLW Repository in Granite: Uncertainties and Relevance for Performance Assessment. Appl. Geochem. 2016, 67, 42–51. [Google Scholar] [CrossRef]
- Montenegro, L.; Samper, J.; Mon, A.; De Windt, L.; Samper, A.-C.; García, E. A Non-Isothermal Reactive Transport Model of the Long-Term Geochemical Evolution at the Disposal Cell Scale in a HLW Repository in Granite. Appl. Clay Sci. 2023, 242, 107018. [Google Scholar] [CrossRef]
- Saltelli, A.; Sobol’, I.M. About the Use of Rank Transformation in Sensitivity Analysis of Model Output. Reliab. Eng. Syst. Saf. 1995, 50, 225–239. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance Based Sensitivity Analysis of Model Output. Design and Estimator for the Total Sensitivity Index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Pianosi, F.; Beven, K.; Freer, J.; Hall, J.W.; Rougier, J.; Stephenson, D.B.; Wagener, T. Sensitivity Analysis of Environmental Models: A Systematic Review with Practical Workflow. Environ. Model. Softw. 2016, 79, 214–232. [Google Scholar] [CrossRef]
- Plischke, E. An Adaptive Correlation Ratio Method Using the Cumulative Sum of the Reordered Output. Reliab. Eng. Syst. Saf. 2012, 107, 149–156. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial Sampling Plans for Preliminary Computational Experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Campolongo, F.; Cariboni, J.; Saltelli, A. An Effective Screening Design for Sensitivity Analysis of Large Models. Environ. Model. Softw. 2007, 22, 1509–1518. [Google Scholar] [CrossRef]
- Uddameri, V.; Hernandez, E.A.; Singaraju, S. A Successive Steady-State Model for Simulating Freshwater Discharges and Saltwater Wedge Profiles at Baffin Bay, Texas. Environ. Earth Sci. 2014, 71, 2535–2546. [Google Scholar] [CrossRef]
- Rabitz, H.; Aliş, Ö.F. General Foundations of High-Dimensional Model Representations. J. Math. Chem. 1999, 25, 197–233. [Google Scholar] [CrossRef]
- Dai, H.; Ye, M. Variance-Based Global Sensitivity Analysis for Multiple Scenarios and Models with Implementation Using Sparse Grid Collocation. J. Hydrol. 2015, 528, 286–300. [Google Scholar] [CrossRef]
- Gatel, L.; Lauvernet, C.; Carluer, N.; Weill, S.; Paniconi, C. Sobol Global Sensitivity Analysis of a Coupled Surface/Subsurface Water Flow and Reactive Solute Transfer Model on a Real Hillslope. Water 2020, 12, 121. [Google Scholar] [CrossRef]
- Dell’Oca, A.; Riva, M.; Guadagnini, A. Moment-Based Metrics for Global Sensitivity Analysis of Hydrological Systems. Hydrol. Earth Syst. Sci. 2017, 21, 6219–6234. [Google Scholar] [CrossRef]
- Maina, F.Z.; Guadagnini, A. Uncertainty Quantification and Global Sensitivity Analysis of Subsurface Flow Parameters to Gravimetric Variations during Pumping Tests in Unconfined Aquifers. Water Resour. Res. 2018, 54, 501–518. [Google Scholar] [CrossRef]
- Razavi, S.; Gupta, H.V. A New Framework for Comprehensive, Robust, and Efficient Global Sensitivity Analysis: 1. Theory. Water Resour. Res. 2016, 52, 423–439. [Google Scholar] [CrossRef]
- Razavi, S.; Gupta, H.V. A New Framework for Comprehensive, Robust, and Efficient Global Sensitivity Analysis: 2. Application. Water Resour. Res. 2016, 52, 440–455. [Google Scholar] [CrossRef]
- Razavi, S.; Gupta, H.V. A Multi-Method Generalized Global Sensitivity Matrix Approach to Accounting for the Dynamical Nature of Earth and Environmental Systems Models. Environ. Model. Softw. 2019, 114, 1–11. [Google Scholar] [CrossRef]
- Puy, A.; Becker, W.; Piano, S.L.; Saltelli, A. A Comprehensive Comparison of Total-Order Estimators for Global Sensitivity Analysis. Int. J. Uncertain. Quantif. 2022, 12, 1–18. [Google Scholar] [CrossRef]
- Malaguerra, F.; Albrechtsen, H.-J.; Binning, P.J. Assessment of the Contamination of Drinking Water Supply Wells by Pesticides from Surface Water Resources Using a Finite Element Reactive Transport Model and Global Sensitivity Analysis Techniques. J. Hydrol. 2013, 476, 321–331. [Google Scholar] [CrossRef]
- Zou, Y.; Yousaf, M.S.; Yang, F.; Deng, H.; He, Y. Surrogate-Based Uncertainty Analysis for Groundwater Contaminant Transport in a Chromium Residue Site Located in Southern China. Water 2024, 16, 638. [Google Scholar] [CrossRef]
- Wang, Y.; Bian, J.; Sun, X.; Ruan, D.; Gu, Z. Sensitivity-Dependent Dynamic Searching Approach Coupling Multi-Intelligent Surrogates in Homotopy Mechanism for Groundwater DNAPL-Source Inversion. J. Contam. Hydrol. 2023, 255, 104151. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, J.; Tang, H. Global Sensitivity Analysis of the Hydraulic Parameters of the Reservoir Colluvial Landslides in the Three Gorges Reservoir Area, China. Landslides 2020, 17, 483–494. [Google Scholar] [CrossRef]
- Mishra, S.; Deeds, N.; Ruskauff, G. Global Sensitivity Analysis Techniques for Probabilistic Ground Water Modeling. Ground Water 2009, 47, 727–744. [Google Scholar] [CrossRef]
- Samper, J.; López-Vázquez, C.; Mon, A.; Pisani, B.; Samper-Pilar, A.-C.; Samper-Pilar, J.; Lentijo, F. VARS global sensitivities for reactive transport simulations in a HLW repository in granite. In Proceedings of the 18th International Conference on Chemistry and Migration Behaviour of Actinides and Fission Products in the Geosphere, Migration 2023, Nantes, France, 24–29 September 2023; pp. 433–434. [Google Scholar]
- Santos, A.; Fernández, J.; Guadaño, J.; Lorenzo, D.; Romero, A. Chlorinated Organic Compounds in Liquid Wastes (DNAPL) from Lindane Production Dumped in Landfills in Sabiñanigo (Spain). Environ. Pollut. 2018, 242, 1616–1624. [Google Scholar] [CrossRef]
- Sobral, B.; Samper, J.; Montenegro, L.; Mon, A.; Guadaño, J.; Gómez, J.; San Román, J.; Delgado, F.; Fernández, J. 2D Model of Groundwater Flow and Total Dissolved HCH Transport through the Gállego Alluvial Aquifer Downstream the Sardas Landfill (Huesca, Spain). J. Contam. Hydrol. 2024, 265, 104370. [Google Scholar] [CrossRef]
- Fernández, J.; Arjol, M.A.; Cacho, C. POP-Contaminated Sites from HCH Production in Sabiñánigo, Spain. Environ. Sci. Pollut. Res. 2013, 20, 1937–1950. [Google Scholar] [CrossRef]
- Biosca, B.; Arévalo-Lomas, L.; Izquierdo-Díaz, M.; Díaz-Curiel, J. Detection of Chlorinated Contaminants Coming from the Manufacture of Lindane in a Surface Detritic Aquifer by Electrical Resistivity Tomography. J. Appl. Geophys. 2021, 191, 104358. [Google Scholar] [CrossRef]
- Samper, J.; Sobral, B.; Pisani, B.; Naves, A.; Guadaño, J.; Gómez, J.; Fernández, J. Groundwater Flow Model along a Vertical Profile of the Sardas Landfill in Sabiñánigo, Huesca, Spain. Water 2023, 15, 3457. [Google Scholar] [CrossRef]
- Guadaño, J.; Gómez, J.; Fernández, J.; Lorenzo, D.; Domínguez, C.M.; Cotillas, S.; García-Cervilla, R.; Santos, A. Remediation of the Alluvial Aquifer of the Sardas Landfill (Sabiñánigo, Huesca) by Surfactant Application. Sustainability 2022, 14, 16576. [Google Scholar] [CrossRef]
- Pankow, J.F.; Cherry, J.A. Dense Chlorinated Solvents and Other DNAPLs in Groundwater: History, Behavior, and Remediation; Waterloo Press: Portland, OR, USA, 1996; ISBN 978-0-9648014-1-7. [Google Scholar]
- Casado, I.; Mahjoub, H.; Lovera, R.; Fernández, J.; Casas, A. Use of Electrical Tomography Methods to Determinate the Extension and Main Migration Routes of Uncontrolled Landfill Leachates in Fractured Areas. Sci. Total Environ. 2015, 506–507, 546–553. [Google Scholar] [CrossRef] [PubMed]
- Julià, X.; González, G.; Alonso, M. Estudio Batimétrico y de Caracterización de Sedimentos Del Embalse de Sabiñánigo; Technical Report for the Ebre River Water District; URS: Zaragoza, Spain, 2009. [Google Scholar]
- Shuai, P.; Chen, X.; Song, X.; Hammond, G.E.; Zachara, J.; Royer, P.; Ren, H.; Perkins, W.A.; Richmond, M.C.; Huang, M. Dam Operations and Subsurface Hydrogeology Control Dynamics of Hydrologic Exchange Flows in a Regulated River Reach. Water Resour. Res. 2019, 55, 2593–2612. [Google Scholar] [CrossRef]
- Espinha Marques, J.; Samper, J.; Pisani, B.; Alvares, D.; Carvalho, J.M.; Chaminé, H.I.; Marques, J.M.; Vieira, G.T.; Mora, C.; Sodré Borges, F. Evaluation of Water Resources in a High-Mountain Basin in Serra Da Estrela, Central Portugal, Using a Semi-Distributed Hydrological Model. Environ. Earth Sci. 2011, 62, 1219–1234. [Google Scholar] [CrossRef]
- Plischke, E.; Röhlig, K.-J. Methodological Approaches to Uncertainty and Sensitivity Analysis. Final Version as of 07.05.2024 of Deliverable D10.4 of the HORIZON 2020 Project EURAD. EC Grant Agreement No: 847593. Available online: https://www.ejp-eurad.eu/publications/eurad-d104-methodological-approaches-uncertainty-and-sensitivity-analysis (accessed on 2 August 2024).
- Sobol’, I.M. On the Distribution of Points in a Cube and the Approximate Evaluation of Integrals. USSR Comput. Math. Math. Phys. 1967, 7, 86–112. [Google Scholar] [CrossRef]
- Sobol’, I.M. Sensitivity Analysis for Non-Linear Mathematical Models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Homma, T.; Saltelli, A. Importance Measures in Global Sensitivity Analysis of Nonlinear Models. Reliab. Eng. Syst. Saf. 1996, 52, 1–17. [Google Scholar] [CrossRef]
- Razavi, S.; Sheikholeslami, R.; Gupta, H.V.; Haghnegahdar, A. VARS-TOOL: A Toolbox for Comprehensive, Efficient, and Robust Sensitivity and Uncertainty Analysis. Environ. Model. Softw. 2019, 112, 95–107. [Google Scholar] [CrossRef]
- Halton, J.H. On the Efficiency of Certain Quasi-Random Sequences of Points in Evaluating Multi-Dimensional Integrals. Numer. Math. 1960, 2, 84–90. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of Different Efficiency Criteria for Hydrological Model Assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Samper, J.; Xu, T.; Yang, C. A Sequential Partly Iterative Approach for Multicomponent Reactive Transport with CORE2D. Comput. Geosci. 2009, 13, 301–316. [Google Scholar] [CrossRef]
- Poonoosamy, J.; Wanner, C.; Alt Epping, P.; Águila, J.F.; Samper, J.; Montenegro, L.; Xie, M.; Su, D.; Mayer, K.U.; Mäder, U.; et al. Benchmarking of Reactive Transport Codes for 2D Simulations with Mineral Dissolution–Precipitation Reactions and Feedback on Transport Parameters. Comput. Geosci. 2021, 25, 1337–1358. [Google Scholar] [CrossRef]
- Idiart, A.; Laviña, M.; Kosakowski, G.; Cochepin, B.; Meeussen, J.C.L.; Samper, J.; Mon, A.; Montoya, V.; Munier, I.; Poonoosamy, J.; et al. Reactive transport modelling of a low-pH concrete/clay interface. Appl. Geochem. 2020, 115, 104562. [Google Scholar] [CrossRef]
- Molinero, J.; Samper, J.; Zhang, G.; Yang, C. Biogeochemical reactive transport model of the redox zone experiment of the Äspö hard rock laboratory in Sweden. Nucl. Technol. 2004, 148, 151–165. [Google Scholar] [CrossRef]
- Mon, A.; Samper, J.; Montenegro, L.; Naves, A.; Fernández-Águila, J. Long-term non-isothermal reactive transport model of compacted bentonite, concrete and corrosion products in a HLW repository in clay. J. Cont. Hydrol. 2017, 197, 1–16. [Google Scholar] [CrossRef]
- González, P.; Prado-Rodriguez, R.; Gábor, A.; Saez-Rodriguez, J.; Banga, J.R.; Doallo, R. Parallel Ant Colony Optimization for the Training of Cell Signaling Networks. Expert. Syst. Appl. 2022, 208, 118199. [Google Scholar] [CrossRef]
- Vourlioti, P.; Kotsopoulos, S.; Mamouka, T.; Agrafiotis, A.; Nieto, F.J.; Sánchez, C.F.; Llerena, C.G.; García González, S. Maximizing the Potential of Numerical Weather Prediction Models: Lessons Learned from Combining High-Performance Computing and Cloud Computing. Adv. Sci. Res. 2023, 20, 1–8. [Google Scholar] [CrossRef]
- Herman, J.; Usher, W. SALib: An Open-Source Python Library for Sensitivity Analysis. J. Open Source Softw. 2017, 2, 97. [Google Scholar] [CrossRef]
- Ziehn, T.; Tomlin, A.S. GUI–HDMR—A Software Tool for Global Sensitivity Analysis of Complex Models. Environ. Model. Softw. 2009, 24, 775–785. [Google Scholar] [CrossRef]
- Kocis, L.; Whiten, W.J. Computational Investigations of Low-Discrepancy Sequences. ACM Trans. Math. Softw. 1997, 23, 266–294. [Google Scholar] [CrossRef]






| Parameter | Minimum | Maximum | Unit | Distribution |
|---|---|---|---|---|
| Aquifer conductivity in material zone 1, K1 | 10 | 103 | m/d | Log-uniform |
| Aquifer conductivity in material zone 2, K2 | 10 | 103 | m/d | Log-uniform |
| Aquifer conductivity in material zone 3, K3 | 10 | 103 | m/d | Log-uniform |
| Aquifer conductivity in material zone 4, K4 | 10 | 103 | m/d | Log-uniform |
| Storage coefficient Ss | 10−5 | 10−3 | 1/m | Log-uniform |
| Aquitard conductivity KVs1 | 10−3 | 1 | m/d | Log-uniform |
| Aquitard conductivity KVs2 | 10−3 | 1 | m/d | Log-uniform |
| Aquitard conductivity KVs3 | 10−4 | 10−1 | m/d | Log-uniform |
| Leakage coefficient αr | 10 | 103 | m2/d | Log-uniform |
| Conductance αd | 1 | 100 | m2/d | Log-uniform |
| Boundary inflow Q6 | 3 × 10−3 | 0.05 | m3/d/m | Uniform |
| Boundary inflow Q7 | 2 × 10−3 | 0.20 | m3/d/m | Uniform |
| Boundary inflow Q9 | 0.25 | 1.00 | m3/d/m | Uniform |
| Boundary inflow Q2 | 1.70 × 10−2 | 1.70 | m3/d/m | Uniform |
| Boundary inflow Q1 | 2 × 10−3 | 10−1 | m3/d/m | Uniform |
| Recharge rc | 5 | 200 | mm/year | Uniform |
| Recharge ru | 20 | 401.5 | mm/year | Uniform |
| Output | Methods | K1 | K2 | K3 | K4 | Ss | KVs1 | KVs2 | KVs3 | αr | αd | Q6 | Q7 | Q9 | Q2 | Q1 | rc | ru |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ST1Ct1 | VARS-TO | 17 | 4 | 1 | 6 | 13 | 3 | 8 | 7 | 5 | 9 | 16 | 11 | 14 | 2 | 10 | 12 | 15 |
| IVARS50 | 16 | 4 | 1 | 6 | 12 | 3 | 8 | 7 | 5 | 9 | 17 | 11 | 14 | 2 | 10 | 13 | 15 | |
| VARS-ABE | 17 | 5 | 1 | 6 | 9 | 4 | 11 | 10 | 3 | 8 | 16 | 12 | 14 | 2 | 7 | 13 | 15 | |
| SALib | 17 | 5 | 1 | 10 | 6 | 3 | 13 | 7 | 4 | 8 | 15 | 12 | 14 | 2 | 9 | 11 | 16 | |
| GUI-HDMR | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| CUSUNORO | 17 | 5 | 1 | 6 | 13 | 3 | 11 | 9 | 4 | 7 | 16 | 10 | 14 | 2 | 8 | 12 | 15 | |
| MAEg | VARS-TO | 14 | 3 | 1 | 7 | 16 | 5 | 8 | 6 | 4 | 9 | 17 | 12 | 13 | 2 | 11 | 10 | 15 |
| IVARS50 | 14 | 4 | 1 | 7 | 16 | 5 | 8 | 6 | 3 | 9 | 17 | 12 | 13 | 2 | 11 | 10 | 15 | |
| VARS-ABE | 14 | 4 | 1 | 6 | 16 | 5 | 11 | 8 | 3 | 10 | 17 | 12 | 13 | 2 | 9 | 7 | 15 | |
| SALib | 14 | 5 | 1 | 6 | 17 | 4 | 12 | 7 | 3 | 10 | 16 | 11 | 13 | 2 | 9 | 8 | 15 | |
| GUI-HDMR | 14 | 4 | 1 | 7 | 17 | 5 | 11 | 6 | 3 | 8 | 15 | 12 | 13 | 2 | 10 | 9 | 16 | |
| CUSUNORO | 14 | 5 | 1 | 6 | 17 | 4 | 12 | 7 | 3 | 10 | 16 | 11 | 13 | 2 | 8 | 9 | 15 | |
| Qt1 | VARS-TO | 17 | 9 | 4 | 6 | 5 | 1 | 14 | 12 | 2 | 8 | 16 | 7 | 10 | 3 | 11 | 13 | 15 |
| IVARS50 | 17 | 9 | 4 | 6 | 5 | 1 | 14 | 11 | 2 | 7 | 16 | 8 | 10 | 3 | 12 | 13 | 15 | |
| VARS-ABE | 17 | 11 | 5 | 7 | 4 | 1 | 14 | 13 | 2 | 8 | 16 | 6 | 12 | 3 | 9 | 10 | 15 | |
| SALib | 17 | 9 | 13 | 10 | 6 | 1 | 15 | 12 | 2 | 5 | 16 | 4 | 11 | 3 | 7 | 8 | 14 | |
| GUI-HDMR | 17 | 9 | 5 | 8 | 4 | 1 | 14 | 13 | 2 | 7 | 16 | 6 | 11 | 3 | 10 | 12 | 15 | |
| CUSUNORO | 17 | 8 | 13 | 10 | 6 | 1 | 15 | 12 | 2 | 5 | 16 | 4 | 11 | 3 | 7 | 9 | 14 | |
| qav | VARS-TO | 4 | 3 | 2 | 7 | 16 | 5 | 9 | 10 | 6 | 8 | 17 | 14 | 13 | 1 | 11 | 12 | 15 |
| IVARS50 | 4 | 3 | 2 | 8 | 16 | 6 | 9 | 10 | 5 | 7 | 17 | 14 | 13 | 1 | 11 | 12 | 15 | |
| VARS-ABE | 4 | 3 | 2 | 7 | 16 | 6 | 12 | 11 | 5 | 9 | 17 | 14 | 13 | 1 | 8 | 10 | 15 | |
| SALib | 4 | 3 | 2 | 9 | 16 | 6 | 13 | 10 | 5 | 8 | 15 | 17 | 12 | 1 | 7 | 11 | 14 | |
| GUI-HDMR | 4 | 3 | 2 | 7 | 14 | 6 | 12 | 10 | 5 | 8 | 15 | 17 | 13 | 1 | 9 | 11 | 16 | |
| CUSUNORO | 4 | 3 | 2 | 8 | 17 | 6 | 13 | 11 | 5 | 9 | 16 | 15 | 12 | 1 | 7 | 10 | 14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samper, J.; Sobral, B.; Pisani, B.; Mon, A.; López-Vázquez, C.; Samper-Pilar, J. VARS and HDMR Sensitivity Analysis of Groundwater Flow Modeling through an Alluvial Aquifer Subject to Tidal Effects. Water 2024, 16, 2526. https://doi.org/10.3390/w16172526
Samper J, Sobral B, Pisani B, Mon A, López-Vázquez C, Samper-Pilar J. VARS and HDMR Sensitivity Analysis of Groundwater Flow Modeling through an Alluvial Aquifer Subject to Tidal Effects. Water. 2024; 16(17):2526. https://doi.org/10.3390/w16172526
Chicago/Turabian StyleSamper, Javier, Brais Sobral, Bruno Pisani, Alba Mon, Carlos López-Vázquez, and Javier Samper-Pilar. 2024. "VARS and HDMR Sensitivity Analysis of Groundwater Flow Modeling through an Alluvial Aquifer Subject to Tidal Effects" Water 16, no. 17: 2526. https://doi.org/10.3390/w16172526
APA StyleSamper, J., Sobral, B., Pisani, B., Mon, A., López-Vázquez, C., & Samper-Pilar, J. (2024). VARS and HDMR Sensitivity Analysis of Groundwater Flow Modeling through an Alluvial Aquifer Subject to Tidal Effects. Water, 16(17), 2526. https://doi.org/10.3390/w16172526







