Real-Time Optimal Scheduling of a Water Diversion System Using an Improved Wolf-Pack Algorithm and Scheme Library
Abstract
1. Introduction
2. Mathematical Model
2.1. Inner-Layer Model
2.1.1. Optimal Model of Single-Stage Pumping Station
2.1.2. Model of Channel Water Level–Flow Rate
2.2. Outer-Layer Model
3. Methodology
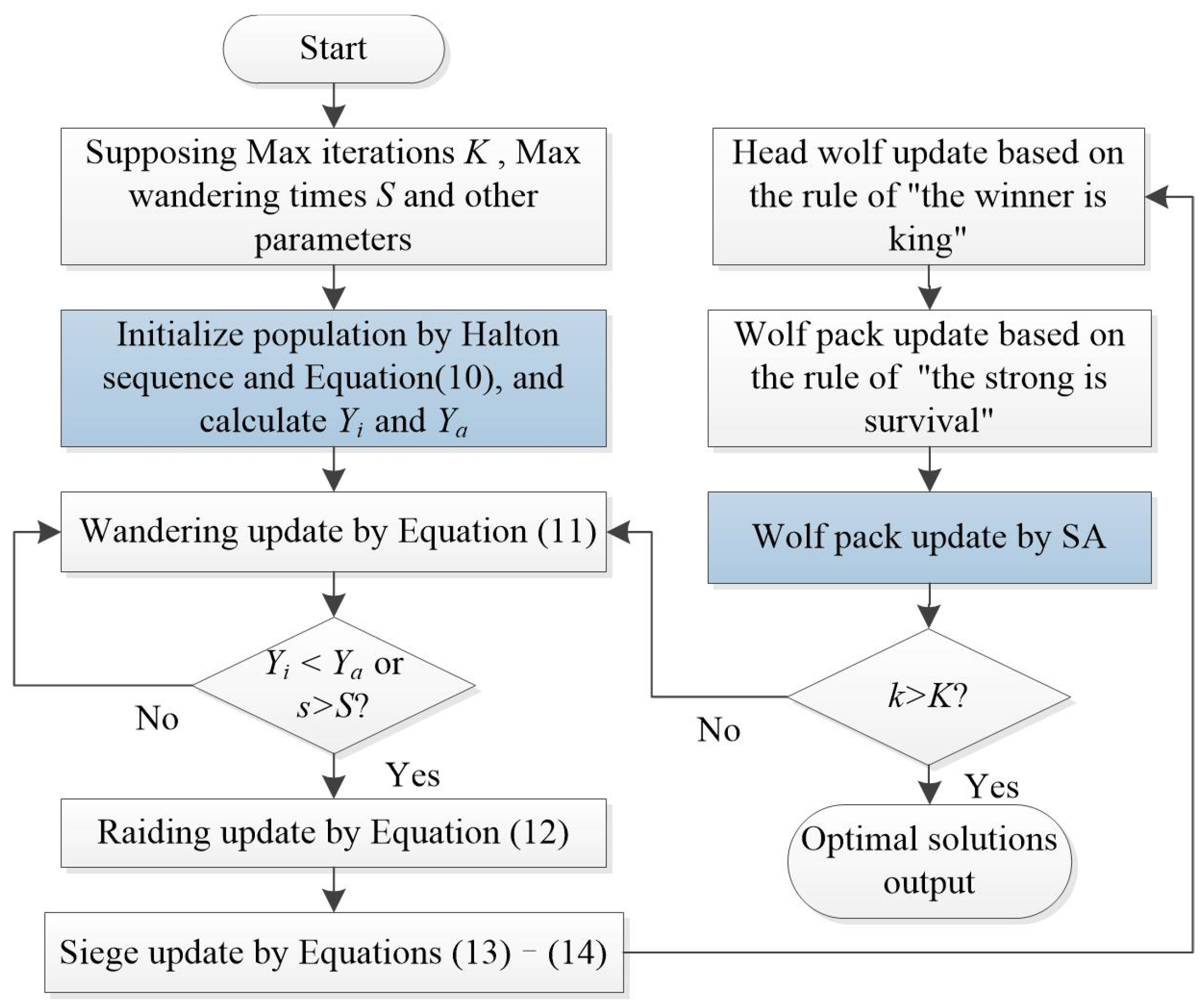
3.1. Wolf-Pack Algorithm
- (1)
- Population initialization
- (2)
- Head wolf spawn rules
- (3)
- Wandering update
- (4)
- Raiding update
- (5)
- Siege update
- (6)
- Wolves elimination mechanism
- (7)
- Optimal solution output.
3.2. Improved Wolf-Pack Algorithm
3.3. Performance Evaluation
3.4. Solution Process of Models with IWPA
4. Computational Application
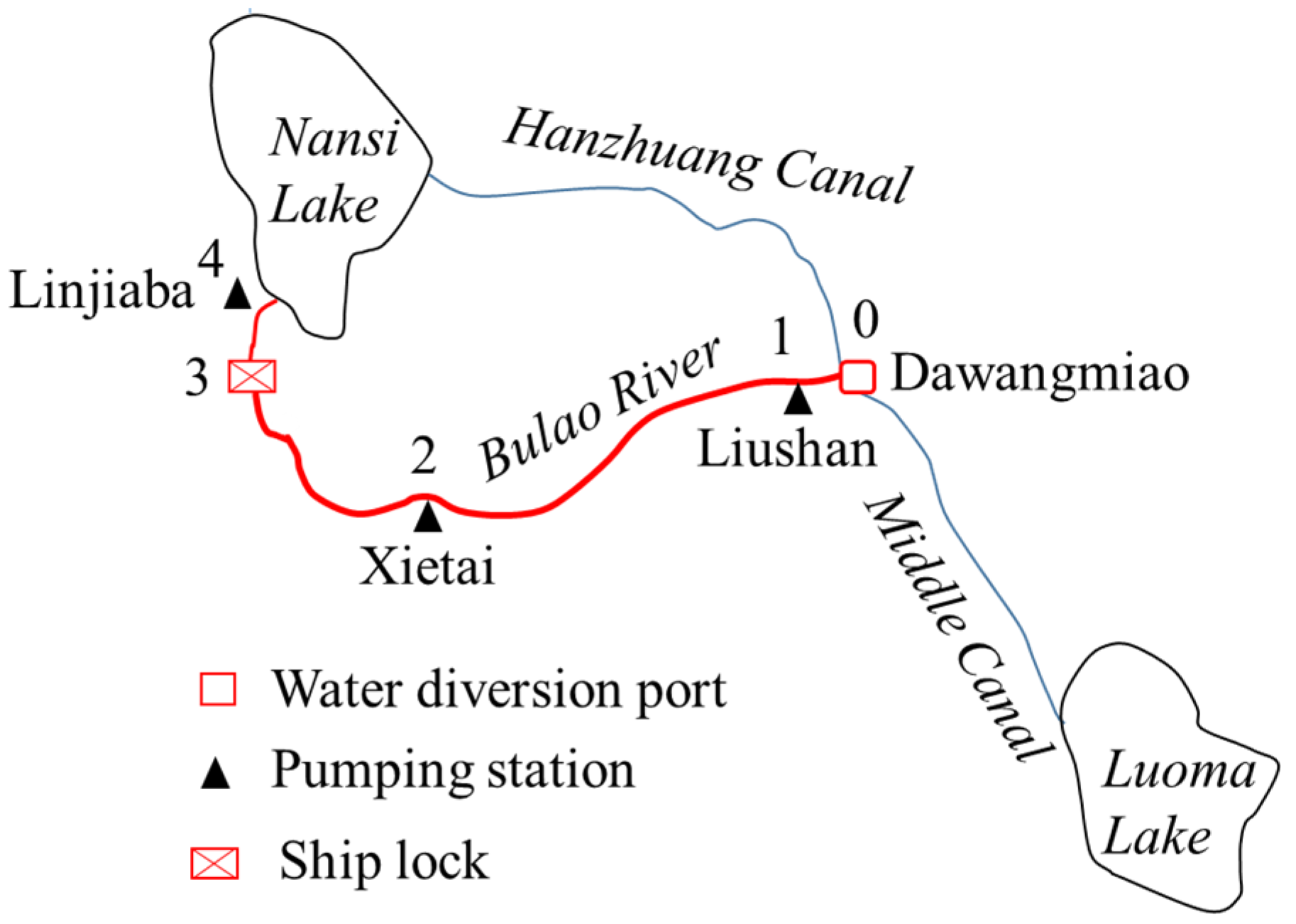
4.1. Case System
4.2. Calculation Results
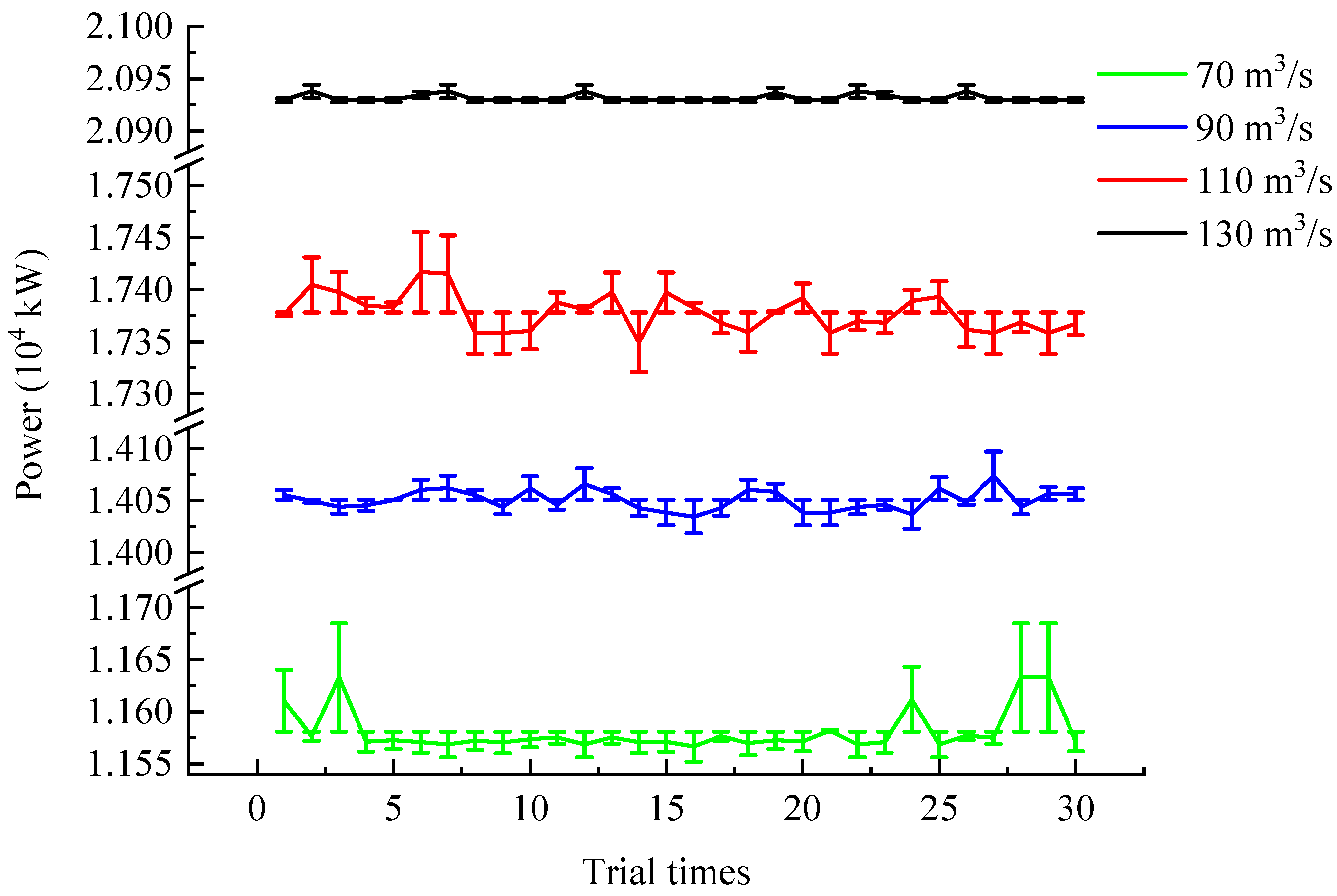
4.2.1. Scheme Library
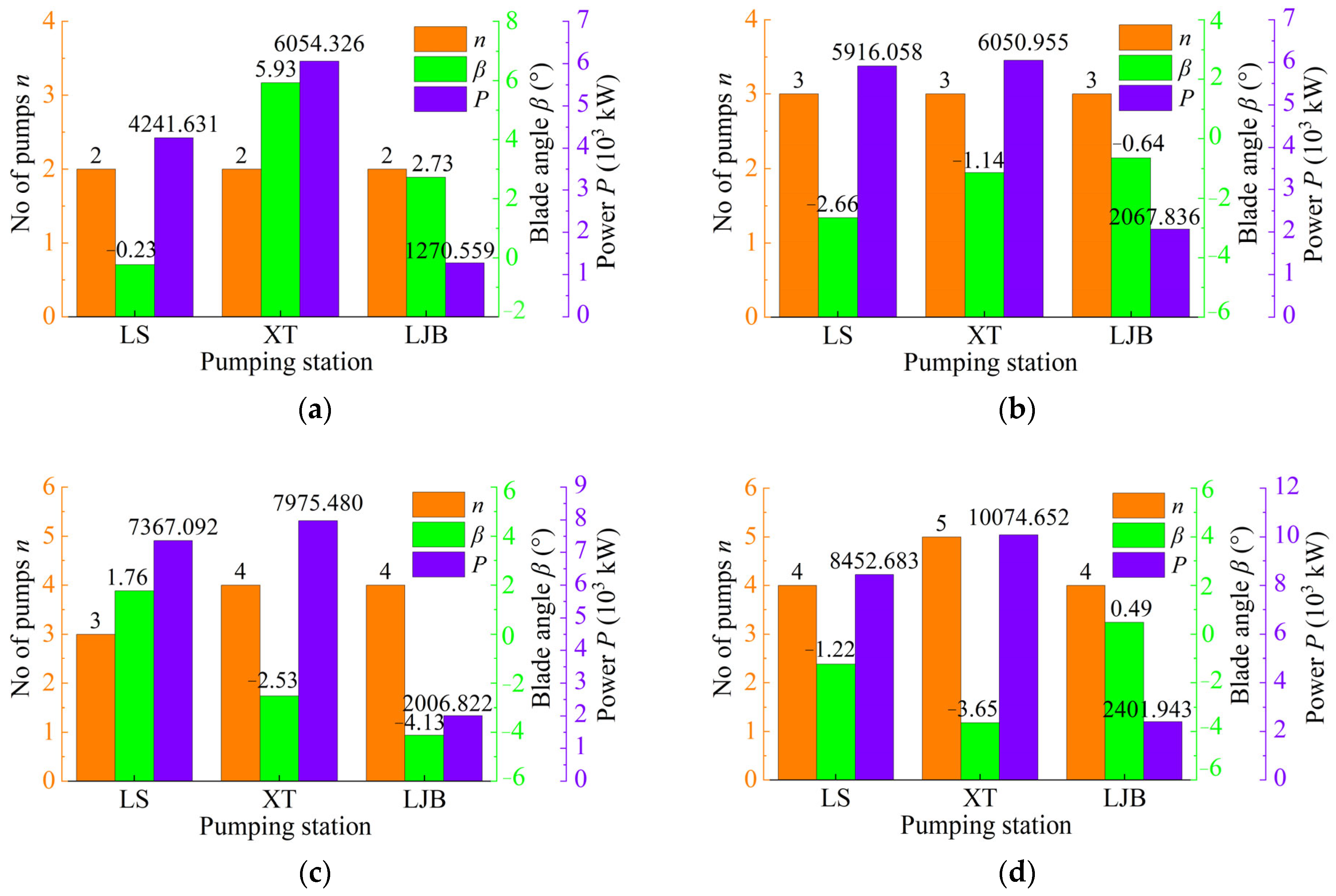
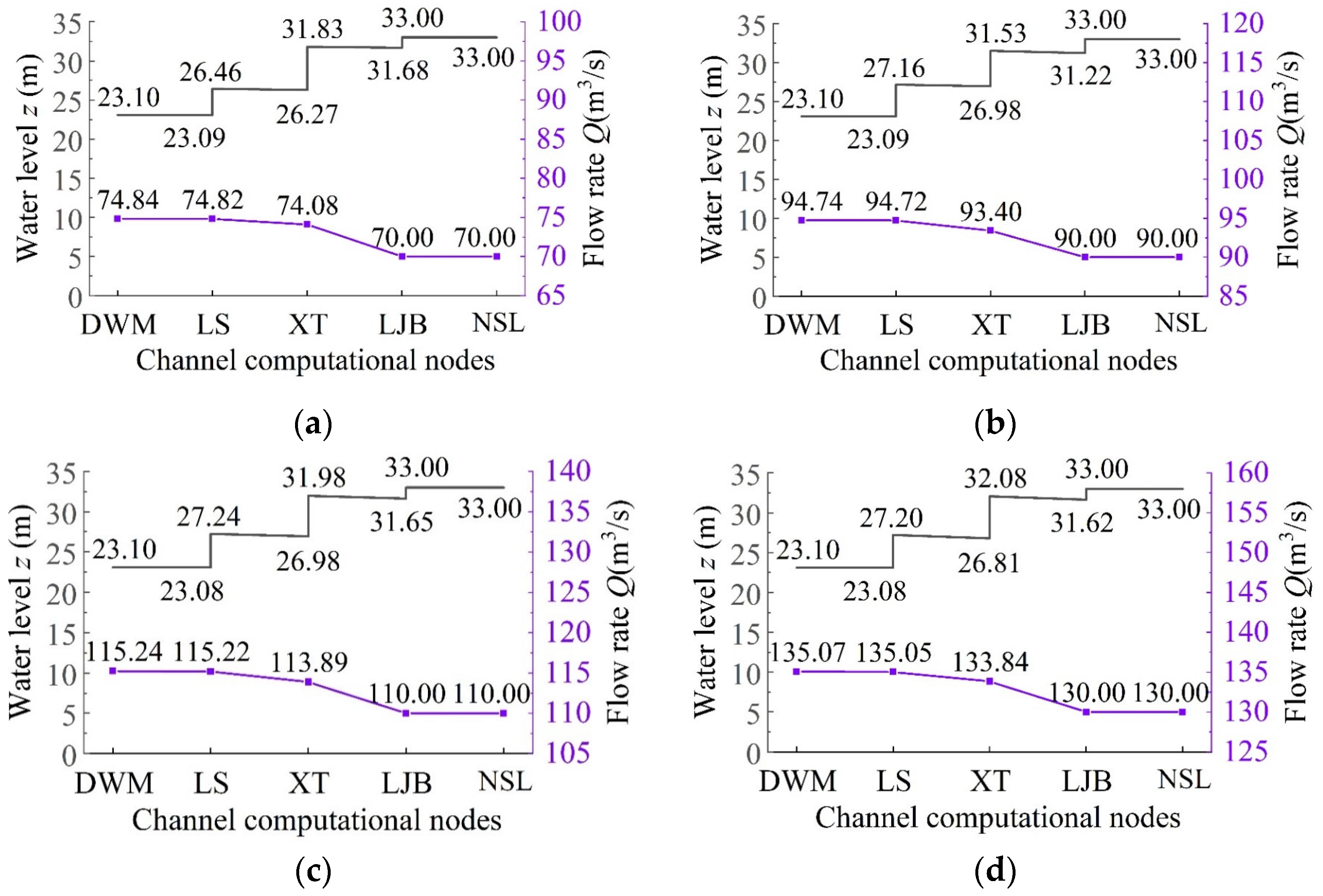
4.2.2. Optimal Schemes
- (1)
- Using scheme library method
- (2)
- Using the double-nesting method
5. Analysis and Discussion
6. Conclusions
- The IWPA was proposed by incorporating the Halton sequence and SA and was tested using ten benchmark functions with varying peaks and dimensions. Compared to PSO, GA, and WPA, the IWPA demonstrated superior convergence ability with respect to the global minimum value and exhibited better stability based on the mean value and standard deviation. Therefore, the IWPA is effective for solving multimodal and high-dimensional models of a WDS with CPSs.
- For the WDS case, double-layer optimal models were developed and solved using the IWPA. To achieve real-time optimal solutions, a method for pre-establishing a scheme library was proposed to avoid repeated calculations. Compared to the double-nesting method, the time complexity was reduced from quadratic to square order, and the CPU time decreased from 10 h to 380 s using the optimal method, demonstrating the time-efficiency of the new approach.
- By considering adjustable pump blade angles and head matching among pumping stations, the optimal schemes were obtained using the IWPA method and the scheme library. Compared to actual schemes, the optimal schemes resulted in power savings of 14.37~20.39% and the flow rate reduction of 0.14~18.34%, translating to a decrease in CO2 emissions of 13~32 tons per day. Overall, the proposed method significantly contributes to energy and water resource savings and environmental protection.
- This study has some limitations. First, the precision of the scheme library was set to 0.01. Higher precision increases CPU time and memory requirements. Therefore, future work will focus on developing machine-learning techniques to reduce the scale of scheme libraries. Second, the water surface line was calculated using iterative methods. Incorporating high-precision hydrodynamic simulations could better account for water and hydraulic losses. Finally, energy savings was the only objective function considered. Future research could explore multi-objective optimization problems considering the reliability and practical of the schemes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khadra, R.; Moreno, M.A.; Awada, H.; Lamaddalena, N. Energy and hydraulic performance-based management of large-scale pressurized irrigation systems. Water Resour. Manag. 2016, 30, 3493–3506. [Google Scholar] [CrossRef]
- Turci, L.D.; Wang, J.C.; Brahmia, I. Adaptive and improved multi-population based nature-inspired optimization algorithms for water pump station scheduling. Water Resour. Manag. 2020, 34, 2869–2885. [Google Scholar] [CrossRef]
- Truettner, C.B.; Barkdoll, B.D. Economic feasibility analysis of variable-speed pumps by simulating 15 multiple water distribution systems. AQUA—Water Infrastruct. Ecosyst. Soc. 2022, 71, 664–670. [Google Scholar] [CrossRef]
- Martin-Candilejo, A.; Martin-Carrasco, F.J. Optimization of a pumping system using convex hyperbola charts: A case study application in Tres Cantos, Madrid, Spain. J. Water Resour. Plan. Manag. 2024, 150, 05023024. [Google Scholar] [CrossRef]
- Feng, X.; Qiu, B.; Wang, Y. Optimizing parallel pumping station operations in an open-channel water transfer system using an efficient hybrid algorithm. Energies 2020, 13, 4626. [Google Scholar] [CrossRef]
- Wang, Y.; Yok, K.T.; Wu, W.Y.; Simpson, A.R.; Weyer, E.; Manzie, C. Minimizing pumping energy cost in real-time operations of water distribution systems using economic model predictive control. J. Water Resour. Plan. Manag. 2021, 147, 04021042. [Google Scholar] [CrossRef]
- Gong, Y.; Zou, W.H. Optimal operation of urban tidal drainage pumping station based on genetic algorithm coupled with head-water level successive approximation. Front. Energy Res. 2023, 10, 1074529. [Google Scholar] [CrossRef]
- Zhao, F.L.; Qiu, B.Y.; Wang, H.J.; Yan, T.X. Energy saving based on a multi-objective optimization model of the tidal pumping station along the coastal area. J. Clean. Prod. 2023, 421, 138513. [Google Scholar] [CrossRef]
- Alsanabani, H.; Iskefiyeli, M.; Yarali, K.; Küçük, H.; Turan, M. A new approach for optimum operation of multi-stage water pump stations. J. Fac. Eng. Archit. Gazi Univ. 2024, 39, 1179–1191. [Google Scholar] [CrossRef]
- Kong, L.Z.; Li, Y.Q.; Chen, R.B. Predictive control for the operation of cascade pumping stations in water supply canal systems considering energy consumption and costs. Appl. Energy 2023, 341, 121103. [Google Scholar] [CrossRef]
- Luna, T.; Ribau, J.; Figueiredo, D.; Alves, R. Improving energy efficiency in water supply systems with pump scheduling optimization. J. Clean. Prod. 2019, 213, 342–356. [Google Scholar] [CrossRef]
- Navarro-Gonzalez, F.J.; Pardo, M.A.; Chabour, H.E.; Alskaif, T. An irrigation scheduling algorithm for sustainable energy consumption in pressurised irrigation networks supplied by photovoltaic modules. Clean Technol. Environ. Policy 2023, 25, 2009–2024. [Google Scholar] [CrossRef]
- Ahcene, B.; Saadia, B. Energetic optimization and evaluation of a drinking water pumping system: Application at the Rassauta station. Water Supply 2019, 19, 472–481. [Google Scholar] [CrossRef]
- Cimorelli, L.; D‘Aniello, A.; Cozzolino, L. Boosting genetic algorithm performance in pump scheduling problems with a novel decision-variable representation. J. Water Resour. Plan. Manag. 2020, 146, 04020023. [Google Scholar] [CrossRef]
- Zhao, Y.P.; Zhang, P.L.; Pu, Y.J.; Lei, H.; Zheng, X.B. Unit operation combination and flow distribution scheme of water pump station system based on Genetic Algorithm. Appl. Sci. 2023, 13, 11869. [Google Scholar] [CrossRef]
- Zhang, Z.; Lei, X.H.; Tian, Y.; Wang, L.L.; Wang, H. Optimized scheduling of cascade pumping stations in open-channel water transfer systems based on station skipping. J. Water Resour. Plan. Manag. 2019, 145, 05019011. [Google Scholar] [CrossRef]
- Yan, P.R.; Zhang, Z.; Lei, X.H.; Hou, Q.Z.; Wang, H. A multi-objective optimal control model of cascade pumping stations considering both cost and safety. J. Clean. Prod. 2022, 345, 131171. [Google Scholar] [CrossRef]
- Liu, X.L.; Tian, Y.; Lei, X.H.; Wang, H. An improved self-adaptive grey wolf optimizer for the daily optimal operation of cascade pumping stations. Appl. Soft Comput. 2019, 75, 473–493. [Google Scholar] [CrossRef]
- Wang, X.N.; Ma, X.M.; Liu, X.L.; Zhang, L.K.; Tian, Y.; Ye, C. Research on optimal operation of cascade pumping stations based on an improved sparrow search algorithm. Water Sci. Technol. 2023, 88, 1982–2001. [Google Scholar] [CrossRef]
- Yu, Z.W.; Yu, J.H.; Liu, J.J.; Hu, C.L.; Hu, S.S.; Wang, J.J.; Zhang, H.H.; Lu, H.T. Prediction model for safe operation of pumping stations optimized by the Sparrow Search Algorithm and BP Neural Network. Adv. Civ. Eng. 2024, 2024, 5358915. [Google Scholar] [CrossRef]
- Creaco, E.; Campisano, A.; Fontana, N.; Marini, G.; Page, P.R.; Walski, T. Real time control of water distribution networks: A state-of-the-art review. Water Res. 2019, 161, 517–530. [Google Scholar] [CrossRef] [PubMed]
- Galuppini, G.; Creaco, E.; Toffanin, C.; Magni, L. Service pressure regulation in water distribution networks. Control Eng. Pract. 2019, 86, 70–84. [Google Scholar] [CrossRef]
- Galuppini, G.; Magni, L.; Creaco, E. Stability and robustness of real-time pressure control in water distribution systems. J. Hydraul. Eng.—ASCE 2020, 146, 04020023. [Google Scholar] [CrossRef]
- Wu, H.S.; Xiao, R.B. Flexible wolf pack algorithm for dynamic multidimensional knapsack problems. Research 2020, 2020, 1762107. [Google Scholar] [CrossRef]
- Chen, X.; Cheng, F.; Liu, C.; Cheng, L.; Mao, Y. An improved wolf pack algorithm for optimization problems: Design and evaluation. PLoS ONE 2021, 16, e0254239. [Google Scholar] [CrossRef] [PubMed]
- Lu, N.; Ma, L. Quantum wolf pack evolutionary algorithm of weight decision-making based on fuzzy control. Chin. J. Electron. 2022, 31, 635–646. [Google Scholar] [CrossRef]
- Fong, S.; Deb, S.; Yang, X.S. A heuristic optimization method inspired by wolf preying behavior. Neural Comput. Appl. 2015, 26, 1725–1738. [Google Scholar] [CrossRef]
- Herrero-Collantes, M.; Garcia-Escartin, J.C. Quantum random number generators. Rev. Mod. Phys. 2017, 89, 015004. [Google Scholar] [CrossRef]
- Kromer, P.; Platos, J.; Snasel, J. Differential evolution for the optimization of low-discrepancy generalized Halton sequences. Swarm Evol. Comput. 2020, 54, 100649. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Kheyrandish, A.; Jamei, M.; Gharabaghi, B. Optimizing operating rules for multi-reservoir hydropower generation systems: An adaptive hybrid differential evolution algorithm. Renew. Energy 2021, 167, 774–790. [Google Scholar] [CrossRef]
- Pang, J.W.; Li, X.H.; Han, S. PSO with mixed strategy for global optimization. Complexity 2023, 2023, 7111548. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Awad, N.H.; Ali, M.Z.; Suganthan, P.N. Ensemble sinusoidal differential covariance matrix adaptation with Euclidean neighborhood for solving CEC2017 benchmark problems. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017; pp. 372–379. [Google Scholar] [CrossRef]






| Function | Algorithm | Min | Mean | SD |
|---|---|---|---|---|
| Matyas: , m = 2, fmin = 0 | PSO | 2.74 × 10−14 | 7.42 × 10−12 | 1.42 × 10−12 |
| GA | 3.15 × 10−9 | 6.57 × 10−8 | 3.59 × 10−8 | |
| WPA | 4.75 × 10−12 | 9.13 × 10−11 | 7.22 × 10−11 | |
| IWPA | 1.34 × 10−14 | 2.37 × 10−12 | 5.96 × 10−13 | |
| Sum squares: , m = 4, fmin = 0 | PSO | 8.14 × 10−8 | 9.06 × 10−6 | 4.22 × 10−6 |
| GA | 1.27 × 10−6 | 9.13 × 10−4 | 7.92 × 10−5 | |
| WPA | 6.32 × 10−10 | 9.75 × 10−7 | 6.56 × 10−8 | |
| IWPA | 2.79 × 10−11 | 5.47 × 10−9 | 8.49 × 10−9 | |
| Trid: , m = 6, fmin = −50 | PSO | −50 | −49.8728 | 3.71 × 10−3 |
| GA | −50 | −49.7453 | 4.79 × 10−3 | |
| WPA | −50 | −50 | 9.16 × 10−7 | |
| IWPA | −50 | −50 | 1.24 × 10−10 | |
| Zakharov: , m = 10, fmin = 0 | PSO | 9.58 × 10−3 | 9.65 × 10−2 | 6.79 × 10−2 |
| GA | 1.58 × 10−3 | 2.71 × 10−2 | 7.40 × 10−2 | |
| WPA | 9.57 × 10−8 | 4.85 × 10−6 | 6.56 × 10−6 | |
| IWPA | 8.00 × 10−11 | 1.42 × 10−10 | 7.06 × 10−11 | |
| Sphere: , m = 30, fmin = 0 | PSO | 0.0277 | 1.7625 | 0.3709 |
| GA | 8.24 × 10−3 | 0.0276 | 0.0680 | |
| WPA | 6.95 × 10−5 | 3.17 × 10−4 | 6.55 × 10−5 | |
| IWPA | 9.50 × 10−9 | 3.44 × 10−8 | 1.19 × 10−8 | |
| Booth: , m = 2, fmin = 0 | PSO | 4.39 × 10−8 | 3.82 × 10−7 | 9.60 × 10−7 |
| GA | 7.66 × 10−9 | 7.95 × 10−7 | 5.85 × 10−7 | |
| WPA | 1.87 × 10−12 | 4.90 × 10−9 | 7.51 × 10−9 | |
| IWPA | 0 | 0 | 0 | |
| Michalewicz: , m = 4, fmin = −9.6602 | PSO | −8.6493 | 0.6376 | 3.1924 |
| GA | −9.6441 | −1.6237 | 3.8752 | |
| WPA | −9.6602 | −9.6599 | 7.98 × 10−7 | |
| IWPA | −9.6602 | −9.6602 | 6.24 × 10−13 | |
| Rastrigin: , m = 10, fmin = 0 | PSO | 7.4229 | 27.2533 | 7.3257 |
| GA | 0.1707 | 10.9961 | 5.5383 | |
| WPA | 1.82 × 10−7 | 2.64 × 10−6 | 1.84 × 10−6 | |
| IWPA | 1.42 × 10−11 | 4.22 × 10−9 | 9.16 × 10−9 | |
| Dixon-price: , m = 10, fmin = 0 | PSO | 17.8003 | 62.9730 | 10.6977 |
| GA | 14.5011 | 39.7565 | 15.5096 | |
| WPA | 8.17 × 10−4 | 8.69 × 10−3 | 8.53 × 10−3 | |
| IWPA | 7.09 × 10−11 | 4.58 × 10−10 | 1.19 × 10−10 | |
| Styblinski-tang: , m = 30, fmin = −1175 | PSO | −1210.10 | −1289.90 | 23.3371 |
| GA | −1221.30 | −1390.80 | 63.3567 | |
| WPA | −1175.40 | −1185.90 | 5.1424 | |
| IWPA | −1175 | −1175 | 6.37 × 10−7 |
| Station Name | Pump Type | Main Transformer | In-Station Transformer | Cables | Number of Pumps N | Head Hz (m) |
|---|---|---|---|---|---|---|
| LS | 2900ZLQ32–6 | S10–20000/110 | SCB10–630/10 | YJV–3 × 150 | 5 | 2.5–6.5 |
| XT | 2900ZLQ32–6 | S10–20000/110 | SCB10–630/10 | YJV–3 × 150 | 5 | 4.0–6.08 |
| LJB | 2800ZGQ–2.5 | S10–M–6300/35 | SCB9–800/10 | YJV–3 × 185 | 4 | 0.1–3.0 |
| Channel Segment | Length L (km) | Bottom Elevation zb (m) | Bottom Width B (m) | Slope Factor m | Groundwater Level zg (m) | Soil Permeability C |
|---|---|---|---|---|---|---|
| 0~1 | 5.30 | 16.50 | 60 | 3 | 24.02~25.02 | 0.0017 |
| 1~2 | 39.90 | 22.00 | 60 | 3 | 25.02~28.20 | 0.0016 |
| 2~3 | 26.02 | 27.00 | 60 | 3 | 28.20~30.10 | 0.0029 |
| 3~4 | 8.50 | 27.00 | 40 | 3 | 30.10~31.50 | 0.0014 |
| Station Name | Head Hz (m) | Flow Rate Qr (m3/s) | Blade Angles β (°) | No. of Pumps n | Power P (kW) |
|---|---|---|---|---|---|
| LS | 2.50 | 70.00 | −2.70 | 2 | 3401.01 |
| 90.00 | 4.00 | 2 | 4615.88 | ||
| 110.00 | −1.59 | 3 | 5317.40 | ||
| 130.00 | 2.94 | 3 | 6697.54 | ||
| XT | 4.00 | 70.00 | 1.13 | 2 | 4496.11 |
| 90.00 | −3.06 | 3 | 5393.64 | ||
| 110.00 | 2.74 | 3 | 7425.57 | ||
| 130.00 | −0.94 | 4 | 7738.75 | ||
| LJB | 3.00 | 70.00 | −2.17 | 3 | 6165.04 |
| 90.00 | −3.06 | 4 | 7668.11 | ||
| 110.00 | 1.76 | 4 | 9337.32 | ||
| 130.00 | 0.36 | 5 | 11,163.96 |
| Channel Segment | End Level Z2 (m) | End Flowrate Q2 (m3/s) | Starting Level Z1 (m) | Starting Flowrate Q1 (m3/s) | Hydraulic Loss ΔH (m) | Water Loss ΔQ (m3/s) |
|---|---|---|---|---|---|---|
| 0~1 | 21.00 | 70.00 | 21.02 | 70.01 | 0.02 | 0.01 |
| 90.00 | 21.03 | 90.01 | 0.03 | 0.01 | ||
| 110.00 | 21.05 | 110.01 | 0.05 | 0.01 | ||
| 130.00 | 21.06 | 130.01 | 0.06 | 0.01 | ||
| 1~2 | 26.00 | 70.00 | 26.22 | 70.56 | 0.22 | 0.56 |
| 90.00 | 26.34 | 90.61 | 0.34 | 0.61 | ||
| 110.00 | 26.48 | 110.66 | 0.48 | 0.66 | ||
| 130.00 | 26.62 | 130.72 | 0.62 | 0.72 | ||
| 2~3 | 30.90 | 70.00 | 31.06 | 72.81 | 0.16 | 2.81 |
| 90.00 | 31.15 | 92.75 | 0.25 | 2.75 | ||
| 110.00 | 31.26 | 112.71 | 0.36 | 2.71 | ||
| 130.00 | 31.38 | 132.70 | 0.48 | 2.70 | ||
| 3~4 | 31.40 | 70.00 | 31.47 | 70.21 | 0.07 | 0.21 |
| 90.00 | 31.52 | 90.21 | 0.12 | 0.21 | ||
| 110.00 | 31.57 | 110.21 | 0.17 | 0.21 | ||
| 130.00 | 31.63 | 130.21 | 0.23 | 0.21 |
| Operations | Time Complexity |
|---|---|
| Population initialization | O (1) |
| Selecting head wolf | O (M) |
| Wandering update | O (K × M × D) ≈O (M) |
| Raiding update | O (K × M × D) ≈ O (M) |
| Siege update and elimination mechanism | O (K × M + K × M2) ≈ O (M2) |
| SA | O (K × D × L) ≈ O (1) |
| Operations | Time Complexity |
|---|---|
| Population initialization | O (1) |
| Selecting head wolf | O (M × (M12 + R1)) ≈ O (M3) |
| Wandering update | O (M × (M12 + R1)) ≈ O (M3) |
| Raiding update | O (M × (M12 + R1)) ≈ O (M3) |
| Siege update and elimination mechanism | O (M2 × (M12 + R1)) ≈ O (M4) |
| SA | O (1 × (M12 + R1)) ≈ O (M2) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, X.; Wang, Y.; Sun, X.; Qiu, B. Real-Time Optimal Scheduling of a Water Diversion System Using an Improved Wolf-Pack Algorithm and Scheme Library. Water 2024, 16, 2420. https://doi.org/10.3390/w16172420
Feng X, Wang Y, Sun X, Qiu B. Real-Time Optimal Scheduling of a Water Diversion System Using an Improved Wolf-Pack Algorithm and Scheme Library. Water. 2024; 16(17):2420. https://doi.org/10.3390/w16172420
Chicago/Turabian StyleFeng, Xiaoli, Yongxing Wang, Xiaoyu Sun, and Baoyun Qiu. 2024. "Real-Time Optimal Scheduling of a Water Diversion System Using an Improved Wolf-Pack Algorithm and Scheme Library" Water 16, no. 17: 2420. https://doi.org/10.3390/w16172420
APA StyleFeng, X., Wang, Y., Sun, X., & Qiu, B. (2024). Real-Time Optimal Scheduling of a Water Diversion System Using an Improved Wolf-Pack Algorithm and Scheme Library. Water, 16(17), 2420. https://doi.org/10.3390/w16172420







