A Theoretical Derivation and Comparison Method for the Optimal Location for Energy Dissipation Boxes
Abstract
1. Introduction
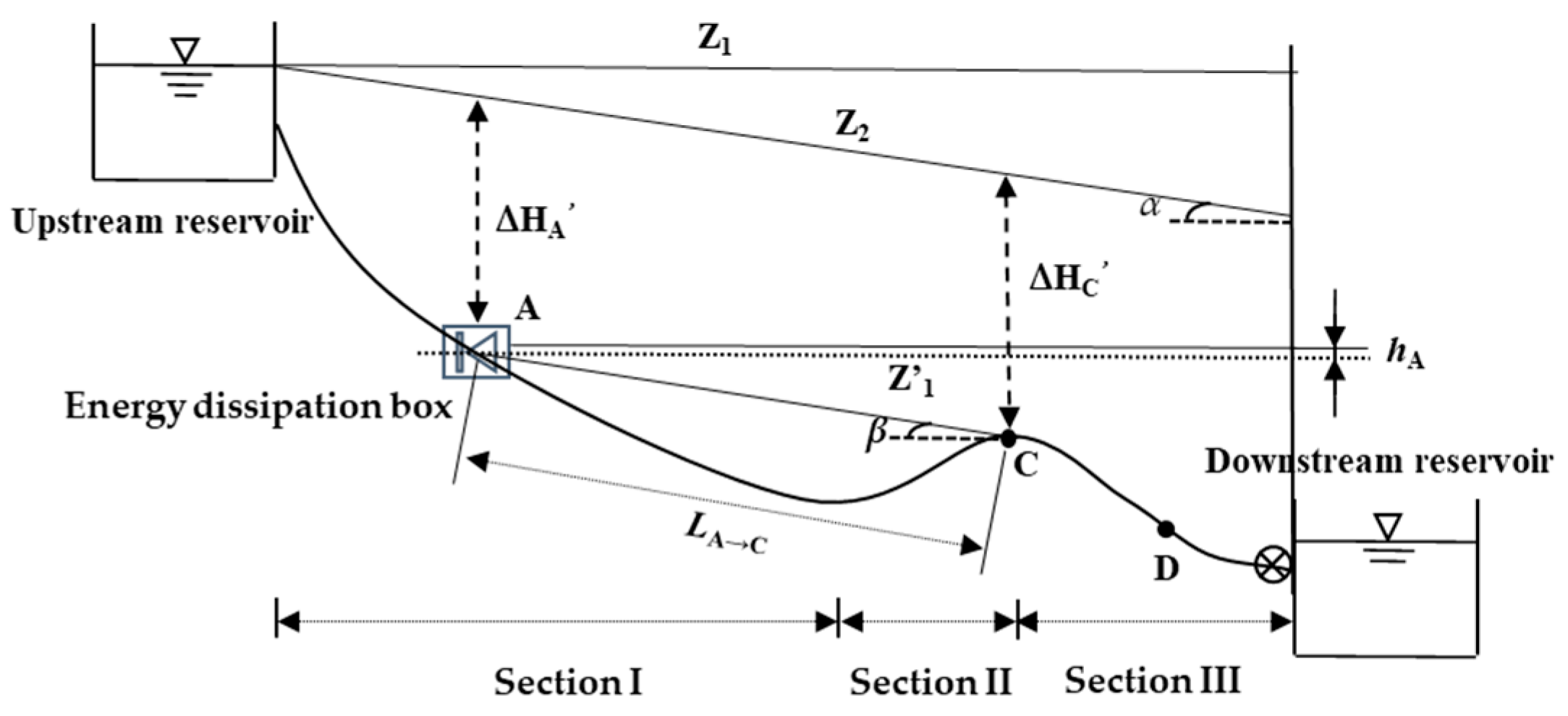
2. Theoretical Equations for the OL of the EDB
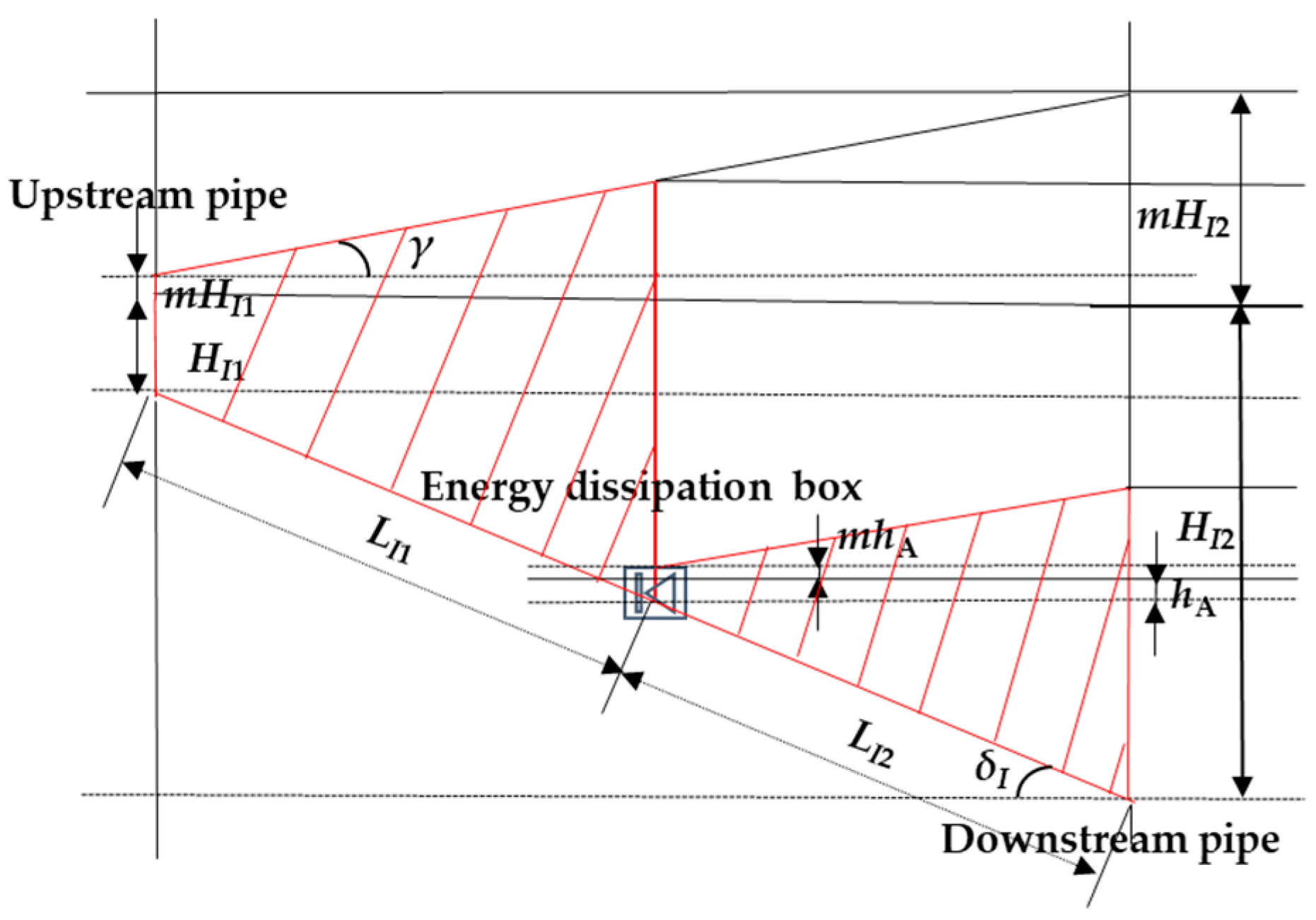
2.1. Theoretical Equations for the EDB’s Critical Location
2.2. Theoretical Equations for the EDB’s Extreme Location
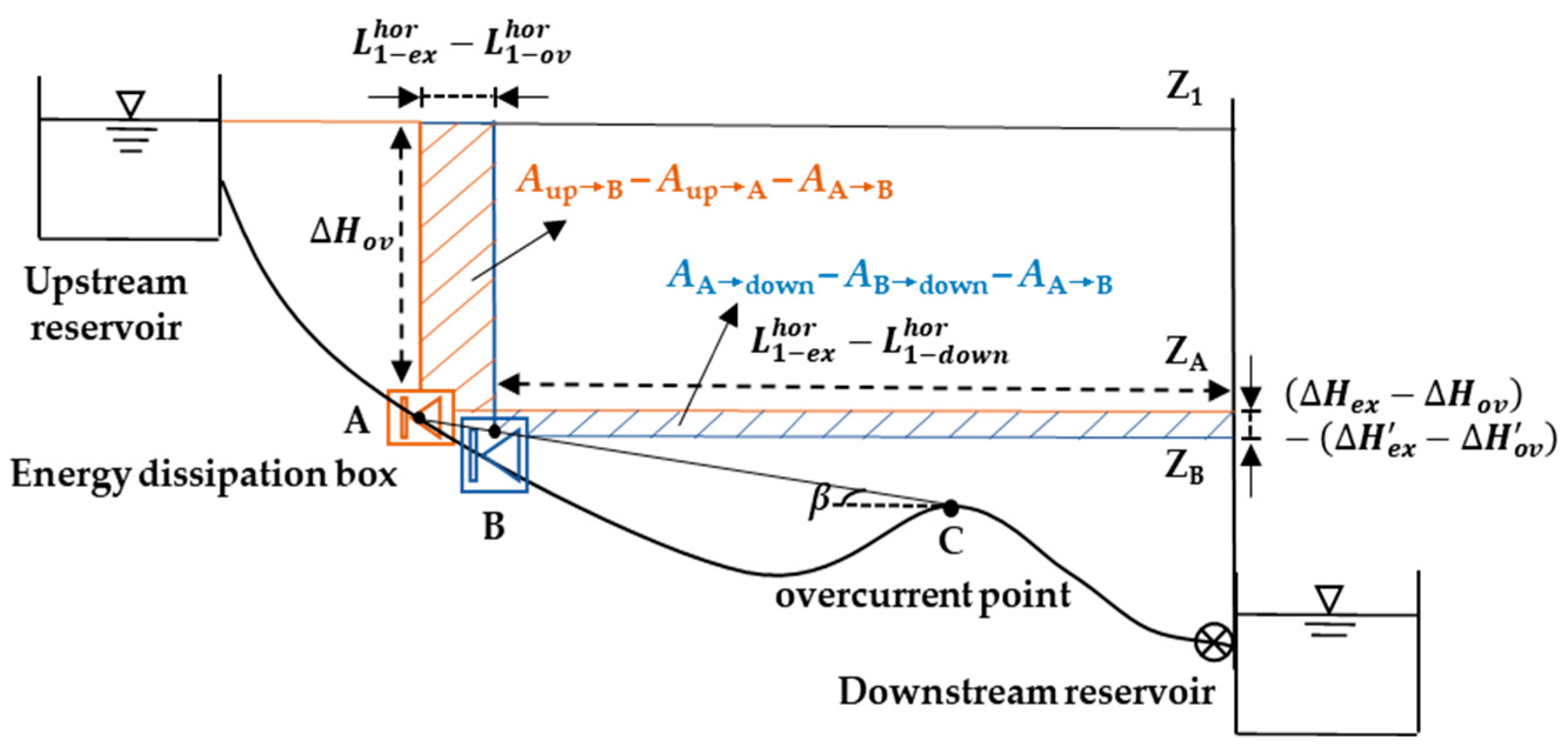
2.3. Comparison Method for OL of the EDB
- (1)
- When , the extreme location coincides with the critical location.
- (2)
- When , the comparison of SMHPHs for EDBs located at the extreme location and critical location is between Aup→A Aup→B AB→A and AB→down AA→down AB→A, i.e., and . If , the OL of the EDB is at the extreme point where the SMHPH reaches the minimum.
3. Impact of EDB Position on the Water Transition System
3.1. Constant Flow Assessment of Gravity Flow System with No EDB
3.2. Theoretical Evaluation of the EDB’s OL
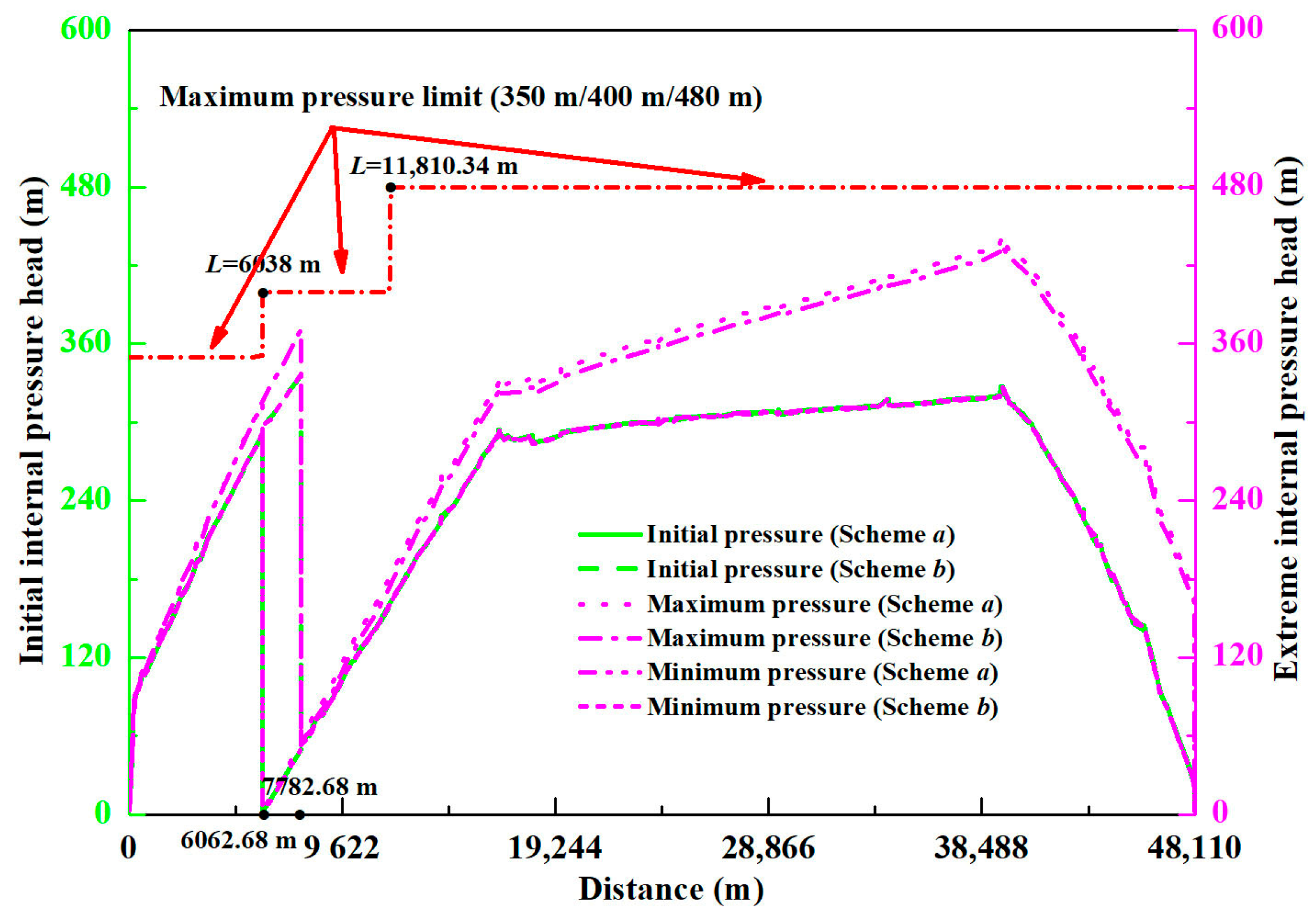
3.3. Comparative Study of Protective Effects at Various EDB Locations
4. Conclusions
- A simplified theoretical equation for the extreme location of the EDB is derived by assuming that the local topographic trend of the gravity flow system can be disregarded. This equation is based on a straight line connecting the starting and ending centerline elevations in each refining divided section, with the aim of minimizing SMHPHs along the overall pipe.
- Given that the pipeline remains under positive pressure during regular operations and SMHPHs reach a lower value, we propose a comprehensive comparison method for assessing the OL of EDBs between the critical and the extreme locations. It is preferable to position an EDB as proximate to the lower reservoir as feasible to alleviate pressure fluctuations. Therefore, when the difference in SMHPHs is negligible, the OL is preferably closer to the downstream. When there is a significant difference between these two locations, the control indicator of SMHPHs in the design stage and the PH fluctuation in the pipelines and the WL fluctuation inside an EDB in the transition process should be considered to determine the OL. In particular, we propose methods for addressing the situation where the initial water depth of the theoretical extreme location downstream of the critical location is excessively large: adjusting the position of the extreme location by disregarding the certain end segment pipelines and determining whether the SMHPH at the adjusted extreme location is lower than that at the critical location.
- Taking the following project as an example, through the utilization of the comprehensive comparison method, the OL of an EDB is located at the extreme location in the design stage. The SMHPH of the OL is smaller than that of the upstream critical location in terms of lowering the initial PH in a broader range of the pipeline, and the result validates the feasibility of the position adjustment methodology. Under the same cross-sectional area of the EDB, the OL could mitigate the pressure oscillations along the pipeline compared to the upstream position. Additionally, due to the larger water depth in the box, given a fixed initial water volume in the box through reducing the cross-sectional area, the OL provides superior protection from water hammer positive pressure compared to the precise location with a larger area. It maximizes the utilization of water depth in the box, reducing the total volume and saving in project investment.
- This research offers a certain theoretical and numerical backing for choosing the OL for an EDB in an LHGWSS rather than exclusively positioning the EDB at the designated places or critical location that meets the overcurrent capacity along the pipe. This approach can reduce the design workload associated with positioning the EDB to some extent.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PH | pressure head |
| OL | optimal location |
| EDB | energy dissipation box |
| EDV | energy dissipation valve |
| LHGWSS | long-distance and high-drop gravitational flow transition system |
| PRV | pressure relief valve |
| SMHPH | sum-of-maximum hydrostatic pressure head |
References
- Fan, J.L.; Wang, J.D.; Zhang, X.; Kong, L.S.; Song, Q.Y. Exploring the changes and driving forces of water footprints in China from 2002 to 2012: A perspective of final demand. Sci. Total Environ. 2019, 650, 1101–1111. [Google Scholar] [CrossRef] [PubMed]
- Swamee, P.K.; Sharma, A.K. Gravity flow water distribution system design. J. Water Supply Res. Technol. AQUA 2000, 49, 169–179. [Google Scholar] [CrossRef]
- Hashemi, S.; Filion, Y.; Speight, V.; Long, A. Effect of pipe size and location on water-main head loss in water distribution systems. J. Water Resour. Plann. Manag. 2020, 146, 06. [Google Scholar] [CrossRef]
- Zhang, K.Q.; Karney, B.W.; Mcpherson, D.L. Pressure-relief valve selection and transient pressure control. J. Am. Water Works Assoc. 2008, 100, 62–69. [Google Scholar] [CrossRef]
- Kim, H.; Kim, S. Optimization of pressure relief valve for pipeline system under transient induced cavitation condition. Urban Water J. 2020, 16, 718–726. [Google Scholar] [CrossRef]
- Zhang, B.; Wan, W.; Shi, M. Experimental and Numerical Simulation of Water Hammer in Gravitational Pipe Flow with Continuou Air Entrainment. Water 2018, 10, 928. [Google Scholar] [CrossRef]
- Desai, S.; Desai, A.; Karande, V. Design and weight optimization of buffer relief valve using FEA with experimental validation. Mater. Today Proc. 2020, 27, 1466–1472. [Google Scholar] [CrossRef]
- Jia, W. Dynamic Characteristics and Stability Analysis of Conical Relief Valve. Mechanika 2019, 25, 25–31. [Google Scholar] [CrossRef]
- Izuchi, H. Stability analysis of safety valve. In Proceedings of the 10th Topical Conference on Gas Utilization, San Antonio, TX, USA, 21–25 March 2010; AICE: Sydney, NSW, Australia, 2010. [Google Scholar]
- Li, D.F.; Xia, X.L.; Dai, G.L.; Ruan, L.M. Numerical simulation on fluid dynamic behavior of high-pressure safety valves. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010; IEEE: New York, NY, USA, 2010; pp. 1–4. [Google Scholar]
- Foster, R.S. Surge protection design for the city and county of San Francisco water transmission system. Pipelines Constr. Environ. 1998, 103–112. Available online: https://trid.trb.org/view/498654 (accessed on 30 June 2024).
- Riasi, A.; Tazraei, P. Numerical analysis of the hydraulic transient response in the presence of surge tanks and relief valves. Renew. Energy 2017, 107, 138–146. [Google Scholar] [CrossRef]
- Geng, Y.F.; Wang, Z.L.; Jin, S. FVS scheme for severe transient flow in pipe networks. J. Hydrodyn. 2005, 17, 621–628. [Google Scholar]
- Gang, H.; Meiling, D.; Jinliang, G.; Guobin, L. Optimization of multi-level pressure reduction program with super high drop gravity in long distance distribution pipelines. Water Technol. 2012, 6, 51–53. (In Chinese) [Google Scholar]
- Jiang, G.; BaoJun, Z.; Tao, Y. Study on water hammer elimination in long distance water pipeline with combined application of various protection measures. Jiangsu Vocat. Inst. Archit. Technol. 2019, 19, 38–41. (In Chinese) [Google Scholar]
- Elshorbagy, W.E.; Al Maamari, M.S. Pressure Utilization In Water Transmission Pipelines considering Transient Conditions. In Proceedings of the Water Distribution System Analysis 2010—WDSA2010, Tucson, AZ, USA, 12–15 September 2010. [Google Scholar]
- Bolin, C.; Engeda, A. Analysis of flow-induced instability in a redesigned steam control valve. Appl. Therm. Eng. 2015, 83, 40–47. [Google Scholar] [CrossRef]
- Yanting, L. Calculation and analysis of gravitational flow transition of Yintao water supply project in Tianshui city. Water Conserv. Sci. Technol. Econ. 2016, 22, 31–36. (In Chinese) [Google Scholar]
- Jiang, X.; Jie, S. Research on water hammer characteristics of long distance water supply system with high fall head. Yellow River 2015, 37, 103–106. (In Chinese) [Google Scholar]
- Ni, W.; Zhang, J.; Chen, S. Optimal Location of Energy Dissipation Box in Long Distance and High Drop Gravitational Water Supply System. Water 2021, 13, 461. [Google Scholar] [CrossRef]
- Zhang, J.; Suo, L.; Hu, J.; Ma, S. Study on water hammer control by one-way surge tank in long-distance water-supply project. J. Hydroelectr. Eng. 2011, 30, 49–56. (In Chinese) [Google Scholar]
- Zhang, J.; Zhu, X.; Qu, X.; Ma, S. Study on theoretical analysis of air valve in long-distance water-supply project. J. Hydraul. Eng. 2011, 9, 1025–1033. (In Chinese) [Google Scholar]
- SL 511-2011; Technical Code for Mechanical and Electrical Design of Water Conservancy and Hydropower Projects. National Standards of the People ‘s Republic of China: Beijing, China, 2011.

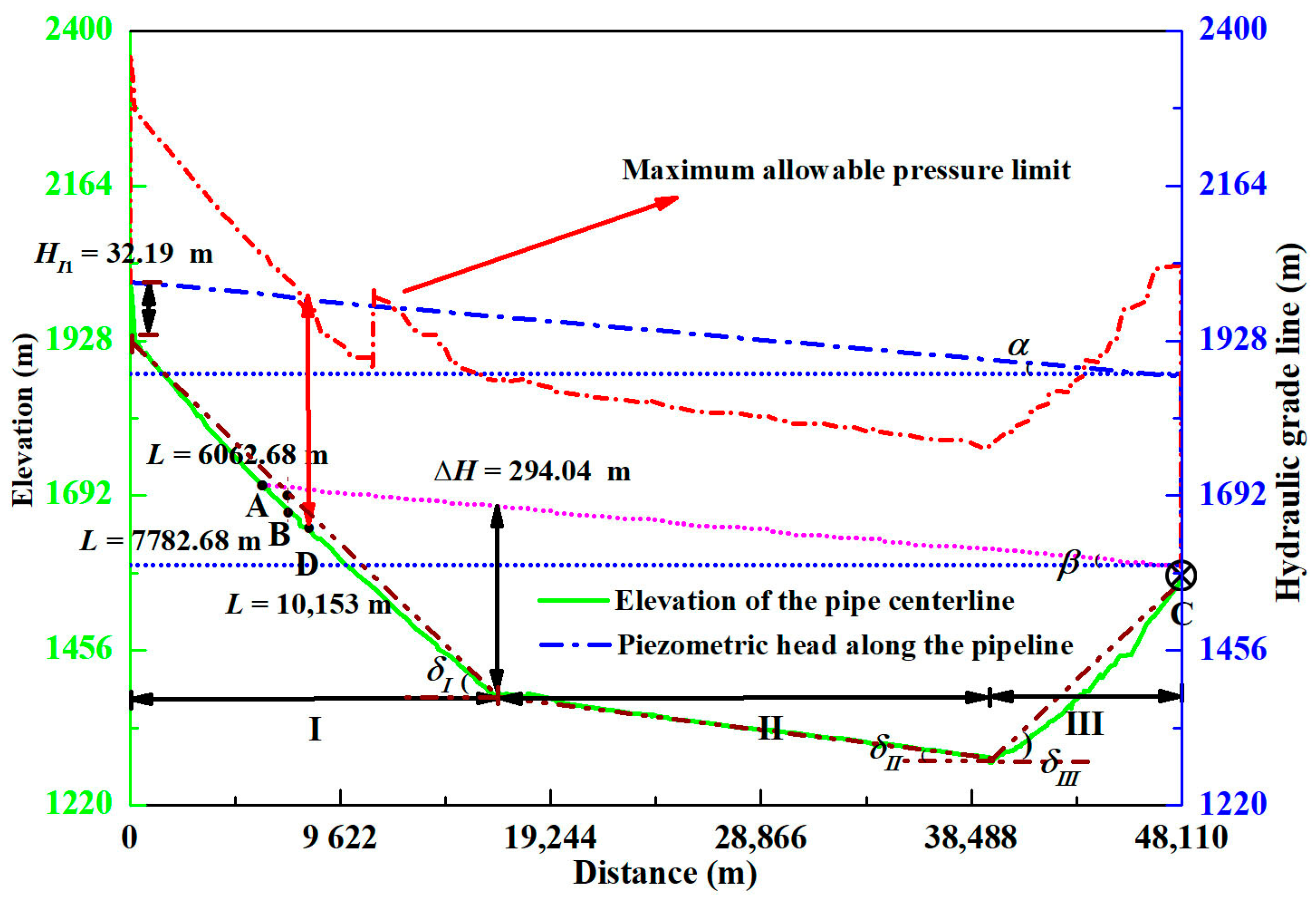


| Section I | Section II | Section III | Water Depth | |||||
|---|---|---|---|---|---|---|---|---|
| LI (m) | HI1 (m) | sinδI | cosδI | LII (m) | sinδII | LIII (m) | sinδIII | hA (m) |
| 16,626.56 | 32.19 | 0.033 | 0.999 | 22,701.44 | 0.004 | 8684.41 | −0.032 | 3.26 |
| Valve Diameter | Opening Degree | Action Time (s) | Valve Closing Slope | Valve Closing Time (s) | |
|---|---|---|---|---|---|
| Model a | DN1000 | 1 | 120 | 1/400 | 400 |
| DN1200 | 0.9766 | 0 | 1/600 | 585 | |
| DN800 | 0.6928 | 415 | |||
| Models b and c | DN1000 | 1 | 120 | 1/400 | 400 |
| DN1200 | 0.9984 | 0 | 1/586 | 585 | |
| DN800 | 0.6996 | 1/593 | 415 |
| Model | Maximum PH before Box (m) | Minimum PH before Box (m) | Maximum PH behind Box (m) | Minimum PH behind Box (m) |
|---|---|---|---|---|
| Model a | 304.06 | 2.27 | 442.29 | 1.47 |
| Model b | 344.9 | 2.26 | 435.39 | 3.81 |
| Model c | 344.99 | 2.24 | 421.64 | 3.93 |
| Model | Initial Water Depth | Cross-Sectional Region | Maximum Water Depth | Minimum Water Depth | Highest Water Depth Amplitude | Lowest Water Depth Amplitude | Volume |
|---|---|---|---|---|---|---|---|
| Model a | 3.26 m | 25 m2 25 m2 | 3.73 m | 2.01 m | 0.47 m | 1.25 m | 85.75 m2 |
| Model b | 54.5 m | 54.93 m | 53.19 m | 0.43 m | 1.31 m | 1364.5 m2 | |
| Model c | 54.5 m | 1.5 m2 | 59.04 m | 36.73 m | 4.54 m | 17.77 m | 87.42 m2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, W.; Hu, Y.; Li, Z. A Theoretical Derivation and Comparison Method for the Optimal Location for Energy Dissipation Boxes. Water 2024, 16, 2189. https://doi.org/10.3390/w16152189
Ni W, Hu Y, Li Z. A Theoretical Derivation and Comparison Method for the Optimal Location for Energy Dissipation Boxes. Water. 2024; 16(15):2189. https://doi.org/10.3390/w16152189
Chicago/Turabian StyleNi, Weixiang, Yanan Hu, and Zhonghua Li. 2024. "A Theoretical Derivation and Comparison Method for the Optimal Location for Energy Dissipation Boxes" Water 16, no. 15: 2189. https://doi.org/10.3390/w16152189
APA StyleNi, W., Hu, Y., & Li, Z. (2024). A Theoretical Derivation and Comparison Method for the Optimal Location for Energy Dissipation Boxes. Water, 16(15), 2189. https://doi.org/10.3390/w16152189





