Tree-Based Machine Learning and Nelder–Mead Optimization for Optimized Cr(VI) Removal with Indian Gooseberry Seed Powder

Abstract

Wastewater containing a mixture of heavy metals, a byproduct of chemical, petrochemical, and refinery activities driven by urbanization and industrial expansion, poses significant environmental threats. Analyzing such wastewater through adsorbate-adsorbent experiments yields extensive datasets. However, traditional methodologies like the Box–Behnken design (BBD) within the response surface methodology (RSM) struggle with managing large datasets and capturing the complex, nonlinear relationships inherent in such experimental data. To address these challenges, ML techniques have emerged as promising tools for accurately predicting the removal percentage of heavy metals from wastewater. In this study, we utilized tree-based regression models—specifically decision tree regression (DTR), random forest regression (RFR), and extra tree regression (ETR)—to forecast the efficiency of gooseberry seed powder in removing chromium (Cr(VI)) from wastewater. Additionally, we employed an ML-based Nelder–Mead optimization approach to identify the optimal values for key features (initial Cr(VI) concentration, pH, and Indian gooseberry powder dosage) which maximized the Cr(VI) removal percentage. Our experimental results reveal that the ETR model achieved an impressive $R^2$ score of 0.99, demonstrating a low error rate in predicting the Cr(VI) removal percentage. Furthermore, we used DTR-Nelder–Mead, RFR-Nelder–Mead, and ETR-Nelder–Mead optimization approaches on a synthesized dataset of 2000 instances while varying the initial Cr(VI) concentration, pH, and Indian gooseberry powder dosage. The analysis determined that the DTR-Nelder–Mead and RFR-Nelder–Mead approaches yielded the highest Cr(VI) removal percentages of 78.21% and 78.107% at an initial concentration of 95.55 mg/L, respectively, a pH level of four, and an adsorbent dosage of 8 g/L of gooseberry seed powder. Furthermore, the ETR-Nelder–Mead approach obtained the maximum Cr(VI) removal percentage of 85.11% at an initial concentration of 99.25 mg/L, a pH level of 4.97, and an adsorbent dosage of 9.62 g/L of gooseberry seed powder. These results reported an increase in the Cr(VI) removal percentage ranging from 4.66% to 11.56% more than the Cr(VI) removal percentage obtained by experimentation. These findings underscore the efficacy of tree-based regression models and ML-based Nelder–Mead optimization in elucidating chromium removal processes from wastewater, offering valuable insights into effective treatment strategies.

1. Introduction

The surge in urbanization and industrial activities has triggered a notable upsurge in wastewater volumes stemming from chemical, petrochemical, and refinery processes. Within this wastewater milieu, heavy metals stand out as significant environmental hazards, often being discharged into water bodies without adherence to stringent environmental regulations [1,2]. Among these, hexa-valent chromium (Cr(VI)), notorious for its high toxicity, carcinogenicity, and mutagenicity, poses a particular concern [3]. For instance, $C{r}_2{O}_7^{2-}$ has been implicated in the onset of lung cancer [4,5]. Activities such as metal finishing, leather tanning, electroplating, and textile production are recognized as common sources of chromium contamination in wastewater. Moreover, both Cr(III) and Cr(VI) have been identified as pertinent constituents in terms of toxicity risks within wastewater. It is widely acknowledged that Cr(VI) exhibits significantly higher toxicity compared with Cr(III), mainly due to its high solubility in water, mobility, and facile reduction properties [6]. The toxicity of Cr(VI) arises from its oxidizing nature and its potential to generate free radicals during the reduction process from Cr(VI) to Cr(III) within living cells [7]. The standard tolerance limit for Cr(VI) in wastewater streams is typically set to 0.05 mg/L [8].

1.1. Motivation

The conventional experimental methods for Cr(VI) removal using bio-absorption often lack a comprehensive understanding of the interactions between various process parameters and their optimal values within the experimental parameter range. Consequently, significant additional time is required to gain insights into these issues and identify the optimal combination of process parameters which maximizes Cr(VI) removal. Such insights are crucial for reducing process costs and improving process efficiency, enabling the treatment of larger volumes of wastewater. One effective approach for obtaining deeper insights into the interaction and significance of various process parameters, as well as identifying optimal parameter values, is the implementation of RSM using multivariable statistical approaches, which has proven valuable in achieving these objectives.

However, traditional statistical tools such as BBD in the RSM [9,10,11,12,13] have inherent limitations when it comes to predicting removal efficiency, while ML models offer significant advantages in this regard. The BBDs in the RSM rely on the assumption of linearity, which constrains their ability to capture nonlinear relationships, ultimately compromising their accuracy and adaptability. In contrast, ML models excel in capturing complex nonlinear patterns and interactions, enabling more precise and flexible forecasts of removal efficiency. Furthermore, ML models leverage a data-driven approach, allowing them to adapt to diverse datasets and uncover subtle patterns which may be overlooked by traditional designs, such as BBDs in the RSM. Moreover, the versatility of ML models extends to their ability to handle high-dimensional data effortlessly, automatically discerning pertinent features and interactions sans manual intervention. Their resilience to noise and outliers stems from their capacity to glean patterns from diverse datasets, mitigating the impact of erroneous measurements.

Additionally, ML models can seamlessly incorporate temporal dynamics, adapting their predictions in response to evolving conditions or system behavior. This adaptability proves invaluable when the removal efficiency is subject to factors which fluctuate over time, such as fouling or aging effects. Furthermore, the innate generalization capability of ML models empowers them to furnish reliable forecasts for removal efficiency across novel scenarios beyond the confines of experimental design constraints. Nonetheless, it is imperative to acknowledge that the efficacy of ML models hinges on various factors, including the quality of training data, adept feature engineering, judicious model selection, and rigorous validation. Domain expertise and interpretability considerations also warrant attention when weighing the merits of ML models against traditional methodologies like the RSM and BBDs. Connected to this, a proposed work considered the experimental data, which was carried out by Krishna et al. [14]. These data were analysed thoroughly through ML and optimization approaches in order to determine the optimal parameters and their impact along with prediction analysis.

1.2. The Literature

Traditional methods for Cr(VI) removal from wastewater encompass various techniques, such as chemical precipitation [15], ion exchange [16], reduction processes [17], electro-chemical methods [18], extraction techniques [19], membrane processes [20], evaporation methods [21], and foam separation processes [22]. While these methods offer advantages, they often encounter limitations like high costs or inefficiency at lower concentrations. An alternative approach to addressing these challenges is bio-absorption, which has been proven to be effective and cost-efficient in Cr(VI) removal from wastewater, employing naturally available agricultural waste materials. Numerous bio-materials, including tamarind seeds, rice husk, maize bran, walnut hull, groundnut hull, Limonia acidissima hull powder, and Ragi husk powder, have been explored as adsorbents for Cr(VI) removal from aqueous solutions [23]. Furthermore, the experiments conducted by Krishna et al. [14] extensively explored batch adsorption studies using Indian gooseberry seed powder for Cr(VI) adsorption from synthetic wastewater solutions. These studies involved varying parameters such the as initial Cr(VI) solution concentration, pH level, and biomass dosage to examine their influence on the adsorption process.

In the context of advocating for ML over BBDs in the RSM for predicting chromium removal, several studies have delved into the advantages of ML models in this realm. Notably, Haripriyan Uthayakumar et al. [24], Meghna Datta et al. [25], and Mohd Zafar et al. [26] successfully harnessed artificial neural networks (ANNs) to accurately forecast chromium removal efficiency based on experimental data. Similarly, Xinzhe Zhu et al. [27] leveraged ML models to attain precise predictions of chromium removal. Additionally, Mohammad Mahbub Kabir et al. [28] employed a tea waste-polyvinyl alcohol (TW-PVA) mixture to eliminate Cr(VI) from aqueous solutions. Furthermore, R. Ali Khan Rao et al. [29,30] proposed the removal of Cr(VI) through the medicinal plant materials of Artimisia absinthium and Litchi chinensis fruit peels. Moreover, as can be gleaned from the literature [14,24,25,26,27], a detailed batch experimental study was carried out for the removal of Cr(VI) from wastewater using Indian gooseberry seed powder.

1.3. Research Gaps

The following are the research gaps identified from the literature:

• The literature indicates that the traditional statistical approach of BBDs in the RSM for optimizing Cr(VI) removal from wastewater struggle to capture nonlinear relationships between the process parameters and removal efficiency.
• In addition, the focus of conventional experimental approaches for Cr(VI) removal using bio-absorption materials, which are lacking in terms of identifying optimal combinations of process parameters, may lead to increased experimentation time and cost.
• Furthermore, previous research by Krishna et al. [14], which explored the use of Indian gooseberry seed powder as an adsorbent for Cr(VI) removal, had a gap in the application of ML models for analyzing and optimizing this process. Similarly, the existing literature also does not fully capture the intricate interactions between various process parameters (such as the initial Cr(VI) concentration, pH level, and adsorbent dosage) and their impact on removal efficiency.

1.4. Novelty

The objective of the present study was to find out the optimum process parameters when using ML models and Nelder–Mead optimization for the removal of chromium (VI) from wastewater with Indian gooseberry seed powder as an adsorbent. Aligned with this research trend, the present study utilizes ML models to scrutinize experimental data pertaining to Cr(VI) removal, as delineated in [14]. Notably, the application of ML models and ML-based Nelder–Mead optimization for Cr(VI) removal using Indian gooseberry seed powder represents a novel approach, which is corroborated by the literature review. By harnessing ML and Nelder–Mead optimization techniques, this study contributes to the burgeoning knowledge in predicting and attaining optimal feature values to enhance chromium removal efficiency, particularly within the specific context of Indian gooseberry seed powder.

1.5. Major Contributions

This work addresses the research gaps stated in Section 1.3 by exploring the capabilities of tree-based ML models and Nelder–Mead optimization approaches for maximization of Cr(VI) removal when using Indian gooseberry seed powder as an adsorbent. The contributions of this study are aimed to achieve following key issues:

• Better prediction of efficiency in removing Cr(VI): ML models outperform conservative BBD approaches in realizing sophisticated nonlinear connections. Consequently, this permits more exact estimations of Cr(VI) removal efficiency using different process parameters.
• Improved maximization through optimization: The proposed approach employs ML-based Nelder–Mead optimization for maximizing Cr(VI) removal, and it reduces the experimentation time and treatment cost and allows efficient processing of larger wastewater volumes.
• Integration of ML models with optimization: The combination of ML models with optimization is a novel approach which has not been previously reported in the literature. Moreover, it offers a new direction for exploring this bio-absorption material.

1.6. Organization

The remainder of this work is structured as follows. Section 2 presents the experimentation procedure and data collection methodology. Section 3 elucidates the architecture and functionality of the proposed approach. Subsequently, Section 4 delineates the experimental results, their comparison, and the ensuing analysis. Finally, Section 5 encapsulates the key findings of this study and offers concluding remarks.

2. Materials and Methods

In this work, the results obtained from the experimentation have been organized and presented in

Table 1. The instances of the dataset.

Sno	Initial Concentration of Cr(VI)	pH	Adsorbent Dosage (g/L)	Percentage Removal of Cr(VI)	Sno	Initial Concentration of Cr(VI)	pH	Adsorbent Dosage (g/L)	Percentage Removal of Cr(VI)
1	20	2	8	73.55	29	100	1	6	59.35
2	20	2	6	65.09	30	100	2	6	60.94
3	60	2	8	71.53	31	20	1	6	63.47
4	100	2	8	69.44	32	20	2	4	61.48
5	20	2	10	72.47	33	60	1	6	61.46
6	80	2	8	70.32	34	40	2	6	64.27
7	80	1	8	68.71	35	20	1	8	71.98
8	20	1	10	70.85	36	80	1	6	60.24
9	80	3	10	66.45	37	80	2	6	61.83
10	100	1	8	67.85	38	20	3	6	62.33
11	100	3	8	64.93	39	20	4	8	65.51
12	40	1	8	71.14	40	20	5	8	60.88
13	40	2	10	71.68	41	20	1	2	51.23
14	60	1	10	68.83	42	100	3	6	58.17
15	40	3	8	68.25	43	20	2	2	52.82
16	80	2	10	69.25	44	20	4	2	47.82
17	80	1	10	67.62	45	80	3	6	59.05
18	100	2	10	68.37	46	20	1	6	63.47
19	100	1	10	66.74	47	60	3	6	60.26
20	80	3	8	65.82	48	20	4	6	59.09
21	20	3	10	69.71	49	20	5	6	55.32
22	60	3	10	67.66	50	40	2	8	72.74
23	100	3	10	65.54	51	40	1	6	62.65
24	60	2	8	71.53	52	60	3	8	67.02
25	80	2	8	70.32	53	20	3	8	69.07
26	20	2	8	73.55	54	60	1	8	69.9
27	60	2	10	70.48	55	60	2	6	63.05
28	100	2	8	69.44	56	40	3	8	68.81

[14]. Additionally, as explained in Section 3.1, the curve-fitting technique was applied to the experimental data. Subsequently, data synthesis was performed using the fitted curve as described in Section 3.2.

2.1. Summary of Experimental Investigations

Indian gooseberry seeds sourced from local markets underwent a rigorous preparation process. Initially, they were meticulously washed, dried, and subjected to crushing using primary crushers. Subsequently, the crushed seeds were air-dried under sunlight until reaching a constant weight. Further grinding was accomplished using roll crushers and hammer mills. The resultant material underwent screening through British Standard screen meshes to achieve the desired particle sizes of 63 µm, 89 µm, and 125 µm. Finally, the processed products were stored in glass bottles in preparation for the heavy metal removal investigations.

A stock solution of chromium (VI) was prepared by dissolving 2.835 g of 99% $K_{2}C{r}_2{O}_7$ in double distilled water within a 1.0 L volumetric flask, yielding a concentration of 1000 ppm (mg/L). Synthetic samples with varying concentrations of chromium (VI) were derived from this stock solution through appropriate dilutions.

Batch mode adsorption studies were conducted to explore chromium removal from wastewater, examining the influence of several parameters. These parameters included the initial concentration of the metal (ranging from 20 to 100 mg/L), adsorbent dosage (ranging from 0.05 to 0.5 g in 50 mL of solution), agitation time (ranging from 5 to 120 min), adsorbent size (utilizing mesh sizes of 63 µm, 89 µm, and 125 µm), and pH level (ranging from 1 to 9). The experiments were conducted at a consistent temperature of 303 K.

2.2. Dataset

The experimental dataset [14], as shown in Table 1, consisted of 56 instances and 4 features, in which 3 features, namely “initial concentration of Cr(VI)”, “pH”, and “adsorbent dosage”, are the independent features and “percentage removal of Cr(VI)” is a dependent feature, and its statistics are as reported in

Table 2. The statistical description of the dataset.

	Initial Concentration of Cr(VI)	pH	Adsorbent Dosage (g/L)	Percentage Removal of Cr(VI)
Count	2000	2000	2000	2000
Mean	58.62	2.52	5.50	52.14
Std	22.98	1.14	2.31	16.15
Min	20.00	1.00	2.00	19.30
25%	39.00	1.00	4.00	38.50
50%	58.00	3.00	5.00	52.42
75%	79.00	4.00	8.00	65.22
Max	100	5	10	73.55

.

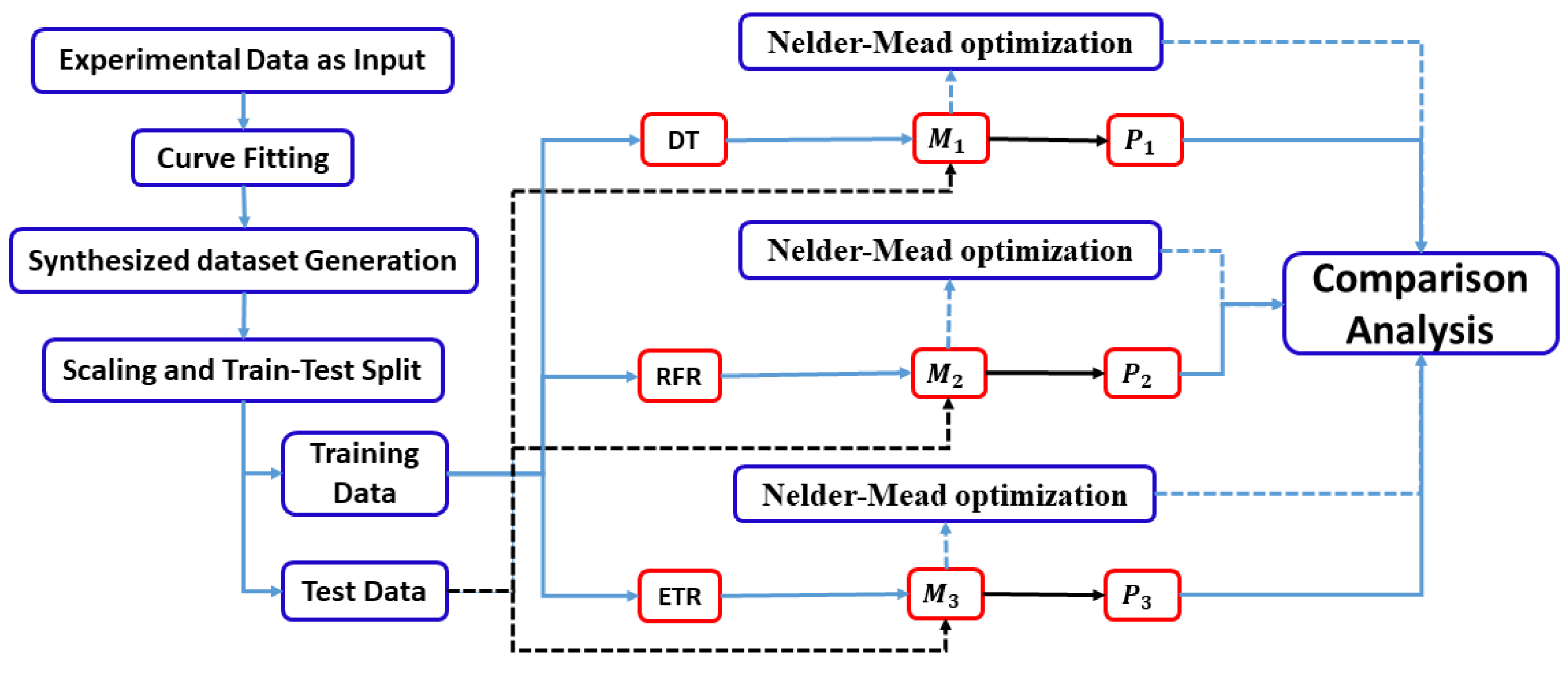
3. Proposed Model

The proposed approach reported in Figure 1 consists of seven phases, namely (1) curve fitting, (2) synthesizing the dataset, (3) scaling and splitting, (4) model building and training, (5) model testing, (6) optimization, and (7) comparison analysis.

3.1. Curve Fitting

In the context of experimental data comprising a limited number of instances, such as 55, curve fitting emerges as a valuable approach to uncovering the underlying trends and relationships between variables. This methodological strategy allows deriving a mathematical model that captures the essence of the observed data, providing insights into the behavior of the system under investigation. Furthermore, curve fitting serves as an effective tool for generating synthesized data related to experimentation and guiding subsequent data-driven analyses. Hence, this work applied curve fitting on experimental data to enable quantification of the relationships between the independent variables (initial concentration of Cr(VI) (IC), pH, and adsorbent dosage (AD)) and the percentage removal of Cr(VI) observed in experimental studies. This approach can precisely describe the dependencies and assess the impact of each factor on the removal efficiency by establishing the mathematical model as reported in Equation (1), where a, b, and c are the weights associated with each independent feature. In this case, the mathematical model is a linear combination of the independent variables (“IC”, “pH’’, and “AD’’) weighted by the parameters (“a’’, “b’’, and “c’’). This mathematical model is expressed as shown in Equation (1):

$$\mathrm{Percentage}\mathrm{removal}\mathrm{of}Cr\left(VI\right)=\left(\right(a\ast IC)+(b\ast pH)+(c\ast AD\left)\right)$$

(1)

3.2. Synthesized Dataset

In this work, a synthesized dataset of 2000 instances with three features, namely “initial concentration of Cr(VI)”, “pH”, and “adsorbent dosage (g/L)” of varying feature values, was built as presented in

Table 3. The range of feature values to synthesize the dataset.

Feature Name	Starting Value	End Value	Number of Instances
Initial concentration of Cr(VI)	20	100	2000
pH	1	5	2000
Adsorbent dosage (g/L)	2	10	2000

. The randomization technique was applied to create a dataset with 2000 instances using these starting and ending values. This dataset was given as initial_data to the Nelder–Mean optimization approach as shown in Algorithm  1. These data underwent the four steps in Algorithm 1—simplex, reflection, expansion, shrinkage, and termination—after reaching the optimal solution.

Algorithm 1: Nelder–Mead optimization for maximum Cr(VI) removal.

1: Inputs: model: Trained ML models $M_1$–$M_3$ which predict Cr(VI) removal percentage based on input parameters initial_data: Dataset with 20,000 instances containing: –Initial concentration of Cr(VI) (mg/L) –pH –Adsorbent dosage (g/L) (Indian gooseberry seed powder) 2: Outputs: –optimal_dosing_parameters: Optimal values for initial concentration, pH, and adsorbent dosage that maximize Cr(VI) removal. 3: Initialization: Extract initial values for the independent variables (concentration, pH, dosage) from the dataset: –initial_values = get_cr6_removal_parameters(initial_data) Initialize the simplex using the initial values: –simplex = initialize_simplex(initial_values) 4: Optimization Loop: 5: while termination criteria not met do 6:     for each vertex in the simplex: do 7:         worst_condition = find_worst_vertex(simplex) 8:         centroid=calculate_centroid(simplex,worst_condition) 9:         new_candidate=reflect_vertex(worst_condition,centroid) 10:       Predicted_Cr(VI)_removal%=ML_model(new_candidate) 11:       if Predicted_Cr(VI)_removal% is higher then 12:            replace_worst_vertex(simplex,new_candidate) 13:       else 14:            alternative_operation(simplex,worst_condition,model) 15:       end if 16:     end for 17: end while 18: Output Optimal Values: Extract the optimal values for the independent variables (concentration, pH, dosage) from the vertex with the highest predicted removal percentage: optimal_dosing_parameters =get_cr6_removal_parameters(best_vertex_in_simplex) 19: Return: Return the optimal values for maximizing Cr(VI) removal: 20: return optimal_dosing_parameters

3.3. Scaling and Splitting

The data values of the initial concentration of Cr(VI), pH, and adsorbent dosage input parameters were in different scales. Hence, models trained with features which are in different scales may not contribute equally to learning and, in turn, model fitting. This may incur adverse effects on model performance. Hence, standardization or Z score normalization was applied to the input parameters to convert the entire input space to equal scale values through Equation (2) below. Here, $f_i$ is the $i^{th}$ independent feature, ${\mu }_{f_i}$ is the mean of the $i^{th}$ independent feature, N is number of instances, and $f_{{\sigma }_i}$ is the standard deviation of the $i^{th}$ independent feature:

$$\begin{array}{c}\hfill Z={\displaystyle \frac{f_i-{\mu }_{f_i}}{f_{{\sigma }_i}}}\mathrm{where}1\le i\le N\\ \hfill \mathrm{mean}{\mu }_{f_i}={\displaystyle \frac{1}{N}}\sum _{i=1}^N\\ \hfill \mathrm{and}\mathrm{standard}\mathrm{deviation}{f}_{{\sigma }_i}=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N}{\left(f_i-{\mu }_{f_i}\right)}^2}\end{array}$$

(2)

After scaling, the proposed approach separated data into two portions: the training data (80%) with 1400 instances and test data (20%) with 600 instances.

3.4. Model Building and Training

The proposed work employed tree-based regression models (as reported in Figure 1) to attain higher prediction accuracy for Cr(VI) removal. The synthesized dataset was divided into training (85%) and testing (15%) sets. Furthermore, each model was trained on the trained portion of data, with their performance evaluated with the testing data, and finally the model’s performance was analyzed. As shown in Figure 1, models $M_1$–$M_3$ are the trained models for DTR, RFR, and ETR, respectively. Moreover, $P_1$–$P_3$ are the predicted results on the testing data for DTR, RFR, and ETR, respectively.

3.5. Model Testing

The chromium removal efficiency of each ML model was evaluated on the testing and synthesized data using metrics such as the mean absolute error (MAE), mean squared error (MSE), root mean squared error (RMSE), $R^2$ score, and finally the relative root mean squared error (RRMSE). The notations used in the calculation of each metric are presented in

Table 4. The notations used in this work.

Notations	Description
$ACrV{I}_i$	The $i^{th}$ instance of actual chromium VI removal percentage
$PCrV{I}_i$	The $i^{th}$ instance of predicted chromium VI removal percentage
$d_i$	The difference between the $i^{th}$ instance of $ACrV{I}_i$ and $PCrV{I}_i$
m	The number of samples or instances in the dataset
$\overline{ACrVI}$	The average or mean of all chromium VI removal percentage values of a given dataset
$MA{E}_{RCrVI}$	The MAE of the chromium removal percentage
$MS{E}_{RCrVI}$	The MSE of the chromium removal percentage
$RMS{E}_{RCrVI}$	The RMSE of the chromium removal percentage
$RRMS{E}_{RCrVI}$	The RMSE of the chromium removal percentage
$R_{RCrVI}^2$	The Coefficient of determination of the chromium removal percentage
$I_{Cr}$	Initial concentration of Cr(VI)
$F_{Cr}$	Final concentration of Cr(VI)

. The regression model is said to be best when its $R^2$ score is close to one and the values are small for the remaining metrics (MAE, MSE, and RMSE).

• Mean Absolute Error (MAE): The absolute average of the difference between the ACrVI and PCrVI of all testing data instances divided by the total number of instances, as shown in Equations (3) and (4), is known as the MAE:

$$d_i={ACrVI}_i-{PCrVI}_i$$

(3)

$$MA{E}_{RCrVI}={\displaystyle \frac{1}{m}}\sum _{i=1}^m\left|d_i\right|$$

(4)

• Mean Squared Error (MSE): The summation of the squares of the differences of all the actual and predicted chromium VI removal percentages, as shown in Equation (1), divided by number of testing samples, as reported in Equation (5), is known as the MSE.

$$MS{E}_{RCrVI}={\displaystyle \frac{1}{m}}\sum _{i=1}^m{\left(d_i\right)}^2$$

(5)

• Root Mean Squared Error (RMSE): Also called the root mean square deviation (RMSD) or root mean squared error on prediction (RMSE), the square root of summation of the squared residuals divided by the total number of instances, as reported in Equation (6), is known as the RMSE:

$$RMSE=\sqrt{MSE}=\sqrt{{\displaystyle \frac{1}{m}}\sum _{i=1}^m{\left(d_i\right)}^2}$$

(6)

• ${\mathbf{R}}^{\mathbf{2}}$–Score: Also called the coefficient of determination, this specifies the variance or score of a model based on given test data and indicates how much of the variance in the dependent features is explained by an independent feature. Equations (7) and (8) show the mathematical formulas for the $R^2$ score’s calculation, where a continuous value between 0 and 1 indicates model score and a model score near one indicates that the model performance is good with minimal error:

$$R_{RCrVI}^2=1-{\displaystyle \frac{{\sum }_{i=1}{\left(d_i\right)}^2}{{\sum }_{i=1}{(ACrV{I}_i-\overline{ACrV{I}_i})}^2}}$$

(7)

$$\overline{ACrVI}={\displaystyle \frac{1}{m}}\sum _{i=1}^{m}ACrV{I}_i$$

(8)

• Relative Root Mean Squared Error (RRMSE): The RRMSE is calculated as stated in Equation (9). The model performance is expressed as a percentage. A model with a value < 10% is said to be excellent, while it is good if it is between 10% and 20%, fair if it is between 20% and 30%, and poor if it is above 30%:

$$RRMS{E}_{ACrVI}={\displaystyle \frac{RMSE}{\sqrt{{\sum }_{i=1}^m{\left(PCrV{I}_i\right)}^2}}}$$

(9)

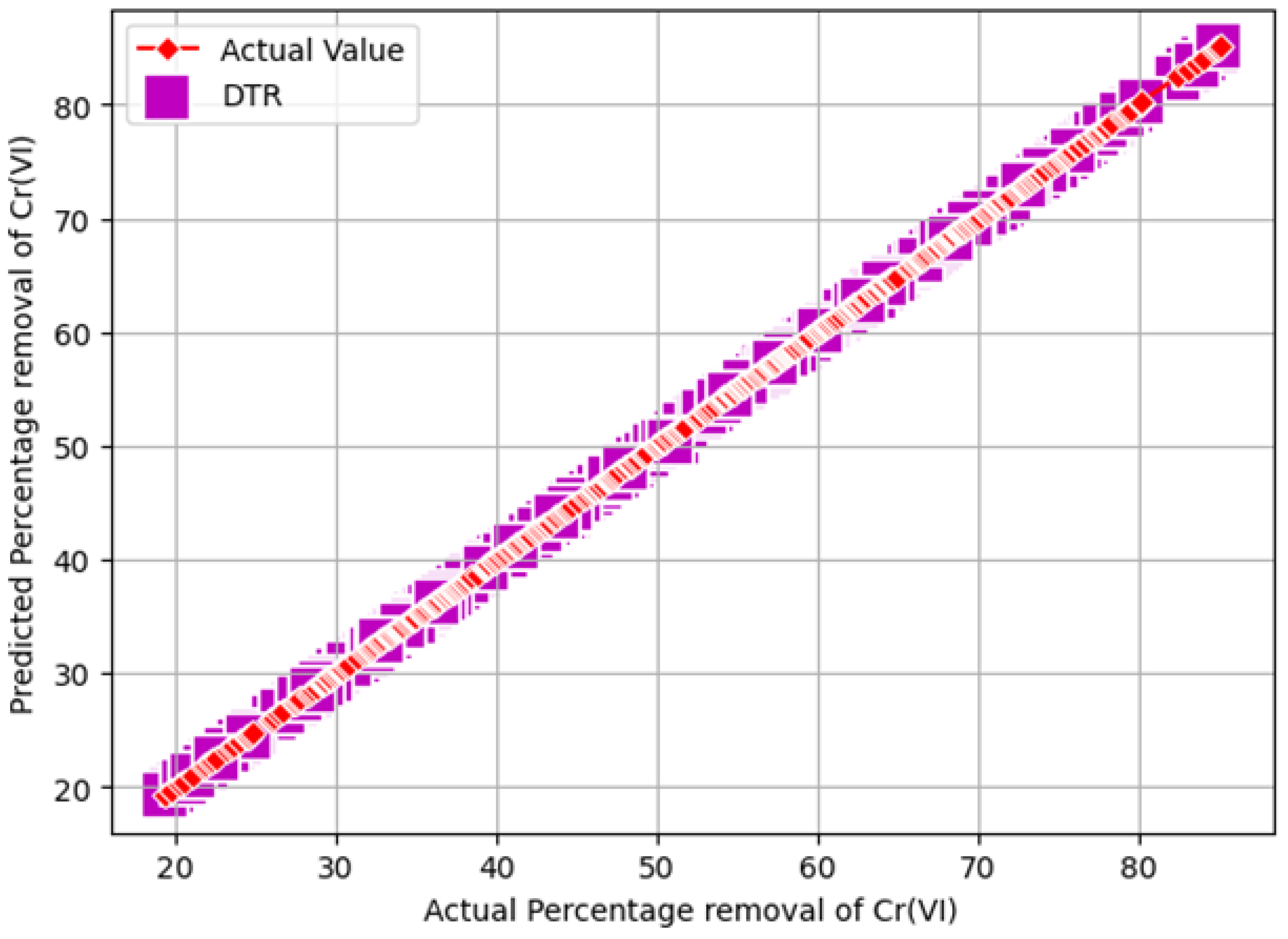
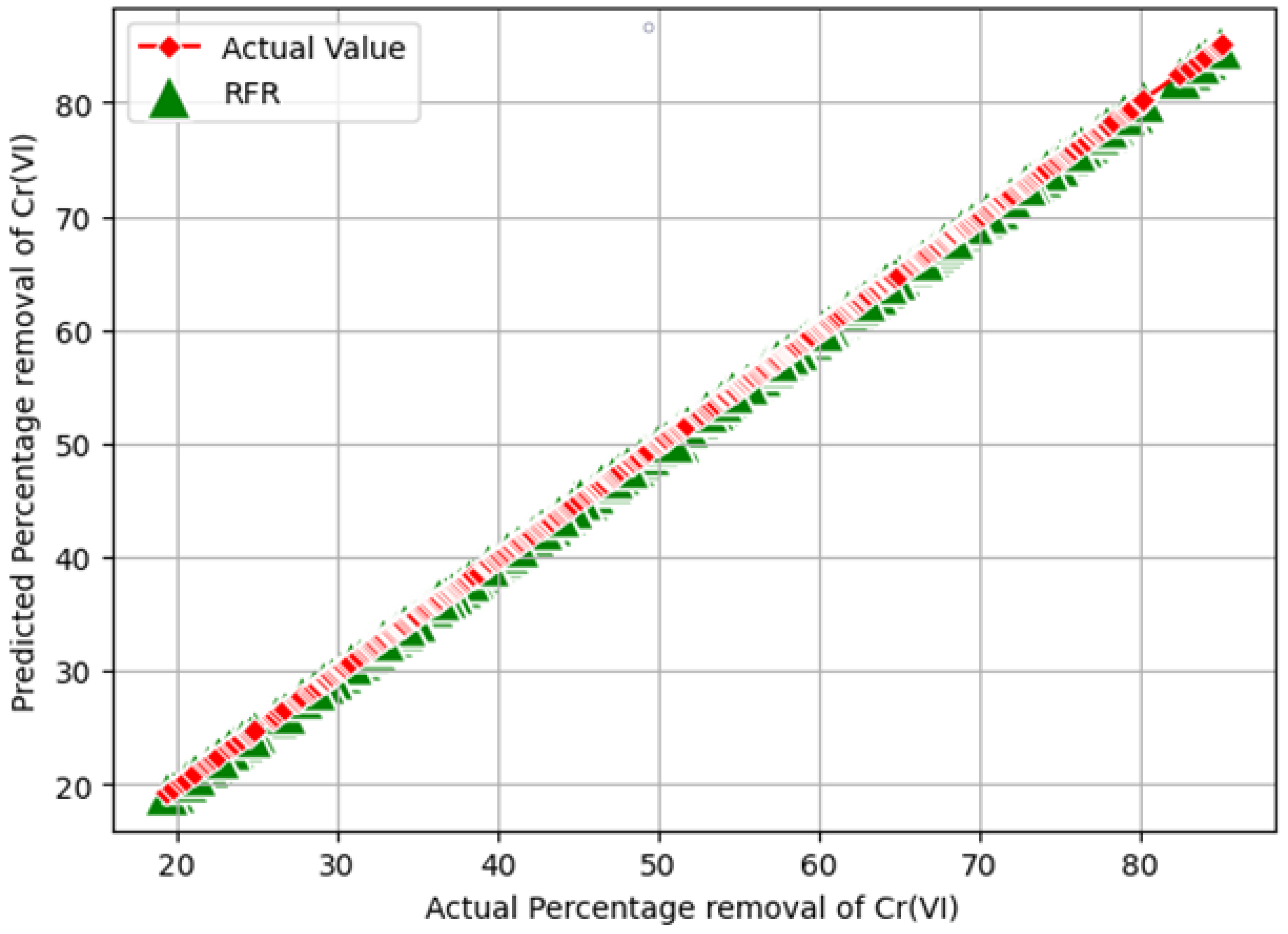
• Chromium (VI) removal percentage: In the traditional approach, chromium (VI) removal efficiency [14,31] is measured as shown in Equation (10). However, in this work, the synthesized dataset with 2000 instances was built using original experimental data (shown in Table 1) by varying the initial chromium (VI) concentration (20–100 mg/L), pH level (1–5), and Indian gooseberry powder dosage (2–10 g/L). The synthesized data samples were given as testing data to all trained ML models to determine the optimal values which removed the highest percentage of chromium (VI) from synthetic wastewater for the three independent features (“initial concentration of Cr(VI)”, “pH”, and “Adsorbent dosage”). During the prediction procedure, comparison analysis of the three ML models through six evolution metrics—the MAE, MSE, RMSE, $R^2$–Score, and RRMSE—is presented in

  Table 5. Performance of DTR, RFR, and ETR models.

  Evolution Metrics	DTR	RFR	ETR
  MAE	0.06	0.06	0.01
  MSE	0.01	0.01	0.00
  R2–Score	0.999960	0.999968	0.99990
  RRMSE	0.01	0.01	0.01

  and the optimal values for the maximum percentage of chromium (VI) removal are presented in

  Table 6. The optimal values obtained by Nelder–Mead optimization with DTR, RFR, and ETR.

  	Optimal Initial Concentration of Cr(VI)	Optimal pH	Optimal Adsorbent Dosage (g/L)	Obtained Cr(VI) Removal %
  DTR-Nelder–Mead	95.55	4.0	8.0	78.21
  RFR-Nelder–Mead	95.55	4.0	8.0	78.11
  ETR-Nelder–Mead	91.0	4.0	8.4	80.63
  	89.99	3.67	9.12	83.09
  	88.978	3.94	9.43	84.08
  	99.25	4.97	9.62	85.11

  .

$$\mathrm{Percentage}\mathrm{Removal}\mathrm{of}\mathrm{Cr}\left(\mathrm{VI}\right)={\displaystyle \frac{I_{Cr}-F_{Cr}}{I_{Cr}}}\times 100$$

(10)

3.6. Nelder–Mead Optimization

The proposed work implemented ML-based Nelder–Mead optimization as reported in Algorithm 1 to determine the optimal feature values (initial concentration of Cr(VI), pH, and adsorbent dosage (g/L)) which obtained maximum Cr(VI) removal from wastewater. In this approach, ML models were added in place of the actual objective function of the Nelder–Mead optimization algorithm. This work applied DTR-Nelder–Mead optimization, RFR-Nelder–Mead optimization, and ETR-Nelder–Mead optimization approaches on a synthesized dataset as depicted in Figure 1 to determine the optimal values for maximization of Cr(VI) removal. The implementation of a Nelder–Mead optimization algorithm to determine the maximum removal of Cr(VI) is as follows. This optimization is a powerful tool for finding the best combination of settings (independent variables) to achieve a desired outcome. In this case, we were using it to identify the optimal values for the initial concentration, pH, and adsorbent dosage (Indian gooseberry Seed Powder) which maximized the removal percentage of Cr(VI) from synthetic wastewater.

The algorithm relies on a trained ML model. This model takes a specific combination of concentration, pH, and dosage values as the input and predicts the resulting Cr(VI) removal percentage. The Nelder–Mead algorithm starts by creating a geometric shape called a simplex in the parameter space. This simplex contains several points, each representing a different combination of the three independent variables. The algorithm then iteratively refines the simplex to identify the region which maximizes Cr(VI) removal. In each iteration, it evaluates the predicted removal percentage for each point (vertex) in the simplex using the ML model. The point with the lowest predicted removal (since we are maximizing) is identified as the “worst vertex”. The algorithm then reflects this worst vertex through the centroid (average) of the remaining points, creating a new candidate solution. This new candidate is evaluated using the ML model.

If the new candidate predicts a higher Cr(VI) removal percentage than the worst vertex, then it replaces the worst vertex within the simplex. This effectively moves the simplex toward a more promising region of the parameter space. However, if the new candidate does not lead to improvement, then the algorithm might explore further by either expanding the reflected vertex or contracting the entire simplex. This exploration helps the algorithm avoid getting stuck in local optima and find the true optimal combination which maximizes Cr(VI) removal. The loop continues until a termination criterion is met, such as an extrmeely small change in the predicted removal percentage observed between iterations. Finally, the vertex within the simplex with the highest predicted Cr(VI) removal percentage represents the optimal combination of the three independent variables for maximizing Cr(VI) removal in this experiment.

Furthermore, the synthesized dataset was given as initial_data to the Nelder–Mead optimization to evaluate the performance of the optimization algorithm. These input data underwent five steps in the algorithm—simplex, reflection, expansion, shrinkage, and termination—after reaching the optimal solution.

4. Results and Discussions

The proposed approach splits the dataset into training and testing, as reported in Figure 1. Each model built trained models, such as $M_1$–$M_3$, after training on the trained data and then tested their performance through test data to obtain predicted outputs, such as $P_1$–$P_3$, as shown in Figure 1. The evolution metrics applied on each predicted result to evaluate the performance of each ML model are as reported in Table 5. The results demonstrate that all models achieved a high $R^2$ score of 99%. Additionally, the MAE remained below 0.06, while the mean squared error (MSE) and root mean squared error (RMSE) were 0.01 and 0.41, respectively. Moreover, Figure 2, Figure 3 and Figure 4 depict a comparison between the actual and predicted removal percentages of chromium (VI) with the DTR, RFR, and ETR models, respectively. Furthermore, the results reveal that the predicted values of RFR diverged considerably from the actual values, whereas the predicted values of ETR were comparatively better.

Additionally, for a more detailed analysis, Figure 2, Figure 3 and Figure 4 provide individual comparisons of each ML model with the actual chromium removal percentage. These comparisons reaffirm the superior performance by DTR, RFR, and ETR, exhibiting a high $R^2$ score and a lower error rate. Through the graphical comparison, it can be observed that the DTR, RFR, and ETR models yielded predictions which closely matched the actual values. The ETR model, however, consistently performed well by closely approximating the actual removal percentage of chromium VI. Furthermore, the removal efficiency of the model was tested for a sample size of 600 instances with three features: the initial concentration of Cr(VI), pH level, and adsorbent dosage (g/L). This sample was synthesized in a random manner, assuming the range of the initial concentration of Cr(VI) was 20–100 ppm. Similarly, the pH range was assumed to be between 1 and 5. Likewise, the considered range for the adsorbent dosage was from 2 to 10 g/L. The DTR, RFR, and ETR approach took this entire sample and predicted the chromium (VI) removal percentage. The performance of these models is tabulated in Table 5.

Furthermore, the Nelder–Mead optimization with DTR, RFR, and ETR was run on the test dataset, and its results are presented in Table 6. From the results, it can be observed that the DTR-Nelder–Mead and RFR-Nelder–Mead optimization methods obtained maximums of 78.21% and 78.11% Cr(VI) removal for an initial Cr(VI) concentration of 95.55 mg/L, pH level of four, and adsorbent dosage of 8 g/L. Moreover, the ETR-Nelder–Mead optimization approach obtained 85.11% as the maximum Cr(VI) removal for an initial Cr(VI) concentration of 99.25 mg/L, pH level of 4.97, and adsorbent dosage of 9.62 g/L.

Similarly, the DTR–Nelder-Mead, RFR-Nelder–Mead, and ETR-Nelder–Mead optimization approaches were able to obtain maximums of 78.107–85.11% Cr(VI) removal, with reported increases in the Cr(VI) removal percentage ranging from 4.66% to 11.56% over the Cr(VI) removal percentage of 73.55% obtained by experimentation for an initial Cr(VI) concentration of 20 mg/L, pH level of 2.0, and adsorbent dosage of 8.0 g/L. In summary, based on the comprehensive evaluation, it is concluded that the ML models exhibited strong performance overall. ETR and ETR-Nelder–Mead optimization in particular stood out as the top performers, demonstrating superior accuracy with minimal error rates while obtaining higher Cr(VI) removal percentages than all of the other models.

Furthermore, the surface morphology of the Indian gooseberry seed powder was examined using SEM analysis both before and after Cr(VI) adsorption, as reported in Figure 5. The SEM images before and after Cr(VI) adsorption confirm that the morphology seemed to be an irregularly shaped sheet-like structure, and we did not find any significant changes after the adsorption process. This confirms that the material exhibited the same morphology before and after the reaction.

Validation of the Optimization Results

The results obtained from ETR-Nelder–Mead optimization were validated through experimentation, as reported in

Table 7. Validation of optimization results through experimentation.

Optimal Initial Concentration of Cr(VI)	Optimal pH	Optimal Adsorbent Dosage (g/L)	Optimal Cr(VI) Removal %	Cr(VI) Removal % through Experimentation	% Error
99.25	4.97	9.62	85.11	79.75	6.72

, since a strong prediction framework for the adsorption process was provided by the tree-based machine learning model, which further validated the results. The results show that the experimental outcomes for the optimal parameters, such as the optimal initial Cr(VI) concentration (99.25), optimal pH level (4.97), and optimal adsorbent dosage (9.62 g/L), strongly aligned with a 6.56% error rate. In light of the experimental results as well as the model values, Indian gooseberry seed powder is an effective and low-cost adsorbent, and we suggest using it for the removal of hexavalent chromium from water, as hexavalent chromium has a carcinogenic nature.

5. Conclusions

This study examined a novel approach for Cr(VI) removal efficiency (expressed as a percentage) from wastewater by employing ML models combined with Nelder–Mead optimization. This particular combined strategy for adsorption capacity estimation using any solute or material has not been previously reported in the literature. This research not only leverages the power of ML for accurately predicting the Cr(VI) removal efficiency percentage but also utilizes Nelder–Mead optimization to identify optimal process parameters which maximize Cr(VI) removal efficiency, ultimately achieving a significant enhancement in Cr(VI) removal efficiency compared with standalone experimentation. In this work, ETR in particular achieved outstanding performance in predicting Cr(VI) removal. The ETR model exhibited a remarkable $R^2$ score of 99% and significantly lower error rates compared with the other models. Furthermore, ML-based Nelder–Mead optimization identified the optimal process parameters, leading to a maximum Cr(VI) removal efficiency of 85.11%. This represents an improvement of up to 11.56% compared with standalone experimentation. These results demonstrate the effectiveness of the combined ML and optimization approach for maximizing Cr(VI) removal using Indian gooseberry seed powder. This research work paves the way for further exploration of ML-driven strategies in wastewater treatment applications.