Calcium Carbonate Formation in Groundwater-Supplied Drinking Water Systems: Role of CO2 Degassing Rate and Scaling Indices Applicability
Abstract
1. Introduction
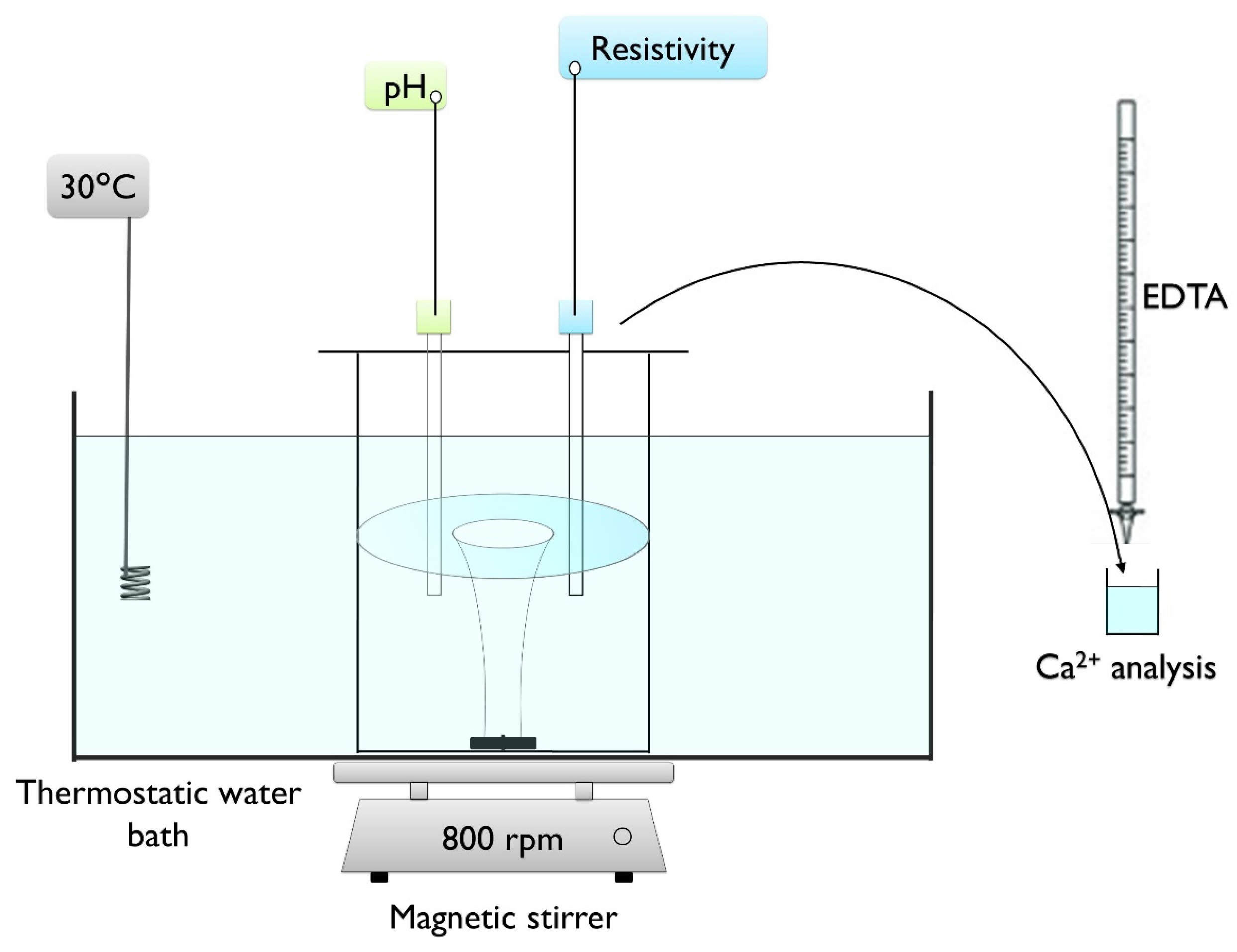
2. Materials and Methods
3. Theoretical Calculations for Thermodynamic Analysis
3.1. Supersaturation Coefficient
3.2. Scaling Indices
3.3. Discussion on the Prediction of the Water-Scaling Power Using Different Indices
4. Results and Discussion
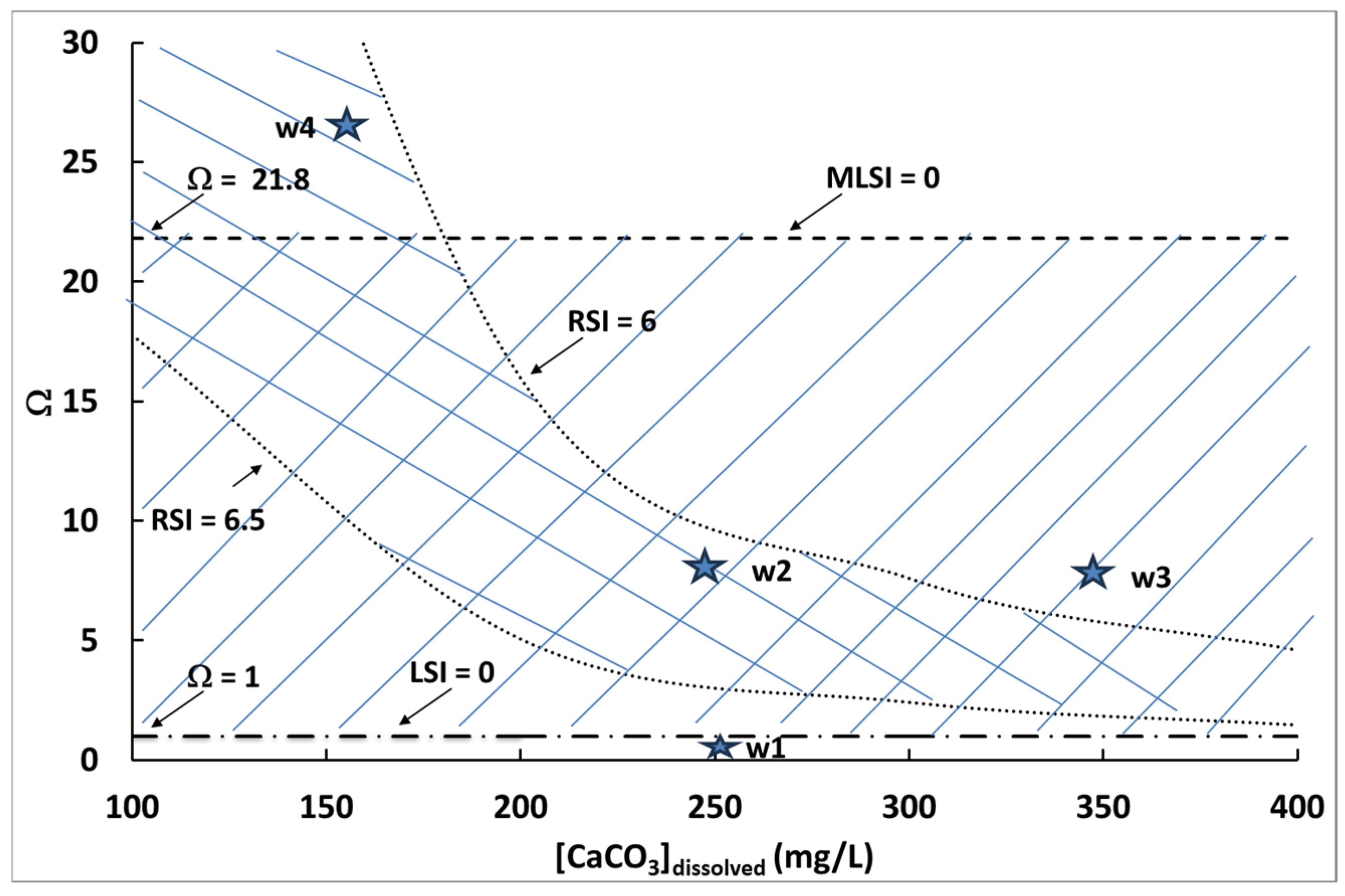
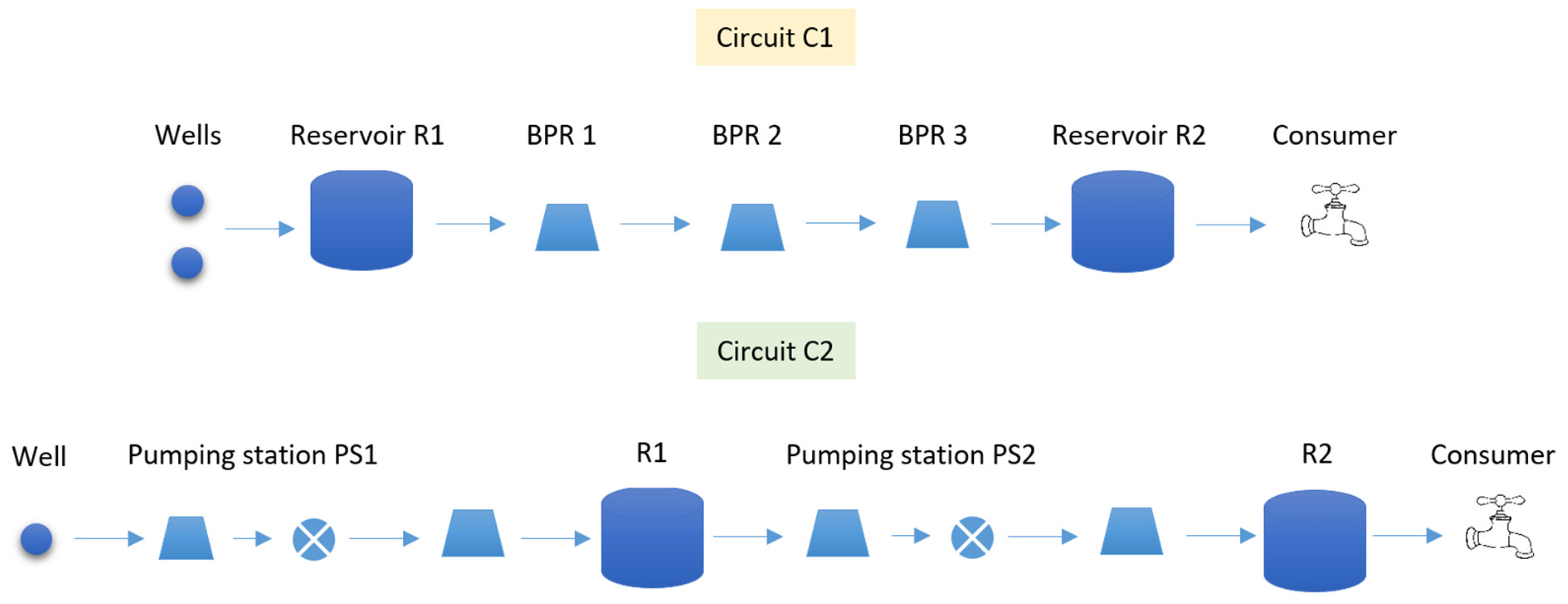
4.1. Scale Prediction in Drinking Water Systems: Case Study
4.2. Effect of CO2 Degassing Rate on CaCO3 Nucleation Kinetics and Precipitation Threshold
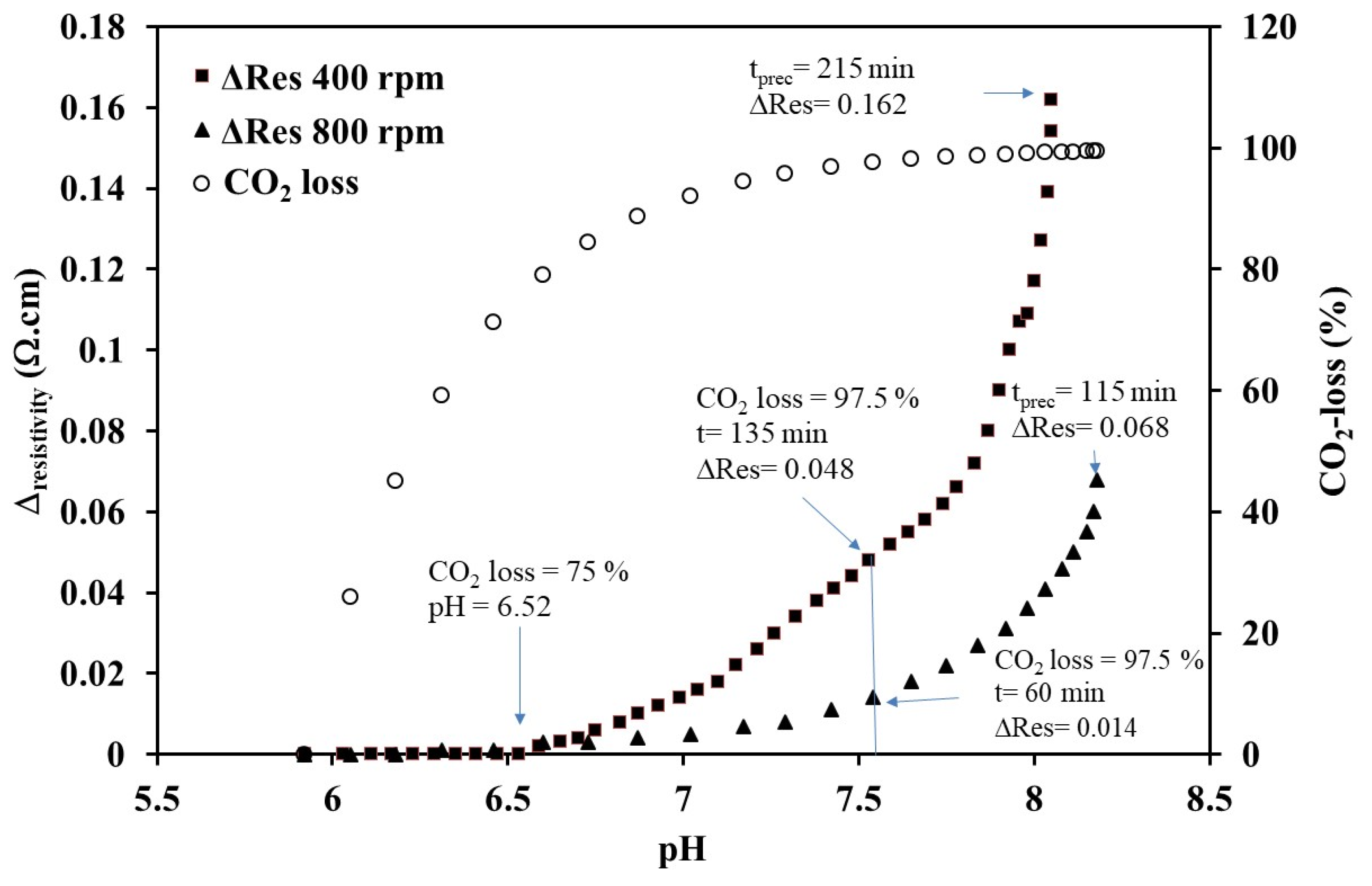
4.2.1. Effect of the Stirring Rate
4.2.2. Effect of the Saturation State on Precipitation Threshold Time
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chhim, N.; Haddad, E.; Neveux, T.; Bouteleux, C.; Teychené, S.; Biscans, B. Performance of green antiscalants and their mixtures in controlled calcium carbonate precipitation conditions reproducing industrial cooling circuits. Water Res. 2020, 186, 116334. [Google Scholar] [CrossRef] [PubMed]
- Kum, S.; Tang, X.; Liu, H. Treatment of brackish water inland desalination brine via antiscalant removal using persulfate photolysis. Environ. Sci. Water Res. Technol. 2023, 9, 1137–1146. [Google Scholar] [CrossRef]
- Chang, B.; Li, G.; Guo, F.; Lu, S.; Peng, Y.; Hou, J. Research on Carbon Dioxide-Assisted Electrocoagulation Technology for Treatment of Divalent Cations in Water. Water 2024, 16, 1715. [Google Scholar] [CrossRef]
- Gebauer, D.; Völkel, A.; Cölfen, H. Stable prenucleation calcium carbonate clusters. Science 2008, 322, 1819–1822. [Google Scholar] [CrossRef] [PubMed]
- Pouget, E.M.; Bomans, P.H.H.; Goos, J.A.C.M.; Frederik, P.M.; de With, G.; Sommerdijk, N.A.J.M. The Initial Stages of Template-Controlled CaCO3 Formation Revealed by Cryo-TEM. Science 2009, 323, 1455–1458. [Google Scholar] [CrossRef] [PubMed]
- Hamdi, R.; Tlili, M.M. Influence of foreign salts on the CaCO3 pre-nucleation stage: Application of the conductometric method. CrystEngComm 2022, 24, 3256–3267. [Google Scholar] [CrossRef]
- Hamdi, R.; Tlili, M.M. Conductometric study of calcium carbonate prenucleation stage: Underlining the role of CaCO3o ion pairs. Cryst. Res. Technol. 2016, 51, 99–109. [Google Scholar] [CrossRef]
- Mazziotti di Celso, G.; Prisciandaro, M.; Karatza, D.; Musmarra, D.; Lancia, A. Study of the Effect of Leucine on Calcium Carbonate Precipitation in a Circular Economy Perspective. Water 2022, 14, 270. [Google Scholar] [CrossRef]
- Hamdi, R.; Tlili, M.M. Influence of Foreign Salts and Antiscalants on Calcium Carbonate Crystallization. Crystals 2023, 13, 516. [Google Scholar] [CrossRef]
- Al-Hashim, M.H.; Al-Aidaros, A.; Zaidi, F.K. Geological and Hydrochemical Processes Driving Karst Development in Southeastern Riyadh, Central Saudi Arabia. Water 2024, 16, 1937. [Google Scholar] [CrossRef]
- Eichinger, S.; Boch, R.; Leis, A.; Koraimann, G.; Grengg, C.; Domberger, G.; Nachtnebel, M.; Schwab, C.; Dietzel, M. Scale deposits in tunnel drainage systems—A study on fabrics and formation mechanisms. Sci. Total Environ. 2020, 718, 137140. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, G.; Mecik, M. The chemistry of scale prediction. J. Pet. Sci. Eng. 1997, 17, 113–121. [Google Scholar] [CrossRef]
- Zhang, F.; Dai, Z.; Zhang, Z.; Al-Saiari, H.; Yan, F.; Bhandari, N.; Ruan, G.; Liu, Y.; Lu, Y.-T.; Deng, G.; et al. Scaling Risk and Inhibition Prediction of Carbonate Scale at High Temperature. In Proceedings of the SPE International Conference on Oilfield Chemistry, Montgomery, TX, USA, 3–5 April 2017. [Google Scholar]
- Coto, B.; Martos, C.; Peña, J.L.; Rodríguez, R.; Pastor, G. Effects in the solubility of CaCO3: Experimental study and model description. Fluid Phase Equilibria 2012, 324, 1–7. [Google Scholar] [CrossRef]
- Grimes, C.J.; Hardcastle, T.; Manga, M.S.; Mahmud, T.; York, D.W. Calcium Carbonate Particle Formation through Precipitation in a Stagnant Bubble and a Bubble Column Reactor. Cryst. Growth Des. 2020, 20, 5572–5582. [Google Scholar] [CrossRef]
- Cosmo, R.d.P.; Ressel Pereira, F.d.A.; Ribeiro, D.d.C.; Barros, W.Q.; Martins, A.L. Estimating CO2 degassing effect on CaCO3 precipitation under oil well conditions. J. Pet. Sci. Eng. 2019, 181, 106207. [Google Scholar] [CrossRef]
- Cosmo, R.d.P.; Pereira, F.d.A.R.; Soares, E.J.; Ferreira, E.G. Addressing the root cause of calcite precipitation that leads to energy loss in geothermal systems. Geothermics 2022, 98, 102272. [Google Scholar] [CrossRef]
- Cosmo, R.d.P.; Rinaldi, R.; Pereira, F.d.A.R.; Soares, E.J.; Martins, A.L. CO2 degassing in CaCO3 precipitation in the presence of oil: Implications, modeling, numerical simulation, validation, prototype development, and experimental results. Geoenergy Sci. Eng. 2023, 228, 211885. [Google Scholar] [CrossRef]
- Davies, C.W. Ion Association; Butterworths: London, UK, 1962. [Google Scholar]
- Malmberg, C.G.; Maryott, A.A. Dielectric constant of water from 0° to 100°C. J. Res. Natl. Inst. Stand. Technol. 1956, 56, 1–8. [Google Scholar] [CrossRef]
- Plummer, L.N.; Busenberg, E. The solubilities of calcite, aragonite and vaterite in CO2-H2O solutions between 0 and 90°C, and an evaluation of the aqueous model for the system CaCO3-CO2-H2O. Geochim. Cosmochim. Acta 1982, 46, 1011–1040. [Google Scholar] [CrossRef]
- Langelier, W.F. The analytical control of anti-corrosion water treatment. J. Am. Water Work. Assoc. 1936, 28, 1500–1521. [Google Scholar] [CrossRef]
- Ryznar, J.W. A new index for determining amount of calcium carbonate scale formed by a water. J.-Am. Water Work. Assoc. 1944, 36, 140–153. [Google Scholar] [CrossRef]
- Larson, T.E.; Buswell, A.M. Calcium Carbonate Saturation Index and Alkalinity Interpretations. J. AWWA 1942, 34, 1667–1678. [Google Scholar] [CrossRef]
- Gal, J.Y.; Bollinger, J.C.; Tolosa, H.; Gache, N. Calcium carbonate solubility: A reappraisal of scale formation and inhibition. Talanta 1996, 43, 1497–1509. [Google Scholar] [CrossRef] [PubMed]
- Elfil, H.; Roques, H. Prediction of the limit of the metastable zone in the “CaCO3-CO2-H2O” system. AIChE J. 2004, 50, 1908–1916. [Google Scholar] [CrossRef]
- Elfil, H.; Hannachi, A. Reconsidering water scaling tendency assessment. AIChE J. 2006, 52, 3583–3591. [Google Scholar] [CrossRef]
- Tlili, M.M. Etude des mécanismes de précipitation de carbonate de calcium. Application à l′entartrage. Phi Thesis, University of Paris, Paris, France, 2002. [Google Scholar]
- Manzola, A.S. Contribution à l’étude de la prévention de l’entartrage par les eaux géothermales du sud Tunisien. Ph.D. Thesis, Faculté des Sciences de Tunis, Tunis, Tunisia, 2003. [Google Scholar]
- Nefzi, M. Contribution à l’étude de la prévention de l’entartrage des eaux potables : Moyens chimiques et physiques—Étude de cas. Ph.D. Thesis, Faculté des Sciences de Tunis, Tunis, Tunisia, 2004. [Google Scholar]
- Gal, J.-Y.; Fovet, Y.; Gache, N. Mechanisms of scale formation and carbon dioxide partial pressure influence. Part II. Application in the study of mineral waters of reference. Water Res. 2002, 36, 764–773. [Google Scholar] [CrossRef]
- Hamdi, R.; Khawari, M.; Hui, F.; Tlili, M. Thermodynamic and kinetic study of CaCO3 precipitation threshold. Desalination Water Treat. 2016, 57, 6001–6006. [Google Scholar] [CrossRef]
- Gache, N. Rôle des formes hydratées du carbonate de calcium dans la rupture de l’état métastable des solutions sursaturées. Ph.D. Thesis, Université Montpellier II, Montpellier, France, 1998. [Google Scholar]


| θ °C | pH | TDS mg·L−1 | Ca2+ mg·L−1 | Mg2+ mg·L−1 | Na+ mg·L−1 | HCO3− mg·L−1 | SO42− mg·L−1 | Cl− mg·L−1 | K+ mg·L−1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Circuit 1 | 20 | 7.48 | 698 | 106 | 46 | 87 | 239 | 144 | 177 | - |
| Circuit 2 | 24 | 6.90 | 701 | 166 | 20 | 62 | 452 | 93 | 136 | 2 |
| Circuit 1 | R1 | BPR1 | BPR2 | BPR3 | R2 | Consumer |
| pH | 7.48 | 8.15 | 8.30 | 8.23 | 8.12 | 7.8 |
| Ω | 1.93 | 9.0 | 12.7 | 10.8 | 8.4 | 4.0 |
| LSI | 0.28 | 0.95 | 1.10 | 1.03 | 0.92 | 0.6 |
| RSI | 6.92 | 6.25 | 6.10 | 6.17 | 6.28 | 6.60 |
| MLSI | −1.05 | −0.38 | −0.23 | −0.30 | −0.41 | −0.73 |
| Circuit 2 | Well | PS1 | R1 | PS2 | R2 | Consumer |
| pH | 6.95 | 7.1 | 7.52 | 7.78 | 7.6 | 7.45 |
| Ω | 1.68 | 2.75 | 7.22 | 13.14 | 8.68 | 6.15 |
| LSI | 0.29 | 0.44 | 0.86 | 1.12 | 0.94 | 0.79 |
| RSI | 6.37 | 6.22 | 5.80 | 5.54 | 5.72 | 5.87 |
| MLSI | −1.05 | −0.90 | −0.48 | −0.22 | −0.40 | −0.55 |
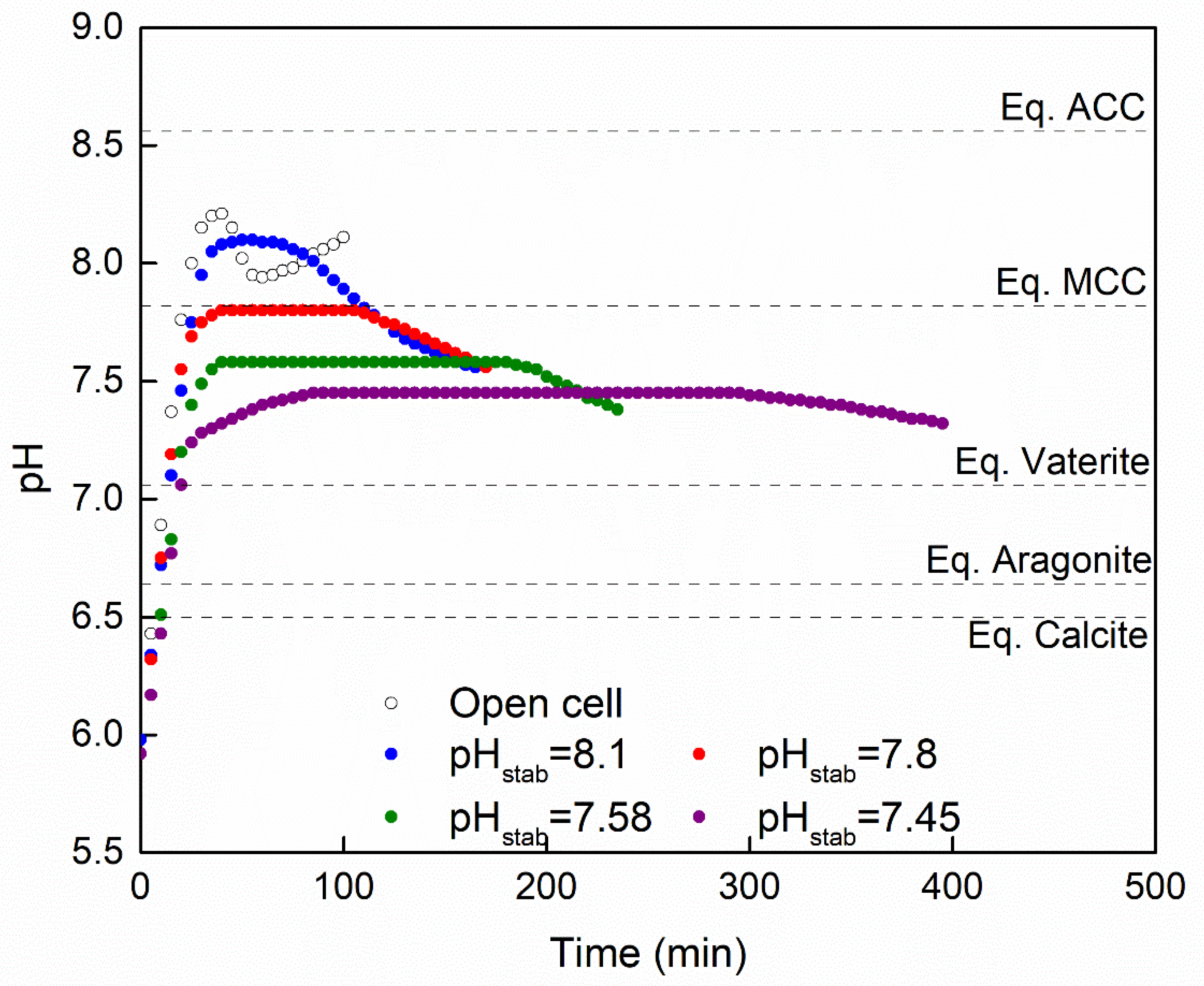
| pHstab | tprec (min) | Ωprec | LSI | RSI | MLSI |
|---|---|---|---|---|---|
| 8.18 (open cell) | 46 | 48 | 1.66 | 3.78 | 0.34 |
| 8.10 | 55 | 40 | 1.58 | 3.86 | 0.26 |
| 7.80 | 105 | 20 | 1.28 | 4.16 | −0.03 |
| 7.58 | 180 | 12 | 1.06 | 4.38 | −0.25 |
| 7.45 | 295 | 9 | 0.93 | 4.51 | −0.38 |
| 7.17 | - | 4.7 | 0.64 | 5.87 | −0.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamdi, R.; Tlili, M.M. Calcium Carbonate Formation in Groundwater-Supplied Drinking Water Systems: Role of CO2 Degassing Rate and Scaling Indices Applicability. Water 2024, 16, 2159. https://doi.org/10.3390/w16152159
Hamdi R, Tlili MM. Calcium Carbonate Formation in Groundwater-Supplied Drinking Water Systems: Role of CO2 Degassing Rate and Scaling Indices Applicability. Water. 2024; 16(15):2159. https://doi.org/10.3390/w16152159
Chicago/Turabian StyleHamdi, Raghda, and Mohamed Mouldi Tlili. 2024. "Calcium Carbonate Formation in Groundwater-Supplied Drinking Water Systems: Role of CO2 Degassing Rate and Scaling Indices Applicability" Water 16, no. 15: 2159. https://doi.org/10.3390/w16152159
APA StyleHamdi, R., & Tlili, M. M. (2024). Calcium Carbonate Formation in Groundwater-Supplied Drinking Water Systems: Role of CO2 Degassing Rate and Scaling Indices Applicability. Water, 16(15), 2159. https://doi.org/10.3390/w16152159





