Abstract
Deep learning models possess the capacity to accurately forecast various hydrological variables, encompassing flow, temperature, and runoff, notably leveraging Long Short-Term Memory (LSTM) networks to exhibit exceptional performance in capturing long-term dynamics. Nonetheless, these deep learning models often fixate solely on singular predictive tasks, thus overlooking the interdependencies among variables within the hydrological cycle. To address this gap, our study introduces a model that amalgamates Multitask Learning (MTL) and LSTM, harnessing inter-variable information to achieve high-precision forecasting across multiple tasks. We evaluate our proposed model on the global ERA5-Land dataset and juxtapose the results against those of a single-task model predicting a sole variable. Furthermore, experiments explore the impact of task weight allocation on the performance of multitask learning. The results indicate that when there is positive transfer among variables, multitask learning aids in enhancing predictive performance. When jointly forecasting first-layer soil moisture (SM1) and evapotranspiration (ET), the Nash–Sutcliffe Efficiency (NSE) increases by 19.6% and 4.1%, respectively, compared to the single-task baseline model; Kling–Gupta Efficiency (KGE) improves by 8.4% and 6.1%. Additionally, the model exhibits greater forecast stability when confronted with extreme data variations in tropical monsoon regions (AM). In conclusion, our study substantiates the applicability of multitask learning in the realm of hydrological variable prediction.
1. Introduction
Accurate prediction of hydrological variables plays an irreplaceable role in areas such as drought prevention, flood warning, and water resource management (Samaniego et al., 2019 [1]; Cloke et al., 2015 [2]; Blöschlet al., 2019 [3]). Over the years, process-based physical models have been employed for forecasting various hydrological variables (Talchabhadel et al., 2018 [4]; Sirisena et al., 2018 [5]). These models, deeply rooted in scientific theory, establish a theoretical statistical model based on physical formulas, yielding results with high reliability and interpretability. In recent years, advancements in remote sensing technologies have enhanced the capability of physical models to describe hydrological processes at finer scales (Khatakho et al., 2021 [6]; Tarek et al., 2020 [7]). However, limitations persist within these models. They are grounded in scientific theory, often representing or achieving merely a subset of the true processes within the ecosystem, leading to a number of constraints (Hilborn & Mangel, 1997 [8]). Simultaneously, the calibration of these models may be significantly influenced by real-world processes not encompassed within the model itself (Arhonditsis & Brett, 2004 [9]).
In recent years, the rapid expansion of data and continuous innovations in computational technology have led to the emergence of a powerful tool, namely deep learning (DL) models. DL models possess the capability to effectively capture complex, nonlinear spatial and temporal correlations within hydrological processes (Shen et al., 2018 [10]). They exhibit the ability to forecast occurrences beyond sampled situations (Herrnegger et al., 2019 [11]). Hence, DL models are considered excellent alternatives for predicting hydrological variables instead of relying solely on physical models. Deep learning (DL) is widely used in hydrology, offering precise predictions of runoff and groundwater levels. These predictions aid governments in planning water resource management strategies (Bai et al., 2016 [12]; Kratzert et al., 2018 [13]). Additionally, DL models can accurately forecast floods and droughts, providing valuable information for disaster preparedness and sustainable agricultural development (Zhang et al., [14]). Furthermore, DL models help researchers gain deeper insights into regional hydrological behavior (Kratzert, Klotz, Herrnegger, et al., 2019; Kratzert, Klotz, Shalev, et al., 2019 [15]; Read et al., 2019 [16]; Shen, 2018; Shen et al., 2018 [17]; Lees et al., 2021 [18]; Nearing et al., 2021 [19]; Yang et al., 2020 [20]; Huang et al., 2023 [21]). The application of various deep learning models in hydrology, such as ANNs (Yang et al., 2020; Majid et al., 2024 [22]), CNNs (Jiang et al., 2020 [23]), and RNNs (Sadeghi Tabas & Samadi, 2022 [24]; Shah et al., 2024 [25]), further underscores their applicability and extensive prospects in hydrological variable prediction. Among these models, RNNs are particularly suited for handling hydrological variable data with high temporal dependency due to their sequential processing of input data. However, their effectiveness in modeling hydrological processes with larger time scales is constrained by their difficulty in retaining time series information beyond 10 time steps (Bengio et al., 1994 [26]). Long Short-Term Memory (LSTM) networks, an advanced iteration of Recurrent Neural Networks (RNNs), feature innovative internal gating architecture pioneered by Hochreiter and Schmidhuber in 1997 [27], which effectively surmounts the challenge of capturing long-term dependencies in sequential data, setting a new standard for time series analysis. Owing to its exceptional ability to handle time series data, LSTM has achieved significant success in hydrological forecasting. Liu and colleagues successfully employed the LSTM model to simulate runoff phenomena in Wuhan, China (2021 [28]). Similar initiatives were undertaken in the United Kingdom and the United States, as demonstrated by Lees et al. (2021) and Kratzert et al. (2018), respectively. Lees and colleagues applied the same LSTM methodology across a broad dataset of 669 basins in the UK, while in the US, Kratzert and associates adeptly used LSTM models for accurate runoff predictions in various basins. Moreover, LSTM’s versatility is further demonstrated by its exceptional predictive performance in groundwater and rainfall forecasting. Kapoor et al. led pioneering efforts by integrating deep learning with traditional rainfall runoff modeling, as highlighted in their 2023 study [29]. In addition, they made significant advancements in accurately predicting cyclonic trajectories and intensities using variational recurrent neural networks, a study they published in the same year (Kapoor et al., 2023 [30]).
Up to this point, the majority of deep learning models in the hydrology domain have typically operated independently on a single variable, such as water level (Bowes et al., 2019 [31]), groundwater (Ali et al., 2022 [32]), evapotranspiration (Zhao et al., 2019 [33]), and soil moisture (Fang & Shen, 2020 [34]; Li et al., 2022 [35]; Li et al., 2024 [36]). Nevertheless, the hydrological system is an extensive and intricate framework where crucial interactions typically exist among various hydrological variables. Solely modeling one hydrological variable can result in models neglecting the interactions between different hydrological processes. In physical models predicting evapotranspiration, incorporating runoff as an auxiliary variable enhances the model’s understanding of the hydrological processes linking runoff and evapotranspiration, thereby improving prediction accuracy (Herman et al., 2018 [37]; Nesru et al., 2020 [38]).
In deep learning, multitask learning helps models better understand the interactions among variables, thereby enhancing the efficiency and accuracy of predictions for each task (Zhang and Yang, 2021 [39]). Additionally, studies in hydrology have shown that multitask learning enhances the understanding of hydrological processes and improves model performance. Salder et al. (2022) conducted experiments with simple deep learning models on data from 101 sites across the US mainland, revealing that at 56 sites, the Nash–Sutcliffe efficiency of multitask models exceeded that of single-task models. Li et al. (2023 [40]) tested multitask learning with LSTM models in three large mountainous basins on the Tibetan Plateau, showing that LSTM models combined with multitask learning exhibited superior accuracy in estimating runoff volume and performance compared to pure LSTM models, with NSEs increasing by approximately 0.02. However, these studies only discuss the interactions between two variables and improve the prediction accuracy of the primary variable. They do not demonstrate the generalizability of multitask learning in hydrology. Furthermore, they do not delve into the factors and reasons that affect the performance of multitask learning in forecasting hydrological variables.
In this study, we developed a multitask learning model comprising an LSTM at the base and multiple parallel fully connected layers at the output. This model utilizes multitask learning to capture interactions between variables, strengthening the LSTM’s capacity to model diverse hydrological processes. Consequently, it enhances prediction accuracy across multiple tasks. During the experimental phase, we performed dual-task modeling for soil moisture and evapotranspiration, regulating the task loss weight allocation to investigate its impact on the multitask model’s performance. Furthermore, we explored the interaction relationships among four hydrological variables (volumetric soil water layer 1 (SM1), soil temperature level 1 (ST1), evapotranspiration (ET), and surface sensible heat flux (SSHF)), including their correlation and transfer directions. To assess the model’s generalizability, we test its ability to predict in diverse climates and extreme events. Furthermore, we evaluate its data utilization efficiency and robustness by expanding the number of prediction tasks. Our overarching goal is to demonstrate the broad applicability of multitask learning in hydrological variable prediction tasks through various experimental perspectives. Additionally, we will conduct an in-depth analysis of the factors influencing the performance of multitask learning. In the subsequent sections of this paper, we first introduce the utilized datasets, the designed deep learning model, and the detailed configurations of all experiments (Section 2). Subsequently, we showcase and analyze the experimental outcomes on the LandBench1.0 dataset (Section 3), followed by an in-depth discussion of the results (Section 4), concluding with a summary of this work in Section 5.
2. Materials and Methods
2.1. Data Sources
This study utilized the LandBench1.0 dataset for experimental data. Created by Li et al. in 2023, LandBench1.0 is a benchmark dataset designed to facilitate research in predicting land surface variables (LSVs) (Li et al., 2023 [41]). This dataset addresses the need for a comprehensive and standardized resource to evaluate the performance of various data-driven deep learning models in hydrological and atmospheric sciences. By offering extensive coverage of variables and multiple resolutions (0.5°, 1°, 2°, and 4°), along with various lead times, LandBench1.0 improves the consistency of data-driven deep learning models for LSVs, making it a robust platform for developing and comparing predictive models.
The primary components of LandBench1.0 include data from the ERA5-Land reanalysis dataset, which provides global land surface data such as soil moisture, soil temperature, surface latent heat flux, surface sensible heat flux, and runoff. These data, derived from a combination of satellite and ground-based observations and numerical weather prediction models, ensure consistency and reliability (Muñoz-Sabater et al., 2021 [42]). Additionally, LandBench1.0 incorporates static physiographic attributes, including soil texture, soil water capacity, and vegetation type, sourced from datasets such as SoilGrid and MODIS (Rasp et al., 2020 [43]).
ERA5 reanalysis datasets combine various observational data sources, such as ground stations, satellites, ships, and aircraft, with numerical weather prediction models to produce globally consistent atmospheric and hydrological data with high spatial and temporal resolution. Recent studies have demonstrated that models trained with reanalysis datasets perform similarly or even better than those trained with observational datasets. For instance, Lee et al. (2021 [44]) evaluated the reliability of ERA5 reanalysis data by comparing the performance of deep learning models trained with ERA5 data to those trained with Global Historical Climatology Network (GHCN) observational data. The study focused on temperature data from temperate (Dublin) and tropical (Singapore) regions between 2015 and 2019. Results indicated that models trained with ERA5 data performed similarly to those trained with GHCN data in temperate regions, effectively replicating the seasonal temperature trends captured by observational datasets. Yilmaz et al. (2023 [45]) assessed the performance of deep learning models trained with ERA5 and ERA5-Land reanalysis datasets against those trained with ground-based observations from Turkey between 1951 and 2020. The study demonstrated that models trained with reanalysis datasets could accurately capture long-term trends and seasonal variations. Furthermore, the reanalysis datasets slightly outperformed observational data in capturing mean trends and temporal variability. These findings indicate that reanalysis datasets can enhance model performance, especially in regions with sparse or unavailable observational data. In 2023, Bi and colleagues introduced the Pangu weather forecasting system, trained using a 39-year reanalysis dataset ([46]). The results showed that Pangu produced more accurate deterministic forecasts on reanalysis data compared to the world’s leading Numerical Weather Prediction (NWP) system, the ECMWF’s operational IFS, and did so at a faster speed. Notably, Pangu demonstrated comparable performance to the IFS for deterministic forecasts up to 7 days in advance. Furthermore, the Fuxi system (Chen et al. (2024) [47]) extended this advance forecast capability to 15 days. These findings indicate that deep learning models can effectively learn the complex uncertainties and multivariable interactions present in the real atmospheric environment from reanalysis data. These studies indicate that deep learning models trained on reanalysis datasets can accurately simulate real atmospheric and hydrological environments to enhance forecast performance. Additionally, these models perform similarly to, or even surpass, those trained on observational data.
Ground station observational data often have temporal discontinuities, with missing days of data. In contrast, reanalysis datasets do not have these gaps, ensuring temporal continuity in model training data. Additionally, reanalysis datasets lack the pronounced regional differences found in ground station data, which facilitates better training and evaluation of models for global generalization. Therefore, we utilized the LandBench1.0 dataset, which spans from 1979 to 2020, focusing on data from 2000 to 2020 with a resolution of 1°. To accurately represent the complex interactions within the hydrological and atmospheric environment, we selected 15 variables, including surface, atmospheric, and static variables, as inputs for our model. Details of all selected variables are presented in Table 1.

Table 1.
Input variables for the multitask forecasting model.
2.2. Model Development
We developed a multitask learning model based on LSTM to improve the accuracy of hydrological variable forecasting by leveraging the strengths of both LSTM and multitask learning. LSTM focuses on learning long-term dependencies, while multitask learning considers interactions among multiple variables. The model’s primary architecture includes an LSTM layer as the shared layer and multiple parallel fully connected layers as the output layers (see Figure 1). In our model, the LSTM layer assimilates all input sequences (atmospheric forcing, road surface variables, and static terrain), processing them into intermediary sequences. As the shared layer, the LSTM learns rich representations across tasks and captures relationships between variables, enhancing performance in simulating hydrological processes. The intermediary sequences serve as inputs for all output modules, with each task having a dedicated module to ensure independent outputs. Next, we will detail the model’s design intricacies.
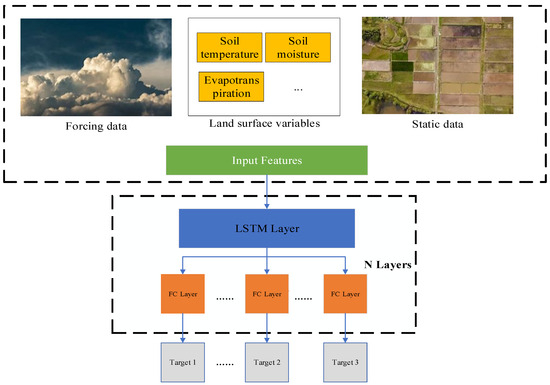
Figure 1.
The concept diagram of a multitask model, with an LSTM layer serving as the information sharing layer, and N fully connected layers serving as the output layer. The “N” depends on the desired forecast variable.
2.2.1. Long Short-Term Memory (LSTM) Networks
In Recurrent Neural Networks (RNNs), each time step’s information often includes the previous step’s data as part of its input. This aspect holds significant importance in hydrological variable forecasting due to the high auto-correlation present in these variables (that is, a high degree of correlation between the current time’s value and the value from the previous time step). LSTM, a variant of RNNs, addresses RNNs’ weakness in handling long-term dependencies (Sherstinsky, 2020 [48]). LSTM’s capability in dealing with long-term dependencies lies in the coordinated operation of its internal memory units (c(t) in Figure 1) and hidden units (h(t) in Figure 1), capturing slow- and fast-evolving processes, respectively. Moreover, its internal three-gate structure (i.e., input, forget, and output gates) regulates the storage, deletion, and transmission of information within each unit. These frameworks contribute to enhancing the LSTM model’s ability to handle long-term dependency relationships.
2.2.2. Multitask Learning
Multitask learning involves configuring multiple tasks as optimization objectives within deep learning models (Caruana, 1997 [49]). This approach enables models to leverage information contained within certain tasks to enhance the predictive performance of most tasks. Moreover, compared to single-task approaches, multitask learning has been proven in fields such as natural language processing (Chen et al., 2014 [50]; Seltzer & Droppo, 2013 [51]) and computer vision (Girshick, 2015 [52]) to achieve higher computational efficiency, reduced overfitting, and improved generalization. This is because multitask learning guides models to acquire generic features favored by the majority of relevant tasks (Li et al., 2021 [53]). Furthermore, multitask learning can alleviate a limitation of deep learning models, wherein deep learning typically requires a substantial amount of observational data for model training. In the field of earth sciences, acquiring data might be prohibitively expensive. Through the multitask learning approach, it might be possible to utilize variables abundant in data to assist in training the relevant variables that suffer from data scarcity, thereby enhancing the model’s predictive capacity for these data-scarce variables.
2.2.3. Model Training
Deep learning models have typically been one model per variable. Hence, we trained four single-task models to predict SM1, ST1, ET, and SSHF. Each single-task model comprises an LSTM layer, a Dropout layer, and a fully connected layer, with the loss calculation formula outlined below:
represents the observed value of round i training and represents the predicted value of round i training. In our experiments, we employed cross-entropy for loss calculation, as indicated by the following formula:
The multitask model comprises an LSTM layer and multiple parallel fully connected layers equal to the number of input variables (for instance, if the input variables are SM1 and ET, then the multitask model has two fully connected layers) to simultaneously predict multiple variables (as illustrated in Figure 1). The model’s loss function formula is expressed as follows:
represents the loss for the i-th round of the j-th task (Equation (1)). represents the loss weight for the j-th task.
In traditional multitask models, parameters are typically updated by computing the losses for all tasks and then collectively updating the entire model’s parameters. However, in our model, for each output layer, only the loss gradient related to the corresponding variable is used to update that layer’s parameters. For example, only the error in predicting SM1 is employed to update the parameters of the SM1 output layer. Conversely, all variable losses are aggregated (Equation (3)) to update the shared layer, namely the LSTM layer’s parameters. We adopted this approach because the LSTM layer processes data from all variables, necessitating all task losses for parameter updates, whereas each output layer is dedicated to forecasting a single task. Therefore, only the loss associated with the predicted task is used for parameter updates to ensure the independence of output results. Through experimentation, we have demonstrated that employing this parameter update methodology yields superior predictive performance compared to the traditional approach.
2.3. Experimental Setting
To comprehensively examine the applicability of multitask learning in hydrology, we designed four experiments from various perspectives.
Experiment A and Experiment B discuss factors affecting multitask learning, specifically task weighting and the impact of different variable combinations (Li et al., 2023 [54]). Experiment C explores how the size of the dataset constrains the performance of multitask models (Sadler et al., 2022 [55]). Finally, Experiment D examines the inclusiveness of multitask models regarding the number of tasks.
2.3.1. Experiment A: Multitask Modeling with Different Weight Allocation Schemes
In Experiment A, we aimed to investigate the degree to which the magnitude of loss weights assigned to different variables within a multitask model affects its performance and the specific reasons behind this impact. When modeling SM1 (Task 1) and ET (Task2), we manually controlled the loss weights for these two variables, adhering to the weight allocation conditions outlined in the following formula:
represents the loss weight for the i-th task. We allocated weights to the two variables across five ratios (28, 37, 55, 73, and 82), where a ratio of 28 signifies a loss weight assignment of 0.2 for Task 1 and 0.8 for Task 2. This experiment aimed to alter the proportion of ET and SM1 in the total loss by assigning different weights to them (as indicated in Formula 3). The goal was to explore how varying proportions of ET and SM1, through different weight assignments, impact the model’s performance.
Due to the substantial influence of task weights on multitask learning, numerous studies are dedicated to devising balanced algorithms for task weight allocation in multitask models. These algorithms can generally be categorized into three types: learning-based, optimization-based, and computation-based approaches.
Learning-based approaches consider task loss weights as learnable parameters, optimizing them explicitly through gradient descent. Notable methods representing this approach include Gradient Normalization (GradNorm) (Chen et al., 2018b [56]) and Uncertainty Weights (UW) (Kendall et al., 2018 [57]). Optimization-based approaches transform task weight allocation into a multi-objective optimization problem, directly deriving task weights by solving equations, such as MGDA (Sener & Koltun, 2018 [58]). Computation-based methods are among the most widely used in current multitask weight allocation algorithms. Their principle involves computing the most suitable weights by aggregating gradients or losses from all tasks. Representative methods include Dynamic Weight Average (DWA) (Liu et al., 2019 [59]), Projecting Conflicting Gradient (PCGrad) (Yu et al., 2020 [60]), and Gradient sign Dropout (GradDrop) (Chen et al., 2020 [61]).
However, most current weight allocation algorithms dynamically balance different tasks (Xin et al., 2022 [62]) without specifically emphasizing the dominant role of a particular variable in weight allocation. Therefore, in Experiment A, we did not utilize weight allocation algorithms. Instead, we manually controlled weight assignments to observe the performance of the model when a specific variable dominates the model’s parameter updates.
2.3.2. Experiment B: Multitask Modeling with Different Variable Combinations
The relationships among different variables vary in strength, and multitask learning is a method that leverages these relationships to enhance model performance by utilizing information from related variables. Therefore, the varying closeness of relationships among different variable combinations can lead to changes in the performance of multitask models. In Experiment B, we combined and modeled four important and correlated hydrological variables (SM1, ET, ST1, and SSHF) (Zhang et al., 2005 [63]), as detailed in Table 2. The aim was to assess the transfer trends of relationships between different variable combinations by contrasting the performance of models formed by these combinations (Chen et al., 2020).

Table 2.
Results of task combinations in multitask models.
In multitask learning, relationships among variables typically fall into three categories: positive transfer, negative transfer, and no significant transfer. Positive transfer might exhibit unidirectional transfer, where multitask learning can only utilize information from one variable to aid in training another variable.
2.3.3. Experiment C: Multitask Modeling with Varied Data Quantities
During model training, every iteration involves randomly selecting N points from the global grid and extracting consecutive seven-day data from these points spanning the years 2015 to 2019, serving as input sequences. This means that each iteration incorporates N sequences of seven days’ worth of data for model training.
Multitask learning has demonstrated its efficacy in effectively utilizing data to aid model training in domains such as natural language processing (Chen et al., 2014; Seltzer & Droppo, 2013) and computer vision (Girshick, 2015), particularly in scenarios where data are sparse. To assess the extent of information utilization of hydrological variables through multitask learning within the hydrology domain, Experiment C employs five values of N (64, 128, 256, 512, and 1024, representing five training datasets ranging from low to high amounts of training data) to model variables SM1 and ET. This experiment aims to evaluate the degree to which the multitask model utilizes data and the performance of the multitask model in cases of data sparsity in the hydrology domain.
2.3.4. Experiment D: Multitask Modeling with Three Variables
In Experiment D, we expanded the forecasting tasks to three, organized into two groups based on relationships among variables (the first group comprises: SM1–ET–ST1; the second group comprises: SM1–ST1–SSHF). This experiment aims to assess the model’s performance in predicting three tasks, investigating the model’s generalizability concerning the number of forecasting tasks. Additionally, it explores the multitask model’s capacity to learn complex task relationships as the prediction tasks increase.
2.4. Experimental Details
We conducted experiments using global surface data from the LandBench1.0 dataset with a resolution of 1°. The training data spanned from 1 January 2015 to 31 December 2019, with the initial 80% used for training and the remaining 20% for testing. The evaluation data covered the period from 1 January 2020 to 31 December 2020. During both the training and evaluation phases, each input sequence consisted of seven days. Data were input as time series, a crucial format due to the high temporal dependence of hydrological variables, which reflect states from previous periods. To prevent potential numerical overflow or instability during computations, all data were preprocessed using Min-Max Scaling, ensuring the processed data fell within the range of 0 to 1.
Each model underwent a maximum of 1000 training epochs, with 300 iterations per epoch. Following every twenty epochs, the model underwent testing. A stopping criterion, designed as an early stopping mechanism, was implemented during testing. This mechanism compared the loss of the current test to the loss of the previous one, retaining the model parameters associated with the smaller loss. If the same model parameters were preserved for ten consecutive tests, training was halted prematurely, and these preserved parameters constituted the final model parameters. Each model in the experiment was trained five times, each time with a different random initialization of model parameters. This approach aimed to account for the influence of initial parameters on model performance. The resulting metrics were averages derived from the metrics obtained by the five models. Across all experiments, the optimizer was set to Adam, with an initial learning rate of 0.001.
During the model evaluation phase, we assessed global surface grid points every 20 days. To evaluate model performance, we calculated the corresponding metrics for all predicted and actual values at each grid point using the specified formulas. The final results for each metric were obtained by summarizing and outputting the median of these metrics across all global surface grid points.
In Experiments B, C, and D, the weight allocation for tasks within the model remained constant. Specifically, Experiments B and C utilized a weight allocation of 28, while Experiment D utilized a weight allocation of 163 (with 163 allocations mirroring the 28 configuration; meaning the first task had a weight of 0.1, the second task 0.6, and the third task 0.3). These weight allocations in Experiments B, C, and D were determined as optimal through extensive experimentation. Even if they may not represent the best weight allocations for particular task combinations, they are considered suboptimal solutions.
2.5. Evaluation Metrics
This study employed various evaluation metrics for assessing and comparing single-task and multitask models: the Kling–Gupta Efficiency coefficient (KGE; Equation (5)), Nash–Sutcliffe Efficiency (NSE; Equation (6)), coefficient of determination (R2; Equation (7)), Bias (Equation (8)), and Root Mean Square Error (RMSE; Equation (9)).
where represents the linear relationship between predicted and observed values; represents the proportional relationship between the predicted mean and the observed mean, where is the mean of the predicted value and is the mean of the observed value; represents the proportional relationship between predicted and observed variability, and std is the standard deviation. The KGE (Kling et al., 2012 [64]) value signifies the degree of agreement between predicted and observed values in terms of correlation, bias, and variability ratio. This metric offers a comprehensive assessment of model performance, ranging from −∞ to 1, where a value closer to 1 indicates a higher level of agreement between simulated and observed values.
NSE (Nash–Sutcliffe Efficiency) assesses the prediction accuracy of a model, ranging from negative infinity to 1. A value of 1 indicates a perfect match between the model simulation and observed values. When NSE equals 0, the model’s performance is equivalent to using the mean of the observed values, and when NSE becomes negative, the model’s performance is even worse than simply using the mean of the observed values.
R2 evaluates the goodness of fit between predicted and actual values.
The Bias metric clearly indicates the deviation of model predictions and the extent of overestimation or underestimation concerning observed values.
RMSE (Root Mean Square Error) emphasizes the average difference between model predictions and observed values. This metric evaluates the model’s average predictive capability by measuring the square root of the average squared differences between predicted and observed values.
3. Results
3.1. Experiment A: Multitask Modeling with Different Weight Allocation Schemes
3.1.1. The Effect of Multitask Learning
Among the five weight allocation schemes, the multitask model consistently outperforms the single-task model in forecasting SM1. Furthermore, under schemes 28, 37, and 55, the multitask model exhibits superior predictive capabilities for ET compared to the single-task model (refer to Figure 2). Across all weight allocation schemes, the multitask model consistently surpasses the single-task model in forecasting SM1 based on R2, KGE, and NSE metrics. Notably, under the 28-weight allocation scheme, the multitask model achieves significant improvements of 65.7%, 8.4%, and 19.6% in R2, KGE, and NSE for forecasting SM1, respectively, compared to the single-task model. Similarly, for predicting ET, the multitask model demonstrates enhancements of 9.3%, 6.1%, and 4.1% in R2, KGE, and NSE metrics, respectively, under the same scheme. These improvements indicate that multitask learning effectively leverages interactions between variables, enhancing the LSTM model’s ability to simulate multiple hydrological processes. Additionally, the multitask model exhibits higher NSE and reduced overall errors compared to the single-task model, indicating enhanced prediction accuracy and stability. Figure 2 illustrates that, except for schemes 73 and 82, the multitask model shows reduced dispersion in the prediction results, highlighting its greater stability in predictive capabilities compared to the single-task model.
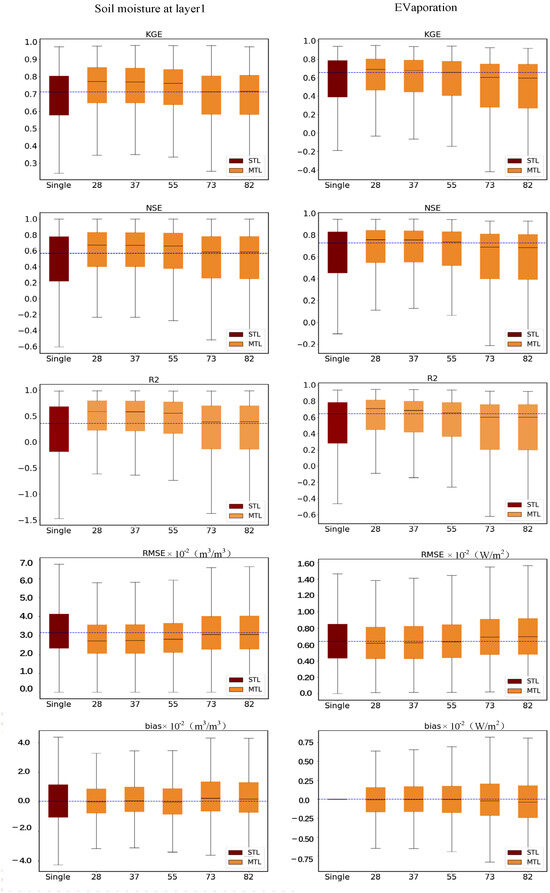
Figure 2.
Under various weight allocation schemes, the performance evaluation of the multitask model modeled with SM1 and ET encompasses metrics such as KGE, NSE, R, RMSE, and Bias.
The substantial performance improvement achieved by our proposed multitask model in joint forecasting of SM1 and ET underscores the wealth of potentially beneficial information inherent in the data of these variables. Moreover, it highlights the model’s capacity to leverage such information through multitask learning. This finding also suggests a positive correlation between SM1 and ET, affirming that multitask learning can enhance the accuracy of forecasting both tasks concurrently.
3.1.2. Influence of Loss Weight
The weight allocation of tasks within the multitask model significantly influences its performance. Across weight allocation schemes 28, 37, and 55, the multitask model exhibits substantial improvements in predictive performance compared to the single-task model. However, in schemes 73 and 82, the multitask model’s performance in forecasting SM1 remains largely on par with the single-task model, and for ET variables, it even falls below that of the single-task model. For instance, when assigning task loss weights in the 28 scheme, the multitask model shows enhancements of 9.3%, 6.1%, and 4.1% in R2, KGE, and NSE, respectively, for forecasting ET compared to the single-task model. Conversely, in the 82 scheme, the multitask model’s forecast for ET yields metrics of 0.6, 0.59, and 0.68, indicating decreases of 6.2%, 9.2%, and 5.5%, respectively, compared to the single-task model. These differences, reflecting a 0.1, 0.1, and 0.07 variance between the two allocation schemes for the same variables, underscore the pivotal role of task weights within the multitask model; improper weight allocation schemes may constrain the model’s performance.
We observe a gradual decrease in the median values of R2, KGE, and NSE for both SM1 and ET predictions in the multitask model as the proportion of SM1 task weight increases (refer to Figure 2). This trend indicates that as the LSTM layer becomes more influenced by the gradient from SM1 during parameter updates, the predictive performance for both SM1 and ET diminishes. This decline is particularly noticeable when SM1 dominates the model’s parameter updates (when SM1’s loss weight exceeds 0.5). Across schemes 28, 37, and 55, the performance of the multitask and single-task models remains comparable until the SM1 task weight reaches 0.7, at which point there is a sharp decline in R2, KGE, and NSE for both SM1 and ET. This scenario likely arises because SM1 is comparatively more challenging to predict (its single-task model’s NSE of 0.56 is significantly lower than ET’s 0.72). Therefore, when the SM1 task carries substantial weight during parameter updates in the LSTM layer, the adjustments in parameters during gradient descent prioritize reducing the prediction error for SM1. This aligns with Salder’s findings in 2022, where assistance variables that are easier to predict should be given higher weights when aiding in stream prediction. Our experimental results echo this, suggesting that when the lower accuracy SM1 task loss dominates the parameter updates in the multitask model, it leads to a decline in predictive performance.
3.2. Experiment B: Multitask Modeling with Different Variable Combinations
3.2.1. The Impact of Inter-Task Relationships on Multitask Model Performance
In Experiment B, multiple trials were conducted using the same dataset (Table 2), and the outcomes are depicted in Figure 3. For the majority of combinations, the model performances surpassed those of the single-task model: the SM1-ST1 model (Figure 3a) exhibited median increments of 57.1%, 5.6%, and 17.8% in R2, KGE, and NSE metrics, respectively, when forecasting SM1. Similarly, the SSHF-ET model (Figure 3c) demonstrated median improvements of 9.3%, 4.6%, and 5.5% in R2, KGE, and NSE for predicting ET, while the ET-ST1 model (Figure 3d) showed respective median enhancements of 14%, 7.6%, and 6.9% in R2, KGE, and NSE for forecasting ET. However, within the SSHF and ET combination (Figure 3c), while the accuracy in predicting ET increased, conversely, the forecast accuracy of SSHF declined (SSHF’s R2, KGE, and NSE decreased from 0.31, 0.49, and 0.55 to 0.23, 0.46, and 0.54). This phenomenon may stem from the lack of shared information in ET data that is beneficial for improving SSHF prediction accuracy, while SSHF data contain useful information for enhancing ET prediction accuracy. This suggests a potentially one-way relationship between SSHF and ET variables, where only self-contained information is utilized to improve predictive capabilities for other variables. In cases where ET variables lack relevant information for SSHF prediction, the loss gradients of ET interfere with parameter adjustments in the LSTM layer, leading to a decrease in SSHF predictive accuracy compared to the single-task model. These findings highlight multitask learning’s role in leveraging variable relationships to enhance model performance, emphasizing that the diversity in these relationships significantly impacts the effectiveness of multitask learning.
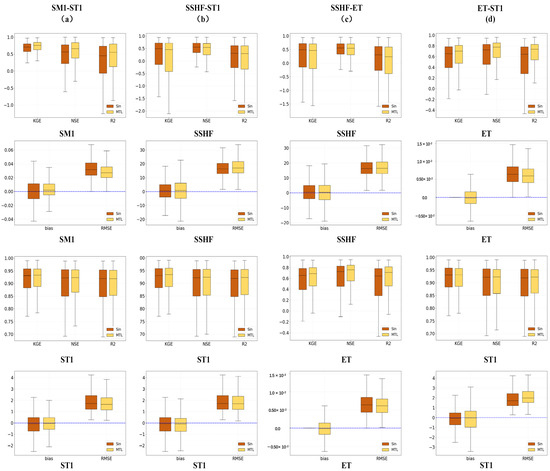
Figure 3.
The performance evaluation of the multitask model, which models five different variable combinations, is compared against the single-task model. Evaluation metrics encompass KGE, NSE, R2, Bias, and RMSE. The five variable combinations are as follows: (a) SM1-ST1, (b) SSHF-ST1, (c) SSHF-ET, and (d) ET-ST1.
Furthermore, we observed a significant enhancement in the predictive efficacy of the multitask model when ST1 was coupled with either SM1 or ET (Figure 3a,d) and assigned a greater task weight. This observation aligns with the findings of Experiment A, indicating a positive correlation between ST1, SM1, and ET, which contributes valuable data for predicting SM1 and ET. Furthermore, owing to the stable data range of ST1, it inherently lends itself to more accurate predictions. Consequently, when ST1 is assigned a higher weight in the overall loss function, the LSTM model prioritizes leveraging the high-accuracy gradient of ST1 during parameter updates, thereby augmenting the model’s predictive prowess.
Conversely, in the combination of ST1 and SSHF (Figure 3b), we found that when ST1 had a high weight, the predictive performance of the multitask model was comparable to that of the single-task model. This could be due to the absence of latent information in the ST1 and SSHF data that aids in predicting each other. This underscores the fact that the relationships between variables are pivotal factors in determining the effective application of multitask learning. If there is no clear relationship or a negative transfer among variables, even when the parameter updates of the multitask model are dominated by high-accuracy loss gradients, it does not guarantee an enhancement in predictive performance for most variables.
3.2.2. The Multitask Model’s Capability in Handling Extreme Situations
Figure 4 demonstrates the improved forecasting of SM1 by the multitask models, SM1-ET and SM1-ST1, compared to single-task models across global regions. Overall, the multitask models exhibit superior performance metrics in many areas, notably across large parts of North America, northern South America, including Argentina, and significant portions of China.
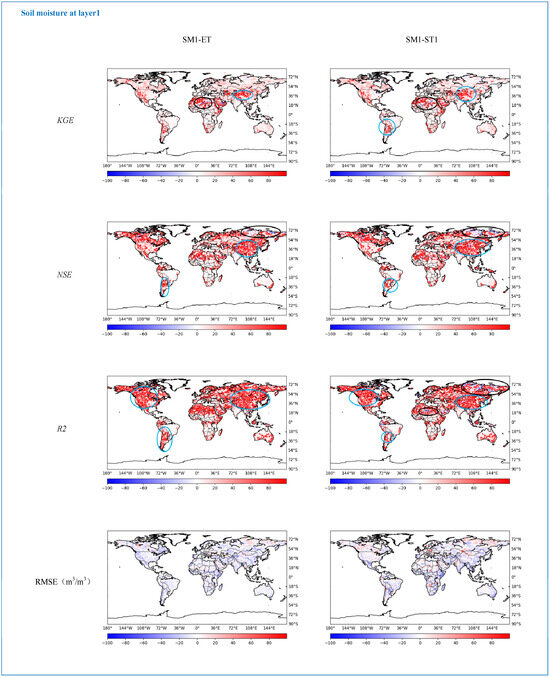
Figure 4.
The differential results showcasing the evaluation metrics for the predictive performance of SM1 by the models SM1-ET and SM1-ST1, in contrast to the evaluation metrics for SM1’s prediction by the single-task model, are presented across global grid points. The evaluation metrics utilized for this presentation encompass R2, KGE, NSE, and RMSE.
However, there are alternating improvements and declines in certain regions of North Africa and North Asia, possibly due to the challenges posed by extreme situations, for example, a sudden increase in rainfall or a drastic drop in temperature. To investigate the multitask model’s capability in handling extreme events further, three regions—Central South America, North Africa, and North Asia—were selected based on Figure 4. These regions represent tropical monsoon (AM), tropical desert (BWH), and subarctic (DFC) climates, respectively. Evaluation of SM1 prediction in 2020 within each region (Figure 5), where random points were selected within the three regions, provides insights into the multitask model’s forecasting performance under various extreme event scenarios.
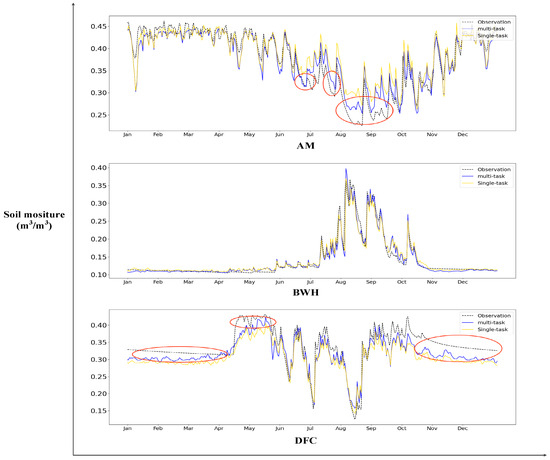
Figure 5.
For the AM, BWH, and DFC climate regions, the predictive outcomes of SM1 by the SM1-ET model are contrasted with those of the single-task model.
In the AM region, rainfall is relatively consistent throughout the year. However, the impact of high summer temperatures leads to a decline in soil moisture content, particularly in surface soil moisture (SM1). Consequently, from summer onwards, observable fluctuations occur in SM1 data. During the sharp decline in SM1 data between August and September, the predictions from the multitask model closely match the observed data from the single-task model. Additionally, between May and August, when observed data undergo frequent and pronounced changes, the multitask model adeptly captures and predicts these trends, resulting in more precise predictions compared to the single-task model.
In the BWH region, where rainfall is scarce throughout the year except for a small amount during the summer, SM1 observations exhibit a sharp increase in the summer. Here, both the multitask and single-task models produce predictions that closely resemble the observed trends. This observation helps explain the fluctuation in predictive accuracy of the multitask model in the northern part of Africa (as depicted in Figure 4), where both improvements and declines in predictive accuracy are evident.
In the DFC region, characterized by harsh winters and consistently low temperatures, weak evapotranspiration results in relatively higher soil moisture. As temperatures rise in summer, evapotranspiration increases, coinciding with seasonal rainfall, leading to a dramatic increase followed by a sharp decrease in soil moisture. Figure 5 and Figure 6 for the DFC region show that, except for the period between June and September, the multitask model consistently outperforms the single-task model in other time periods. However, during the volatile period of intense SM1 observation changes from June to September, the predictive performance of the multitask model does not exhibit significant differences from the single-task model.
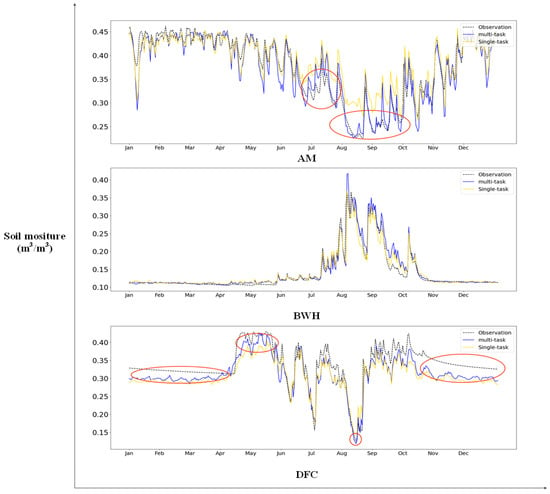
Figure 6.
Similar to Figure 5, this illustration showcases the predictive results of the SM1-ST1 model for forecasting SM1.
Findings from Experiment B highlight a significant advantage of the multitask model over the single-task model in facing extreme conditions, particularly in the AM region (Figure 5, Figure 6, Figure 7 and Figure 8). By evaluating the multitask model’s predictive capabilities across diverse climatic zones, we further confirm the effectiveness of multitask learning in facilitating models to simulate various hydrological processes, even amidst distinct climatic conditions. Moreover, in certain scenarios, the multitask model demonstrates an improved ability to manage extreme situations.
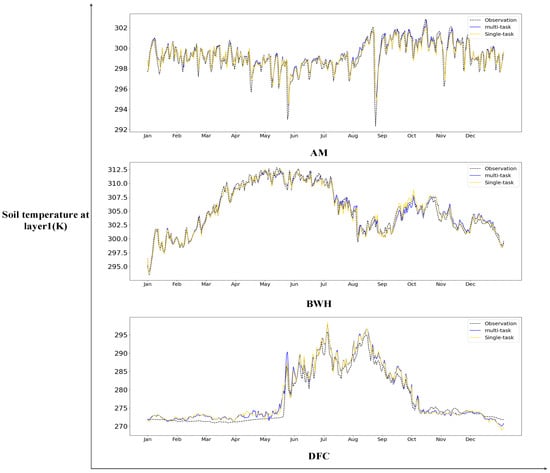
Figure 7.
The results of forecasting ST1 by the SM1-ST1 model in the AM, BWH, and DFC climate regions.
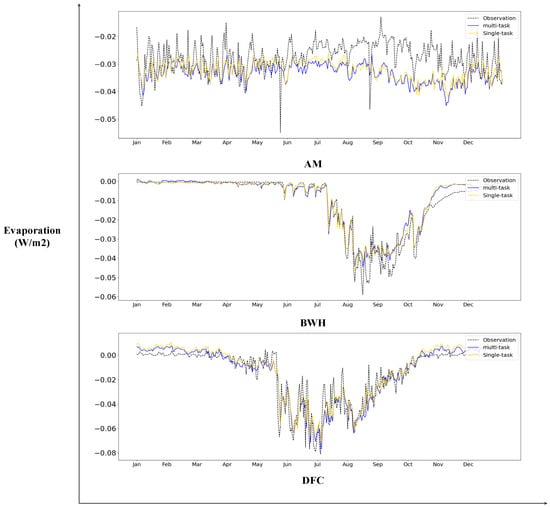
Figure 8.
Similar to Figure 7, this representation displays the forecasting outcomes of ET by the SM1-ET model.
3.3. Experiment C: Multitask Modeling with Varied Data Quantities
Table 3 presents the outcomes of evaluating the performance of single-task and multitask models under varying volumes of training data. The results from Table 3 reveal a consistent enhancement in predictive performance for both single-task and multitask models as the volume of training data increases. This aligns with expectations, given that deep learning models have the capacity to learn hydrological processes from data, whereby larger training data volumes lead to more precise emulation of these hydrological processes. Under equivalent training data conditions, the multitask model outperforms the single-task model across three metrics (R2, NSE, and KGE) for forecasting SM1 and ET. Particularly noteworthy is the considerable improvement of the multitask model in predicting SM1. For instance, considering R2 with an input of 64 grid points, the multitask model exhibits a 45.6% enhancement compared to the single-task model. This augmentation rate remains consistent across varying data volumes. Additionally, even with only 64 grid points per iteration, the multitask model’s evaluation metrics (R2, KGE, and NSE) for forecasting SM1 surpass those of the single-task model using 1024 grid points per iteration. These findings underscore how multitask learning facilitates more effective utilization of training data, leading to a substantial enhancement in model performance.

Table 3.
The evaluation results of single-task and multitask model performances across five different training data volumes. Evaluation metrics include R2, KGE, and NSE.
Concurrently, the performance of multitask models not only escalates with an increase in training data volume but also maintains equivalent enhancement efficiency to single-task models, even when possessing high inherent accuracy. As depicted in Table 3, we observe that with the augmentation of training data volume, multitask models exhibited final increments of 0.07, 0.027, and 0.046 for R2, KGE, and NSE in predicting SM1, and 0.047, 0.054, and 0.03 for the same metrics in predicting ET. In contrast, single-task models displayed enhancements of 0.059, 0.014, and 0.031 for R2, KGE, and NSE in predicting SM1, and 0.072, 0.57, and 0.044 for predicting ET. Noteworthy is that even with a higher predictive accuracy, multitask models showcased a greater increase in R2, KGE, and NSE for predicting SM1 with an augmented data volume compared to single-task models, while the enhancement in predicting ET was slightly lower than that of single-task models. These findings indicate that multitask learning, when applied to models with high precision, can still further augment predictive capabilities by leveraging multi-variable data, affirming its role in enabling models to fully exploit training data.
3.4. Experiment D: Multitask Modeling with Three Variables
Expanding the model’s forecasting tasks from two to three, the multitask model continues to demonstrate superior predictive performance over single-task learning (see Figure 9): within the SM1-ET-ST1 combination, the KGE for SM1 and ET increased from 0.70 and 0.63 to 0.74 and 0.66, respectively, while NSE improved from 0.58 and 0.69 to 0.62 and 0.72, and R2 progressed from 0.36 and 0.62 to 0.51 and 0.66. Likewise, in the SM1-ST1-SSHF combination, SM1’s R2, KGE, and NSE metrics rose from 0.36, 0.70, and 0.58 to 0.48, 0.73, and 0.61. These outcomes underscore the positive relationship between SM1, ET, and ST1, demonstrating that multitask learning aids the model in capturing information conducive to enhancing performance among multiple variables. However, when the number of forecasting tasks increases to three, the improvement in the model due to multitask learning is not as significant as with the dual-task learning model. This situation might arise from (1) the inherent constraints of the simple model structure in learning complex relationships among multiple variables; (2) insufficient hyperparameter tuning specifically for the three-task forecast, instead opting for a simple proportional allocation of weights among the tasks.
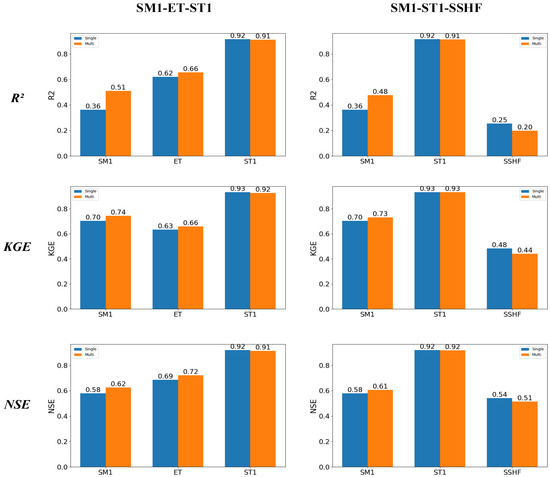
Figure 9.
The performance evaluation results of two three-task models, SM1-ET-ST1 and SM1-ST1-SSHF, are presented using metrics such as R2, KGE, and NSE.
In the SM1-ST1-SSHF combination, we observed slightly lower predictive performance for SM1 compared to the SM1-ET-ST1 combination. This could stem from two reasons: firstly, in the SM1-ST1-SSHF combination, the model lacks information present in ET data that aids in improving SM1 forecasting performance; secondly, there is not a significant relationship between SSHF and ST1/SM1, impeding multitask learning from leveraging SSHF data to enhance SM1 forecasting performance. These factors result in a lesser improvement in SM1’s predictive accuracy compared to the SM1-ET-ST1 combination. This further validates how multitask learning sifts through variable relationships, enabling the model to learn generalized features applicable to most tasks, thus enhancing forecasting accuracy for the majority of tasks.
Furthermore, these experiments also demonstrate a certain robustness in our designed multitask model concerning the number of forecasting tasks.
4. Discussion
We conducted an exhaustive comparative analysis of multitask and single-task models in forecasting hydrological variables, employing various evaluation metrics such as R2, NSE, KGE, RMSE, and Bias. Our findings consistently demonstrate the superior performance of the multitask model across the majority of scenarios. Further discussion will delve into the factors influencing multitask learning, provide further analysis of our experimental results, and shed light on some inherent limitations of our multitask model design.
4.1. Performance of Multitask Models
Figure 2 and Figure 3 clearly show that, compared to single-task models, multitask learning models produce more consistent predictions with fewer outliers and extreme values. This advantage stems from the ability of multitask learning to improve prediction stability by learning the interactions between multiple hydrological variables. Additionally, Figure 4 demonstrates that multitask models achieve higher prediction accuracy than single-task models across most global grid points at a resolution of 1°. This improved accuracy is due to the multitask models receiving information from multiple variables, allowing them to capture features more closely aligned with the actual hydrological cycle, thereby enhancing the models’ generalization performance. Furthermore, the 2020 annual prediction analysis for three climatic regions, as shown in Figure 5 and Figure 6 (highlighted by the red circles), demonstrates the multitask model’s sensitivity to seasonal variability in the variables. Moreover, during periods of significant change, the multitask model exhibits far superior predictive performance compared to the single-task model. Compared to single-task models, multitask models can produce predictions that more closely match real data even when data are sparse (Table 3). This advantage offers a new perspective for addressing the issue of limited data for certain specific variables in the field of hydrology.
4.2. Factors Influencing Multitask Learning
Our research findings indicate that when high-precision tasks predominantly influence parameter updates in a multitask model (where high-precision tasks possess greater task weights), the model’s predictive performance is significantly enhanced. For example, using three variables—SM1, ET, and ST1—evaluated through the NSE metric, we found NSE metrics of 0.58, 0.69, and 0.92, respectively. This indicates that ET’s precision is higher than SM1’s but lower than ST1’s. In our experiments, combining SM1 with either ET or ST1, with higher weights assigned to ET or ST1, greatly improved the model’s performance. When combining ET with ST1, assigning a higher weight to ST1 maximally enhanced the model’s predictive capability.
Furthermore, our results demonstrate that the efficacy of multitask learning relies on the presence of positive transfer relationships among variables. For instance, in the experiment involving SSHF and ST1, the absence of a significant transfer relationship between ST1 and SSHF resulted in no improvement in SSHF’s prediction accuracy, despite the high-precision ST1 dominating the gradient of loss in the LSTM layer’s parameter updates. Hence, the successful application of multitask learning depends on the relationships among variables. Multitask learning can enhance model predictive performance through positive inter-variable relationships; however, in cases of negative transfer or insignificance, it fails to aid in enhancing the model’s performance.
The allocation of task weights can mitigate negative transfer to some extent, where training multiple tasks together leads to a decline in model performance. Alternatively, it helps the model assign greater weights to tasks with positive correlations, thus leveraging task relationships fully to facilitate model training.
4.3. Selection of Multitask Forecasting Variables
To leverage the benefits of multitask learning, the variables involved in forecasting within the multitask model must have some common drivers (such as physical, biological, or chemical relationships). The four hydrological variables selected in this study (SM1, ET, ST1, and SSHF) exhibit close interconnections within the hydrological cycle. Additionally, other relevant observational variables, such as runoff and surface heat radiation, can be incorporated from equations such as the water balance and heat equations. As indicated by the results of Experiment D, the multitask model demonstrates generalizability concerning the number of forecasting tasks. Thus, with an adequate volume of training data for the chosen variables, multitask learning can significantly enhance model performance.
4.4. Task Loss Weight Allocation
In Experiment A, we employed a manual task weight control approach to explore how task loss weighting impacts the performance of multitask models. However, this method, while useful for gaining an overall understanding of weight distribution, falls short in determining precise optimal weight combinations. Therefore, we advocate for using task weight balancing algorithms within multitask learning frameworks when modeling multiple tasks. These algorithms efficiently attain optimal weight combinations and exhibit remarkable generalizability concerning the number of tasks forecasted, automatically considering intricate inter-variable relationships.
4.5. Limitations of the Study and Future Prospects
In this endeavor, we devised a model to assess the feasibility and superiority of multitask learning on hydrological variables. However, the inherent simplicity of the multitask model structure we designed may constrain its capacity to grasp intricate task relationships. In various domains, numerous sophisticated multitask models have been developed to tackle complex and challenging predictions across diverse tasks or scenarios. Take computer vision, for instance. Liu et al. (2019) proposed an End-To-End Multitask Learning With Attention (MTAN) framework comprising a shared network with a global feature pool and a soft attention module for each task. These modules adeptly extract features pertinent to a specific task from the global features, demonstrating exceptional robustness in task loss weighting algorithms. In contrast, within the hydrological domain, multitask learning has largely remained at the stage of employing simplistic models to handle multiple variable features. Consequently, our forthcoming efforts will be directed towards the development of a hydrology-specific multitask learning model, grounded in the distinctive data characteristics of hydrological variables.
5. Conclusions
In this study, we developed an LSTM model based on multitask learning principles to exploit relationships between hydrological variables, enhancing predictive performance. We conducted four experiments using the LandBench1.0 dataset: (A) exploring different weight allocation schemes, (B) investigating variable combinations, (C) analyzing different data volumes, and (D) examining models with three variables. In light of the experiments conducted, our study yields several key findings regarding the application of multitask learning in hydrological variable prediction.
Firstly, employing optimal weights for variables in multitask models results in significant enhancements in predictive performance, as demonstrated by notable improvements in R2, KGE, and NSE metrics for various variable combinations compared to single-task models. Specifically, the SM1-ET model showed improvements of 0.23, 0.06, and 0.11 for SM1, and 0.06, 0.04, and 0.03 for ET. In the SM1-ST1 model, SM1’s metrics improved by 0.2, 0.04, and 0.1, and in the ET-ST1 model, ET’s metrics improved by 0.09, 0.05, and 0.05. These findings underscore the effectiveness of multitask learning in enhancing LSTM model performance for hydrological variables.
Secondly, the multitask model consistently outperforms the single-task model as the number of forecast tasks increases, while maintaining consistent relationships among variables. This highlights the robustness of the multitask model in handling varying task quantities without compromising performance or altering variable relationships.
Thirdly, our findings indicate that multitask learning allows for more effective utilization of training data by the model, as evidenced by superior predictive performance with a smaller training data volume compared to the single-task model. This suggests that multitask learning optimizes data utilization and enhances model efficiency.
Lastly, the allocation of task loss weights significantly influences the effectiveness of multitask learning. Variables with strong positive correlations, such as SM1 with ET and SM1 with ST1, prove advantageous for multitask learning, leading to substantial performance enhancements. Conversely, unidirectional transfer relationships and combinations lacking significant correlation may constrain the efficacy of multitask learning, highlighting the critical role of inter-variable relationships in influencing model performance.
In conclusion, our study underscores the effectiveness of multitask learning in improving hydrological variable prediction, offering insights into its mechanisms and highlighting its potential applications in hydrological modeling and forecasting.
Author Contributions
Y.Y.: Conceptualization, Methodology, Software, Investigation, Formal Analysis, Writing—Original Draft; G.L.: Data Curation, Writing—Original Draft; Q.L.: Visualization, Investigation; J.Z.: Resources, Supervision. All authors have read and agreed to the published version of the manuscript.
Funding
The study was partially supported by the Jilin Provincial Science and Technology Development Plan Project under grants 20230101370JC.
Data Availability Statement
The code for multitask hydrological variable forecasting, developed using Python (version 3.9) based on PyTorch, is available on GitHub: https://github.com/2023ATAI/MTL-LSTM (accessed on 13 May 2023). This repository was created by Qingliang Li (liqingliang@ccsfu.edu.cn) in 2023. The experimental setup of the authors is as follows: OS: Linux 5.4.0; CPU: Intel(R) Xeon(R) Gold 6330 CPU @ 2.00 GHz (Intel, Santa Clara, CA, USA); RAM: 256.00 GB; GPU: NVIDIA A800 80 GB (NVIDIA, Santa Clara, CA, USA). The LandBench1.0 dataset used in the experiment can be downloaded from https://doi.org/10.11888/Atmos.tpdc.300294 (accessed on 13 May 2023).
Acknowledgments
Many thanks to the above institutions for their contributions to this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Samaniego, L.; Thober, S.; Wanders, N.; Pan, M.; Rakovec, O.; Sheffield, J.; Wood, E.F.; Prudhomme, C.; Rees, G.; Houghton-Carr, H.; et al. Hydrological Forecasts and Projections for Improved Decision-Making in the Water Sector in Europe. Bull. Am. Meteorol. Soc. 2019, 100, 2451–2472. [Google Scholar] [CrossRef]
- Pappenberger, F.; Cloke, H.L.; Parker, D.J.; Wetterhall, F.; Richardson, D.S.; Thielen, J. The monetary benefit of early flood warnings in Europe. Environ. Sci. Policy 2015, 51, 278–291. [Google Scholar] [CrossRef]
- Blöschl, G.; Bierkens, M.F.P.; Chambel, A.; Cudennec, C.; Destouni, G.; Fiori, A.; Kirchner, J.W.; McDonnell, J.J.; Savenije, H.H.G.; Sivapalan, M.; et al. Twenty-three unsolved problems in hydrology (UPH)—A community perspective. Hydrol. Sci. J. 2019, 64, 1141–1158. [Google Scholar] [CrossRef]
- Talchabhadel, R.; Karki, R.; Thapa, B.R.; Maharjan, M.; Parajuli, B. Spatio-temporal variability of extreme precipitation in Nepal. Int. J. Climatol. 2018, 38, 4296–4313. [Google Scholar] [CrossRef]
- Sirisena, T.A.J.G.; Maskey, S.; Ranasinghe, R.; Babel, M.S. Effects of different precipitation inputs on streamflow simulation in the Irrawaddy River Basin, Myanmar. J. Hydrol. Reg. Stud. 2018, 19, 265–278. [Google Scholar] [CrossRef]
- Khatakho, R.; Talchabhadel, R.; Thapa, B.R. Evaluation of different precipitation inputs on streamflow simulation in Himalayan River basin. J. Hydrol. 2021, 599, 126390. [Google Scholar] [CrossRef]
- Tarek, M.; Brissette, F.P.; Arsenault, R. Evaluation of the ERA5 reanalysis as a potential reference dataset for hydrological modelling over North America. Hydrol. Earth Syst. Sci. 2020, 24, 2527–2544. [Google Scholar] [CrossRef]
- Hilborn, R.; Mangel, M. (Eds.) The Ecological Detective: Confronting Models with Data, 1st ed.; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- Arhonditsis, G.; Brett, M. Evaluation of the current state of mechanistic aquatic biogeochemical modeling. Mar. Ecol. Prog. Ser. 2004, 271, 13–26. [Google Scholar] [CrossRef]
- Shen, C. A Transdisciplinary Review of Deep Learning Research and Its Relevance for Water Resources Scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Herrnegger, M.; Sampson, A.K.; Hochreiter, S.; Nearing, G.S. Toward Improved Predictions in Ungauged Basins: Exploiting the Power of Machine Learning. Water Resour. Res. 2019, 55, 11344–11354. [Google Scholar] [CrossRef]
- Bai, Y.; Chen, Z.; Xie, J.; Li, C. Daily reservoir inflow forecasting using multiscale deep feature learning with hybrid models. J. Hydrol. 2016, 532, 193–206. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Zhang, L.; Qin, H.; Mao, J.; Cao, X.; Fu, G. High temporal resolution urban flood prediction using attention-based LSTM models. J. Hydrol. 2023, 620, 129499. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Shalev, G.; Klambauer, G.; Hochreiter, S.; Nearing, G. Towards learning universal, regional, and local hydrological behaviors via machine learning applied to large-sample datasets. Hydrol. Earth Syst. Sci. 2019, 23, 5089–5110. [Google Scholar] [CrossRef]
- Read, J.S.; Jia, X.; Willard, J.; Appling, A.P.; Zwart, J.A.; Oliver, S.K.; Karpatne, A.; Hansen, G.J.A.; Hanson, P.C.; Watkins, W.; et al. Process-Guided Deep Learning Predictions of Lake Water Temperature. Water Resour. Res. 2019, 55, 9173–9190. [Google Scholar] [CrossRef]
- Shen, C.; Laloy, E.; Elshorbagy, A.; Albert, A.; Bales, J.; Chang, F.-J.; Ganguly, S.; Hsu, K.-L.; Kifer, D.; Fang, Z.; et al. HESS Opinions: Incubating deep-learning-powered hydrologic science advances as a community. Hydrol. Earth Syst. Sci. 2018, 22, 5639–5656. [Google Scholar] [CrossRef]
- Lees, T.; Buechel, M.; Anderson, B.; Slater, L.; Reece, S.; Coxon, G.; Dadson, S.J. Benchmarking data-driven rainfall–runoff models in Great Britain: A comparison of long short-term memory (LSTM)-based models with four lumped conceptual models. Hydrol. Earth Syst. Sci. 2021, 25, 5517–5534. [Google Scholar] [CrossRef]
- Nearing, G.S.; Kratzert, F.; Sampson, A.K.; Pelissier, C.S.; Klotz, D.; Frame, J.M.; Prieto, C.; Gupta, H.V. What Role Does Hydrological Science Play in the Age of Machine Learning? Water Resour. Res. 2021, 57, e2020WR028091. [Google Scholar] [CrossRef]
- Yang, S.; Yang, D.; Chen, J.; Santisirisomboon, J.; Lu, W.; Zhao, B. A physical process and machine learning combined hydrological model for daily streamflow simulations of large watersheds with limited observation data. J. Hydrol. 2020, 590, 125206. [Google Scholar] [CrossRef]
- Huang, X.; Gao, L.; Zhang, N.; Crosbie, R.S.; Ye, L.; Liu, J.; Guo, Z.; Meng, Q.; Fu, G.; Bryan, B.A. A top-down deep learning model for predicting spatiotemporal dynamics of groundwater recharge. Environ. Model. Softw. 2023, 167, 105778. [Google Scholar] [CrossRef]
- Mirzaei, M.; Shirmohammadi, A. Utilizing Data-Driven Approaches to Forecast Fluctuations in Groundwater Table. Water 2024, 16, 1500. [Google Scholar] [CrossRef]
- Jiang, S.; Zheng, Y.; Solomatine, D. Improving AI System Awareness of Geoscience Knowledge: Symbiotic Integration of Physical Approaches and Deep Learning. Geophys. Res. Lett. 2020, 47, e2020GL088229. [Google Scholar] [CrossRef]
- Sadeghi Tabas, S.; Samadi, S. Variational Bayesian dropout with a Gaussian prior for recurrent neural networks application in rainfall–runoff modeling. Environ. Res. Lett. 2022, 17, 065012. [Google Scholar] [CrossRef]
- Shah, W.; Chen, J.; Ullah, I.; Shah, M.H.; Ullah, I. Application of RNN-LSTM in Predicting Drought Patterns in Pakistan: A Pathway to Sustainable Water Resource Management. Water 2024, 16, 1492. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, T.; Kang, A.; Li, J.; Lei, X. Research on Runoff Simulations Using Deep-Learning Methods. Sustainability 2021, 13, 1336. [Google Scholar] [CrossRef]
- Kapoor, A.; Pathiraja, S.; Marshall, L.; Chandra, R. DeepGR4J: A deep learning hybridization approach for conceptual rainfall-runoff modelling. Environ. Model. Softw. 2023, 169, 105831. [Google Scholar] [CrossRef]
- Kapoor, A.; Negi, A.; Marshall, L.; Chandra, R. Cyclone trajectory and intensity prediction with uncertainty quantification using variational recurrent neural networks. Environ. Model. Softw. 2023, 162, 105654. [Google Scholar] [CrossRef]
- Bowes, B.D.; Sadler, J.M.; Morsy, M.M.; Behl, M.; Goodall, J.L. Forecasting Groundwater Table in a Flood Prone Coastal City with Long Short-term Memory and Recurrent Neural Networks. Water 2019, 11, 1098. [Google Scholar] [CrossRef]
- Azari, B.; Alasta, M.S.; Masood Ashiq, M.; Ebrahimi, S.; Shakir Ali Ali, A. CNN-Bi LSTM Neural Network for Simulating Groundwater Level. Comput. Res. Prog. Appl. Sci. Eng. 2022, 8, 1–7. [Google Scholar] [CrossRef]
- Zhao, W.L.; Gentine, P.; Reichstein, M.; Zhang, Y.; Zhou, S.; Wen, Y.; Lin, C.; Li, X.; Qiu, G.Y. Physics-Constrained Machine Learning of Evapotranspiration. Geophys. Res. Lett. 2019, 46, 14496–14507. [Google Scholar] [CrossRef]
- Fang, K.; Shen, C. Near-Real-Time Forecast of Satellite-Based Soil Moisture Using Long Short-Term Memory with an Adaptive Data Integration Kernel. J. Hydrometeorol. 2020, 21, 399–413. [Google Scholar] [CrossRef]
- Li, L.; Dai, Y.; Shangguan, W.; Wei, Z.; Wei, N.; Li, Q. Causality-Structured Deep Learning for Soil Moisture Predictions. J. Hydrometeorol. 2022, 23, 1315–1331. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Z.; Li, Q.; Zhu, J. Enhancing Soil Moisture Forecasting Accuracy with REDF-LSTM: Integrating Residual En-Decoding and Feature Attention Mechanisms. Water 2024, 16, 1376. [Google Scholar] [CrossRef]
- Herman, M.R.; Nejadhashemi, A.P.; Abouali, M.; Hernandez-Suarez, J.S.; Daneshvar, F.; Zhang, Z.; Anderson, M.C.; Sadeghi, A.M.; Hain, C.R.; Sharifi, A. Evaluating the role of evapotranspiration remote sensing data in improving hydrological modeling predictability. J. Hydrol. 2018, 556, 39–49. [Google Scholar] [CrossRef]
- Nesru, M.; Shetty, A.; Nagaraj, M.K. Multi-variable calibration of hydrological model in the upper Omo-Gibe basin, Ethiopia. Acta Geophys. 2020, 68, 537–551. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Q. A survey on multi-task learning. IEEE Trans. Knowl. Data Eng. 2021, 34, 5586–5609. [Google Scholar] [CrossRef]
- Li, B.; Li, R.; Sun, T.; Gong, A.; Tian, F.; Khan, M.Y.A.; Ni, G. Improving LSTM hydrological modeling with spatiotemporal deep learning and multi-task learning: A case study of three mountainous areas on the Tibetan Plateau. J. Hydrol. 2023, 620, 129401. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, C.; Shangguan, W.; Wei, Z.; Yuan, H.; Zhu, J.; Li, X.; Li, L.; Li, G.; Liu, P.; et al. LandBench 1.0: A benchmark dataset and evaluation metrics for data-driven land surface variables prediction. Expert Syst. Appl. 2024, 243, 122917. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Rasp, S.; Dueben, P.D.; Scher, S.; Weyn, J.A.; Mouatadid, S.; Thuerey, N. WeatherBench: A benchmark data set for data-driven weather forecasting. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002203. [Google Scholar] [CrossRef]
- McNicholl, B.; Lee, Y.H.; Campbell, A.G.; Dev, S. Evaluating the reliability of air temperature from ERA5 reanalysis data. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1004505. [Google Scholar] [CrossRef]
- Yilmaz, M. Accuracy assessment of temperature trends from ERA5 and ERA5-Land. Sci. Total Environ. 2023, 856 (Pt. 2), 159182. [Google Scholar] [CrossRef]
- Bi, K.; Xie, L.; Zhang, H.; Chen, X.; Gu, X.; Tian, Q. Accurate medium-range global weather forecasting with 3D neural networks. Nature 2023, 619, 533–538. [Google Scholar] [CrossRef]
- Chen, L.; Zhong, X.; Zhang, F.; Cheng, Y.; Xu, Y.; Qi, Y.; Li, H. FuXi: A cascade machine learning forecasting system for 15-day global weather forecast. NPJ Clim. Atmos. Sci. 2023, 6, 190. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Caruana, R. Multitask learning. Mach. Learn. 1997, 28, 41–75. [Google Scholar] [CrossRef]
- Chen, D.; Mak, B.; Leung, C.; Sivadas, S. Joint acoustic modeling of triphones and trigraphemes by multi-task learning deep neural networks for low-resource speech recognition. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing, Florence, Italy, 4–9 May 2014; pp. 5592–5596. [Google Scholar] [CrossRef]
- Seltzer, M.L.; Droppo, J. Multi-task learning in deep neural networks for improved phoneme recognition. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6965–6969. [Google Scholar] [CrossRef]
- Girshick, R. Fast R-CNN. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; Available online: https://github.com/rbgirshick/ (accessed on 13 May 2023).
- Li, B.; Zhou, X.; Ni, G.; Cao, X.; Tian, F.; Sun, T. A multi-factor integrated method of calculation unit delineation for hydrological modeling in large mountainous basins. J. Hydrol. 2021, 597, 126180. [Google Scholar] [CrossRef]
- Li, L.; Dai, Y.; Wei, Z.; Shangguan, W.; Zhang, Y.; Wei, N.; Li, Q. Enforcing water balance in multitask deep learning models for hydrological forecasting. J. Hydrometeorol. 2023, 25, 89–103. [Google Scholar] [CrossRef]
- Sadler, J.M.; Appling, A.P.; Read, J.S.; Oliver, S.K.; Jia, X.; Zwart, J.A.; Kumar, V. Multi-Task Deep Learning of Daily Streamflow and Water Temperature. Water Resour. Res. 2022, 58, e2021WR030138. [Google Scholar] [CrossRef]
- Chen, Z.; Badrinarayanan, V.; Lee, C.-Y.; Rabinovich, A. Gradnorm: Gradient normalization for adaptive loss balancing in deep multitask networks. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 794–803. [Google Scholar]
- Kendall, A.; Gal, Y.; Cipolla, R. Multi-task learning using uncertainty to weigh losses for scene geometry and semantics. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7482–7491. [Google Scholar]
- Sener, O.; Koltun, V. Multi-task learning as multi-objective optimization. In Proceedings of the 31st Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 525–536. [Google Scholar]
- Liu, S.; Johns, E.; Davison, A.J. End-To-End Multi-Task Learning with Attention. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 1871–1880. [Google Scholar]
- Yu, T.; Kumar, S.; Gupta, A.; Levine, S.; Hausman, K.; Finn, C. Gradient surgery for multi-task learning. In Proceedings of the 33rd Advances in Neural Information Processing Systems, Virtual, 6–12 December 2020. [Google Scholar]
- Chen, Z.; Ngiam, J.; Huang, Y.; Luong, T.; Kretzschmar, H.; Chai, Y.; Anguelov, D. Just pick a sign: Optimizing deep multitask models with gradient sign dropout. In Proceedings of the 33rd Advances in Neural Information Processing Systems, Virtual, 6–12 December 2020. [Google Scholar]
- Xin, D.; Ghorbani, B.; Garg, A.; Firat, O.; Gilmer, J. Do current multi-task optimization methods in deep learning even help? Neural Inf. Process. Syst. 2022, 35, 13597–13609. [Google Scholar]
- Zhang, Y.; Chen, W.; Smith, S.L.; Riseborough, D.W.; Cihlar, J. Soil temperature in Canada during the twentieth century: Complex responses to atmospheric climate change. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an eNSEmble of climate change scenarios. J. Hydrol. 2012, 424–425, 264–277. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).