1. Introduction
With the increasing scarcity of coal and oil resources, hydropower has become one of the resources that are encouraged to be developed and utilized first. The turbine is the core component of hydropower equipment that realizes the mutual conversion between fluid energy and mechanical energy. Its performance has an important impact on the rational development and utilization of hydropower and the safe, reliable and stable operation of power grids and generators [
1,
2].
During the operation of the Kaplan turbine, the runner blades are subjected to pressure changes caused by changes in head height [
3,
4,
5,
6], as well as pressure changes caused by changes in speed and flow. Therefore, the blades are affected by pressure pulsation, dynamic loads generated by various hydraulic phenomena, and the combined effects of dynamic loads and water pressure generated by various mechanical disturbances during operation, resulting in a very complex stress state [
7,
8,
9].
Due to the complex spatial structure of the Kaplan turbine runner [
10] and the long-term exposure to complex load conditions, its fatigue strength and stability cannot be guaranteed. After a period of operation, the runner blades will successively develop different crack damages. As the size of the unit increases, the rigidity is relatively weakened, the head amplitude of the power station increases, and the unit operating conditions become more complex. There will be more and more abnormal vibration and fatigue crack problems during unit operation [
11]. In order to more clearly understand the vibration problems of hydropower generator sets, major companies and research institutions at home and abroad have conducted field research and statistical analysis on some power stations [
12,
13].
Cracks occur in the welding area between the stay vanes and the upper and lower rings. This is because the natural frequency of the stay vanes is close to the Karman vortex frequency of the runner blades [
14,
15,
16,
17,
18]. Therefore, it is very important to analyze the natural frequencies of the fixed structure and the rotating components. In the actual design process of the turbine, modal analysis generally takes the hydraulic design into consideration first. If resonance occurs during operation, the design scheme needs to be modified, and the runner needs to be redesigned or modified. The model test is to build a runner model based on the hydraulic similarity theory. Then, the relevant characteristic parameters of the real runner are equivalent by analyzing the law of water flow movement inside the model runner. The hydraulic characteristics of the analysis are well consistent with the real machine. However, due to the difference in geometric dimensions between the model and the real machine, it is difficult to achieve a simulation similar to the blades of the real machine in its dynamic characteristics analysis. Numerical calculation is a computer-based and finite element analysis method that has developed rapidly in recent years [
19,
20]. It analyzes the dynamic characteristics of blades through numerical calculation to achieve the purpose of solving abnormal vibration cracks. With the maturity and development of finite element methods and computing technology, the dynamic characteristics and dynamic stress analysis calculation of turbine runner blades will replace model tests and power station measurements.
During operation, the turbine transfers energy to the surrounding waters, causing the surrounding waters to exert energy on the turbine, which greatly affects the dynamic characteristics of the turbine itself. If the calculation model is to achieve a certain accuracy, the interaction between the turbine and the surrounding waters must be considered in the dynamic characteristics analysis of the turbine. A large number of studies have used finite element numerical simulation methods and fluid–structure interaction technology to analyze the dynamic stress of blades [
21,
22]. Wang [
23] used velocity potential to describe the fluid and analyzed the coupled vibration of the runner blades in the fluid. A finite element mathematical model for the numerical calculation of the three-dimensional fluid–structure interaction vibration during the operation of the runner and the dynamic control equations of the coupling system were established. A modal analysis of a certain mixed flow runner was also performed.
At present, there is little analysis on the dynamic response of the fixed and rotating components of the Kaplan turbine under different heads, and there is a lack of analysis on the source of structural vibration. So in this paper, a Kaplan turbine is taken as the research object, and the natural frequency characteristics and dynamic stress characteristics of the fixed parts (bottom ring, head cover and support cover) and the rotating components (blades, runner body and main shaft) are analyzed. The influence of the exciting force caused by hydraulic phenomena, such as blade channel vortex and draft tube vortex on the vibration, is studied. The pressure changes under low-flow conditions are verified to have a certain impact on the stress of the runner structure. This method of observing the change in the flow channel pressure section can be extended to other turbines to study the cause of the change in the runner dynamic stress. The structural displacement and stress fluctuation characteristics and sources of fluctuations under medium and low heads are analyzed compared with those under high head, providing a reference for the safe and stable operation of the turbine.
2. Numerical Calculation Methods
2.1. Model
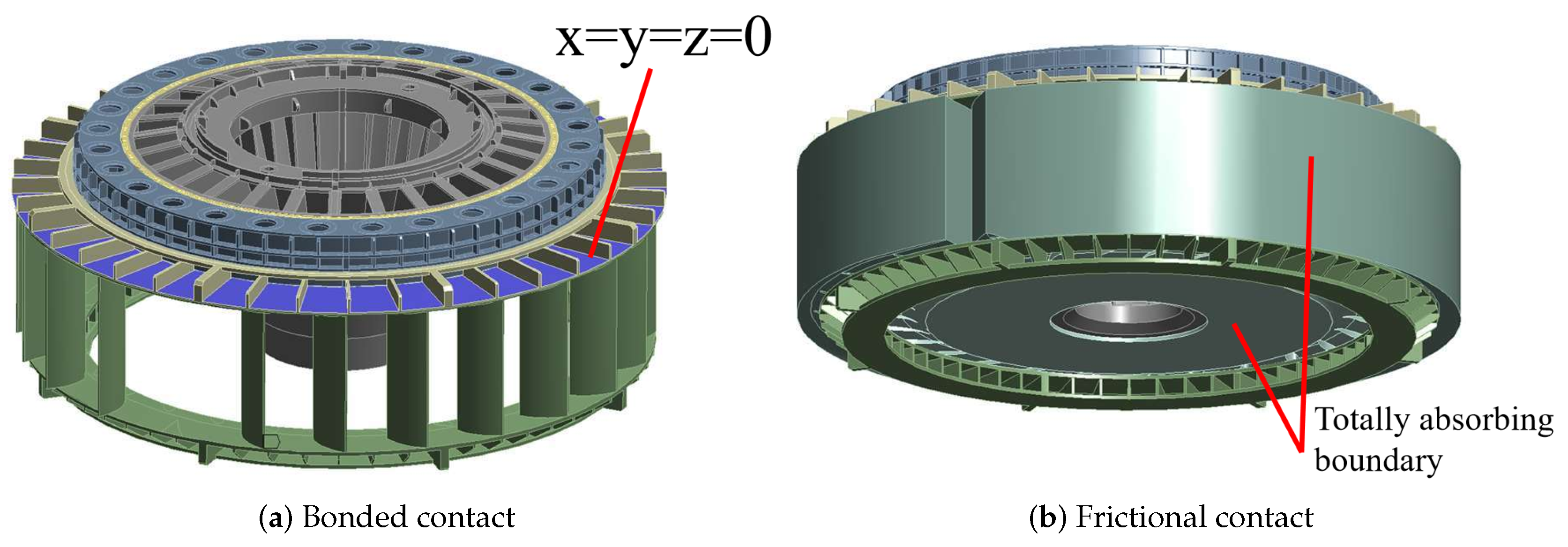
In this paper, a three-dimensional model of the key components of a prototype Kaplan turbine, including the runner blades, runner body, main shaft and head cover, support cover and bottom ring, and connecting bolts, is established as shown in
Figure 1. In actual engineering, the above components are all surrounded by water. Therefore, when the model is established, the outer surface of the structural component must coincide with the surface of the water body in order to accurately construct a fluid–structure interaction model. The three-dimensional fluid–structure interaction model is shown in
Figure 2.
2.2. Calculation of Flow Field and Structural Field
In this paper, the transient results of the flow field are calculated by the software ANSYS CFX 19.1, and then the software ANSYS APDL 19.1 is used to calculate the fluid–solid coupling. In the calculation of the flow field, the Reynolds-averaged Navier–Stokes (RANS) equation is mainly used. The turbulence model is the SST
model, which combines the characteristics of the
model and the
model [
24,
25]. The boundary conditions for the flow field calculation are full pressure inlet and static pressure outlet. Except the runner flow field, which is set to rotate, the other fluid domains are set to be stationary. The runner speed of the Kaplan turbine is 68.2 r/min, the number of stay vanes is 25, the number of guide vanes is 28, the number of runner blades is 6, and the rated head is 25 m. The walls of the flow field are set to non-slip walls. The top of the main shaft of the structure field is set as a fixed support. The position in contact with the radial bearing is set as a radial support.
The main feature of the fluid–structure interaction is the interaction between the two phases of media. At the interface of the fluid–structure interaction, the fluid and the structure have the same velocity and pressure. Therefore, a fluid structure is “constructed” at the interface between the structure and the fluid. This is the physical condition of the fluid–structure interaction. When calculating the structural field, the D’Alembert principle is used to add inertial forces
and damping forces
to a continuous medium point. This yields:
where
is the solid density.
u,
and
are the local displacement, velocity, and acceleration vectors in the solid domain.
is the Cauchy stress tensor, which establishes a connection with strain
.
is the volumetric force. It can be expressed in discrete form as [
26]:
where
is the mass matrix,
is the damping matrix, and
is the stiffness matrix.
,
,
represent the acceleration, velocity, and displacement, respectively.
is a node load vector.
2.3. Mesh of Flow and Structural Fields
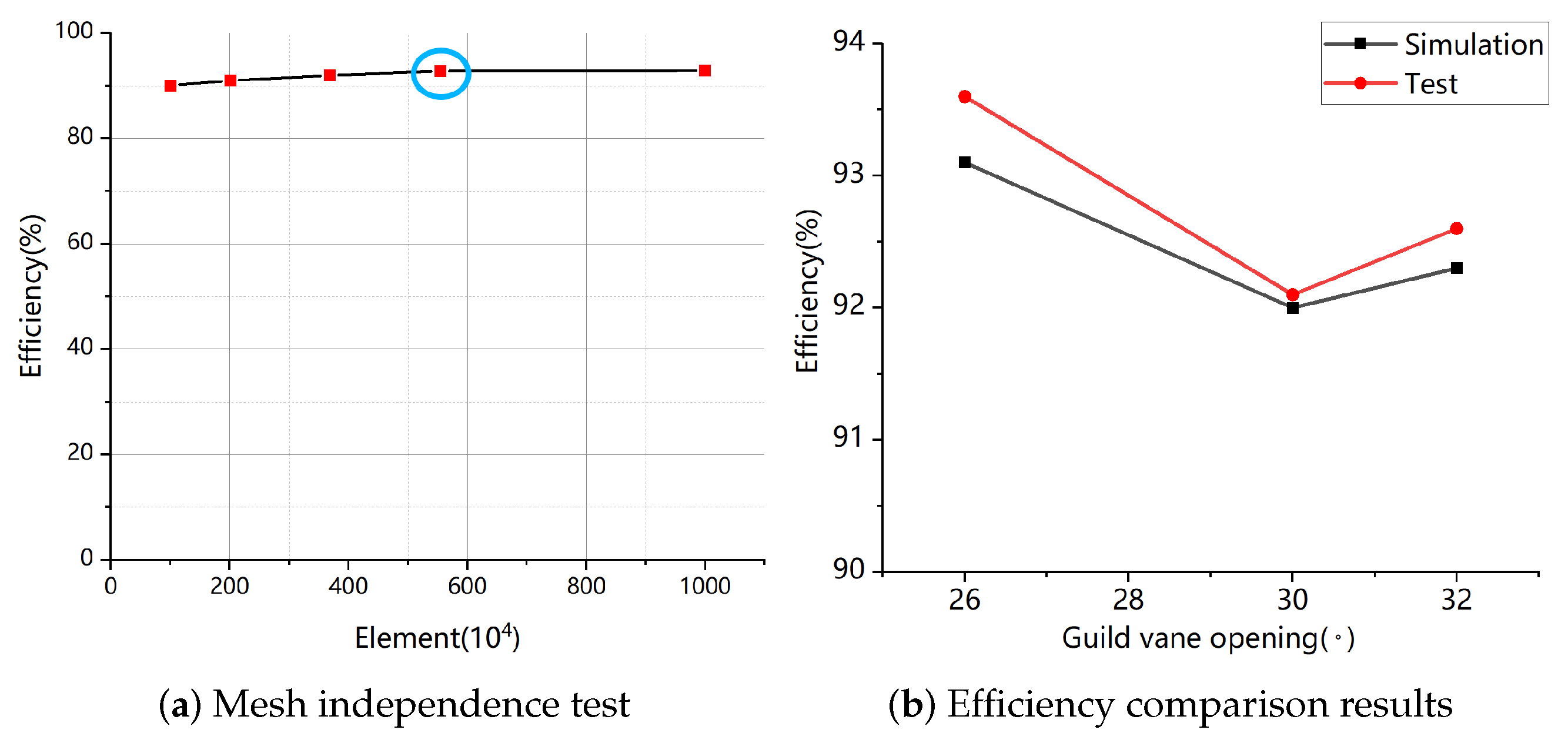
In fluid–solid coupling analysis, in order to improve the solution efficiency, the mesh nodes of the flow field and the structural field on the fluid–solid coupling surface correspond one to one. Therefore, it is necessary to directly mesh the entire complex fluid–solid coupling domain. Since the calculation domain is too complex, tetrahedral mesh is mainly used for discretization. The model is discretized into finite elements, and all calculations and analyses are performed on this model. The selection of element type and mesh division will affect the speed and accuracy of finite element analysis. The mesh independence of the flow field is verified by the efficiency of the Kaplan turbine under the rated condition [
27,
28].
Figure 3 shows the mesh independence verification results and efficiency comparison results. Under the premise of ensuring accurate and reliable calculation results and fast convergence speed, about 5.54 million elements are selected for calculation this time so that the accuracy requirements can be met with a smaller number of units. In this article, the efficiency values of three types of guide vane openings are calculated under the rated head and opening, and the calculated efficiency is compared with the experimental results. The results show that the error is small and meets the reliability requirements of numerical simulation. Among them, the elements of the spiral case are about 550,000, the elements of the guide vane area are 1.88 million, the elements of the runner area are 2.40 million, the elements of the draft tube are 0.71 million, the elements of the support cover, head cover and bottom ring structure are 680,000, and the elements of the runner and main shaft are 1.56 million. The meshes of each component are shown in
Figure 4.
2.4. Operating Conditions
In the normal continuous operation area of the unit in the real machine operation characteristic curve, three representative heads of the power station are selected in this paper (maximum head Hmax = 37.79 m, rated head Hr = 25 m and minimum head Hmin = 12.91 m). The high-head condition OP1, the small-flow condition OP2 under the medium head, and the two flow conditions OP3 and OP4 under the low head are selected for unsteady flow and structural dynamic response characteristics analysis as shown in
Table 1. The mesh and boundary conditions of this dynamic response analysis are consistent with those in the modal analysis of the corresponding components. In addition, the effects of water pressure, gravity and centrifugal force are considered. The corresponding positions of each operating point on the characteristic curve are shown in
Figure 5.
3. Results
3.1. Modal Analysis
3.1.1. Runner Modes in the Flow Channel
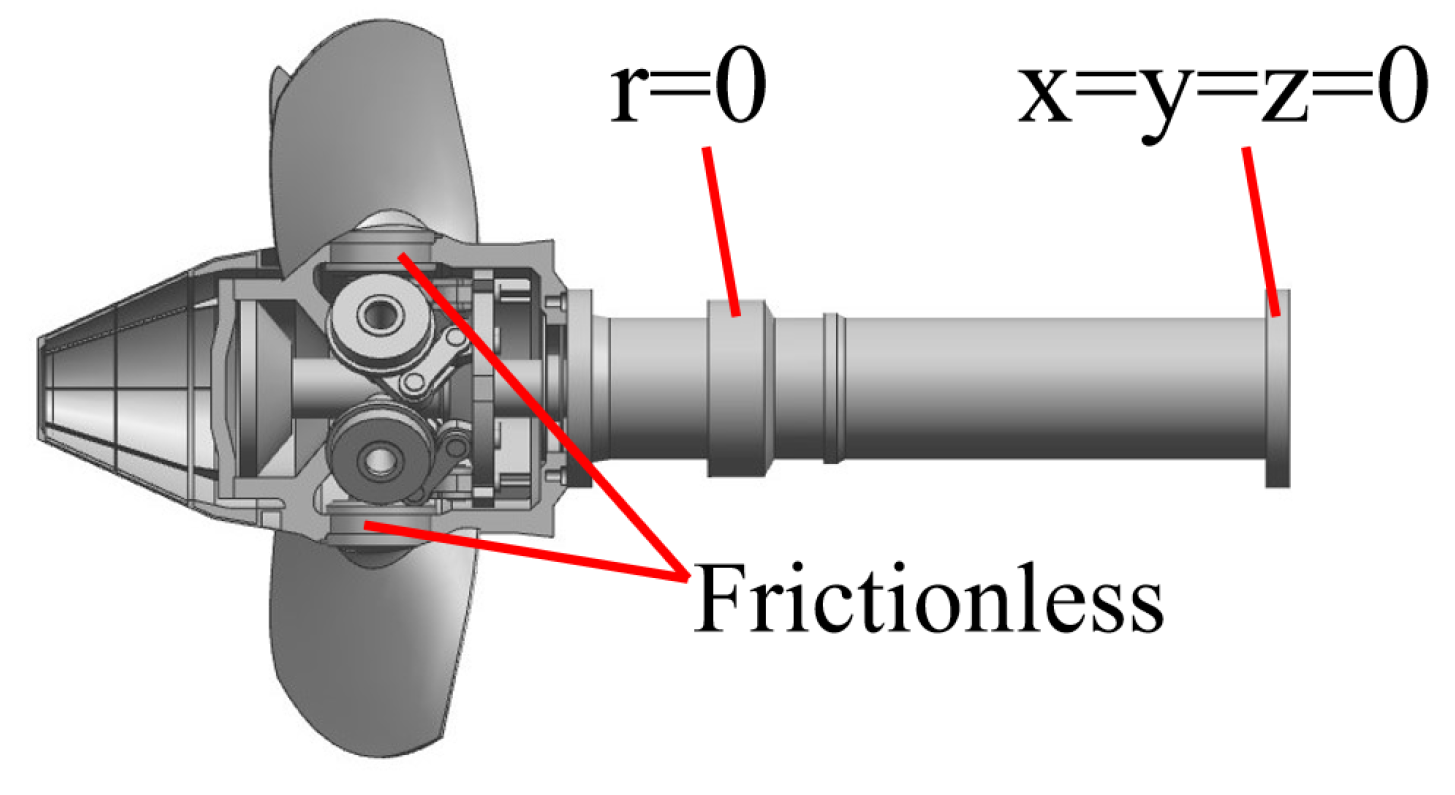
Modal analysis is a method for studying the dynamic characteristics of structures, and is generally used in the field of engineering vibration. Among them, mode refers to the natural vibration characteristics of mechanical structures. The runner of a Kaplan turbine is prone to large deformation under the impact of water flow. Therefore, evaluating the modal characteristics of the runner is crucial to understanding the dynamic response characteristics of the Kaplan turbine. In this paper, the natural modes of the runner in the flow channel are calculated. When the runner modes are calculated, the complex blade operating mechanism inside the runner and part of the main shaft is taken into account to ensure the relative authenticity of the research object and boundary conditions. The finite element model of the runner modal analysis is shown in
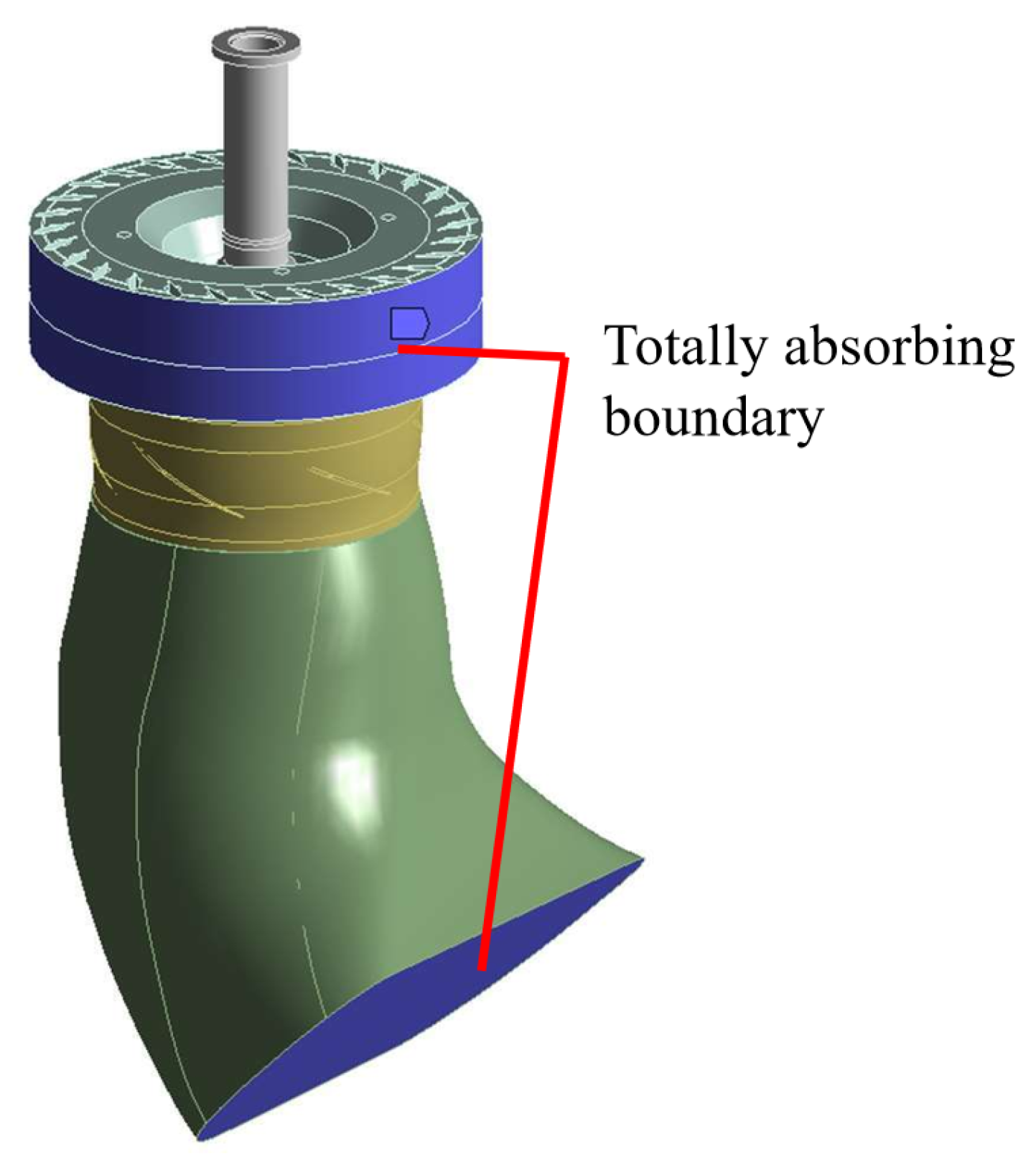
Figure 6. The top of the main shaft is set as a fixed support. The position in contact with the radial bearing is set as a radial support. The contact between the blade lever and the runner body is set to be frictionless. Acoustic fluid units in the guide vane channel, runner channel, and draft tube channel are added for fluid–solid coupling analysis. The finite element model of the runner wet modal analysis is shown in
Figure 7.
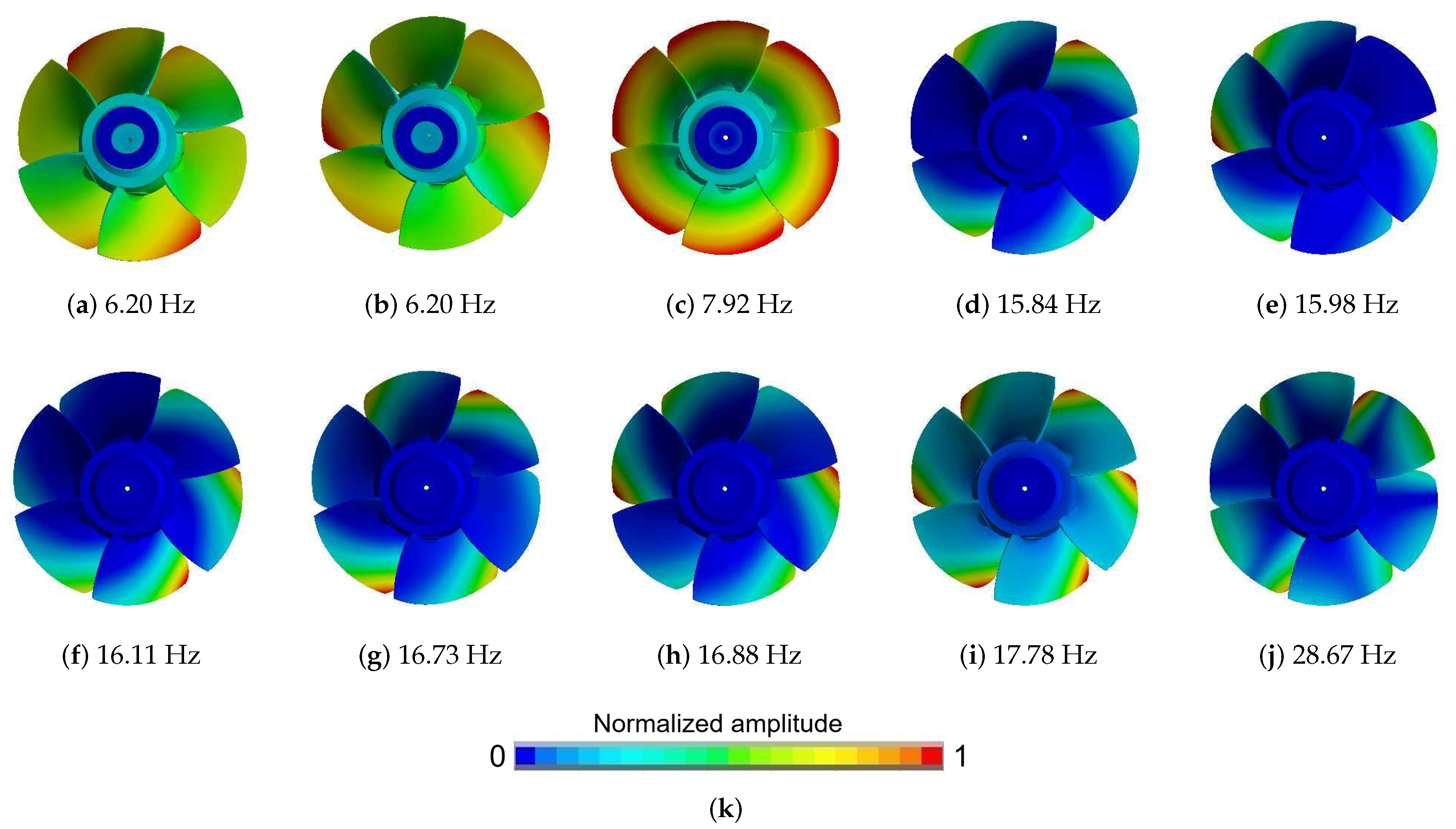
The first ten modes of the runner in water are shown in
Figure 8. Among them, the first and second orders are the same mode, which is manifested as the vibration of the runner as a whole in the radial direction. The third order is a torsional mode. The 4th to 10th orders are all modes dominated by blade vibration. From the vibration mode of a single blade, the blades from the fourth- to the ninth-order modes all exhibit first-order bending vibration modes. The fourth order is quite special. In addition to the vibration of the blade, the runner also vibrates back and forth along the main shaft. In the 10th order mode, the vibration mode of the blade is between the first-order bending and the second-order bending, and the blade head exhibits more obvious vibration.
3.1.2. Fixed Component Modes in the Flow Channel
The finite element model of the modal analysis of the bottom ring, head cover and support cover in water is shown in
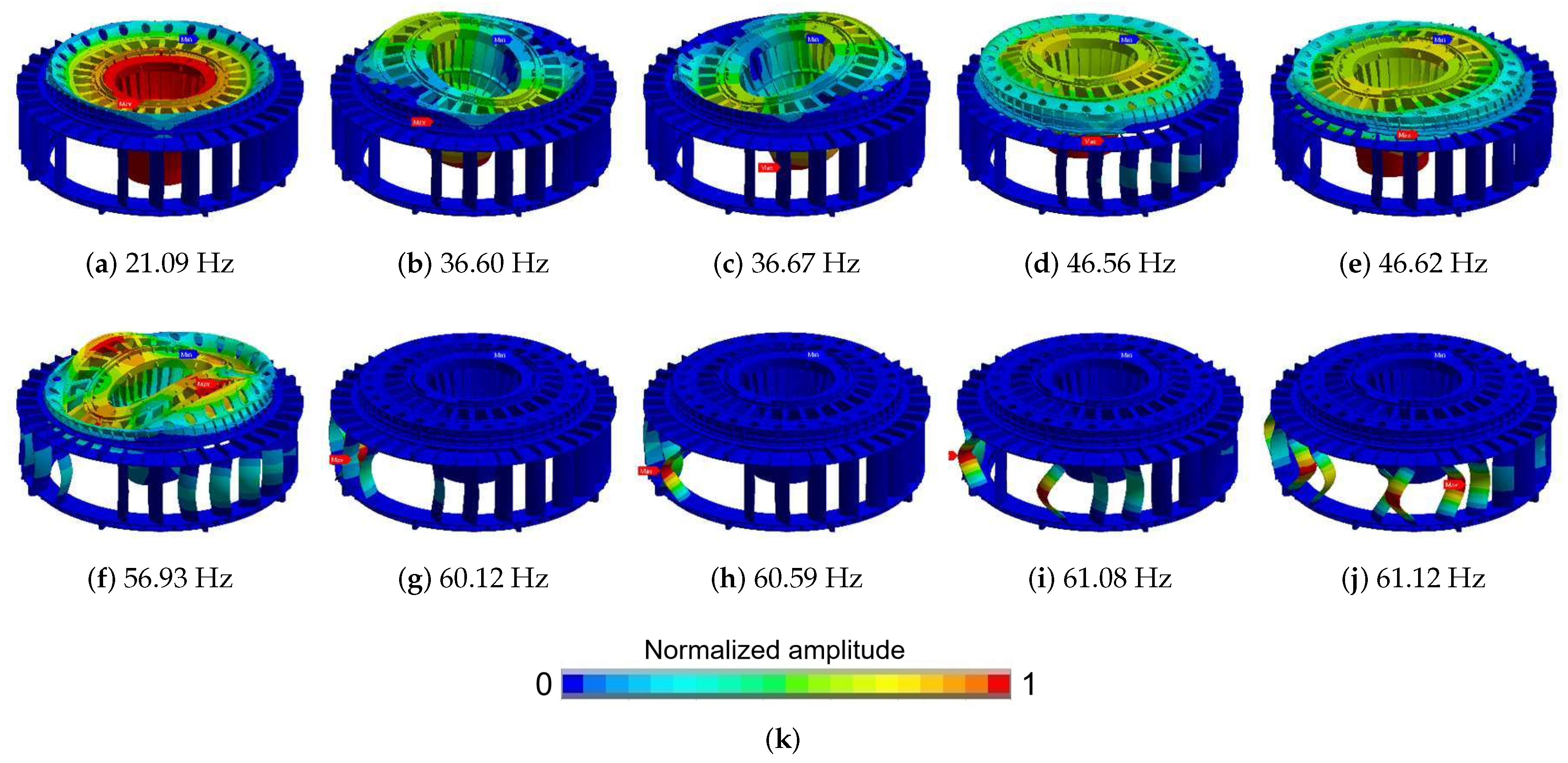
Figure 9. The outer side of the bottom ring is set as fixed support, and the contact relationship between the components is simplified to bond. On the basis of the fixed components, the acoustic fluid unit of the guide vane channel is added to perform fluid–solid coupling analysis. The first 10 natural modes of the bottom ring, head cover and support cover in the flow channel are shown in
Figure 10. Among them, the first order is an axial vibration. The second and third orders are similar to the one-diameter mode in the disk vibration mode. The fourth and fifth orders are mainly radial vibrations. The sixth order is a two-diameter mode. And the 7th to 10th sections are modes dominated by the vibration of multiple stay vanes.
3.2. Dynamic Response Analysis of Structural Components
3.2.1. Dynamic Response of Fixed Structures
The boundary conditions for flow field calculation in this article are the full pressure inlet and static pressure outlet. Then, the flow field pressure result on the fluid structure coupling surface is transmitted to the structural surface as the pressure boundary condition of the structure.
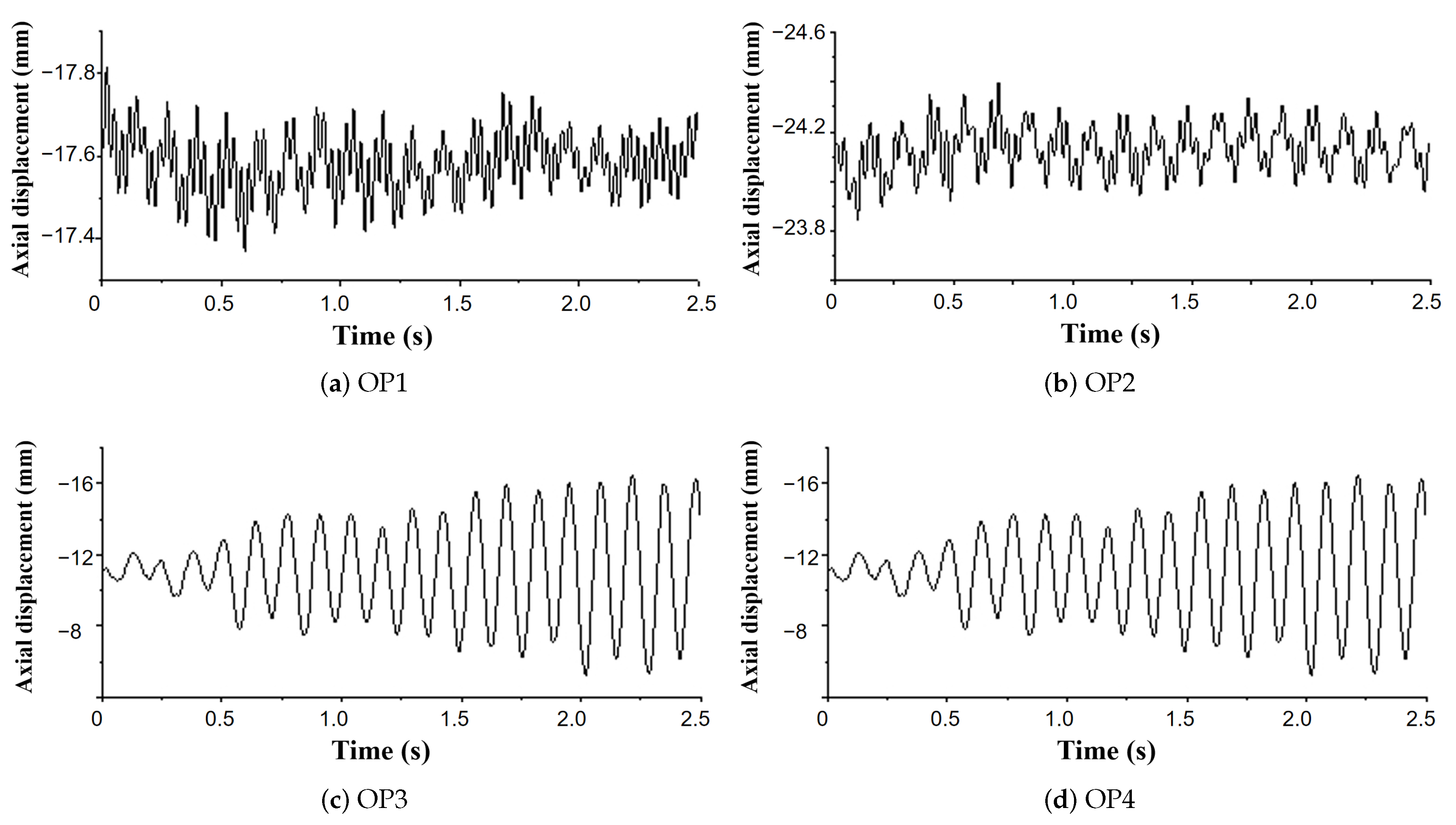
Figure 11 shows the displacement of the rotating components in operating condition OP1. Under the combined effects of water flow impact, gravity and centrifugal force, the displacement of the rotating components is mainly concentrated at the tail of the blade near the shroud. The maximum displacement is about 19.4 mm, of which the axial component accounts for about 95%. Relatively speaking, the displacement of the blade head is smaller than that of the tail, and the displacement near the hub is smaller than that near the shroud. The displacement distribution of the rotating components is similar under the four operating conditions. The maximum displacements of operating conditions OP2, OP3 and OP4 are approximately 24.6 mm, 18.8 mm and 20.8 mm.
Figure 12 and
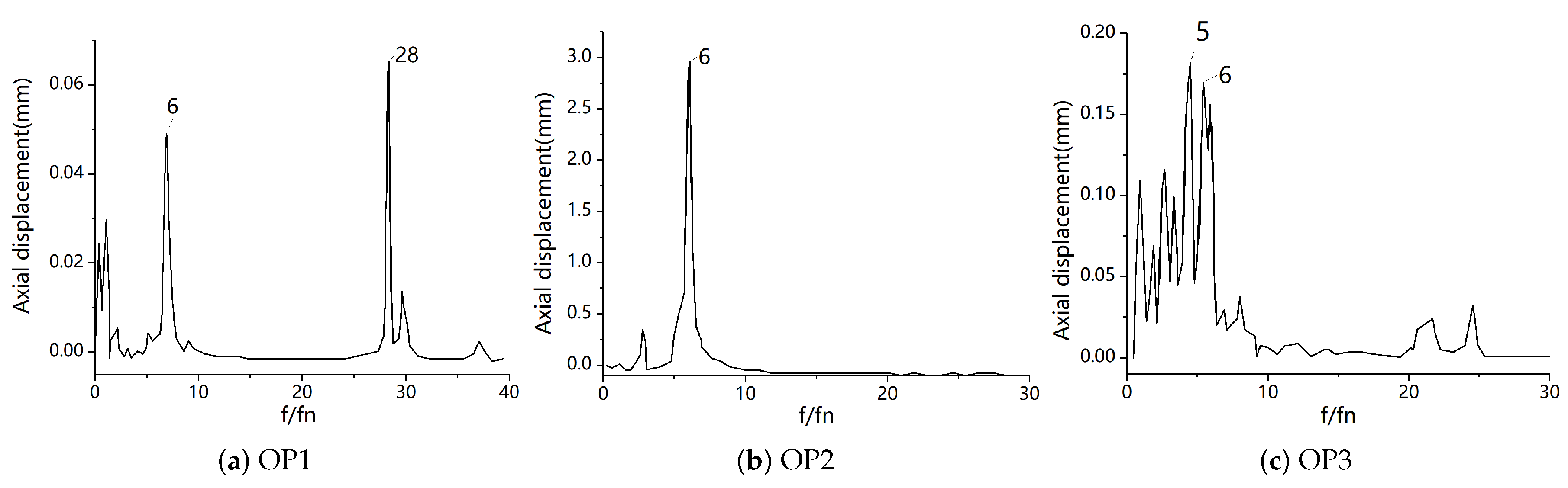
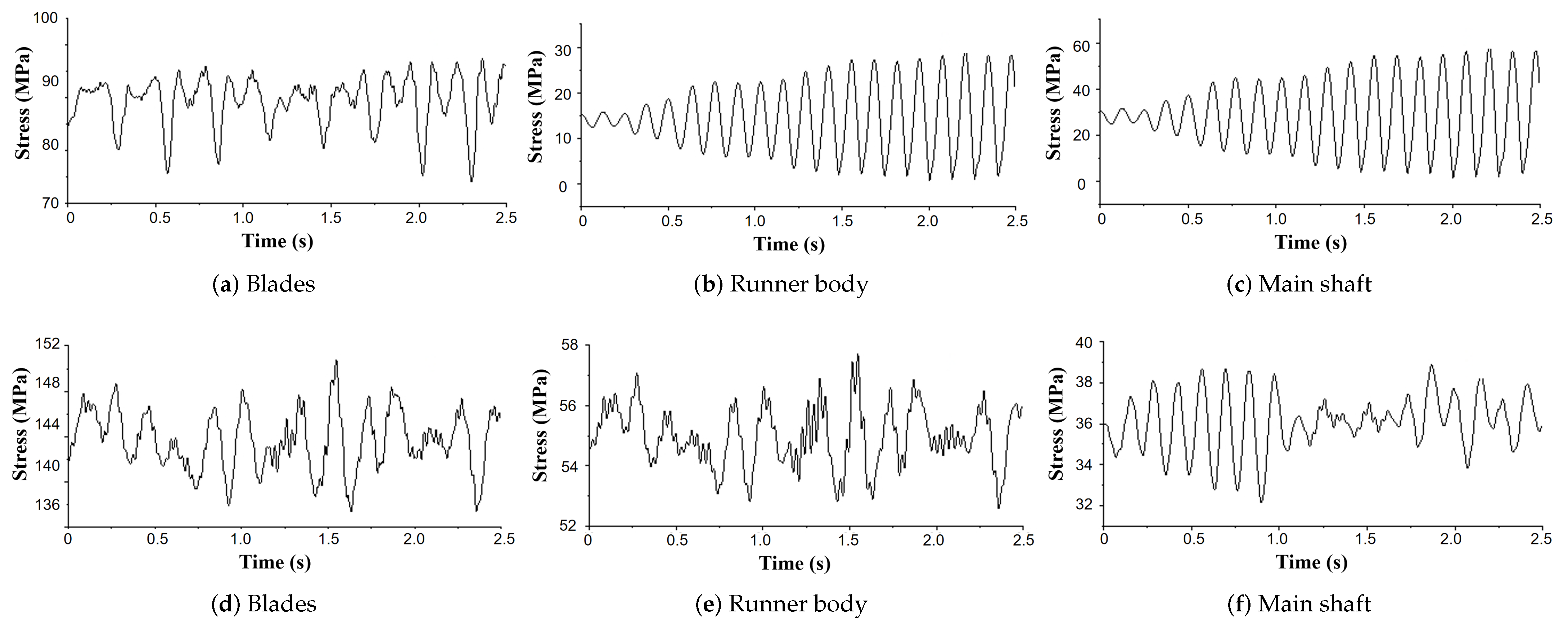
Figure 13 show the time history and frequency domain signal of the axial displacement at the maximum displacement point on the blade under different working conditions. The main vibration frequency of the blade in working condition OP1 is 28 fn, that is, the guide vane passing frequency, and the amplitude is 0.065 mm. In addition, 6 fn and 1 fn also show relatively large amplitudes, which means that the displacement amplitude is greatly affected by the rotation of the runner and blade, but the displacement amplitude of OP1 is much smaller than that of other unstable working conditions. The axial vibration of the maximum displacement point on the blade in OP2 is similar to that in OP1, but the vibration amplitude is twice that of OP1. Although the axial displacement is the smallest in OP3, the amplitude is much larger than that of other working conditions. The main frequency of the axial vibration of the runner blade in OP3 is 6 fn, and the amplitude is 3 mm. It can be seen from OP4 that the vibration frequency of the axial vibration is relatively complex, with a main frequency of 5 fn. In addition, there are frequency components such as 1 fn and 6 fn.
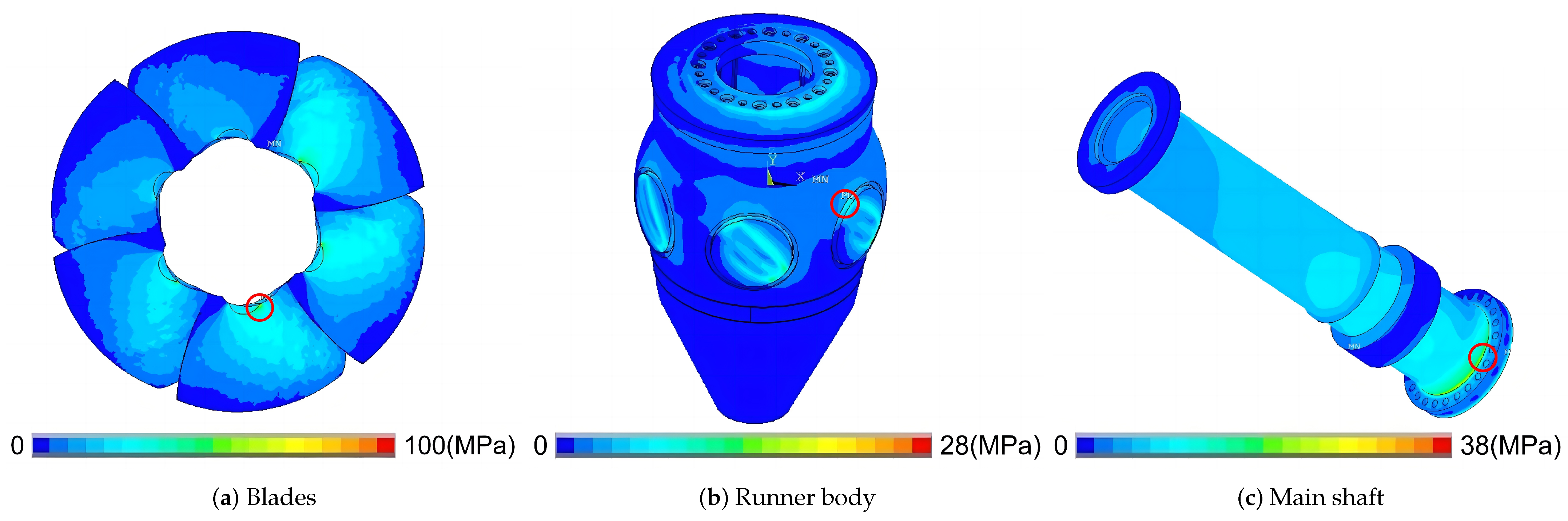
Figure 14 shows the equivalent stress distribution on the rotating components of OP1. The red circle is the maximum stress. It can be seen that the maximum stress on the blade is greater than that on the runner body and the main shaft. The stress at the head and tail of the blade is small, and the stress in the middle is large. The stress at the shroud is very small, and the stress at the hub is very large. Stress concentration occurs at the weld in the hub area. The maximum stresses on the blades, runner body and main shaft are approximately 94 MPa, 27.5 MPa and 38 MPa. The stress distribution on the rotating components of OP2 and OP1 is similar, but the stress values are larger. The maximum stresses on the blades, rotor body, main shaft and bolts of OP2 are approximately 186.5 MPa, 59.3 MPa and 36.5 MPa.
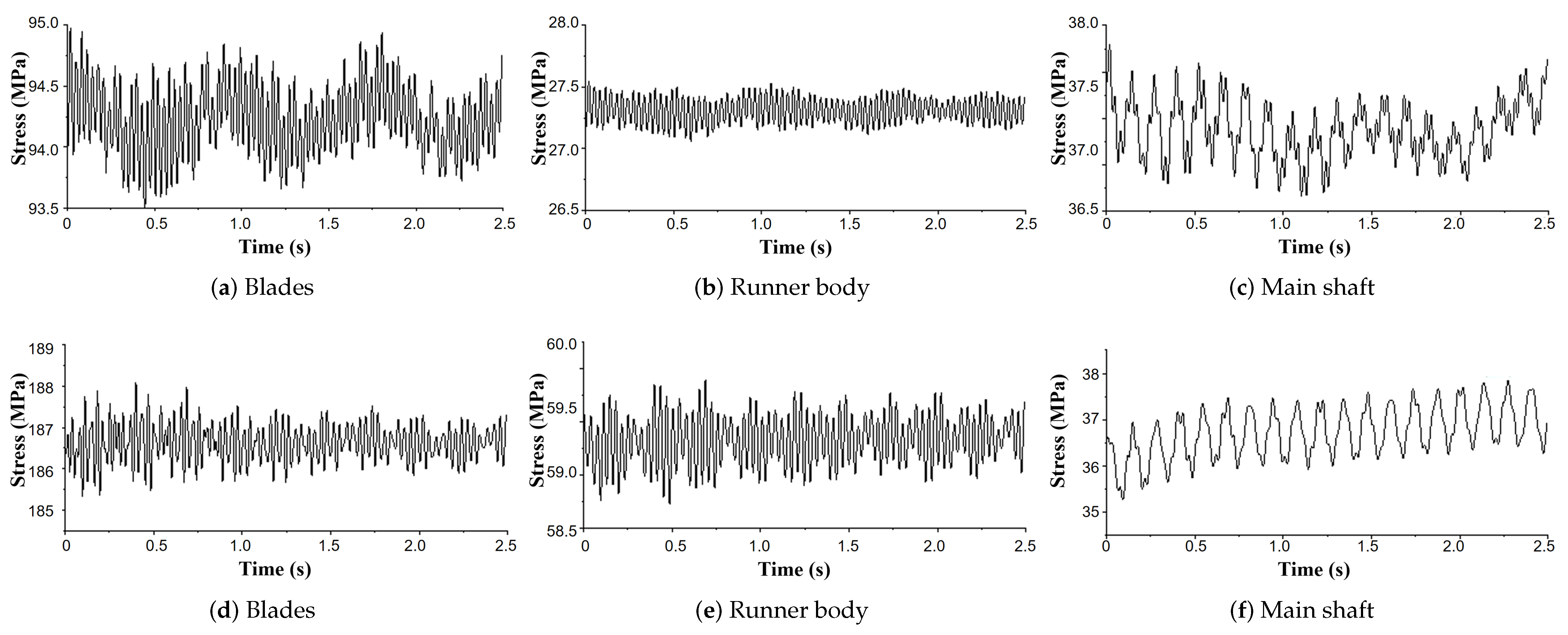
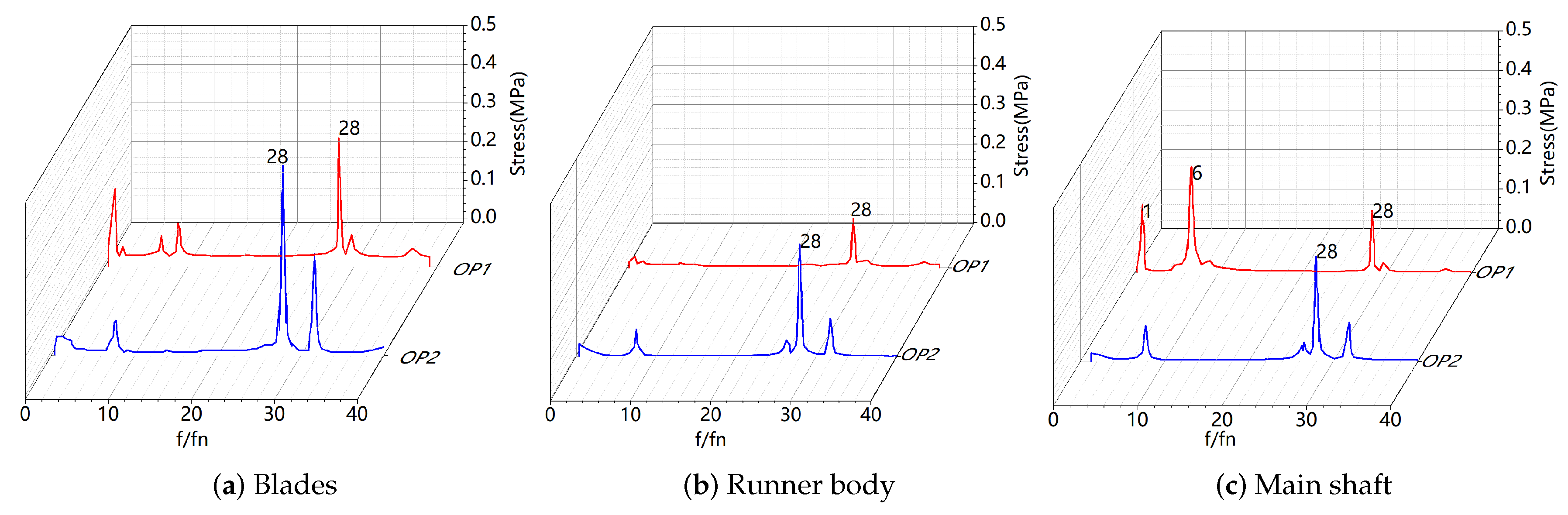
Figure 15 and
Figure 16 show the time domain and frequency domain diagrams of the dynamic stress at the maximum stress point on the rotating components of OP1 and OP2. The main frequency of the dynamic stress on the blade and main shaft in OP1 is 28 fn, with an amplitude of approximately 0.33 MPa and 0.13 MPa. The main frequencies of the dynamic stress on the main shaft are 28 fn and 6 fn, with an amplitude of approximately 0.16 MPa for 28 fn and approximately 0.27 MPa for 6 fn. This shows that the main shaft stress is more easily affected by the rotation of the runner than the stay vanes. The main frequencies of dynamic stress on the blades, rotor body and main shaft in OP2 are all 28 fn, with amplitudes of approximately 0.48 MPa, 0.28 MPa and 0.27 MPa. All three working conditions have a large value of 28 fn, indicating that the guide vanes have a greater influence. The vibration amplitudes of the three components of OP2 are greater than those of OP1.
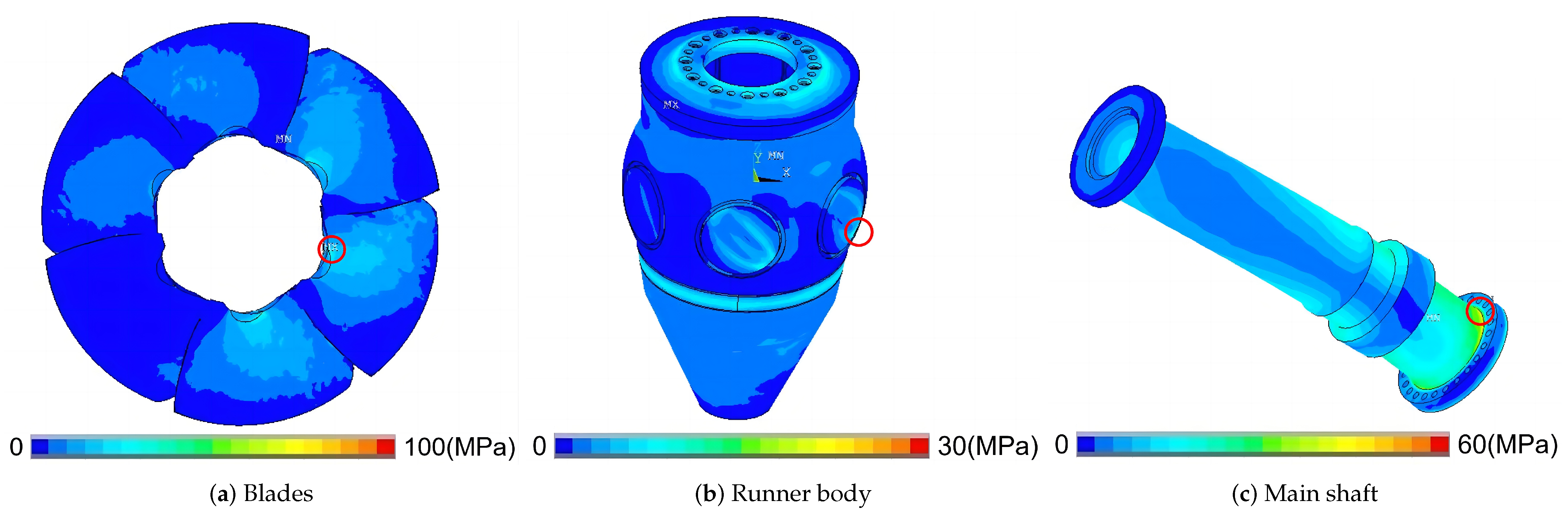
Figure 17 shows the stress distribution on the rotating components of OP3. The distribution of blades and runner body is similar to that of OP1. The dynamic stress on the blades is greater than that on the runner body and main shaft, but the main shaft of OP3 is in a greater bending state. The dynamic stress on the blades, runner body and main shaft of OP3 reaches 92 MPa, 28 MPa and 55 MPa, respectively. The stress distribution on the rotating components of OP4 and OP3 is similar, but the stress value of OP4 is larger. The maximum stress on the blade, rotor body and main shaft of OP4 is about 144 MPa, 55 MPa and 36 MPa.
Figure 18 and
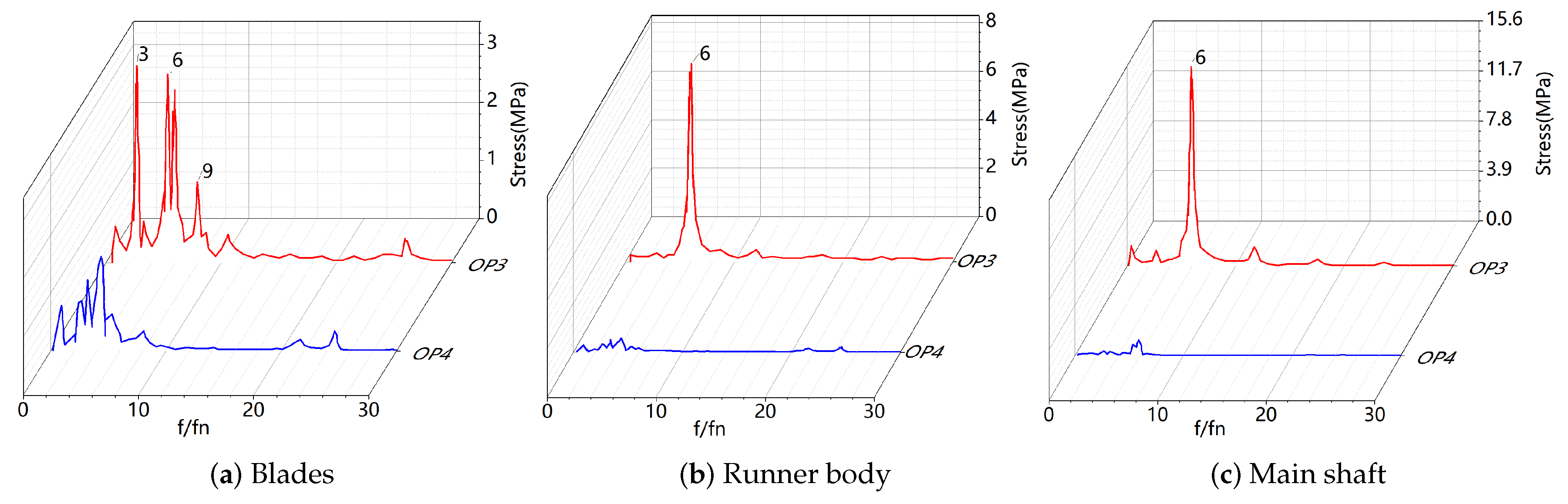
Figure 19 shows the time domain diagram of the dynamic stress at the maximum stress point on the rotating components of OP3 and OP4 and the frequency domain diagram of OP3. The frequency components of the dynamic stress on the runner body and the main shaft of OP3 are relatively simple, with a main frequency of 6 fn and an amplitude of approximately 8.16 Mpa and 15.7 Mpa. In addition to 6 fn, the frequency components of the dynamic stress on the blades also include 3 fn and 9 fn. Although the stress of OP3 is not as large as that of the other three working conditions, the fluctuation amplitude is much larger than that of the other working conditions. The amplitude of the dynamic stress on the rotor body and the main shaft of OP4 is relatively small, and only the dynamic stress on the blades has a large amplitude, with a frequency of 5 fn and an amplitude of approximately 1.6 Mpa.
3.2.2. Analysis of the Causes of Resonance of Rotating Components
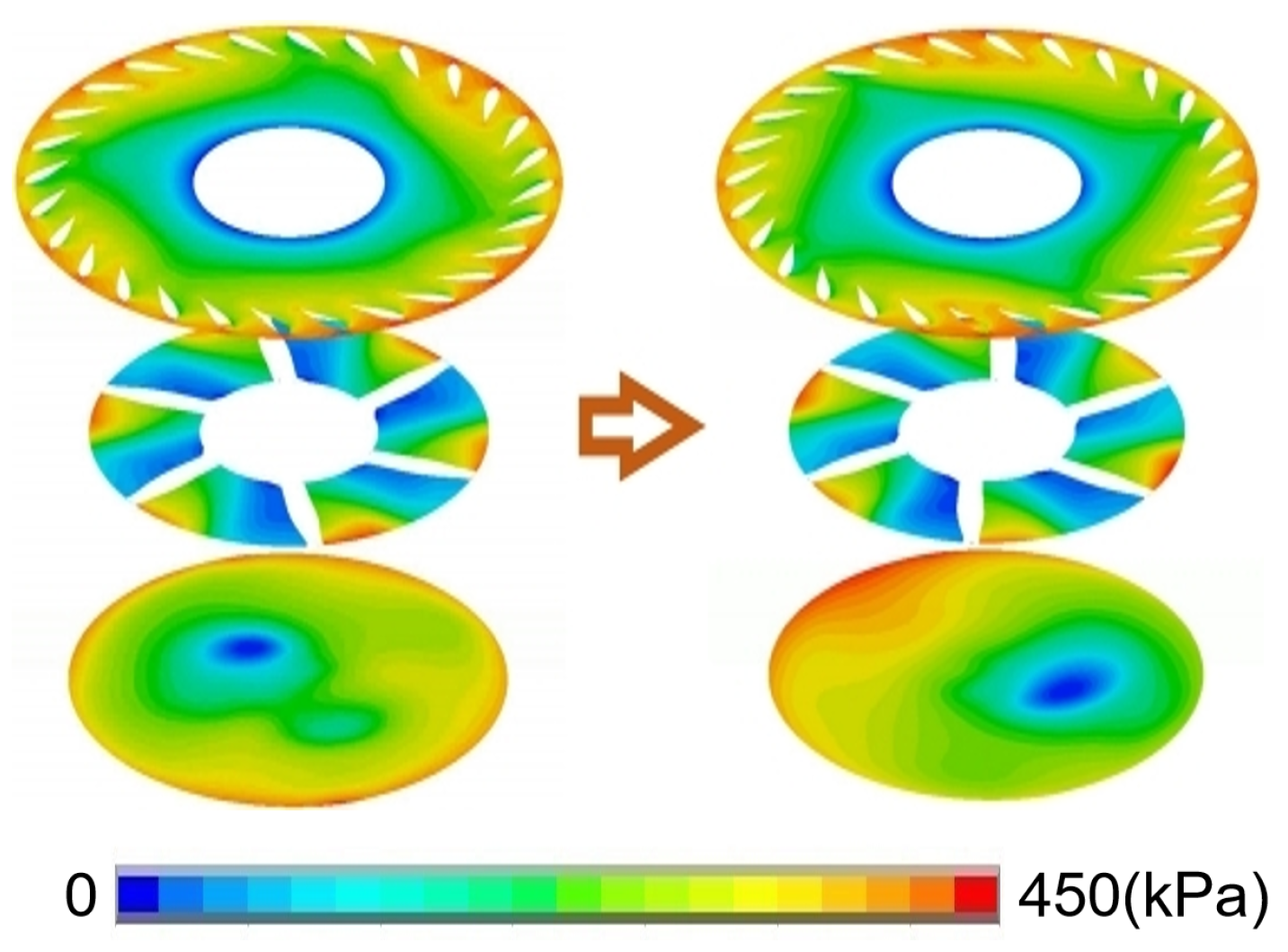
From the above calculation results, it can be seen that when the unit is running at medium and high heads, the vibration response of the runner is weak. When the unit is running at low head, it is easy to vibrate significantly. In order to study the cause of abnormal vibration of the runner under low-head conditions, the pressure of the vortex in the draft tube and vaneless zone of OP4 is analyzed as shown in
Figure 20. It is found that the pressure and pressure distribution in the vaneless area and the draft tube changed periodically on the cross section. Therefore, the low-frequency excitation is caused by the combined action of the vortex in the draft tube and the vaneless zone. This method of observing the change in the flow channel pressure section can be extended to other turbines to study the cause of the change in the runner dynamic stress.
3.2.3. Dynamic Response Analysis of Fixed Components
The displacement results of the fixed structures (including the bottom ring, head cover and support cover) under four working conditions are calculated. The displacement results at OP2, -3 and -4 are similar.
Figure 21 shows the displacement of the fixed components of OP1 and -4. It can be seen that under OP1, the displacement of the fixed components is mainly concentrated on the stay vanes, and the maximum displacement is about 2.1 mm. The displacement of the fixed components of OP2 is mainly concentrated on the support cover. Under the impact of water flow, the support cover moves upward, and the maximum combined displacement is about 2.5 mm. Therefore, under medium- and low-head conditions, the support cover is prone to upward displacement under the impact of water flow.
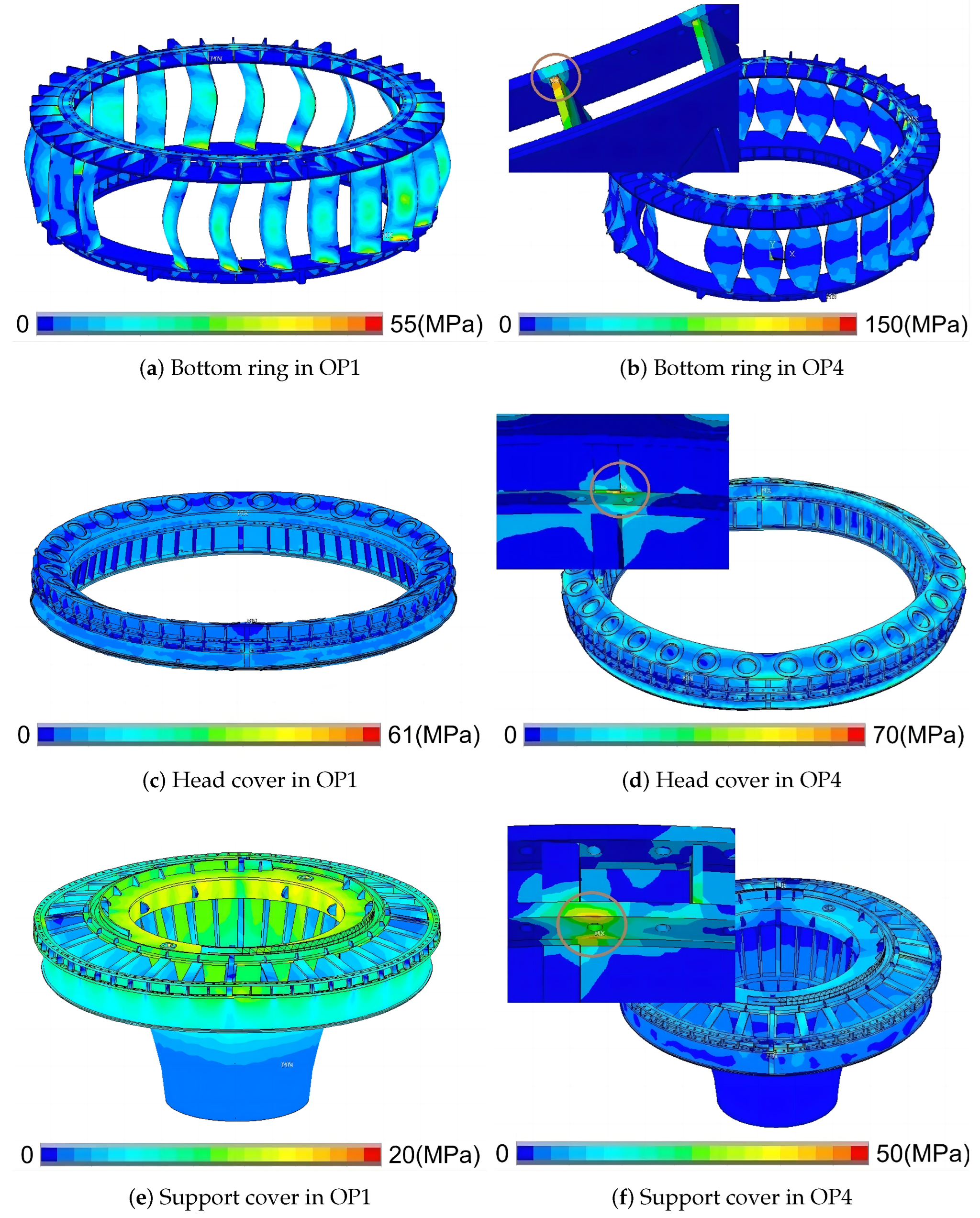
Figure 22 shows the stress distribution of the fixed components (including bottom ring, head cover and support cover) of OP1 and 4. In OP1, a relatively obvious stress concentration appears at the root of the stay vane, and a large stress is also found on the head cover. The stress on the support cover is relatively small, with a maximum stress of about 20 Mpa. Therefore, in OP1, the dynamic stress at the stress concentration point on the stay vane and head cover components is mainly analyzed. For OP2, OP3 and OP4 with smaller load rates, it can be seen that the stability of the unit is poor when operating under low-load conditions. The displacement in OP2 causes obvious stress concentration on the bottom ring, head cover and support cover. The maximum stresses are 150 MPa, 69 MPa and 47 MPa, respectively. Compared with the stable working condition, the stress distribution of the fixed structure under the low load condition of medium and low head changes significantly, the maximum stress on the stay vane and head cover components increases slightly, and the stress on the support cover is significantly greater than the result of OP1.
3.2.4. Time Domain and Frequency Domain Analysis of Stress Points of Fixed Components
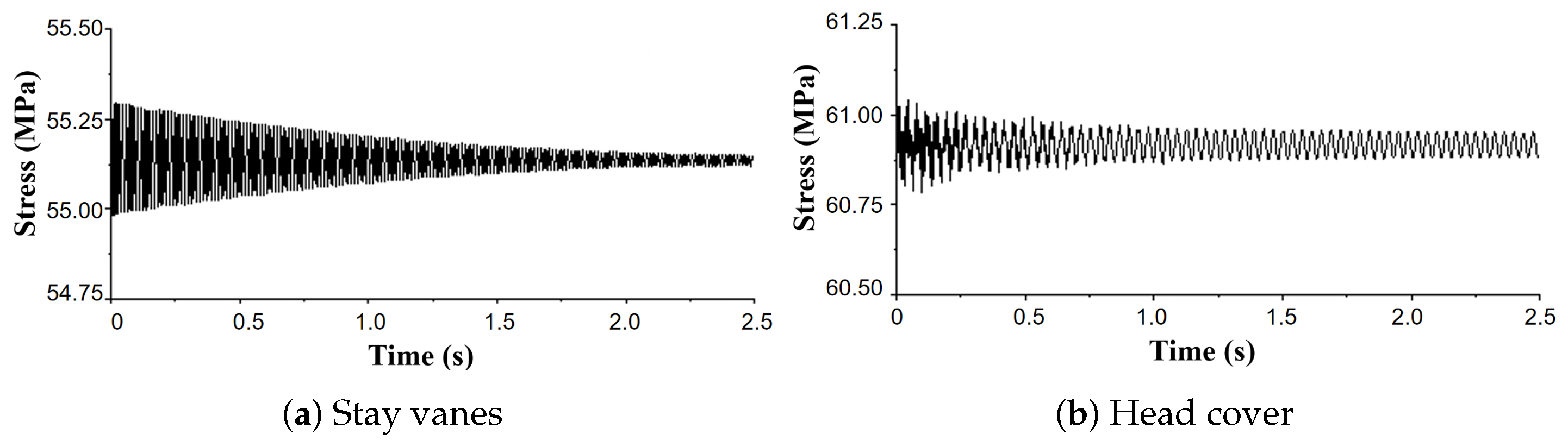
The dynamic stress–time history curves of the stress concentration points on the stay vanes and head cover of OP1 are shown in
Figure 23. It can be seen that under stable working conditions, the stress of the fixed components is relatively stable. Under the impact of water flow, a certain amplitude of dynamic stress first appears on the guide vanes and head cover, and then gradually decays. The amplitude of dynamic stress on the stay vanes and head cover is very small and can be basically ignored.
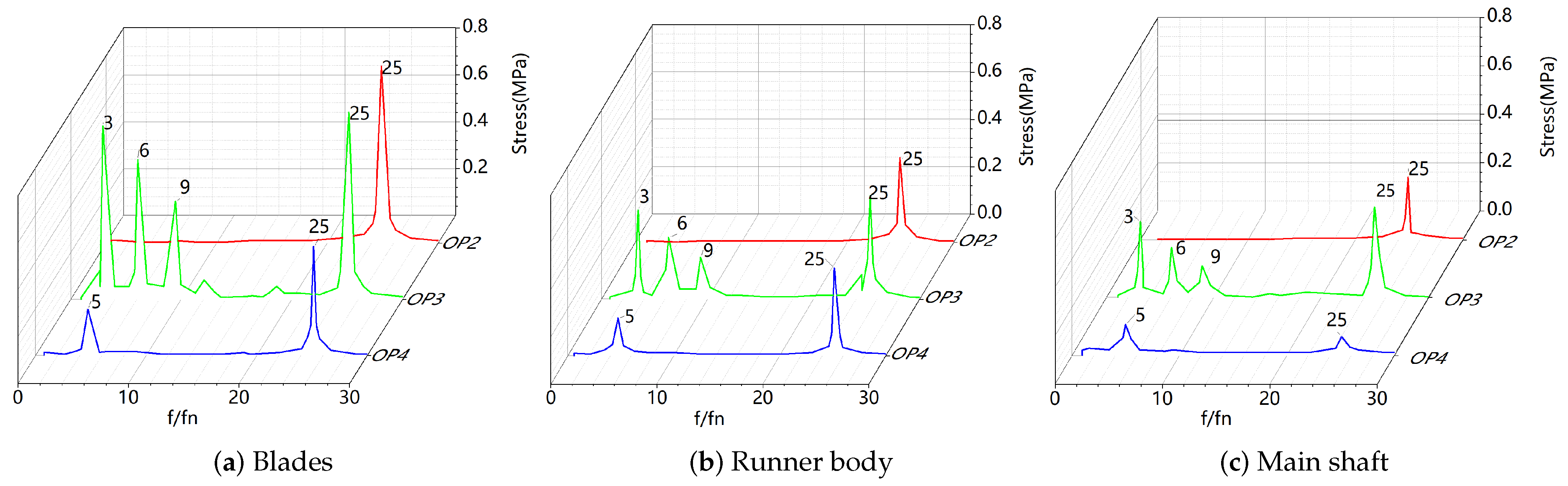
Figure 24 and
Figure 25 show the dynamic stress–time domain and frequency domain of the stress concentration points on the bottom ring, head cover and support cover of OP2, -3 and -4. Under the three working conditions, the stress and stress amplitude are that the stress of the bottom ring is the largest, the stress of the head cover is the second, and the stress at the support cover is the smallest. The main frequency of the dynamic stress on the bottom ring, head cover and support cover of OP2 is 25 fn, and the corresponding amplitudes are 0.75 MPa, 0.36 MPa and 0.26 MPa. In addition to 25 fn, the dynamic stress on the bottom ring, head cover and support cover of OP3 also has high amplitudes corresponding to 3 fn, 6 fn and 9 fn. This shows that in addition to the rotation of the runner, the stress of the fixed parts is greatly affected by the stay vane. OP4 has a main stress frequency with a large amplitude on the bottom ring and head cover, with a main frequency of 25 fn and a secondary frequency of 5 fn.
4. Conclusions
1. Under medium and low heads, the first 10 natural frequencies of rotating and fixed components both avoid various excitation force frequencies, making it difficult to induce components resonance.
2. The displacement distribution of rotating components under different heads is similar. Under medium and high heads, the displacement of rotating components changes little, mainly affected by the stay vanes. The displacement of rotating components under low heads is most affected by the rotation of the runner, and the displacement fluctuation value is greater than that of medium and high heads, and increases as the load decreases.
3. Under medium and high heads, the main frequency of stress pulsation of the blades and runner body is 28 fn, the main frequency of the main shaft is 1 fn, and the secondary frequency is 28 fn. Under low heads, the stress fluctuation amplitude of rotating components is much greater than that of medium and high heads. The main frequency of the blade and runner body stress is 6 fn, and the stress of blades 3 fn, 6 fn, and 9 fn all show high amplitudes, indicating that the rotating components under low heads are mainly affected by the rotation of the runner body and produce large stress fluctuations. Some low-frequency excitations are generated by the combined action of the vortex in the draft tube vaneless zone.
4. The displacement of fixed components under high head is mainly concentrated on the stay vanes. The displacement distribution of fixed components under medium and low heads is different from that under high heads. The displacement of fixed components under medium and low heads is mainly concentrated on the support cover, which moves upward under the impact of water flow.
5. The stress of fixed parts under high head is mainly concentrated on the root of the stay vanes and head cover, and the stress of the support cover is relatively small. However, the working condition with a small load under low head is changed significantly compared with the stable working condition. The stress and stress amplitude on the bottom ring, head cover and support cover increase significantly, and the main frequency of stress is 25 fn. In addition to 25 fn, the dynamic stress on the fixed parts of OP3 also has high amplitudes corresponding to 3 fn, 6 fn, and 9 fn. This indicates that in addition to being affected by the stay vanes, the stress of the fixed components in OP3 is greatly affected by the rotor–stator interference. There is also an obvious amplitude corresponding to 5 fn in OP4.
Author Contributions
Conceptualization, Z.W., G.W. and L.Z.; methodology, G.W., C.L. and H.L.; investigation, C.L. and X.C.; validation, H.L. and C.L.; writing—original draft preparation, C.L.; writing—review and editing, C.L., X.C. and H.L.; supervision, L.Z. and Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by National Natural Science Foundation of China (No. 51876099).
Data Availability Statement
Data are contained within the article.
Acknowledgments
The author sincerely thanks the project support: “Research on the Safe and Stable Operation of the Datongxia Large Kaplan Tubrbine Project” from Guangxi Datengxia Gorge Water Conservancy Development Co., Ltd.
Conflicts of Interest
Author Hongyun Luo, Guiyu Wang and Xiaobin Chen were employed by the company Guangxi Datengxia Gorge Water Conservancy Development Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Valentín, D.; Presas, A.; Egusquiza, M. Benefits of battery hybridization in hydraulic turbines. Wear and tear evaluation in a Kaplan prototype. Renew. Energy 2022, 199, 35–43. [Google Scholar] [CrossRef]
- Cui, R.G.; Guo, J.; Cheng, L.H. Status and Trends Analysis of Global Clean Energies. Acta Geosci. Sin. 2021, 42, 179–186. [Google Scholar]
- Iovǎnel, R.G.; Bucur, D.M.; Cervantes, M.J. Study on the accuracy of RANS modelling of the turbulent flow developed in a Kaplan turbine operated at BEP. Part 1—Velocity field. J. Appl. Fluid Mech. 2019, 12, 1449–1461. [Google Scholar] [CrossRef]
- Ma, W.S. Simulation of the Whole Passage in Prototype Turbine and Analysis of Precision in Calculation; China Agricultural University: Beijing, China, 2005. [Google Scholar]
- Estevez, E.E. Comportament Dinàmic de Màquines Hidràuliques; Universitat Politècnica de Catalunya: Barcelona, Spain, 2004. [Google Scholar]
- Abeykoon, C. Modelling and optimisation of a Kaplan turbine—A comprehensive theoretical and CFD study. Clean. Energy Syst. 2022, 3, 100017. [Google Scholar] [CrossRef]
- Altimemy, M.; Watheq, S.; Caspar, J. Performance of Kaplan Turbine Operating at Design Condition. In Proceedings of the Fluids Engineering Division Summer Meeting, Virtual Online, 10–12 August 2021; Volume 85307, p. V003T05A018. [Google Scholar]
- Petit, O.; Mulu, B.; Nilsson, H. Comparison of numerical and experimental results of the flow in the U9 Kaplan turbine model. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012024. [Google Scholar] [CrossRef]
- Puolakka, O.; Keto-Tokoi, J.; Matusiak, J. Unsteady load on an oscillating Kaplan turbine runner. J. Fluids Struct. 2013, 37, 22–23. [Google Scholar] [CrossRef]
- Liu, S.; Mai, J.; Shao, J. Pressure pulsation prediction by 3D turbulent unsteady flow simulation through whole flow passage of Kaplan turbine. Eng. Comput. 2009, 26, 1006–1025. [Google Scholar] [CrossRef]
- David, F.; Neil, B.; Bede, G. Fitness for purpose assessment after an over pressure incident at Arapuni Power Station. Int. J. Press. Vessel. Pip. 2004, 81, 471–479. [Google Scholar]
- Urquiza, G.; Garcia, J.C.; Gonzalez, J.G. Failure analysis of a hydraulic Kaplan turbine shaft. Eng. Fail. Anal. 2014, 41, 108–117. [Google Scholar] [CrossRef]
- Zhu, G.J.; Li, K.; Feng, J.J. Influence of cavitation on pressure fluctuation of draft tube and runner vibration of Kaplan turbine. Trans. Chin. Soc. Agric. Eng. 2021, 37, 40–49. [Google Scholar]
- Motycak, L.; Skotak, A.; Kupcik, R. Kaplan turbine tip vortex cavitation-analysis and prevention. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 32060. [Google Scholar] [CrossRef]
- Kumar, P.; Saini, R.P.; Cheng, L.H. Study of cavitation in hydro turbines—A review. Renew. Sustain. Energy Rev. 2010, 14, 374–383. [Google Scholar] [CrossRef]
- Wang, Z.W.; Luo, Y.Y.; Zhou, L.J. Computation of dynamic stresses in piston rods caused by unsteady hydraulic loads. Eng. Fail. Anal. 2008, 15, 28–37. [Google Scholar] [CrossRef]
- Liu, X.; Presas, A.; Luo, Y. Crack growth analysis and fatigue life estimation in the piston rod of a Kaplan hydro turbine. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 2402–2417. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, Z.; Zeng, J. Fatigue of piston rod caused by unsteady, unbalanced, unsynchronized blade torques in a Kaplan turbine. Eng. Fail. Anal. 2010, 17, 192–199. [Google Scholar] [CrossRef]
- Shigley, J.E.; Mischke, C.R. Mechanical Engineering Design; McGraw-Hill: New York, NY, USA, 1989. [Google Scholar]
- Sines, G.; Ohgi, G. Fatigue criteria under combined stresses or strains. J. Eng. Mater. Technol. 1981, 103, 82–90. [Google Scholar] [CrossRef]
- Gehrer, A.; Schmidl, R.; Sadnik, D. Kaplan turbine runner optimization by numerical flow simulation (CFD) and an evolutionary algorithm. In Proceedings of the 23rd IAHR Symposium on Hydraulic Machinery and Systems, Yokohama, Japan, 17–21 October 2006. [Google Scholar]
- Shingai, K.; Katayama, K.; Shimmei, K. Optimization of axial turbine runner blade using a simulated annealing algorithm. In Proceedings of the 23rd IAHR Symposium on Hydraulic Machinery and Systems, Yokohama, Japan, 17–21 October 2006. [Google Scholar]
- Liang, Q.W.; Wang, Z.W.; Fang, Y. Modal analysis of Francis turbine with considering FSI. J. Hydroelectr. Eng. 2004, 23, 116–120. [Google Scholar]
- Menter, F.R. Zonal Two-Equation k-ω Turbulence Model for Aerodynamic Flows; AIAA Paper; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1993. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures; Klaus-Jurgen Bathe: Cambridge, MA, USA, 2006. [Google Scholar]
- Roache, P.J. Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid. Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Kim, H.-H.; Rakibuzzaman, M.; Kim, K.; Suh, S.-H. Flow and Fast Fourier Transform Analyses for TipClearance Effect in an Operating Kaplan Turbine. Energies 2019, 12, 264. [Google Scholar] [CrossRef]
Figure 1.
Fixed and rotating components of the Kaplan turbine.
Figure 1.
Fixed and rotating components of the Kaplan turbine.
Figure 2.
Flow field profile and structural field.
Figure 2.
Flow field profile and structural field.
Figure 4.
Mesh for fluid–structure interaction.
Figure 4.
Mesh for fluid–structure interaction.
Figure 5.
The operating region of the prototype Kaplan turbine.
Figure 5.
The operating region of the prototype Kaplan turbine.
Figure 6.
Boundary conditions for rotating components.
Figure 6.
Boundary conditions for rotating components.
Figure 7.
Finite element model of wet modes of rotating components.
Figure 7.
Finite element model of wet modes of rotating components.
Figure 8.
Low-order wet modes of rotating components.
Figure 8.
Low-order wet modes of rotating components.
Figure 9.
Finite element model of wet modes of fixed components.
Figure 9.
Finite element model of wet modes of fixed components.
Figure 10.
Low-order wet modes of fixed components.
Figure 10.
Low-order wet modes of fixed components.
Figure 11.
Displacement of rotating parts (OP1).
Figure 11.
Displacement of rotating parts (OP1).
Figure 12.
Time domain of axial displacement at the maximum displacement point of the blade.
Figure 12.
Time domain of axial displacement at the maximum displacement point of the blade.
Figure 13.
Frequency domain of axial displacement at the maximum displacement point of the blade.
Figure 13.
Frequency domain of axial displacement at the maximum displacement point of the blade.
Figure 14.
Stress in rotating parts (OP1).
Figure 14.
Stress in rotating parts (OP1).
Figure 15.
Stress–time domain of components (OP1 and OP2).
Figure 15.
Stress–time domain of components (OP1 and OP2).
Figure 16.
Stress–frequency domain of components (OP1 and OP2).
Figure 16.
Stress–frequency domain of components (OP1 and OP2).
Figure 17.
Stress in rotating parts (OP3).
Figure 17.
Stress in rotating parts (OP3).
Figure 18.
Stress–time domain of components (OP3 and OP4).
Figure 18.
Stress–time domain of components (OP3 and OP4).
Figure 19.
Stress–frequency domain of components (OP3 and OP4).
Figure 19.
Stress–frequency domain of components (OP3 and OP4).
Figure 20.
Pressure distribution on different cross sections of OP4.
Figure 20.
Pressure distribution on different cross sections of OP4.
Figure 21.
Displacement of fixed components.
Figure 21.
Displacement of fixed components.
Figure 22.
Stress in fixed components.
Figure 22.
Stress in fixed components.
Figure 23.
Stress–time domain (OP1).
Figure 23.
Stress–time domain (OP1).
Figure 24.
Time domain of stress on fixed components.
Figure 24.
Time domain of stress on fixed components.
Figure 25.
Frequency domain of stress on fixed components.
Figure 25.
Frequency domain of stress on fixed components.
Table 1.
Operating conditions.
Table 1.
Operating conditions.
| | Head (m) | Angle of Guide Vane (°) | Angle of Runner Vane (°) |
|---|
| OP1 | 37.79 | 0 | 28 |
| OP2 | 25 | −10 | 25 |
| OP3 | 12.91 | 0 | 52 |
| OP4 | 12.91 | −10 | 38 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).