Comprehensive Review for Energy Recovery Technologies Used in Water Distribution Systems Considering Their Performance, Technical Challenges, and Economic Viability
Abstract
1. Introduction
2. Pressure Management Devices and Techniques
3. State of the Art
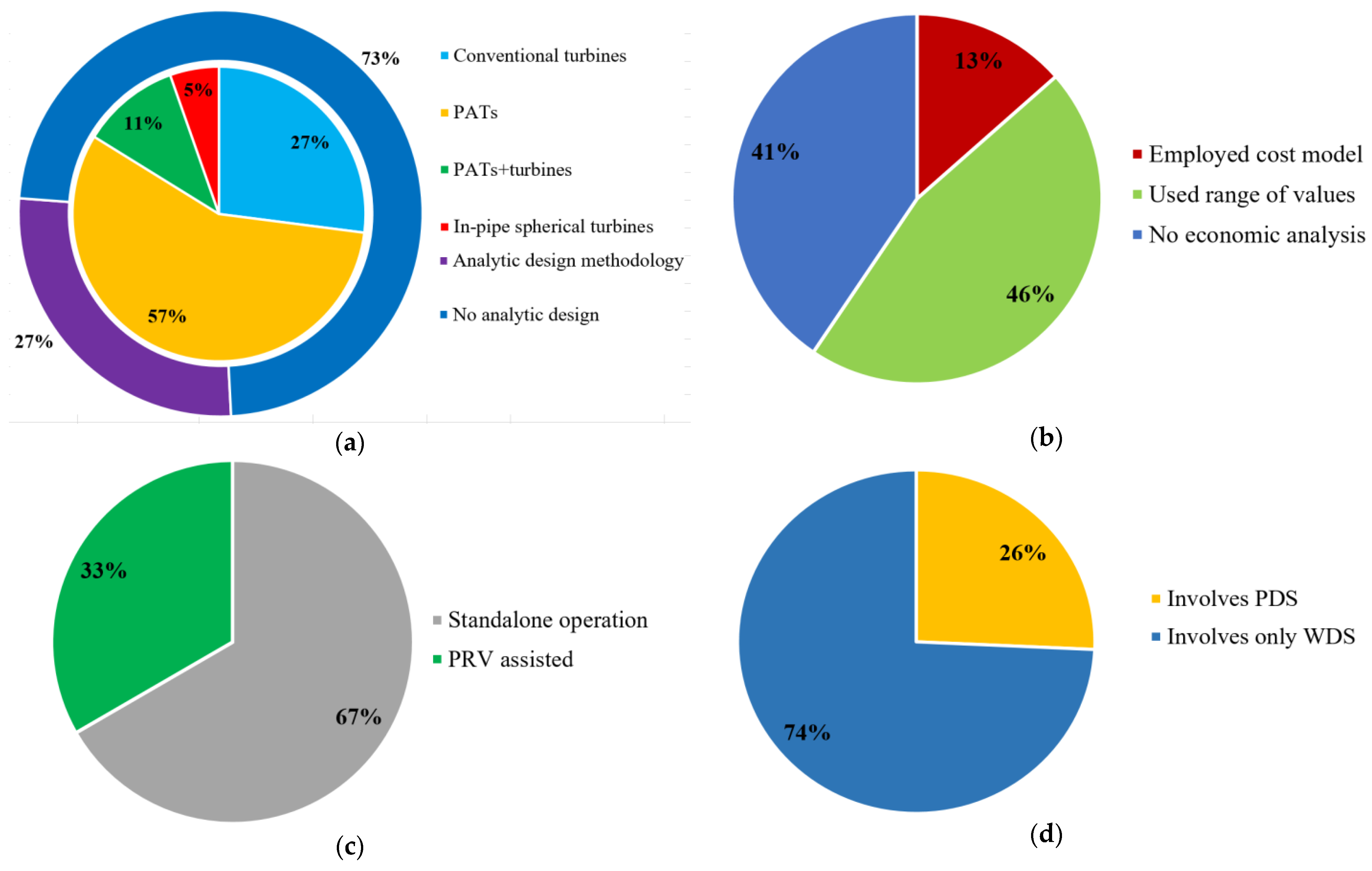
3.1. Energy Recovery Technologies in WDS
3.2. Studies Involving WDSs and PDSs
3.3. Infrastructure Requirements of Pressure-Regulating Devices
3.4. Turbine Types
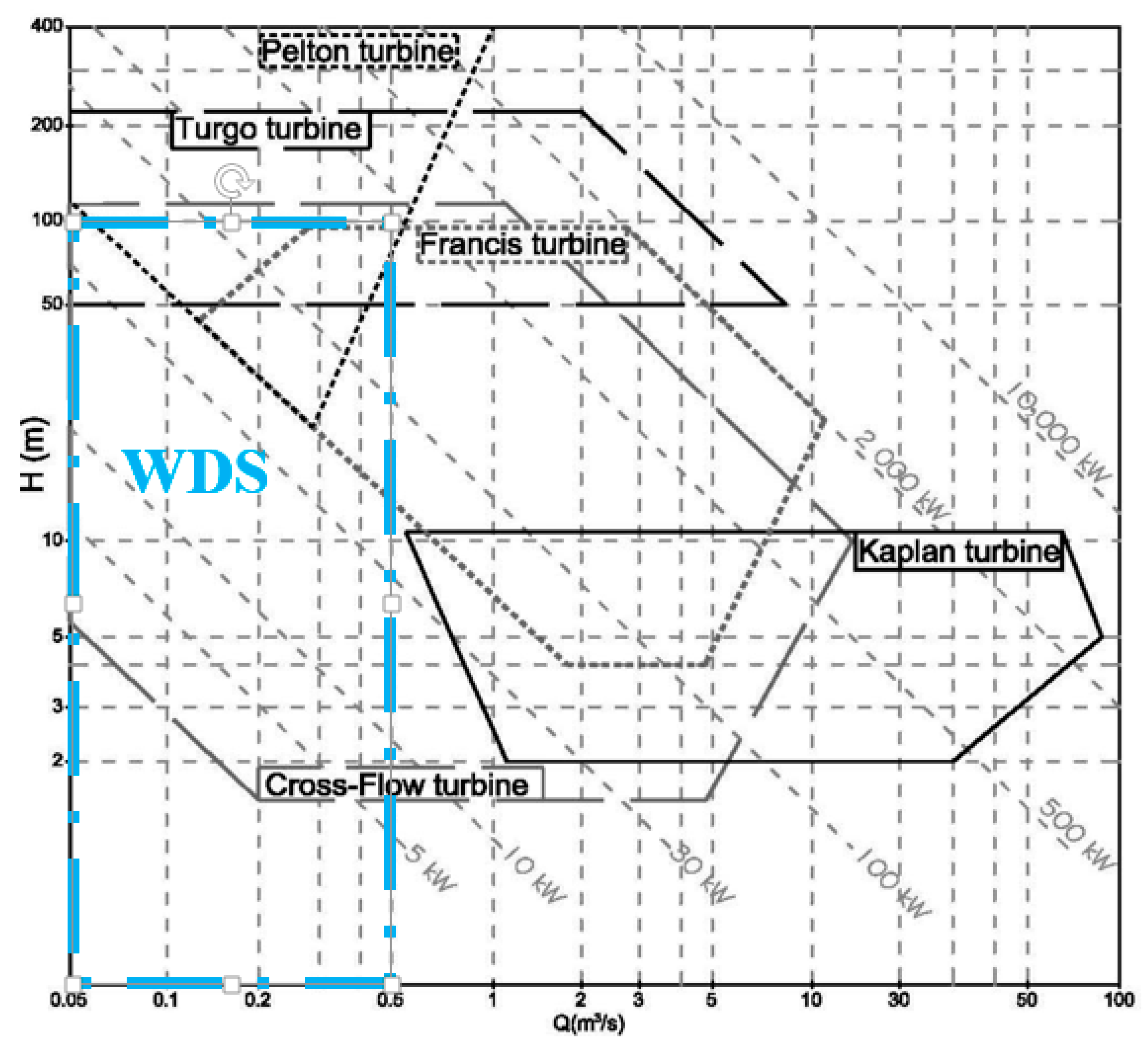
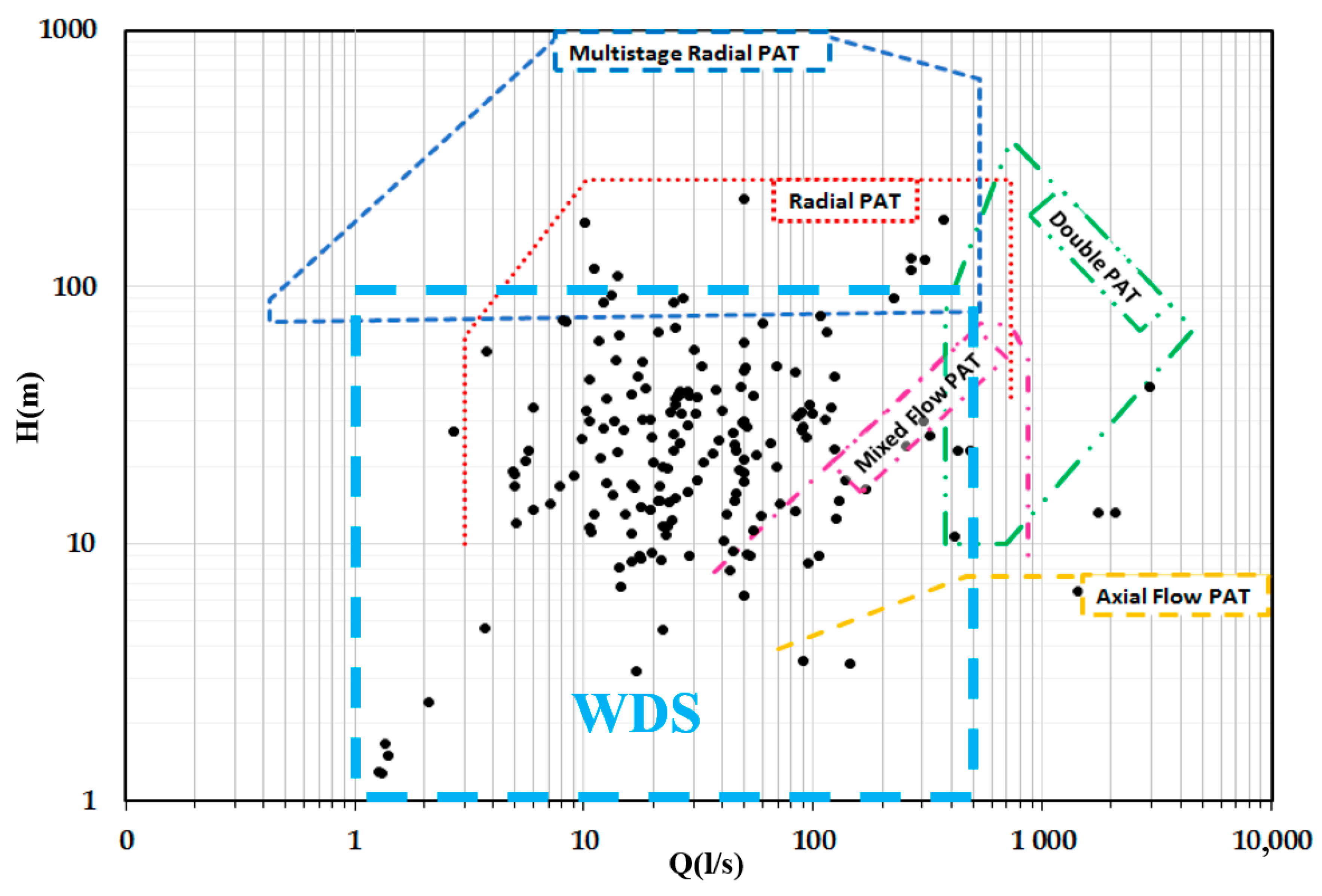
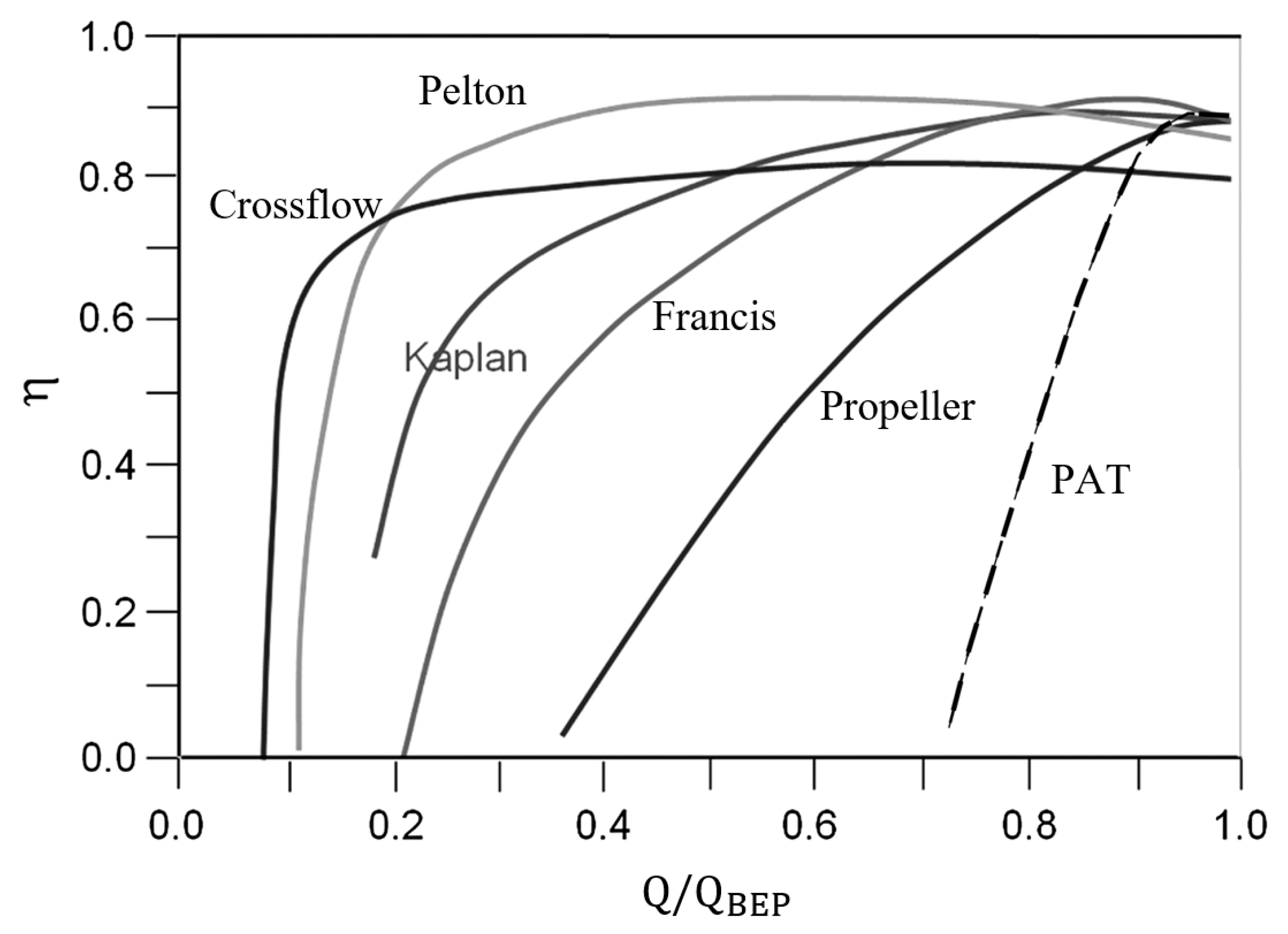
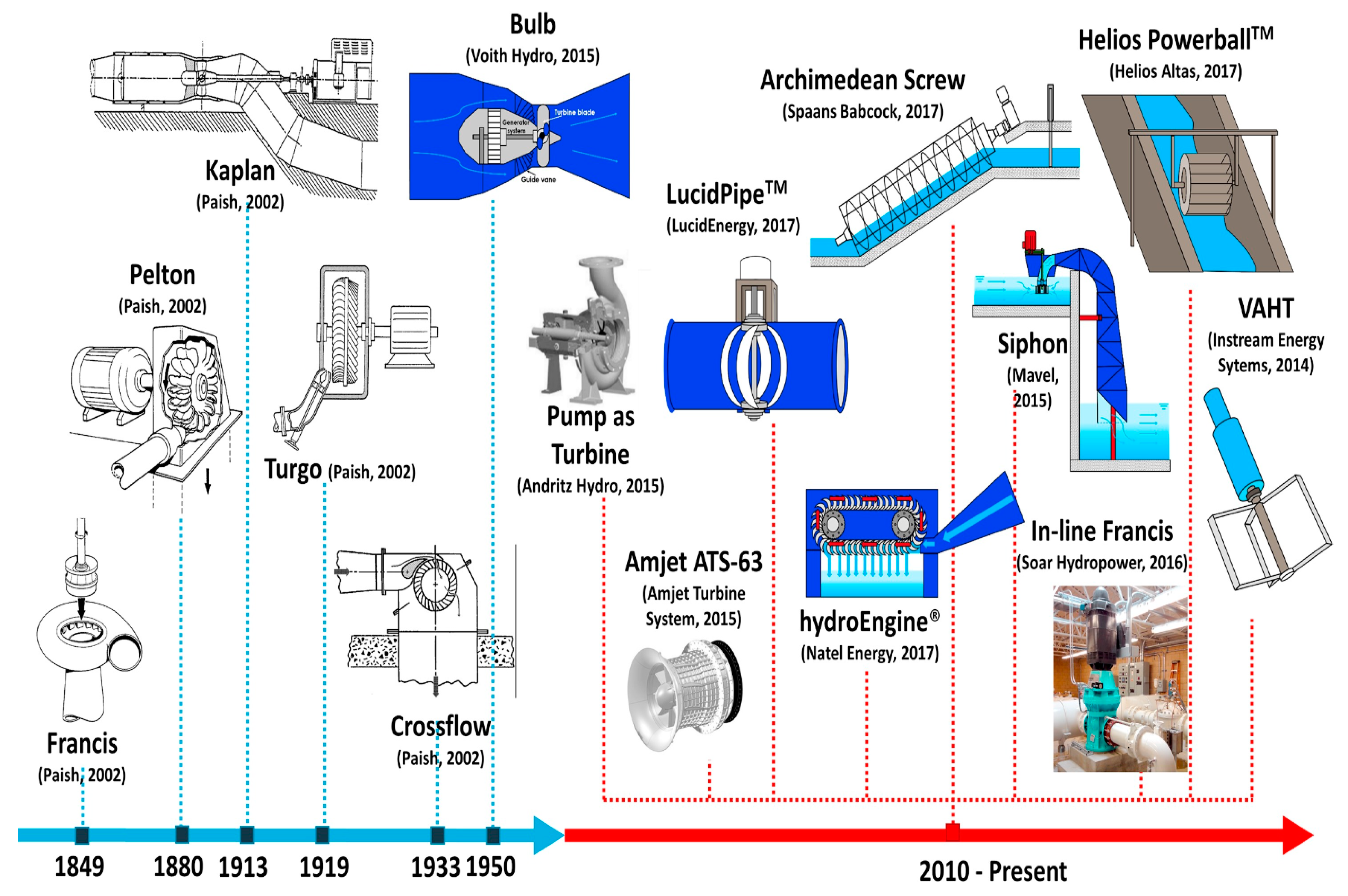
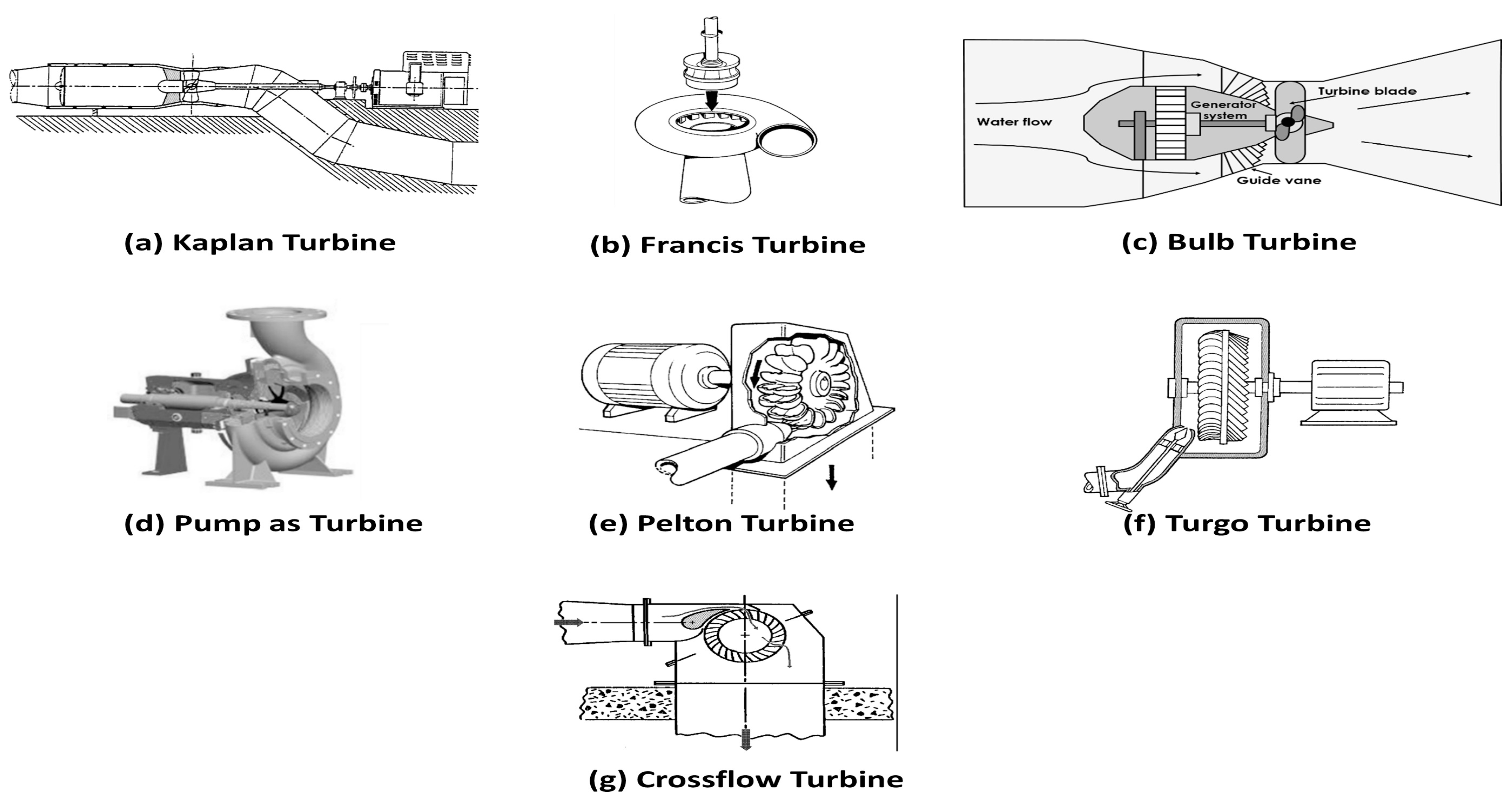
| Name | Type | Head (m) | Flow Rate | Efficiency at Design Point (%)/Part Flow | Pressure Regulation Ability | Installation Point |
|---|---|---|---|---|---|---|
| Pelton | Impulse | 7–1500 | 0.001–100 | 70–90/Very High | No | BPTs, in-pipe |
| Turgo | Impulse | 3–250 | 0.001–10 | 70–90/High–Very High | No | Only in BPTs |
| Crossflow | Impulse | 2–200 | 0.04–13 | 80/Medium | Low | BPTs, in-pipe * |
| Francis | Reaction | 30–700 | 0.07–100 | 80–90/Medium–High | High | BPTs, PRVs, in-pipe |
| Kaplan | Reaction | 1–70 | 0.05–1000 | 80–90/High | Very high | BPTs, PRVs, in-pipe |
| Semi-Kaplan | Reaction | 1–70 | 0.05–1000 | 80–90/Low | Medium | BPTs, PRVs, in-pipe |
| PAT | Reaction | 2–400 | 0.03–0.5 | 40–75/Very low | Limited | BPTs, PRVs, in-pipe |
| Spherical | Reaction | 1–4 | 0.5–10 | 10–50/NS | Νο | In-pipe |
| Turbine | PAT | |
|---|---|---|
| Efficiency | Higher efficiency at BEP and part-load conditions 1 | Inferior hydraulic efficiency 2 |
| Simulation/modeling | Well-documented and supported by CFD results | Characteristic curves not typically provided by manufacturer |
| Cost | High purchase cost 3 | Low purchase cost |
| Design | Complex design | Simple design |
| Maintenance | Maintenance requires a certain level of expertise | Easy maintenance |
| Pressure regulation ability | Can provide pressure regulation without PRV assistance | Requires additional hydraulic equipment (PRVs or more PATs) for accurate pressure regulation |
| Performance | Operational flexibility and wide range of applications | Narrow operating range and performance prediction still based on empirical relations and prediction methods |
| Market availability | Usually requires ad hoc design (limited range of standard diameters and power capacities in market) | Mass-produced with wide commercial availability 4 |
| Turbine | |||
| Expression | |||
| Reference | Type | , | |
| [51] * | Francis | ||
| [51] * | Kaplan | ||
| PAT | |||
| Expression | |||
| Reference | |||
| [52] | |||
| [15] | |||
| [53] | |||
| [7] | |||
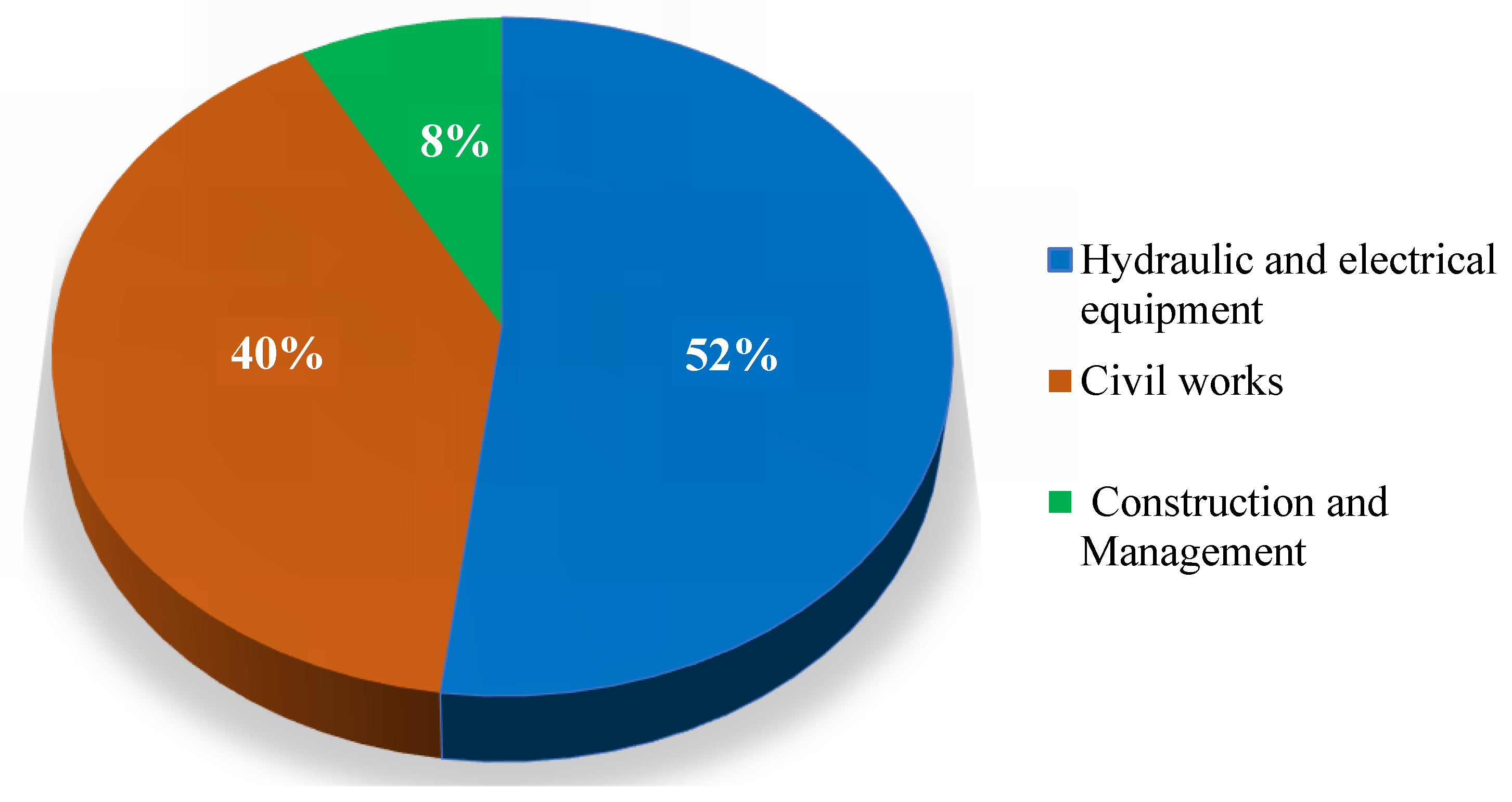
4. Cost Models
- They are often drawn from projects completed long ago, and they may need to be updated to current market prices in order to reflect the present cost of electro-mechanical equipment.
- Civil work cost is site-dependent, and every turbine installation may utilize a variety of components and characteristics, and thus the distribution of the various costs over the total cost may vary significantly from site to site.
- Most of the available capital cost functions are derived from small hydropower plants that often require the construction of dams and reservoirs, and thus their employment in the economic assessment of micro-turbine schemes installed in a WDS may lead to an overestimation of the total cost. Only in [60,62] is an estimation method developed specifically for the cost of the electro-mechanical equipment of micro-turbine projects.
- Civil work and electro-mechanical equipment cost is highly dependent on the location and country. In [60], it was demonstrated that when applying the models derived from data sets based on countries with different economic profiles to the country where the project will be deployed, like the ones of [61,63], the estimated cost may deviate by a factor greater than 2.5. This is mainly caused by the significantly different cost of electro-mechanical equipment, materials, and labor in the country of deployment (Nepal) in comparison to the counties that the data set is based (e.g., such as [61,63] for Europe).
- Many cost models use a single expression for all turbines, ignoring the impact of certain correlation constants that depend on turbine type. For example, the cost of Pelton turbines is more sensitive to flow rate variation, while the cost of Kaplan turbines is more sensitive to mechanical power variation. Such correlations often decrease the accuracy of such expressions.
- Cost models in the literature show great variety in their expressions. Therefore, determining which expression is more suitable to better estimate real costs may be challenging. According to [61], involving more parameters into the expressions, like flow rate, tends to make the expressions to follow the cost variation more accurately. However, such a detailed input data set is not always available or complete, especially during preliminary analysis.
5. Discussion
- The energy yield of the site should typically exceed 3 kW, otherwise the project’s financial viability is highly uncertain.
- For sites with insignificant variation in operating conditions (flow and head) and an installed capacity smaller than 20 kW, PATs are the most cost-efficient solution. However, when accurate pressure regulation is also required, low-cost reaction turbines are a better choice.
- During a preliminary cost assessment analysis, it is better to deploy a cost model derived from data sets that are closer to those of the case under study. This ensures a lower discrepancy between expected and actual cost.
- Impulse turbines should be considered at locations without any downstream pressure requirements, such as, BPTs.
- Especially for PATs, whose performance prediction is still accompanied with uncertainties, optimal placement is crucial for the economic feasibility of the project.
- When estimating the total cost of the turbine, the contribution of the associated costs should be determined with caution for each scenario, as they differ for each turbine type (Pelton and Francis), country (materials price and labor wage), and WDS location (whether they employ existing infrastructure or not). For example, when a turbine is specifically designed to replace a PRV, it will be accommodated within the existing PRV station, so civil work costs are already paid; hydraulic equipment and pipes in parallel are already in place. Conversely, at BPT locations, such hydraulic equipment will be required, as well as the installation of a bypass system, introduction of gate valves, etc.
- A turbine architecture with fewer moving parts is simpler and cheaper. Therefore, when the flow and head variation is not significant, electrical regulation (electronic load controllers) should be preferred over the more expensive hydraulic regulation (hydraulic and mechanical governors) required for part-flow operation.
- In order to ensure the economic feasibility of the project, the payback period should be at least two times lower than the turbine’s expected lifespan.
- During all instances, the turbine design and operation should be carefully considered, so that the minimum pressure requirements of the WDS are not violated, thus preventing any kind of disruption to the service quality of the network.
- During the assessment of the economic viability of pressure-regulating turbines replacing existing PRVs, the significant shadow cost of avoiding the purchase and O&M cost of a PRV should be considered over the turbine’s service lifetime. Under the same rationale, the environmental repercussions should be considered as well (e.g., the reduction in CO2 emissions and potential water savings created by the turbine pressure regulation).
- The selection of the appropriate turbine type, design, and dimension relies heavily upon site conditions, and thus there is need for extensive hydraulic data (water flow rate and head) from several years before the installation [12].
- The number of installed micro-hydropower projects within WDSs is restricted, and the commercial availability of pico-hydroturbines is limited. As a result, an investment from private owners will become less probable.
- Many institutional and regulatory aspects are still unresolved: no licensing protocols, lack of subsidies for the development of such mini projects, ambiguity on how the profits will be shared between water and electric system operators, etc.
- Turbines generally require well-trained manpower with a certain level of expertise in order to perform their installation and maintenance.
- The connection point of the turbine to the PDS should be appropriately selected, so that it allows full absorption of the produced energy, without creating adverse effects on bus voltage levels. This way, the net monetary benefit of the turbine operation will be maximized [39].
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stefanizzi, M.; Capurso, T.; Balacco, G.; Binetti, M.; Camporeale, S.M.; Torresi, M. Selection, Control and Techno-Economic Feasibility of Pumps as Turbines in Water Distribution Networks. Renew. Energy 2020, 162, 1292–1306. [Google Scholar] [CrossRef]
- Itani, Y.; Soliman, M.R.; Kahil, M. Recovering Energy by Hydro-Turbines Application in Water Transmission Pipelines: A Case Study West of Saudi Arabia. Energy 2020, 211, 118613. [Google Scholar] [CrossRef]
- Lahimer, A.; Alghoul, M.; Sopian, K.; Amin, N.; Asim, N.; Fadhel, M. Research and Development Aspects of Pico-Hydro Power. Renew. Sustain. Energy Rev. 2012, 16, 5861–5878. [Google Scholar] [CrossRef]
- Ferrarese, G.; Malavasi, S. Perspectives of Water Distribution Networks with the GreenValve System. Water 2020, 12, 1579. [Google Scholar] [CrossRef]
- Hamlehdar, M.; Yousefi, H.; Noorollahi, Y.; Mohammadi, M. Energy Recovery from Water Distribution Networks Using Micro Hydropower: A Case Study in Iran. Energy 2022, 252, 124024. [Google Scholar] [CrossRef]
- Boroomandnia, A.; Rismanchi, B.; Wu, W. A Review of Micro Hydro Systems in Urban Areas: Opportunities and Challenges. Renew. Sustain. Energy Rev. 2022, 169, 112866. [Google Scholar] [CrossRef]
- Le Marre, M.; Mandin, P.; Lanoisellé, J.-L.; Bezuglov, R. Experimental Study on Performance Predictions of Pumps as Turbine. Energy Convers. Manag. 2023, 292, 117235. [Google Scholar] [CrossRef]
- Poullikkas, A. A Comparative Assessment of Net Metering and Feed in Tariff Schemes for Residential PV Systems. Sustain. Energy Technol. Assessments 2013, 3, 1–8. [Google Scholar] [CrossRef]
- McNabola, A.; Coughlan, P.; Williams, A.P. The Technical and Economic Feasibility of Energy Recovery in Water Supply Networks. Renew. Energy Power Qual. J. 2011, 1, 1123–1127. [Google Scholar] [CrossRef]
- McNabola, A.; Coughlan, P.; Williams, A.P. Energy Recovery in the Water Industry: An Assessment of the Potential of Micro-Hydropower. Water Environ. J. 2013, 28, 294–304. [Google Scholar] [CrossRef]
- Voltz, T.J.; Grischek, T. Microturbines at Drinking Water Tanks Fed by Gravity Pipelines: A Method and Excel Tool for Maximizing Annual Energy Generation Based on Historical Tank Outflow Data. Water 2019, 11, 1403. [Google Scholar] [CrossRef]
- Ramos, H.M.; Borga, A.; Simão, M. New Design Solutions for Low-Power Energy Production in Water Pipe Systems. Water Sci. Eng. 2009, 2, 69–84. [Google Scholar] [CrossRef]
- Morani, M.C.; Carravetta, A.; Fecarotta, O. A Mixed Integer Non-Linear Programming Model for the Optimal Valve Placement within Water Distribution Networks. Environ. Sci. Proc. 2022, 21, 2. [Google Scholar] [CrossRef]
- García, I.F.; Novara, D.; Mc Nabola, A. A Model for Selecting the Most Cost-Effective Pressure Control Device for More Sustainable Water Supply Networks. Water 2019, 11, 1297. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Improved Planning of Energy Recovery in Water Systems Using a New Analytic Approach to PAT Performance Curves. Water 2020, 12, 468. [Google Scholar] [CrossRef]
- Algieri, A.; Zema, D.A.; Nicotra, A.; Zimbone, S.M. Potential Energy Exploitation in Collective Irrigation Systems Using Pumps as Turbines: A Case Study in Calabria (Southern Italy). J. Clean. Prod. 2020, 257, 120538. [Google Scholar] [CrossRef]
- Barbarelli, S.; Amelio, M.; Florio, G. Predictive Model Estimating the Performances of Centrifugal Pumps Used as Turbines. Energy 2016, 107, 103–121. [Google Scholar] [CrossRef]
- Venturini, M.; Manservigi, L.; Alvisi, S.; Simani, S. Development of a physics-based model to predict the performance of pumps as turbines. Appl. Energy 2018, 231, 343–354. [Google Scholar] [CrossRef]
- Venturini, M.; Alvisi, S.; Simani, S.; Manservigi, L. Energy production by means of Pumps As Turbines in water distribution networks. Energies 2017, 10, 1666. [Google Scholar] [CrossRef]
- Nasir, A.; Salau, A.O.; Dribssa, E.; Girma, M. Technical and Economic Analysis of a Pump as a Turbine for Rural Electrification. Int. J. Sustain. Energy 2023, 42, 914–928. [Google Scholar] [CrossRef]
- Muhammetoglu, A.; Karadirek, I.E.; Ozen, O.; Muhammetoglu, H. Full-Scale PAT Application for Energy Production and Pressure Reduction in a Water Distribution Network. J. Water Resour. Plan. Manag. 2017, 143, 04017040. [Google Scholar] [CrossRef]
- Lima, G.M.; Luvizotto, E.; Brentan, B.M. Selection and Location of Pumps as Turbines Substituting Pressure Reducing Valves. Renew. Energy 2017, 109, 392–405. [Google Scholar] [CrossRef]
- Rodríguez-Pérez, M.; Pulido-Calvo, I.; Cáceres-Ramos, P. A Computer Program to Support the Selection of Turbines to Recover Unused Energy at Hydraulic Networks. Water 2021, 13, 467. [Google Scholar] [CrossRef]
- Bideris-Davos, A.A.; Vovos, P.N. Algorithm for Appropriate Design of Hydroelectric Turbines as Replacements for Pressure Reduction Valves in Water Distribution Systems. Water 2023, 15, 554. [Google Scholar] [CrossRef]
- Morani, M.C.; Simão, M.; Gazur, I.; Santos, R.S.; Carravetta, A.; Fecarotta, O.; Ramos, H.M. Pressure Drop and Energy Recovery with a New Centrifugal Micro-Turbine: Fundamentals and Application in a Real WDN. Energies 2022, 15, 1528. [Google Scholar] [CrossRef]
- Mosbahi, M.; Ayadi, A.; Mabrouki, I.; Driss, Z.; Tucciarelli, T.; Abid, M.S. Effect of the Converging Pipe on the Performance of a Lucid Spherical Rotor. Arab. J. Sci. Eng. 2018, 44, 1583–1600. [Google Scholar] [CrossRef]
- Oladosu, T.L.; Koya, O.A. Numerical Analysis of Lift-Based In-Pipe Turbine for Predicting Hydropower Harnessing Potential in Selected Water Distribution Networks for Waterlines Optimization. Eng. Sci. Technol. Int. J. 2018, 21, 672–678. [Google Scholar] [CrossRef]
- Muratoglu, A.; Demir, M.S. Modeling Spherical Turbines for In-Pipe Energy Conversion. Ocean Eng. 2022, 246, 110497. [Google Scholar] [CrossRef]
- Sari, M.A.; Badruzzaman, M.; Cherchi, C.; Swindle, M.; Ajami, N.; Jacangelo, J.G. Recent innovations and trends in in-conduit hydropower technologies and their applications in water distribution systems. J. Environ. Manag. 2018, 228, 416–428. [Google Scholar] [CrossRef] [PubMed]
- Casini, M. Harvesting Energy from In-Pipe Hydro Systems at Urban and Building Scale. Int. J. Smart Grid Clean Energy 2015, 4, 316–327. [Google Scholar] [CrossRef]
- Saini, G.; Saini, R.P. A Review on Technology, Configurations, and Performance of Cross-Flow Hydrokinetic Turbines. Int. J. Energy Res. 2019, 43, 6639–6679. [Google Scholar] [CrossRef]
- Zamzam, A.S.; Dall’Anese, E.; Zhao, C.; Taylor, J.A.; Sidiropoulos, N.D. Optimal Water–Power Flow-Problem: Formulation and Distributed Optimal Solution. IEEE Trans. Control Netw. Syst. 2019, 6, 37–47. [Google Scholar] [CrossRef]
- Singh, M.K.; Kekatos, V. Optimal Scheduling of Water Distribution Systems. IEEE Trans. Control Netw. Syst. 2020, 7, 711–723. [Google Scholar] [CrossRef]
- Menke, R.; Abraham, E.; Parpas, P.; Stoianov, I. Demonstrating Demand Response from Water Distribution System through Pump Scheduling. Appl. Energy 2016, 170, 377–387. [Google Scholar] [CrossRef]
- Oikonomou, K.; Parvania, M. Optimal Coordinated Operation of Interdependent Power and Water Distribution Systems. IEEE Trans. Smart Grid 2020, 11, 4784–4794. [Google Scholar] [CrossRef]
- Li, Q.; Yu, S.; Al-Sumaiti, A.S.; Turitsyn, K. Micro Water–Energy Nexus: Optimal Demand-Side Management and Quasi-Convex Hull Relaxation. IEEE Trans. Control Netw. Syst. 2019, 6, 1313–1322. [Google Scholar] [CrossRef]
- Majidi, M.; Rodriguez-Garcia, L.; Mosier, T.; Parvania, M. Coordinated Operation of Pumped-Storage Hydropower with Power and Water Distribution Systems. Int. J. Electr. Power Energy Syst. 2022, 142, 108297. [Google Scholar] [CrossRef]
- Najafi, J.; Peiravi, A.; Anvari-Moghaddam, A.; Guerrero, J. An Efficient Interactive Framework for Improving Resilience of Power-Water Distribution Systems with Multiple Privately-Owned Microgrids. Int. J. Electr. Power Energy Syst. 2020, 116, 105550. [Google Scholar] [CrossRef]
- Bideris-Davos, A.A.; Vovos, P.N. Co-Optimization of Power and Water Distribution Systems for Simultaneous Hydropower Generation and Water Pressure Regulation. Energy Rep. 2024, 11, 3135–3148. [Google Scholar] [CrossRef]
- Petrollese, M.; Seche, P.; Cocco, D. Analysis and Optimization of Solar-Pumped Hydro Storage Systems Integrated in Water Supply Networks. Energy 2019, 189, 116176. [Google Scholar] [CrossRef]
- Marini, G.; Di Menna, F.; Maio, M.; Fontana, N. HYPER: Computer-Assisted Optimal Pump-as-Turbine (PAT) Selection for Microhydropower Generation and Pressure Regulation in a Water Distribution Network (WDN). Water 2023, 15, 2807. [Google Scholar] [CrossRef]
- Saidur, R.; Mekhilef, S.; Ali, M.; Safari, A.; Mohammed, H. Applications of Variable Speed Drive (VSD) in Electrical Motors Energy Savings. Renew. Sustain. Energy Rev. 2012, 16, 543–550. [Google Scholar] [CrossRef]
- Du, J.; Yang, H.; Shen, Z.; Chen, J. Micro Hydro Power Generation from Water Supply System in High Rise Buildings Using Pump as Turbines. Energy 2017, 137, 431–440. [Google Scholar] [CrossRef]
- Laghari, J.; Mokhlis, H.; Bakar, A.; Mohammad, H. A Comprehensive Overview of New Designs in the Hydraulic, Electrical Equipments and Controllers of Mini Hydro Power Plants Making It Cost Effective Technology. Renew. Sustain. Energy Rev. 2013, 20, 279–293. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Energy Recovery in Existing Water Networks: Towards Greater Sustainability. Water 2017, 9, 97. [Google Scholar] [CrossRef]
- Elbatran, A.; Yaakob, O.; Ahmed, Y.M.; Shabara, H. Operation, Performance and Economic Analysis of Low Head Micro-Hydropower Turbines for Rural and Remote Areas: A Review. Renew. Sustain. Energy Rev. 2015, 43, 40–50. [Google Scholar] [CrossRef]
- Samora, I.; Hasmatuchi, V.; Münch-Alligné, C.; Franca, M.J.; Schleiss, A.J.; Ramos, H.M. Experimental Characterization of a Five Blade Tubular Propeller Turbine for Pipe Inline Installation. Renew. Energy 2016, 95, 356–366. [Google Scholar] [CrossRef]
- Postacchini, M.; Darvini, G.; Finizio, F.; Pelagalli, L.; Soldini, L.; Di Giuseppe, E. Hydropower Generation Through Pump as Turbine: Experimental Study and Potential Application to Small-Scale WDN. Water 2020, 12, 958. [Google Scholar] [CrossRef]
- Ávila, C.A.M.; Sánchez-Romero, F.-J.; López-Jiménez, P.A.; Pérez-Sánchez, M. Definition of the Operational Curves by Modification of the Affinity Laws to Improve the Simulation of PATs. Water 2021, 13, 1880. [Google Scholar] [CrossRef]
- Yang, S.-S.; Derakhshan, S.; Kong, F.-Y. Theoretical, Numerical and Experimental Prediction of Pump as Turbine Performance. Renew. Energy 2012, 48, 507–513. [Google Scholar] [CrossRef]
- Papantonis, D. Hydraulic Turbomachines: Pumps, Turbines-Hydrodynamic Transmissions, 2nd ed.; Tsotras: Athens, Greece, 2016; Chapter 6. (In Greek) [Google Scholar]
- Rossi, M.; Nigro, A.; Renzi, M. A Predicting Model of PaTs’ Performance in Off-Design Operating Conditions. Energy Procedia 2019, 158, 123–128. [Google Scholar] [CrossRef]
- Novara, D.; McNabola, A. A Model for the Extrapolation of the Characteristic Curves of Pumps as Turbines from a Datum Best Efficiency Point. Energy Convers. Manag. 2018, 174, 1–7. [Google Scholar] [CrossRef]
- Novara, D.; McNabola, A. The Development of a Decision Support Software for the Design of Micro-Hydropower Schemes Utilizing a Pump as Turbine. Proceedings 2018, 2, 678. [Google Scholar] [CrossRef]
- Carravetta, A.; Conte, M.; Fecarotta, O.; Ramos, H. Evaluation of PAT Performances by Modified Affinity Law. Procedia Eng. 2014, 89, 581–587. [Google Scholar] [CrossRef]
- Fecarotta, O.; Carravetta, A.; Ramos, H.M.; Martino, R. An Improved Affinity Model to Enhance Variable Operating Strategy for Pumps Used as Turbines. J. Hydraul. Res. 2016, 54, 332–341. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; López-Jiménez, P.A.; Ramos, H.M. Modified Affinity Laws in Hydraulic Machines towards the Best Efficiency Line. Water Resour. Manag. 2017, 32, 829–844. [Google Scholar] [CrossRef]
- Tahani, M.; Kandi, A.; Moghimi, M.; Houreh, S.D. Rotational speed variation assessment of centrifugal pump-as-turbine as an energy utilization device under water distribution network condition. Energy 2020, 213, 118502. [Google Scholar] [CrossRef]
- Fontanella, S.; Fecarotta, O.; Molino, B.; Cozzolino, L.; Della Morte, R. A Performance Prediction Model for Pumps as Turbines (PATs). Water 2020, 12, 1175. [Google Scholar] [CrossRef]
- Butchers, J.; Williamson, S.; Booker, J.; Maitland, T.; Karki, P.B.; Pradhan, B.R.; Pradhan, S.R.; Gautam, B. Cost Estimation of Micro-Hydropower Equipment in Nepal. Dev. Eng. 2022, 7, 100097. [Google Scholar] [CrossRef]
- Cavazzini, G.; Santolin, A.; Pavesi, G.; Ardizzon, G. Accurate Estimation Model for Small and Micro Hydropower Plants Costs in Hybrid Energy Systems Modelling. Energy 2016, 103, 746–757. [Google Scholar] [CrossRef]
- Malhan, P.; Mittal, M. Evaluation of Different Statistical Techniques for Developing Cost Correlations of Micro Hydro Power Plants. Sustain. Energy Technol. Assessments 2021, 43, 100904. [Google Scholar] [CrossRef]
- Ogayar, B.; Vidal, P. Cost Determination of the Electro-Mechanical Equipment of a Small Hydro-Power Plant. Renew. Energy 2009, 34, 6–13. [Google Scholar] [CrossRef]
- Aggidis, G.; Luchinskaya, E.; Rothschild, R.; Howard, D. The Costs of Small-Scale Hydro Power Production: Impact on the Development of Existing Potential. Renew. Energy 2010, 35, 2632–2638. [Google Scholar] [CrossRef]
- Gordon, J.L.; Penman, A.C. Quick estimating techniques for small hydro potential. J. Water Power Dam Constr. 1979, 31, 46–51. [Google Scholar]
- Lasu, S.; Persson, T. Mini Power Station in Sweden. Int. Fachtag Uber Umbau Erweitrung Wasserkr. 1979, 34, 163–172. [Google Scholar]
- Gulliver, J.S.; Dotan, A. Cost estimated for hydropower at existing dams. J. Energy Eng. 1984, 110, 204–214. [Google Scholar] [CrossRef]
- Wallace, A.R.; Whittington HW, P.; Henderson, D.S. An Economic Analysis of the Capital Cost in Micro Hydro. Proceedings 3rd Int. Conf. Small Hydro. 1988, p. 8. Available online: https://www.research.ed.ac.uk/en/publications/an-economic-analysis-of-the-capital-cost-in-micro-hydro (accessed on 20 June 2024).
- Chenal, R. Evaluation du Cout de Construction D’une Petite Centrale Hydroelectrique Nouvelle et Complete et du Prix de Revient du kwh (p < d 1000 kw). Suisse: MHylab. 2000. Available online: https://www.mhylab.ch/images/public/images/cout_PCH.pdf (accessed on 20 June 2024).
- Voros, N.; Kiranoudis, C.; Maroulis, Z. Short-Cut Design of Small Hydroelectric Plants. Renew. Energy 2000, 19, 545–563. [Google Scholar] [CrossRef]
- Papantonis, D. Small Hydro Power Station; Simeon: Athens, Greece, 2001. [Google Scholar]
- Gordon, J.L. Determining Ballpark costs for a proposed project. Hydro Rev. Worldwide 2003, 11, 37–41. [Google Scholar]
- Kaldellis, J.; Vlachou, D.; Korbakis, G. Techno-Economic Evaluation of Small Hydro Power Plants in Greece: A Complete Sensitivity Analysis. Energy Policy 2005, 33, 1969–1985. [Google Scholar] [CrossRef]
- Singal, S.; Saini, R. Analytical Approach for Development of Correlations for Cost of Canal-Based SHP Schemes. Renew. Energy 2008, 33, 2549–2558. [Google Scholar] [CrossRef]
- Filho, G.L.T.; dos Santos, I.F.S.; Barros, R.M. Cost Estimate of Small Hydroelectric Power Plants Based on the Aspect Factor. Renew. Sustain. Energy Rev. 2017, 77, 229–238. [Google Scholar] [CrossRef]
- Alzohbi, G. The Cost of Electromechanical Equipment in a Small Hydro Power Storage Plant. J. Energy Syst. 2018, 2, 238–259. [Google Scholar] [CrossRef]
- Novara, D.; Carravetta, A.; McNabola, A.; Ramos, H.M. Cost Model for Pumps as Turbines in Run-of-River and In-Pipe Microhydropower Applications. J. Water Resour. Plan. Manag. 2019, 145, 04019012. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H.M. PAT Design Strategy for Energy Recovery in Water Distribution Networks by Electrical Regulation. Energies 2013, 6, 411–424. [Google Scholar] [CrossRef]
- Gagliano, A.; Tina, G.; Nocera, F.; Patania, F. Technical and Economic Perspective for Repowering of Micro Hydro Power Plants: A Case Study of an Early XX Century Power Plant. Energy Procedia 2014, 62, 512–521. [Google Scholar] [CrossRef][Green Version]
- De Marchis, M.; Freni, G. Pump as turbine implementation in a dynamic numerical model: Cost analysis for energy recovery in water distribution network. J. Hydroinform. 2015, 17, 347–360. [Google Scholar] [CrossRef]
- De Marchis, M.; Fontanazza, C.M.; Freni, G.; Messineo, A.; Milici, B.; Napoli, E.; Notaro, V.; Puleo, V.; Scopa, A. Energy Recovery in Water Distribution Networks. Implementation of Pumps as Turbine in a Dynamic Numerical Model. Procedia Eng. 2014, 70, 439–448. [Google Scholar] [CrossRef]
- Crespo Chacón, M.; Rodríguez Díaz, J.A.; García Morillo, J.; McNabola, A. Pump-as-Turbine Selection Methodology for Energy Recovery in Irrigation Networks: Minimising the Payback Period. Water 2019, 11, 149. [Google Scholar] [CrossRef]
- Hatata, A.; El-Saadawi, M.; Saad, S. A Feasibility Study of Small Hydro Power for Selected Locations in Egypt. Energy Strat. Rev. 2019, 24, 300–313. [Google Scholar] [CrossRef]
- Zema, D.A.; Nicotra, A.; Tamburino, V.; Zimbone, S.M. A Simple Method to Evaluate the Technical and Economic Feasibility of Micro Hydro Power Plants in Existing Irrigation Systems. Renew. Energy 2016, 85, 498–506. [Google Scholar] [CrossRef]
- Pugliese, F.; Giugni, M. An Operative Framework for the Optimal Selection of Centrifugal Pumps As Turbines (PATs) in Water Distribution Networks (WDNs). Water 2022, 14, 1785. [Google Scholar] [CrossRef]
- Kramer, M.; Terheiden, K.; Wieprecht, S. Pumps as turbines for efficient energy recovery in water supply networks. Renew. Energy 2018, 122, 17–25. [Google Scholar] [CrossRef]
- Klein, S.; Fox, E. A Review of Small Hydropower Performance and Cost. Renew. Sustain. Energy Rev. 2022, 169, 112898. [Google Scholar] [CrossRef]
- Kaldellis, J. The contribution of small hydro power stations to the electricity generation in Greece: Technical and economic considerations. Energy Policy 2007, 35, 2187–2196. [Google Scholar] [CrossRef]
- Forouzbakhsh, F.; Hosseini, S.; Vakilian, M. An Approach to the Investment Analysis of Small and Medium Hydro-Power Plants. Energy Policy 2007, 35, 1013–1024. [Google Scholar] [CrossRef]

| Reference | Equipment | |
|---|---|---|
| [41] | PRV | |
| Calculated from [14] | Total PRV installation | |
| [42] | Inverter |
| Cost Function | Turbine Types Considered /Project Classification | Country | Year | Reference |
|---|---|---|---|---|
| Various/Micro-small | Canada | 1979 | [65] | |
| () | Various/Small | Sweden | 1979 | [66] |
| Various/Micro-Small | U.S.A. | 1984 | [67] | |
| NS/Small | U.K. | 1998 | [68] | |
| NS/Micro-small | Switzerland | 2000 | [69] | |
| Francis, Pelton, Kaplan/ Small | Greece | 2000 | [70] | |
| Various/small ( | Greece | 2001 | [71] | |
| NS/Small | U.S.A. | 2003 | [72] | |
| S-type Kaplan/Small | Greece | 2005 | [73] | |
| + ++ | NS/Small | India | 2008 | [74] |
| Pelton/Micro to small | Spain | 2009 | [63] | |
| Francis/Mini to small | ||||
| Kaplan/Micro to small | ||||
| Semi-Kaplan/Micro to small | ||||
| /Mini to small | U.K. | 2010 | [64] | |
| , Q = (0.5–2.5) | ||||
| , Q = (2.5–10) | ||||
| , Q > 10 | ||||
| , Q = (0.5–5) | ||||
| , Q = (5–30) | ||||
| Pelton/Micro to small | Italy | 2016 | [61] | |
| Francis/Small | ||||
| Kaplan, Semi-Kaplan/Micro to small | ||||
| Various/Small | India | 2017 | [75] | |
| In-line turbine: PAT: | Turbine+PAT/Pico-mini (<120 kW) | Switzerland | 2019 | [11] |
| 69,040 − 1180P − 596H + 127.6 − 124.6PH + 44.94 − 1.02 + 0.6473H + 0.3239P − 0.2877 | Various/Micro | India | 2021 | [62] |
| ) ( | Crossflow/Micro Pelton/Micro | Nepal | 2022 | [60] |
| PAT/Pico-mini (550 kW) | Europe | 2018 | [76] | |
| Radial with 1 pair of poles: Radial with 2 pairs of poles: Radial with 3 pairs of poles: Vertical with 1 pair of poles: | PAT (PAT+gen)/Micro | Italy | 2019 | [77] |
| PAT (PAT+gen)/Micro | Italy | 2020 | [16] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bideris-Davos, A.A.; Vovos, P.N. Comprehensive Review for Energy Recovery Technologies Used in Water Distribution Systems Considering Their Performance, Technical Challenges, and Economic Viability. Water 2024, 16, 2129. https://doi.org/10.3390/w16152129
Bideris-Davos AA, Vovos PN. Comprehensive Review for Energy Recovery Technologies Used in Water Distribution Systems Considering Their Performance, Technical Challenges, and Economic Viability. Water. 2024; 16(15):2129. https://doi.org/10.3390/w16152129
Chicago/Turabian StyleBideris-Davos, Admitos A., and Panagis N. Vovos. 2024. "Comprehensive Review for Energy Recovery Technologies Used in Water Distribution Systems Considering Their Performance, Technical Challenges, and Economic Viability" Water 16, no. 15: 2129. https://doi.org/10.3390/w16152129
APA StyleBideris-Davos, A. A., & Vovos, P. N. (2024). Comprehensive Review for Energy Recovery Technologies Used in Water Distribution Systems Considering Their Performance, Technical Challenges, and Economic Viability. Water, 16(15), 2129. https://doi.org/10.3390/w16152129







