Abstract
The efficiency of beach recovery during a time of moderate waves following storm waves is closely related to the interaction between dynamics, sediment, and the landform. The existing studies mainly focus on the description of erosion and accretion characteristics, while the response and feedback mechanism of beach berm sediment have not been elucidated. The main controlling factors of recovery efficiency are not clear. In this paper, field observation and the XBeach numerical model are utilized on the sandy beach in Puqian Bay, China, to capture high-frequency cross-shore data during the post-storm recovery period. The variation characteristics and rules of berm elements, including berm ridge height and slope on two sides of the berm ridge, are analyzed. It is observed that the berm constantly changes to adapt to dynamic conditions. Additionally, a correlation between volume change and certain landform parameters is proposed, leading to the identification of a new relationship in wave run-up. The new forum reflects berm influence and considers the berm ridge and berm width.
1. Introduction
The pivotal role in the profile between the nearshore and backshore areas is held by the berm, which is situated within the swash zone and spans from the low water level (LWL) to the high water level (HWL). Wave run-up following the initial break of waves reaches the berm. Sediment erosion occurs during storm waves, resulting in the formation of offshore sandbars. Then, restoration takes place through onshore transport during moderate waves, thus creating berm accretion above the mean water level (MWL). During the recovery phase after storm-induced wave action, the beach berm undergoes its most significant changes in sediment volume. Despite restoration attempts, effectively recovering berm height and platform width proves challenging, even in monthly and seasonal evolution. Challenges in the study of geomorphic dynamics arise from the randomness of sediment particles and macroscopic variation in coastal landform evolution. The evolution of erosion and accretion is influenced by a combination of multiple factors. Understanding the natural recovery power of coastal areas and maintaining coastal resilience are significant in coastal management [1,2]. A global increase in tropical cyclone-associated wave hazards has significantly increased [3] various engineering measures, such as constructing ecological seawalls [4], artificial beaches [5], check dams [6,7], and artificial submerged sandbars [8,9], to enhance the original functionality of the coastal zone and maintain berm width. Koster [10] described in detail the wave-clipping action of the artificial submerged sandbar and the physical process of the sandbar as a source of sand that continuously replenishes the berm. Dette [11] studied the influence of the width of an artificial submerged sandbar on the berm maintenance effect through physical experiments. Based on the particle size composition of sediment, Žilinskas [12] analyzed the movement trend of a bar and obtained the best berm maintenance location for the bar. Pan [13] conducted physical models and EOF analysis of the migration law of sand bars on low-energy beaches, revealing that berm elevation is controlled by velocity skewness, wave height, and water depth. Wave height plays a leading role in onshore sediment transport for low-energy beaches. Based on coastal sandy–muddy transitional (SMT) beaches on South China coasts, Li [14] focused on the grain size distribution and put forward a predictive function for the equilibrium configurations of SMT beach berm. This function was proposed in an exponential form that combined boundary, tidal ranges, and wave heights. It was able to effectively predict the configurations of SMT beach berm. Zhu [15] observed that berm height significantly affects the degree of erosion and accretion in the beach profile during storms. Through measured data analysis and numerical simulation, he proposed that berm height is dominated by wave height and water level. He established an empirical relationship between the berm height parameter and the erosion capacity parameter. Li [16] found that wave characteristics were highly modulated by changing tidal levels in the intertidal zone of the dissipative beach berm. Li’s study showed that breaking dissipation increases from the offshore boundary to the intertidal sandbar, reaching a local maximum at the bar and then decreasing in berms onshore. This rule can guide us in making stronger sandbars to weaken offshore wave height and decrease the risk of berm erosion.
Numerous empirical models exist for predicting beach erosion and accretion under storm wave conditions. You [17] found berm sand size correlated with shore-normal wave direction, and a majority of the coast faces into the direction of predominant waves. He also proposed a conceptual model for the assessment of beach-dune storm erosion. But in his model, wave run-up was directly observed and measured. We can evaluate the volume change from this model but cannot build a relation between berm morphology and volume change. Zhu [15] defined erosion efficiency with eroded volume and wave power. Then, he found a statistical relationship between berm height and erosion efficiency from numerical simulation. In Zhu’s model, profile erosion is stronger with higher berm. But if the berm forms a ridge, wave run-up cannot easily go over the ridge and the erosion might be smaller. In other words, berm formation has a very strong relation with profile volume change. However, we do not clearly understand the berm function in profile recovery. There remains a gap in in-depth research and discussion on the primary controlling factors. Previous investigations have primarily focused on changes in total profile sediment volume, offering limited accuracy in explaining the rapid evolution of the berm due to wave actions. Understanding this evolution is crucial for a comprehensive understanding of beach erosion and recovery.
This study focused on Puqian Bay Beach in Haikou City as an example. Using measurement data and a numerical model, the following activities were conducted: (1) The identification of the law of beach volume change during the recovery period after storm waves. Then, revealing which part experiences dramatic sediment volume changes. From these characters, we try to find the crucial factors driving these changes. (2) Focusing on berm change (the most significant volume alteration area) and utilizing two shape parameters (berm ridge height and two sides of the berm ridge slope) to analyze recovery efficiency during the recovery period. (3) The determination of the parameters affecting sediment volume alteration in different parts of the profile. Try to find how they influence wave run-up in the berm, and the relationship between berm form and run-up limit location. (4) A discussion on how to improve coastal resilience using green plants.
2. Study Site
Haikou in China was selected as our study area due to its curved shorelines. Over the past few years, a long-term field observation plan was implemented to continuously obtain data. The impact of storm waves, which caused significant erosion, as well as the recovery time during moderate wave periods, were captured by our measurement data.
Puqian Bay is situated to the north of Hainan Island, with its bay mouth open to the north, facing the Qiongzhou Strait. The shoreline starts from Haikou Xinbu island in the west and continues to Wenchang Xinbuhai in the east, covering a width of 20 km. The water depth is less than 10 m, and encompasses a water area of nearly 80 km2. The landforms in Puqian Bay are predominantly composed of shallow sea plains, and the shoreline is primarily sandy coastal with a median grain diameter (D50) of 0.3 mm. The prevailing wind direction is from the northeast (NE), followed by south-southeast (SSE) and north-northeast (NEE). The wave direction in the N-NNE-NE sector accounts for 64%, with NNE being the most frequent at 29%, followed by N at 18% and NE at 17%. The mean wave height in the NNE, NE, and W directions is 0.7 m. The maximum wave height was observed in the N direction, reaching about 3.5 m, while smaller wave heights, ranging from 0.6 to 1.0 m, are experienced in the SSW, ESE, and SE directions. The wave period falls within the range of 2.7 to 4.0 s. Tides in the study area follow irregular half-day patterns, with a small average tidal difference of 0.89 m and a maximum tidal difference of 1.80 m. Despite the narrow mouth effect of the Qiongzhou Strait, the current in the strait is predominantly dominated by reflux, with flow velocities at the mouth of Puqian Bay exceeding 1.0 m/s [18] (Figure 1).
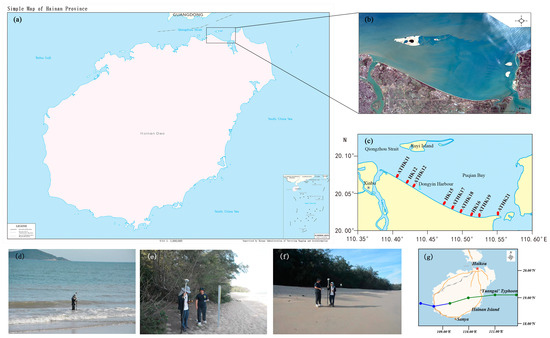
Figure 1.
Study area. (a) Simple map of Hainan Province in China and of our study area (in rectangular box). (b) Satellite sensing image of Puqian Bay. (c) Simple map of our study area. (d–f) Our filed measurement photo taken by group members. (g) Tracking of storm “Kompasu” No. 2118.
3. Methods
3.1. RTK-GPS Profiles Survey
The beach profile measurement data (Figure 1c) were acquired using the RTK (real-time kinematic) linear lofting function for navigation and positioning. We used the brand-new GALAXY G2 diminutive RTK receiver produced by South Surveying & Mapping Instrument Co., Ltd., in Guangzhou, China with a GNSS code differential of 0.5 mm. RTK technology’s direct coordinate method was employed to record and collect the data. The coordinate system utilized was the 2000 National Geodetic Coordinate System (CGCS2000), with the results projected according to the 6° belt, a central longitude of 111°, and the elevation datum from the 1985 National Elevation Datum. Differential signals were received through the Chihiro CORS network signal. Typically, the starting point for beach slope measurement is situated 3 to 10 m behind the line of the beach windbreak trees. In cases where there are no windbreak trees on the beach profile, we selected a starting point 2 to 3 m behind the steep ridge or buildings. If distinct dunes were present in certain profiles, we selected a starting point 2 to 8 m behind the dune. The end point of the survey line was generally positioned at 0.5 to 1.0 m MWL, with a point distance on the profile typically ranging from 0.5 to 1.0 m. Feature points indicating terrain changes were encrypted and measured. Where the same measurement line was used for both conventional measurement and measurement before and after a storm, the starting and ending point coordinates for each phase should remain consistent throughout the measurement process.
3.2. XBeach Model
The XBeach model was utilized as a resource to supplement the interval of measurement data. Originally developed to simulate hydrodynamic and morphodynamic processes impacting sandy coasts with a domain size of kilometers and on the time scale of storms, XBeach is an open-source numerical model and has been applied to the simulations of sandy beaches [19,20,21,22]. Employing the surfbeat version of the model, the time-dependent, short-wave action balance equation is solved for the wave group envelope. It is coupled with non-linear shallow water equations to resolve mean currents and infragravity waves. Sediment transport is modeled using a depth-averaged advection–diffusion equation [23], and morphology change is calculated based on gradients in sediment transport at each time step. Dune erosion in XBeach occurs directly from these transport gradients, as well as from avalanching induced when a critical angle of repose is exceeded. Detailed model formulations are described by Roelvink [24,25] and are not reiterated here. XBeach has undergone extensive validation for dune erosion processes in numerous coastal settings.
3.3. Dynamic Database
Wave data for Puqian Bay were derived from the ERA5 reanalysis dataset at 110°30′ E, 20°11′ N by the European Centre for Medium-Range Weather Forecasts. We focused on the time-averaged wave data within half a year after 13 October 2021, encompassing effective wave height and average period. Wind field data from 110°30′ E, 20°00′ N, including average wind speed and wind direction, were also sourced from the ERA5 reanalysis dataset. The selected time, region, and accuracy were aligned with the wave data. Tide level data were collected from 109°29′ E, 20°03′ N utilizing the measured data from the tide level station at Haikou during the corresponding period on Changdi Road. Elevation data were converted to the 1985 National Elevation Datum.
The study period for Puqian Bay spanned six months, ranging from October 2021 to April 2022, including one storm event along with five months of moderate wave events following the last storm. The analysis revealed that most wave periods were below 10 s, and wave height increased with the wave period in synchrony without a phase difference (Figure 2).
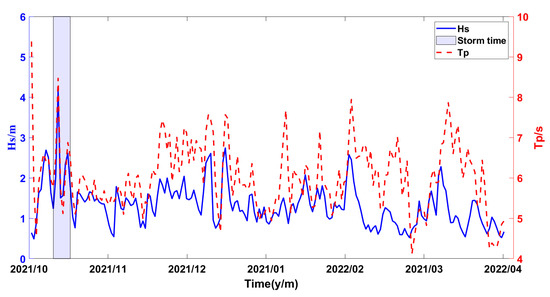
Figure 2.
Wave climate in the study area. Significant wave height and wave period in time series in Puqian Bay; the only storm, named “Kompasu” No. 2118, was a severe tropical storm.
3.4. Model Setup
Nine profiles with measurement data were selected in Puqian Bay, and their cross-shore elevation changes were measured before and after storm waves. Their evolution was tracked during a six-month-long period of moderate wave activity. The terrain was updated every 100 s, allowing oblique incidence and reflected waves to pass through the maritime boundary, while the outer boundary conditions were set as uniform domain models along the coast using Neumann boundary conditions. Both the offshore and land boundaries were equipped with weakly reflective boundaries, while the horizontal boundaries utilized Neumann boundaries with a constant water gradient. The mesh accuracy of the one-dimensional profile model was set at 1 m. The model accounted for tidal effects, fluctuations in wave height, wave run-up, and local wind and wave conditions. Utilizing the measured storm profile terrain as the initial terrain, the model simulated the storm and recovery process. The parameters listed in Table 1 were used as the primary input parameters to validate the model’s recovery period. There were not any storm events occurring during the validation period, which represents the parameters were used under moderate waves.

Table 1.
Main parameter settings.
3.5. Model Validation
Model validation based on a one-dimensional profile used the wave, wind, and tidal level as boundary conditions (Figure 3). Compared with the moderate wave period in April 2022, after a storm in October 2021, the berm became higher, and the foreshore slope became steeper. Our model reflected this trend effectively. However, when sediment collected over the berm (HK12 and ATHK19) and formed more than one berm ridge (ATHK17 and HK16) (Figure 3b,e,g,h), we could not accurately simulate the precise point on the ridge where this occurred. This likely occurred because we did not update the parameters closely connected with the profiles’ morphological change, such as the critical collapse slopes (wetslp and dryslp), which are related to sediment form and erosion volume. Instead, due to limited computing resources, we considered them as constants during the model period.
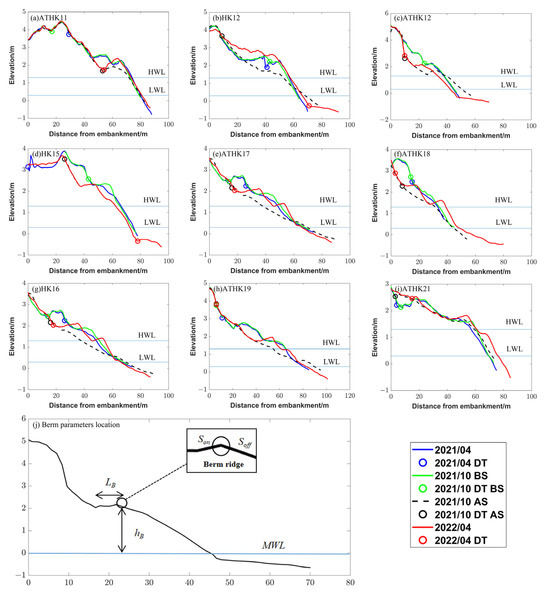
Figure 3.
(a–i) are profiles evolution in study area, (j) is berm parameters location concept figure, LB is berm platform length, hB is berm ridge height, Soff is berm slope, Soff is berm ridge slope. BS indicates before storm, AS indicates after storm, and DT indicates dune toe location; we show them in a circle.
4. Results
4.1. Volume Change
According to the methodology outlined by Stockdon [26], in our study, the location of maximal curvature within a geomorphological profile is defined as the dune toe. Considering the spatial resolution of the measurements, the dune toe positions are computed through data interpolation. The dune toe delineates the upper limit of sedimentary accretion and erosion processes, with its precise spatial positioning intricately linked to HWL and wave run-up.
The dynamic morphological transformations of beach profiles from west to east in response to storm wave influences are shown in Figure 4. Erosion predominantly targets the berm situated between the HWL and the dune toe. This erosion results in a concomitant narrowing of the berm and the steepening of its gradient, culminating in shoreward migration and elevation increase in the dune toe. Furthermore, the area of erosion observed in the supratidal zone surpasses that within the intertidal zone between the HWL and LWL. The western profiles ATHK11, HK12, and ATHK12 (Figure 4a–c) are geographically positioned west of Dongyin Habour, the western part of Puqian Bay, within the wave shadow zone of Ruyi Island. The storm “Kompasu”, passing through this area, induced a higher storm surge water level. In ATHK11, HK12, and ATHK12, the dune toe height increased, and strong erosion occurred below the dune toe. After the storm “Kompasu”, a moderate wave period of more than six months was required to recover the sediment volume. However, the volume of these profiles did not recover over pre-erosion levels. Instead, they formed a lower berm slope that was higher in elevation and demonstrated a gradation in recovery efficiency from west to east. The recovery rate of berm elevation was more rapid than the recovery of berm width, which indicates that it is easier for berms to increase in steepness than it is for berms to form a smooth and wide platform. At the same time, the intertidal zone demonstrated a quicker recovery than the area over the HWL. Due to the wave shadow area influenced by Ruyi Island, the volume in the profiles ATHK11 and ATHK12 accreted rapidly and the height of the berm increased. Six months after the storm event, the berm width and elevation in HK12 completely recovered compared to their pre-storm levels. The central profiles (HK15, ATHK17, and ATHK18 (Figure 4d–f)) and eastern parts (ATHK19 and ATHK21 (Figure 4h,i)) are situated to the east of Dongyin Habour, in the eastern edge of Puqian Bay. Remote sensing analyses [27] using suspended particulate matter inversion techniques revealed different sediment transport pathways from the Nandu River to the eastern Haikou Bay during flood and dry seasons: During the flood season, sediment flux occurs through Nandu River–Haidian Stream–eastern Haikou Bay. In the dry season, it occurs via Nandu River–Puqian Bay (around Haidian Island)–eastern Haikou Bay. Numerical simulations revealed a clockwise residual current flow in Puqian Bay [28] transitioning from east to west. After the construction of Ruyi Island, an anticlockwise flow around the island was observed, and the seabed level eroded between the land and the island. This persistent scouring offshore cut the sand supply and influenced the accretion rate in the intertidal zones of the profiles ATHK11, HK12, and ATHK12, rendering the slopes steeper.
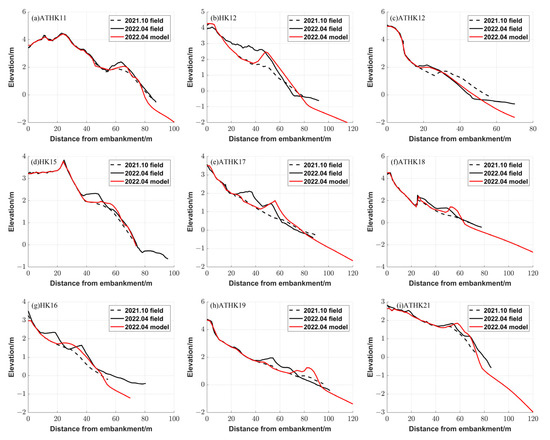
Figure 4.
(a–i) are model validation in each profile.
A one-dimensional water and sediment transport model was built using the XBeach model and based on the profiles measured after the storm. Monthly variations in sediment in the intertidal and supratidal zones for all the measured profiles were simulated (Table 2). The sediment volume in the intertidal zone was integrated based on the area enclosed by the HWL, the measured profile, and the vertical coordinate axis. The sediment volume in the supratidal zone was integrated based on the area enclosed by the HWL and LWL, the measured profile, and the vertical coordinate axis. During the six-month period of moderate wave recovery, the recovery characteristics of each profile varied, and they could be divided into three types of phenomenon: (1) The profiles with rapid recovery (ATHK11, ATHK12, and HK15) were mainly distributed in the western part of Puqian Bay. In the first month (October–November 2021), the total sediment amount in both the intertidal and supratidal zones recovered the fastest, even exceeding the total sediment balance of the final profile. From the second month onwards (December 2021 to April 2022), although the total sediment in the supratidal zone fluctuated monthly, the mean value remained basically unchanged, decreasing to the level after storm erosion at the end of the simulation period. The sediment volume in the intertidal zone recovered rapidly within the first month. Compared to the subsequent recovery period, the sediment volume changes stabilized. This stabilization may be attributed to the absence of high storm surges during the regular wave period, with beach profile recovery dominated by the mean water level. The range of wave and current erosion decreased compared to the storm period, thereby reducing the range of sediment initiation and transport. (2) The profiles with sustained recovery (HK12 and ATHK18) were primarily distributed in the central part of Puqian Bay. During the six-month recovery period, sediment in both the intertidal and supratidal zones continued to increase, with no period of basic stability in sediment volume. This continuous increase may be due to the matching slope of the beach and wave conditions, resulting in continuous sediment transport and accumulation towards the shore. Notably, the increase in sediment in the intertidal and supratidal zones was synchronous, indicating a cohesive sediment transport process. However, whether there was a limit threshold for the continuous accumulation of sediment ultimately depends on the steepness of the beach berm slope and the angle of repose of the sediment. The collapse may be caused by the inability to accumulate more sediment, but from the measured profiles (Figure 4b,h), it can be observed that the beach berm ridge continuously rose during the recovery period, accompanied by the gradual steepening of the beach berm slope, and sediment continuously accumulated on both sides of the beach berm ridge. (3) Profiles with intertidal zone accumulation (ATHK17, ATHK19, HK16, and ATHK21) were mainly distributed in the eastern part of Puqian Bay. During the regular wave recovery period, a gentle and broad beach berm gradually developed, resulting in a higher sediment volume in the intertidal zone compared to the supratidal zone.

Table 2.
Volume changes in different parts of profiles.
4.2. Berm Recovery
The berm is a crucial component of the beach profile and possesses a morphology that has a strong relation with nearshore dynamics. It can be observed from each profile that the elevation of the berm ridge in each profile ranged from 2.0 to 2.4 m before the storm. Typically, following storm events, berm erosion occurs, resulting in a gradual reduction in berm ridge height, causing the elevation of the berm ridge to fall below 2.0 m. Simultaneously, there is a tendency for the berm to move seaward. Over the half-year recovery period, the berm ridge was raised even higher than before the storm event. Under the influence of storm waves, the slopes on both sides of the berm changed in opposite directions (Table 3): during the storm period, berm erosion led to a decrease in elevation, seaward slope (Soff), and foreshore slope (Son). During moderate wave periods, the berm gradually recovered, and the elevation of the berm ridge increased due to recovery dynamics. This was accompanied by an increase in seaward slope (Soff) and foreshore slope (Son). The elevation of the berm ridge and the slopes on both sides of the berm ridge adapt to the changes in the erosion–recovery wave cycle.

Table 3.
Seaward slope (Soff) and foreshore slope (Son) change during wave action.
Laboratory experiments of an artificial profile were conducted by Li [29], revealing a relative trend in the sandbar slopes on both the seaward and shore sides. Gradual stabilization occurred under the influence of constant waves, indicating the attainment of a steady state by the landform after adapting to dynamic conditions. A comparison with Li’s findings suggests significant differences in the evolution characteristics between the supratidal and subtidal zones of the sandbar. Under the influence of continuous moderate waves, Soff and Son gradually undergo changes in opposite directions due to onshore accumulation, leading to the formation of a steep berm ridge. Subsequently, they revert to their pre-storm state, completing a periodic cycle of storm–moderate waves. This observation underscores the inherent difficulty in achieving absolute equilibrium and stability in natural beach evolution, with continual adjustments required to accommodate dynamic conditions.
4.3. How the Berm Effects Wave Run-Up and Volume Change
In this section, the aim is to identify the primary factors that induce volume changes in profiles and to explore methods for their evaluation. The correlation between sediment volume above the HWL and various parameters such as berm platform length (LB), berm ridge height (hB), berm slope (Soff), berm ridge slope (Son), wave run-up (R2%), and Iribarren number (ξ) was examined, as well as the correlation between the HWL and LWL (Table 4). There were many differences in the two parts of the profile: LB demonstrated almost no relation with volume change above the HWL but was much more strongly related to volume change between the HWL and LWL (in the index of approximately 0.397). LB always plays an important role due to its position below the HWL. hB correction in two parts of the berm reached 0.408. Soff is much more important and accounts for most relations above the HWL, which directly reflect R2% and ξ. When the slope became steeper, waves could not easily pass over it, which prevented erosion from occurring on the berm. Notably, R2% and ξ were relatively lower than Soff in terms of their wave height and wave period, except for Soff. This reduced relation indicates that the importance of dynamic parameters such as waves is lesser than that of landform parameters. Beach nearshore slope plays a critical role in profile morphology control.

Table 4.
The correlation between volume change and berm parameters.
Berm evolution occurs in the surf zone and has a strong relation to wave run-up. Generally, wave run-up is characterized by the Iribarren number [30], which is defined as follows:
The wave run-up model was based on field experiments from 10 beaches spanning a wide range of environmental conditions, which provide a general idea of the run-up on all the beaches. The empirical equation (S-model) can be written as follows [31]:
For beaches, H and L can use H0 and L0 in deep water. is the nearshore slope (below the MWL). This indicates that in the S-model, R2% is controlled by wave conditions and the beach nearshore slope. However, in the surf zone, two conditions are always present during storm waves with no nearshore slope change: (1) The whole berm erodes and retreats with no slope change (Figure 5a). (2) Erosion occurs above the HWL, with the berm volume reduced and the platform shortened but no sediment transport in the nearshore area (Figure 5b). These two ways in which beach erosion occurs are more common in Puqian Bay. Prior studies have focused on wave conditions and beach surfaces to calculate wave run-up (R2%). As a result, they cannot reflect true conditions when berm erosion occurs but the foreshore slope does not change. In other words, R2% and ξ will not change even though the berm eroded dramatically. Thus, we must combine berm conditions such as berm height (hB), berm platform length (LB), and berm ridge slope (Soff) to re-evaluate the berm’s contribution to reducing the erosion of the profiles.
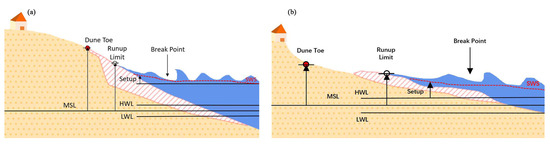
Figure 5.
Two conditions of berm erosion without foreshore slope change (a). Strong erosion with no nearshore sediment transport. (b) Shoreline totally retreats without nearshore slope change. Stripe area is volume loss after storm “Kompasu” compared with pre-storm. The red circle is dune toe, the white circle is wave run-up limit.
In this section, a new run-up relation was developed. It is based on hB, LB, and Soff using measurement data from Puqian Bay spanning from October 2021 to April 2022, including both measurement data and model results. In the development of this new relation, wave run-up elevation and non-dimensional parameters were employed. The significant offshore wave height was (R2%/H0) and expressed as a function of the Iribarren number corresponding to the berm, defined as ξB. It was determined that redefining the run-up using this new equation, which accounts for changes in the berm, is meaningful. A further explanation is provided in the subsequent section.
In Figure 6a, it can be observed that R2% is linearly related to ξ. This implies that as the nearshore slope becomes steeper or H/L decreases, the wave run-up elevation will be higher. Park [32] introduced a constant as a reduction factor to reflect the berm width and made a new run-up equation. Park made dimensionless berm width a constant, but he did not consider berm ridge height and seaward slope. We used measurement data and model results with data per month (Figure 6b) to demonstrate a new relationship between R2%/H and ξB. This is demonstrated in the following equation:
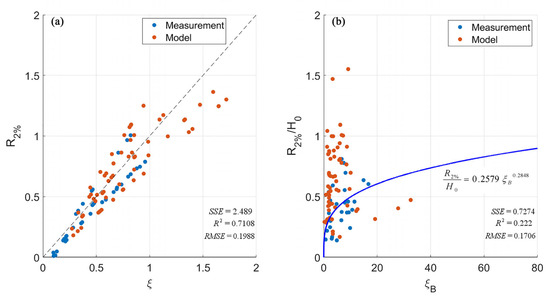
Figure 6.
(a) Relation between R2% and ξ in Stockdon model. (b) Relation between R2%/H0 and ξB in new model. Black dotted line in (a) with slope = 1. Blue line is the fitted curve with the equation in (b).
This new model shows that R2% is decreased when hB becomes higher or LB becomes wider, suggesting that the actual run-up peaks should be close to the berm ridge height and platform width. Run-up peaks tend to be underestimated by the S-model when the berm width is long and the platform is smooth with a low slope. This occurs because the equation fails to consider the location of the berm platform, resulting in a lower run-up limit that is distant from the berm ridge. Conversely, when the platform is not prominent or extended, the S-model may overestimate run-up peaks. The S-model neglects the berm ridge point, which acts as a hump that effectively reduces overtopping. The new model incorporates berm functionality, accounting for the berm ridge in reducing run-up peaks and the berm platform in damping run-up transport. In fact, the berm is a very important part of the profiles that can break waves and protect sand dunes. Our new model effectively considers changes in berm width and berm ridge and can more accurately reflect the interaction between the berm and dynamic elements.
5. Discussion: How to Improve Coast Resilience
The erosion range of the berms and dunes was limited by the width of the profile. Sparse coastal vegetation results in an increased length of the beach wind zone, which exacerbates wind force and wind-driven erosion. Furthermore, a low-slope backshore and increased berm width provide sufficient space for wave run-up and overtopping, extending the distance and depth of beach surface seepage and, consequently, increasing erosion range and depth. Based on our satellite image (Figure 7), the nine measured profiles in Puqian Bay can be classified into three kinds: (1) Dunes that were mostly bare (HK15 and ATHK17). (2) Dunes covered by shrubs, but sparsely (ATHK11, HK12, and ATHK19). (3) Dunes covered by windbreak trees on the landward side (ATHK12, HK16, ATHK18, and ATHK21). The bare dune profiles (HK15 and ATHK17) demonstrate a sharp drop in sediment that moves away from the embankment during storm waves. Sediment is lost on the beach surface; some of these dunes were accumulated by means of prior man-made sediment supply engineering. In other words, due to bare profiles lacking protection on the landward side, storm erosion caused a wider range to be influenced on the beach surface and an increased slope. Their volume is reduced compared to those with a green and fully protected profile. The difference was approximately 1–2 m in the vertical direction. In profiles covered by shrubs (ATHK11, HK12, and ATHK19), changes in the beach surface above the dune toe were relatively minor. The upper limit of the profile erosion was lower than that of bare beaches: approximately 0.5–1.0 m above the HWL, with a depth that was reduced by 0.5–1.0 m, indicating that the resilience of vegetation cover significantly reduces the range and depth of wave erosion during storms. In profiles protected by windbreak trees (ATHK12, HK16, ATHK18, and ATHK21), the front edge of the windbreak trees above the dune toe caused erosion leading to significant sediment loss on the beach surface. Some of these dunes were accumulated by means of prior man-made sediment supply engineering. In other words, due to bare profiles lacking protection on the landward side, storm erosion caused a wider range to be influenced on the beach surface and an increased slope. Their volume was reduced compared to those with a green and fully protected profile. Pits of about 1 m in depth formed during storms, but the volume decreased in the profile due to sharp waves and wind damping throughout the windbreak forest area. It is worth noting that the erosion pits caused by storms are difficult to recover throughout a long period of moderate waves because the wave overtopping and sediment movement caused by waves cannot easily pass over the dune toe to compensate for the lost volume. Hence, there is a significant difference between the protective effects and coastal resilience of bare beaches, grass-covered beaches, and windbreak forest profiles. Grass and other vegetation covering the coastal zone exhibited the most pronounced coast resilience effect, and reduced disasters compared to windbreak forests planted behind the dunes and bare beaches lacking protective measures.

Figure 7.
(a–i) are location of nine measurement profiles shown on MAP WORLD before storm “Kompasu”.
The berm in ATHK12 (Figure 8a,b) was covered by grass before the storm, which included small shrubs and some small trees. However, after the storm, both the ground cover and small shrubs disappeared, and the small trees were toppled. This highlights the formidable destructive force of the storm. In the case of the ATHK19 profile (Figure 8c,d), a distinct transformation is evident post-storm, with the complete disappearance of ground cover grass and leaving a bare beach. Additionally, the cutting depth at the front edge of the windbreak forest exceeded 1.5 m (approximately the height of an adult). The effective role of the windbreak forest is in preventing further inland erosion during storms and controlling the upper limit of beach erosion. The contribution of ground cover grass should not be underestimated, as it plays a significant role in enhancing coastal resilience. Thorough research on local tree species coupled with hydrodynamic analysis is essential in the context of coastal zone ecological restoration and resilience enhancement. Planting a suitable range and density of vegetation combinations on the beach berm and dune to create a diverse vertical ecological protection belt is a useful method to mitigate storm-induced erosion effectively and reduce threats to the beach profile.

Figure 8.
(a) Photo before storm in ATHK12; (b) photo after storm in ATHK12; (c) photo before storm in ATHK19; (d) photo after storm in ATHK19.
6. Conclusions
The evolution of beaches, including changes in the berm and backshore slope during storms and moderate wave conditions, is closely related to wave conditions and beach characteristics. This research is based on the measurement data of typical beach profiles before and after storm events, as well as on-field measurements obtained during moderate wave conditions. The recovery characteristics and the main factors affecting the recovery efficiency during storms were analyzed. The main conclusions are as follows:
- Supratidal erosion and intertidal accretion are induced by storm waves in the profile. The recovery efficiency of berm elevation exceeds that of the beach berm platform width, with the intertidal zone demonstrating the fastest overall recovery efficiency while that above the HWL is slower.
- The height of the berm ridge is shifted landward and increased during storm waves, while it is lowered and shifted seaward during moderate waves. This movement is governed by a periodic cycle aligned with the circulation of the storm–moderate waves.
- Under the influence of storms, the slopes on both sides of the berm ridge point change in opposite directions. However, during the accumulation of moderate waves, the slopes on both sides of the berm ridge gradually change in the opposite direction.
- The empirical wave run-up model of Stockdon neglects berm conditions, resulting in the underestimation of smooth and wide berm platforms and the overestimation of non-platform berms. The new model, which combines the berm ridge and platform width, reflects the dynamic interaction between waves and profiles. The new model modifies the elevation of the run-up peaks to align more closely with the berm ridge point.
The profile data in this study were obtained solely using RTK and the permeate function of the beach could not be assessed. The importance of understanding the role of permeability, particularly in the wave run-up area, which influences sediment transport in the dry–wet zone, cannot be overstated. Further investigations into the mechanisms of permeation and its effects on sediment transport with different diameters and gradings should be pursued. Precise field observation instruments, laboratory experiments, or numerical model tests need more attention.
Author Contributions
Conceptualization, Y.Z. (Yu Zhu) and Y.Z. (Yingtao Zhou) methodology, Y.Z. (Yingtao Zhou).; writing—original draft preparation, Y.Z. (Yingtao Zhou) and Y.J.; writing—review and editing, Y.Z. (Yu Zhu) and Y.J.; figure, Y.Z. (Yu Zhu); supervision, W.Z. and W.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by Hainan Provincial Natural Science Foundation of China (No. 423QN322); Hainan Provincial Natural Science Foundation of China (No. 421QN369); Fund of Key Laboratory of Marine Ecological Conservation and Restoration, Ministry of Natural Resources/Fujian Provincial Key Laboratory of Marine Ecological Conservation and Restoration (EPR2023009); Fund of Hainan Key Laboratory of Marine Geological Resources and Environment (22-HNHYDZZYHJKF028).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available upon request.
Acknowledgments
The authors are very much grateful to the three anonymous reviewers for their constructive comments that significantly improved the quality of this paper. We also thank Maoyuan Liu for his kind support in the conception figure drawing.
Conflicts of Interest
Author Yingtao Zhou was employed by the company Shanghai Urban Construction Design & Research Institute (Group) Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Smart, L.S.; Vukomanovic, J.; Sills, E.O.; Sanchez, G. Cultural ecosystem services caught in a ‘coastal squeeze’ between sea level rise and urban expansion. Glob. Environ. Chang. 2021, 66, 102209. [Google Scholar] [CrossRef]
- Rangel-Buitrago, N.; Williams, A.T.; Anfuso, G. Hard protection structures as a principal coastal erosion management strategy along the Caribbean coast of Colombia. A chronicle of pitfalls. Ocean Coast. Manag. 2017, 156, 58–75. [Google Scholar] [CrossRef]
- Shi, J.; Feng, X.; Toumi, R.; Zhang, C.; Hodges, K.I.; Tao, A.; Zhang, W.; Zheng, J. Global increase in tropical cyclone ocean surface waves. Nat. Commun. 2024, 15, 174. [Google Scholar] [CrossRef]
- Clifton, G.A.; Dafforn, K.A.; Bishop, M.J. The ecological benefits of adding topographic complexity to seawalls vary across estuarine gradients. Ecol. Eng. J. Ecotechnol. 2022, 182, 106735. [Google Scholar] [CrossRef]
- Zhou, Y.; Feng, X.; Liu, M.; Wang, W. Influence of Beach Erosion during Wave Action in Designed Artificial Sandy Beach Using XBeach Model: Profiles and Shoreline. J. Mar. Sci. Eng. 2023, 11, 984. [Google Scholar] [CrossRef]
- Peng, S.; Tang, C. Blending the analytic hierarchy process and fuzzy logical systems in scenic beauty assessment of check dams in streams. Water 2015, 7, 6983–6998. [Google Scholar] [CrossRef]
- Djuma, H.; Bruggeman, A.; Camera, C.; Eliades, M.; Kostarelos, K. The impact of a check dam on groundwater recharge and sedimentation in an ephemeral stream. Water 2017, 9, 813. [Google Scholar] [CrossRef]
- Kuang, C.; Ma, Y.; Han, X.; Pan, S.; Zhu, L. Experimental observation on beach evolution process with presence of artificial submerged sand bar and reef. J. Mar. Sci. Eng. 2020, 8, 1019. [Google Scholar] [CrossRef]
- Kuang, C.; Mao, X.; Gu, J.; Niu, H.; Ma, Y.; Yang, Y.; Qiu, R.; Zhang, J. Morphological processes of two artificial submerged shore-parallel sandbars for beach nourishment in a nearshore zone. Ocean Coast Manag. 2019, 179, 104870. [Google Scholar] [CrossRef]
- Koster, L. Humplike Nourishing of the Shoreface. A Study on More Efficient Nourishing of the Shoreface. 2006. Available online: https://repository.tudelft.nl/record/uuid:e354c6da-99bb-4419-8419-31654896027f (accessed on 9 April 2024).
- Dette, H.H.; Larson, M.; Murphy, J.; Newe, J.; Peters, K.; Reniers AJ, H.M.; Steetzel, H. Application of prototype flume tests for beach nourishment assessment. Coast. Eng. 2002, 47, 137–177. [Google Scholar] [CrossRef]
- Žilinskas, G.; Pupienis, D.; Jarmalavičius, D. Possibilities of regeneration of Palanga coastal zone. J. Environ. Eng. Landsc. Manag. 2010, 18, 92–101. [Google Scholar] [CrossRef]
- Pan, Y.; Yin, S.; Chen, Y.; Yang, Y.; Xu, C.; Xu, Z. An experimental study on the evolution of a submerged berm under the effects of regular waves in low-energy conditions. Coast. Eng. 2022, 176, 104169. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, C.; Zhao, S.; Qi, H.; Cai, F.; Zheng, J. Equilibrium configurations of sandy-muddy transitional beaches on South China coasts: Role of waves in formation of sand-mud transition boundary. Coast. Eng. 2024, 187, 104401. [Google Scholar] [CrossRef]
- Zhu, J.; Shi, F.; Cai, F.; Wang, Q.; Qi, H.; Zhang, C.; Liu, J.; Liu, G.; Lei, G. Influences of beach berm height on beach response to storms: A numerical study. Appl. Ocean Res. 2022, 121, 103090. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, C.; Song, J.; Chi, S.; Zhao, S.; Qi, H.; Shi, J. Tide-modulated wave characteristics and breaking regimes in the intertidal zone of a dissipative beach. Ocean Eng. 2022, 266, 113055. [Google Scholar] [CrossRef]
- You, Z.; Laine, R.; Hanslow, D.J.; Baldock, T.; Wiecek, D. Field measurements of beach-dune dynamic profiles to assess erosion hazard on the coast of NSW, Australia. Coast. Eng. Proc. 2014, 34, 23. [Google Scholar] [CrossRef]
- Chen, J.M. Numerical simulation of tidal current and sediment movement in Ruyi island of Haikou bay. Water 2018, 15, 2516. [Google Scholar]
- Duo, E.; Sanuy, M.; Jiménez, J.A.; Ciavola, P. How good are symmetric triangular synthetic storms to represent real events for coastal hazard modelling. Coast. Eng. 2020, 159, 103728. [Google Scholar] [CrossRef]
- Van Ormondt, M.; Nelson, T.R.; Hapke, C.J.; Roelvink, D. Morphodynamic modelling of the wilderness breach, Fire Island, New York. Part I: Model set-up and validation. Coast. Eng. 2020, 157, 103621. [Google Scholar] [CrossRef]
- Bennett, W.G.; Karunarathna, H.; Reeve, D.E.; Mori, N. Computational modelling of morphodynamic response of a macro-tidal beach to future climate variabilities. Mar. Geol. 2019, 415, 105960. [Google Scholar] [CrossRef]
- Didier, D.; Baudry, J.; Bernatchez, P.; Dumont, D.; Sadegh, M.; Bismuth, E.; Bandet, M.; Dugas, S.; Sévigny, C. Multihazard simulation for coastal flood mapping: Bathtub versus numerical modelling in an open estuary, Eastern Canada. J. Flood Risk Manag. 2019, 12 (Suppl. S1), e12505. [Google Scholar] [CrossRef]
- Galappatti, G.; Vreugdenhil, C.B. A depth-integrated model for suspended sediment transport. J. Hydraul. Res. 1985, 23, 359–377. [Google Scholar] [CrossRef]
- Roelvink, D.; Reniers, A.; Van Dongeren, A.; van Thiel De Vries, J.; McCall, R.; Lescinski, J. Modelling storm impacts on beaches, dunes and barrier islands. Coast. Eng. 2009, 56, 1133–1152. [Google Scholar] [CrossRef]
- Lu, Y.; Li, S.; Zuo, L.; Liu, H.; Roelvink, J. Advances in sediment transport under combined action of waves and currents. Int. J. Sediment Res. 2015, 30, 351–360. [Google Scholar] [CrossRef]
- Stockdon, H.F.; Sallenger, A.H., Jr.; Holman, R.A.; Howd, P.A. A simple model for the spatially-variable coastal response to hurricanes. Mar. Geol. 2007, 238, 1–20. [Google Scholar] [CrossRef]
- Cao, Y.G.; Bai, Y.C.; Chen, Y.Z.; Ouyang, Y.Z.; Feng, Y.; Jiang, L.; Liao, S.; Xiao, Z. Analysis of siltation trend and mechanism in the eastern sea area of Haikou Bay, Hainan, China. Oceanol. Limnol. Sin. 2022, 53, 906–916. [Google Scholar]
- Chen, L.H.; Lin, G.Y.; Gong, W.P. The impact of artificial island construction on the headland vortex and bed level change in headland-bay coastal systems: A case study in Puqian Bay, Hainan Island. Haiyang Xuebao 2019, 41, 41–50. [Google Scholar]
- Li, Y.; Zhang, C.; Dai, W.; Chen, D.; Sui, T.; Xie, M.; Chen, S. Laboratory investigation on morphology response of submerged artificial sandbar and its impact on beach evolution under storm wave condition. Mar. Geol. 2022, 443, 106668. [Google Scholar] [CrossRef]
- Battjes, J.A. Surf similarity. Coast. Eng. 1974, 1974, 466–480. [Google Scholar]
- Stockdon, H.F.; Holman, R.A.; Howd, P.A.; Sallenger, J.A. Empirical parameterization of setup, swash, and runup. Coast. Eng. 2006, 53, 573–588. [Google Scholar] [CrossRef]
- Park, H.; Cox, D.T.; Petroff, C.M. An empirical solution for tsunami run-up on compound slopes. Nat. Hazards 2015, 76, 1727–1743. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).