Seepage and Stability Analysis of Earth Dams’ Downstream Slopes, Considering Hysteresis in Soil–Water Characteristic Curves under Reservoir Water Level Fluctuations
Abstract
1. Introduction
2. Materials and Methods
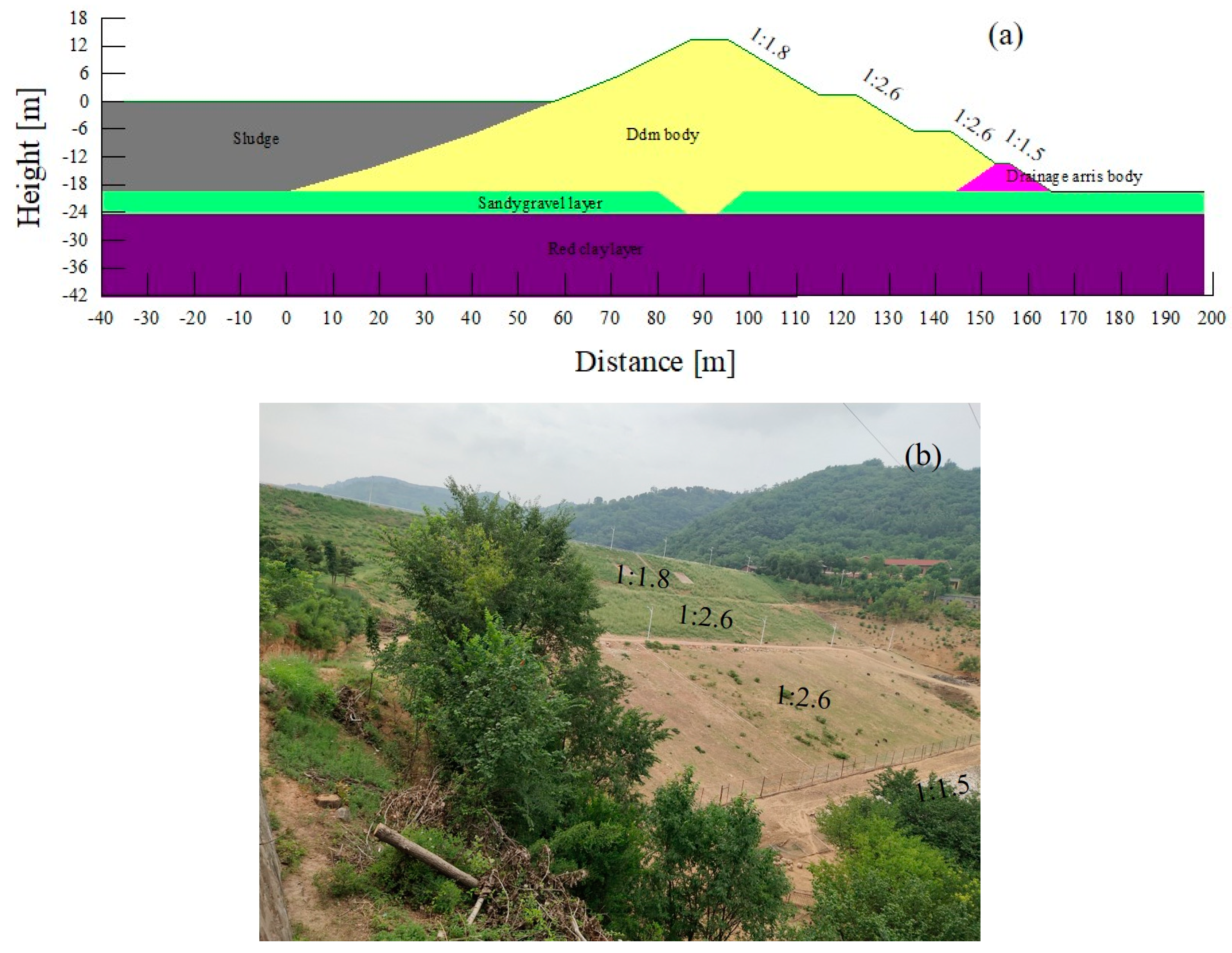
2.1. Project Profile
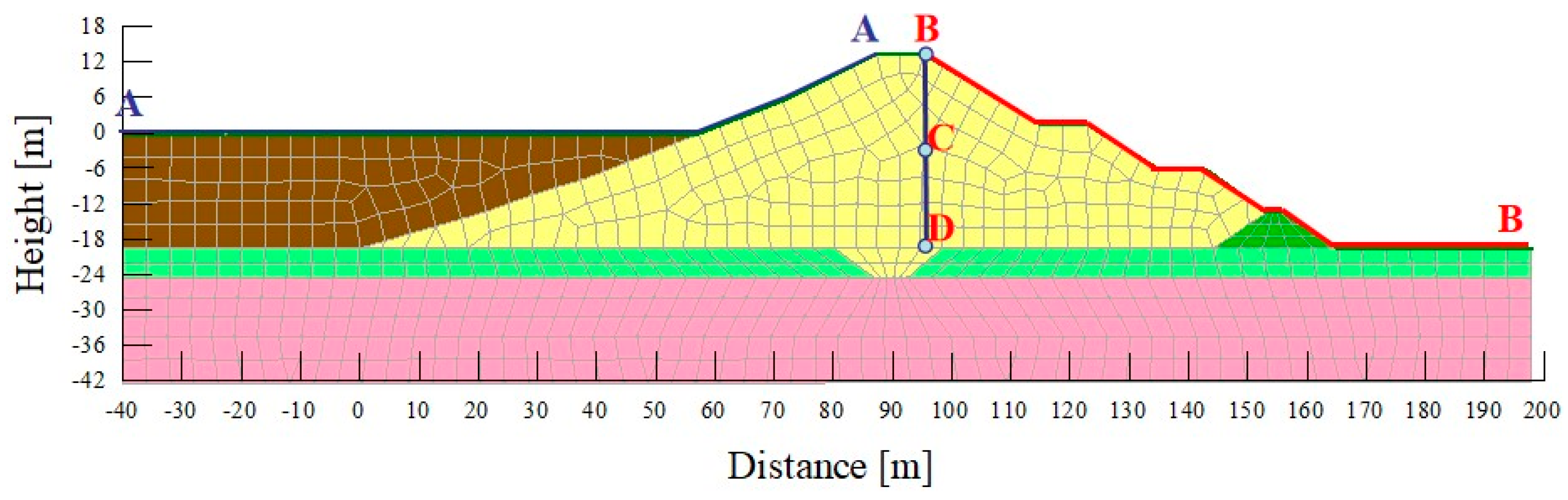
2.2. Analysis Scheme and Calculation Theory
2.3. Material Properties
3. Results
3.1. Downstream Slope Stability under Water Level Fluctuations
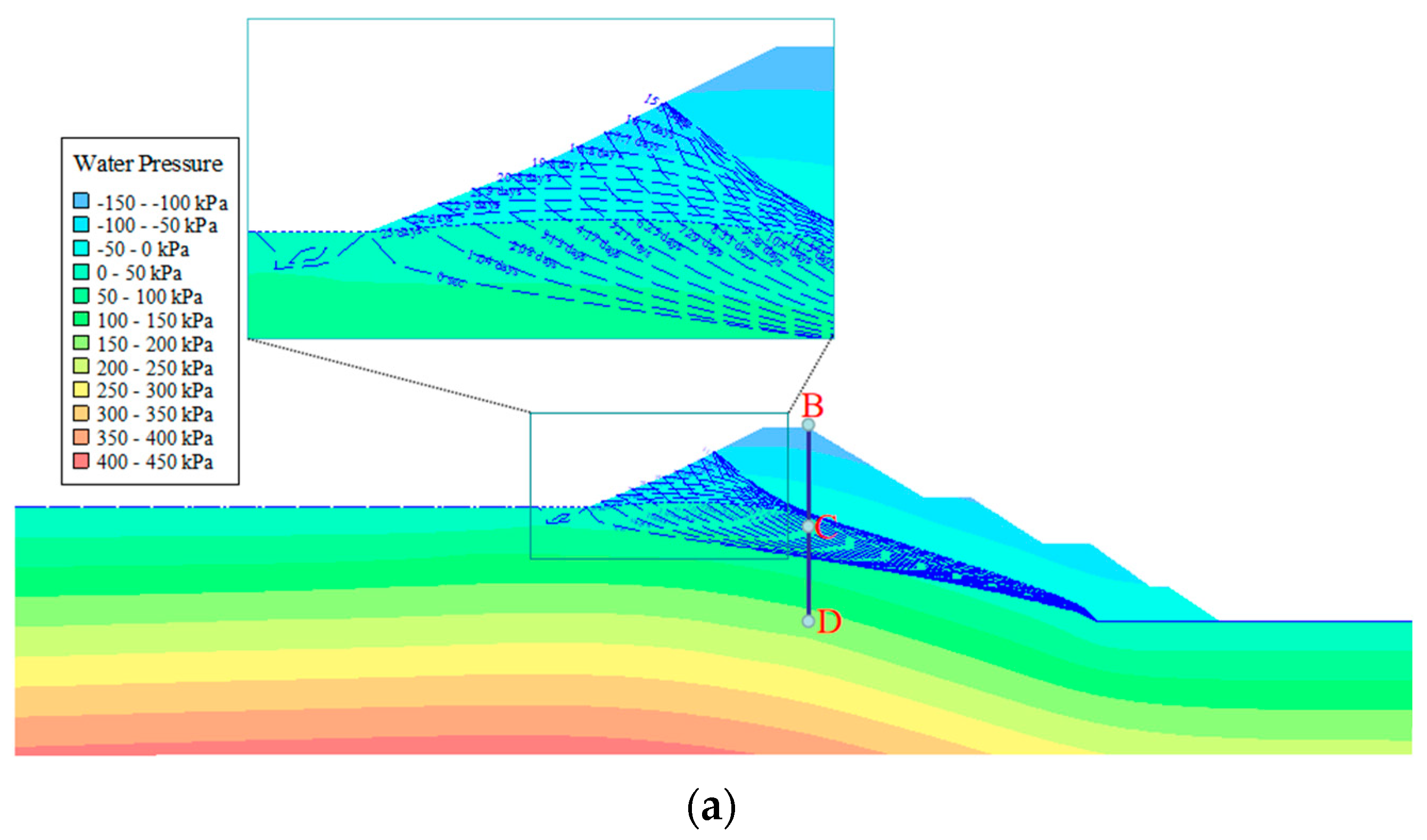
3.1.1. Seepage under Water Level Fluctuations
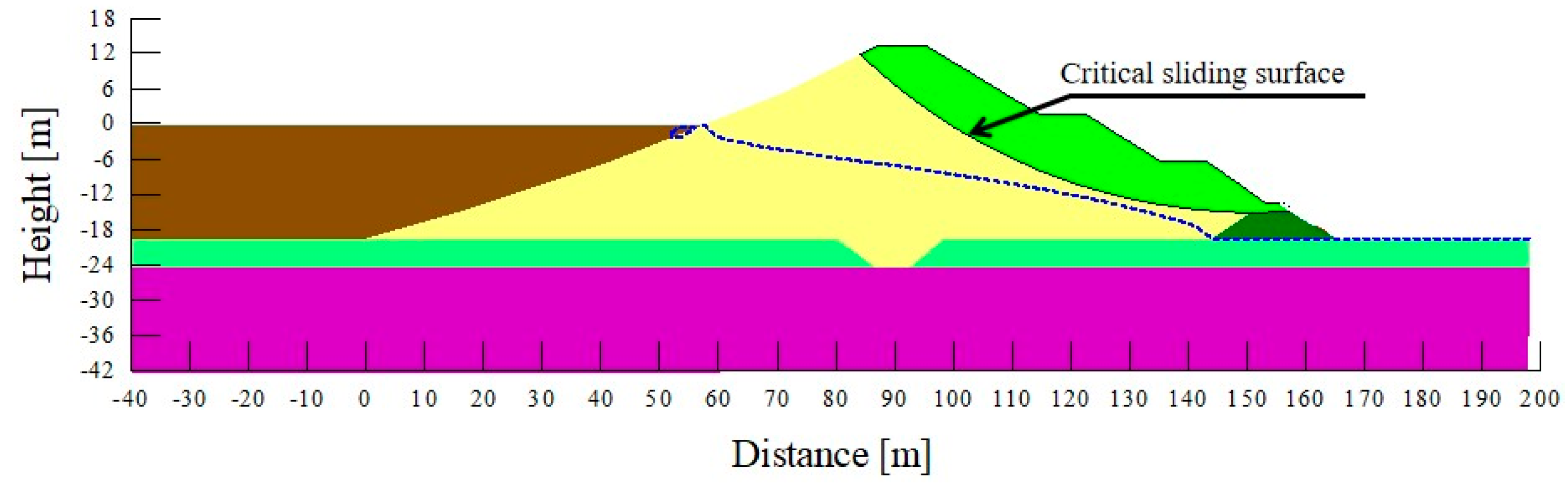
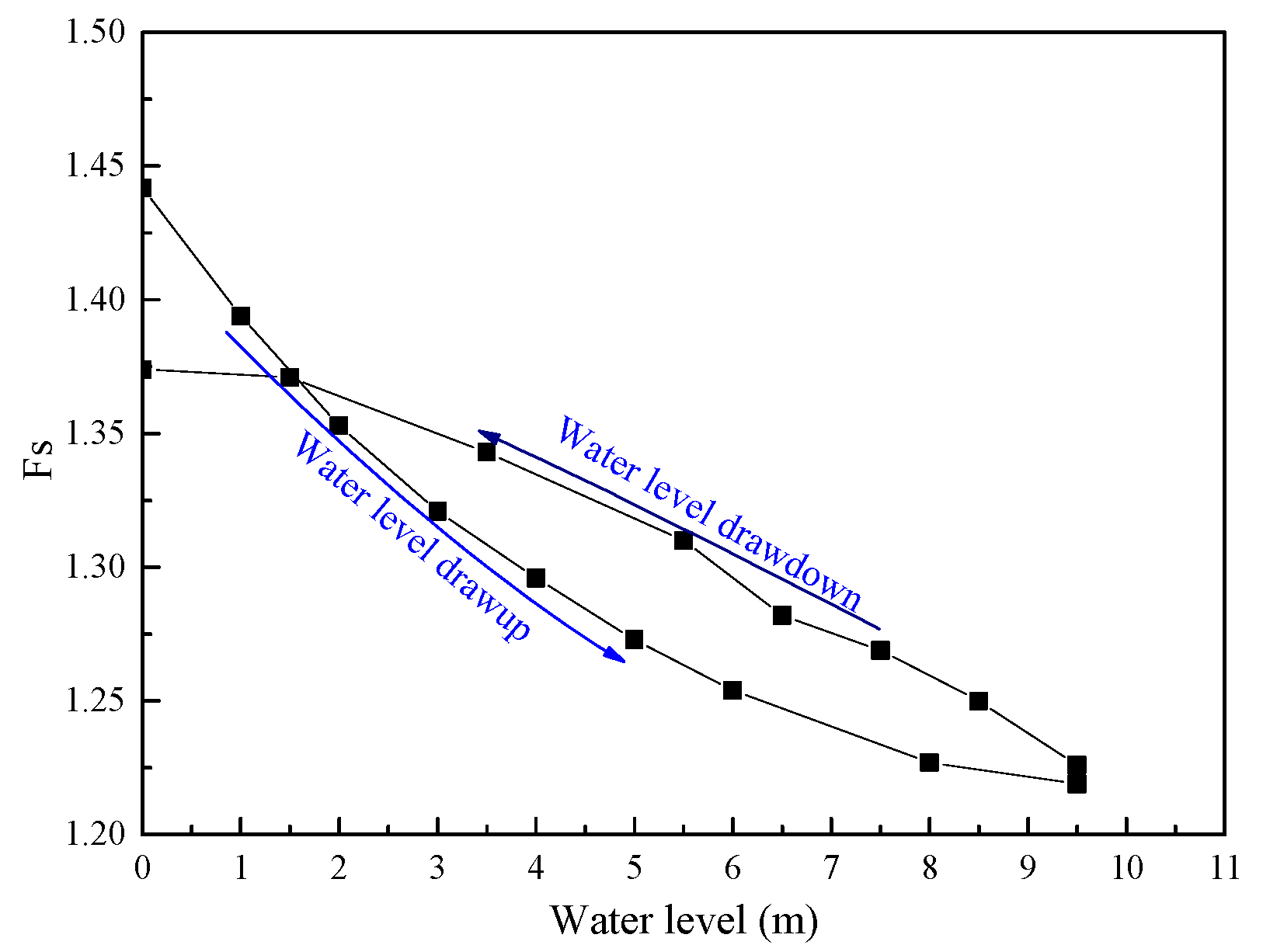
3.1.2. Fs of the Downstream Slope under Water Level Fluctuations
3.2. Influence of the Water Level Fluctuation Rate on the Downstream Slope Stability
3.2.1. Influence of the Water Level Fluctuation Rate on Seepage
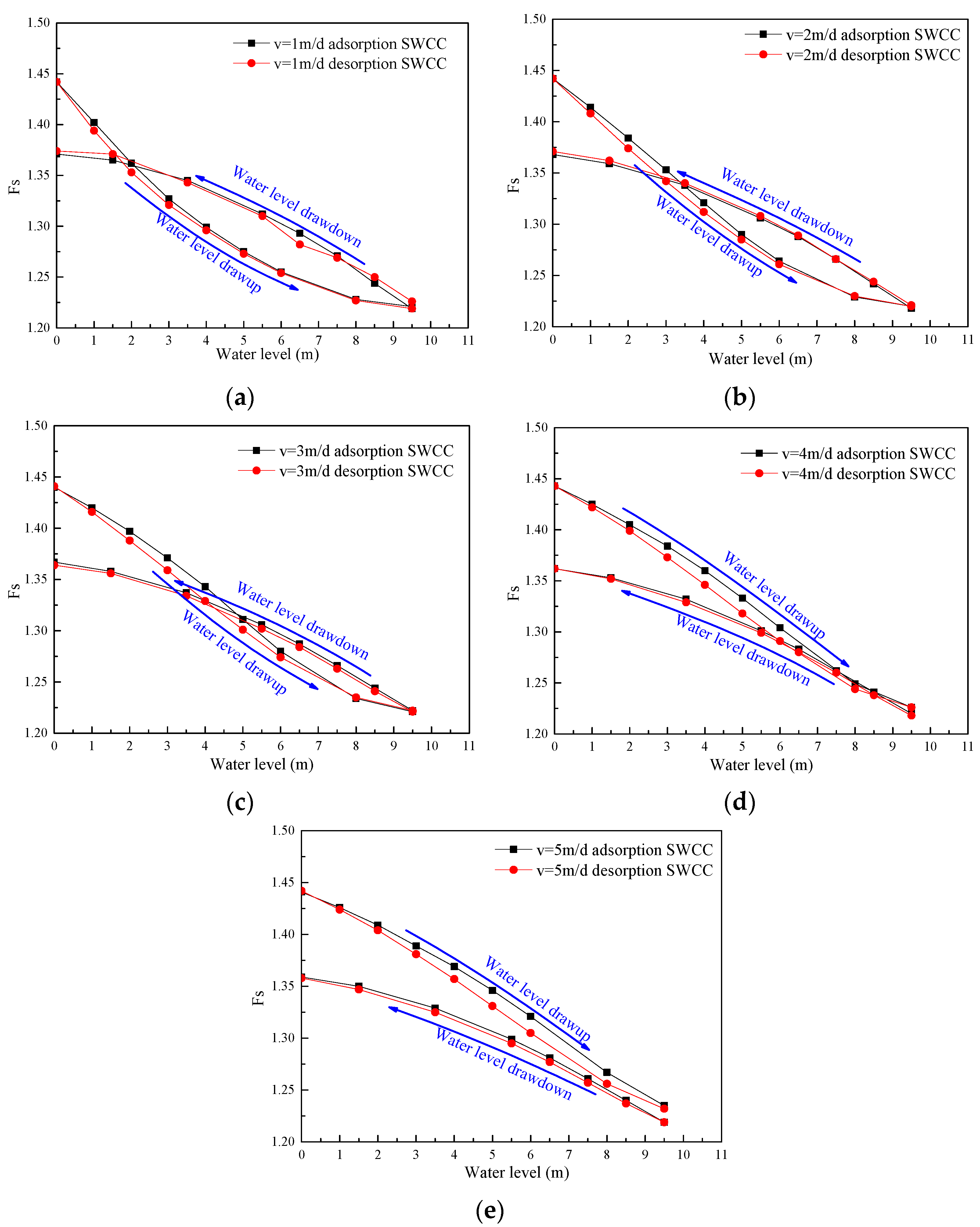
3.2.2. Influence of the Water Level Fluctuation Rate on the Fs of the Downstream Slope
3.3. Influence of SWCC Hysteresis on the Stability of the Downstream Slope
3.3.1. Influence of SWCC Hysteresis on the Seepage
3.3.2. Influence of SWCC Hysteresis on the Fs of the Downstream Slope
4. Discussion
5. Conclusions
- With the fluctuation in the reservoir water level, the phreatic line inside the dam shows a profile of a horn shape, while the variation curves of the PWP of the representative points form a hysteresis loop. The deeper the representative point inside the dam, the larger the hysteresis loop.
- As the water level variation rate increases, the PWP hysteresis loop becomes smaller. When the water level rises, the pore water pressures of the desorption SWCC are greater than those of the adsorption SWCC. However, the difference in the pore water pressures is negligible when the water level is falling.
- The variation curve of the Fs of the downstream slope also forms a hysteresis loop with the water level fluctuation. Within the Fs hysteresis loop, the Fs value of the falling water level is larger than that for a rising water level, which is converse outside the hysteresis loop. The hysteresis loop of Fs becomes smaller with the increase in the water level variation rate. When the water level fluctuation rate increases to 4 m/d, the Fs variation curves of the rising and falling water levels are tangent; the Fs of the rising water level is always greater than that of the falling water level.
- The SWCC hysteresis mainly influences the slope’s Fs as the water level rises, but it has little effect on the Fs as the water level falls. As the water level rises, the Fs value from the desorption SWCC is smaller than that from the adsorption SWCC.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, S.; Ren, X.; Zhang, J.; Wang, H.; Wang, J.; Zhu, W. Seepage, deformation, and stability analysis of sandy and clay slopes with different permeability anisotropy characteristics affected by reservoir water level fluctuations. Water 2020, 12, 201. [Google Scholar] [CrossRef]
- Chen, M.L.; Qi, S.C.; Lv, P.F.; Yang, X.G.; Zhou, J.W. Hydraulic response and stability of a reservoir slope with landslide potential under the combined effect of rainfall and water level fluctuation. Environ. Earth Sci. 2021, 80, 25. [Google Scholar] [CrossRef]
- Liu, D.; Lin, T.; Gao, J.; Xue, B.; Yang, J.; Chen, C.; Zhang, W.; Sun, W. Study on the influence of water level on earth dam reinforced by cut-off wall: A case study in Wujing reservoir. Water 2022, 15, 140. [Google Scholar] [CrossRef]
- Liu, G.; Zhou, Z.; Xu, S.; Mi, W. Hysteresis of dam slope safety factor under water level fluctuations based on the LEM coupled with FEM Method. CMES-Comp. Model. Eng. 2022, 133, 351–375. [Google Scholar] [CrossRef]
- Huang, F.; Luo, X.; Liu, W. Stability analysis of hydrodynamic pressure landslides with different permeability coefficients affected by reservoir water level fluctuations and rainstorms. Water 2017, 9, 450. [Google Scholar] [CrossRef]
- Xiong, X.; Shi, Z.; Xiong, Y.; Peng, M.; Ma, X.; Zhang, F. Unsaturated slope stability around the Three Gorges Reservoir under various combinations of rainfall and water level fluctuation. Eng. Geol. 2019, 261, 105231. [Google Scholar] [CrossRef]
- Mao, J.Z.; Guo, J.; Fu, Y.; Zhang, W.P.; Ding, Y.N. Effects of rapid water-level fluctuations on the stability of an unsaturated reservoir bank slope. Adv. Civ. Eng. 2020, 2020, 6661593. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z.; Xue, S.; Wang, R.; Xiao, M. Stability analysis of a typical landslide mass in the Three Gorges Reservoir under varying reservoir water levels. Environ. Earth Sci. 2020, 79, 42. [Google Scholar] [CrossRef]
- Su, Z.; Chen, G.; Meng, Y. Study on seepage characteristics and stability of core dam under the combined action of the variation of reservoir water level and rainfall. Geotech. Geol. Eng. 2021, 39, 193–211. [Google Scholar] [CrossRef]
- Li, D.; Li, L.; Xu, L.; Li, C.; Meng, K.; Gao, Y.; Yang, Z. Stability analysis of upstream and downstream dam slopes with water level drawdown using response surface function. Geotech. Geol. Eng. 2022, 40, 3107–3123. [Google Scholar] [CrossRef]
- Fredlund, D.; Morgenstern, N.; Widger, R. The shear strength of unsaturated soils. Can. Geotech. J. 1978, 15, 313–321. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, J.; Chai, H. Influence of water level fluctuation on phreatic line in silty soil model slope. Eng. Geol. 2010, 113, 90–98. [Google Scholar] [CrossRef]
- Xia, M.; Ren, G.; Zhu, S.; Ma, X. Relationship between landslide stability and reservoir water level variation. Bull. Eng. Geol. Environ. 2015, 74, 909–917. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, L. Bayesian back analysis of unsaturated hydraulic parameters for rainfall-induced slope failure: A review. Earth-Sci. Rev. 2024, 251, 104714. [Google Scholar] [CrossRef]
- Gharehdaghi, M.; Shahbodagh, B.; Khalili, N. Pore pressure parameters for unsaturated soils. Comput. Geotech. 2024, 172, 106441. [Google Scholar] [CrossRef]
- Ye, Z.; Liu, X.; Dong, Q.; Wang, E.; Sun, H. Hydro-damage properties of red-bed mudstone failures induced by nonlinear seepage and diffusion effect. Water 2022, 14, 351. [Google Scholar] [CrossRef]
- Sun, H.; Liu, X.; Ye, Z.; Wang, E. A new proposed method for observing fluid in rock fractures using enhanced x-ray images from digital radiography. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 10. [Google Scholar] [CrossRef]
- Duncan, J.M.; Wright, S.G. The accuracy of equilibrium methods of slope stability analysis. Eng. Geol. 1980, 16, 5–17. [Google Scholar] [CrossRef]
- Song, K.; Yan, E.; Zhang, G.; Lu, S.; Yi, Q. Effect of hydraulic properties of soil and fluctuation velocity of reservoir water on landslide stability. Environ. Earth Sci. 2015, 74, 5319–5329. [Google Scholar] [CrossRef]
- Zhou, C.; Cao, Y.; Yin, K.; Intrieri, E.; Catani, F.; Wu, L. Characteristic comparison of seepage-driven and buoyancy-driven landslides in Three Gorges Reservoir area, China. Eng. Geol. 2022, 301, 106590. [Google Scholar] [CrossRef]
- Miao, F.; Wu, Y.; Li, L.; Tang, H.; Li, Y. Centrifuge model test on the retrogressive landslide subjected to reservoir water level fluctuation. Eng. Geol. 2018, 245, 169–179. [Google Scholar] [CrossRef]
- Li, S.; Xu, Q.; Tang, M.; Li, H.; Yang, H.; Wei, Y. Centrifuge modeling and the analysis of ancient landslides subjected to reservoir water level fluctuation. Sustainability 2020, 12, 2092. [Google Scholar] [CrossRef]
- Fang, K.; An, P.; Tang, H.; Tu, J.; Jia, S.; Miao, M.; Dong, A. Application of a multi-smartphone measurement system in slope model tests. Eng. Geol. 2021, 295, 106424. [Google Scholar] [CrossRef]
- Wang, Y.; Shen, D.; Chen, J.; Pei, L.; Li, Y.; Lu, X.; Zhang, L. Research and application of a smart monitoring system to monitor the deformation of a dam and a slope. Adv. Civ. Eng. 2020, 2020, 9709417. [Google Scholar] [CrossRef]
- Adamo, N.; Al-Ansari, N.; Sissakian, V.; Laue, J.; Knutsson, S. Geophysical methods and their applications in dam safety monitoring. J. Earth Sci. Geotech. Eng. 2021, 11, 291–345. [Google Scholar] [CrossRef]
- Vazquez-Ontiveros, J.R.; Martinez-Felix, C.A.; Vazquez-Becerra, G.E.; Gaxiola-Camacho, J.R.; Melgarejo-Morales, A.; Padilla-Velazco, J. Monitoring of local deformations and reservoir water level for a gravity type dam based on GPS observations. Adv. Space Res. 2022, 69, 319–330. [Google Scholar] [CrossRef]
- Wang, L.; Wu, C.; Gu, X.; Liu, H.; Mei, G.; Zhang, W. Probabilistic stability analysis of earth dam slope under transient seepage using multivariate adaptive regression splines. Bull. Eng. Geol. Environ. 2020, 79, 2763–2775. [Google Scholar] [CrossRef]
- Kumar, V.; Samui, P.; Himanshu, N.; Burman, A. Reliability-based slope stability analysis of Durgawati Earthen Dam considering steady and transient state seepage conditions using MARS and RVM. Indian Geotech. J. 2019, 49, 650–666. [Google Scholar] [CrossRef]
- Zewdu, A. Modeling the slope of embankment dam during static and dynamic stability analysis: A case study of Koga dam, Ethiopia. Model. Earth Syst. Environ. 2020, 6, 1963–1979. [Google Scholar] [CrossRef]
- Hailu, M.B. Modeling assessment of seepage and slope stability of dam under static and dynamic conditions of Grindeho Dam in Ethiopia. Earth Syst. Environ. 2021, 7, 2231–2239. [Google Scholar]
- Pakmanesh, M.; Jahromi, S.H.M.; Khosrojerdi, A.; Darvishi, H.H.; Babazadeh, H. Experimental and numerical study of upstream slope stability in an earth dam reservoir under rapid drawdown conditions. Prog. Comput. Fluid Dyn. 2021, 21, 248–260. [Google Scholar] [CrossRef]
- Izumi, A.; Sawada, Y.; Hori, T.; Maki, R. Centrifuge modelling of small earth dams subjected to the combined effects of rainfall and earthquakes. Soil Dyn. Earthq. Eng. 2021, 151, 106963. [Google Scholar] [CrossRef]
- Chen, J.; Cai, X.; Lale, E.; Yang, J.; Cusatis, G. Centrifuge modeling testing and multiscale analysis of cemented sand and gravel (CSG) dams. Constr. Build. Mater. 2019, 223, 605–615. [Google Scholar] [CrossRef]
- Jia, C.; Chen, F.; Zhang, Q.; Gu, J.; Hu, J.; Chen, H.; Cheng, W. Centrifuge modeling and numerical analysis of reservoir bank landslides triggered by a fast two-step drop in water level. Bull. Eng. Geol. Environ. 2023, 82, 465. [Google Scholar] [CrossRef]
- Miao, F.; Wu, Y.; Török, Á.; Li, L.; Xue, Y. Centrifugal model test on a riverine landslide in the Three Gorges Reservoir induced by rainfall and water level fluctuation. Geosci. Front. 2022, 13, 101378. [Google Scholar] [CrossRef]
- Harada, Y.; Goto, H.; Sawada, S. Initiation process of tension cracks in soil embankment on liquefied sandy ground investigated from centrifuge model test. Soil Dyn. Earthq. Eng. 2022, 161, 107444. [Google Scholar] [CrossRef]
- Lee, Y.H.; Yamakawa, S.; Tobita, T.; Hong, H.K.; Song, H.S.; Kim, J.J.; Lee, D.W. Centrifugal model study of seepage and seismic behavior in a homogeneous reservoir dam with parapet. Appl. Sci. 2023, 13, 6347. [Google Scholar] [CrossRef]
- Abdoun, T.; Bennett, V.; Desrosiers, T.; Simm, J.; Barendse, M. Asset management and safety assessment of levees and earthen dams through comprehensive real-time field monitoring. Geotech. Geol. Eng. 2013, 31, 833–843. [Google Scholar] [CrossRef]
- Wang, Q.; Gao, Y.; Gong, T.; Liu, T.; Sui, Z.; Fan, J.; Wang, Z. Dam surface deformation monitoring and analysis based on PS-InSAR technology: A case study of xiaolangdi reservoir dam in China. Water 2023, 15, 3298. [Google Scholar] [CrossRef]
- Su, H.; Hu, J.; Yang, M. Dam seepage monitoring based on distributed optical fiber temperature system. IEEE Sens. J. 2014, 15, 9–13. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]





| Materials | Kh m/s | Kr | Desorption SWCC | ||||
|---|---|---|---|---|---|---|---|
| a kPa | m | n | θs | θr | |||
| Dam body | 5.41 × 10−6 | 0.22 | 869.55 | 0.51 | 2.03 | 0.520 | 0.213 |
| Drainage arris | 6.11 × 10−4 | 1.00 | 1266.77 | 0.90 | 10.40 | 0.250 | 0.153 |
| Sludge | 1.50 × 10−8 | 0.93 | 6576.95 | 0.15 | 1.17 | 0.446 | 0.002 |
| Sandy gravel | 6.00 × 10−4 | 1.00 | 1265.80 | 0.92 | 10.40 | 0.251 | 0.153 |
| Red clay | 1.00 × 10−8 | 1.01 | 6576.95 | 0.65 | 2.77 | 0.430 | 0.201 |
| Materials | Kh m/s | Kr | Adsorption SWCC | ||||
|---|---|---|---|---|---|---|---|
| a′ kPa | m′ | n′ | θs | θr | |||
| Dam body | 5.41 × 10−6 | 0.22 | 510.00 | 0.64 | 2.77 | 0.430 | 0.213 |
| Materials | γ kN/m3 | γs kN/m3 | C′ kPa | Φ′ ° | Φb ° |
|---|---|---|---|---|---|
| Sludge | 17.0 | 18.20 | 17.22 | 18.21 | 9.20 |
| Dam body material | 18.87 | 19.61 | 14.15 | 21.00 | 10.75 |
| Drainage arris | 21.62 | 22.50 | 0.00 | 35.21 | 17.52 |
| Sandy gravel layer | 21.62 | 22.10 | 0.00 | 33.00 | 17.22 |
| Red clay layer | 21.55 | 21.30 | 58.21 | 16.53 | 8.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Zhou, Z.; Zhang, J.; Jiang, G.; Mi, W. Seepage and Stability Analysis of Earth Dams’ Downstream Slopes, Considering Hysteresis in Soil–Water Characteristic Curves under Reservoir Water Level Fluctuations. Water 2024, 16, 1811. https://doi.org/10.3390/w16131811
Liu G, Zhou Z, Zhang J, Jiang G, Mi W. Seepage and Stability Analysis of Earth Dams’ Downstream Slopes, Considering Hysteresis in Soil–Water Characteristic Curves under Reservoir Water Level Fluctuations. Water. 2024; 16(13):1811. https://doi.org/10.3390/w16131811
Chicago/Turabian StyleLiu, Guodong, Zhijun Zhou, Jiarong Zhang, Guan Jiang, and Wenjing Mi. 2024. "Seepage and Stability Analysis of Earth Dams’ Downstream Slopes, Considering Hysteresis in Soil–Water Characteristic Curves under Reservoir Water Level Fluctuations" Water 16, no. 13: 1811. https://doi.org/10.3390/w16131811
APA StyleLiu, G., Zhou, Z., Zhang, J., Jiang, G., & Mi, W. (2024). Seepage and Stability Analysis of Earth Dams’ Downstream Slopes, Considering Hysteresis in Soil–Water Characteristic Curves under Reservoir Water Level Fluctuations. Water, 16(13), 1811. https://doi.org/10.3390/w16131811






