Stability Analysis of Breakwater Armor Blocks Based on Deep Learning
Abstract
1. Introduction
- It is used to assess the ability of breakwaters to resist wave forces. This ensures structural integrity over time.
- It ensures the breakwaters are safe and capable of protecting coastal regions from waves. This reduces the risk of flooding and erosion.
- It helps in the optimal design of breakwaters, which permits experts to prefer suitable materials and construction methods.
2. Literature Review
3. Research Model
3.1. Analysis of Influencing Factors on the Stability of Breakwater Armor Blocks
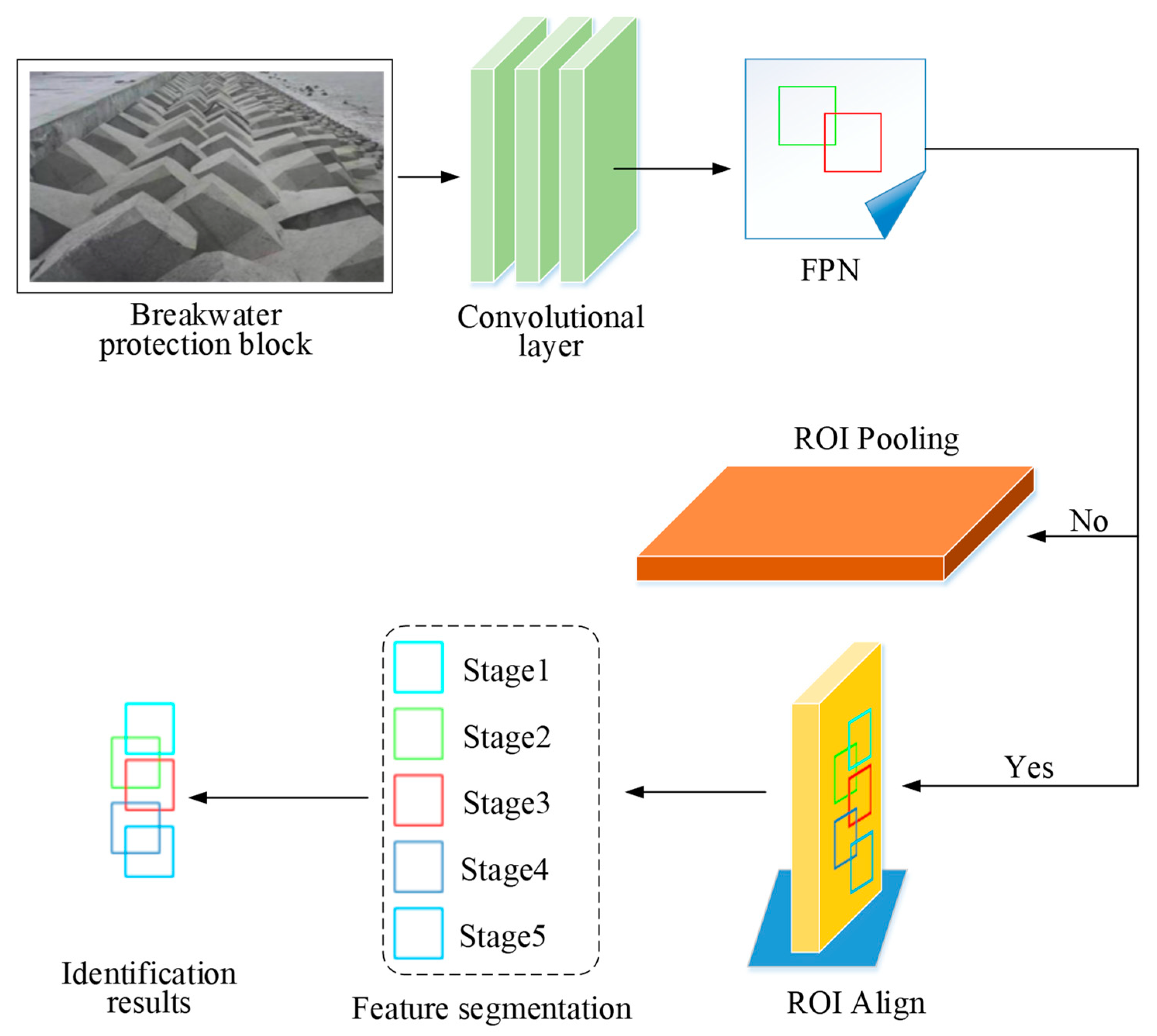
3.2. Identification and Analysis of Face Protection Block Posture Using Mask R-CNN
3.3. Wave Prediction and Analysis of Breakwaters Based on Bidirectional Encoder Representations from Transformer and BiLSTM
3.4. Experimental Design and Evaluation
4. Results and Discussion
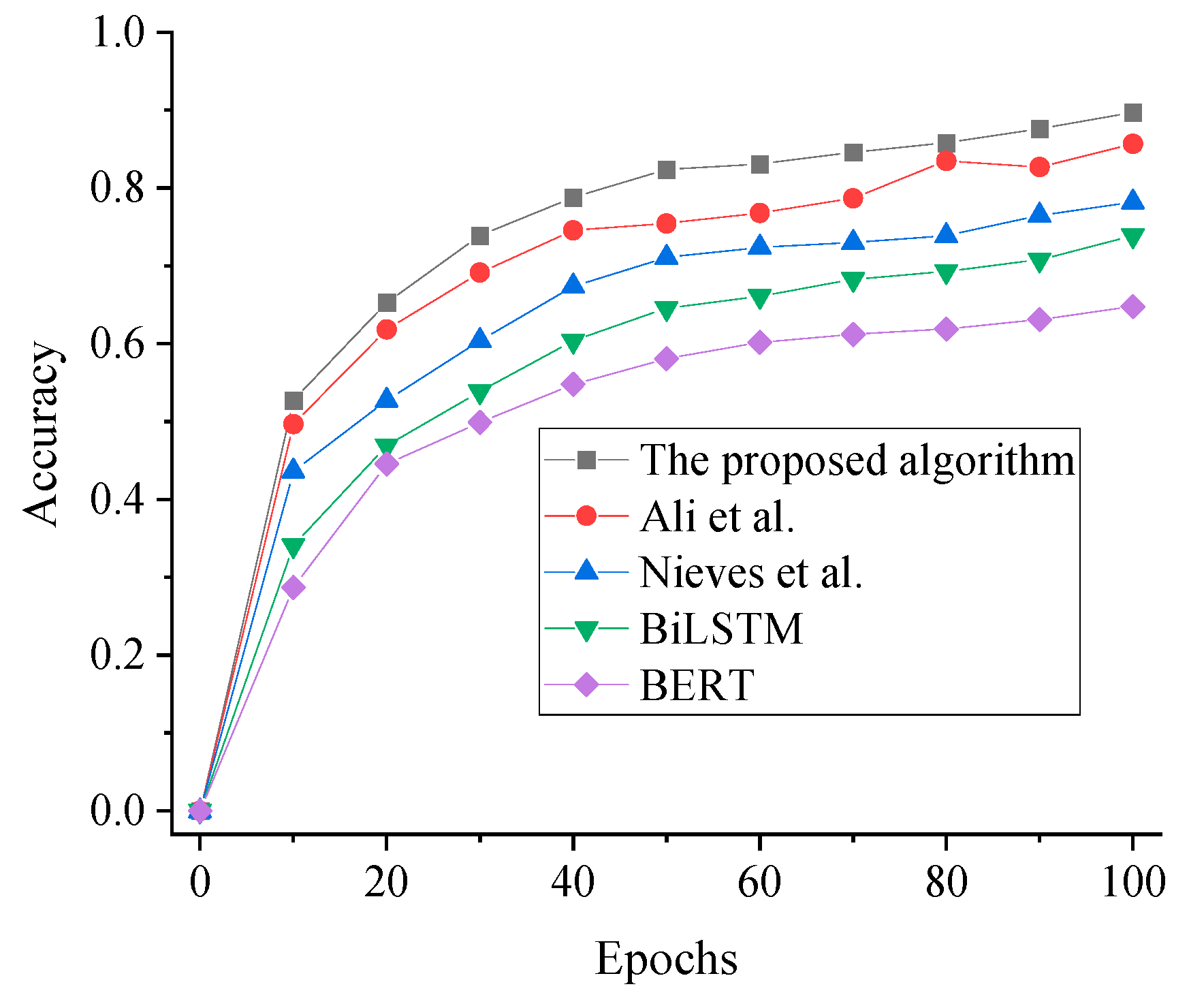
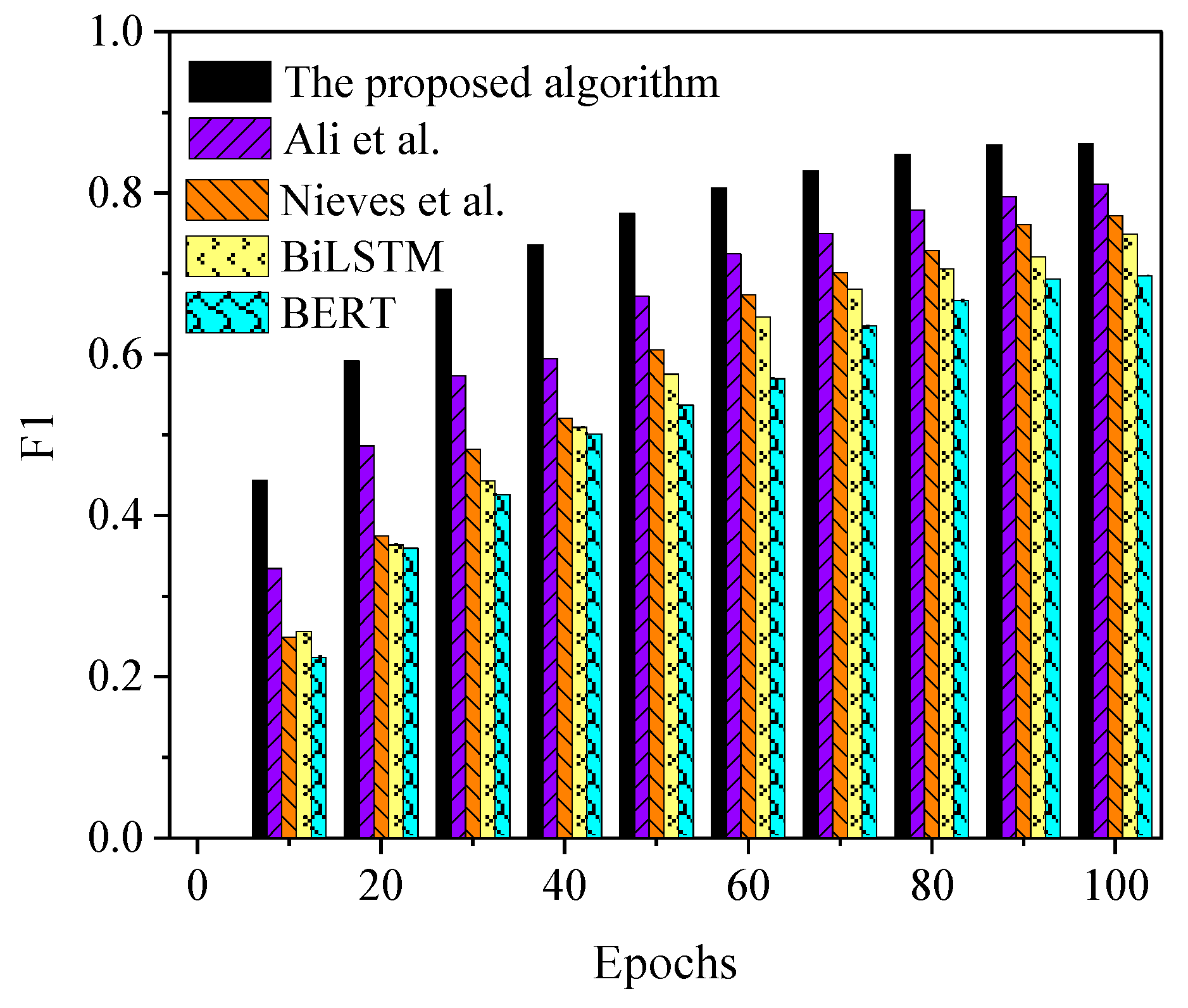
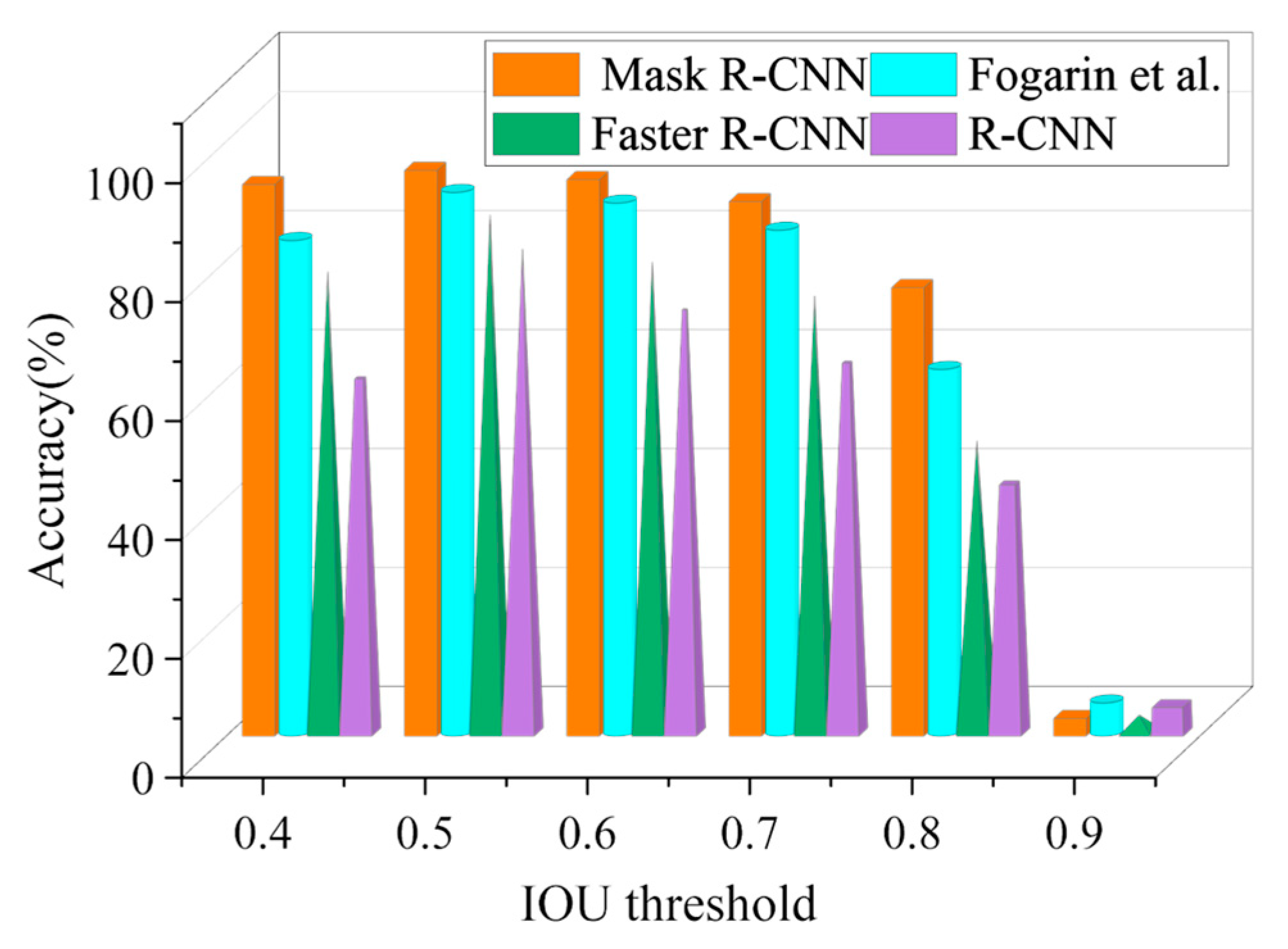
4.1. Performance Analysis
4.2. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cantasano, N.; Boccalaro, F.; Ietto, F. Assessing of detached breakwaters and beach nourishment environmental impacts in Italy: A review. Environ. Monit. Assess. 2023, 195, 127. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhao, X.; Geng, J.; Göteman, M.; Tao, L. Wave power extraction and coastal protection by a periodic array of oscillating buoys embedded in a breakwater. Renew. Energy 2022, 190, 434–456. [Google Scholar] [CrossRef]
- Repousis, E.; Roupas, I.; Memos, C. Wave Transmission over Rubble-Mound Submerged Breakwaters. J. Mar. Sci. Eng. 2023, 11, 1346. [Google Scholar] [CrossRef]
- Han, X.; Dong, S. Wave Force on the Crown Wall of Rubble Mound Breakwaters at Intermediate Depths. J. Ocean Univ. China 2023, 22, 53–64. [Google Scholar] [CrossRef]
- Le Xuan, T.; Le Manh, H.; Ba, H.T.; Van, D.D.; Vu, H.T.D.; Wright, D.; Bui, V.H.; Anh, D.T. Wave energy dissipation through a hollow triangle breakwater on the coastal Mekong Delta. Ocean Eng. 2022, 245, 110419. [Google Scholar] [CrossRef]
- Hudson, J. Waterway Port Coast. Ocean Eng. 1959, 271, 610–659. [Google Scholar]
- Thompson, D.M.; Shuttler, R.M. Riprap Design for Wind Wave Attack, A Laboratory Study in Random Waves; HR Wallingford Report EX 707; HR Wallingford: Wallingford, UK, 1975. [Google Scholar]
- Ahrens, J.P. Large Wave Tank Tests of Riprap Stability CERC; Technical Memorandum No. 51; DTIC: Fort Belvoir, VA, USA, 1975. [Google Scholar]
- Vidal, C.; Medina, R.; Lomónaco, P. Wave height parameter for damage description of rubble-mound breakwaters. Coast. Eng. 2006, 53, 711–722. [Google Scholar] [CrossRef]
- Tsai, C.-P.; Chen, Y.-C.; Ko, C.-H. Prediction of Bay-Shaped Shorelines between Detached Breakwaters with Various Gap Spacings. Sustainability 2023, 15, 6218. [Google Scholar] [CrossRef]
- Liu, H.; Liu, T.; Zhang, Z.; Sangaiah, A.K.; Yang, B.; Li, Y. Arhpe: Asymmetric relation-aware representation learning for head pose estimation in industrial human–computer interaction. IEEE Trans. Ind. Inform. 2022, 18, 7107–7117. [Google Scholar] [CrossRef]
- Dong, Y.; Liu, J.; Yan, W. Dynamic hand gesture recognition based on signals from specialized data glove and deep learning algorithms. IEEE Trans. Instrum. Meas. 2021, 70, 2509014. [Google Scholar] [CrossRef]
- Liu, W.; Bao, Q.; Sun, Y.; Mei, T. Recent advances of monocular 2d and 3d human pose estimation: A deep learning perspective. ACM Comput. Surv. 2022, 55, 1–41. [Google Scholar] [CrossRef]
- van Gent, M.R.; van den Bogar, H.F.; Pozueta, B.; Medina, J.R. Neural network modelling of wave overtopping at coastal structures. Coast. Eng. 2007, 54, 586–593. [Google Scholar] [CrossRef]
- Romano, A.; Bellotti, G.; Briganti, R.; Franco, L. Uncertainties in the physical modelling of the wave overtopping over a rubble mound breakwater: The role of the seeding number and of the test duration. Coast. Eng. 2015, 103, 15–21. [Google Scholar] [CrossRef]
- Musumeci, R.E.; Molti Santi, D.; Foti, E.; Battiato, S.; Farinella, G.M. 3-D monitoring of rubble mound breakwater damages. Measurement 2018, 117, 347–364. [Google Scholar] [CrossRef]
- Vieira, F.; Taveira-Pinto, F.; Rosa-Santos, P. Single-layer cube armored breakwaters: Critical review and technical challenges. Ocean Eng. 2020, 216, 108042. [Google Scholar] [CrossRef]
- Stagnitti, M.; Lara, J.L.; Musumeci, R.E.; Foti, E. Numerical modeling of wave overtopping of damaged and upgraded rubble-mound breakwaters. Ocean Eng. 2023, 280, 114798. [Google Scholar] [CrossRef]
- Stagnitti, M.; Musumeci, R.; Foti, E. Surface roughness measurement for the assessment of damage dynamics of existing and upgraded cube-armored breakwaters. Coast. Eng. 2023, 179, 104226. [Google Scholar] [CrossRef]
- Galiatsatou, P.; Makris, C.; Prinos, P. Optimized reliability based upgrading of rubble mound breakwaters in a changing climate. J. Mar. Sci. Eng. 2018, 6, 92. [Google Scholar] [CrossRef]
- Campos, Á.; Molina-Sanchez, R.; Castillo, C. Damage in rubble mound breakwaters. Part II: Review of the definition, parameterization, and measurement of damage. J. Mar. Sci. Eng. 2020, 8, 306. [Google Scholar] [CrossRef]
- Sujantoko; Armono, H.D.; Djatmiko, E.B.; Putra, R.D. Stability Analysis of Concrete Block Anchor on Steep-Slope Floating Breakwater. Fluids 2022, 7, 259. [Google Scholar] [CrossRef]
- Zhao, E.; Mu, L.; Hu, Z.; Wang, X.; Sun, J.; Zhang, Z. Physical and Numerical Investigations on Wave Run-Up and Dissipation under Breakwater with Fence Revetment. J. Mar. Sci. Eng. 2021, 9, 1355. [Google Scholar] [CrossRef]
- Hasan, M.K.; Rahman, M.A.; Womera, S.A. Experimental Study on the Stability of Concrete Block Revetment for High Waves Propagating over Submerged Geotube Breakwater. Int. J. Coast. Offshore Environ. Eng. 2022, 7, 15–22. [Google Scholar]
- Saha, S.; Changdar, S.; De, S. Prediction of the stability number of conventional rubble-mound breakwaters using machine learning algorithms. J. Ocean Eng. Sci. 2022; in press. [Google Scholar] [CrossRef]
- Van der Meer, J.W. Rock Slopes and Gravel Beaches under Wave Attack. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1988. [Google Scholar]
- Saha, S.; De, S. Damage Level Estimation of Rubble-Mound Breakwaters Using Deep Artificial Neural Network. In Proceedings of the International Conference on Mathematics and Computing, Pilani, India, 6–8 January 2023; Springer Nature: Singapore, 2023; pp. 57–68. [Google Scholar]
- Saha, S.; De, S.; Changdar, S. An Application of Machine Learning Algorithms on the Prediction of the Damage Level of Rubble-Mound Breakwaters. J. Offshore Mech. Arct. Eng. 2024, 146, 011202. [Google Scholar] [CrossRef]
- Nieves, V.; Radin, C.; Camps-Valls, G. Predicting regional coastal sea level changes with machine learning. Sci. Rep. 2021, 11, 7650. [Google Scholar] [CrossRef] [PubMed]
- Calkoen, F.; Luijendijk, A.; Rivero, C.R.; Kras, E.; Baart, F. Traditional vs. machine-learning methods for forecasting sandy shoreline evolution using historic satellite-derived shorelines. Remote Sens. 2021, 13, 934. [Google Scholar] [CrossRef]
- Fogarin, S.; Zanetti, M.; Barco, M.K.D.; Zennaro, F.; Furlan, E.; Torresan, S.; Pham, H.V.; Critto, A. Combining remote sensing analysis with machine learning to evaluate short-term coastal evolution trend in the shoreline of Venice. Sci. Total. Environ. 2023, 859, 160293. [Google Scholar] [CrossRef] [PubMed]
- Ali, S.I.; Lalji, S.M.; Awan, Z.; Qasim, M.; Alshahrani, T.; Khan, F.; Ullah, S.; Ashraf, A. Prediction of asphaltene stability in crude oils using machine learning algorithms. Chemom. Intell. Lab. Syst. 2023, 235, 104784. [Google Scholar] [CrossRef]
- Le Xuan, T.; Ba, H.T.; Thanh, V.Q.; Wright, D.P.; Tanim, A.H.; Anh, D.T. Evaluation of coastal protection strategies and proposing multiple lines of defense under climate change in the Mekong Delta for sustainable shoreline protection. Ocean Coast. Manag. 2022, 228, 106301. [Google Scholar] [CrossRef]
- Wang, G.; Ge, L.; Yu, T.; Zhang, Y.; Chen, S. Experimental Study on the Stability and Wave Force of a Breakwater Transition under Multiangle Oblique Waves. J. Mar. Sci. Eng. 2023, 11, 631. [Google Scholar] [CrossRef]
- Dang, B.-L.; Nguyen-Xuan, H.; Wahab, M.A. An effective approach for VARANS-VOF modelling interactions of wave and perforated breakwater using gradient boosting decision tree algorithm. Ocean Eng. 2023, 268, 113398. [Google Scholar] [CrossRef]
- Salauddin, M.; O’Sullivan, J.J.; Abolfathi, S.; Peng, Z.; Dong, S.; Pearson, J.M. New insights in the probability distributions of wave-by-wave overtopping volumes at vertical breakwaters. Sci. Rep. 2022, 12, 16228. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Zheng, Z.; Zhang, Q.; Jin, P.; Wang, L.; Ning, D. Wave attenuation and amplification by an abreast pair of floating parabolic breakwaters. Energy 2023, 271, 127077. [Google Scholar] [CrossRef]
- Wiener, G.F.; Teixeira, P.R.F.; Didier, E. Numerical Evaluation of Optimal Sizes of Wells Turbine and Chamber of a Cluster of Oscillating Water Columns Integrated into a Breakwater on the Southern Brazilian Coast. J. Waterw. Port Coast. Ocean Eng. 2022, 148, 04022009. [Google Scholar] [CrossRef]
- He, K.; Ye, J. Physical modeling of the dynamics of a revetment breakwater built on reclaimed coral calcareous sand foundation in the South China Sea—Tsunami wave. Bull. Eng. Geol. Environ. 2021, 80, 3315–3330. [Google Scholar] [CrossRef]
- Ghasemi, A.; Amirabadi, R.; Kamalian, U.R.; Mazyak, A.R. Numerical modeling investigation of perforated geometry of caisson breakwater under irregular waves by considering porous media. Ocean Eng. 2023, 269, 113558. [Google Scholar] [CrossRef]
- Barman, K.K.; Bora, S.N. Elastic bottom effects on ocean water wave scattering by a composite caisson-type breakwater placed upon a rock foundation in a two-layer fluid. Int. J. Appl. Mech. 2021, 13, 2150114. [Google Scholar] [CrossRef]
- Brancasi, A.; Leone, E.; Francone, A.; Scaravaglione, G.; Tomasicchio, G.R. On Formulae for Wave Transmission at Submerged and Low-Crested Breakwaters. J. Mar. Sci. Eng. 2022, 10, 1986. [Google Scholar] [CrossRef]
- Martins, J.C.; Fragassa, C.; Goulart, M.M.; dos Santos, E.D.; Isoldi, L.A.; Gomes, M.d.N.; Rocha, L.A.O. Constructal design of an overtopping wave energy converter incorporated in a breakwater. J. Mar. Sci. Eng. 2022, 10, 471. [Google Scholar] [CrossRef]
- Madjidi, H.; Laroussi, T. Approximate MLE based automatic bilateral censoring CFAR ship detection for complex scenes of log-normal sea clutter in SAR imagery. Digit. Signal Process. 2023, 136, 103972. [Google Scholar] [CrossRef]
- Peng, J.; Zhao, Y.; Zhang, D.; Li, F.; Sangaiah, A.K. DSAFF-Net: A Backbone Network Based on Mask R-CNN for Small Object Detection. Comput. Mater. Contin. 2023, 74, 3405–3419. [Google Scholar] [CrossRef]
- Gao, L.; Wang, S.; Chen, S.; Zhao, X.; Chen, H. Identification and segmentation technology of complex armour blocks of rubble mound breakwater based on Mask R-CNN. J. Hohai Univ. Nat. Sci. 2022, 50, 121–126. [Google Scholar]
- Bello, R.-W.; Mohamed, A.S.A.; Talib, A.Z. Contour extraction of individual cattle from an image using enhanced mask R-CNN instance segmentation method. IEEE Access 2021, 9, 56984–57000. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Z.; Feng, L.; Lin, K.-Y.; Liu, P. Development of technology opportunity analysis based on technology landscape by extending technology elements with BERT and TRIZ. Technol. Forecast. Soc. Chang. 2023, 191, 122481. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Miyamoto, H.; Oishi, T. Using Simple LSTM Models to Evaluate Effects of a River Restoration on Groundwater in Kushiro Wetland, Hokkaido, Japan. Water 2023, 15, 1115. [Google Scholar] [CrossRef]
- Hosseinzadeh, S.; Etemad-Shahidi, A.; Koosheh, A. Prediction of mean wave overtopping at simple sloped breakwaters using kernel-based methods. J. Hydroinform. 2021, 23, 1030–1049. [Google Scholar] [CrossRef]
- Lee, Y.-S.; Park, W.-H. Diagnosis of depressive disorder model on facial expression based on fast R-CNN. Diagnostics 2022, 12, 317. [Google Scholar] [CrossRef]
- Zaman, K.; Sun, Z.; Shah, S.M.; Shoaib, M.; Pei, L.; Hussain, A. Driver emotions recognition based on improved faster R-CNN and neural architectural search network. Symmetry 2022, 14, 687. [Google Scholar] [CrossRef]
- Hu, G.; Wang, T.; Wan, M.; Bao, W.; Zeng, W. UAV remote sensing monitoring of pine forest diseases based on improved Mask R-CNN. Int. J. Remote Sens. 2022, 43, 1274–1305. [Google Scholar] [CrossRef]
- Tao, P.; Ma, H.; Li, C.; Liu, L. Intelligent grid load forecasting based on BERT network model in low-carbon economy. Front. Energy Res. 2023, 11, 1197024. [Google Scholar] [CrossRef]
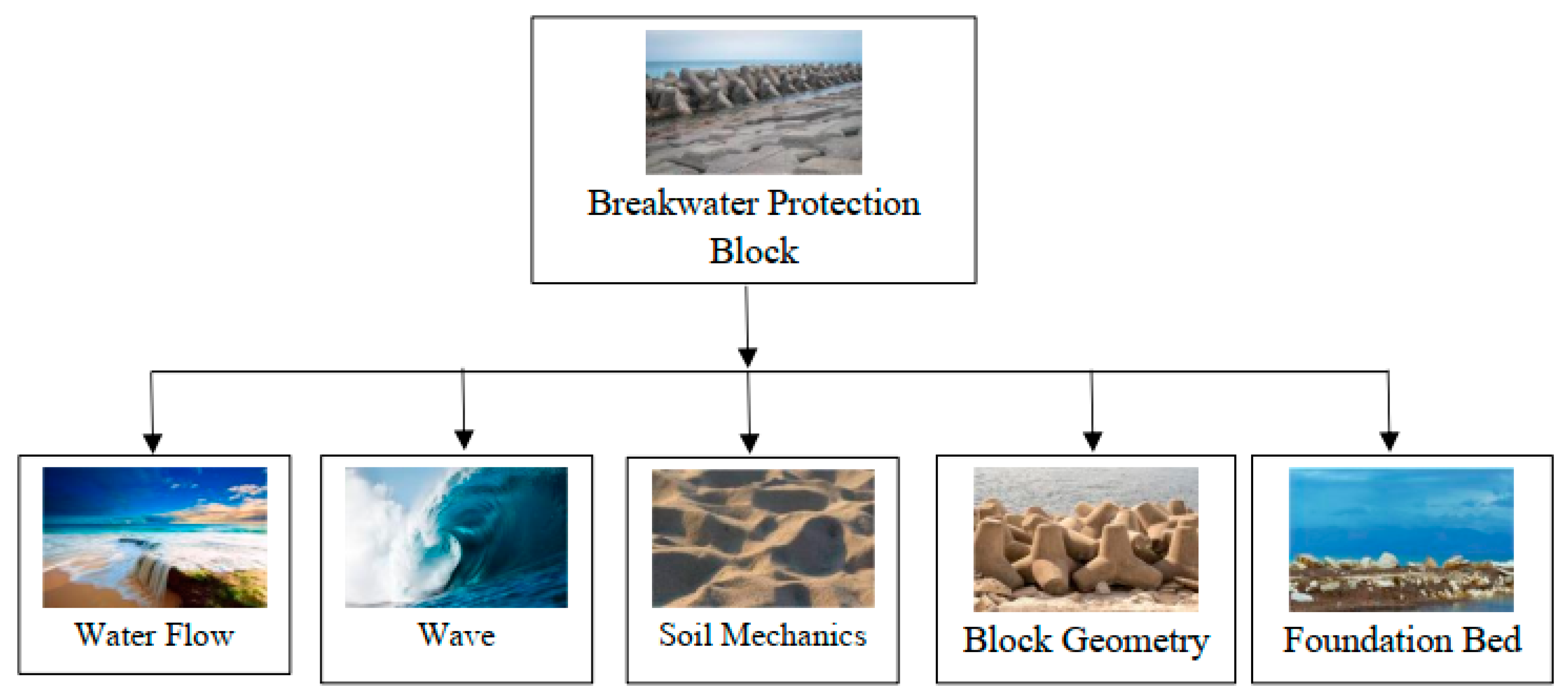

| Influence Factor | Description | Influence Mode |
|---|---|---|
| Wave characteristics | Wave height, period, incident angle, and spectrum characteristics | Affect the force and displacement of the block |
| Water flow characteristics | Velocity, direction, scouring, vortex formation | Affect the stability and failure of the block |
| Soil mechanical properties | Strength, shear parameters, pore water pressure, type, and composition | Affect the shear strength and bearing capacity of soil |
| Geometric characteristics of block | Geometry, size, arrangement, block spacing and connection | Affect block stability and interaction between blocks |
| Characteristics of foundation bed | Bed hardness, bed stability, bed deformability, settlement, and erosion. The armor blocks are not placed directly on the foundation bed. Instead, intermediary layers like filter layers or bedding materials are typically incorporated between the foundation bed and the armor blocks. | Affect block support and displacement |
| Condition | Waterline (z/Dn) | Wave Height (m) | Stability Coefficient | Number of Collisions | Maximum Impact Velocity (m/s) |
|---|---|---|---|---|---|
| W 1-1 | −2 | 0.50 | 1.563 | 0.517 | 0.214 |
| W 1-2 | −2 | 0.55 | 1.719 | 0.556 | 0.231 |
| W 1-3 | −2 | 0.60 | 1.875 | 0.583 | 0.245 |
| W 1-4 | −2 | 0.65 | 2.031 | 0.635 | 0.253 |
| W 1-5 | −2 | 0.70 | 2.188 | 0.657 | 0.260 |
| W 1-6 | −2 | 0.75 | 2.344 | 0.678 | 0.271 |
| W 1-7 | −2 | 0.80 | 2.500 | 0.712 | 0.284 |
| W 1-8 | −2 | 0.85 | 2.656 | 0.734 | 0.288 |
| W 1-9 | −2 | 0.90 | 2.813 | 0.764 | 0.295 |
| W 1-10 | 0 | 0.50 | 1.563 | 0.421 | 0.254 |
| W 1-11 | 0 | 0.55 | 1.719 | 0.435 | 0.283 |
| W 1-12 | 0 | 0.60 | 1.875 | 0.471 | 0.312 |
| W 1-13 | 0 | 0.65 | 2.031 | 0.493 | 0.334 |
| W 1-14 | 0 | 0.70 | 2.188 | 0.514 | 0.349 |
| W 1-15 | 0 | 0.75 | 2.344 | 0.529 | 0.353 |
| W 1-16 | 0 | 0.80 | 2.500 | 0.546 | 0.367 |
| W 1-17 | 0 | 0.85 | 2.656 | 0.563 | 0.371 |
| W 1-18 | 0 | 0.90 | 2.813 | 0.578 | 0.380 |
| W 1-19 | +2 | 0.50 | 1.563 | 0.254 | 0.183 |
| W 1-20 | +2 | 0.55 | 1.719 | 0.261 | 0.194 |
| W 1-21 | +2 | 0.60 | 1.875 | 0.293 | 0.205 |
| W 1-22 | +2 | 0.65 | 2.031 | 0.322 | 0.217 |
| W 1-23 | +2 | 0.70 | 2.188 | 0.343 | 0.224 |
| W 1-24 | +2 | 0.75 | 2.344 | 0.356 | 0.235 |
| W 1-25 | +2 | 0.80 | 2.500 | 0.370 | 0.256 |
| W 1-26 | +2 | 0.85 | 2.656 | 0.394 | 0.263 |
| W 1-27 | +2 | 0.90 | 2.813 | 0.413 | 0.270 |
| Model | ||
|---|---|---|
| Software | Operating system | Windows 10 |
| Image processing library | OpenCV 4.2.0 | |
| Python version | Python 3.7 | |
| Deep learning framework | TensorFlow 2.3.0 | |
| Hardware | CPU | Intel core i5-7400 CPU @ 3.0 GHz (Santa Clara, CA, USA) |
| Memory | 512 GB SSD | |
| Internal storage | Kingston ddr4 2400 MHz 8 G (Santa Clara, CA, USA) | |
| GPU | Nvidia GeForce GTX 1080 Ti (Santa Clara, CA, USA) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, P.; Bai, X.; Liu, H.; Zhao, Y. Stability Analysis of Breakwater Armor Blocks Based on Deep Learning. Water 2024, 16, 1689. https://doi.org/10.3390/w16121689
Zhu P, Bai X, Liu H, Zhao Y. Stability Analysis of Breakwater Armor Blocks Based on Deep Learning. Water. 2024; 16(12):1689. https://doi.org/10.3390/w16121689
Chicago/Turabian StyleZhu, Pengrui, Xin Bai, Hongbiao Liu, and Yibo Zhao. 2024. "Stability Analysis of Breakwater Armor Blocks Based on Deep Learning" Water 16, no. 12: 1689. https://doi.org/10.3390/w16121689
APA StyleZhu, P., Bai, X., Liu, H., & Zhao, Y. (2024). Stability Analysis of Breakwater Armor Blocks Based on Deep Learning. Water, 16(12), 1689. https://doi.org/10.3390/w16121689