Seepage–Deformation Coupling Analysis of a Core Wall Rockfill Dam Subject to Rapid Fluctuations in the Reservoir Water Level
Abstract
1. Introduction
2. Methodology
2.1. Unsaturated Soil Seepage Equation
- (1)
- Initial condition
- (2)
- Boundary condition
2.2. Constitutive Equation of Unsaturated Soil
2.3. Seepage and Stress Coupling Governing Equation
3. Numerical Model of a CWRD
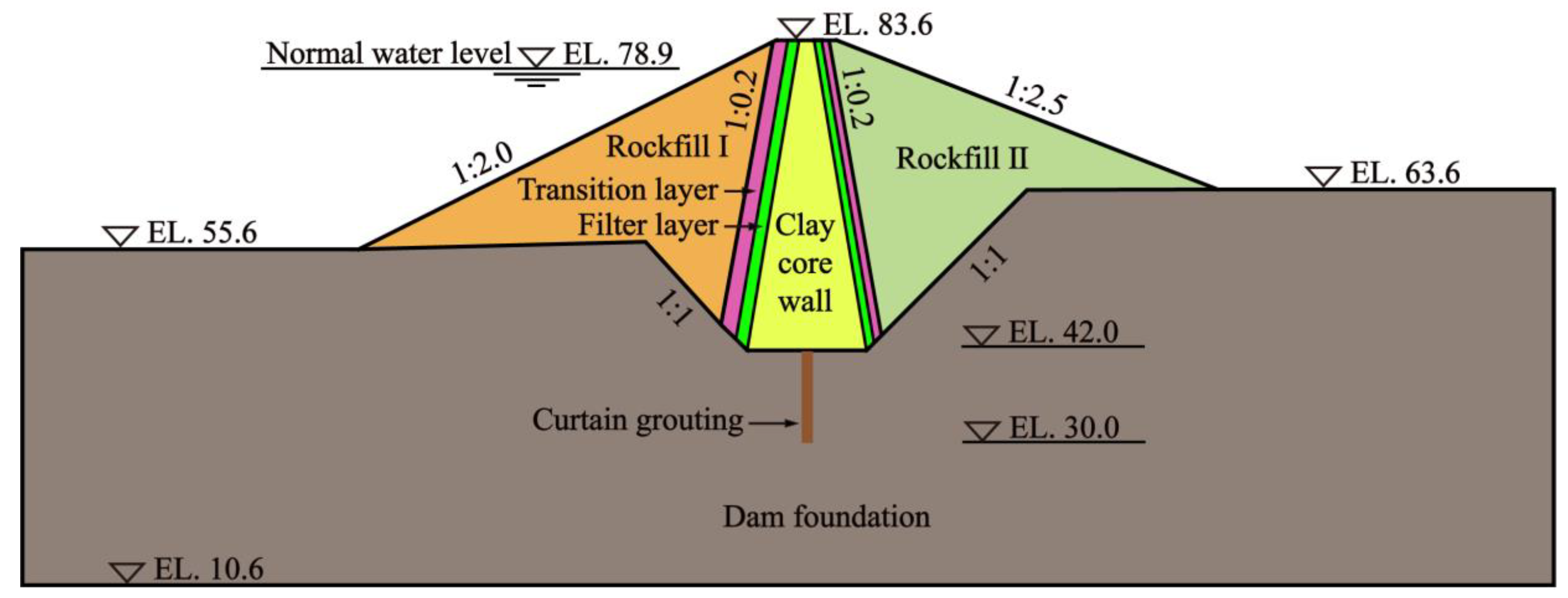
3.1. Summary of the Project
3.2. Material Parameters and Boundary Conditions
3.3. Process of Numerical Simulation
4. Results of Numerical Simulation and Analysis of Monitoring Data
4.1. Analysis of the Seepage Field
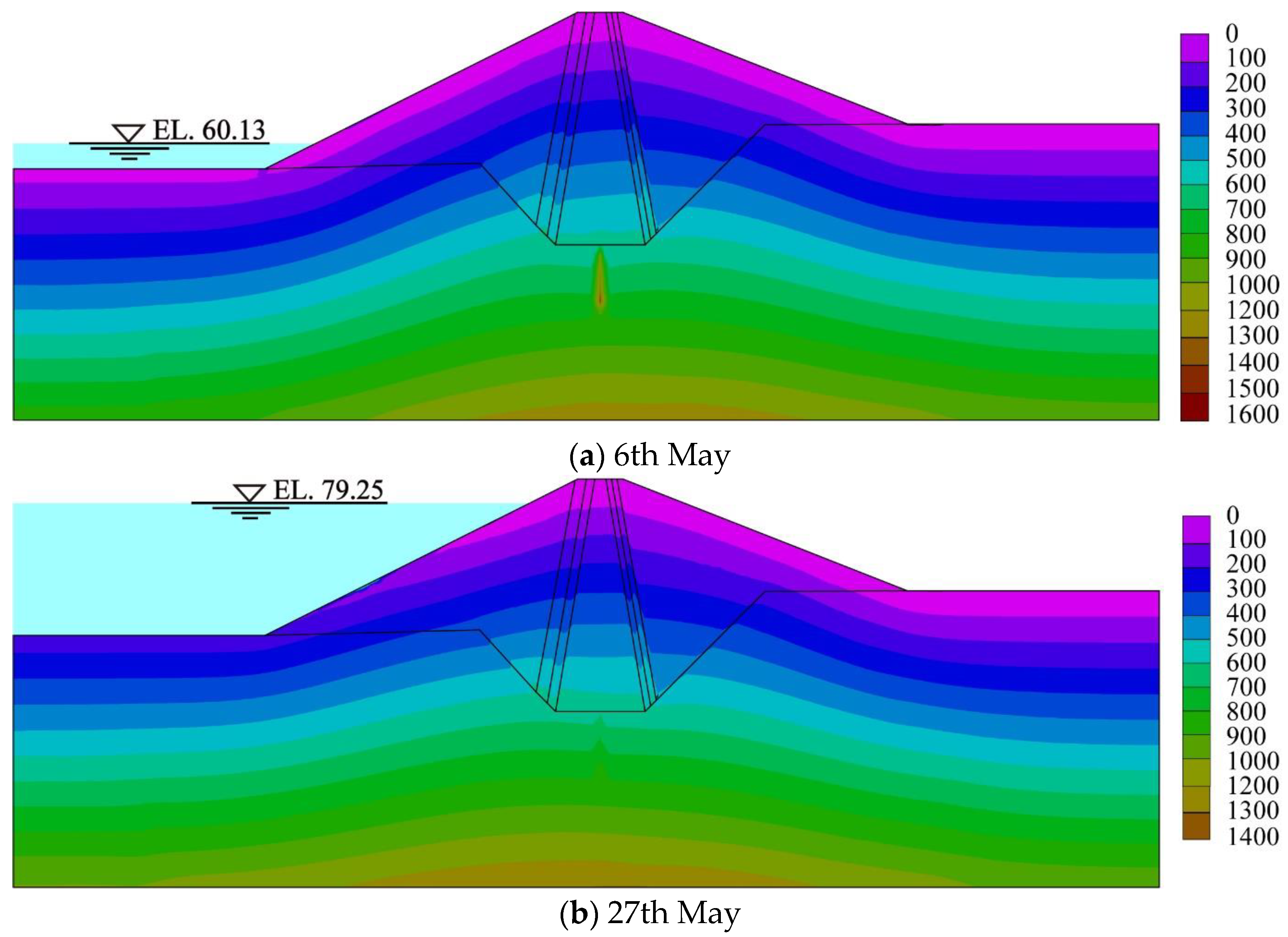
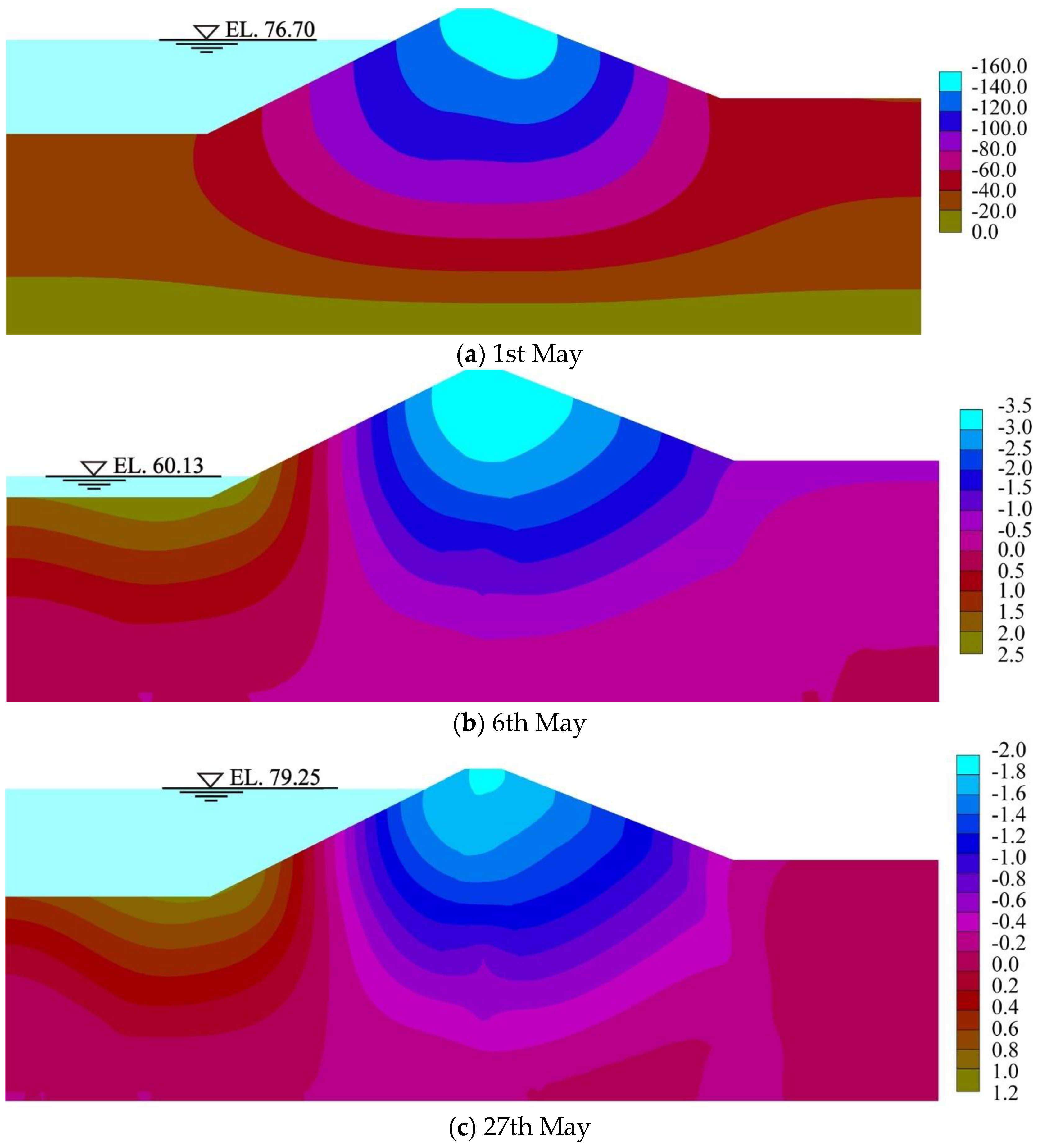
4.1.1. Analysis of the Results of Simulating Pore Water Pressure
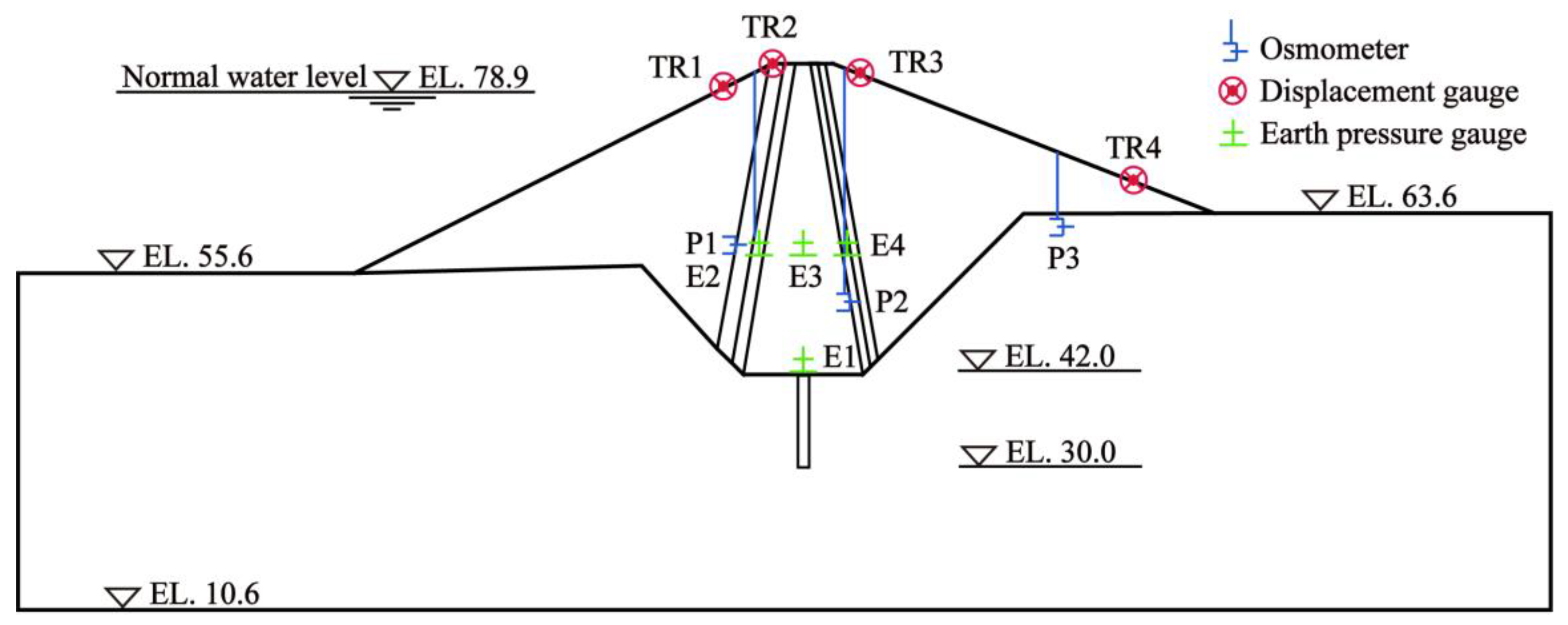
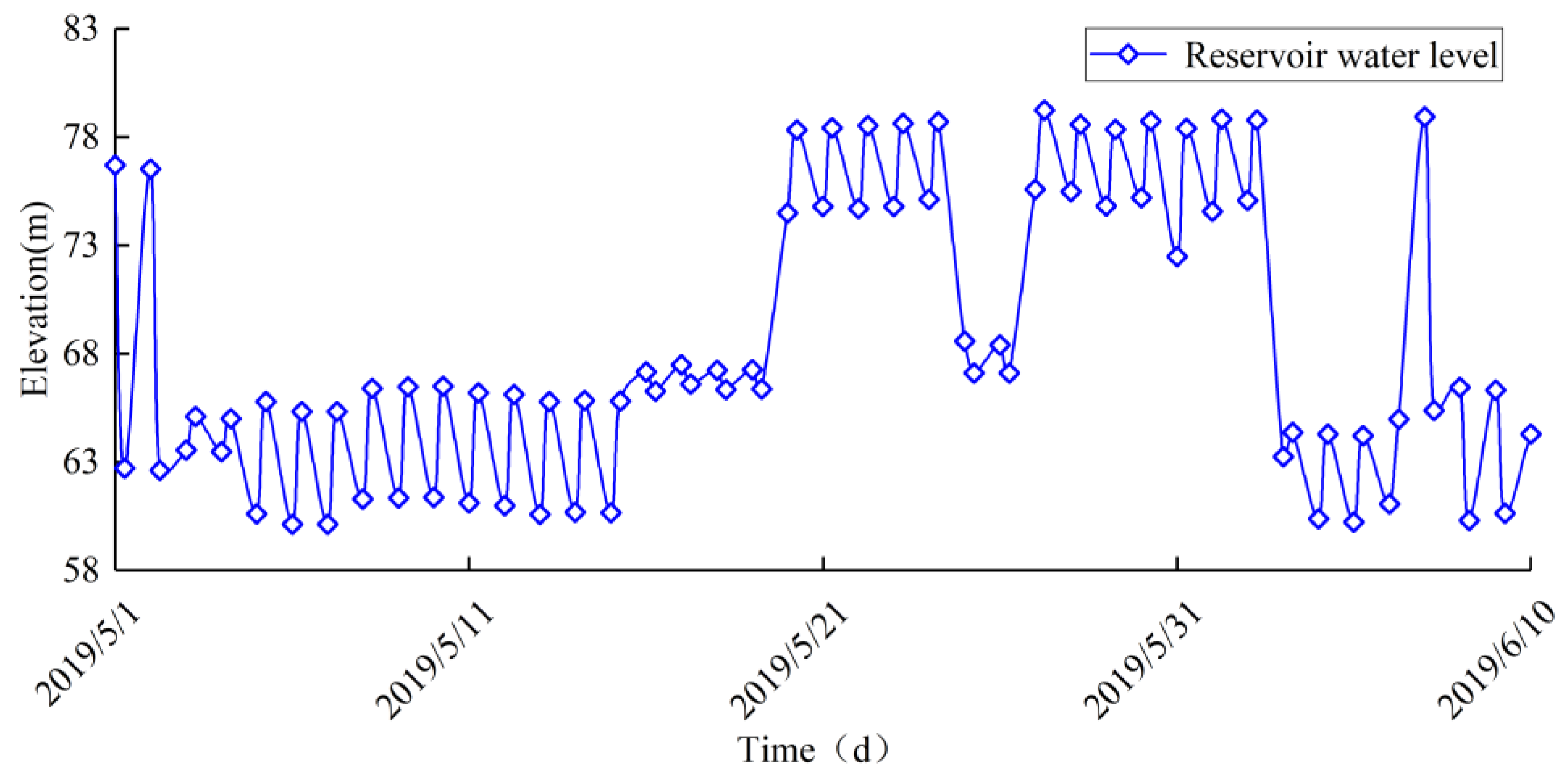
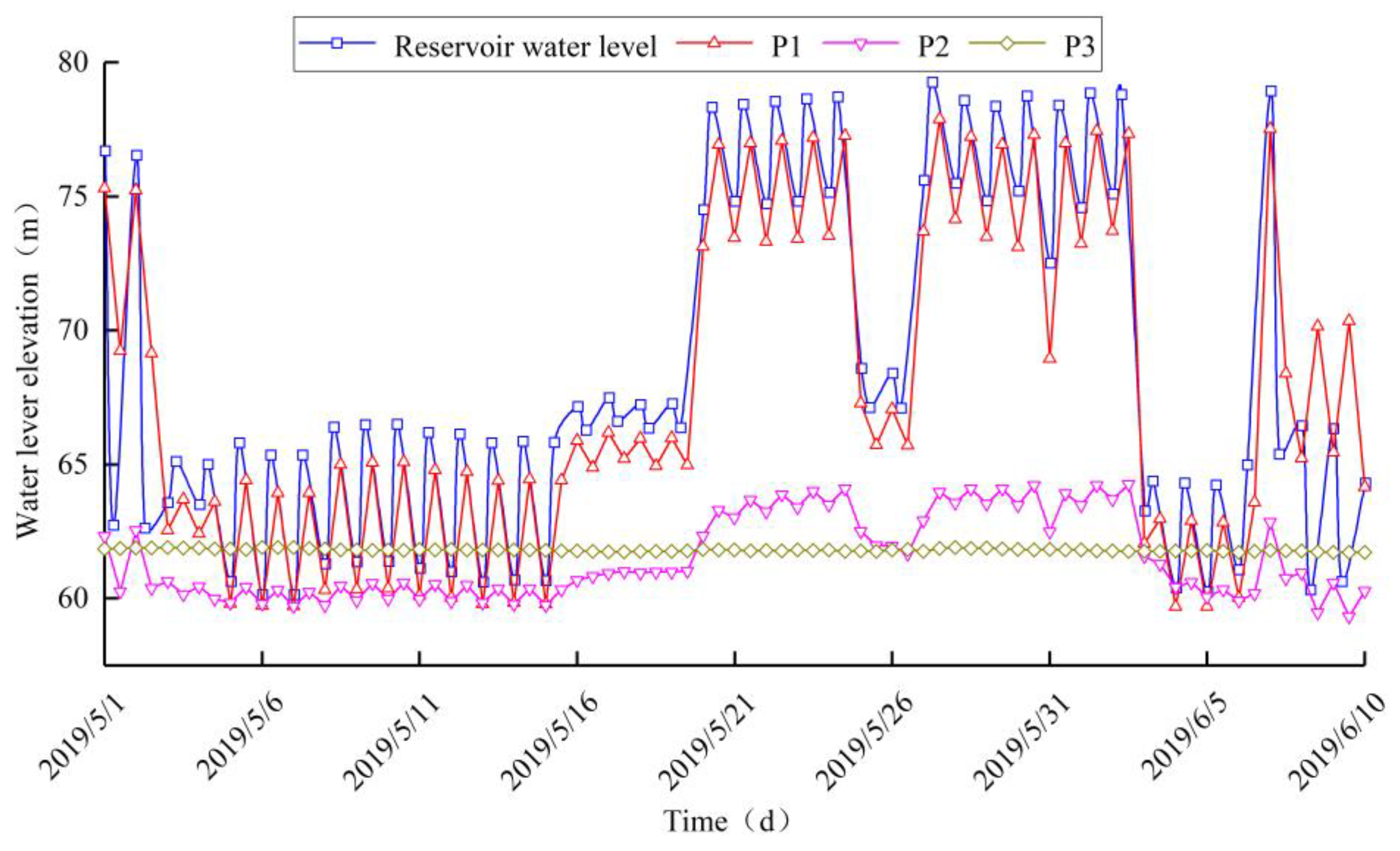
4.1.2. Analysis of the Monitoring Data of Seepage Pressure
4.2. Analysis of the Stress Field
4.2.1. Analysis of the Results of Simulating Vertical Soil Pressure
4.2.2. Analysis of the Monitoring Data of Vertical Soil Pressure
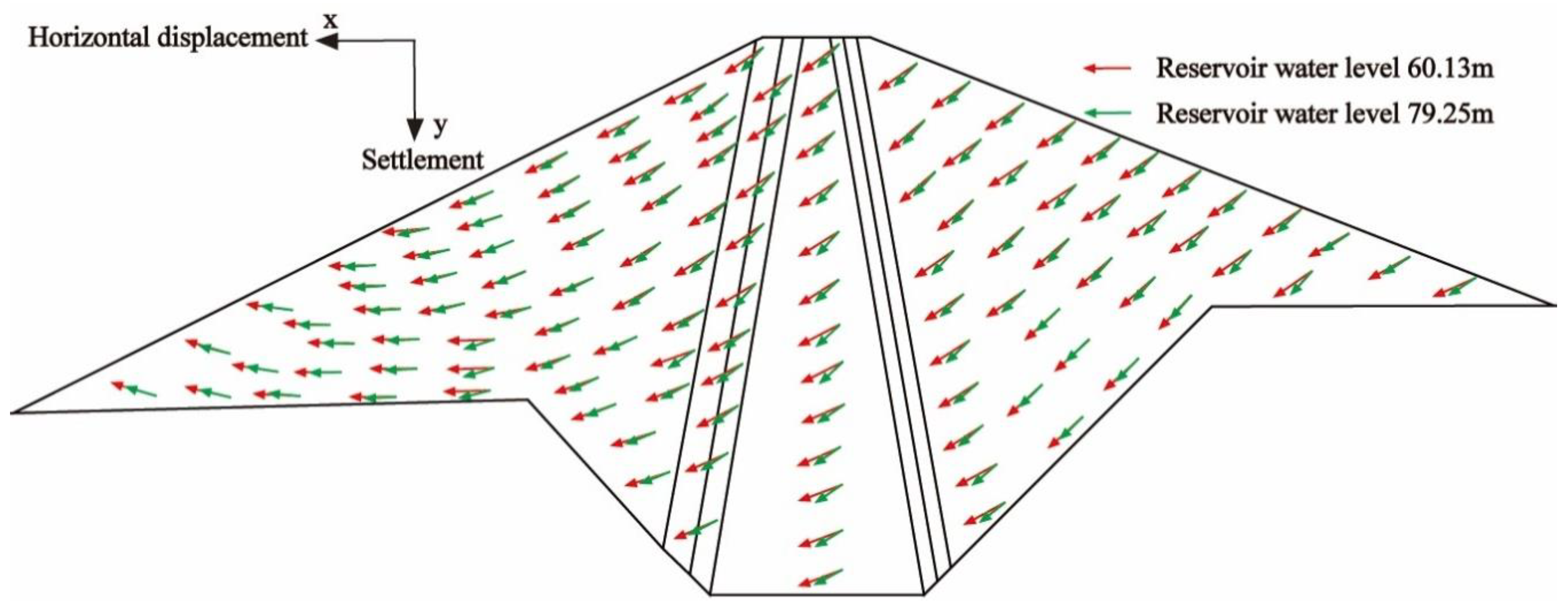
4.3. Analysis of the Displacement Field
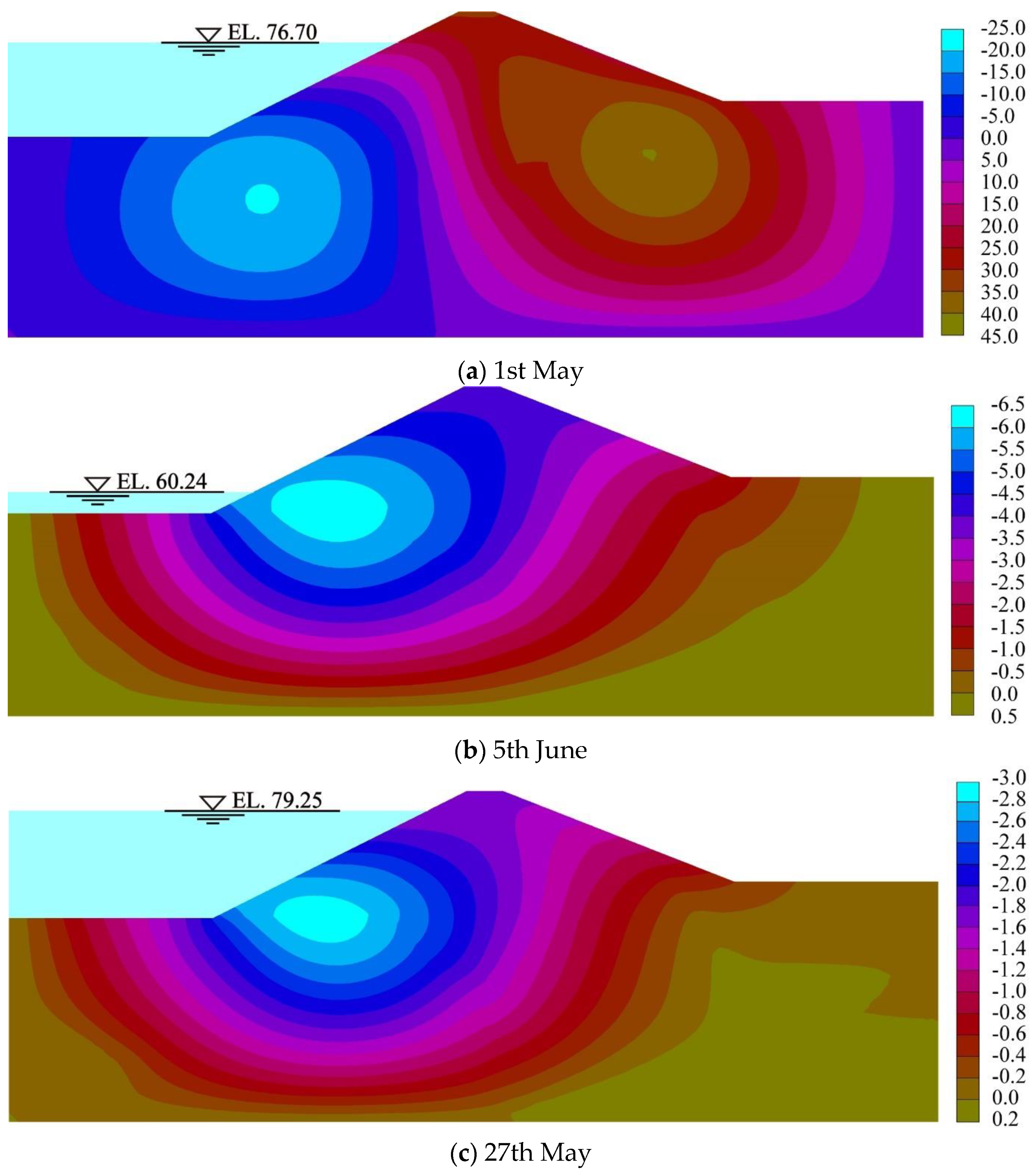
4.3.1. Analysis of the Results of Simulating Horizontal Displacement and Settlement
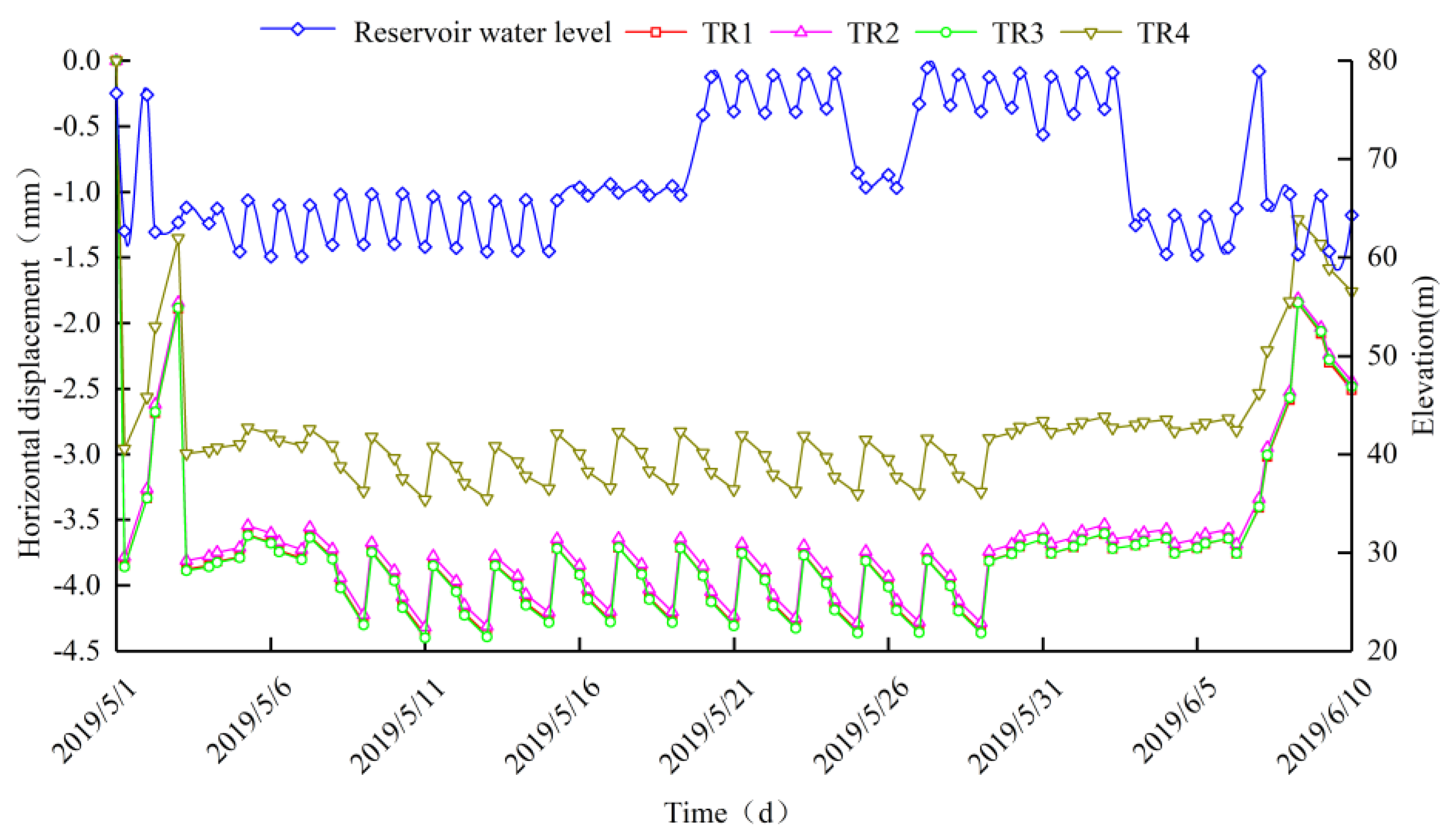
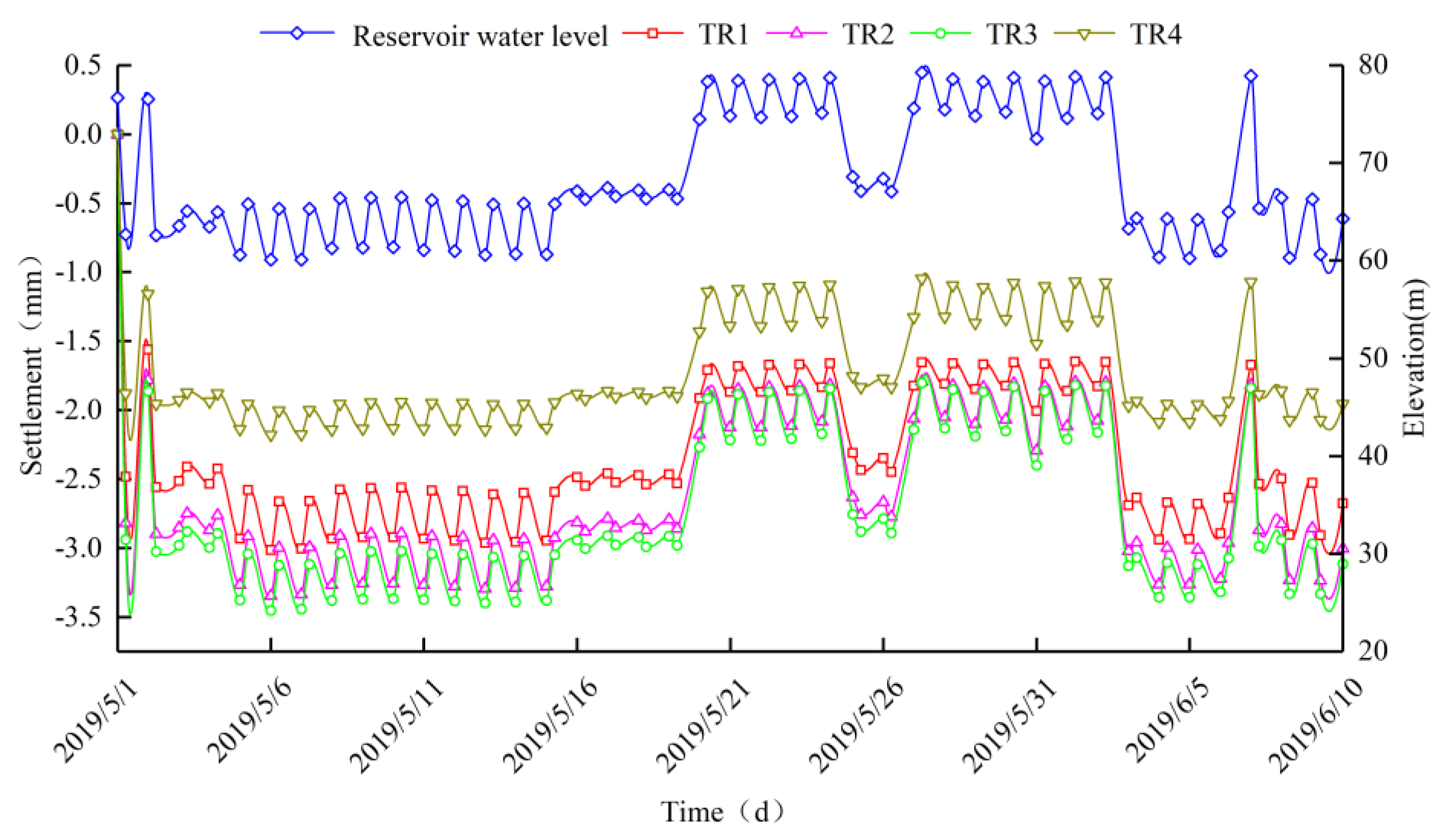
4.3.2. Analysis of the Monitoring Data of Displacement
5. Conclusions and Prospects
5.1. Conclusions
- (1)
- When the reservoir’s water level dropped sharply, the decline in the phreatic line in the rockfill lagged, creating a large hydraulic gradient and a reverse seepage field on the surface of the dam’s slope. This resulted in a dragging force directed upstream, with a noticeable deformation trend of the lower core wall and rockfill towards the upstream. One-third of the surface of the upstream slope of the dam and the curtain grouting experienced significant concentrations of stress. Consequently, bending of the core wall could easily produce horizontal cracks, and there was a risk of longitudinal cracks separating from the rockfill, greatly affecting the stability of the rockfill on the upstream slope of the dam.
- (2)
- Upon a sudden decrease in the reservoir’s water level, the dam’s deformation showed increased sensitivity to the lowest elevation point, compared with the peak rate of decline in the water level. The peak increase in horizontal displacement of 6.5 mm occurred one-third up Rockfill I, while the maximum increase in settlement at the dam’s crest was 3.5 mm. Hence, close scrutiny is warranted for cracks or voids at the dam’s crest and near one-third of the dam’s height within Rockfill I.
- (3)
- A sudden increase in the reservoir’s water level led to a reduction in both the upstream and downstream horizontal displacement, as well as decreased in settlement. For both the core wall and the rockfill, the ratio of cumulative maximum settlement to the dam’s height was less than 0.5%. Furthermore, the absence of tensile stress zones or cracks at the dam’s crest aligned with the established deformation principles of CWRDs.
- (4)
- Under the influence of rapid fluctuations in the reservoir’s water level, the variation in vertical earth pressure at the bottom of the core wall was more pronounced than at its midsection. This was because the soil at the bottom of the core wall had a higher initial density, smaller porosity, and lower permeability due to greater gravity and pressure from the overlying soil. Consequently, when the reservoir’s water level changed, the pore water pressure in the bottom soil adjusted more slowly than in the middle, resulting in more significant changes in soil pressure at the bottom.
- (5)
- The safety monitoring data for dam seepage pressure, earth pressure, and displacement aligned closely with the finite element model’s simulated values for the infiltration line, earth pressure, and deformation. This concordance verified the finite element model’s accuracy.
5.2. Prospects
- (1)
- The deformation characteristics of a PSPS’s CWRD under earthquake conditions when the reservoir’s water level fluctuates during the service period were not discussed in this study. This aspect should be further investigated in future studies.
- (2)
- Due to the lack of detailed 3D geological data, a two-dimensional finite element model was used in this study. This model could not fully capture the distribution of stress and deformation in the dam’s three-dimensional space, and should be improved in future research.
- (3)
- This study used the Duncan–Chang E-B model for the stress–strain relationship of rockfill, which could not accurately describe particle breakage and other characteristics of rockfill. Future research should propose a constitutive model that accounts for all the characteristics of rockfill to enhance the accuracy of finite element calculations.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, H.; Chi, F. Major Technologies for Safe Construction of High Earth-Rockfill Dams. Engineering 2016, 2, 498–509. [Google Scholar] [CrossRef]
- Wang, X. Discussion on Some Problems Observed in High Earth-Rockfill Dams. Chin. J. Geotech. Eng. 2018, 40, 203–222. [Google Scholar] [CrossRef]
- Rahmani, H.; Panah, A. Effect of Particle Size and Saturation Conditions on the Breakage Factor of Weak Rockfill Materials Under One-Dimensional Compression Testing. Geomech. Eng. 2020, 4, 315–326. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Wu, Z.; Chen, J.; Yin, C.; Bian, K. Dynamic Risk Evaluation and Early Warning of Crest Cracking for High Earth-Rockfill Dams through Bayesian Parameter Updating. Appl. Sci. 2020, 10, 7627. [Google Scholar] [CrossRef]
- Zhang, H.; Jing, Y.; Chen, J.; Gao, Z.; Xu, Y. Characteristics and Causes of Crest Cracking on A High Core-Wall Rockfill Dam: A Case Study. Eng. Geol. 2022, 297, 106488. [Google Scholar] [CrossRef]
- Naylor, D.; Maranha das Neves, E.; Mattar, J.; Veiga Pinto, A. Prediction of Construction Performance of Beliche Dam. Geotechnique 1986, 36, 359–376. [Google Scholar] [CrossRef]
- Naylor, D.; Maranha, J.; Maranha das Neves, E.; Veiga Pinto, A. A Back-Analysis of Beliche Dam. Geotechnique 1997, 47, 221–233. [Google Scholar] [CrossRef]
- Maranha das Neves, E.; Veiga Pinto, A. Modeling Collapse on Rockfill Dams. Comput. Geotech. 1988, 6, 131–153. [Google Scholar] [CrossRef]
- Alonso, E.; Olivella, S.; Pinyol, N. A Review of Beliche Dam. Geotechnique 2005, 55, 267–285. [Google Scholar] [CrossRef]
- Cetin, H.; Laman, M.; Ertunc, A. Settlement and Slaking Problems in the World’s Fourth Largest Rock-Fill Dam, the Ataturk Dam in Turkey. Eng. Geol. 2000, 56, 225–242. [Google Scholar] [CrossRef]
- Kartal, M.; Çavusli, M.; Genis, M. 3D Nonlinear Analysis of Atatürk Clay Core Rockfill Dam Considering Settlement Monitoring. Int. J. Geomech. 2019, 19, 04019034. [Google Scholar] [CrossRef]
- Leonards, G.; Davidson, L. Reconsideration of Failure Initiating Mechanisms for Teton Dam. Int. J. Rock. Mech. Min. Sci. Geomech. Abstr. 1986, 23, A27. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, C.; Wong, H.; Jiang, T.; Dong, J. Modeling Dam Deformation in the Early Stage of Internal Seepage Erosion—Application to the Teton Dam, Idaho, Before the 1976 Incident. J. Hydrol. 2022, 605, 127378. [Google Scholar] [CrossRef]
- Jia, Y.; Xu, B.; Chi, S.; Xiang, B.; Xiao, D.; Zhou, Y. Joint Back Analysis of the Creep Deformation and Wetting Deformation Parameters of Soil Used in the Guanyinyan Composite Dam. Comput. Geotech. 2018, 96, 167–177. [Google Scholar] [CrossRef]
- Zhou, X.; Chi, S.; Jia, Y.; Shao, X. A New Wetting Deformation Simulation Method Based on Changes in Mechanical Properties. Comput. Geotech. 2020, 117, 103261. [Google Scholar] [CrossRef]
- Zhou, X.; Chi, S.; Wang, M.; Jia, Y. Study on Wetting Deformation Characteristics of Coarse Granular Materials and Its Simulation in Core-Wall Rockfill Dams. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 851–873. [Google Scholar] [CrossRef]
- Squier, L. Load Transfer in Earth and Rockfill Dams. J. Soil Mech. Found. 1970, 96, 213–233. [Google Scholar] [CrossRef]
- Ding, N.; Duan, J.; Xue, S.; Zeng, M.; Shen, J. Overall Review of Peaking Power in China: Status Quo, Barriers and Solutions. Renew. Sustain. Energy Rev. 2015, 42, 503–516. [Google Scholar] [CrossRef]
- Kong, Y.; Kong, Z.; Liu, Z.; Wei, C.; Zhang, J.; An, G. Pumped Storage Power Stations in China: The Past, the Present, and the Future. Renew. Sustain. Energy Rev. 2017, 71, 720–731. [Google Scholar] [CrossRef]
- Jia, J. A Technical Review of Hydro-Project Development in China. Engineering 2016, 2, 302–312. [Google Scholar] [CrossRef]
- Xu, Z.; Cao, C.; Li, K.; Cai, J.; Xiong, W.; Zhao, J.; Qin, R. Simulation of Drainage Hole Arrays and Seepage Control Analysis of the Qingyuan Pumped Storage Power Station in China: A Case Study. Bull. Eng. Geol. Environ. 2019, 78, 6335–6346. [Google Scholar] [CrossRef]
- Feng, W.; Chi, S.; Jia, Y. Random Finite Element Analysis of A Clay-Core-Wall Rockfill Dam Considering Three-Dimensional Conditional Random Fields of Soil Parameters. Comput. Geotech. 2023, 159, 105437. [Google Scholar] [CrossRef]
- Larese, A.; Rossi, R.; Oñate, E.; Toledo, M.; Morán, R.; Campos, H. Numerical and Experimental Study of Overtopping and Failure of Rockfill Dams. Int. J. Geomech. 2015, 15, 04014060. [Google Scholar] [CrossRef]
- Mohammad Rashidi, S.; Mohsen, H. Evaluation of Behaviors of Earth and Rockfill Dams During Construction and Initial Impounding Using Instrumentation Data and Numerical Modeling. J. Rock. Mech. Geotech. Eng. 2017, 9, 709–725. [Google Scholar] [CrossRef]
- Xu, M.; Pang, R.; Zhou, Y.; Xu, B. Seepage Safety Evaluation of High Earth-Rockfill Dams Considering Spatial Variability of Hydraulic Parameters Via Subset Simulation. J. Hydrol. 2023, 626, 130261. [Google Scholar] [CrossRef]
- Wu, Z.; Chen, C.; Zheng, Y.; Chen, J.; Bian, K.; Li, J. Analysis of Seepage Failure Probability for High Core Rockfill Dams During Rapid Drawdown of Reservoir Water level. J. Hydrol. 2024, 633, 131046. [Google Scholar] [CrossRef]
- Reza, M.; Ali, A.; Behrouz, G. Simulation of Collapse Settlement of First Filling in a High Rockfill Dam. Eng. Geol. 2015, 187, 32–44. [Google Scholar] [CrossRef]
- Akhtarpour, A.; Salari, M. The Deformation Mechanism of A High Rockfill Dam During the Construction and First Impounding. Sci. Iran. 2020, 27, 566–587. [Google Scholar] [CrossRef]
- Qiu, T.; Wang, W.; Höeg, K.; Feng, S.; Zhao, R. 3D Analysis of the 174-m High Quxue Asphalt-Core Rockfill Dam in A Narrow Canyon. Soils Found. 2021, 61, 1645–1659. [Google Scholar] [CrossRef]
- Zhou, X.; Wu, B.; Li, L. Study on Influence of Numerical Simulation Accuracy on High Core Wall Rockfill Dam Deformation and Crack Analysis. Buildings 2022, 12, 1494. [Google Scholar] [CrossRef]
- Zhou, X.; He, J.; Chi, S.; Wang, J. Study on Collapse Settlement and Cracks of Core Wall Rockfill Dams Under Wetting Deformation. Int. J. Numer. Anal. Methods Geomech. 2023, 47, 106–128. [Google Scholar] [CrossRef]
- Liu, S.; He, W.; Sun, Y.; Shen, C.; Wang, L. Analysis of the Behavior of A High Earth-Core Rockfill Dam Considering Particle Breakage. Comput. Geotech. 2023, 157, 105320. [Google Scholar] [CrossRef]
- Pan, L.; Fan, Z.; Wang, D.; Zhou, X. The Wetting Deformation Model of Rockfill and Its Two Methods for Simulating Rock-fill Dam Collapse Settlement. Sci. World J. 2023, 2023, 5593636. [Google Scholar] [CrossRef] [PubMed]
- Pan, L.; Wu, B.; Wang, D.; Zhou, X.; Wang, L.; Zhang, Y. Study on Impoundment Deformation Characteristics and Crack of High Core Rockfill Dam Based on Inversion Parameters. Water 2024, 16, 188. [Google Scholar] [CrossRef]
- Ai, Z.; Ma, G.; Zhang, G.; Liu, R.; Deng, S.; Chang, X.; Zhou, W. Multi-Source Monitoring Data Filtering Assisted Deformation Analysis Model Updating of Ultra-High Rockfill Dam. Comput. Geotech. 2024, 171, 106323. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, B.; Yu, Y.; Zhang, Z. Consolidation Analysis of Nuozhadu High Earth-Rockfill Dam Based on the Coupling of Seepage and Stress-Deformation Physical State. Int. J. Geomech. 2016, 16, 04015085. [Google Scholar] [CrossRef]
- Dong, Y.; Xing, H.; Liu, J. With FLAC3D Simulating Analysis the Rock Stability by Stretching Anchor Cables Reinforce on the Reservoir Dam Abutment. Appl. Mech. Mater. 2011, 90–93, 2670–2676. [Google Scholar] [CrossRef]
- Li, M.; Xue, B.; Fang, H.; Zhang, S.; Wang, F. Parameter Sensitivity Analysis of Polyurethane Cutoff Walls for Earth Dams under Multifield Coupling. Int. J. Geomech. 2023, 23, 04023206. [Google Scholar] [CrossRef]
- Liu, S.; Wang, L.; Wang, Z.; Bauer, E. Numerical Stress-Deformation Analysis of Cut-Off Wall in Clay-Core Rockfill Dam on Thick Overburden. Water Sci. Eng. 2016, 9, 219–226. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, G.; Lu, Y. Deformation and Stability Analysis of a Core Rockfill Dam with Leakage. Shock. Vib. 2022, 2022, 6944442. [Google Scholar] [CrossRef]
- Ri, Y.; Han, U.; Jang, U.; Jong, D.; Kim, C. Study on Stability Reduction Characteristics of Earth and Rockfill Dams under Rapid Drawdown Using Fully Coupled Seepage-Stress Analysis. Adv. Civil. Eng. 2022, 2022, 7954991. [Google Scholar] [CrossRef]


| Dam Materials | , kN•m−3 | c, kPa | /° | /° | K | n | Rf | Kb | m | Kur |
|---|---|---|---|---|---|---|---|---|---|---|
| Rockfill I | 22.1 | 0 | 39.8 | 10.5 | 960 | 0.49 | 0.74 | 490 | 0.42 | 2K |
| Transition layer | 22.5 | 120 | 40.2 | 7.7 | 780 | 0.47 | 0.75 | 475 | 0.37 | 2K |
| Filter layer | 18.1 | 133 | 43.7 | 8.5 | 840 | 0.42 | 0.80 | 450 | 0.43 | 2K |
| Clay core wall | 16.2 | 154 | 44 | 7.8 | 500 | 0.35 | 0.77 | 240 | 0.35 | 2K |
| Rockfill II | 21.8 | 0 | 43.9 | 9.6 | 660 | 0.49 | 0.70 | 258 | 0.28 | 2K |
| Dam’s foundation | 21.8 | 55 | 43.9 | 9.6 | 660 | 0.49 | 0.70 | 258 | 0.28 | 2K |
| Time | Reservoir’s Water Level, m | P1 | P2 | P3 | |||
|---|---|---|---|---|---|---|---|
| Simulated Value, m | Monitored Value, m | Simulated Value, m | Monitored Value, m | Simulated Value, m | Monitored Value, m | ||
| 5/1 | 76.70 | 75.40 | 75.31 | 62.60 | 62.33 | 61.87 | 61.85 |
| 5/6 | 60.13 | 73.60 | 73.39 | 62.80 | 62.31 | 61.76 | 61.90 |
| 5/27 | 79.25 | 77.38 | 77.87 | 64.44 | 63.97 | 61.94 | 61.86 |
| Time | Reservoir’s Water Level, m | Rate of Decline in the Reservoir’s Water Level, (m•d−1) | Maximum Increase in Horizontal Displacement, mm | Maximum Increase in Settlement, mm | ||
|---|---|---|---|---|---|---|
| Upstream Point | Downstream Point | Upstream Point | Downstream Point | |||
| 6/5 | 60.24 | 4.06 | 6.5 | 0.5 | / | / |
| 5/6 | 60.13 | 4.38 | / | / | 2.5 | 3.5 |
| 6/2 | 63.26 | 15.53 | 5.5 | 0.5 | 2.0 | 3.0 |
| Time | TR2 Horizontal Displacement, mm | TR2 Settlement, mm | TR3 Horizontal Displacement, mm | TR3 Settlement, mm | ||||
|---|---|---|---|---|---|---|---|---|
| Simulated Value, m | Monitored Value, m | Simulated Value, m | Monitored Value, m | Simulated Value, m | Monitored Value, m | Simulated Value, m | Monitored Value, m | |
| 5/1 | 24.88 | 23.65 | 154.78 | 150.73 | 25.04 | 24.13 | 156.35 | 151.67 |
| 5/15 | 20.60 | 18.95 | 151.84 | 148.32 | 20.68 | 19.74 | 154.47 | 149.23 |
| 5/30 | 22.87 | 21.63 | 152.38 | 149.30 | 23.01 | 22.60 | 154.83 | 149.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Yan, B.; Wang, W.; Du, K.; Fang, Y. Seepage–Deformation Coupling Analysis of a Core Wall Rockfill Dam Subject to Rapid Fluctuations in the Reservoir Water Level. Water 2024, 16, 1621. https://doi.org/10.3390/w16111621
Zheng X, Yan B, Wang W, Du K, Fang Y. Seepage–Deformation Coupling Analysis of a Core Wall Rockfill Dam Subject to Rapid Fluctuations in the Reservoir Water Level. Water. 2024; 16(11):1621. https://doi.org/10.3390/w16111621
Chicago/Turabian StyleZheng, Xueqin, Bin Yan, Wei Wang, Kenan Du, and Yixiang Fang. 2024. "Seepage–Deformation Coupling Analysis of a Core Wall Rockfill Dam Subject to Rapid Fluctuations in the Reservoir Water Level" Water 16, no. 11: 1621. https://doi.org/10.3390/w16111621
APA StyleZheng, X., Yan, B., Wang, W., Du, K., & Fang, Y. (2024). Seepage–Deformation Coupling Analysis of a Core Wall Rockfill Dam Subject to Rapid Fluctuations in the Reservoir Water Level. Water, 16(11), 1621. https://doi.org/10.3390/w16111621





