A Modified Manning’s Equation for Estimating Flow Rate in Grass Swales under Low Inflow Rate Conditions
Abstract
1. Introduction
2. Materials and Methods
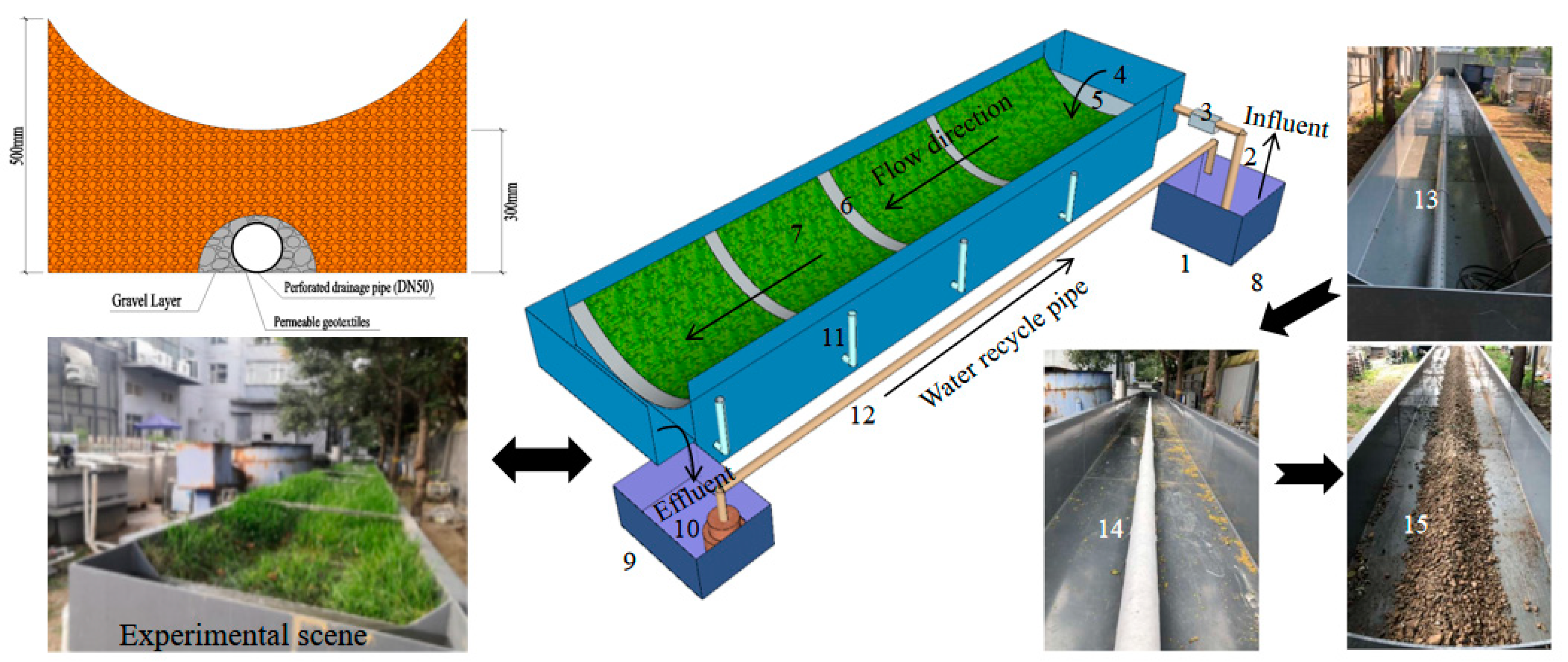
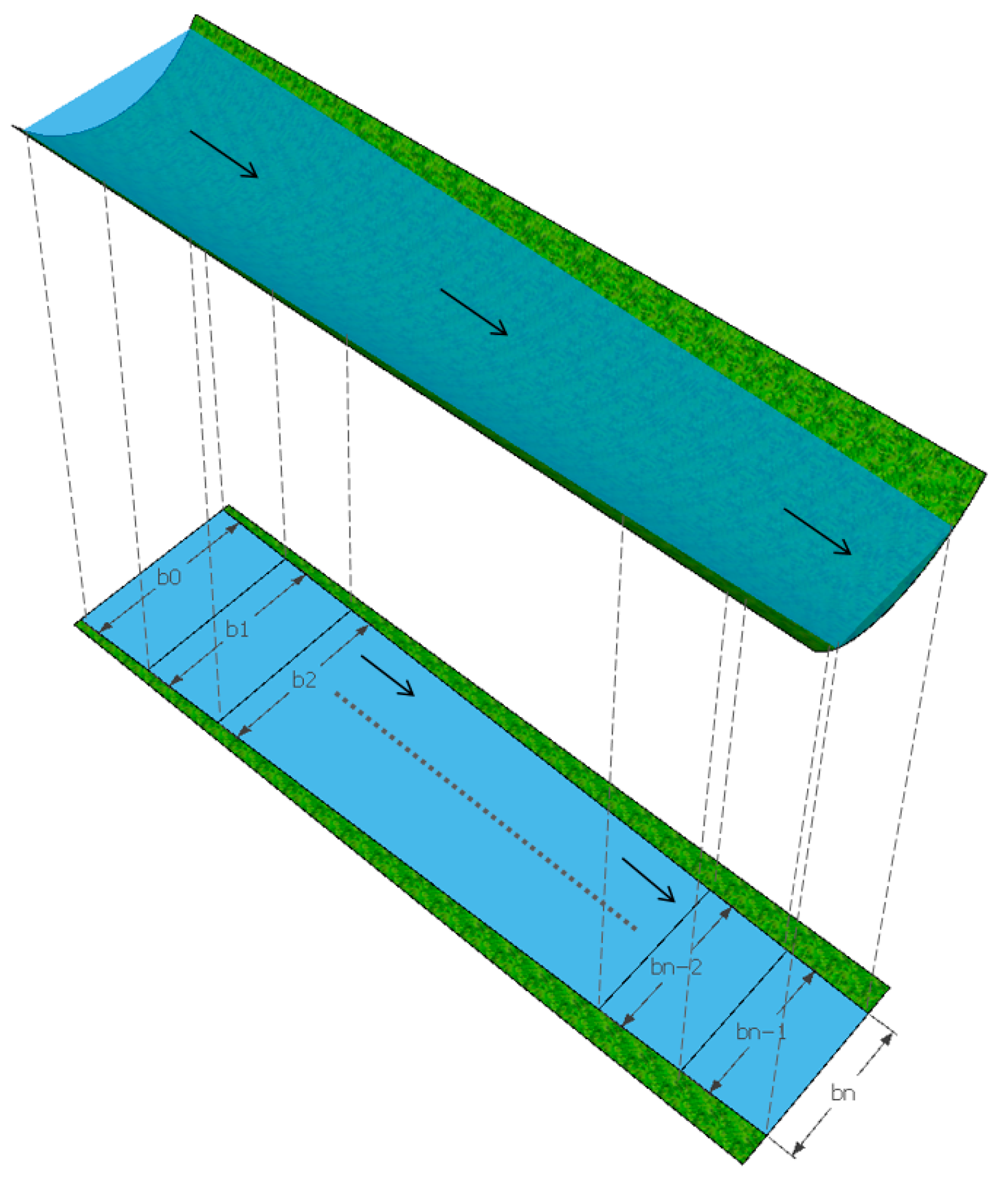
2.1. Experimental Device
2.2. Flow Rate Measurement Method
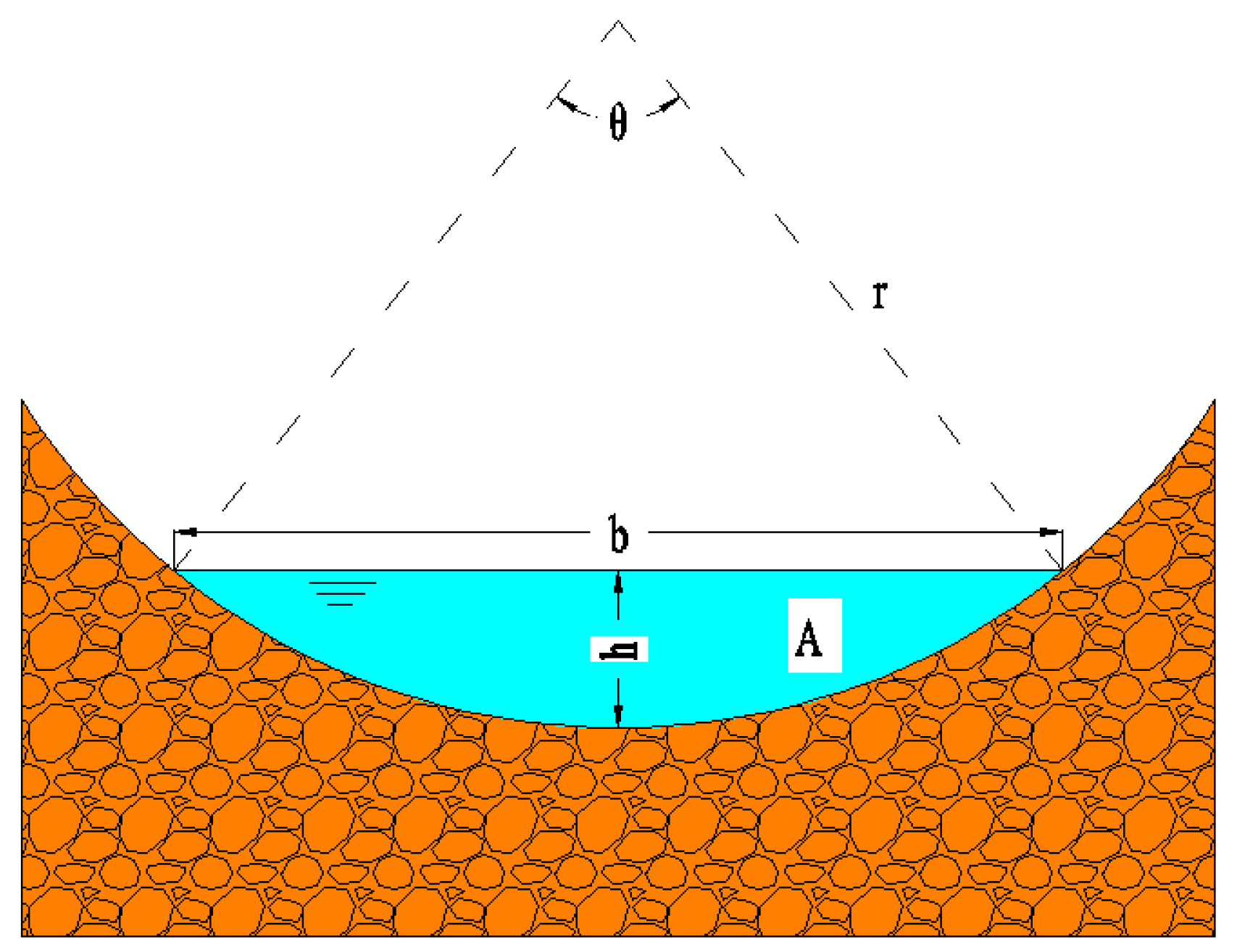
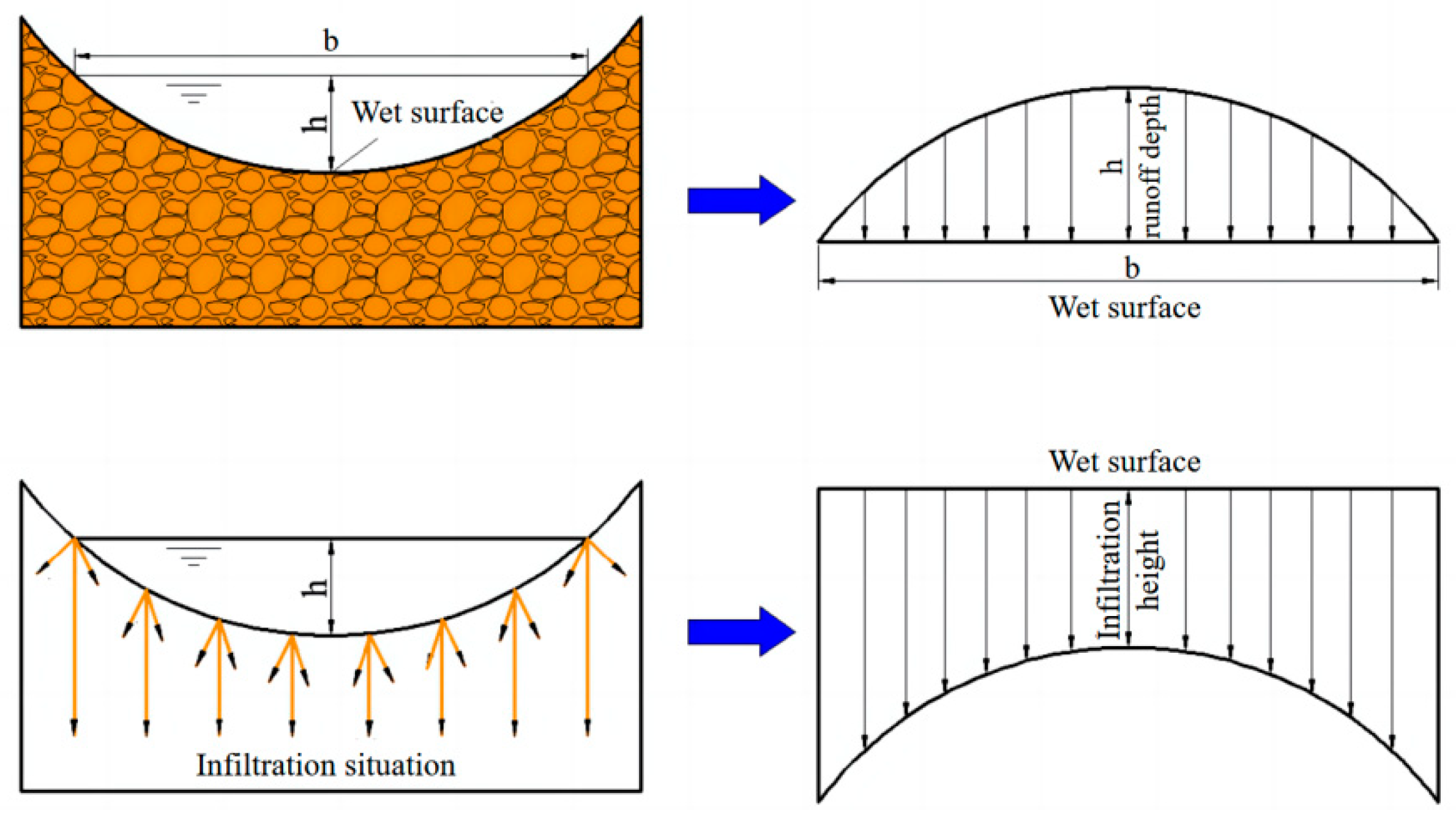
2.3. Manning’s Equation
3. Results and Discussion
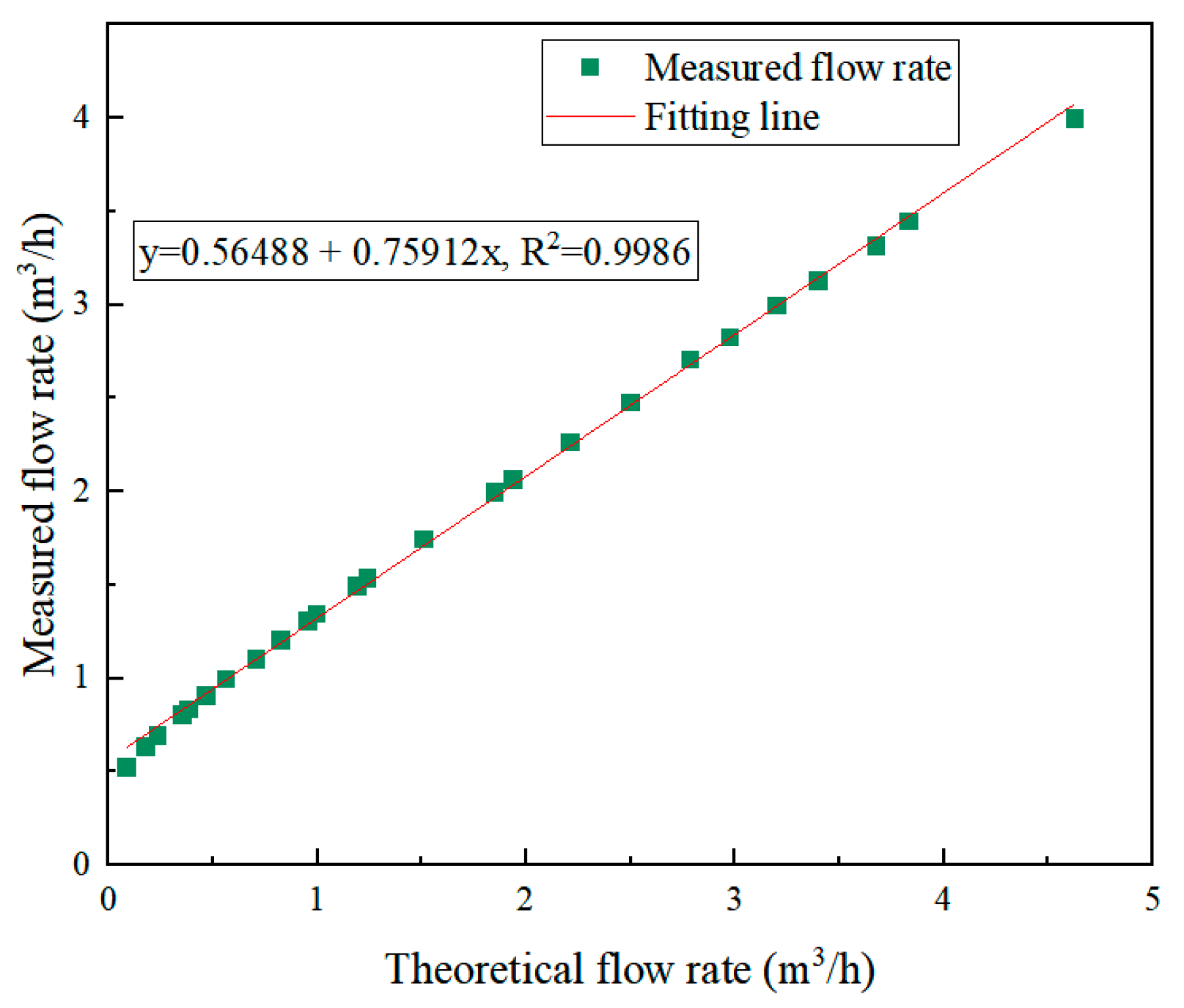
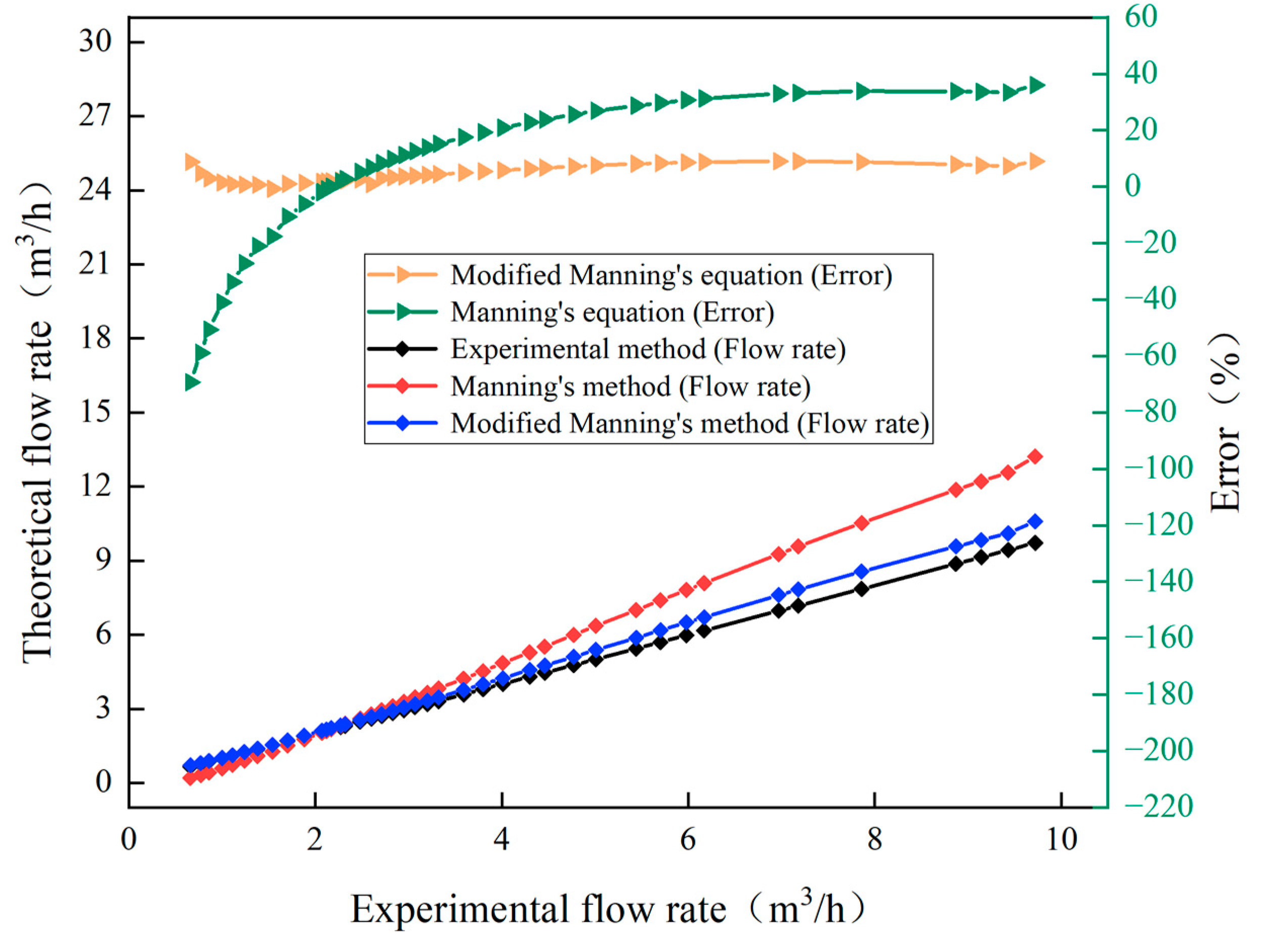
3.1. Comparison between Calculated Results and Experimental Data
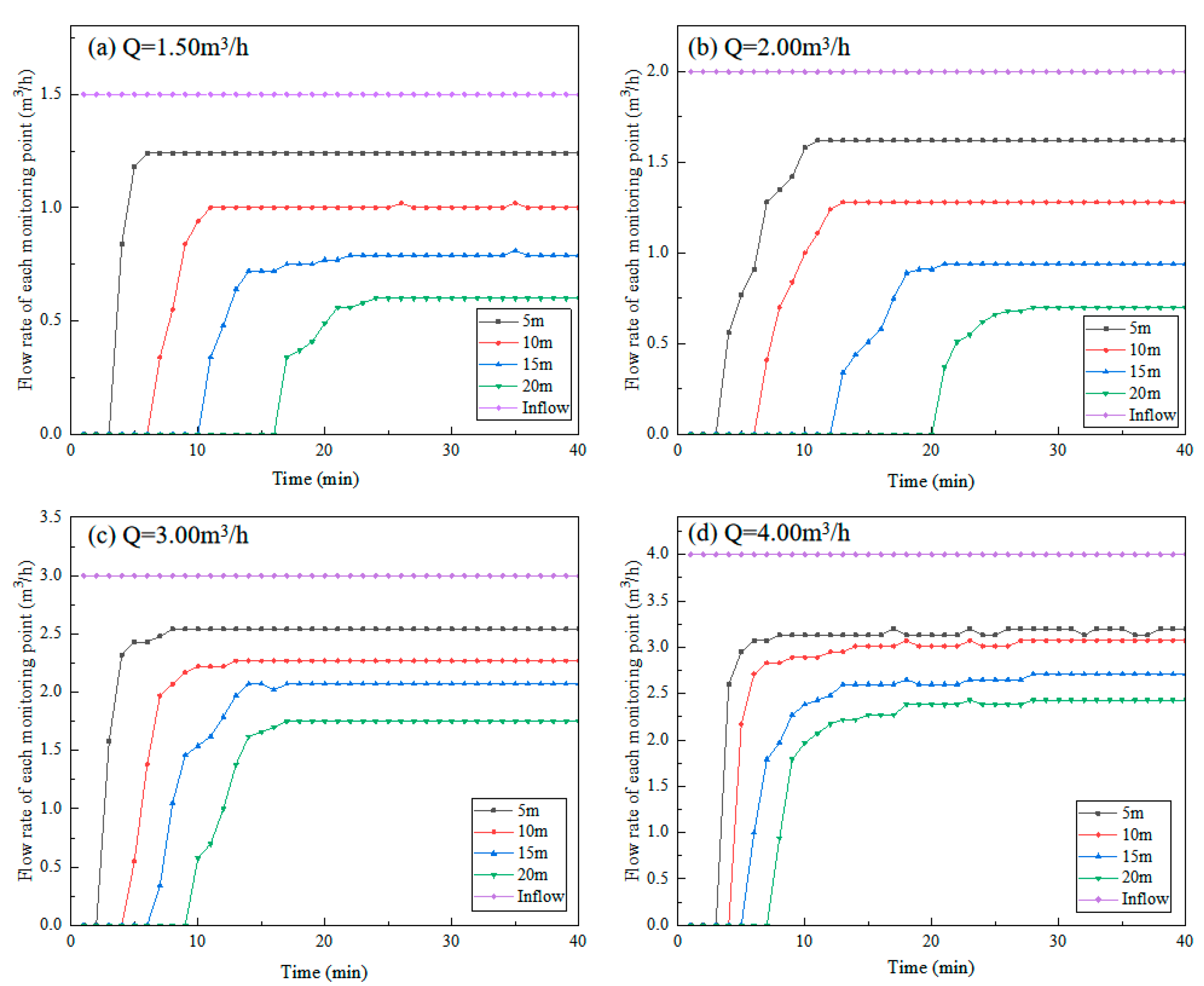
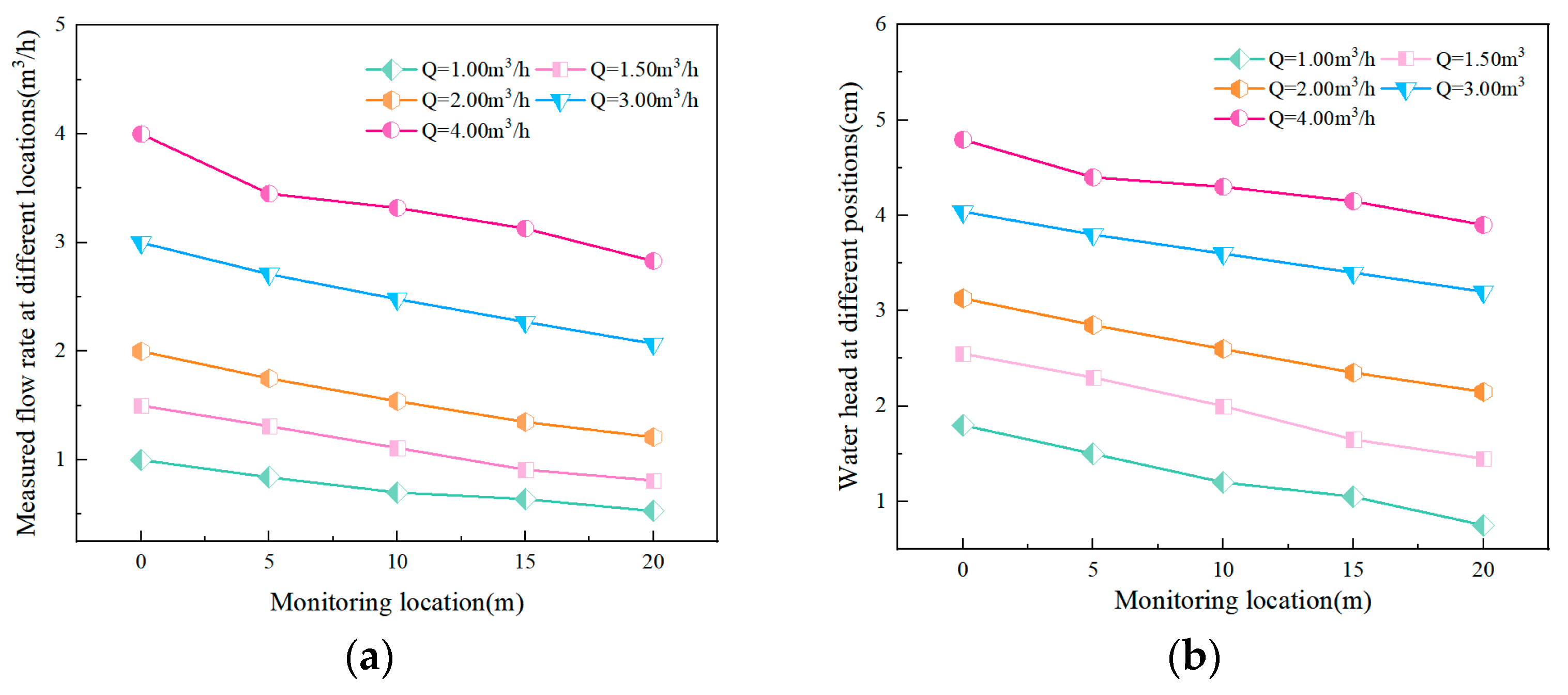
3.2. Characteristics of Flow Rate and Water Depth along the Grass Swale
3.3. Modified Method for Flow Rate Calculation along the Grass Swale
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Margerum, R.D. Integrated Approaches to Environmental Planning and Management. J. Plan. Lit. 1997, 11, 459–475. [Google Scholar] [CrossRef]
- Zhao, H.; Zou, C.; Zhao, J.; Li, X. Role of Low-Impact Development in Generation and Control of Urban Diffuse Pollution in a Pilot Sponge City: A Paired-Catchment Study. Water 2018, 10, 852. [Google Scholar] [CrossRef]
- Che, W.; Zhao, Y.; Yang, Z.; Li, J.; Shi, M. Integral stormwater management master plan and design in an ecological community. J. Environ. Sci. 2014, 26, 1818–1823. [Google Scholar] [CrossRef]
- Wang, J.; Wang, M.; Che, W.; Li, J.; Zhao, Y.; Wang, W. Discussion on key issues of low-impact development rainwater system construction. China Water Wastewater 2015, 31, 6–12. [Google Scholar] [CrossRef]
- Pitt, R.; Nara, Y.; Kirby, J.; Durrans, S. Particulate Transport in Grass Swales; Low Impact Development, 2012; pp. 191–204. Available online: https://ascelibrary.org/doi/10.1061/41007%28331%2917 (accessed on 18 March 2024). [CrossRef]
- Davis Allen, P. Field Performance of Bioretention: Hydrology Impacts. J. Hydrol. Eng. 2008, 13, 90–95. [Google Scholar] [CrossRef]
- Kirby Jason, T.; Durrans, S.R.; Pitt, R.; Johnson Pauline, D. Hydraulic Resistance in Grass Swales Designed for Small Flow Conveyance. J. Hydraul. Eng. 2005, 131, 65–68. [Google Scholar] [CrossRef]
- Cheng, N.-S.; Nguyen Hoai, T. Hydraulic Radius for Evaluating Resistance Induced by Simulated Emergent Vegetation in Open-Channel Flows. J. Hydraul. Eng. 2011, 137, 995–1004. [Google Scholar] [CrossRef]
- Ahmed, F.; Gulliver John, S.; Nieber John, L. Determining Infiltration Loss of a Grassed Swale. In Proceedings of the World Environmental and Water Resources Congress 2014, Portland, Oregon, 1–5 June 2014; pp. 8–14. [Google Scholar] [CrossRef]
- Yang, F.; Fu, D.; Zevenbergen, C.; Boogaard, F.C.; Singh, R.P. Time-varying characteristics of saturated hydraulic conductivity in grassed swales based on the ensemble Kalman filter algorithm—A case study of two long-running swales in Netherlands. J. Environ. Manag. 2024, 351, 119760. [Google Scholar] [CrossRef] [PubMed]
- Deletic, A. Modelling of water and sediment transport over grassed areas. J. Hydrol. 2001, 248, 168–182. [Google Scholar] [CrossRef]
- Deletic, A.; Fletcher, T.D. Performance of grass filters used for stormwater treatment—A field and modelling study. J. Hydrol. 2006, 317, 261–275. [Google Scholar] [CrossRef]
- Zhang, W.; Hao, W.; Yan, W.; LI, S. Influence of Influent Load on Stormwater Runoff Control in Grassed Swales. Water Resour. Power 2020, 38, 22–25. [Google Scholar]
- Järvelä, J. Determination of flow resistance caused by non-submerged woody vegetation. Int. J. River Basin Manag. 2004, 2, 61–70. [Google Scholar] [CrossRef]
- Hu, Y.; Huai, W.; Han, J. Analytical solution for vertical profile of streamwise velocity in open-channel flow with submerged vegetation. Environ. Fluid Mech. 2013, 13, 389–402. [Google Scholar] [CrossRef]
- Bi, Y.; Zou, H.; Zhu, C. Dynamic monitoring of soil bulk density and infiltration rate during coal mining in sandy land with different vegetation. Int. J. Coal Sci. Technol. 2014, 1, 198–206. [Google Scholar] [CrossRef]
- Rujner, H.; Leonhardt, G.; Marsalek, J.; Perttu, A.-M.; Viklander, M. The effects of initial soil moisture conditions on swale flow hydrographs. Hydrol. Process. 2018, 32, 644–654. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Q.; Li, J. Study on the Runoff Generation Process on the Slope with Numerical Method. J. Sediment Res. 2001, 4, 61–67. [Google Scholar] [CrossRef]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef]
- Rujner, H.; Leonhardt, G.; Marsalek, J.; Viklander, M. High-resolution modelling of the grass swale response to runoff inflows with Mike SHE. J. Hydrol. 2018, 562, 411–422. [Google Scholar] [CrossRef]
- García-Serrana, M.; Gulliver John, S.; Nieber John, L. Calculator to Estimate Annual Infiltration Performance of Roadside Swales. J. Hydrol. Eng. 2018, 23, 04018017. [Google Scholar] [CrossRef]
- Wilson, C.A.M.E. Flow resistance models for flexible submerged vegetation. J. Hydrol. 2007, 342, 213–222. [Google Scholar] [CrossRef]
- Seo, Y.; Park, S.Y.; Schmidt, A.R. Implication of the flow resistance formulae on the prediction of flood wave propagation. Hydrol. Sci. J. 2016, 61, 683–695. [Google Scholar] [CrossRef]
- Elmoaty, M.; Elsamman, T. Manning roughness coefficient in vegetated open channels. Water Sci. 2020, 34, 121–128. [Google Scholar] [CrossRef]
- Cowan, W.L. Estimating Hydraulic Roughness Coefficients. Agric. Eng. 1956, 121, 473–475. [Google Scholar]
- Yousef, Y.A.; Wanielista, M.P.; Harper, H.H.; Pearce, D.; Tolbert, R.D. Best Management Practices: Removal of Highway Contaminants by Roadside Swales; Final Report; University of Central Florida, Florida Department of Transportation: Orlando, FL, USA, 1985; p. 166. [Google Scholar]
- Deletic, A. Sediment Behaviour in Overland Flow over Grassed Areas; University of Aberdeen (United Kingdom): Aberdeen, UK, 2000. [Google Scholar]
- Davis, A.P.; Stagge, J.H.; Jamil, E.; Kim, H. Hydraulic performance of grass swales for managing highway runoff. Water Res. 2012, 46, 6775–6786. [Google Scholar] [CrossRef]
- Stagge, J. Field Evaluation of Hydrologic and Water Quality Benefits of Grass Swales for Managing Highway Runoff. Master’s Thesis, Department Civil & Environmental Engineering, University of Maryland, College Park, MD, USA, 2006. [Google Scholar]
- Shafique, M.; Kim, R.; Kyung-Ho, K. Evaluating the Capability of Grass Swale for the Rainfall Runoff Reduction from an Urban Parking Lot, Seoul, Republic of Korea. Int. J. Environ. Res. Public Health 2018, 15, 537. [Google Scholar] [CrossRef]





| Fitting Formula | ||
|---|---|---|
| Q = 1.00 m3/h | h-L | h = −3.00 × 10−5L4 + 1.10 × 10−3L3 − 1.12 × 10−2L2 − 2.75 × 10−2L + 1.80 |
| Q-L | Q = −1.27 × 10−5L4 + 4.60 × 10−4L3 − 4.28 × 10−3L2 − 2.05 × 10−2L + 1.00 | |
| Q = 1.50 m3/h | h-L | h = 1.33 × 10−5L4 − 4.00 × 10−4L3 + 2.67 × 10−3L2 − 5.50 × 10−2L + 2.55 |
| Q-L | Q = 6.00 × 10−6L4 − 1.67 × 10−4L3 + 1.25 × 10−3L2 − 4.10 × 10−2L + 1.50 | |
| Q = 2.00 m3/h | h-L | h = 5.33 × 10−6L4 − 2.00 × 10−4L3 + 2.67 × 10−3L2 − 6.50 × 10−2L + 3.13 |
| Q-L | Q = 3.33 × 10−6 L4 − 1.27 × 10−4L3 + 2.12 × 10−3L2 − 5.78 × 10−2L + 2.00 | |
| Q = 3.00 m3/h | h-L | h = 2.67 × 10−6 L4 − 1.33 × 10−4L3 + 2.33 × 10−3L2 − 5.67 × 10−2L + 4.04 |
| Q-L | Q = 2.00 × 10−6L4 − 1.13 × 10−4L3 + 2.55 × 10−3L2 − 6.82 × 10−2L + 3.00 | |
| Q = 4.00 m3/h | h-L | h = 1.97 × 10−5L4 − 1.05 × 10−3L3 + 1.82 × 10−2L2 − 1.46 × 10−1L + 4.80 |
| Q-L | Q = 2.87 × 10−5L4 − 1.50 × 10−3L3 + 2.59 × 10−2L2 − 2.06 × 10−1L + 4.00 | |
| Distance from Inlet (m) | Inflow Rate (m3/h) | ||||
|---|---|---|---|---|---|
| 1.00 | 1.50 | 2.00 | 3.00 | 4.00 | |
| 5 | 16.00 | 12.67 | 12.50 | 9.67 | 8.75 |
| 10 | 30.00 | 26.00 | 23.00 | 17.33 | 17.00 |
| 15 | 36.00 | 39.33 | 32.50 | 24.33 | 21.75 |
| 20 | 47.00 | 46.00 | 39.50 | 31.00 | 29.25 |
| Inflow Rate (m3/h) | a′ | b′ | R2 |
|---|---|---|---|
| 1.00 | 0.978 | 0.462 | 0.996 |
| 1.50 | 0.824 | 0.526 | 0.999 |
| 2.00 | 0.773 | 0.579 | 0.999 |
| 3.00 | 0.740 | 0.638 | 0.999 |
| 4.00 | 0.709 | 0.725 | 0.999 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Qiu, R.; Xia, X.; Li, X.; Zhang, C.; Wang, W. A Modified Manning’s Equation for Estimating Flow Rate in Grass Swales under Low Inflow Rate Conditions. Water 2024, 16, 1613. https://doi.org/10.3390/w16111613
Wang J, Qiu R, Xia X, Li X, Zhang C, Wang W. A Modified Manning’s Equation for Estimating Flow Rate in Grass Swales under Low Inflow Rate Conditions. Water. 2024; 16(11):1613. https://doi.org/10.3390/w16111613
Chicago/Turabian StyleWang, Jianlong, Rongting Qiu, Xu Xia, Xiaoning Li, Changhe Zhang, and Wenhai Wang. 2024. "A Modified Manning’s Equation for Estimating Flow Rate in Grass Swales under Low Inflow Rate Conditions" Water 16, no. 11: 1613. https://doi.org/10.3390/w16111613
APA StyleWang, J., Qiu, R., Xia, X., Li, X., Zhang, C., & Wang, W. (2024). A Modified Manning’s Equation for Estimating Flow Rate in Grass Swales under Low Inflow Rate Conditions. Water, 16(11), 1613. https://doi.org/10.3390/w16111613







