An Evaluation and Reduction Approach for the Ground Vibration Induced by High Dam Flood Discharge
Abstract
1. Introduction
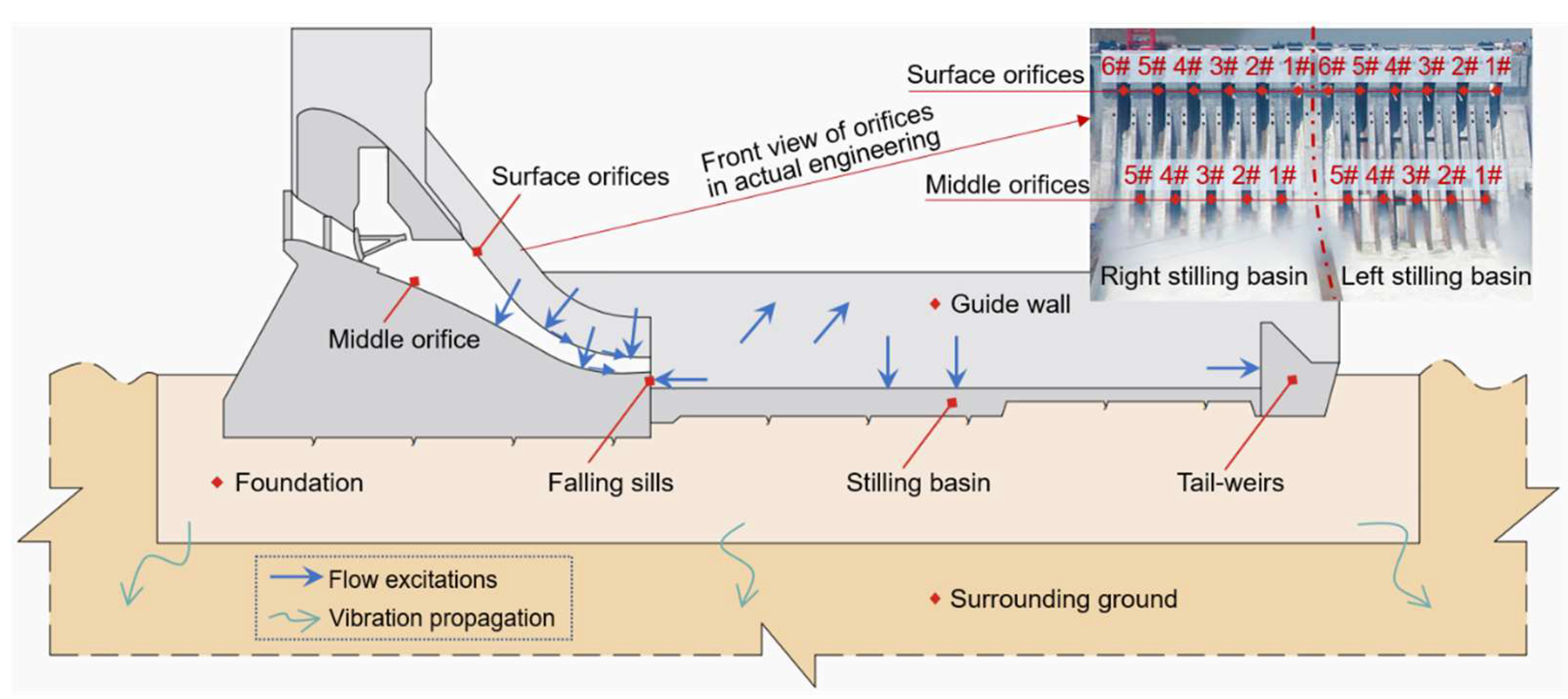
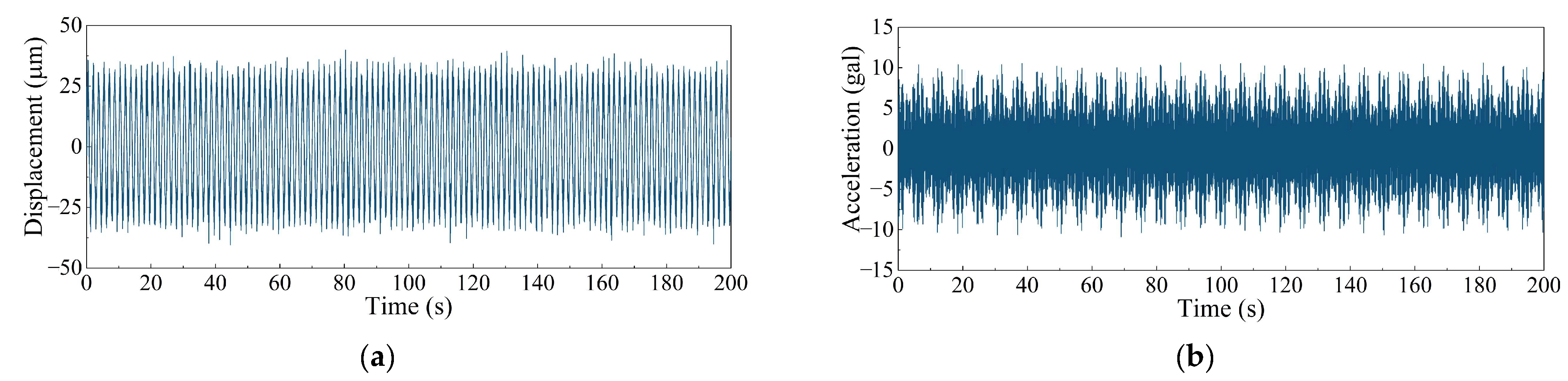
2. Measurement and Processing of Hydrodynamic Loads
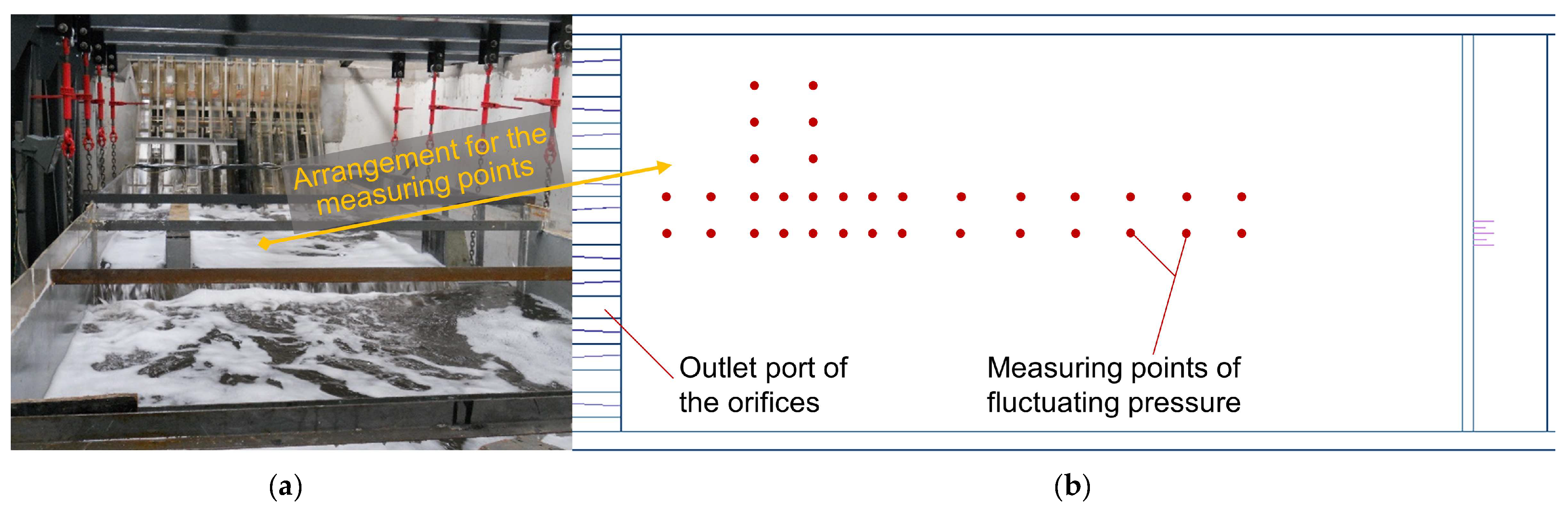
2.1. Measurement of the Hydrodynamic Load in the Stilling Basin
2.2. Three-Dimensional Least Squares Fitting
2.3. Analytical Expression of Hydrodynamic Loads
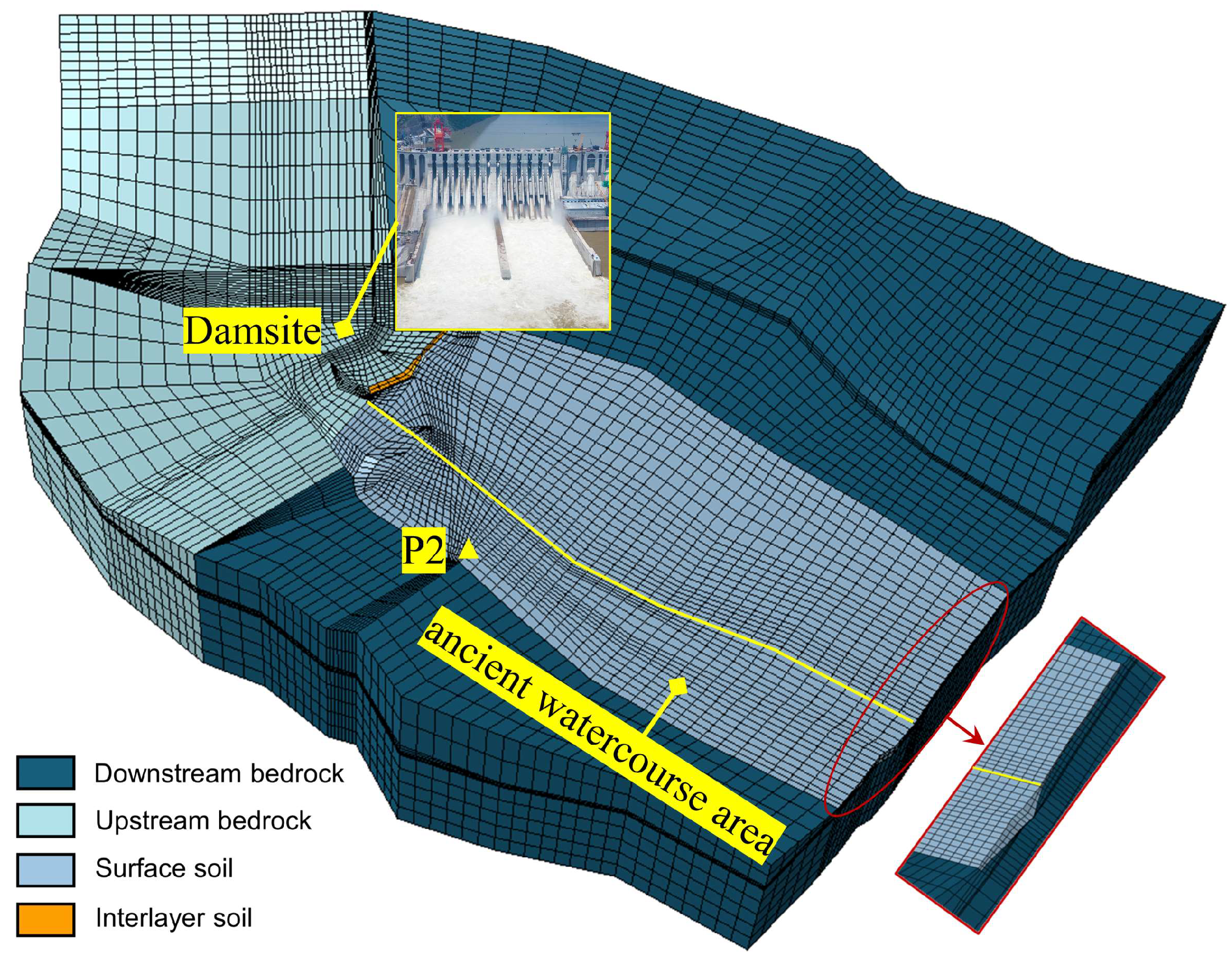
3. Evaluation Approach for Ground Vibration Based on the SBP–Foundation Coupled System
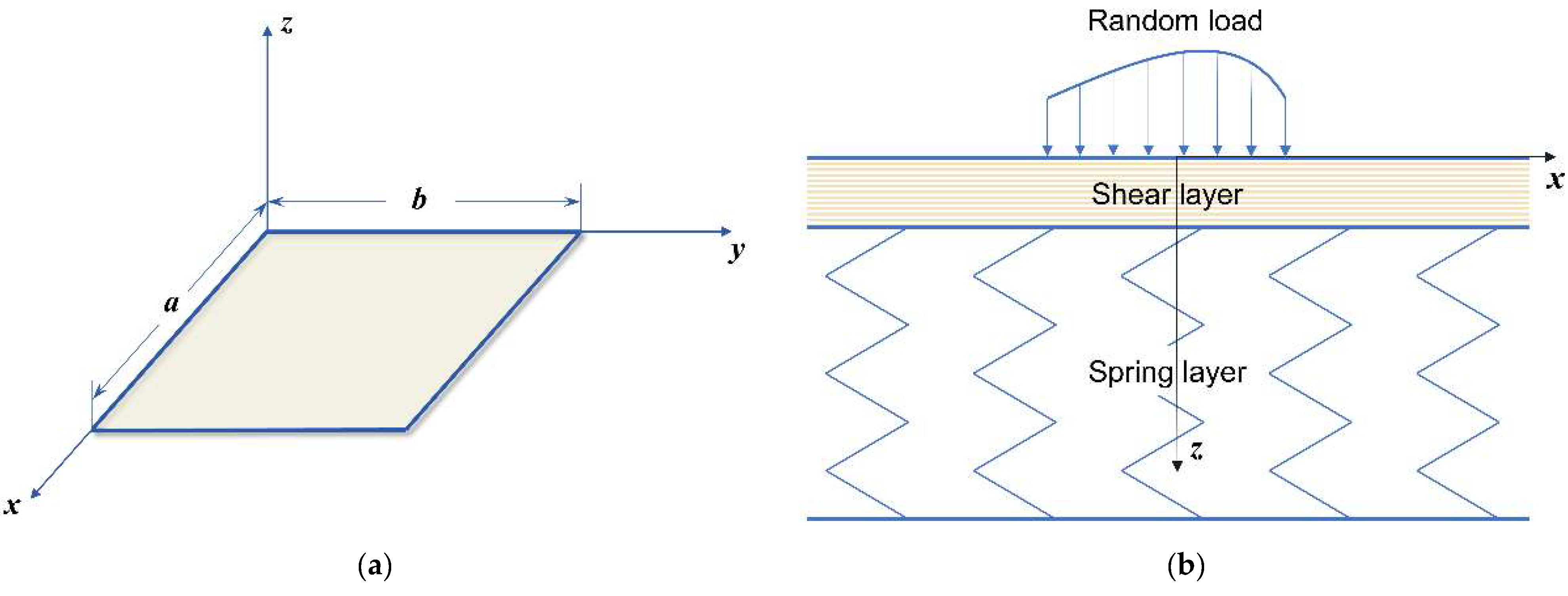
3.1. Theoretical Model of SBP–Foundation Coupled System
3.1.1. Assumptions Applied to the SBP and Foundation
3.1.2. Dynamic Analysis of the SBP–Foundation Coupled System
3.2. Calculation of the Dynamic Response of SBP
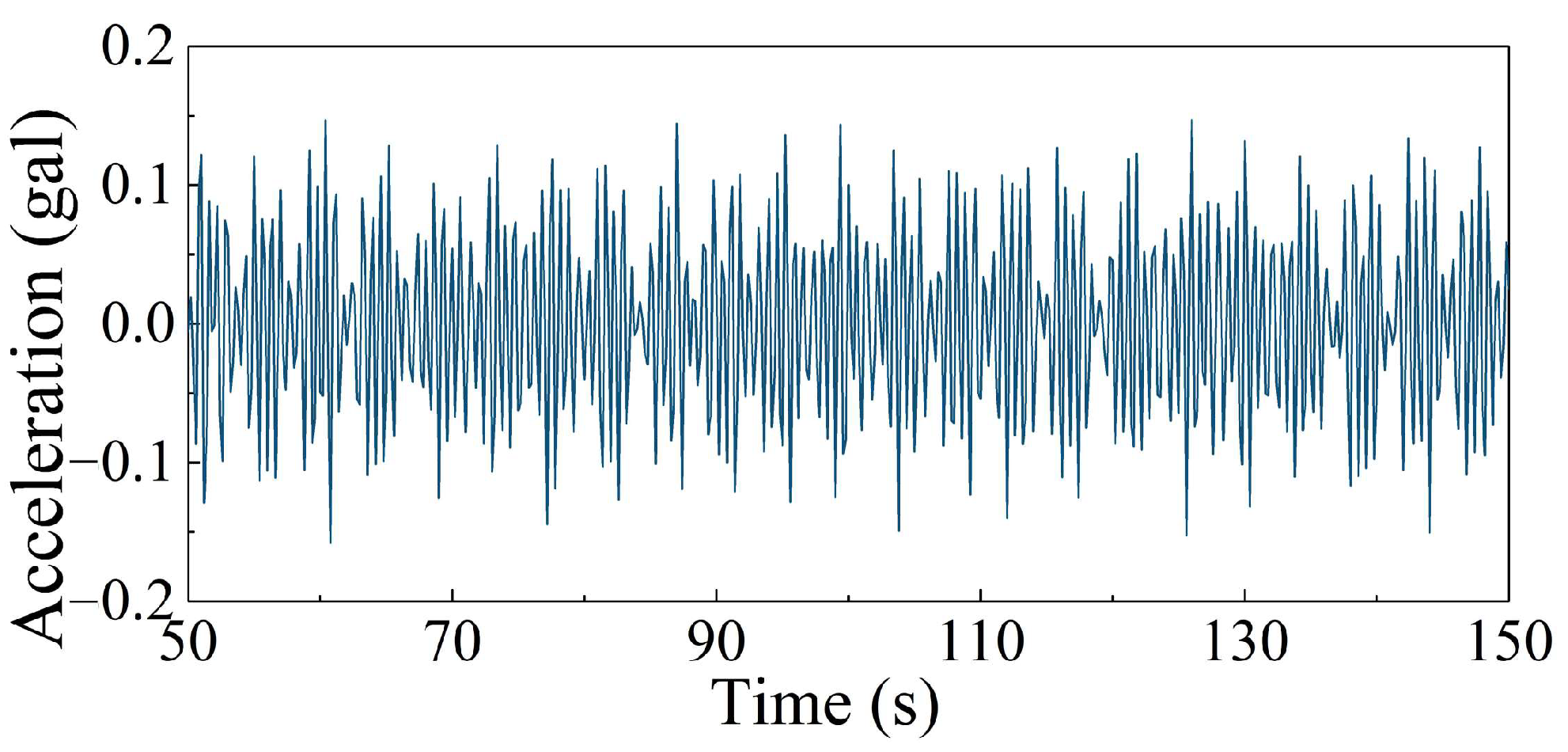
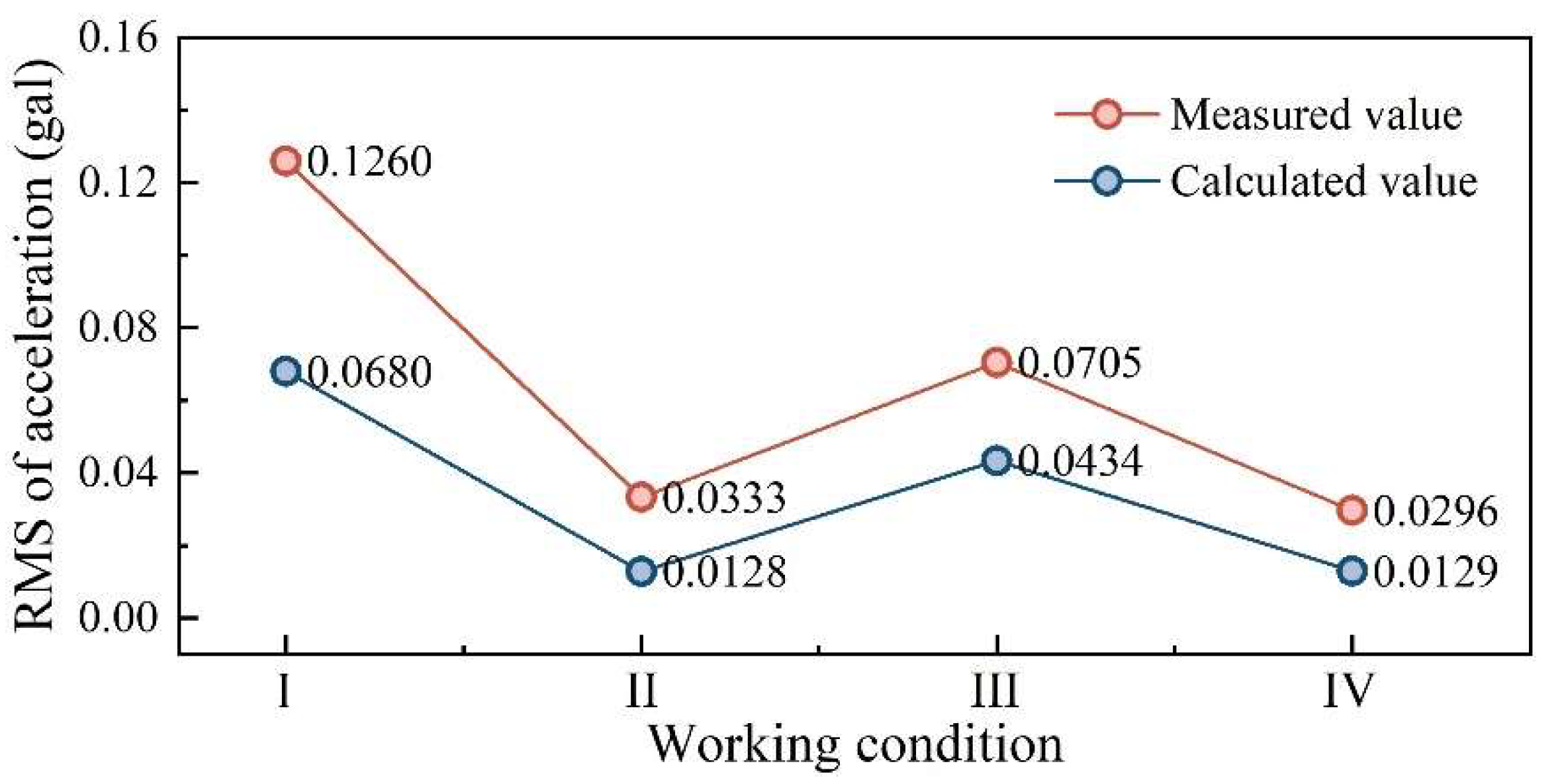
3.3. Verification of the Effectiveness of Evaluation Approach
4. Results and Discussions—Ground Vibration Reduction Based on SBP Optimization
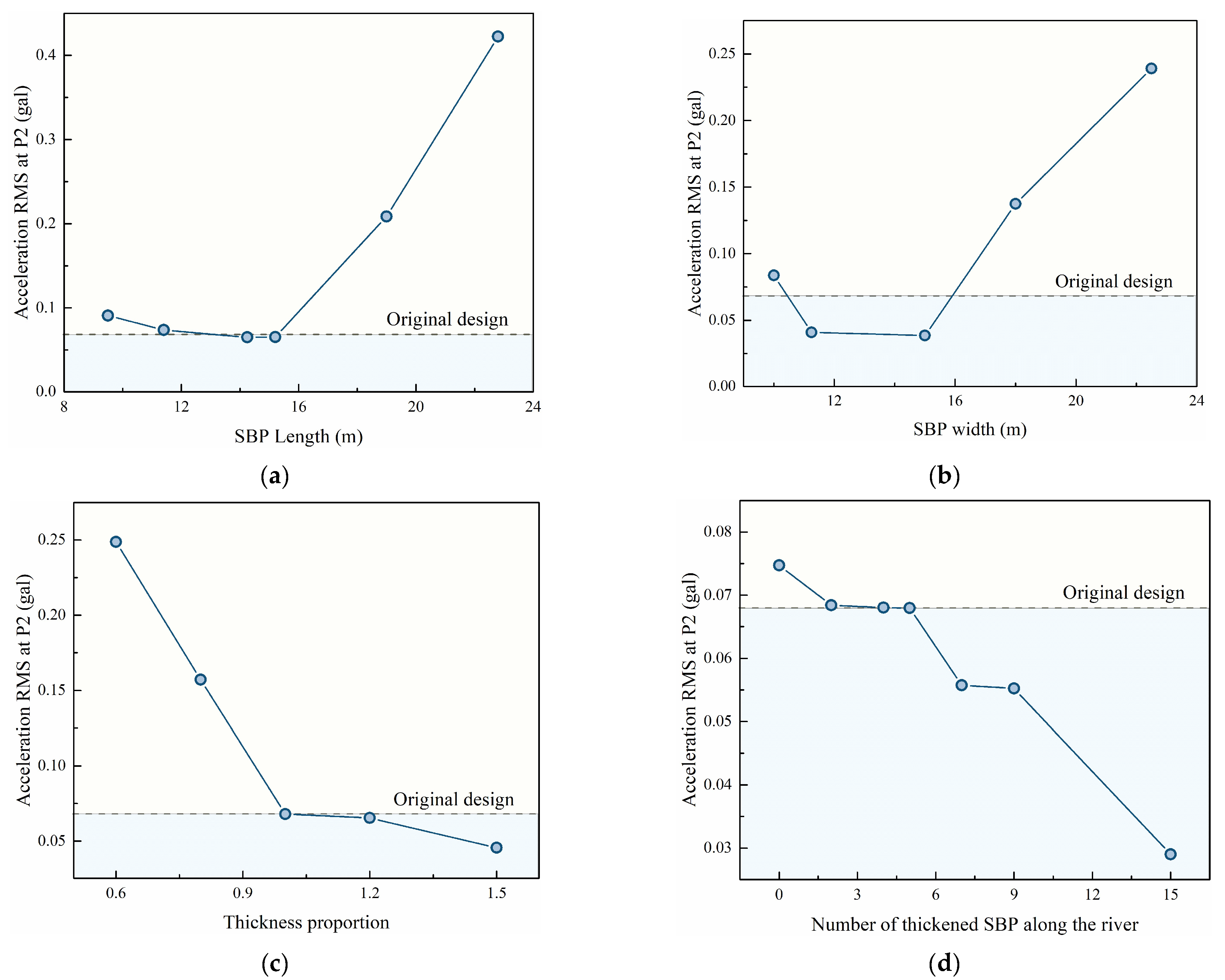
4.1. Sensitivity Analysis for SBP Physical Dimensions to Ground Vibration
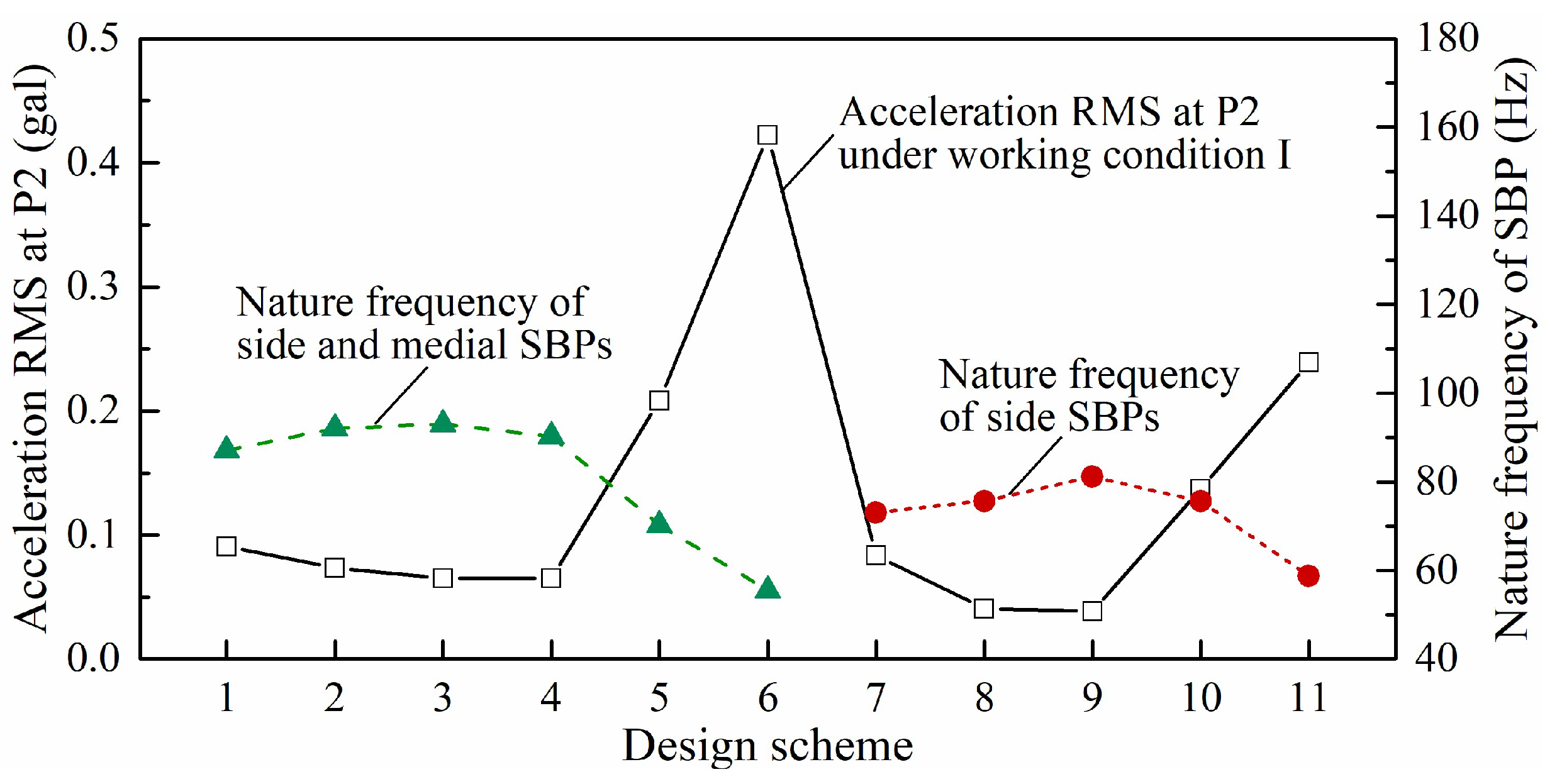
4.2. Discussions on the Ground Vibration Reduction Mechanism Based on SBP Optimization
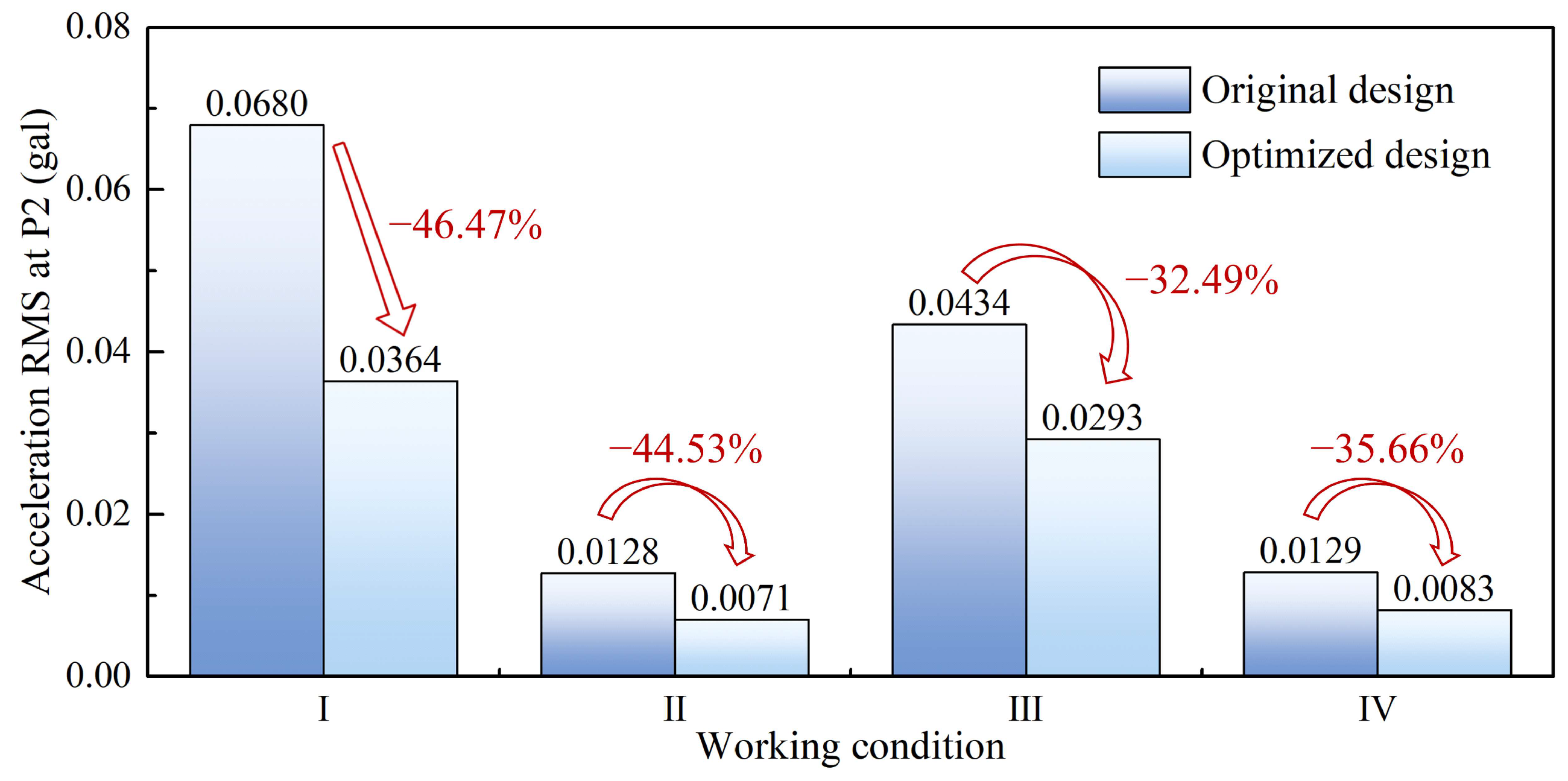
4.3. An Optimized SBP Design and Its Vibration Reduction Effect
5. Conclusions
- (1)
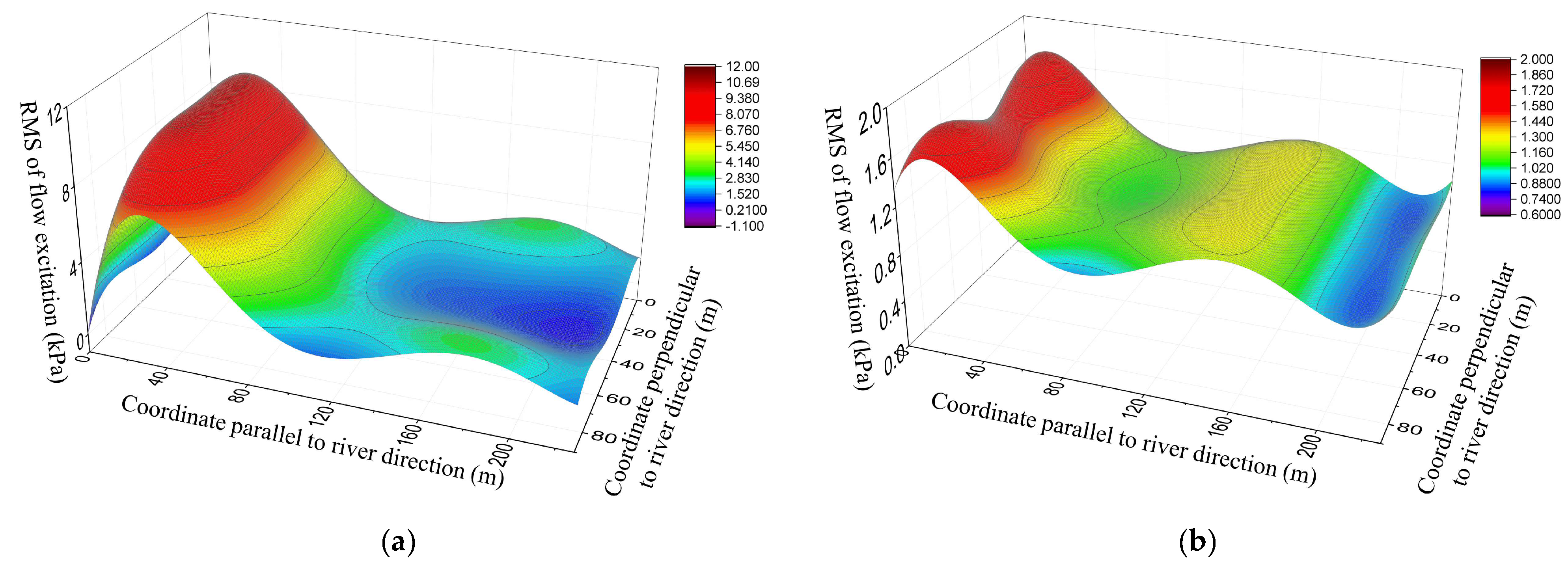
- Based on the hydraulic model tests of Xiangjiaba Hydropower Station (XHS), the spatial distribution for the root-mean-squares (RMSs) of fluctuating pressures acting on the SBPs is obtained and further fitted in the form of polynomials by employing the three-dimensional least squares method. Afterward, the hydrodynamic load is analytically expressed as spatially variable harmonic excitation. As the R2 values corresponding to the data fitting under different working conditions are all close to 1, it is believed that the polynomial fitting functions are sufficiently accurate.
- (2)
- The theoretical model for the SBP–foundation dynamic coupling system is established by considering the SBP as a rectangular plate satisfying the Kirchhoff hypothesis and the SBP as the Pasternak foundation. Thereafter, the dynamic response of SBP is deduced and considered to be the forced vibration under the analytical excitation input. Accordingly, ground vibration is evaluated by applying the acceleration response of every SBP to the corresponding position in the finite element model with infinite element boundary conditions. Compared to some of the available prototype measurement results, the variation trend of evaluation results under different working conditions is consistent with the actual situation, which verifies the effectiveness of the evaluation approach.
- (3)
- In order to investigate ground vibration reduction based on the SBP–foundation coupled system, sensitivity analyses of the physical dimensions of SBPs to ground vibration are conducted. It is found that there is an optimal length and width for the SBP that are beneficial to ground vibration reduction, because the natural frequency of SBP is relatively at a maximum when adopting the optimal length or width. The increase in SBP thickness can also reduce ground vibration, but only a substantial increase in the number of thickened SBPs has a significant vibration reduction effect. Based on the above results, an optimized design for SBP is presented. The analysis result shows that the optimized design can effectively reduce the ground vibration component induced by SBP.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Darbre, G.; De Smet, C.; Kraemer, C. Natural frequencies measured from ambient vibration response of the arch dam of Mauvoisin. Earthq. Eng. Struct. Dyn. 2000, 29, 577–586. [Google Scholar] [CrossRef]
- Zhang, J.W.; Hou, G.; Wang, H.; Zhao, Y.; Huang, J.L. Operation feature extraction of flood discharge structure based on improved variational mode decomposition and variance dedication rate. J. Vib. Control 2019, 26, 229–240. [Google Scholar] [CrossRef]
- Li, H.K.; Liu, B.; Huang, W.; Liu, H.; Wang, G. Vibration load identification in the time-domain of high arch dam under discharge excitation based on hybrid LSQR algorithm. Mech. Syst. Sig. Process. 2022, 177, 109193. [Google Scholar] [CrossRef]
- Kotlyakov, A.V.; Shumakova, E.M.; Artem’Ev, S.A. Dynamics of the coastal zone of the Kuibyshev and Saratov reservoirs in the Tolyatti area and its correlation with the operation regime of the Zhigulevskaya HPP. Water Resour. 2007, 34, 657–662. [Google Scholar] [CrossRef]
- Shumakova, E.M.; Kotlyakov, A.V.; Shumakov, G.V. The effect of vibrations in the Zhigulevskii hydropower structure on soils in the nearby territories of Tolyatti City. Water Resour. 2010, 37, 306–310. [Google Scholar] [CrossRef]
- Lyatkher, V.M.; Komel’kov, L.V.; Mazhbits, G.L. Seismic effects caused by discharged water through the waterworks. Int. J. Altern. Energy Ecol. 2015, 165, 70–84. [Google Scholar] [CrossRef]
- Wang, X.; Hu, Y.A.; Luo, S.Z.; Zhang, L.C.; Wu, B. Prototype observation and influencing factors of environmental vibration induced by flood discharge. Water Sci. Eng. 2017, 10, 78–85. [Google Scholar] [CrossRef]
- Liang, C.; Zhang, J.L.; Lian, J.J.; Liu, F.; Li, X.Y. Probabilistic analysis for the response of nonlinear base isolation system under the ground excitation induced by high dam flood discharge. Earthq. Eng. Eng. Vib. 2017, 16, 841–857. [Google Scholar] [CrossRef]
- Lian, J.J.; Chen, L.; Liang, C.; Liu, F. Presentation and verification of an optimal operating scheme aiming at reducing the ground vibration induced by high dam flood discharge. Int. J. Environ. Res. Public Health 2020, 17, 377. [Google Scholar] [CrossRef]
- Zhang, C. Recent developments on seismic safety evaluation of concrete dams. Earthq. Eng. Resil. 2022, 1, 7–20. [Google Scholar] [CrossRef]
- Fernández-Ruiz, J.; Rodríguez, L.E.M.; Costa, P.A.; Martínez-Díaz, M. Benchmarking of two three-dimensional numerical models in time/space domain to predict railway-induced ground vibrations. Earthq. Eng. Eng. Vib. 2021, 20, 242–256. [Google Scholar] [CrossRef]
- Colaço, A.; Costa, P.A.; Ferreira, C.; Parente, C.; Fernandez-Ruiz, J. Prediction of ground-borne vibration induced by impact pile driving: Numerical approach and experimental validation. Earthq. Eng. Eng. Vib. 2023, 22, 921–935. [Google Scholar] [CrossRef]
- Zhang, Y.; Lian, J.J.; Liu, F.; Zhang, W.J.; Li, S.H. Influencing factors of the ground vibration induced by flood discharge of high dams based on model experiments. J. Vib. Shock 2016, 35, 30–47. (In Chinese) [Google Scholar]
- Zhang, L.C.; Fan, X.M.; Luo, S.Z.; Wang, Y.J. Prediction method of ground vibration induced by flood discharge and energy dissipation of high dams. Adv. Sci. Technol. Water Resour. 2018, 38, 66–69. (In Chinese) [Google Scholar]
- Yin, R.G.; Zhang, J.H.; Zhang, J.M. Vibration source and shock absorption scheme research of near-field vibration caused by flood discharge and energy dissipation of a stilling pool. In Proceedings of the Geo-Shanghai 2014, Shanghai, China, 26–28 May 2014. [Google Scholar]
- Lian, J.J.; Zhang, Y.; Liu, F.; Zhao, Q. Analysis of the ground vibration induced by high dam flood discharge using the cross wavelet transform method. J. Renew. Sustain. Energy 2015, 7, 043146. [Google Scholar] [CrossRef]
- Narayanan, R. Pressure fluctuations beneath submerged jump. J. Hydraul. Div. 1978, 104, 1331–1342. [Google Scholar] [CrossRef]
- Armenio, V.; Toscano, P.; Fiorotto, V. On the effects of a negative step in pressure fluctuations at the bottom of a hydraulic jump. J. Hydraul. Res. 2000, 38, 359–368. [Google Scholar] [CrossRef]
- Liu, P.Q.; Li, A.H. Fluctuating uplift acting on rock blocks at the bottom of river bed and estimation of the limiting scour depth. J. Hydraul. Res. 2007, 45, 478–485. [Google Scholar]
- Frýba, L. History of Winkler Foundation. Veh. Syst. Dyn. 1995, 24, 7–12. [Google Scholar] [CrossRef]
- Filonenko-Borodich, M.M. Some approximate theories of elastic foundation. Uchenyie Zap. Mosk. Gos. Univ. Mekhanika 1940, 46, 3–18. [Google Scholar]
- Pasternak, P.L. On a New Method of Analysis of an Elastic Foundation by Means of Two Foundation Constants; Gosudarstvennoe Izdatelstvo Literaturi po Stroitelstvu I Arkhitekture: Moskow, Russia, 1954; pp. 1–56. (In Russian) [Google Scholar]
- Hetényi, M. Beams on Elastic Foundations; The University of Michigan Press: Ann Arbor, MI, USA, 1946. [Google Scholar]
- Zhang, J.M.; Peng, Y.; Xu, W.L. Hydraulic prediction of near-field vibrations induced by releasing flood. J. Hydraul. Eng. 2017, 143, 05017002. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, J.M.; Xu, W.L.; Rubinato, M. Experimental optimization of gate-opening modes to minimize near-field vibrations in hydropower stations. Water 2018, 10, 1435. [Google Scholar] [CrossRef]
- Ministry of Water Resources of the People’s Republic of China. Specification for Normal Hydraulic Model Test (SL 155-2012); China Water & Power Press: Beijing, China, 2012.
- Xu, Z.G. Elasticity; Higher Education Press, Inc.: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Cao, Z.Y.; Yang, S.T. The Theory of Thick Plate Dynamics and Its Applications; Science Press: Beijing, China, 1983. [Google Scholar]
- Wang, X.; Luo, S.Z.; Zhang, L.C.; Chen, C.; Li, Z.Y.; Wu, X.Y. Flow-induced Vibration of Stilling Basin in One of Giant Hydropower Stations. In Proceedings of the Earth and Space, St. Louis, MI, USA, 27–29 October 2014; pp. 563–570. [Google Scholar]
- Biot, M.A. Bending of an Infinite Beam on an Elastic Foundation. J. Appl. Mech. 1937, 4, A1–A7. [Google Scholar] [CrossRef]
- Dong, J.; Peng, L. Researches on two-parameter model and foundation beams. J. Wuhan Univ. Hydraul. Electr. Eng. 1991, 24, 427–438. (In Chinese) [Google Scholar]
- Lin, J.Y.; Lian, J.J. Calculation for the amplitudes of fluctuating pressures acting at a single point and on an area under the impact of binary jet. J. Hydraul. Eng. 1988, 12, 34–40. (In Chinese) [Google Scholar]
- Sheng, Y.; Huang, Y. A free rectangular plate on the two-parameter elastic foundation. Appl. Math. Mech. 1987, 8, 325–338. [Google Scholar] [CrossRef]
- Cheng, X.S. A free rectangular plate on elastic foundation. Appl. Math. Mech. 1992, 13, 977–982. [Google Scholar] [CrossRef]
- Qu, Q.Z.; Liang, X.F.; Dong, X.J. Problem of rectangular plates with four free edges on Winkler elastic foundations. Struct. Environ. Eng. 1998, 2, 31–37. (In Chinese) [Google Scholar]
- Bhat, R.B. Natural frequencies of rectangular plates using characteristic orthogonal polynomials in Rayleigh-Ritz method. J. Sound Vib. 1985, 102, 493–499. [Google Scholar] [CrossRef]
- Liu, P.Q.; Li, A.H. Model discussion of pressure fluctuations propagation within lining slab joints in stilling basins. J. Hydral. Eng. 2007, 133, 618–624. [Google Scholar] [CrossRef]
- Yao, Z. Research on the Flow-Induced Vibration Response Characteristics of Slabs in Plunge Pool of Jinping-I High Arch Dam; Tianjin University: Tianjin, China, 2013. (In Chinese) [Google Scholar]
- Zhao, C.B. Coupled method of finite and dynamic infinite elements for simulating wave propagation in elastic solids involving infinite domains. Sci. China Ser. E Technol. Sci. 2010, 53, 1678–1687. [Google Scholar]
- Ministry of Water Resources of the People’s Republic of China. Design Specification for Spillway (SL253-2018); China Water & Power Press: Beijing, China, 2018.
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering; Prentice Hall: Bergen, NJ, USA, 2001. [Google Scholar]

| Discharge Scheme | Upstream Water Level (m) | Downstream Water Level (m) | Opening Ratios of Orifices | Degree of Fitting (R2) | |
|---|---|---|---|---|---|
| 1#–6# Surface Orifices (m) | 1#–5# Middle Orifices (m) | ||||
| (a) | 372.78 | 275.85 | Fully opened | Closed | 0.9661 |
| (b) | 380 | 277.15 | Fully opened | Closed | 0.9786 |
| (c) | 353 | 271.81 | Closed | 2.5 | 0.8981 |
| (d) | 353 | 272.89 | Closed | Fully opened | 0.9318 |
| (e) | 370 | 274.30 | Closed | Fully opened | 0.9459 |
| (f) | 380 | 276.11 | Fully opened | Fully opened | 0.9120 |
| Parameters of SBP | Parameters of Foundation | ||||
|---|---|---|---|---|---|
| Parameter | Notation | Value | Parameter | Notation | Value |
| Elasticity modulus | E | 30 GPa | Compression modulus | 10 GPa | |
| Poisson’s ratio | μ | 0.167 | Poisson’s ratio | 0.3 | |
| Density | ρ | 2450 kg/m3 | |||
| Material | Geotechnical Type | Density (kg/m3) | Elastic Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|---|
| Surface soil of the ancient watercourse area | Gravel clay | 1670 | 60 | 0.38 |
| Interlayer soil of the ancient watercourse area | Sand gravel | 2125 | 90 | 0.39 |
| Downstream bedrock | Silty mudstone | 2580 | 11,300 | 0.3 |
| Upstream bedrock | Weak-weathered medium-fine sandstone | 2600 | 38,000 | 0.225 |
| Working Condition | Stilling Basin Put into Operation |
Discharge Scheme |
|---|---|---|
| I | Right | (a) |
| II | (c) | |
| III | Left | (a) |
| IV | (c) |
| Optimization Type | Design Schemes | SBP Length (m) | SBP Width (m) | Thickened SBP | Downstream SBP | Acceleration RMS at P2 (gal) | ||
|---|---|---|---|---|---|---|---|---|
| Thickness (m) | SBP Number Along River | Thickness (m) | SBP Number Along River | |||||
| Length change | 1 | 9.5 | U | U | U | U | U | 0.09083 |
| 2 | 11.4 | U | U | U | U | U | 0.07376 | |
| 3 | 14.25 | U | U | U | U | U | 0.06503 | |
| 4 | 15.2 | U | U | U | U | U | 0.06531 | |
| 5 | 19 | U | U | U | U | U | 0.20859 | |
| 6 | 22.8 | U | U | U | U | U | 0.42226 | |
| Width change | 7 | U | 10 | U | U | U | U | 0.08364 |
| 8 | U | 11.25 | U | U | U | U | 0.04092 | |
| 9 | U | 15 | U | U | U | U | 0.03856 | |
| 10 | U | 18 | U | U | U | U | 0.13738 | |
| 11 | U | 22.5 | U | U | U | U | 0.23907 | |
| Thickness change (of equal proportions) | 12 | U | U | 6 | U | 3.6 | U | 0.24868 |
| 13 | U | U | 8 | U | 4.8 | U | 0.15715 | |
| 14 | U | U | 10 | U | 6 | U | 0.06802 | |
| 15 | U | U | 12 | U | 7.2 | U | 0.06541 | |
| 16 | U | U | 15 | U | 9 | U | 0.04560 | |
| Thickness change (in the number of thickened SBPs) | 17 | U | U | U | 0 | U | 15 | 0.07473 |
| 18 | U | U | U | 2 | U | 13 | 0.06842 | |
| 19 | U | U | U | 4 | U | 11 | 0.06802 | |
| 20 | U | U | U | 5 | U | 10 | 0.06795 | |
| 21 | U | U | U | 7 | U | 8 | 0.05573 | |
| 22 | U | U | U | 9 | U | 6 | 0.05524 | |
| 23 | U | U | U | 15 | U | 0 | 0.02899 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lian, J.; Zheng, Y.; Liang, C.; Li, Y.; Ma, B.; Liu, F.; Yao, Y. An Evaluation and Reduction Approach for the Ground Vibration Induced by High Dam Flood Discharge. Water 2024, 16, 1559. https://doi.org/10.3390/w16111559
Lian J, Zheng Y, Liang C, Li Y, Ma B, Liu F, Yao Y. An Evaluation and Reduction Approach for the Ground Vibration Induced by High Dam Flood Discharge. Water. 2024; 16(11):1559. https://doi.org/10.3390/w16111559
Chicago/Turabian StyleLian, Jijian, Yan Zheng, Chao Liang, Yutong Li, Bin Ma, Fang Liu, and Ye Yao. 2024. "An Evaluation and Reduction Approach for the Ground Vibration Induced by High Dam Flood Discharge" Water 16, no. 11: 1559. https://doi.org/10.3390/w16111559
APA StyleLian, J., Zheng, Y., Liang, C., Li, Y., Ma, B., Liu, F., & Yao, Y. (2024). An Evaluation and Reduction Approach for the Ground Vibration Induced by High Dam Flood Discharge. Water, 16(11), 1559. https://doi.org/10.3390/w16111559







