Risk Identification of Mountain Torrent Hazard Using Machine Learning and Bayesian Model Averaging Techniques

Abstract

Frequent mountain torrent disasters have caused significant losses to human life and wealth security and restricted the economic and social development of mountain areas. Therefore, accurate identification of mountain torrent hazards is crucial for disaster prevention and reduction. In this study, based on historical mountain torrent hazards, a mountain torrent hazard prediction model was established by using Bayesian Model Average (BMA) and three classic machine learning algorithms (gradient-boosted decision tree (GBDT), backpropagation neural network (BP), and random forest (RF)). The mountain torrent hazard condition factors used in modeling were distance to river, elevation, precipitation, slope, gross domestic product (GDP), population, and land use type. Based on the proposed BMA model, flood risk maps were produced using GIS. The results demonstrated that the BMA model significantly improved upon the accuracy and stability of single models in identifying mountain torrent hazards. The F1-values (comprehensively displays the Precision and Recall) of the BMA model under three sets of test samples at different locations were 3.31–24.61% higher than those of single models. The risk assessment results of mountain torrents found that high-risk areas were mainly concentrated in the northern border and southern valleys of Yuanyang County, China. In addition, the feature importance analysis result demonstrated that distance to river and elevation were the most important factors affecting mountain torrent hazards. The construction of projects in mountainous areas should be as far away from rivers and low-lying areas as possible. The results of this study can provide a scientific basis for improving the identification methods of mountain torrent hazards and assisting decision-makers in the implementation of appropriate measures for mountain torrent hazard prevention and reduction.

1. Introduction

Globally, a mountain torrent hazard is one of the most serious natural disasters [1,2]. Their extremely destructive and sudden nature makes mountain torrent hazards more prone to causing enormous numbers of casualties and immense property loss [3]. Mountain torrent hazards have become a crucial problem restricting human safety and healthy economic and social development in mountainous areas. The mountain torrent hazard statistics in 136 countries according to the World Meteorological Organization (WMO) show that the losses caused by mountain torrent hazards have reached millions of dollars annually and more than 70% of countries consider mountain torrent hazards the most serious natural disaster [4]. Recent studies have demonstrated that climate change in the future will further increase the risk of mountain torrents [5,6]. Therefore, it is necessary to explore accurate and stable prediction methods of mountain torrent hazards in order to reduce the losses caused by mountain torrent hazards.

In order to understand the risk of mountain torrents, scholars have developed various risk assessment methods, including disaster investigation, numerical simulation, and indicator evaluation methods [7,8,9]. These methods have played a very important role in the prevention and management of mountain torrent hazards. The disaster investigation method evaluates the regional mountain torrent risk mainly by collecting historical mountain flood, hydrological, meteorological, and socio-economic data, which is the most classic and traditional method for assessing the risk of mountain torrents [3]. This method can accurately reflect the risk of the surveyed object. Due to the limitations of disaster investigation points, there may be significant deviation in the estimated risk at uninvestigated points. The numerical simulation method characterizes the risk of mountain torrents based on the results of mountain flood processes (such as inundation depth and duration) simulated by a hydrodynamic model [10]. The numerical simulation results of mountain torrent hazards can characterize the risk of each grid. These results can compensate for the shortcomings of disaster investigation methods in terms of investigation points. However, the parameter uncertainty of hydrological models and the limitations of validation data [11] may affect the reliability of mountain torrent risk assessment results based on numerical simulation methods. The indicator evaluation method is one of the most widely used methods for mountain torrent risk assessment [12]. This method is constructed by the evaluation model by selecting indicators based on risk theory and the research area to assess mountain torrent risk. The core of the indicator weight method is the determination of the weight [13]. The Analytic Hierarchy Process [14], Entropy Weight [15], and CRITIC Method [16] are commonly used methods for determining weights. However, there is no unified paradigm for indicator selection and weight determination in mountain torrent risk assessment [17]. The indicator selection and weight determination method mainly relies on researchers’ understanding of the problem, leading to uncertainty in the evaluation results.

In recent years, with the rapid development of big data and machine learning methods, research on mountain torrent risk based on machine learning methods has attracted the attention of many scholars [18,19,20]. Machine learning methods can accurately predict mountain torrent hazards by capturing the non-linear relationship between conditional factors and feature variables by using sufficient training samples, which provides a new concept for accurately identifying mountain torrent hazards [21]. Many scholars have attempted to apply some machine learning methods to identify the mountain torrent hazard [22,23]. Youssef et al. [22] constructed landslide and flood identification models using logistic regression (LR), random forest (RF), and support vector machine (SVM) algorithms, and plotted multi-hazard maps using the proposed models. The results indicated that RF has the best predictive performance for landslides and floods, with an AUC of 94.9% and 98.7%. Salvati et al. [24] constructed a watershed flood-prone area identification model using support vector regression and three optimization methods (linear kernel, basic classifier, and hyperparameter optimization) based on 201 historical flood maps. The results demonstrated that this method effectively identified floods in the watershed, and the AUC of the test results was above 0.9. Li et al. [18] established a mountain flood susceptibility model using LR and RF, and mapped flash flood susceptibility for the Songhua River. They found that the RF model provided better predictive ability than the LR model. These machine learning methods have achieved good results in the identification, prediction, and risk assessment of mountain torrents. Zhou et al. [25] focused on the Lianggoushan watershed at the southern foot of Boroconu Mountain as the research subject and constructed a flood-level prediction model using six machine learning methods, including artificial neural network (ANN), k-nearest neighbor (KNN), recurrent neural network (RNN), long short-term memory neural network (LSTM), support vector regression (SVR), and RF. The results showed that LSTM and RF have better predictive performance. It can be found from the above literature that a single machine learning method may have significant uncertainty in different prediction tasks [26,27]. The model often performs well under given test samples, but may perform poorly under new test events [28]. Zhou et al. [29] pointed out that it is almost impossible to find a model that is applicable to all situations. Therefore, the uncertainty of the prediction results of a single model may pose great challenges to the accurate identification and risk assessment of mountain torrents.

In order to overcome this issue, several technologies and methods (such as BMA or frequency model average) have been developed to integrate results from different sources [30]. Among them, BMA is one of the most widely used methods to reduce model uncertainty [29,31,32]. BMA is a statistical method that uses probability density functions (PDFs) to provide probability results [27,33]. In the field of hydrology, BMA is often used for improving the prediction and reducing the uncertainty of analyses [28]. For example, Asfaw et al. [34] used BMA to fuse four high-resolution satellite rainfall estimation (SRE) products to improve the estimation of rainfall. The results showed that the BMA model significantly reduced the error in estimating rainfall. Moknatian and Mukundan [30] applied the BMA method and streamflow simulations of the SWAT-hillslope model (SWAT-HS) to integrated daily runoff prediction. The results found that the application of BMA can better understand the reliability and accuracy of SWAT-HS. Huang and Merwade [30] proposed a new algorithm (Metropolis–Hastings) to estimate BMA parameters in order to resolve the insufficient research on the uncertainty of traditional expectation–maximization (EM) algorithms in estimating BMA parameters. They used numerical experiments and system models to test the applicability of the Metropolis–Hastings algorithm under multiple independent Markov chains. The results indicated that the Metropolis–Hastings method provided more information related to the uncertainty of BMA parameters. These studies indicated that the BMA method can effectively improve model stability, which is very useful for improving the credibility of mountain torrent risk identification results. However, to the best of the authors’ knowledge, there are few studies that combine BMA with machine learning methods to accurately identify and assess the risk of mountain torrents.

In summary, the single machine learning method has significant uncertainty in different prediction tasks, which affects the prediction accuracy of mountain torrent models. Therefore, this study attempts to combine BMA with powerful machine learning models to study more accurate and stable methods for identifying mountain torrent hazards, reveal the potential relationship between risks and driving factors, and explore mountain torrent risk assessment methods based on BMA models. Firstly, seven indicators (distance to river, elevation, precipitation, slope, gross domestic product (GDP), population, and land use type) were selected as the conditional factors for predicting mountain torrent hazards, and combined with historical disaster data, three mountain torrent hazard prediction models were constructed based on gradient-boosted decision tree (GBDT), backpropagation neural network (BP), and RF. On this basis, an integrated mountain torrent hazard identification model was established by integrating the results of the three machine learning methods using the BMA method. Finally, the main driving factors affecting mountain torrent hazards were analyzed, and the risk of mountain torrents in Yuanyang County was evaluated using the proposed BMA model. This study can serve as a reference for improving mountain torrent hazard prediction methods.

2. Materials and Methods

2.1. Study Area

Yuanyang is located in the southern part of Yunnan Province, China (102°27′–103°13′ E, 22°49′–23°19′ N). The lowest altitude is 112 m and the highest altitude is 2939.6 m, with a relative elevation difference of 2795.6 m. The annual average temperature is 24.4 °C. The average annual rainfall is 899.5 mm, and rainfall is mainly concentrated from July to September. The terrain of Yuanyang is characterized by a prominent center and lower sides, with a V-shaped development. The rivers of Yuanyang are the Red River and the Fuji River, two major rivers that meander from west to east (Figure 1).

2.2. Data

The research data mainly include digital elevation model (DEM) data, slope, land use type, population, GDP, rainfall, river distribution, historical flooding points, etc. The sources of the above data are as follows. DEM data are obtained via regional and provincial DEM data sharing in China, with a spatial resolution of 12.5 m (Figure 1). River data are provided by the Yunnan Provincial Geographic Information Public Service Platform. The slope and distance to the river are obtained using ArcGIS based on DEM and river data, respectively. The land use, population, and GDP data are sourced from the Resource and Environmental Science Data Registration and Publishing System (https://www.resdc.cn/DOI/DOI.aspx?DOIID=54; https://www.resdc.cn/DOI/DOI.aspx?DOIID=32; https://www.resdc.cn/DOI/DOI.aspx?DOIID=33, accessed on 1 January 2024). The rainfall, historical flooding point, and non-flooded point data are sourced from the evaluation report on flash floods in Yuanyang provided by Yunnan Provincial Hydrological Bureau. The statistical characteristics of 116 sample points (50% of which are mountain torrent hazard points and 50% which are non-mountain torrent hazard points) are shown in

Table 1. Statistical characteristics of sample data.

Statistical Indicator	Elevation (m)	Slope	Population	Rainfall (mm)	Distance to River (m)
Max	2518	0.60	4952	105.5	10,824
Min	164	0.02	0	80	0
Average	1124.62	0.22	386	93.11	2534.02

.

2.3. Applied Machine Learning Method

The selection of candidate models is the foundation for constructing mountain torrent hazard prediction models and also one of the most critical factors affecting model performance. The neural network represented by BP is one of the most widely used methods in machine learning prediction models, which can better capture the non-linear relationship between input and output variables [35]. In recent years, scholars have found that GBDT and RF models that integrate multiple decision trees have higher robustness and are suitable for mining potential relationships between multiple environmental variables and disasters [36,37]. In addition, recent research has shown that among classic machine learning and deep learning methods, GBDT, RF, and BP exhibit superior performance in prediction accuracy [38]. Therefore, considering the significant non-stationarity, non-linearity, and non-periodicity of environmental variable data and flash flood data, combined with the characteristics and applicable conditions of various methods, GBDT, RF, and BP algorithms were selected to construct mountain torrent hazard prediction models as benchmark models for the BMA model.

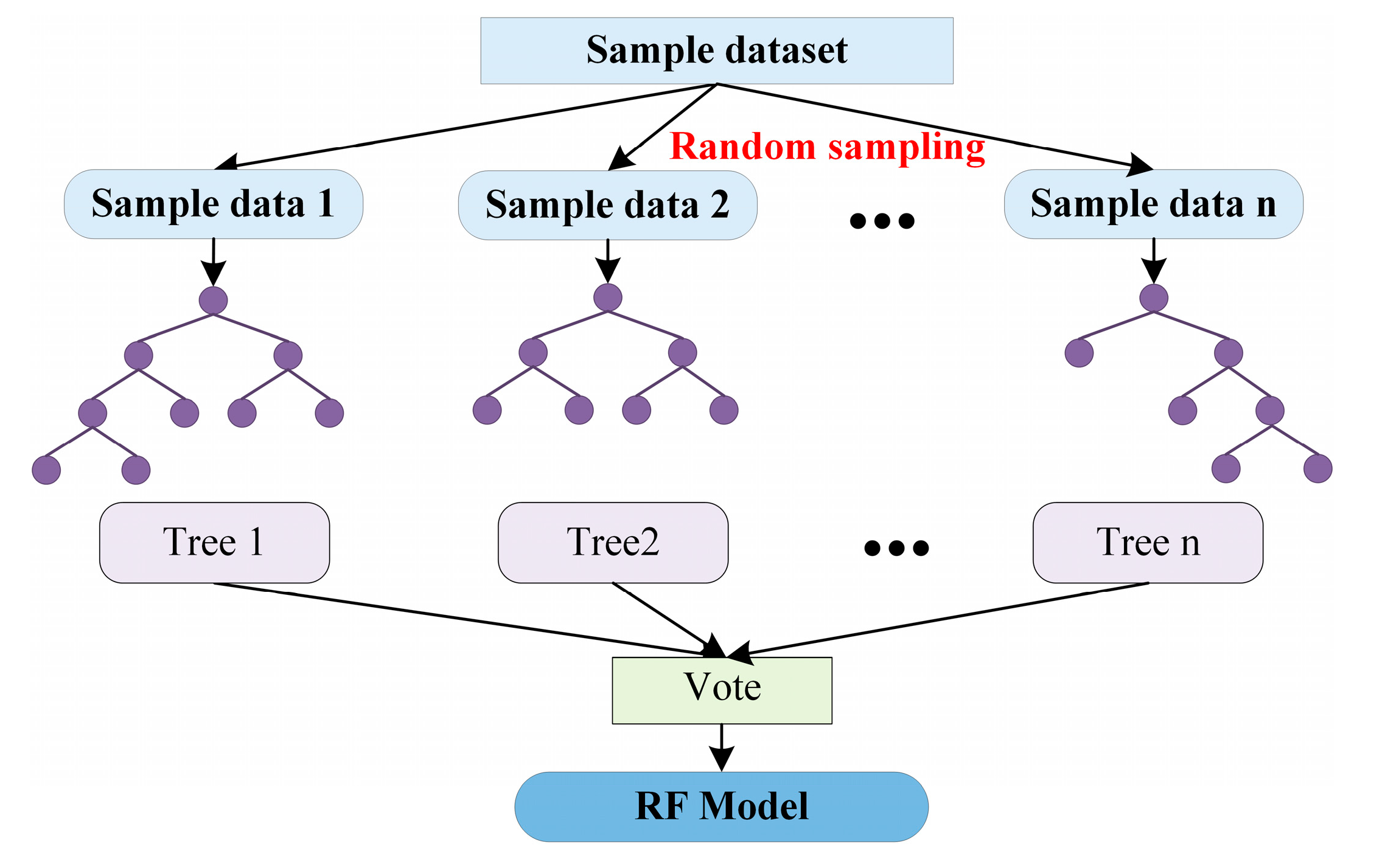
2.3.1. Machine Learning Models

The GBDT algorithm is an ensemble learning algorithm that combines decision tree (DT) and gradient boosting (GB) algorithms. The core of this algorithm is to use the GB algorithm to fit the residuals predicted by the DT in each iteration process. As shown in Figure 2, during each iteration of the GBDT model, the DT always fits the residual of the previous DT along the direction of maximum gradient descent. This process makes the residual of the DT gradually decrease as the number of iterations increase. Finally, the DTs in each iteration process are accumulated to obtain the integrated GBDT model. This algorithm effectively integrates the advantages of DT and GB algorithms, and has been proven to be a high-precision and low-bias model in many classification prediction practices [36,39,40]. In this study, the classification model of GBDT was used to predict mountain torrent hazards. The number of iterations, learning rate, and depth of tree are the main hyperparameters of the GBDT algorithm. The number of iterations and learning rate are a set of related constraints, and the lower the learning rate, the higher the number of iterations. To prevent the model from becoming stuck in overfitting, the number of iterations was set to 10–1000, and the learning rate was between 0 and 1. The depth of tree refers to the maximum depth of the subtree, and excessive depth may cause overfitting in the model. Therefore, the depth of tree was set to 10–100. The detailed modeling process and mathematical description of the GBDT algorithm can be found in Wu et al. [41] and Zhou et al. [29].

The BP neural network is a multi-layer feedforward neural network based on error backpropagation, which is considered the representative of machine learning in the field of data mining [42]. This algorithm utilizes the backpropagation of errors to continuously adjust the weights and thresholds of the network, thereby reducing the sum of squared errors between the output and the expected value. The advantage of the BP neural network is that it can also handle non-linear problems by setting training times or error limits in complex situations, which is particularly suitable for using historical data to find the laws of matter. These characteristics indicate that it can be used in mountain torrent hazard prediction. The BP neural network consists of three parts: input layer, hidden layer, and output layer [35] (Figure 3). The input layer refers to the indicator variables used for mountain torrent hazard prediction; the output layer refers to the predicted mountain torrent hazard. The learning rate, number of hidden layers, and number of nodes in the hidden layers are the main hyperparameters of the BP neural network. The core of BP neural network training lies in continuously adjusting the weights and biases of the network to continuously approach the expected output.

RF is a machine learning algorithm proposed by Leo Breiman in 2001, which combines ensemble learning and random subspace theory [43]. This algorithm introduces random attribute features during the training process of DTs based on the Bagging algorithm. The main idea of the RF algorithm is to use an autonomous sampling method to extract samples from the original training set, making the sample selection random. Based on this, the DT model is established for each sample, and all DT models are combined through voting to obtain the final result (Figure 4). In addition, the optimal cutoff point of the RF algorithm is determined by randomly extracting feature attributes. The randomness of feature selection improves the independence of each DT and enhances the model’s generalization ability. The number of trees and depth of trees are the main hyperparameters of RF. The number of trees refer to the number of decision trees in the forest, with a default value of 100. In this study, the classification model of RF was used to predict mountain torrent hazards.

2.3.2. Model Training and Parameter Optimization

When constructing mountain torrent hazard prediction models using GBDT, BP, and RF algorithms, the sample dataset is input into these models. The x refers to the input variable (seven selected flood sensitivity indicators); y refers to the output variable (whether flood has occurred). On this basis, 70% of the data are selected as training data to construct the mountain torrent hazard prediction models, and 30% of the data are used as validation data to test the performance of GBDT, BP, and RF (

Table 2. Statistical differences between training and testing samples.

Data	Statistical Indicator	Elevation (m)	Slope	Population	Rainfall (mm)	Distance to River (m)
Training	Max	2518	0.60	4952	105.5	10,824
	Min	164	0.02	0	80	0
	Average	1124.62	0.22	386	93.11	2534.02
Testing	Max	2277	0.43	2043	103	8343
	Min	174	0.02	0	80	0
	Average	1321	0.24	255	92	3111

). In addition, in order to test the comprehensive performance of each model under different sample data, three validation samples were extracted from sample dataset D using 3-fold cross-validation. As shown in Figure 5, three sets of training and testing samples were formed by selecting three different test data. GBDT, BP, and RF algorithms were used to construct mountain torrent hazard prediction models for each training sample, and the performance differences of each model were tested on three test samples.

Parameter optimization is also an important factor affecting the difference in model performance. In order to minimize the impact of parameter selection on analyzing the performance differences of different models, the grid search algorithm is used to quantify the optimal parameters of each model. The grid search algorithm is one of the most commonly used methods for parameter optimization in machine learning algorithms [44]. This method divides the parameters to be optimized into grids of equal step size within a fixed range. And the optimal parameter values that meet the conditions are calculated by traversing all grid points using the grid search method. The detailed process and mathematical description of the grid search algorithm’s optimization can be found in Min and Lee [45].

2.4. Construction of the BMA Model

Bayesian Model Average (BMA) is a probabilistic post-processing technique that generates probability predictions by quantifying prediction uncertainty [46]. The Bayesian formula was used to combine the prior distribution with the likelihood function in the BMA method, which aims to obtain the posterior distribution of the predicted object. The BMA method has been proven to be a more effective and efficient way to improve prediction accuracy. It can provide clearer and more reliable prediction density functions (PDFs) for probability prediction. In the process of using BMA for multi-model ensemble prediction, it is assumed that $y$ is the predictive variable of the multiple models, $S=[y_1,y_2,\dots ,y_T]$ is the mountain flood data required for the calibration model, $f=[f_1,f_2,\dots ,f_k]$ represents the model space composed of candidate models (GBDT, BP, and RF), and $p_k(y|f_k,S)$ is the posterior distribution of the predictive variable $y$ under the given conditions of mountain flood data $S$ and model $f_k$. The posterior probability of predictor variable y is as follows:

$$p(y|S)={\displaystyle \sum _{k=1}^{K}p(f_k|S)}·p_k(y|f_k,S)$$

(1)

where $p(f_k|S)$ is the posterior probability given the mountain flood data $S$ and the prediction results of the k-th model $f_k$.

The magnitude of the posterior probability reflects the importance of the candidate model. The posterior probability obtained in Equation (1) is the weighted sum of the posterior probabilities of the model, and this weighting method is Bayesian model averaging. According to the posterior probability distribution formula, the expectation and variance of BMA can be expressed as follows:

$$E(y|\mathrm{S})={\displaystyle \sum _{k=1}^{K}p(f_k|\mathrm{S})}·E[p_k(y|f_k,S)]={\displaystyle \sum _{k=1}^K{w}_k·f_k}$$

(2)

$$Var[y|S]={\displaystyle \sum _{k=1}^K{(f_k-{\displaystyle \sum _{k=1}^K{w}_i{f}_i})}^2}+{\displaystyle \sum _{k=1}^K{w}_k·f_k}$$

(3)

The expectation of BMA represents the average impact of the candidate model on the predicted variable, and the variance represents the dispersion degree of the posterior mean distribution. Therefore, the core of the BMA algorithm is the calculation of the probability distribution parameters $w_k$ and ${{\sigma }_k}^2$ of the predicted variable $y$. The expectation–maximization (EM) algorithm is used to calculate the parameters of BMA, and the likelihood function can be expressed as follows:

$$l(\theta )=\ln \{p(y|\mathrm{S})\}=\ln \{{\displaystyle \sum _{k=1}^K{w}_k}·p_k(y|f_k,S)\}$$

(4)

The EM method is a widely used iterative method for calculating maximum likelihood estimation [47]. This algorithm is divided into the E (expectation) step and the M (maximization) step; the analytical solution of the BMA parameters is obtained by repeated iterations through the E step and the M step. The detailed steps of the EM algorithm can be found in Ajami et al. [48].

2.5. Model Performance Evaluation

The performance of the models was assessed and validated using four accuracy criteria of receiver operating characteristic (ROC) curve, F₁-score, Precision, and Recall. The ROC curve is a graphical representation that displays how the binary classifier performs. This method utilizes the classification performance of area under the curve (AUC) to quantify the classification performance of binary classifiers, which is a popular accuracy evaluation method for binary classification problems [49]. The ROC curve is created by plotting the true positive rate (TPR) and false positive rate (FPR) at various threshold settings. Precision is the proportion of true positive samples in the predicted sample and Recall is the proportion of true positive samples in all positive samples [50,51]. Precision and Recall are contradictory measures. In order to better measure the performance of the model in terms of Precision and Recall, the F₁-value is introduced. The F₁-value comprehensively displays the Precision and Recall of the model; the formula of these are as follows:

$$TPR=Recall=\frac{TP}{TP+FN}$$

(5)

$$FPR=\frac{FP}{TN+FP}$$

(6)

$$Precision=\frac{TP}{TP+FP}$$

(7)

$$F_1\mathit{\text{-score}}=\frac{2Precison\times Recall}{(Precison\times Recall)}=\frac{2TP}{2TP+FP+FN}$$

(8)

where TP refers to the number of samples correctly classified as positive, FP refers to the number of samples incorrectly classified as positive because the right category is negative, TN refers to the number of samples correctly classified as negative, and FN refers to the number of samples incorrectly classified as negative because the right class is positive [50].

3. Results and Discussion

3.1. Model Performance of Single Models

Figure 6 shows the accuracy and stability differences of GBDT, BP, and RF models under three different validation samples. In terms of model accuracy (Figure 6a–c), GBDT has the highest F₁-score in the first and third validation samples, demonstrating superior classification performance. RF has the highest accuracy (with a 0.91 F₁-score) in the second validation sample. In contrast, the BP model always has the lowest accuracy among the three validation samples, which may be attributed to the combined influence of model structure and applicability. GBDT and RF have improved the performance of the model to a certain extent by integrating multiple models. And Zhou et al. [29] also reached a similar conclusion in their study using 12 classic machine learning algorithms to build ponding prediction models. In addition, both GBDT and RF are decision tree models, which have better applicability to classification problems than the BP model with a mesh structure. In terms of model stability (Figure 6d), the RF model exhibits the lowest SD and the shortest interval for the F₁-value distribution across the three validation samples, suggesting that the RF model demonstrates more dependable classification prediction performance. On the contrary, the BP model has the lowest stability under three validation samples; the SD of the F₁-value was 18.2–47.7% higher than that of the RF model and GBDT model. Therefore, GBDT and RF may have better performance when using a single model to construct classification prediction problems.

In addition, there are significant fluctuations in the Precision and Recall of GBDT and RF models under the three validation samples. For example, the Recall of GBDT in the second validation sample is 17.64% higher than the Precision, while the Recall in the other two validation samples is 5.5–7.14% lower than the Precision. These values indicate that GBDT and RF still have certain uncertainties in different prediction tasks. Although GBDT and RF integrate multiple decision tree models, these decision tree models used for integration have the same structure, resulting in the integrated GBDT and RF model still being affected by the prediction uncertainty of a single decision tree model. Therefore, it is necessary to explore multiple-model integration methods that include different model structures to improve model stability and support the widespread application of the models.

3.2. Performance of BMA Model

Figure 7 shows the performance of the BMA model in predicting mountain torrent hazards. As shown in Figure 7a–c, the Precision and Recall of the BMA model are all above 0.8 under the three different validation samples, indicating that BMA can accurately and robustly identify mountain torrent hazards. In order to further analyze the differences in mountain torrent hazard prediction performance between the BMA model and individual models, the ROC curve and AUC value of all models were analyzed. As shown in Figure 7d–f, BMA consistently has the highest AUC under the three validation samples. Moreover, compared with the GBDT, BP, and RF models, the F₁-score of the BMA model increases by 3.31–24.61%. Therefore, it can be concluded that the BMA model improves the accuracy and stability of the model in different prediction tasks by integrating GBDT, BP, and RF. This improvement in accuracy and stability can more accurately identify the risk of mountain torrents, which can also provide more accurate technical support for the management and prevention of mountain torrent hazards.

In addition, although the improvement thanks to BMA in the prediction accuracy of some individual models may be limited, the outstanding advantage of BMA in improving the prediction stability significantly enhances the credibility of machine learning model prediction results. In fact, the uncertainty of machine learning model prediction results has always been one of the most concerning key issues for many scholars [52,53] because it may be difficult for individual machine learning methods (including GBDT and RF) to fully explore the potential relationships between data due to the limitation of model structure and parameters. This will lead to significant fluctuations in the performance of the individual model under different verification samples (Figure 6). As Zhou et al. [29] pointed out, the single model may perform well in the current prediction task and perform poorly in another prediction task. The uncertainty of machine learning limits the promotion and application of models. How to reduce the uncertainty of machine learning model predictions is a key issue that machine learning scholars cannot ignore [54,55]. Although this study improved the accuracy and stability of the model to some extent by combining GBDT, BP, and RF models using the BMA method, it is not yet clear whether the BMA model has a similar performance in other types of prediction tasks. Future research can explore the comprehensive performance of the BMA model in different study areas and types of prediction tasks.

3.3. Feature Importance Analysis

The feature importance analysis results in Figure 8 show the influence of seven indicators for mountain torrent hazards. It can be easily found that the distance to the river is the most important factor affecting mountain torrent hazards, which is consistent with the research findings of Li and Hong [56]. The main reason is that the river is the main channel for flood discharge. When mountain torrent hazards occur, areas closer to the river may be washed away. In addition, mountain torrent hazards have strong destructive power and high uncertainty. Under the background of frequent extreme weather, the characteristics of mountain torrent hazards may also undergo significant changes, resulting in areas near rivers where mountain torrent hazards have not occurred also possibly having a high risk of disaster. Moreover, it can be seen from Figure 8 that elevation is also an important factor affecting mountain torrent hazards. Because Yuanyang County is located in the typical plateau mountainous area with steep slopes and deep valleys, mountain torrent hazards often form at the foot of the slopes and valleys. In particular, in the low-lying areas near the river, the broken rock materials and steep terrain create excellent conditions for the formation of mountain torrent hazards. Therefore, the engineering and residential regions in mountain areas should be as far away from rivers as possible in the planning and construction processes, especially in low-lying river valleys that are prone to flash floods.

3.4. Risk Assessment of Mountain Torrent Based on BMA

In this paper, a mountain torrent risk identification model was constructed using BMA; it may forecast the flood risk value of each grid. To be specific, based on verifying the accuracy of the BMA model, the sensitivity factors of all grids in Yuanyang County were input into the BMA model, and the mountain torrent risk values of each grid were obtained. The flood risk value was divided into five types using the natural breaks approach: very high, high, moderate, low, and very low [56]. Figure 9 shows the mountain torrent risk map using the BMA model. It shows that the areas with lower altitude and a smaller distance to the river exhibit a higher risk of mountain torrents, which is consistent with the results of the feature importance analysis. From the perspective of spatial distribution, the high-risk areas are mainly concentrated in the northern boundary and southern parts of Yuanyang County, with relatively a small altitude and distance to the river. And low-risk areas are mainly located in the central part of Yuanyang County, with a high altitude and slope. Therefore, the prevention of mountain torrent hazards in Yuanyang County needs to focus on the low-altitude areas in the north and the areas near the central valleys.

High-risk areas in terms of mountain torrents are often important references for flood control and hazard reduction in mountainous areas. It can be seen from Figure 10a that the high-risk and very high-risk areas have reached 592.72 km², accounting for 24.17% of the total area of Yuanyang. Among them, the very high-risk areas account for 5.15% of the total area of Yuanyang. This indicates that Yuanyang County is facing very severe risks of mountain torrents. From the distribution of very high-risk areas in various townships of Yuanyang County (Figure 10b), the area of very high-risk area in Nansha Town is the greatest, accounting for 25.65% of the total area of very high-risk areas. The very high-risk areas in Xiaoxinjie, Daping, Shangxincheng, and Fengchunling Town are smaller than in Nansha Town. Nonetheless, the very high-risk areas in the four towns account for 43.78% of the total very high-risk area. Therefore, in the prevention and control of mountain torrent hazards, it is necessary to focus on the very high-risk areas of the five townships mentioned above, particularly to strengthen the prevention and monitoring of mountain torrent hazards in Nansha Town, and to reasonably arrange prevention and control measures to minimize the losses caused by mountain torrent hazards.

4. Conclusions

Risk identification of mountain torrents is an important basis for managing flood disasters in mountainous areas. In this study, three classic machine learning methods (GBDT, BP, and RF) were used to construct the mountain torrent hazard identification model, and the integrated model for mountain torrent hazard prediction was proposed by fusing the results of GBDT, BP, and RF using the BMA method. And the risk of mountain torrents was evaluated by using the BMA model in Yuanyang County, China. The main contributions of this study are as follows:

(1)

The proposed BMA model consistently has the highest testing accuracy under the three different test samples; the F₁-score of the BMA model was 3.31–24.61% higher than that of the three single models under the three different test samples. These results demonstrate that the BMA model that integrated multiple machine learning methods significantly improved the accuracy and stability of mountain torrent hazard prediction. This can provide a reference for improving the performance of mountain torrent hazard prediction based on machine learning methods.

(2)

The analysis of feature importance showed that the distance to the river and elevation were the main factors affecting mountain torrent hazards in Yuanyang County. Therefore, the residents in low-lying areas near the river should relocate to safe areas as far away as possible from the river, and the construction of new projects should also avoid low-lying river valleys as much as possible.

(3)

The results of the mountain torrent risk assessment based on the BMA model indicate that very high-risk areas are mainly concentrated near the northern boundary and southern valleys of Yuanyang County. The area of very high-risk areas in Nansha Town is the greatest, accounting for 25.65% of the total area of very high-risk areas in the county. Therefore, the relevant management personnel of Yuanyang County should pay more attention to the prevention and monitoring of mountain torrent hazards in Nansha Town during the flood season.

Although this study found that the BMA model can improve the accuracy of mountain torrent hazard prediction, it only considered seven main factors that affect mountain torrent hazards. However, there are many factors that affect the occurrence of mountain torrent hazards, which may to some extent limit the space for improving model accuracy. Future research can delve into the impact of different indicators and combination schemes on mountain torrent hazard prediction and explore the optimal combination scheme of indicators for mountain torrent hazard prediction. In addition, due to limitations in the research area and subjects, this study only analyzed the performance of the BMA model in predicting mountain torrent hazards in Yuanyang County, China. To fully verify the universality and scalability of the proposed BMA model, future research can attempt to explore the impact of indicator selection, research areas, and prediction tasks on the performance of BMA models, providing support for the promotion and use of BMA models.