Developing Regional Hydrological Drought Risk Models through Ordinary and Principal Component Regression Using Low-Flow Indexes in Susurluk Basin, Turkey
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data Set
2.2. Methods
2.2.1. Brief Methodology
- First, daily streamflow time series were obtained from streamflow observation sites in the Susurluk Basin.
- 7-day, 15-day, 30-day, and 60-day low-flow time series were calculated using daily flow time series to reflect the demand for water resources. Low-flow rates are annual minimum d-day average flows.
- With the help of geographic information systems (GIS), the physical, morphological, and hydrological characteristics of the Susurluk Basin were calculated, and the watersheds were delineated.
- To check whether the data are suitable for statistical analysis, the discordancy measure (Di) was first applied to the data, and discordant sites were determined. Frequency distributions were applied to the d-day low-flow time series of each year. After parameter estimation and a test of goodness-of-fit with distributions, d-day low-flows between the basin’s physical, morphological, and hydrological features at different probability levels (risk) and return periods were estimated at the site.
- Various frequency distribution functions such as Exponential (EXP), 2-parameter exponential (EXP2), Frechet (FRE), 3-parameter Frechet (FRE3), Gamma (G), 3-parameter gamma (G3), Generalized extreme values (GEVs), Generalized gamma (GG), 4-parameter generalized gamma (GG4), Generalized logistic (GLO), Generalized Pareto (GPA), Logarithmic logistic (LLO), 3-parameter logarithmic logistic (LLO3), 3-parameter logarithmic Pearson (LP3), Logistic (LO), Logarithmic normal (LN), 3-parameter logarithmic normal (LN3), Normal (N), Weibull (WE), 3-parameter Weibull (WE3) were used for the estimation of at-site quantities.
- Before regionalization, cluster analysis (CA) and principal component analysis (PCA) were performed on group sites to identify homogeneous regions. To determine whether the regions are homogeneous, the discordancy, heterogeneity test, and goodness-of-fit measure tests for each homogeneous region provided were determined with the L-moment approach, and frequency analysis was performed.
- For each homogeneous region obtained, regional models indicating the relationship between d-day low flows and the basin’s physical, morphological, and hydrological characteristics were developed using ordinary univariate and multivariate linear or univariate non-linear regression and principal component regression analyses [44].
2.2.2. Determination of Watershed Physiographic Parameters
2.2.3. Data Completion
2.2.4. Detection of Annual Minimum d-Day Low Flows
2.2.5. At-Site Frequency Analysis
2.2.6. Regional Analysis
L-Moments and L-Moment Ratios
Discordancy Measure (Di)
Basin Classification
Heterogeneity Measure (H)
The Goodness-of-Fit Measure (ZDIST)
2.2.7. Principal Component Analysis (PCA)
Y2 = t2′X = t12 X1 + t22 X2 + ⋯ + tp2 Xp
Yp = tp′X = t1p X1 + t2p X2 + ⋯ + tpp Xp
2.2.8. Development of Regional Hydrological Drought Models
3. Results
3.1. At-Site Frequency Distribution and Relevant Low-Flow Discharges
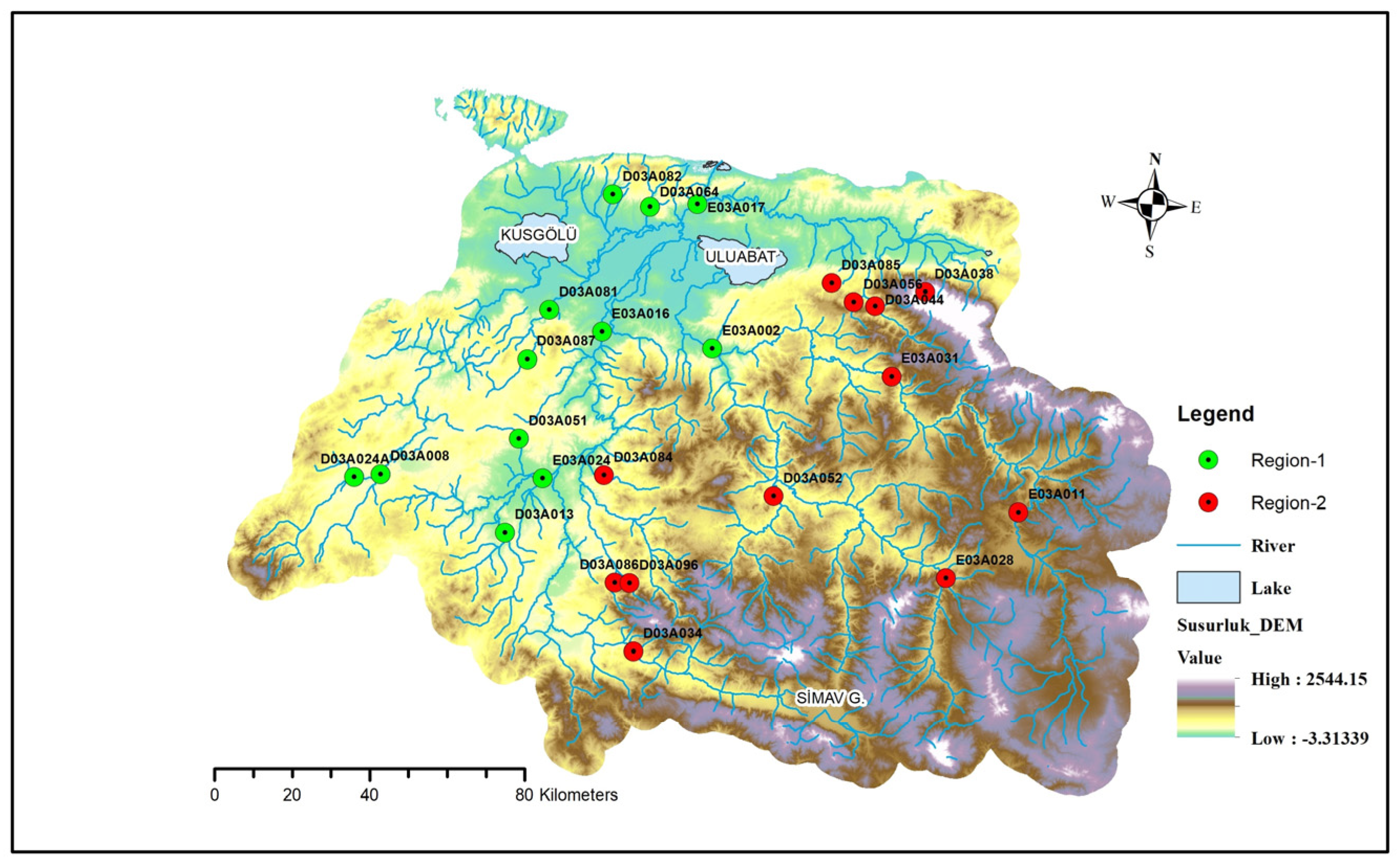
3.2. Determination of Homogeneous Regions
3.3. Regional Hydrological Models for Ungauged Basins via Regression Approaches
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- UNCCD. Zero Net Land Degradation, A Sustainable Development Goal for Rio+20 to Secure the Contribution of Our Planet’s Land and Soil to Sustainable Development, Including Foodsecurity and Poverty Eradication, Bonn. 2012. Available online: https://catalogue.unccd.int/58_Zero_Net_Land_Degradation.pdf (accessed on 19 May 2024).
- Köken, E. Regionalization of Tigris Basin Low Flow Characteristics. Master’s Thesis, Dokuz Eylül University, İzmir, Türkiye, 2009. (In Turkish). [Google Scholar]
- Yıldırımlar, O. Analysis of Low Flows in the Euphrates Basin. Master’s Thesis, Istanbul Technical University, Sarıyer/İstanbul, Türkiye, 2012. (In Turkish). [Google Scholar]
- Bayazit, M.; Onoz, B. Flood and Drought Hydrology; Nobel Publications: Istanbul, Turkey, 2008; 259p. (In Turkish) [Google Scholar]
- Ouarda, T.B.M.J.; Charron, C.; St-Hilaire, A. Statistical models and the estimation of low flows. Can. Water Resour. J. 2008, 33, 195–206. [Google Scholar] [CrossRef]
- Ouarda, T.B.M.J. Handbook of Applied Hydrology, 2nd ed.; Chapter 77, Regional Flood Frequency Modeling; McGraw-Hill Education: New York, NY, USA, 2017. [Google Scholar]
- Gustard, A.; Bullock, A.; Dixon, J.M. Low Flow Estimation in the United Kingdom; IH Report No.108; Institute of Hydrology: Wallingford, UK, 1992; 88p. [Google Scholar]
- Laaha, G.; Bloschl, G. A comparison of low flow regionalization methods–catchment grouping. J. Hydrol. 2006, 323, 193–214. [Google Scholar] [CrossRef]
- Engeland, K.; Hisdal, H. A comparison of low flow estimates in ungauged catchments using regional regression and the HBV-model. Water Resour. Manag. 2009, 23, 2567–2586. [Google Scholar] [CrossRef]
- Mamuna, A.A.; Hashim, A.; Daoud, J.I. Regionalisation of low flow frequency curves for the Peninsular Malaysia. J. Hydrol. 2010, 381, 174–180. [Google Scholar] [CrossRef]
- Ahn, K.; Merwade, V. The effect of land cover change on duration and severity of high and low flows. Hydrol. Process. 2017, 31, 133–149. [Google Scholar] [CrossRef]
- Cammalleri, C.; Vogt, J.; Salamon, P. Development of an operational low-flow index for hydrological drought monitoring over Europe. Hydrolog. Sci. J. 2017, 62, 346–358. [Google Scholar] [CrossRef]
- Anli, A.S.; Modarres, R.; Apaydin, H. A Hybrid Approach for Regional Low-Flow Frequency Analysis for the Upper Tigris and Euphrates Basin. J. Hydrol. Eng. 2023, 28, 04023015. [Google Scholar] [CrossRef]
- Institute of Hydrology. Low Flow Studies; Report No.1 Research Report, (Low Flow Studies 1); Institute of Hydrology: Wallingford, UK, 1980; 55p. [Google Scholar]
- Nathan, R.J.; McMahon, T.A. Overview of a Systems Approach to the Prediction of Low Flow Characteristics in Ungauged Catchments. In National Conference Publication; Institution of Engineers, Australia: Barton, Australia, 1991; Volume 1, pp. 187–192. [Google Scholar]
- Nathan, R.J.; McMahon, T.A. Estimating low flow characteristics in ungauged catchments. Water Resour. Manag. 1992, 6, 85–100. [Google Scholar] [CrossRef]
- Smakhtin, V. Low flow hydrology: A review. J. Hydrol. 2001, 240, 147–186. [Google Scholar] [CrossRef]
- Arbelaez, A.C.; Castro, L.M. Low Flow Discharges Regional Analysis using Wakeby Distribution in an ungauged basin in Colombia. In AGU Hydrology Days; Colorado State University: Fort Collins, CO, USA, 2007. [Google Scholar]
- Castiglioni, S.; Castellarin, A.; Montanari, A. Prediction of low-flow indices in ungauged basins through physiographical space-based interpolation. J. Hydrol. 2009, 378, 272–280. [Google Scholar] [CrossRef]
- Kirkby, M.; Gallart, F.; Kjeldsen, T.; Irvine, B.; Froebrich, J.; Lo Porto, A.; De Girolamo, A. Classifying low flow hydrological regimes at a regional scale. Hydrol. Earth Syst. Sci. 2011, 15, 3741–3750. [Google Scholar] [CrossRef]
- Grandry, M.; Gailliez, S.; Sohier, C.; Verstraete, A.; Degre, A. A method for low-flow estimation at ungauged sites: A case study in Wallonia (Belgium). Hydrol. Earth Syst. Sci. 2013, 17, 1319–1330. [Google Scholar] [CrossRef]
- Sharma, S.; Gajbhiye, S.; Tignath, S. Application of principal component analysis in grouping geomorphic parameters of a watershed for hydrological modeling. Appl. Water Sci. 2015, 5, 89–96. [Google Scholar] [CrossRef]
- Van Lanen, H.A.; Wanders, N.; Tallaksen, L.M.; Van Loon, A.F. Hydrological drought across the world: Impact of climate and physical catchment structure. Hydrol. Earth Syst. Sci. 2013, 17, 1715–1732. [Google Scholar] [CrossRef]
- Bulu, A.; Cokgor, S.; Cigizoglu, H. Statistical analysis of low flows on Thrace Region. In Proceedings of the UNESCO FRIEND-AMHY Conference, Thessalonique, Greece, September 1995; pp. 91–104. [Google Scholar]
- Onoz, B.; Bulu, A. Frequency Analysis of Low Flows in the Thrace Region. Turk. J. Civ. Eng. 1996, 93, 1243–1254. [Google Scholar]
- Sertbas, Y. The investigation of the most suitable probability distribution for the low flows of the Sakarya Basin River flows. Master’s Thesis, Istanbul Technical University, Sarıyer/İstanbul, Türkiye, 1996. (In Turkish). [Google Scholar]
- Bulu, A.; Onoz, B. Frequency analysis of low flows by the PPCC test in Turkey. UNESCO FRIEND-AMHY’97—Reg. Hydrol. Concepts Models Sustain. Water Resour. Manag. 1997, 246, 133–140. [Google Scholar]
- Saris, F. Low Flow Analysis in Porsuk Stream Basin. J. Geogr. 2016, 33, 72–82. (In Turkish) [Google Scholar]
- Durak, S. Low flow hydrology and Aegean Region application. Master’s Thesis, Istanbul Technical University, Sarıyer/İstanbul, Türkiye, 2000. (In Turkish). [Google Scholar]
- Saraçoğlu, Ö. Low Flow Hydrology and Its Application in the Mediterranean Region. Master’s Thesis, Istanbul Technical University, Sarıyer/İstanbul, Türkiye, 2002. (In Turkish). [Google Scholar]
- Yurekli, K.; Kurunc, A.; Gul, S. Frequency analysis of low flow series from Çekerek Stream Basin. J. Agric. Sci. 2005, 11, 72–77. [Google Scholar]
- Eris, E.; Aksoy, H.; Onoz, B.; Cetin, M.; Yuce, M.I.; Selek, B.; Aksu, H.; Burgan, H.I.; Esit, M.; Yildirim, I.; et al. Frequency analysis of low flows in intermittent and non-intermittent rivers from hydrological basins in Turkey. Water Supply 2019, 19, 30–39. [Google Scholar] [CrossRef]
- Anlı, A.S.; Öztürk, F. Regional frequency analysis of annual maximum precipitation measured in Ankara. GOU J. Fac. Agric. 2011, 28, 61–71. (In Turkish) [Google Scholar]
- Şen, O. Determination of Hydrological Homogeneous Regions of Türkiye Flow Variables. Master’s Thesis, Istanbul Technical University, Sarıyer/İstanbul, Türkiye, 2011. (In Turkish). [Google Scholar]
- Aksoy, H.; Çetin, M.; Önöz, B.; Yüce, M.İ.; Eriş, E.; Selek, B.; Çavuş, Y. Low Flows and Drought Analysis in Hydrological Basins. Turkish National Geodesy and Geophysics Union. Turkey National Meteorological and Hydrological Disasters Program-2015-01, 2018. (In Turkish). Available online: https://www.tujjb.org.tr/uploads/files/nationalprojects/hidrolojik-havzalarda-dusuk-akimlar-ve-kuraklik-analizi-tujjb-tumehap-2015-01-2240.pdf (accessed on 19 May 2024).
- Cavus, Y.; Aksoy, H. Spatial Drought Characterization for Seyhan River Basin in the Mediterranean Region of Turkey. Water 2019, 11, 1331. [Google Scholar] [CrossRef]
- Mersin, D.; Gulmez, A.; Safari, M.J.S.; Vaheddoost, B.; Tayfur, G. Drought assessment in the Aegean region of Turkey. Pure Appl. Geophys. 2022, 179, 3035–3053. [Google Scholar] [CrossRef]
- Gulmez, A.; Mersin, D.; Vaheddoost, B.; Safari, M.J.S.; Tayfur, G. A Joint Evaluation of Streamflow Drought and Standard Precipitation Indices in Aegean Region, Turkey. Pure Appl. Geophys. 2023, 180, 4319–4337. [Google Scholar] [CrossRef]
- Yuce, M.I.; Deger, I.H.; Esit, M. Hydrological drought analysis of Yeşilırmak Basin of Turkey by streamflow drought index (SDI) and innovative trend analysis (ITA). Theor. Appl. Climatol. 2023, 153, 1439–1462. [Google Scholar] [CrossRef]
- Bayer Altin, T.; Altin, B.N. Response of hydrological drought to meteorological drought in the eastern Mediterranean Basin of Turkey. J. Arid Land 2021, 13, 470–486. [Google Scholar] [CrossRef]
- Orta, S.; Aksoy, H. Development of Low Flow Duration-Frequency Curves by Hybrid Frequency Analysis. Water Resour. Manag. 2022, 36, 1521–1534. [Google Scholar] [CrossRef]
- Sarigil, G.; Cavus, Y.; Aksoy, H. Frequency curves of high and low flows in intermittent river basins for hydrological analysis and hydraulic design. Stoch Environ. Res. Risk Assess 2024, accepted. [Google Scholar] [CrossRef]
- Ministry of Agriculture and Forestry; General Directorate of Water Management; Department of Flood and Drought Management. Drought Management Planning of Susurluk Basin Projects; General Directorate of Water Management: Ankara, Turkey, 2023. (In Turkish) [Google Scholar]
- Gürler, Ç. Regional Low Flow Frequency Analysis for Water Supply Systems in Susurluk Basin. Master’s Thesis, Ankara University, Ankara, Türkiye, 2022. (In Turkish). [Google Scholar]
- Bhatti, S.J.; Kroll, C.N.; Vogel, R.M.R. Revisiting the probability distribution of low streamflow series in the United States. J. Hydrol. Eng. 2019, 24, 04019043. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R. Some statistics useful in regional frequency analysis. Water Resour. Res. 1993, 29, 271–281. [Google Scholar] [CrossRef]
- Anli, A.S. Regional Frequency Analysis of Rainfall in Ankara Using L Moment Methods. Ph.D. Thesis, Ankara University, Ankara, Türkiye, 2009. (In Turkish). [Google Scholar]
- Hosking, J.R.M. The four-parameter kappa distribution. IBM J. Res. Dev. 1994, 38, 251–258. [Google Scholar] [CrossRef]
- Bulut, H. Multivariate Statistical Methods with R Applications; Multivariate Statistics II Lecture Notes; Academic Publishing: Ankara, Turkey, 2018. (In Turkish) [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Vining, C.G. Introduction to Linear Regression Analysis, 5th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2012; p. 836. [Google Scholar]
- Eslamian, S.; Ghasemizadeh, M.; Biabanaki, M.; Talebizadeh, M. A principal component regression method for estimating low flow index. Water Res. Manag. 2010, 24, 2553–2566. [Google Scholar] [CrossRef]
- Susilawati, S.; Didiharyono, D. Application of Principal Component Regression in Analyzing Factors Affecting Human Development Index. J. Varian 2023, 6, 199–208. [Google Scholar] [CrossRef]
- Hosking, J.R.M. FORTRAN Routines for Use with the Method of L-Moments, Version 3.04; Research Report RC 20525; IBM Research Division, T.C. Watson Research Center: Yorktown Heights, NY, USA, 2005. [Google Scholar]
- Dawson, C.W.; Abrahart, R.J.; See, L.M. HydroTest: A webbased toolbox of evaluation metrics for the standardized assessment of hydrological forecasts. Environ. Modell. Softw. 2007, 22, 1034–1052. [Google Scholar] [CrossRef]
- Li, M.; Li, X.; Ao, T. Comparative Study of Regional Frequency Analysis and Traditional At-Site Hydrological Frequency Analysis. Water 2019, 11, 486. [Google Scholar] [CrossRef]
- Ghabelnezam, E.; Mostafazadeh, R.; Hazbavi, Z.; Huang, G. Hydrological Drought Severity in Different Return Periods in Rivers of Ardabil Province, Iran. Sustainability 2023, 15, 1993. [Google Scholar] [CrossRef]
- Ouarda, T.B.; Charron, C.; Hundecha, Y.; St-Hilaire, A.; Chebana, F. Introduction of the GAM model for regional low-flow frequency analysis at ungauged basins and comparison with commonly used approaches. Environ. Model. Softw. 2018, 109, 256–271. [Google Scholar] [CrossRef]
- Strnad, F.; Moravec, V.; Markonis, Y.; Máca, P.; Masner, J.; Stočes, M.; Hanel, M. An Index-Flood Statistical Model for Hydrological Drought Assessment. Water 2020, 12, 1213. [Google Scholar] [CrossRef]
- Wang, M.; Jiang, S.; Ren, L.; Xu, C.Y.; Shi, P.; Yuan, S.; Fang, X. Nonstationary flood and low flow frequency analysis in the upper reaches of Huaihe River Basin, China, using climatic variables and reservoir index as covariates. J. Hydrol. 2022, 612, 128266. [Google Scholar] [CrossRef]
- Requena, A.I.; Ouarda, T.B.; Chebana, F. Low-flow frequency analysis at ungauged sites based on regionally estimated streamflows. J. Hydrol. 2018, 563, 523–532. [Google Scholar] [CrossRef]
- Laaha, G. A mixed distribution approach for low-flow frequency analysis—Part 1: Concept, performance, and effect of seasonality. Hydrol. Earth Syst. Sci. 2023, 27, 689–701. [Google Scholar] [CrossRef]
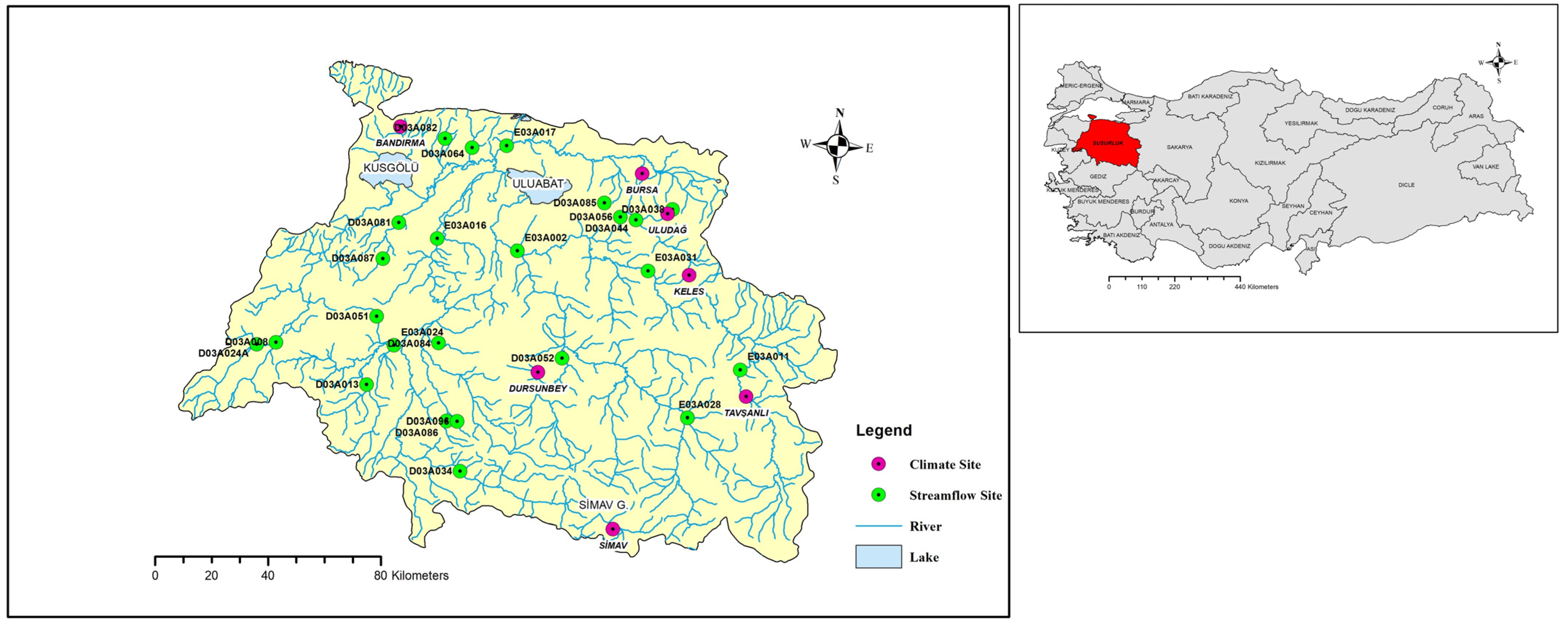


| No | Site Code | Site Name | Longitude–Latitude (°) | Drainage Area (km2) | Elevation (m) | Observation Period | Sample Size | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | D03A008 | Kahve | 27.54 | East | 39.61 | North | 741 | 190 | 1963–2016 | 54 |
| 2 | D03A013 | İkizcetepeler | 27.92 | East | 39.50 | North | 467 | 128 | 1964–2017 | 54 |
| 3 | D03A024 | Ayaklı | 27.36 | East | 39.52 | North | 115 | 250 | 1967–2016 | 50 |
| 4 | D03A034 | Osmanlar Köp. | 28.32 | East | 39.25 | North | 1266 | 277 | 1970–2017 | 48 |
| 5 | D03A038 | Uludağ | 29.14 | East | 40.12 | North | 26 | 1675 | 1972–2017 | 46 |
| 6 | D03A044 | S.Saygı Brj. Gir. | 29.00 | East | 40.08 | North | 377 | 341 | 1982–2017 | 36 |
| 7 | D03A051 | Değirmenboğazı | 27.95 | East | 39.71 | North | 84 | 192 | 1980–2017 | 38 |
| 8 | D03A052 | Sinderler | 28.72 | East | 39.62 | North | 965 | 294 | 1981–2017 | 37 |
| 9 | D03A056 | Sultaniye | 28.94 | East | 40.09 | North | 50 | 368 | 1982–2017 | 36 |
| 10 | D03A064 | Gölecik | 28.28 | East | 39.61 | North | 111 | 27 | 1984–2017 | 34 |
| 11 | D03A081 | Mürvetler | 28.01 | East | 40.02 | North | 289 | 31 | 1986–2017 | 32 |
| 12 | D03A082 | Keçiler | 28.18 | East | 40.30 | North | 21 | 65 | 1986–2017 | 32 |
| 13 | D03A084 | Eyüpbükü | 28.23 | East | 39.65 | North | 241 | 945 | 1987–2017 | 31 |
| 14 | D03A085 | İnegazi | 28.87 | East | 40.13 | North | 15 | 306 | 1988–2017 | 30 |
| 15 | D03A086 | Adalı | 28.26 | East | 39.39 | North | 66 | 375 | 1988–2017 | 30 |
| 16 | D03A087 | Yeşilova | 27.96 | East | 39.90 | North | 141 | 250 | 1989–2017 | 29 |
| 17 | D03A096 | Okçular | 28.30 | East | 39.40 | North | 35 | 405 | 1991–2017 | 27 |
| 18 | E03A002 | Döllük | 28.51 | East | 39.62 | North | 9617 | 40 | 1950–2017 | 68 |
| 19 | E03A011 | Küçükilet | 29.86 | East | 39.12 | North | 1642 | 795 | 1950–2017 | 68 |
| 20 | E03A016 | Yahyaköy | 28.17 | East | 39.98 | North | 6376 | 32 | 1953–2017 | 65 |
| 21 | E03A017 | Akçasusurluk | 28.40 | East | 40.26 | North | 20 | 2 | 1953–2017 | 65 |
| 22 | E03A024 | Balıklı | 28.02 | East | 39.63 | North | 244 | 94 | 1954–2017 | 60 |
| 23 | E03A028 | Dereli | 29.25 | East | 39.46 | North | 1165 | 557 | 1965–2017 | 53 |
| 24 | E03A031 | Dağgüney | 29.06 | East | 39.92 | North | 3493 | 365 | 1993–2017 | 25 |
| No | Site Code | Site Name | Elevation (m) | Longitude (°) | Latitude (°) |
|---|---|---|---|---|---|
| 1 | 17114 | Bandırma | 51 | 27.99 | 40.32 |
| 2 | 17116 | Bursa | 101 | 29.02 | 40.23 |
| 3 | 17676 | Uludağ | 1877 | 29.13 | 40.12 |
| 4 | 17695 | Keles | 1063 | 29.23 | 39.91 |
| 5 | 17700 | Dursunbey | 639 | 28.62 | 39.58 |
| 6 | 17704 | Tavşanlı | 833 | 29.50 | 39.55 |
| 7 | 17748 | Simav | 809 | 28.98 | 39.08 |
| Site Code | Low-Flow Index | |||
|---|---|---|---|---|
| 7-Day | 15-Day | 30-Day | 60-Day | |
| D03A008 | 0.23 | 0.46 | 0.58 | 0.84 |
| D03A013 | 0.08 | 0.04 | 0.08 | 0.27 |
| D03A024 | 0.12 | 0.20 | 0.14 | 0.26 |
| D03A034 | 0.63 | 0.99 | 0.89 | 0.80 |
| D03A038 | 0.21 | 0.28 | 0.08 | 0.20 |
| D03A044 | 1.70 | 2.43 | 1.02 | 0.05 |
| D03A051 | 0.56 | 0.07 | 1.00 | 0.63 |
| D03A052 | 0.11 | 0.16 | 0.17 | 0.39 |
| D03A056 | 0.51 | 0.24 | 0.27 | 0.30 |
| D03A064 | 0.81 | 1.19 | 2.37 | 0.90 |
| D03A081 | 0.45 | 0.69 | 0.78 | 0.84 |
| D03A082 | 0.78 | 1.22 | 1.49 | 0.65 |
| D03A084 | 0.55 | 0.46 | 0.90 | 0.26 |
| D03A085 | 3.50 * | 1.72 | 2.35 | 3.36 * |
| D03A086 | 0.17 | 1.86 | 0.18 | 0.61 |
| D03A087 | 0.08 | 0.26 | 0.42 | 1.30 |
| D03A096 | 0.94 | 0.09 | 0.29 | 0.18 |
| E03A002 | 1.27 | 1.26 | 1.25 | 1.22 |
| E03A011 | 1.02 | 0.78 | 1.02 | 1.08 |
| E03A016 | 1.88 | 1.62 | 0.99 | 0.98 |
| E03A017 | 6.13 * | 6.04 * | 5.82 * | 5.94 * |
| E03A024 | 0.44 | 0.14 | 0.10 | 0.52 |
| E03A028 | 0.28 | 0.33 | 0.39 | 0.38 |
| E03A031 | 1.55 | 1.45 | 1.42 | 2.03 |
| Site Code | Region-1 | Site Code | Region-2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 7-Day | 15-Day | 30-Day | 60-Day | 7-Day | 15-Day | 30-Day | 60-Day | ||
| D03A008 | 0.37 | 1.79 | 1.03 | 1.79 | D03A034 | 1.26 | 1.35 | 1.16 | 1.17 |
| D03A013 | 0.12 | 0.09 | 0.18 | 0.58 | D03A038 | 0.24 | 0.44 | 0.31 | 0.57 |
| D03A024 | 0.33 | 0.42 | 0.26 | 0.42 | D03A044 | 1.08 | 1.94 | 1.67 | 0.33 |
| D03A051 | 1.34 | 0.11 | 1.33 | 0.74 | D03A052 | 0.15 | 0.29 | 0.34 | 0.93 |
| D03A064 | 0.75 | 0.88 | 1.59 | 0.63 | D03A056 | 0.52 | 0.91 | 0.89 | 1.11 |
| D03A081 | 1.22 | 1.61 | 1.47 | 1.09 | D03A084 | 1.96 | 1.28 | 1.86 | 0.62 |
| D03A082 | 0.92 | 1.08 | 0.98 | 0.68 | D03A085 | 2.25 | 1.12 | 1.87 | 2.44 |
| D03A087 | 0.18 | 0.50 | 0.52 | 0.93 | D03A086 | 0.46 | 1.20 | 0.26 | 0.55 |
| E03A002 | 0.68 | 0.68 | 0.57 | 0.59 | D03A096 | 0.70 | 0.21 | 0.23 | 0.45 |
| E03A016 | 2.16 | 1.66 | 1.29 | 1.32 | E03A011 | 0.85 | 0.70 | 0.82 | 0.84 |
| E03A017 | 2.74 | 2.75 | 2.73 | 2.75 | E03A028 | 0.44 | 0.43 | 0.51 | 0.85 |
| E03A024 | 1.01 | 0.26 | 0.05 | 0.41 | E03A031 | 2.08 | 2.14 | 2.07 | 2.15 |
| Low-Flow Index | Region | Number of Sites | Heterogeneity Measure | ||
|---|---|---|---|---|---|
| H1 | H2 | H3 | |||
| 7-day | 1 | 12 | −0.1747 | −0.1772 | 5.5933 |
| 2 | 12 | −0.1811 | −0.1790 | 7.0201 | |
| 15-day | 1 | 12 | −0.1701 | −0.2000 | 4.8446 |
| 2 | 12 | −0.2500 | −0.2605 | 6.7792 | |
| 30-day | 1 | 12 | −0.2245 | −0.2235 | 5.1790 |
| 2 | 12 | −0.3302 | −0.3677 | 6.9218 | |
| 60-day | 1 | 12 | −0.0520 | −0.0538 | 4.1992 |
| 2 | 12 | −0.4101 | −0.4158 | 5.7555 | |
| Low-Flow Index | Region | Number of Sites | ZDIST (Goodness-of-Fit Measure) | ||||
|---|---|---|---|---|---|---|---|
| GLO | GEV | GNO | PE3 | GPA | |||
| 7-day | 1 | 12 | 2.15 | 0.70 * | 0.10 ** | −1.50 * | 2.98 |
| 2 | 12 | 2.19 | 0.77 * | 0.02 ** | −1.32 * | −2.82 | |
| 15-day | 1 | 12 | 3.45 | 1.74 | 0.95 * | −0.47 ** | −2.47 |
| 2 | 12 | 2.67 | 1.19 * | 0.42 ** | −0.94 * | −2.54 | |
| 30-day | 1 | 12 | 3.62 | 1.80 | 1.06 * | −0.31 ** | −2.61 |
| 2 | 12 | 2.28 | 0.67 * | 0.01 ** | −1.19 * | −3.24 | |
| 60-day | 1 | 12 | 3.62 | 1.44 * | 0.78 * | −0.51 ** | −3.66 |
| 2 | 12 | 2.07 | 0.28 * | −0.24 ** | −1.28 * | −3.90 | |
| Low-Flow Index | Region | Ordinary Regression Model (a) | R2 | p-Value | Cross-Validation | ||
| RMSE | MRE | R2 | |||||
| Q7,10 | 1 | Q7,10 = 0.2666 − 0.1192LAF + 0.01208LAF2 − 0.000091LAF3 | 95.64 | 0.0001 | 1.13 | 1.58 | 93.53 |
| 2 | Q7,10 = −0.411268 − 0.0051575WA − 0.932308LAF + 0.048948LSPS + 0.396897LAP | 98.92 | 0.0002 | 0.16 | 7.63 | 96.84 | |
| Q15,7 | 1 | Q15,7 = −100.386 + 0.0074322E + 3.55112X + 0.1835LAF | 97.31 | 0.0001 | 0.92 | −16.31 | 95.14 |
| 2 | Q15,7 = −0.0188402 − 0.00505061WA − 0.927826LAF + 0.390254LAP | 98.47 | 0.0001 | 0.19 | 10.96 | 96.38 | |
| Q30,5 | 1 | Q30,5 = −0.4996 + 0.2636LAF − 0.000632LAF2 | 96.70 | 0.0001 | 1.19 | 0.32 | 93.83 |
| 2 | Q30,5 = −0.00670212 − 0.00526292WA − 0.956042LAF + 0.404939LAP | 98.66 | 0.0001 | 0.19 | 9.47 | 96.48 | |
| Q60,2 | 1 | Q60,2 = −65.3312 + 2.33149X + 0.21396LAF | 97.20 | 0.0003 | 1.11 | −1.36 | 94.99 |
| 2 | Q60,2 = 0.0142909 − 0.0056536WA − 0.996297LAF + 0.429326LAP | 98.90 | 0.0001 | 0.18 | 6.23 | 96.58 | |
| Low-Flow Index | Region | Principal Component Regression Model (b) | R2 | p-Value | Cross-Validation | ||
| RMSE | MRE | R2 | |||||
| Q7,10 | 1 | Q7,10 = 2.85024 − 2.01963PC2 + 4.77548PC3 | 83.97 | 0.0003 | 2.17 | 29.67 | 82.12 |
| 2 | Q7,10 = [0.590891 + 0.624979PC1 − 0.272818PC2]2 | 95.01 | 0.0001 | 0.15 | −0.32 | 91.83 | |
| Q15,7 | 1 | Q15,7 = 2.98478 − 2.11063PC2 + 4.96447PC3 + 1.37115PC5 | 89.70 | 0.0003 | 1.81 | 14.17 | 87.69 |
| 2 | Q15,7 = [0.606588 + 0.63404PC1 − 0.280948PC2]2 | 94.88 | 0.0001 | 0.15 | −0.32 | 91.72 | |
| Q30,5 | 1 | Q30,5 = 3.18191 + 1.24506PC1 − 2.2412PC2 + 5.255PC3 + 1.43846PC5 | 93.71 | 0.0002 | 1.49 | 32.04 | 91.58 |
| 2 | Q30,5 = [0.633935 + 0.645009PC1 − 0.286274PC2]2 | 94.74 | 0.0001 | 0.16 | −0.35 | 91.49 | |
| Q60,2 | 1 | Q60,2 = 3.55864 − 2.5025PC2 + 5.87477PC3 | 84.83 | 0.0002 | 2.59 | 19.79 | 82.91 |
| 2 | Q60,2 = [0.676954 + 0.659337PC1 − 0.292911PC2]2 | 94.40 | 0.0001 | 0.17 | −0.38 | 96.73 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gürler, Ç.; Anli, A.S.; Polat, H.E. Developing Regional Hydrological Drought Risk Models through Ordinary and Principal Component Regression Using Low-Flow Indexes in Susurluk Basin, Turkey. Water 2024, 16, 1473. https://doi.org/10.3390/w16111473
Gürler Ç, Anli AS, Polat HE. Developing Regional Hydrological Drought Risk Models through Ordinary and Principal Component Regression Using Low-Flow Indexes in Susurluk Basin, Turkey. Water. 2024; 16(11):1473. https://doi.org/10.3390/w16111473
Chicago/Turabian StyleGürler, Çiğdem, Alper Serdar Anli, and Havva Eylem Polat. 2024. "Developing Regional Hydrological Drought Risk Models through Ordinary and Principal Component Regression Using Low-Flow Indexes in Susurluk Basin, Turkey" Water 16, no. 11: 1473. https://doi.org/10.3390/w16111473
APA StyleGürler, Ç., Anli, A. S., & Polat, H. E. (2024). Developing Regional Hydrological Drought Risk Models through Ordinary and Principal Component Regression Using Low-Flow Indexes in Susurluk Basin, Turkey. Water, 16(11), 1473. https://doi.org/10.3390/w16111473






