Modeling the Structure and Diffusion of Porous Layers
Abstract
1. Introduction
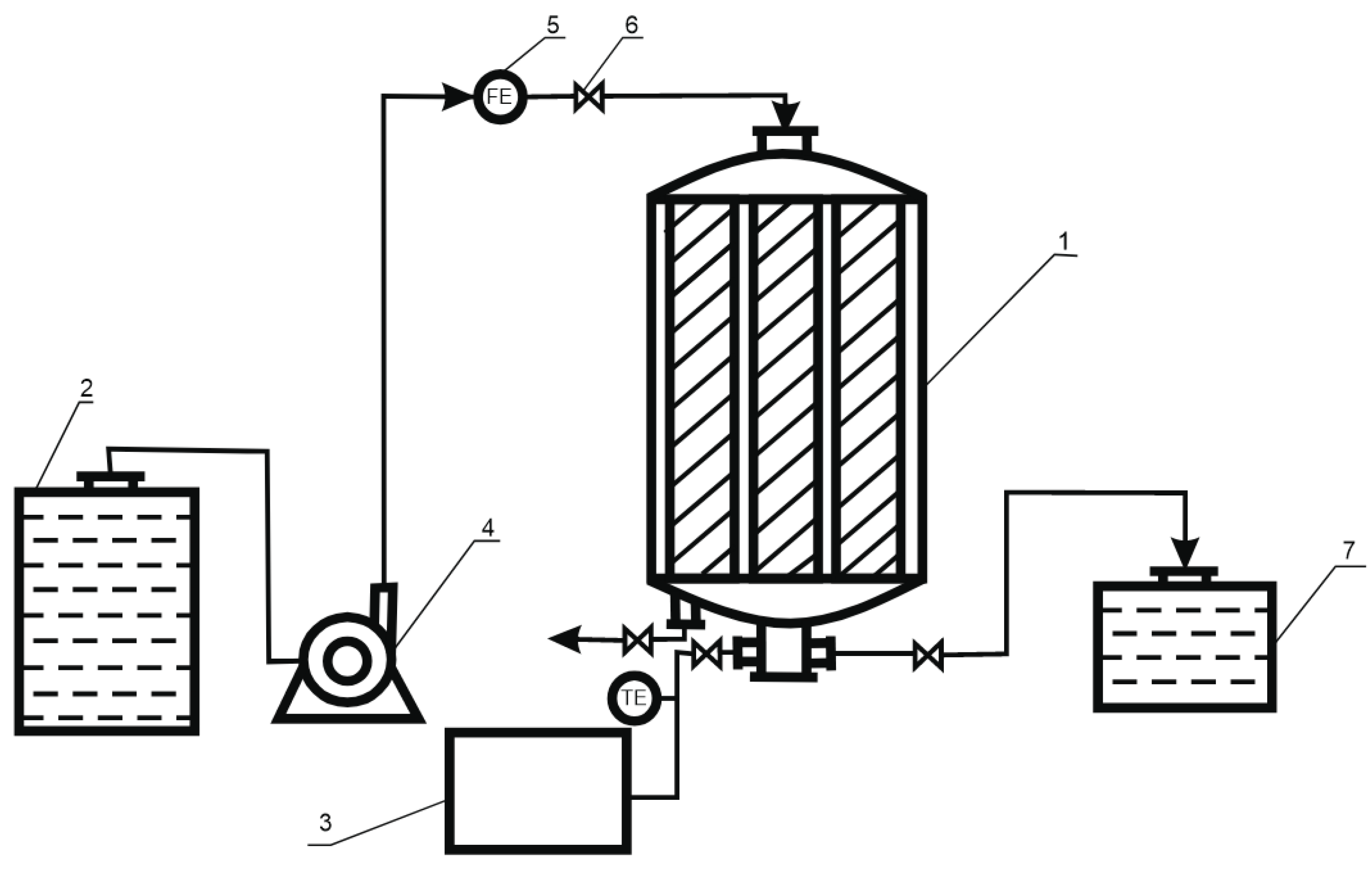
2. Material and Methods
3. Results and Discussion
3.1. Adsorption Layer Model Based on Fractal Theory
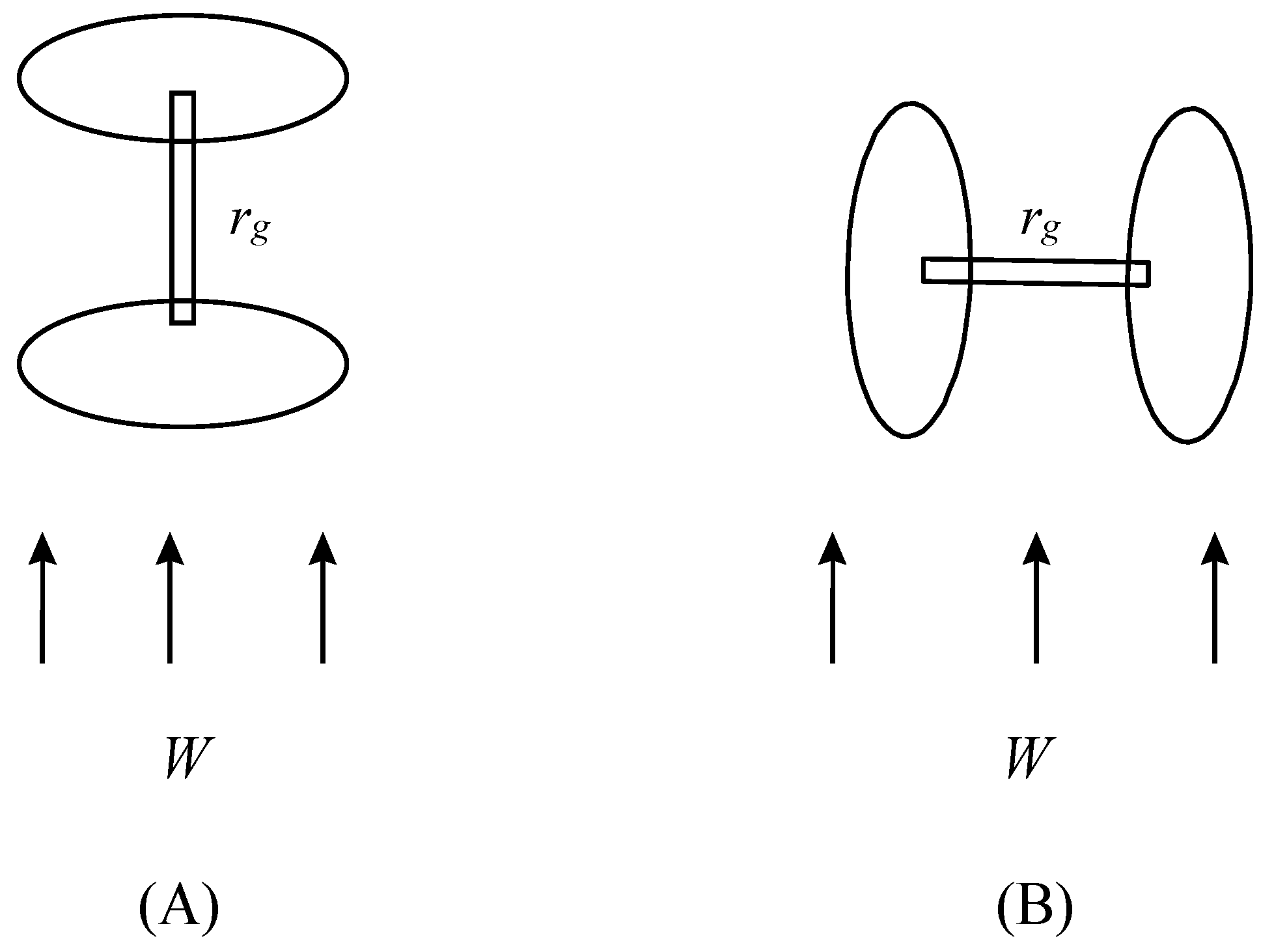
3.2. Development of Mathematical Model of Hydrodynamic Characteristics of a Granular Adsorptive Layer in the Mode of Intensive Loadings
3.3. Modeling of Diffusive Processes in a Layer of Porous Adsorbent
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| thermal diffusivity coefficient, m2/s; | |
| g | the characteristic size of the attached particle (adsorbent grain), m; |
| impurity concentration in the flow core, mol/m3; | |
| concentration of the substance, kg/m3; | |
| Cp | the heat capacity of the adsorbent material, J/C; |
| cs | concentration on the surface of the granule, kg/m2; |
| fractal dimension of the cluster structure; | |
| Dl | diffusion coefficient for the liquid phase, m2/s; |
| diffusion coefficient for the solid phase, m2/s; | |
| Dn | grain diameter, m; |
| Deff | effective diffusion coefficient, m2/s; |
| grain diameter, m; | |
| the characteristic size of the filtration channel, m; | |
| Arrhenius constant; | |
| F | surface, m2; |
| amount of residue on the sieve, kg; | |
| amount of coal weighed, kg; | |
| q | coefficient of curvature of the microchannels of the layer; |
| qr | thermal effect of the reaction, J/kg K; |
| specific enthalpy; | |
| cluster mobility, m3/s; | |
| and | coefficients of proportionality depending on the structure of the granular layer; |
| e | empirical coefficient; |
| kB | Boltzmann constant; |
| k | constant; |
| Km | empirical constant; |
| M | the molecular weight of the solvent; |
| m | molecular weight, kg; |
| L | characteristic size of the adsorption layer, m; |
| the number of particles; | |
| the number of particles depending on the characteristic length; | |
| the number of particles in the cluster; | |
| density of k particle clusters, 1/m3; | |
| the probability of a particle attaching to the cluster “protrusion”; | |
| P | carrier pressure in the granular layer, Pa; |
| average cluster radius, m; | |
| g | characteristic distance between grains, m; |
| R | cluster radius, m; |
| r | grain radius, m; |
| Scp | specific surface area of the adsorbent per unit volume, m2; |
| cross-sectional area of the apparatus, m2; | |
| T | temperature, K; |
| t | process time, s; |
| Ts | the temperature on the surface of the granule, K; |
| V0 | reduced velocity of the main flow of the carrier, m/s; |
| flow rate, m/s. | |
| W | flow velocity, m/s; |
| X | parameter that takes into account the association of molecules in the solvent; |
| mass of adsorbed substance, kg/kg; | |
| heat of adsorption, J/mol; | |
| βe | external mass transfer coefficient, m/s; |
| βi | internal mass transfer coefficient m/s; |
| shear stress, Pa; | |
| γ | bulk density of the undisturbed packing in a static state, kg/m3; |
| specific active surface of the adsorption layer, m2; | |
| an indicator that depends on the characteristic length; | |
| porosity; | |
| fixed stacking porosity; | |
| ξ | coefficient of hydrodynamic resistance; |
| g | coefficient of resistance of the granular layer; |
| concentration, mol/m3; | |
| thermal conductivity coefficient, J·m/K·m2·s; | |
| λeff | effective thermal conductivity coefficient, J·m/K·m2·s; |
| coefficient of dynamic viscosity of the carrier flow, Pa·s; | |
| μl | viscosity for the liquid phase, Pa s; |
| ρl | density for the liquid phase, kg/m3; |
| ρm | true density of the grain material, kg/m3; |
| average volume density of adsorbate, kg/m3; | |
| νk | kinematic viscosity, n·s/m3; |
| carrier pressure in the granular layer, Pa; | |
| core width, m; | |
| anisotropy index of the adsorbent layer; |
References
- Yüksel, Ş.; Orhan, R. The Removal of Cr(VI) from Aqueous Solution by Activated Carbon Prepared from Apricot, Peach Stone and Almond Shell Mixture in a Fixed-Bed Column. Arab. J. Sci. Eng. 2018, 44, 5345–5357. [Google Scholar] [CrossRef]
- Habeeb, O.A.; Olalere, O.A.; Kanthasamy, R.; Ayodele, B.V. Hydrogen Sulfide Removal from Downstream Wastewater Using Calcium-Coated Wood Sawdust-Based Activated Carbon. Arab. J. Sci. Eng. 2019, 45, 501–518. [Google Scholar] [CrossRef]
- Khelifi, O.; Affoune, A.M.; Nacef, M.; Chelaghmia, M.L.; Laksaci, H. Response surface modeling and optimization of Ni (II) and Cu (II) Ions competitive adsorption capacity by sewage sludge activated carbon. Arab J Sci Eng. 2021, 47, 5797–5809. [Google Scholar] [CrossRef]
- Biham, O.; Malcai, O. Emergence of fractal clusters in sequential adsorption processes. In Dynamics and Thermodynamics of Systems with Long-Range Interactions; Dauxois, T., Ruffo, S., Arimondo, E., Wilkens, M., Eds.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2002; Volume 602. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, C.; Liu, Y.; Wang, D.; Liu, J. A model for the effective thermal conductivity of moist porous building materials based on fractal theory. Int. J. Heat Mass Transf. 2018, 125, 387–399. [Google Scholar] [CrossRef]
- Yu, B.; Cheng, P. A fractal permeability model for bi-dispersed porous media. Int. J. Heat Mass Transf. 2002, 45, 2983–2993. [Google Scholar] [CrossRef]
- Jin, Y.; Li, X.; Zhao, M.; Liu, X.; Li, H. A mathematical model of fluid flow in tight porous media based on fractal assumptions. Int. J. Heat Mass Transf. 2017, 108, 1078–1088. [Google Scholar] [CrossRef]
- Yu, B.; Zou, M.; Feng, Y. Permeability of fractal porous media by Monte Carlo simulations. Int. J. Heat Mass Transf. 2005, 48, 2787–2794. [Google Scholar] [CrossRef]
- Zhu, Q.; Xie, M.; Yang, J.; Li, Y. A fractal model for the coupled heat and mass transfer in porous fibrous media. Int. J. Heat Mass Transf. 2010, 54, 1400–1409. [Google Scholar] [CrossRef]
- Kolbanovskii, Y.A.; Bilera, I.V.; Borisov, A.A. The kinetics of adsorption on fractals: A numerical experiment. Russ. J. Phys. Chem. B 2007, 1, 685–691. [Google Scholar] [CrossRef]
- Helwani, Z.; Wiheeb, A.D.; Shamsudin, I.K.; Kim, J.; Othman, M.R. The effects of fractality on hydrogen permeability across meso-porous membrane. Heat Mass Transf. 2014, 51, 751–758. [Google Scholar] [CrossRef]
- Birdi, K.S. Fractals in Chemistry, Geochemistry, and Biophysics; Springer Science and Business Media LLC: Dordrecht, The Netherlands, 1993; ISBN 9781489911247. [Google Scholar]
- Inaba, H.; Seo, J.K.; Horibe, A. Numerical study on adsorption enhancement of rectangular adsorption bed. Heat Mass Transf. 2003, 41, 133–146. [Google Scholar] [CrossRef]
- Wallender, W.W.; Buyuktas, D. Dispersion in spatially periodic porous media. Heat Mass Transf. 2003, 40, 261–270. [Google Scholar] [CrossRef]
- White, S.M.; Tien, C.L. Analysis of flow channeling near the wall in packed beds. Wärme Stoffübertragung 1987, 21, 291–296. [Google Scholar] [CrossRef]
- Chandrasekhara, B.C.; Vortmeyer, D. Flow model for velocity distribution in fixed porous beds under isothermal conditions. Wärme Stoffübertragung 1979, 12, 105–111. [Google Scholar] [CrossRef]
- Samsonov, V.M.; Zubkov, V.V.; Grinev, I.V. Study of structural and thermodynamic characteristics of adsorption layers by the density functional method: Local density in adsorption layer on planar solid surface and adsorption isotherms. Colloid J. 2011, 73, 531–539. [Google Scholar] [CrossRef]
- Khodakov, Y.S.; Berlin, A.A.; Kalyaev, G.I.; Minachev, K.M. Equilibrium in an ideal adsorption layer during multiplet adsorption. Theor. Exp. Chem. 1972, 5, 424–430. [Google Scholar] [CrossRef]
- Avramenko, V.A.; Glushchenko, V.Y.; Golikov, A.P. Selection of a model of the adsorption layer in adsorption of solutions by solids. Russ. Chem. Bull. 1987, 36, 1118–1122. [Google Scholar] [CrossRef]
- Olivier, J.P. Modeling physical adsorption on porous and nonporous solids using density functional theory. J. Porous Mater. 1995, 2, 9–17. [Google Scholar] [CrossRef]
- Dabrowski, A.; Fekner, Z.; Dékány, I. Application of Comparative Method for Estimating Microporosity of Porous Solids in Adsorption from Solutions. J. Porous Mater. 2001, 8, 49–59. [Google Scholar] [CrossRef]
- Scarpa, F.; Tagliafico, L.A. A new procedure to measure water adsorption isotherms of porous fibrous materials. J. Porous Mater. 2007, 15, 451–456. [Google Scholar] [CrossRef]
- Almazán-Almazán, M.C.; Léonard, A.; Job, N.; López-Garzón, J.; Pirard, J.-P.; Blacher, S. Three-dimensional void space structure of activated carbon packed beds. J. Porous Mater. 2010, 18, 761–766. [Google Scholar] [CrossRef]
- Karnaukhov, A.P. Adsorption. The Texture of Dispersed and Porous Materials. The Science. Siberian Enterprise of the Russian Academy of Sciences 1999. p. 470. Available online: https://docplayer.ru/46514225-Adsorbciya-tekstura-dispersnyh-i-poristyh-materialov.html (accessed on 19 September 2023).
- Carrott, P.J.M.; Roberts, R.A.; Sing, K.S.V. Determination of micropore size distributions. In Characterization of Porous Solids; Elsevier: Amsterdam, The Netherlands, 1988; Volume 39, p. 89. Available online: https://www.elsevier.com/books/characterization-of-porous-solids/kral/978-0-444-42953-7 (accessed on 19 September 2023).
- Chandrasekhara, B.C.; Radha, N.; Kumari, M. The effect of surface mass transfer on buoyancy induced flow in a variable porosity medium adjacent to a vertical heated plate. Wärme Stoffübertragung 1992, 27, 157–166. [Google Scholar] [CrossRef]
- Bear, J.; Bachmat, Y. Macroscopic description of transport phenomena in porous media. In Introduction to Modeling of Transport Phenomena in Porous Media. Theory and Applications of Transport in Porous Media; Springer: Dordrecht, The Netherlands, 1990; Volume 4. [Google Scholar] [CrossRef]
- Bear, J.; Bachmat, Y. Transport phenomena in porous media—Basic equations. In Fundamentals of Transport Phenomena in Porous Media; Bear, J., Corapcioglu, M.Y., Eds.; NATO ASI Series (Series E: Applied Sciences); Springer: Dordrecht, The Netherlands, 1984; Volume 82. [Google Scholar] [CrossRef]
- Bachmat, Y.; Bear, J. Macroscopic modelling of transport phenomena in porous media. 1: The continuum approach. Transp. Porous Media 1986, 1, 213–240. [Google Scholar] [CrossRef]
- Bear, J. Modeling transport phenomena in porous media. In Convective Heat and Mass Transfer in Porous Media; Kakaç, S., Kilkiş, B., Kulacki, F.A., Arinç, F., Eds.; NATO ASI Series (Series E: Applied Sciences); Springer: Dordrecht, The Netherlands, 1991; Volume 196. [Google Scholar] [CrossRef]
- Bear, J.; Bachmat, Y. Macroscopic modelling of transport phenomena in porous media. 2: Applications to mass, momentum and energy transport. Transp. Porous Media 1986, 1, 241–269. [Google Scholar] [CrossRef]
- Meftah, F.; Pont, S.D. Staggered Finite Volume Modeling of Transport Phenomena in Porous Materials with Convective Boundary Conditions. Transp. Porous Media 2009, 82, 275–298. [Google Scholar] [CrossRef]
- Gaombalet, J.; Su, K.A. Numerical code for computation of transport phenomena coupled with mechanics in porous media. In Application of Numerical Methods to Geotechnical Problems; Cividini, A., Ed.; International Centre for Mechanical Sciences (Courses and Lectures); Springer: Vienna, Austria, 1998; Volume 397. [Google Scholar] [CrossRef]
- van Brakel, J.; Heertjes, P. Analysis of diffusion in macroporous media in terms of a porosity, a tortuosity and a constrictivity factor. Int. J. Heat Mass Transf. 1974, 17, 1093–1103. [Google Scholar] [CrossRef]
- Carvalho, P.H.; de Lemos, M.J. Role of porosity and solid-to-fluid thermal conductivity ratio on turbulent combined heat and mass transfer in a porous cavity. Int. J. Heat Mass Transf. 2019, 132, 221–237. [Google Scholar] [CrossRef]
- Tang, T.; McDonough, J. A theoretical model for the porosity–permeability relationship. Int. J. Heat Mass Transf. 2016, 103, 984–996. [Google Scholar] [CrossRef]
- Mussabekov, A.A.; Satayev, M.I.; Altynbekov, F.E.; Satayeva, L.M. Adsorber. Preliminary Patent of the Republic of Kazakhstan No. 18435. 2007. Available online: https://kzpatents.com/0-pp18435-adsorber.html (accessed on 19 September 2023).
- Do, D.D. Adsorption Analysis: Equilibria and Kinetics; Imperial College Press: London, UK, 1998; p. 913. [Google Scholar]
- Brener, A.M. Model of many-particle aggregation in dense particle systems. Chem. Eng Trans. 2014, 38, 145. [Google Scholar]
- Tong, X.; Wang, J.; Lin, S.; Guo, B.; Shum, H.Y. Modeling and rendering of quasi-homogeneous materials. ACM Trans. Graph. (TOG) 2005, 24, 1054–1061. [Google Scholar] [CrossRef]
- Ball, J.M.; Carr, J.; Penrose, O.; Ball, J.M.; Carr, J.; Penrose, O.; Ball, J.M.; Carr, J.; Penrose, O.; Ball, J.M.; et al. The Becker-Döring cluster equations: Basic properties and asymptotic behaviour of solutions. Commun. Math. Phys. 1986, 104, 657–692. [Google Scholar] [CrossRef]
- Vaisman, A.M.; Pravdina, M.K. Prelimiting equilibrium of a granular medium. In 5th All-Union Congress on Theoretical and Applied Mechanics; Kniga: Alma-Ata, Kazakhstan, 1981; p. 158. [Google Scholar]
- Frumkin, A.N.; Ponomarenko, E.A.; Burshtein, R.H. Chemisorption of oxygen and adsorption of electrolytes on activated charcoal. Rep. Acad. Sci. USSR 1963, 149, 1123–1126. Available online: http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=dan&paperid=27853&option_lang=eng (accessed on 19 September 2023).
- Goldshtik, M.A. Processes of Transfer in a Granular Layer; Academy of Sciences of the USSR: Novosibirsk, Russia, 1984; p. 163. [Google Scholar]
- Aerov, M.E.; Todes, O.M.; Narinsky, D.A. Devices with a Stationary Granular Layer; Chemistry: Leningrad, Russia, 1979; p. 176. [Google Scholar]
- Dulnev, G.N.; Novikov, V.V. Processes of transfer in non-uniform environments; Energoatomizdat: Leningrad, Russia, 1991; p. 248. [Google Scholar]
- Akhberdiyev, A.S.; Brener, A.M. Hydrodynamic characteristics of a fluidized nozzle with elements of a difficult configuration. Teor. Bases Chem. Technol. 2001, 35, 1–6. [Google Scholar]
- Rubenstein, R.N. Performance in a disskusiya on 3 All-Union conferences on theoretical questions of physical adsorption. In Kinetics and Dynamics of Physical Adsorption; Science: Moscow, Russia, 1972; pp. 168–170. [Google Scholar]
- Aris, R. The Mathematical Theory of Diffusion and Reaction in Permeable Catalists; Clarendon Press: Oxford, UK, 1975; p. 326. [Google Scholar]
- Holodniok, M.; Kubiphek, M.; Marek, M. Methods of the Analysis of Nonlinear Dynamic Models; World: Moscow, Russia, 1991; p. 365. [Google Scholar]
- Flad, E. (Ed.) Interphase Border: Gas—A Firm Body; World: Moscow, Russia, 2010; p. 435. [Google Scholar]
- Schaefer, D.W.; Keefer, K.D. The analysis of fractal characteristics of materials. In Fractals in Physics: Proceedings of the Sixth Trieste International Symposium on Fractals in Physics, ICTP, Trieste, Italy, 9–12 July 1985; University of Michigan: St. Ann Arbor, MI, USA, 1985; pp. 62–71. [Google Scholar]
- Azimov, A.M.; Zhantasov, K.T.; Abiyev, R.S.; Satayeva, L.M.; Khusanov, A.E. Modeling of Water Desalination in the Membranes of a Coaxial Cylindrical Form. 2016. Izvestiya Vysshikh Uchebnykh Zavedenii, Seriya Teknologiya Tekstil’noi Promyshlennosti 2016-January (3), с. 235–241. Available online: https://ttp.ivgpu.com/wp-content/uploads/2016/08/363_47.pdf (accessed on 1 December 2023).












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Satayev, M.; Azimov, A.; Iztleuov, G.; Satayeva, L. Modeling the Structure and Diffusion of Porous Layers. Water 2024, 16, 172. https://doi.org/10.3390/w16010172
Satayev M, Azimov A, Iztleuov G, Satayeva L. Modeling the Structure and Diffusion of Porous Layers. Water. 2024; 16(1):172. https://doi.org/10.3390/w16010172
Chicago/Turabian StyleSatayev, Marat, Abdugani Azimov, Gani Iztleuov, and Lazzat Satayeva. 2024. "Modeling the Structure and Diffusion of Porous Layers" Water 16, no. 1: 172. https://doi.org/10.3390/w16010172
APA StyleSatayev, M., Azimov, A., Iztleuov, G., & Satayeva, L. (2024). Modeling the Structure and Diffusion of Porous Layers. Water, 16(1), 172. https://doi.org/10.3390/w16010172






