Numerical Investigation of Inner Flow Characteristics of a Prototype Pump Turbine with a Single Pier in Draft Tube at Part Load Conditions
Abstract
:1. Introduction
2. Research Object and Numerical Method
3. Results and Discussion
3.1. Field Test Results of Pressure Fluctuation
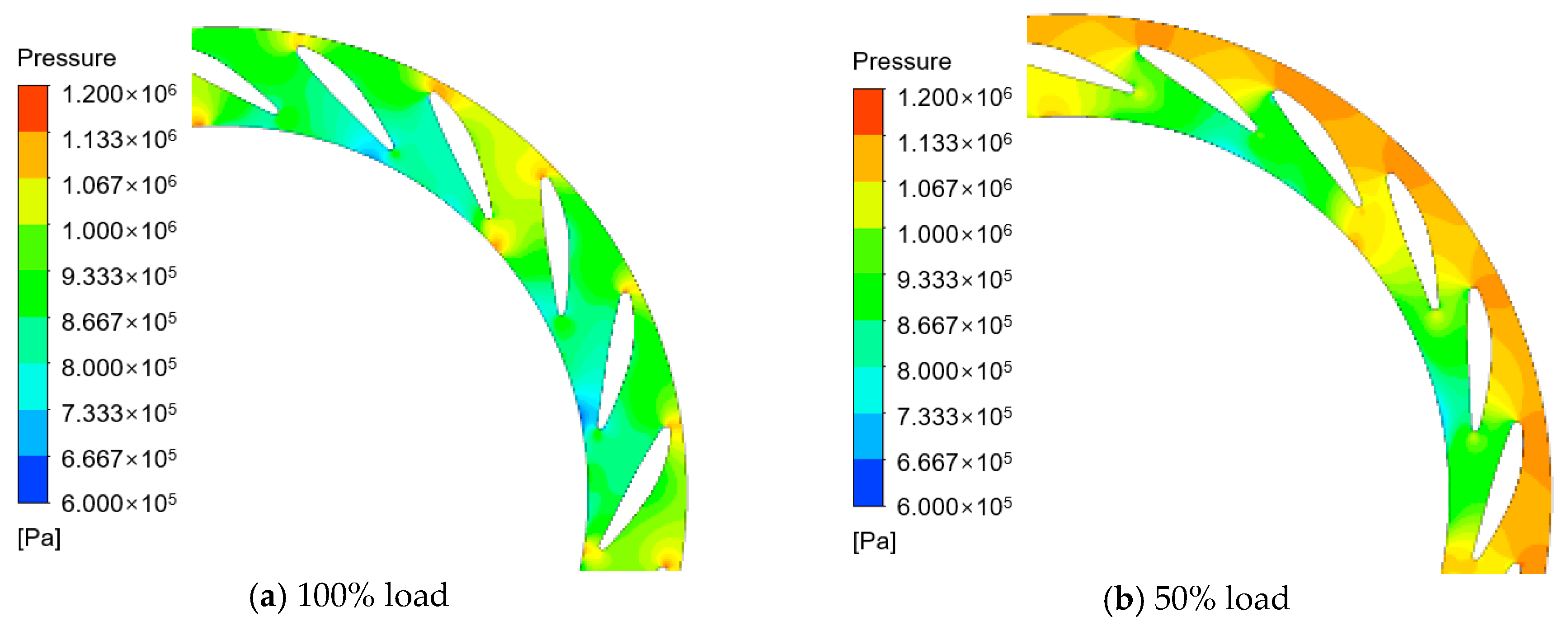
3.2. Internal Flow Characteristic of Ring and Runner
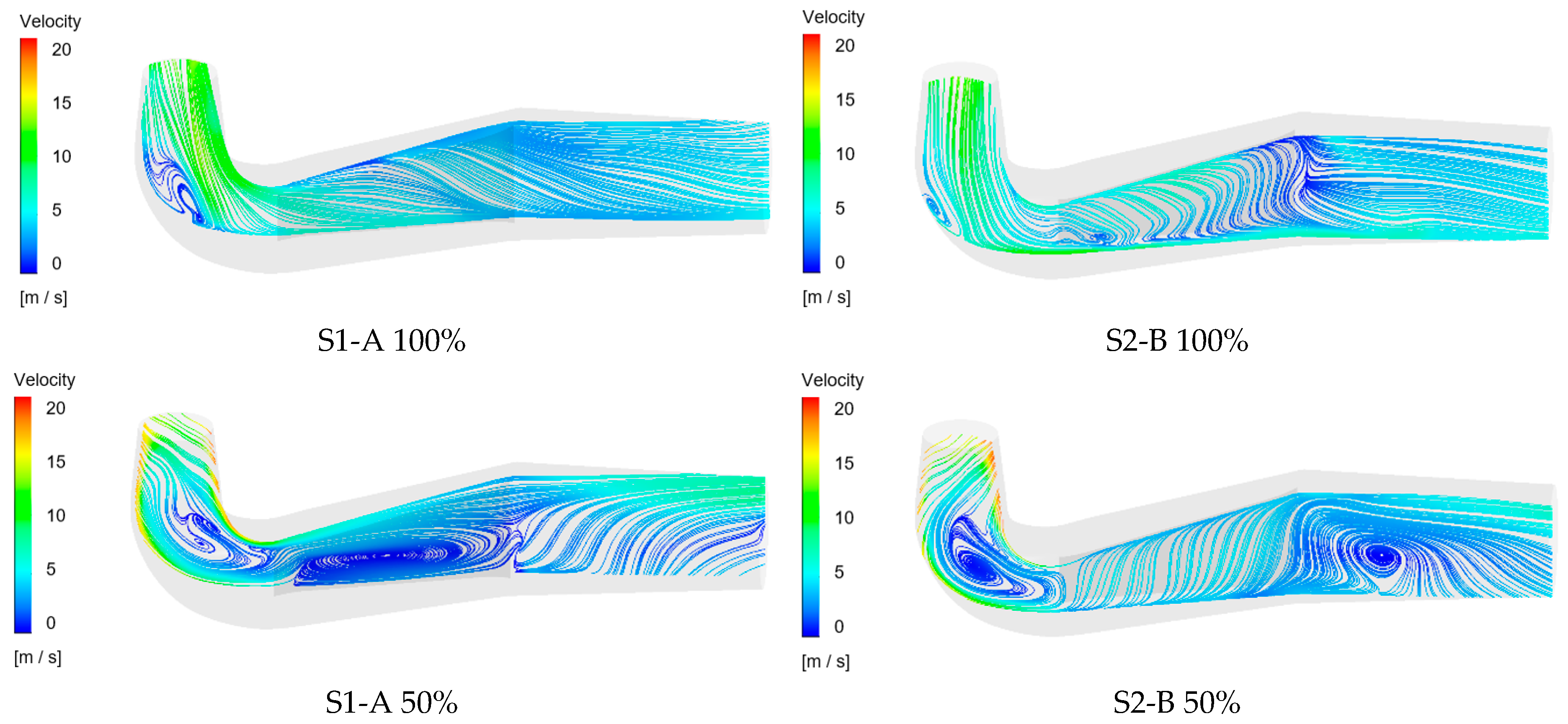
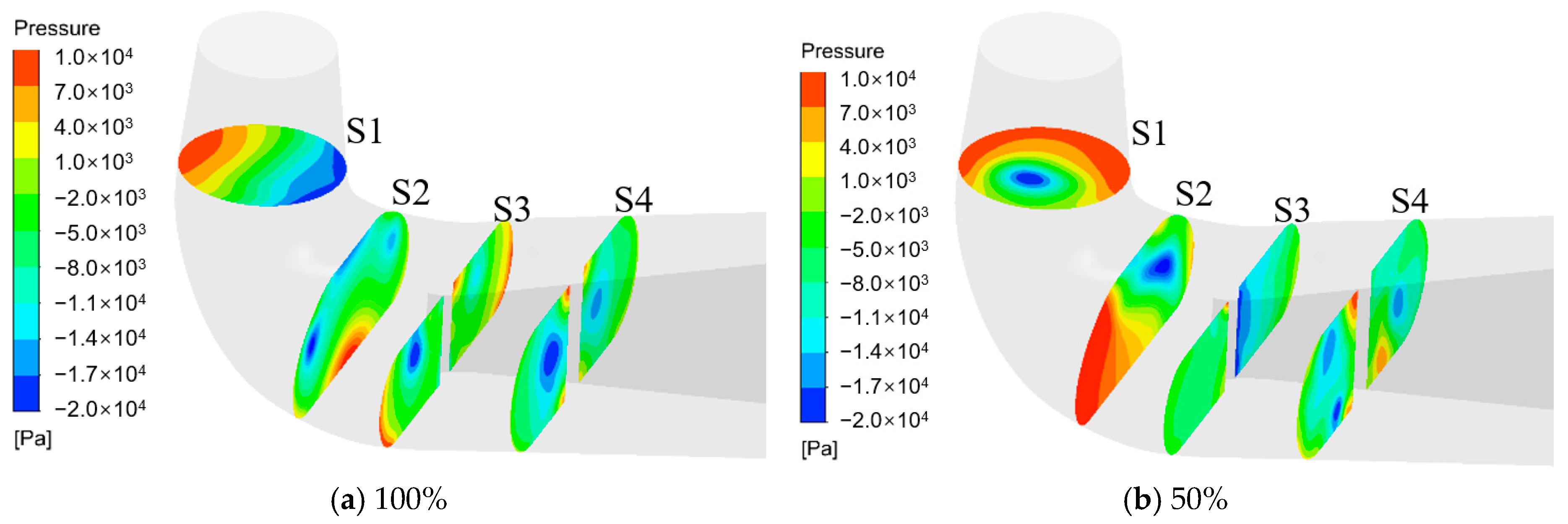
3.3. Internal Flow Characteristic of Draft Tube
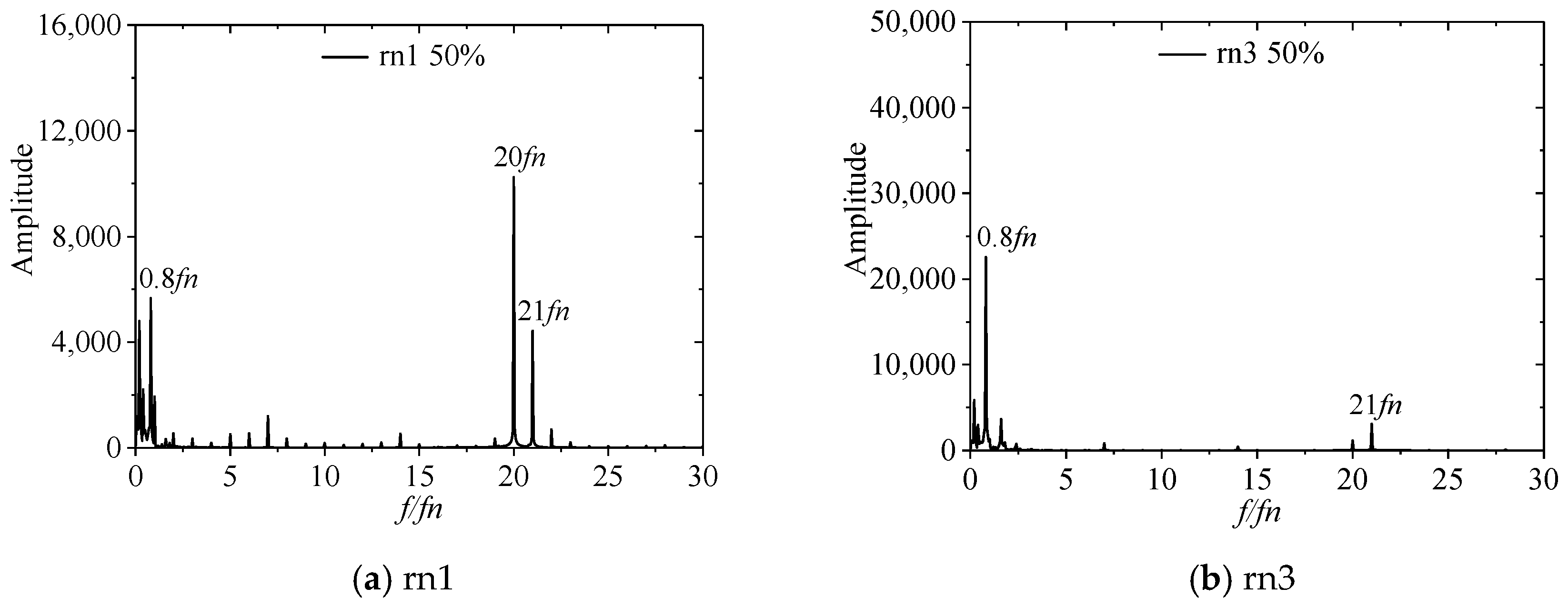
3.4. Spectral Characteristics of Draft Tube Pressure Fluctuation
3.5. Discussion
3.5.1. Evolution Process of Vortex Rope
3.5.2. Complementary Shape of Vortex Rope and Recirculation Zone
3.5.3. Effect on the Runner
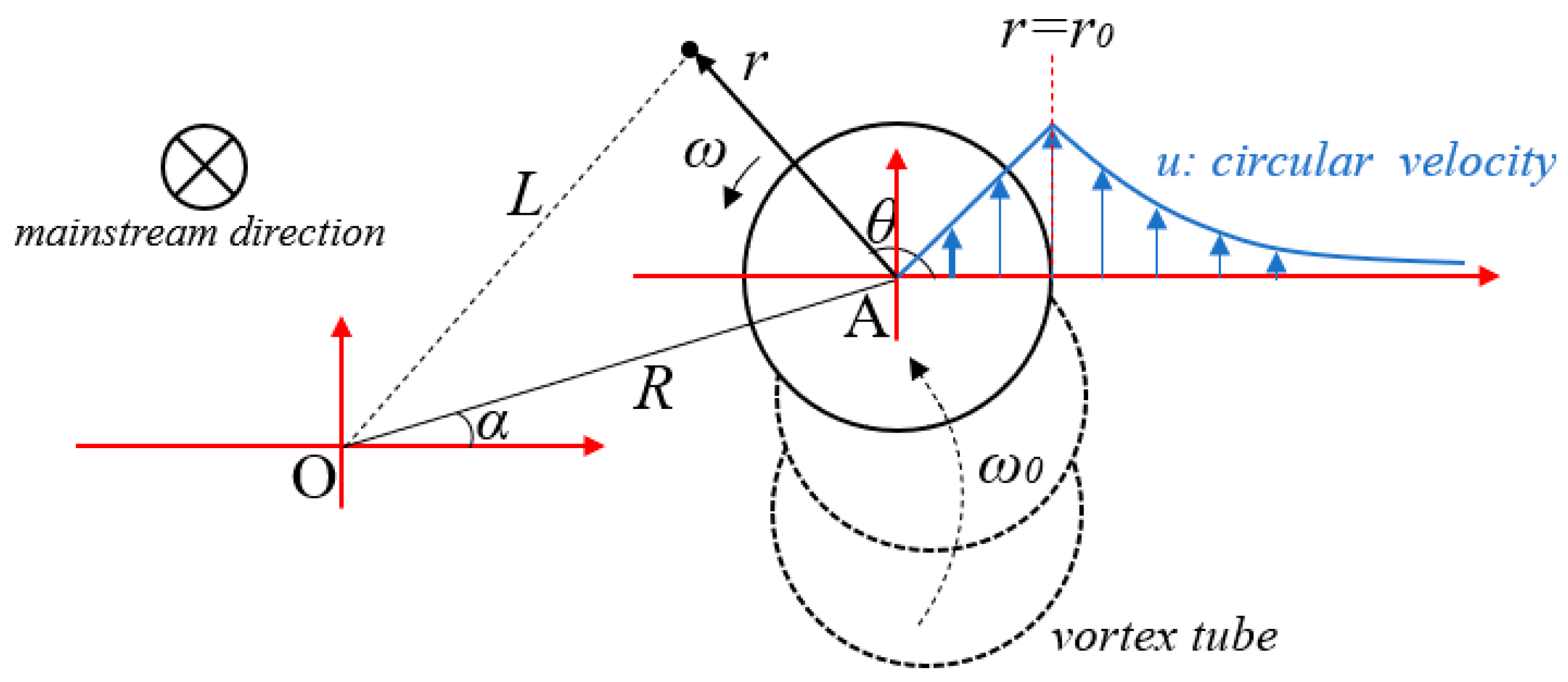
3.5.4. Preliminary Analysis of Fluid Kinematic Progression
3.5.5. Comparability and Limitation of Experimental and Numerical Simulations
4. Conclusions
- (1)
- The asymmetry of the flow is preordained. At 100% load, the flow in Passage A and Passage B on both sides of the pier was relatively consistent with the geometric contour of the draft tube. At 50% load, Passage A had a larger flow rate and generated a large area of vortex near the pier. Passage B mainly exhibited a low-speed spiral motion, mixed with the high-speed area of Passage A, and formed a large-scale vortex at the outlet of the draft tube. The existence of the pier made Passage B reduce the global pressure difference with Passage A through localized pressure adjustments and also reduced the turbulent kinetic energy of the fluid, especially in the front section of Passage B.
- (2)
- Through the analysis of pressure fluctuation, it was found that, at 50% load, the rotor–stator interaction component that dominated at 100% load basically disappeared, and the more pronounced component was the low frequency (0.2fn), which is the evolution period of the process of the generation, movement, and decay of the vortex rope. At the monitoring point in the middle of the pier, the main frequency split into 0.13fn and 0.4fn, which may be due to the kinematic precession originated from the evolution of vortex rope.
- (3)
- The distribution of the vortex rope in the draft tube and the recirculation zone showed a complementary shape. The frequency of the vortex rope had a significant impact on the pressure fluctuation of the runner, and the point near trailing edge of the runner blade showed a high-amplitude vortex rope frequency of 0.8fn.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, J.F.; Oh, U.J.; Park, J.C.; Park, E.S.; Im, H.B.; Lee, K.Y.; Choi, J.S. A Review of World-wide Advanced Pumped Storage Hydropower Technologies. IFAC Pap. 2022, 55, 170–174. [Google Scholar] [CrossRef]
- Hu, J.Y.; Wang, Q.B.; Song, H.G.; Mao, J.H. Effect of wave disturbance on the fluid dynamics of the pump turbine in a seawater pumped storage hydroplant. Front. Earth Sci. 2023, 11, 1220842. [Google Scholar] [CrossRef]
- Hu, J.Y.; Wang, Q.B.; Meng, Z.Z.; Song, H.G.; Chen, B.W.; Shen, H. Numerical Study of the Internal Fluid Dynamics of Draft Tube in Seawater Pumped Storage Hydropower Plant. Sustainability 2023, 15, 8327. [Google Scholar] [CrossRef]
- Zuo, Z.G.; Liu, S.H. Flow-Induced Instabilities in Pump-Turbines in China. Engineering 2017, 3, 504–511. [Google Scholar] [CrossRef]
- Yan, J.P.; Seidel, U.; Koutnik, J. Numerical simulation of hydrodynamics in a pump-turbine at off-design operating conditions in turbine mode. IOP Conf. Ser. Earth Environ. Sci. 2013, 15, 032041. [Google Scholar] [CrossRef]
- Zhu, D.; Yan, W.; Guang, W.L.; Wang, Z.W.; Tao, R. Influence of Guide Vane Opening on the Runaway Stability of a Pump-Turbine Used for Hydropower and Ocean Power. J. Mar. Sci. Eng. 2023, 11, 1218. [Google Scholar] [CrossRef]
- Hu, H.P.; Xia, M.; Qiao, M.; Wang, W.; Wang, J.Z.; Wang, Z.W. A Simulation Study of Hydraulic Vibration caused by Clearance Flow in a Pump Turbine. IOP Conf. Ser. Earth Environ. Sci. 2022, 1079, 012032. [Google Scholar] [CrossRef]
- Asomani, S.N.; Yuan, J.P.; Wang, L.Y.; Appiah, D.; Zhang, F. Geometrical effects on performance and inner flow characteristics of a pump-as-turbine: A review. Adv. Mech. Eng. 2020, 12, 1687814020912149. [Google Scholar] [CrossRef]
- Fu, X.L.; Li, D.Y.; Wang, H.J.; Zhang, G.H.; Li, Z.G.; Wei, X.Z. Influence of the clearance flow on the load rejection process in a pump-turbine. Renew. Energy 2018, 127, 310–321. [Google Scholar] [CrossRef]
- Yang, H.; He, Q.; Bi, H.; Huang, X.; Yang, M.; Zou, M.; Wang, Z. Head-Cover vibration investigation of a Prototype Reversible Pump-Turbine Unit during Start-up in Pump mode. Part I: Fluid dynamic analysis. IOP Conf. Ser. Earth Environ. Sci. 2022, 1037, 012055. [Google Scholar] [CrossRef]
- Yang, M.Q.; Zhao, W.Q.; Bi, H.L.; Yang, H.X.; He, Q.L.; Huang, X.X.; Wang, Z.W. Flow-Induced Vibration of Non-Rotating Structures of a High-Head Pump-Turbine during Start-Up in Turbine Mode. Energies 2022, 15, 8743. [Google Scholar] [CrossRef]
- Zhang, W.W.; Chen, Z.M.; Zhu, B.S.; Zhang, F. Pressure fluctuation and flow instability in S-shaped region of a reversible pump-turbine. Renew. Energy 2020, 154, 826–840. [Google Scholar] [CrossRef]
- Kim, S.J.; Suh, J.W.; Choi, Y.S.; Park, J.; Park, N.H.; Kim, J.H. Inter-Blade Vortex and Vortex Rope Characteristics of a Pump-Turbine in Turbine Mode under Low Flow Rate Conditions. Water 2019, 11, 2554. [Google Scholar] [CrossRef]
- Tridon, S.; Barre, S.; Ciocan, G.D.; Tomas, L. Experimental analysis of the swirling flow in a Francis turbine draft tube: Focus on radial velocity component determination. Eur. J. Mech.-B-Fluids 2010, 29, 321–335. [Google Scholar] [CrossRef]
- Lin, T.; Li, J.; Xie, B.F.; Zhang, J.R.; Zhu, Z.C.; Yang, H.; Wen, X.M. Vortex-Pressure Fluctuation Interaction in the Outlet Duct of Centrifugal Pump as Turbines (PATs). Sustainability 2022, 14, 15250. [Google Scholar] [CrossRef]
- Pang, S.; Zhu, B.; Shen, Y.; Chen, Z. Study on cavitating vortex rope characteristics of reversible pump-turbine under part load turbine condition. Phys. Fluids 2023, 35, 085131. [Google Scholar] [CrossRef]
- Vu, T.C.; Devals, C.; Zhang, Y.; Nennemann, B.; Guibault, F. Steady and unsteady flow computation in an elbow dr aft tube with experimental validation. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012045. [Google Scholar] [CrossRef]
- Ciocan, G.D.; Iliescu, M.S.; Vu, T.C.; Nennemann, B.; Avellan, F. Experimental Study and Numerical Simulation of the FLINDT Draft Tube Rotating Vortex. J. Fluids Eng. 2006, 129, 146–158. [Google Scholar] [CrossRef]
- Foroutan, H.; Yavuzkurt, S. Unsteady Numerical Simulation of Flow in Draft Tube of a Hydroturbine Operating under Various Conditions Using a Partially Averaged Navier–Stokes Model. J. Fluids Eng. 2015, 137, 061101. [Google Scholar] [CrossRef]
- Gagnon, J.-M.; Aeschlimann, V.; Houde, S.; Flemming, F.; Coulson, S.; Deschenes, C. Experimental Investigation of Draft Tube Inlet Velocity Field of a Propeller Turbine. J. Fluids Eng. 2012, 134, 101102. [Google Scholar] [CrossRef]
- Gouin, P.; Deschênes, C.; Iliescu, M.; Ciocan, G.D. Experimental investigation of draft tube flow of an axial turbine by laser doppler velocimetry. In Proceedings of the 3rd IAHR International Meeting of the Workgroup on Cavitation and Dynamic Problems in Hydraulic Machinery and Systems, Brno, Czech Republic, 14–16 October 2009; pp. 87–97. [Google Scholar]
- Lemay, S.; Fraser, R.; Ciocan, G.D.; Aeschlimann, V.; Deschênes, C. Flow field study in a bulb turbine runner using LDV and endoscopic S-PIV measurements. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 022015. [Google Scholar] [CrossRef]
- Vuillemard, J.; Aeschlimann, V.; Fraser, R.; Lemay, S.; Deschênes, C. Experimental investigation of the draft tube inlet flow of a bulb turbine. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 032010. [Google Scholar] [CrossRef]
- Tridon, S.; Barre, S.; Ciocan, G.D.; Leroy, P.; Ségoufin, C. Experimental investigation of draft tube flow instability. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012044. [Google Scholar] [CrossRef]
- Tridon, S.; Barre, S.; Ciocan, G.; Ségoufin, C.; Leroy, P. Discharge Imbalance Mitigation in Francis Turbine Draft-Tube Bays. J. Fluids Eng. 2012, 134, 041102. [Google Scholar] [CrossRef]
- Cedric, D.; Balarac, G.; Metais, O.; Sylvain, T.; Stephane, B.; Ciocan, G.; Thomas, L.; Laurent, T. Large-Eddy Simulations of Draft Tube Flow and Validation from Experimental Results. In Proceedings of the 3rd IAHR International Meeting of the Workgroup on Cavitation and Dynamic Problems in Hydraulic Machinery and Systems, Brno, Czech Republic, 14–16 October 2009. [Google Scholar]
- Li, H.; Xu, L.; Zhao, F.; Zhang, F.; Deng, Y.; Li, H.; Cheng, Y.; Zheng, Y.; Kan, K. Investigation of Flow Characteristics of Flow Passage Components in Francis Turbine under No-load and 50% Load operating conditions. J. Phys. Conf. Ser. 2022, 2285, 012040. [Google Scholar] [CrossRef]
- Wang, L.; Cui, J.; Shu, L.; Jiang, D.; Xiang, C.; Li, L.; Zhou, P. Research on the Vortex Rope Control Techniques in Draft Tube of Francis Turbines. Energies 2022, 15, 9280. [Google Scholar] [CrossRef]
- Paik, J.; Sotiropoulos, F.; Sale Michael, J. Numerical Simulation of Swirling Flow in Complex Hydroturbine Draft Tube Using Unsteady Statistical Turbulence Models. J. Hydraul. Eng. 2005, 131, 441–456. [Google Scholar] [CrossRef]
- Pasche, S.; Gallaire, F.; Avellan, F. Origin of the synchronous pressure fluctuations in the draft tube of Francis turbines operating at part load conditions. J. Fluid Struct. 2019, 86, 13–33. [Google Scholar] [CrossRef]
- Temam, R. Navier-Stokes Equations: Theory and Numerical Analysis; American Mathematical Society: Providence, RI, USA, 2001; Volume 343. [Google Scholar]
- Hu, J.; Luo, X.; Zhao, Y.; Liang, Q.; Liu, D.; He, Q.; Wang, Z.; Guan, Z. Evolution mechanism of unsteady internal flow of an ultra-high head pump-turbine in pump mode. J. Energy Storage 2023, 74, 109309. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Li, J.F.; Zhu, Z.C. The acceleration effect of pump as turbine system during starting period. Sci. Rep. 2023, 13, 4913. [Google Scholar] [CrossRef]
- Chen, W.; Zydek, N.; Parma, F. Evaluation of hydrocyclone models for practical applications. Chem. Eng. J. 2000, 80, 295–303. [Google Scholar] [CrossRef]
- Hu, H.P.; Xia, M.; Song, X.H.; Zhao, W.Q.; Wang, W.; Wang, Z.W. A Field Investigation of Stability Characteristics of Pressure Fluctuation and Vibration in Prototype Pump Turbine at Multiple Working Points. Water 2023, 15, 3378. [Google Scholar] [CrossRef]






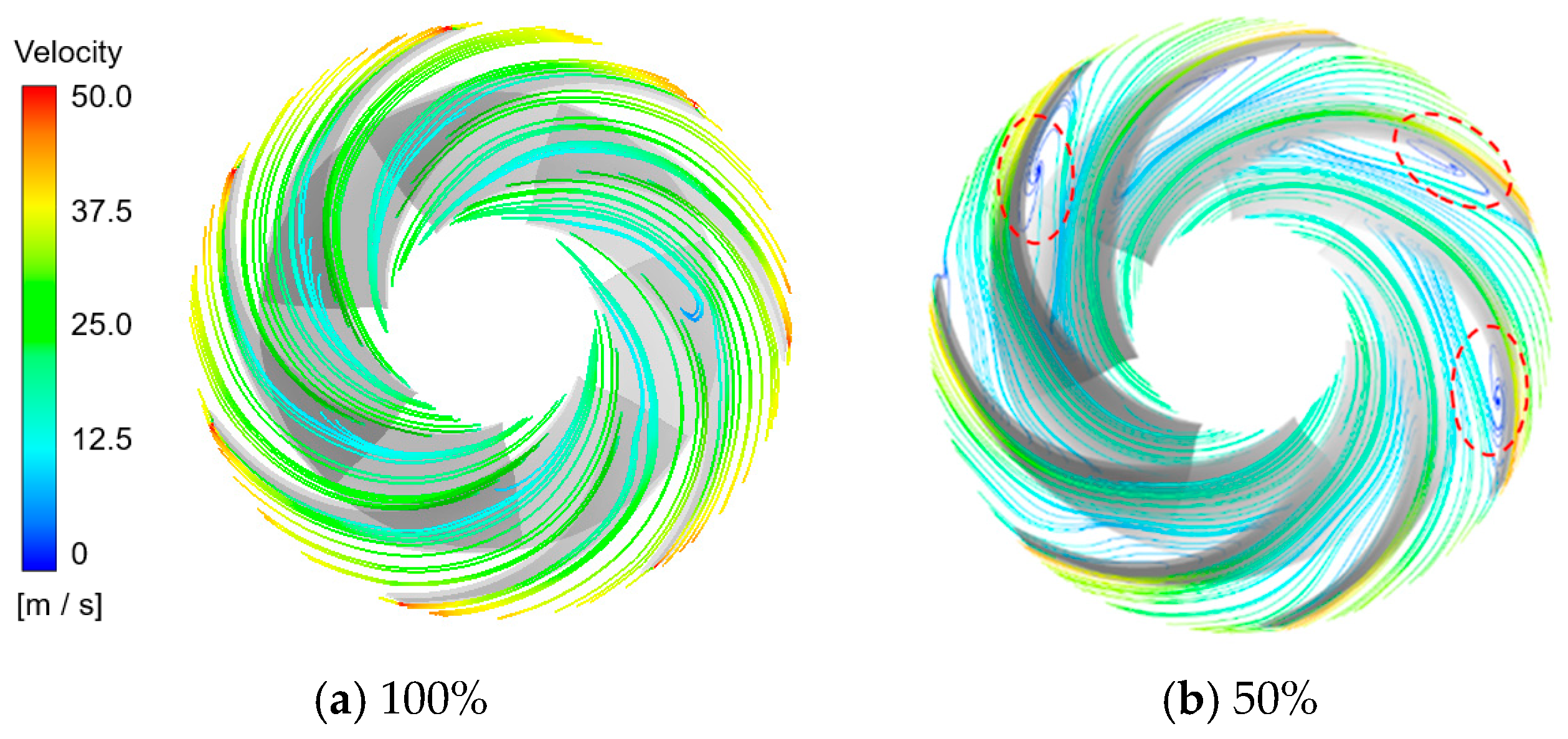













| Parameter | Unit | Value |
|---|---|---|
| Runner inlet diameter (D) | m | 5.22 |
| Rotational speed (n) | r/min | 200 |
| Rated power (P) | MW | 139 |
| Rated flow (Q) | m3/s | 148.8 |
| Number of blades (Zb) | / | 7 |
| Number of stay vanes (Zs) | / | 20 |
| Number of guide vanes (Zg) | / | 20 |
| Rated head (H) | m | 105.8 |
| Fluid Domain | Spiral Case | Stay Vane | Guide Vane | Runner | Draft Tube |
|---|---|---|---|---|---|
| Number of Nodes (×104) | 13.2 | 36.2 | 26.5 | 156 | 26.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Xia, M.; Song, X.; Wang, Z.; Qiao, M. Numerical Investigation of Inner Flow Characteristics of a Prototype Pump Turbine with a Single Pier in Draft Tube at Part Load Conditions. Water 2024, 16, 13. https://doi.org/10.3390/w16010013
Hu H, Xia M, Song X, Wang Z, Qiao M. Numerical Investigation of Inner Flow Characteristics of a Prototype Pump Turbine with a Single Pier in Draft Tube at Part Load Conditions. Water. 2024; 16(1):13. https://doi.org/10.3390/w16010013
Chicago/Turabian StyleHu, Haiping, Ming Xia, Xianghui Song, Zhengwei Wang, and Mu Qiao. 2024. "Numerical Investigation of Inner Flow Characteristics of a Prototype Pump Turbine with a Single Pier in Draft Tube at Part Load Conditions" Water 16, no. 1: 13. https://doi.org/10.3390/w16010013
APA StyleHu, H., Xia, M., Song, X., Wang, Z., & Qiao, M. (2024). Numerical Investigation of Inner Flow Characteristics of a Prototype Pump Turbine with a Single Pier in Draft Tube at Part Load Conditions. Water, 16(1), 13. https://doi.org/10.3390/w16010013







