1. Introduction
Discharge of wastewater has been steadily increasing over the years in China due to urbanization and population growth. There is still a disparity between China’s modern Integrated Water Resources Management (IWRM) and that of some developed countries [
1]. In China, the conventional activated sludge process has been utilized as a crucial treatment to treat over 80% of the wastewater in Wastewater Treatment Plants (WWTPs) [
2]. However, due to the time delay between the monitoring of the biological process and control actions, WWTPs are difficult to attain precise control, resulting in over-aeration and improper dosing which lead to higher energy consumption and overall treatment costs. The average energy consumption of wastewater treatment in China is 0.29 kW-h/m
3 [
3], indicating substantial potential for energy conservation [
4].
Research has demonstrated that applying model predictive control (MPC) in WWTPs can lead to refined control, resulting in energy or material savings under the same influent conditions [
5]. MPC [
6] is a class of control algorithms that uses explicit process models to predict the future response of a system and has been widely applied in various industries. MPC uses process models to predict the future dynamic behavior of a system and combines recursive optimization and feedback emendation strategies to improve system performance within constraints [
7,
8]. A considerable number of studies have applied MPC and mechanism models, e.g., the activated sludge models (ASMs) [
9], to design control strategies for WWTPs. For instance, Holenda et al. [
10] effectively controlled dissolved oxygen in the activated sludge process using MPC combined with the activated sludge model No. 1 (ASM1) model. Liu et al. [
11] demonstrated the effectiveness of ASM1-based MPC in controlling ammonia nitrogen in WWTPs.
However, MPC requires a detailed model whose modeling process is complex due to the nonlinear and time-varying nature of the bioreaction system and the influence of environmental factors [
12]. Despite ASMs being quite refined models for MPCs, they have limitations in accuracy, cumbersome modeling, and computational time. Also, incomplete modeling of certain processes, such as phosphorus removal, further restricts ASM-based MPCs’ potential in controlling variable prediction or optimal control [
13]. Currently, ASM-based MPCs are not widely used in full-flow WWTP bioreactors [
14]. Instead, some studies have utilized linear models in place of ASMs to reduce the computational time [
15,
16,
17].
For the prediction models in MPC, data-driven and artificial intelligence (AI) models have garnered significant attention in the wastewater treatment industry due to the advent of information technology [
18,
19,
20,
21]. Compared to traditional mechanistic models that are characterized by fixed numerous parameters, data-driven models possess powerful fitting ability and adaptability that enable them to effectively learn non-linear and complex biological treatment systems. The simulation models of biological reaction tanks in wastewater treatment plants using artificial intelligence mainly include traditional machine learning models [
20], simple artificial neural network models (ANN) [
18,
19,
21], and deep neural network models (DNN) [
22,
23], etc. These aforementioned studies have shown that the prediction results of neural network models are consistent with the measured values. Moreover, the long short-term memory (LSTM) model has been found to exhibit higher prediction accuracy compared to other simple neural networks [
24,
25,
26]. In recent years, MPC based on the deep neural network has been developed for WWTP [
27,
28,
29]. Pisa et al. [
25] used LSTM in conjunction with model predictive control (MPC) to regulate sulfur emissions from wastewater treatment plants. Literature tends to focus on benchmark simulation model 1 (BSM1) simulation studies or univariate regression tasks using LSTM as a predictive model.
The aforementioned MPC methods overcome the disadvantages of mechanism models in MPC and are capable of effectively utilizing monitoring data from wastewater treatment plants (WWTPs) to model and optimize complex biochemical processes. However, current research on data-driven MPC still have limitations in actual systems and operational challenges still exist.
(1) Existing MPC for WWTP focus on enhancing the effluent quality and reducing energy consumption. For the biological reaction process of Anaerobic-Anoxic-Oxic (AAO), the stability of the dynamic state, e.g., mixed liquor suspended solids (MLSS) and dissolved oxygen in bioreactors, during the operation still lacks further consideration.
(2) Machine learning-based MPC is perceived as a black-box model, whose outputs may not be readily interpretable and reliable, therefore, its decisions may not be trusted by WWTP operators. Moreover, the model’s predictive performance is highly dependent on training data, and it is often difficult to guarantee the safety of the output in case of learning failure. The systematic analysis and solution to the improvement of the control strategy’s safety of data-driven MPC in WWTPs still need further investigation.
To overcome these limitations, an LSTM-based model predictive control method (LSTM-MPC) and its corresponding rationality verification were developed in this study for the biochemical reaction of a real combined sewer system (CSS) WWTP. First, the stability of bioreactor state variables and energy consumption were taken as the objectives of the optimal control. Then, to address concerns about the safety of the black-box control model, three rationality verification methods were designed based on historical monitoring dataset to constrain the output of the control term, providing a reliable MPC model in practical operation.
3. Methodology
3.1. LSTM Stimulatuon Model
The state of the bioreactors at the previous moment in the wastewater treatment process has an impact on the subsequent bioreaction. While the LSTM can achieve the function of filtering and storing information, capturing the long-term dependencies present in the data [
31,
32], and therefore is more suitable for the dynamic of long time series data in this study.
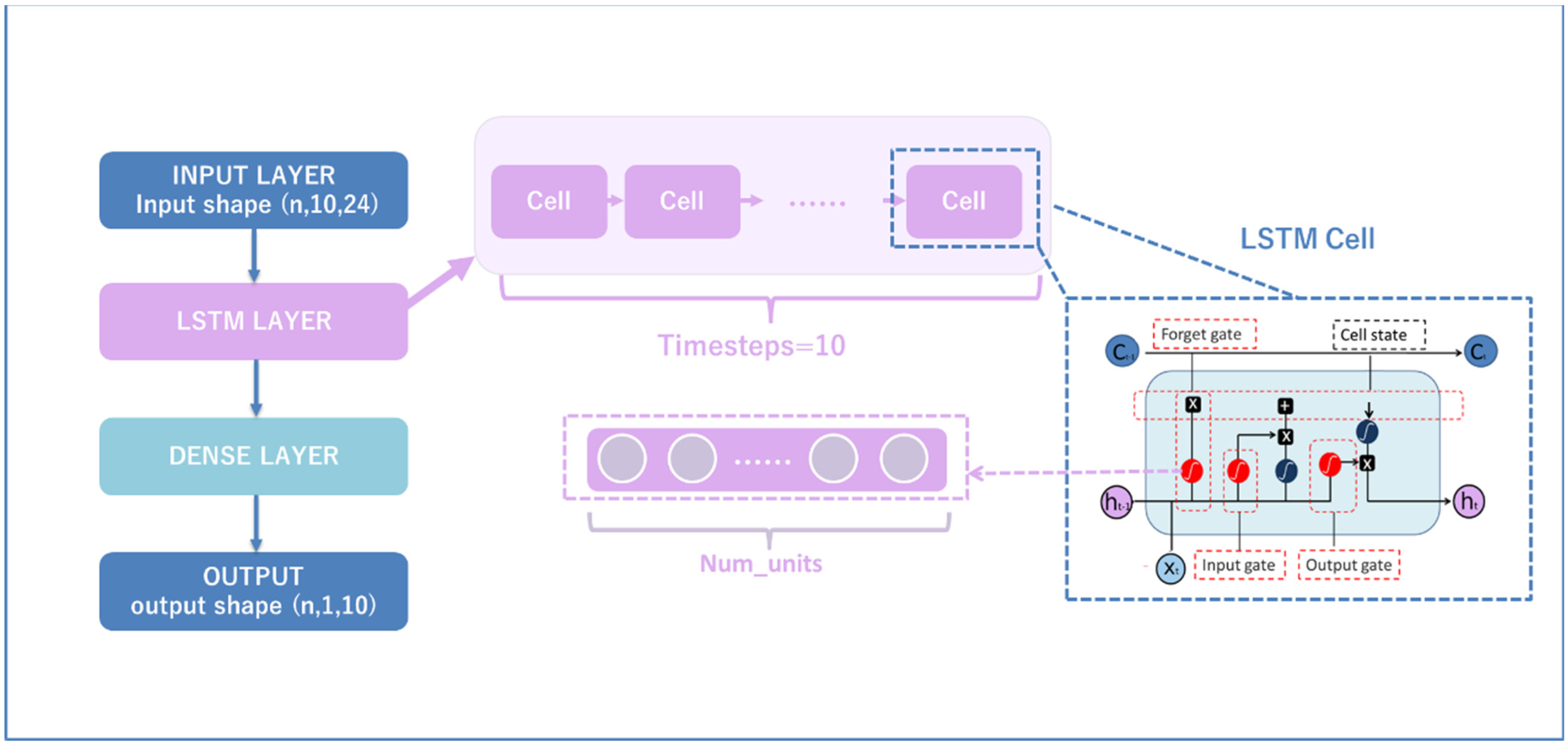
The LSTM neural network was used to predict the state of the bioreactor at the next time step. The construction of LSTM considered the effects of organic nutrients on water quality and operational parameters. In this study, the time series dataset of state variables, influent variables, and control variables was used as inputs, and outputs were the state variables at the next time step. The specific mathematical formula of the model is as follows.
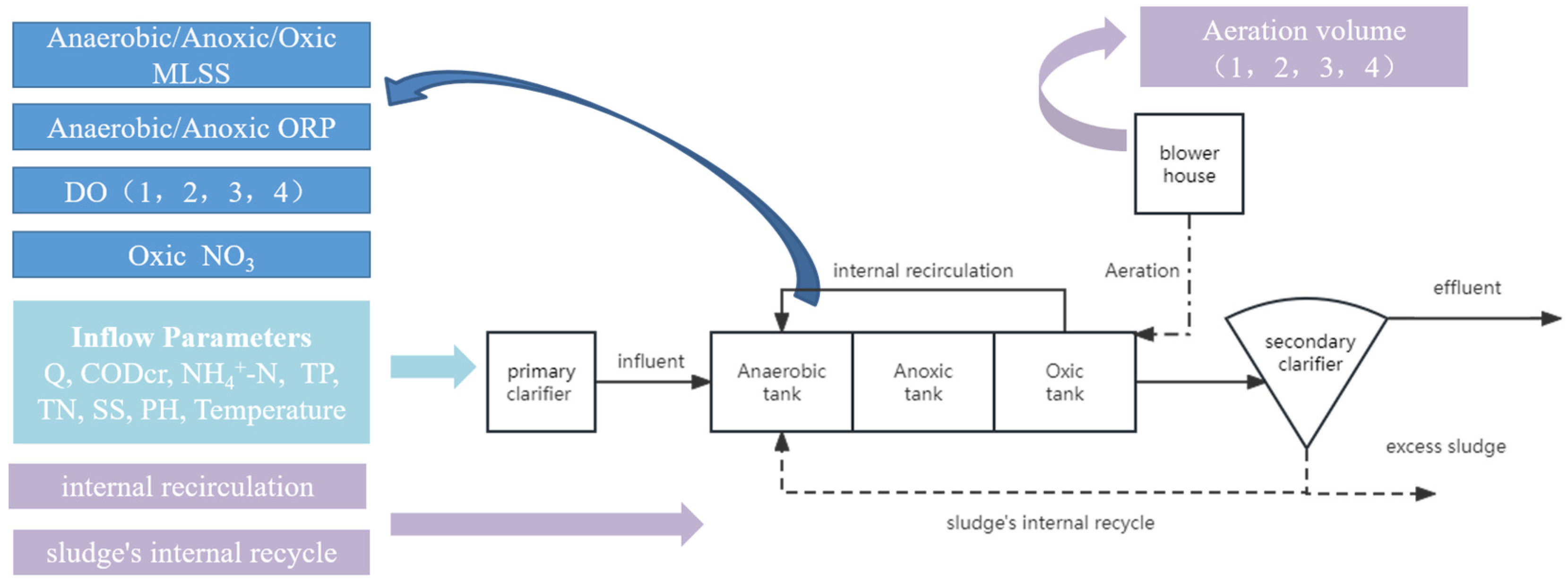
are the state variables, containing: DO, MLSS, ORP, Oxic NO3;
are the influent variables, containing: Qin, COD, TP, TN, NH4+-N, PH, SS;
are the control variables, where is the aeration volume, is the internal return flow rate (Qr), and is the sludge internal recycle flow rate (Qsr);
are the output state variables, containing DO, MLSS, ORP, and Oxic NO3 at the next time step.
is the prediction time step.
is the parameters of LSTM.
Figure 2 shows the schematic diagram of the LSTM model proposed in this study. The structural hyperparameters of LSTM are mainly the number of hidden layer neurons of LSTM cells (Num_units in
Figure 2), so this study used different numbers of LSTM units for testing, and the final output is passed through a dense layer. In this paper, four LSTM model structures (named structure 1–4) were constructed to verify their performance on the prediction. The parameters of each structure, which were gradually adjusted in pre-tests, are shown in
Table 2. All the LSTM models were developed by Python 3.0 and TensorFlow library [
33].
Model performance evaluation aims to assess the effectiveness of model predictions. In this study, the results of the proposed model predictions were evaluated by mean squared error (MSE, Equation (5)) and Nash–Sutcliffe model efficiency coefficient (NSE, Equation (6)), where
n corresponds to the total number of measurements,
is the model predicted value, and
is the sample real value, and
denotes the total average of the sample real values.
3.2. MPC Based on LSTM for Bioreaction Optimal Control
3.2.1. Structure of MPC
Based on the above LSTM, this study used a standard MPC architecture based on recursive optimization [
6,
25] to build a real-time optimization model called LSTM-MPC which can be described by 4 steps and is shown in
Figure 3 below.
Step 1, initialization: The control strategy is randomly initialized within a limited range based on the control variable of the collected dataset.
Step 2, prediction: The real-time monitoring data and initialized control variables are used as inputs and sent into the LSTM for prediction.
Step 3, evaluation: The prediction results are evaluated to determine whether the current state can achieve the goal of optimal control with respect to the control variables in Step 1. If true, the control variables will be output as a control strategy. Otherwise, go to step 4.
Step 4, optimization: The control variables are sent into the optimization algorithm (e.g., PSO in this study) for optimization, and the optimized control variables are used as the new control variables in Step 2.
These four steps should be finished within one control interval (less than or equal to Δt) for real-time control. Through the above process, a sufficiently optimized control strategy will be obtained for system operation.
In this study, considering the characteristics of the bioreactor, the following three control variables are optimized.
(1) Optimization of aeration control
Research shows that biological treatment is the main energy user in Chinese WWTPs [
34]. In the aeration process of the AAO, there are often random factors and lags in human operation, leading to excessive aeration and excessive consumption of electricity. Reducing aeration is one of the most important and feasible steps to achieve energy savings. At the same time, controlling dissolved oxygen in the bioreaction tank through aeration control is the most effective way to control greenhouse gas emissions, which is in line with the sustainable development needs of sewage treatment plants [
35]. Therefore, in the optimization of WWTPs operations, the process control means are recommended to prioritize aeration control.
(2) Optimization of internal recirculation control
The internal recirculation of the AAO process mainly provides nitrogen sources for denitrification reactions in the anoxic tank to achieve nitrogen removal. As this stage requires a low concentration of dissolved oxygen and sufficient nitrogen source input, optimizing internal recirculation can effectively stabilize the operation of the process.
(3) Optimization of sludge’s internal recycle control
The sludge’s internal recycle flow of AAO mainly replenishes the activated sludge in the reaction tanks and maintains the total amount of activated sludge. The control of can ensure stable and qualified effluent to a certain extent in practical reaction conditions of the bioreactors.
3.2.2. Optimization Algorithm
For the control requirements of the biochemical reactor tanks and the control duration, the optimization algorithm selected in this study is the Particle Swarm Optimization (PSO) algorithm [
36,
37]. PSO optimizes the control variables through the particle’s velocity and their best-know positions, and its flow chart is shown in
Figure 4 below.
Since the time interval of control equipment (e.g., blowers and pumps) in the AAO process is 30 min, the control time step . The proposed optimization model was developed in Python. The algorithm parameter configurations were as follows: population size pop_size = 30, inertia weight w = 0.2, acceleration constant C1 = C2 = 0.6, and the maximum number of iterations max_steps = 500. Due to the requirement of the algorithm speed in the actual control, the optimization algorithm was terminated if there was no significant change in the fitness function during 200 iterations.
3.2.3. Fitness Function
In the optimization algorithm, the fitness function was set based on control requirements. In this study, considering both the stability and optimization of the AAO process, a comprehensive optimization fitness function
was designed (Equation (7)). This fitness function consisted of two parts, stable control requirements (
, there are
N of them) and optimization control requirements (
, there are
M of them). The detailed definition of them are given in Equations (8) and (9), where
is the ith state of the system,
is the set target value of control variables.
represents that
needs to be maintained between the artificially specified upper and lower bounds (
and
) which are shown in
Table 3 below. The Parameters Threshold is recommended by engineers in the WWTP and research [
38,
39].
indicates that needs to be as close as possible to the artificially specified target (). In other words, the closer the system’s control variables are to , the higher score the system is. In this study, the parameters for setting were:
(1) The aeration amount should be as low as possible, in Equation (9) ,.
(2) The adjustment range of the Qr and Qsr ratios should be kept relatively stable to reduce the impact of flow rate changes and the large-scale control operation of the pumps. Their in Equation (9) was a ratio determined by certain historical data.
3.3. The Rationality Verification for LSTM-MPC
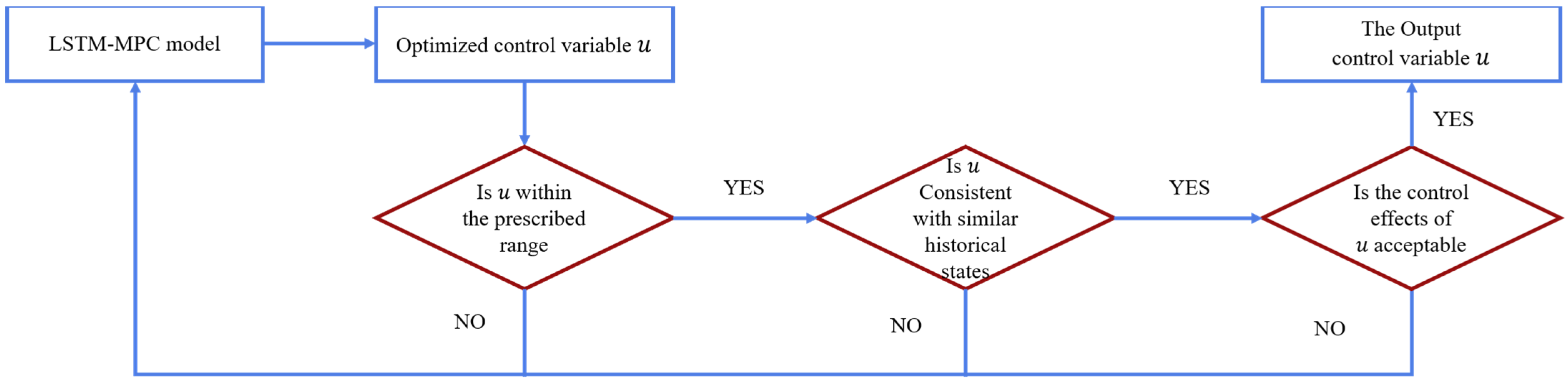
After constructing the LSTM-MPC, it is necessary to preliminarily judge the rationality of its output control variables and control effect to ensure safety and effectiveness.
The rationality verification proposed in this study is mainly based on three aspects: whether the current optimization control variables are within the prescribed range set by engineers, whether they are consistent with similar situations in history, and whether the control effects of the current optimization control variables are acceptable. By checking these three aspects, the evaluation of the effectiveness of optimization control can be made, and its rationality can be determined accordingly, as shown in
Figure 5.
3.3.1. The Prescribed Range of Control Variables
When considering whether optimized control variables meet the standards of the actual production process of the biochemical reactor, it is necessary to evaluate it through the prescribed range.
In this study, the prescribed range is designed based on two parts: a large amount of historical data on the biochemical reactors and recommended process parameters given by engineers. For the first part, historical data and the 3σ principle were used to estimate the prescribed range. The specific method is given as Equations (10) and (11), where
represents the historical data of the control variable, and
represents the average control values of the historical data, and
represents the number of data. The recommended process parameters
is given by engineers and combined with the first part through the intersection in Equation (12) to provide the final prescribed range.
3.3.2. Consistency with Similar Historical States
In this study, the control variables were provided with respect to a given state. Therefore, they should be consistent with themselves in similar situations in history. This study used Euclidean distance
(Equation (13), where
is the system state at the current moment, and
is the historical data of the state) to evaluate the similarity between the current situation and historical situations, through which the similar control variables in history were selected and compared with current control variables, so as to evaluate the rationality. Detailed steps were given as follows.
First, for the current system status (DO, MLSS, COD, etc.), find the historical data of similar states. If the Euclidean distance between the two was less than a given threshold, the two states were considered to be close, and the control variables corresponding to were collected, thereby obtaining the control variables under conditions similar to those in history with the current state. Afterward, the 3σ principle was used to estimate the upper and lower limits of the collected control variables. Finally, this upper and lower limit was taken as the judgment standard to evaluate whether the optimized control variables were within this range, thereby further supplementing the evaluation standard of their rationality.
3.3.3. Evaluation of the Control Effects
For MPC, the optimized control variables are mainly used to control the system in the future period. Therefore, it is necessary to predict and evaluate the effects of the control variables to determine their effectiveness.
The method for predicting and evaluating the control effects was as follows. Firstly, the optimized control variables and the current state variables were used as inputs for the prediction model, i.e., LSTM, to make a one-step prediction (Equation (14), where
represents the optimized control variables). Then, the predicted result was compared with the operating standards of the biochemical reactor. If the predicted state variables (DO, MLSS, etc.) were within the prescribed range of the biochemical reactor, then the optimized control variables were considered acceptable and can be used. Otherwise, it was considered that the current control variables might pose a risk to the system during the actual control process and could not be used as the final output, even though it may save aeration.
4. Results
4.1. LSTM Prediction
Four LSTM models (structure 4 in
Table 2) were trained through the method in
Section 3.1. Combined with the hydraulic retention time (HRT) of the AAO process and the actual operation interval for the WWTP control, the input of the LSTMs in this study was the state variables, the influent variables, and the control variables within the past 10-time steps (
L in Equation (4) is 10, the sum of time span = 300 min), and the output of the LSTMs was the state variables in the bioreactor at the next time step. They were trained and tested on the data from 1 June–1 September 2019 with a monitoring frequency of 5 min, i.e., the size of the full dataset is 30,000. The test set was the full dataset. There are two types of training sets used to establish different LSTMs: Dataset 1 (number n = 1300) and Dataset 2 (number n = 6500). Both of them were randomly selected from the full dataset.
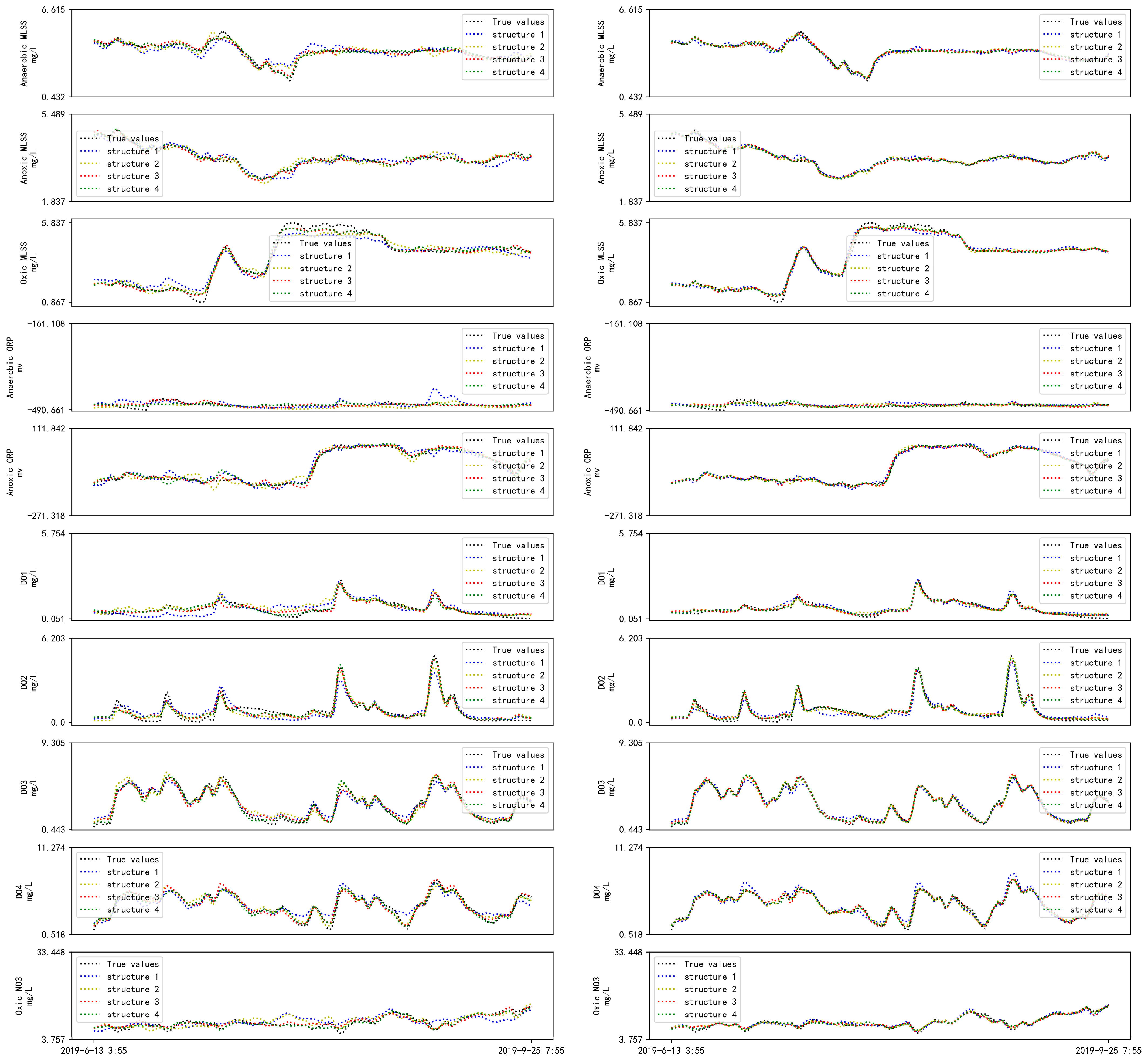
Prediction results of LSTM models on the test dataset were shown in
Figure 6, the curve can measure the fitting degree of the output. All the models proposed in this paper can achieve accurate prediction, and the curves of Dataset 2 generally fit better than Dataset 1.
Table 4 evaluates the results of the proposed models on the test dataset by MSE and NSE.
Structure 1 has the highest MSE in both Dataset 1 and Dataset 2. Although Structure 1 with only 10 hidden layer neurons can learn the patterns of the dataset during the training process, the accuracy of the model is limited. Structures 2–4 have 15–25 hidden layer neurons, so their network structures are more complex respectively. Structure 4 can better learn the nonlinear training dataset, and demonstrate more accurate dynamic characteristics. However, an overly complex network structure can cause overfitting and reduce the model’s prediction performance. In the experiments with Dataset 1, the MSE of Structure 4 is slightly higher than that of Structure 3, resulting in a decrease in the model’s accuracy.
NSE is generally used to verify the fitness of hydrological model simulation results and process simulation errors. An NSE value close to 1 indicates high model quality and reliability. An NSE value close to 0 indicates that the simulation result is close to the average value, which means that the overall result is reliable, but the process simulation is large. The LSTM model with Structure 4 on dataset 2 has an NSE value closest to 1, indicating that compared with other models proposed in this paper, this model has better performance. At the same time, the NSE of Dataset 1 is generally higher than that of Dataset 2, indicating that the model quality is higher after training on Dataset 2 with more data numbers.
The results demonstrate that LSTM had precise and stable predictive capabilities and performed well in predicting system behavior for unseen datasets. Furthermore, selecting an appropriate dataset and structure can enhance the LSTM model’s performance and achieve better results.
4.2. Performance of LSTM-MPC
As shown in
Table 4, the model with structure 4 and dataset 2 is a relatively superior prediction model. Therefore, this study used this model for LSTM-MPC.
(1) One-step optimization: a random time point (2 March 2019, at 17:30) was chosen as the starting time step, and the control variables for the next time step were optimized by LSTM-MPC.
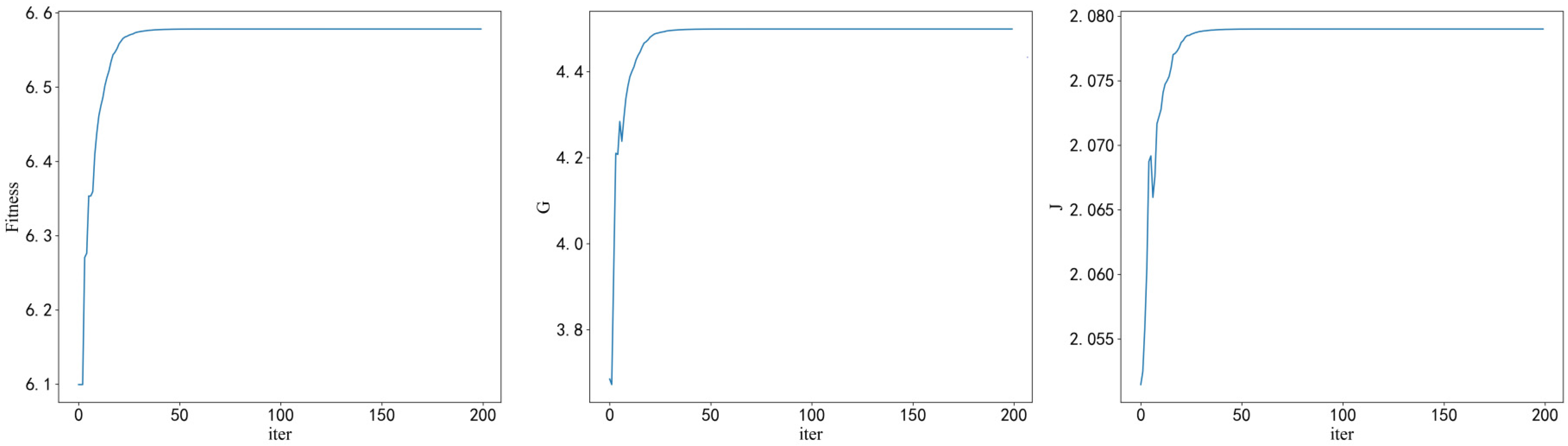
Figure 7 illustrates how the objective function
changed in the iteration.
The fitness function shows an overall significant upward trend, indicating that the whole system was optimized. The objective function corresponding to the optimization requirements increased, indicating that the aeration volume was close to the target value (as low as possible), while the Qr and Qsr ratios remained stable within a certain range. The objective function corresponding to the control requirements also increased but only slightly and with some fluctuations, indicating that the AAO system maintained stability and met the water quality parameters threshold after optimization.
(2) Multi-step optimization: a random time point (7 March 2019, at 22:35:00) was chosen as the starting time step for LSTM-MPC, with a control time interval of 30 min and a control time step of 48 (time span = 24 h).
Table 5 shows the average results of the multi-step control in LSTM-MPC.
As compared to the historical control, the optimized control strategy resulted in a 33% reduction in the average aeration volume in 24 h, accompanied by a slight increase in both Qr and Qsr. As aeration is the main energy-consuming process, this reduction would lead to a decrease in the overall energy consumption of the bioreactor.
The prediction results of the optimized control strategy maintained the state variables within reasonable thresholds and a decrease in DO concentrations, as shown in
Figure 8. Therefore, the proposed LSTM-MPC is feasible and effective for the optimization control of the AAO system.
4.3. The Effect of Rationality Verification
Based on the aforementioned LSTM-MPC, rationality verification was proposed and employed to improve the safety of the optimization control. For the rationality verification proposed in this study, the final optimal control will be output only when it meets all three types of rationality verifications. The same time node (7 March 2019 22:35:00) of the aforementioned LSTM-MPC model was used as the starting time step, the control time interval was 30 min, and the control time step was 48 (24 h).
Table 4 also shows the prediction and control results after rationality verification. Compared with the historical control, the average aeration volume of 24 h after optimization was reduced by 7%, Q
r was slightly reduced, Q
sr was slightly increased, and the overall energy consumption was reduced. The state variables of water quality stayed stable and the DO concentrations decreased after optimal control. After the rationality verification, the optimized control met the safety requirements, but its optimization and energy-saving performance was significantly reduced compared with LSTM-MPC.
Overall, the proposed LSTM-MPC model for the AAO bioreactors was found to be effective in optimizing control variables and reducing energy consumption. And LSTM-MPC with rationality verification improved the stability of bioreaction as well as ensured security.
5. Discussion
5.1. Performance of LSTM Prediction Model
Previously research often focused on the effluent quality of wastewater treatment, considering data-driven models as a soft sensor, while the state variables of the bioreactor were often not included as model outputs [
29]. This study proposes an LSTM model based on historical data. State variables, influent variables, and control variables were used as inputs. On the one hand, the input of state variables compensates for the lack of state variables in the bioreaction process. On the other hand, the control variables make it possible to construct control models such as MPC, which can further assist in optimizing control-related research.
As shown in
Section 4.1, the LSTM model established in this study can accurately predict the changing trends of multiple state variables during the bioreactor operation process. This result is consistent with previous research on the good performance of LSTM models in predicting effluent quality, such as Yaquba et al. [
24,
25]. It is mostly attributable to LSTM’s strong learning capability, training algorithms, and abundant data. As a deep learning neural network, LSTM’s complex network structure allows it to better handle nonlinear datasets, making it easier to identify patterns in the large time-series datasets used in this study, thus improving model performance. The dataset used in this study has a large time span, covering different operational conditions of the WWTP over 3 months. The value of MSE is 2.64 (structure 4, Training Dataset 2) and all values of NSE are close to 1. Since LSTM contains multiple output values and the datasets have different thresholds, the errors are within a reasonable range for the entire AAO system. However, the generalization and overfitting problems faced by deep learning models still exist (
Table 4). For different datasets, using LSTM hyperparameters with the right level of complexity can prevent overfitting and achieve accurate prediction.
Moreover, the reliability of the dataset is one of the challenges in applying data-driven methods to bioreaction processes in real wastewater treatment. WWTPs are many times limited by the environment or the accuracy of the instrumentation and often do not get a sufficient number of accurate datasets. Also in most practical applications, it is difficult to avoid losing data during the long treatment process. Therefore, the method is limited to complex nonlinear systems with insufficient data or untrained conditions.
5.2. Effect of Fitness Function for Stability on LSTM-MPC
The control of actual bioreaction in WWTP involves a wide range of controllable indicators. Existing researches tend to focus on reducing energy consumption rather than paying attention to the stability of the bioreaction tank’s state after control operation changes. In the AAO process, its operation often needs to consider the impact of changes in influent quality and flow. And similarly, large changes in control variables in a short period can also have a negative impact on the stability of the biological reaction tank. Considering the influence of control parameters on the stability of the state is of great significance in the practical operation of WWTPs. In view of the multi-objective characteristics of the optimization control of the AAO process, this study used the PSO optimization algorithm to construct an LSTM-MPC model, taking the operational stability of the bioreactors as one of the objective functions, and optimizing the aeration volume, internal recirculation flow (Qr), and sludge internal recycle flow (Qsr).
LSTM-MPC aims to reduce aeration and save energy based on the stable operation.
Figure 7 shows the fitness function curve of the LSTM-PSO optimization algorithm in one-step optimization. The overall fitness function
increased significantly, guiding the particles to iterate in the direction of the optimal solution. The fitness function
of the optimization control requirements made the main contribution to
, indicating that a significant optimization has been made in the control, i.e., reducing aeration and controlling the ratio of Q
r/Q
in and Q
sr/Q
in. And the fitness function
corresponding to the stable control requirements fluctuated within a small range, indicating that the operational status of the bioreaction tanks did not undergo drastic fluctuations. During the optimization control process, the variations of state variables MLSS and NO
3 in the oxic bioreaction tank were controlled within 15%, and the ORP and DO concentrations in each tank met the threshold requirements for stable operation. The overall bioreaction was running relatively stable after the control variables were changed.
5.3. Effect of Rationality Verification on LSTM-MPC
Numerous studies based on simulation models such as BSM1 have shown excellent optimization results using neural network-based MPC [
17]. However, neural networks are still regarded as black-box models, and their computation process and logic remain opaque. In practical applications, we must focus on the reliability and trustworthiness of data-driven models such as LSTM-MPC. Therefore, further consideration of enhancing the safety and rationality of control outputs is a necessary condition for promoting the application of artificial intelligence methods.
This study proposes three rationality verification methods to ensure that the LSTM-MPC proposed in this study is safe and trustworthy in real-world conditions, which has a practical significance in actual wastewater treatment processes. Comparing the results of
Section 4.2 and
Section 4.3 (
Figure 8 and
Figure 9), the LSTM-MPC combined with rationality verification shows significantly reduced fluctuation in the predicted state variables and better robustness when control operations vary under the same influent conditions. The rationality verification process removes control variables that do not meet the requirements of similar historical conditions, while the overall control variables change more smoothly. It can also reduce the frequency of operations, meet historical operating experience, and improve the acceptance of operation personnel for LSTM-MPC strategies.
However, the optimization efficiency is dramatically decreased in the same state and the optimized control variables offered by LSTM-MPC with rationality verification exhibit a significantly lower decrease in aeration than the model without rationality verification. This is because many operations that do not agree with historical data are eliminated during the rationality verification procedure, producing conservative output control variables. It is not difficult to find that ensuring safety and meeting optimization requirements are a set of conflicting objectives. In this study, we emphasize choosing the best solution that satisfies rationality verification and relatively low energy consumption, which results in excessively conservative operations in some time steps, and the possibility of abandoning the global optimal solution. There is room for further improvement in the balance between safety and optimization performance.
5.4. Calculation Time of LSTM-MPC
In addition, due to the real-time control requirements of WWTPs, the calculation speed of the optimization algorithm must be taken into consideration. In this study, the PSO algorithm was set to terminate if the fitness function did not show significant changes in nearly 200 iterations. The calculation time of the LSTM-MPC was 430 s in one time step of the optimization control at 200 iterations, which was much lower than the control time interval in this case (30 min). Although the calculation speed of LSTM-MPC can meet requirements in this certain WWTP, for more complex conditions, more time-consuming optimization algorithms, and larger nonlinear systems, the calculation time issue cannot be avoided. At this point, more powerful computing hardware or a new optimization algorithm may be needed to improve calculation speed.