Robust Optimal Booster Disinfectant Injection in Water Systems under Uncertainty
Abstract
:1. Introduction
2. Robust Optimization
2.1. RO-A Short Tutorial
Box Uncertainty
3. Problem Formulation
3.1. Optimal Booster Chlorination Problem
3.1.1. Decision and Uncertain Variables
3.1.2. Optimization Problem Formulation
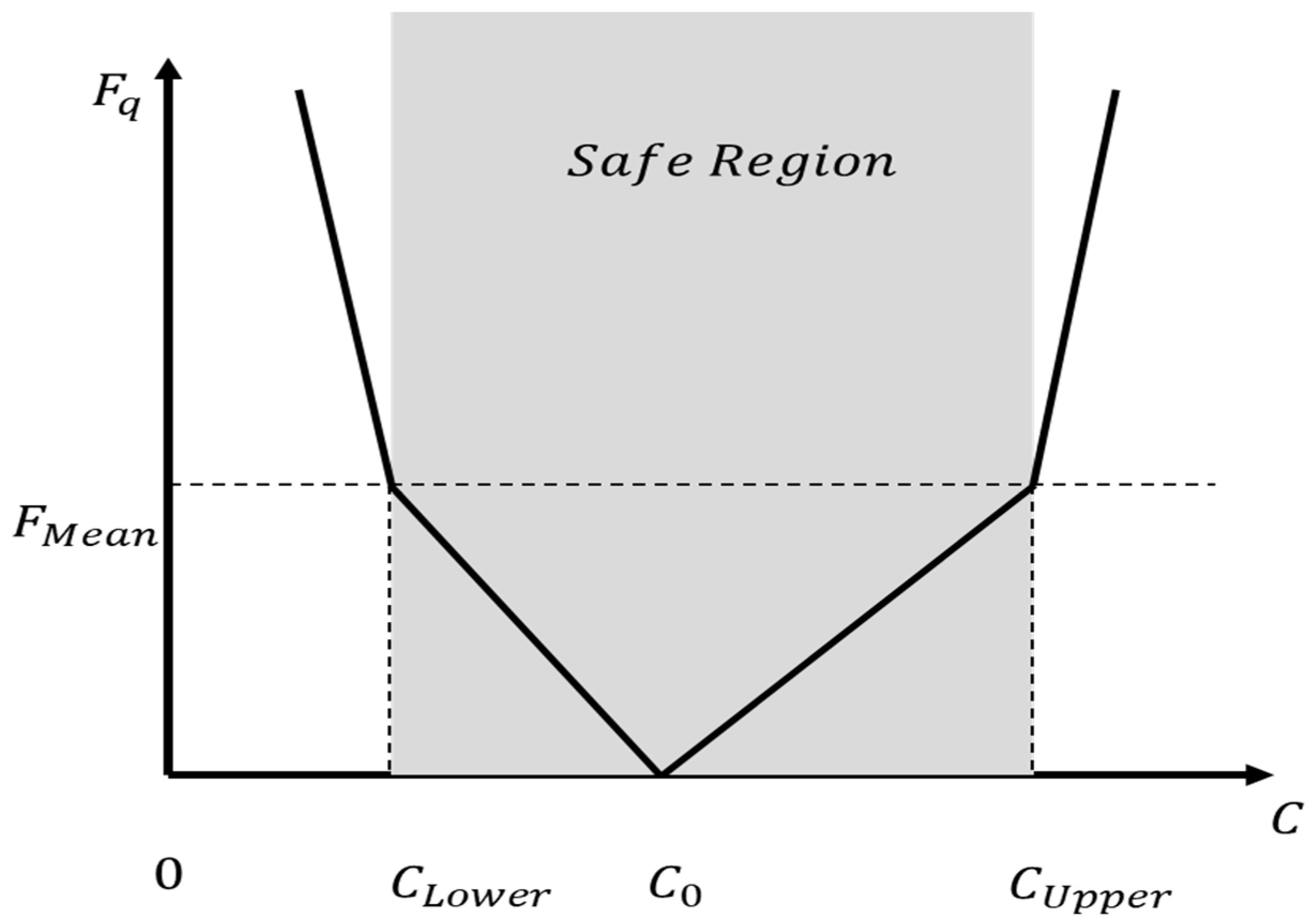
3.1.3. Water Quality Objective
3.1.4. Robust Counterpart Formulation
4. Case Studies
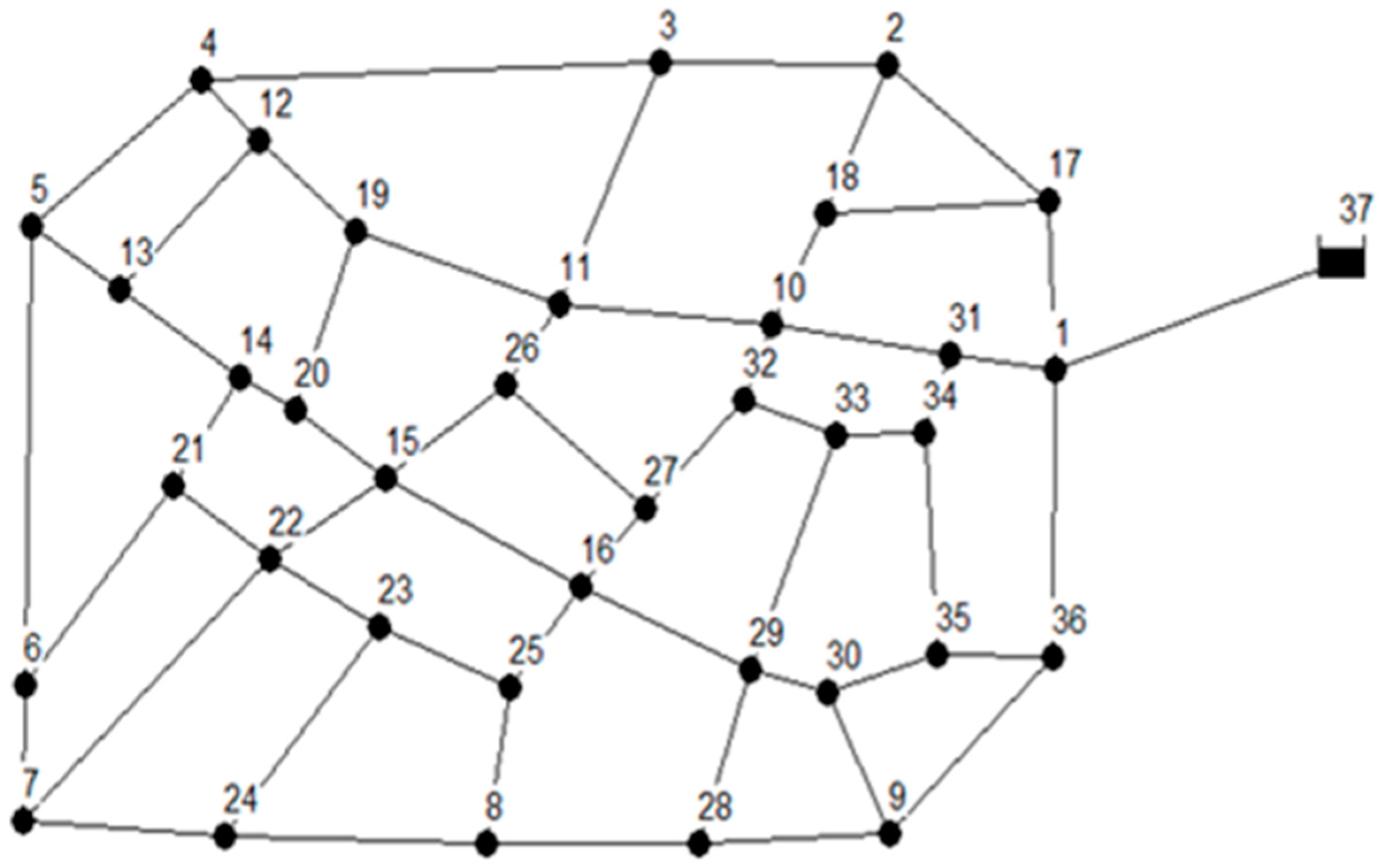
4.1. Network System 1
4.2. Network System 2
5. Results and Discussion
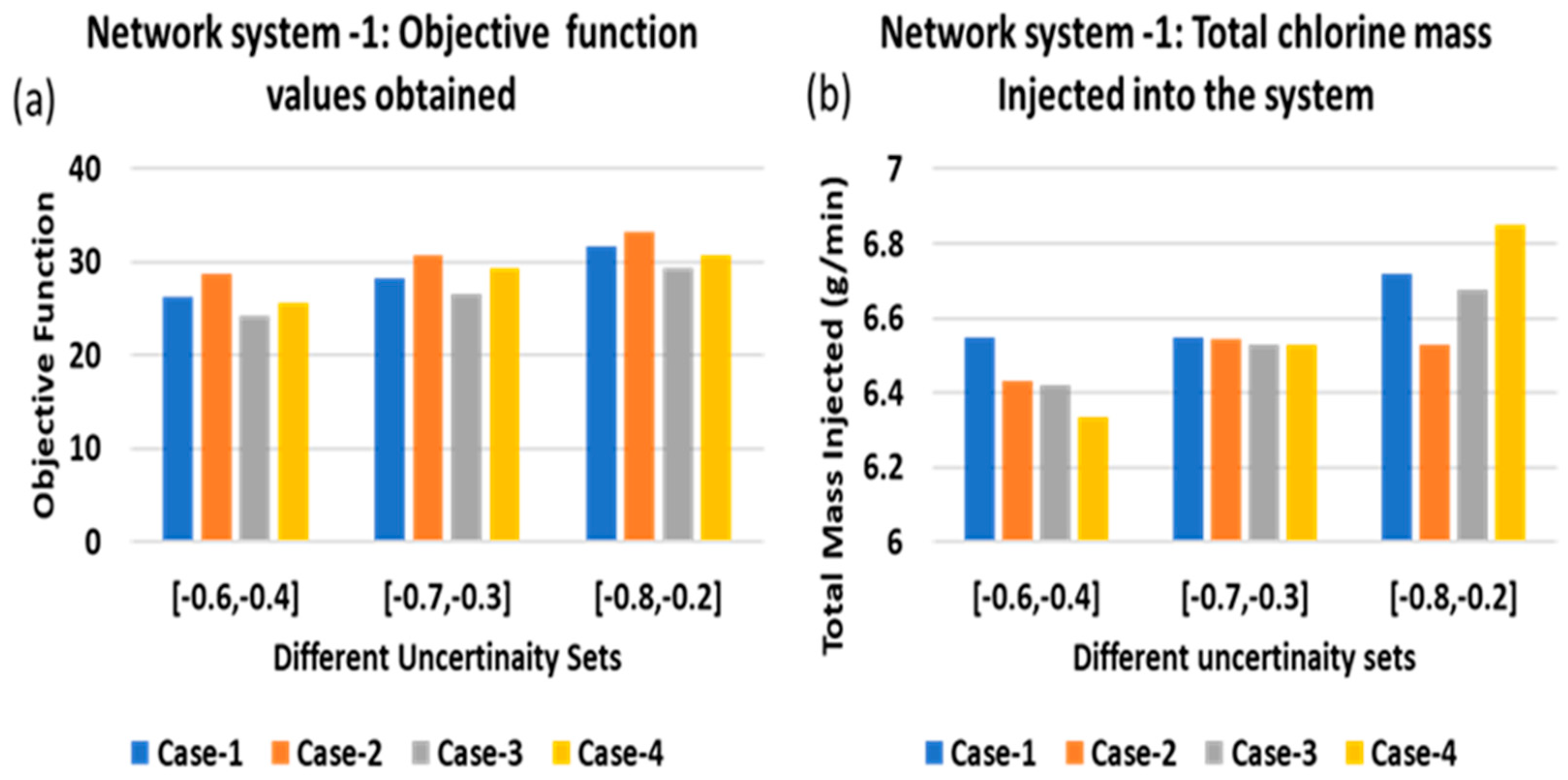
5.1. Network System 1
5.2. Network System 2
5.3. Sensitivity Analysis
5.3.1. Effect of Varying the Desired Residual Chlorine Concentration
5.3.2. Effect of Residual Chlorine Regulation Limits
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tryby, M.E.; Boccelli, D.L.; Koechling, M.T.; Uber, J.G.; Summers, R.S.; Rossman, L.A. Booster Chlorination for Managing Disinfectant Residuals. J. Am. Water Work. Assoc. 1999, 91, 95–108. [Google Scholar] [CrossRef]
- Kang, D.; Lansey, K. Real-Time Optimal Valve Operation and Booster Disinfection for Water Quality in Water Distribution Systems. J. Water Resour. Plan. Manag. 2010, 136, 463–473. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, G.; Engel, B. Variation and Relationship of THMs between Tap Water and Finished Water in Yancheng City, China. Environ. Monit. Assess. 2018, 190, 517. [Google Scholar] [CrossRef] [PubMed]
- Boccelli, D.L.; Tryby, M.E.; Uber, J.G.; Rossman, L.A.; Zierolf, M.L.; Polycarpou, M.M. Optimal Scheduling of Booster Disinfection in Water Distribution Systems. J. Water Resour. Plan. Manag. 1998, 124, 99–111. [Google Scholar] [CrossRef]
- Goyal, R.V.; Patel, H.M. Optimal Location and Scheduling of Booster Chlorination Stations for Drinking Water Distribution System. J. Appl. Water Eng. Res. 2017, 5, 51–60. [Google Scholar] [CrossRef]
- Köker, E.; Altan-Sakarya, A.B. Chance Constrained Optimization of Booster Chlorination in Water Distribution Networks. Clean 2015, 43, 717–723. [Google Scholar] [CrossRef]
- Propato, M.; Uber, J.G. Linear Least-Squares Formulation for Operation of Booster Disinfection Systems. J. Water Resour. Plan. Manag. 2004, 130, 53–62. [Google Scholar] [CrossRef]
- Prasad, T.D.; Walters, G.A.; Savic, D.A. Booster Disinfection of Water Supply Networks: Multiobjective Approach. J. Water Resour. Plan. Manag. 2004, 130, 367–376. [Google Scholar] [CrossRef]
- Chu, C.W.; der Lin, M.; Tsai, K.T. Optimal Scheduling of Booster Chlorination with Immune Algorithm. In Proceedings of the 3rd International Conference on Convergence and Hybrid Information Technology (ICCIT 2008), Busan, Republic of Korea, 11–13 November 2008; Volume 2, pp. 1226–1232. [Google Scholar]
- Harmant, P.; Nace, A.; Kiene, L. An Algorithm to Optimize Booster Chlorination in Water Distribution Network. In Building Partnerships; American Society of Civil Engineers: Reston, VA, USA, 2000; Volume 104, pp. 1–10. [Google Scholar]
- Ohar, Z.; Ostfeld, A. Optimal Design and Operation of Booster Chlorination Stations Layout in Water Distribution Systems. Water Res. 2014, 58, 209–220. [Google Scholar] [CrossRef]
- Wang, H.; Guo, W.; Xu, J.; Gu, H. A Hybrid PSO for Optimizing Locations of Booster Chlorination Stations in Water Distribution Systems. In Proceedings of the 2010 International Conference on Intelligent Computation Technology and Automation (ICICTA 2010), Changsha, China, 11–12 May 2010; Volume 1, pp. 126–129. [Google Scholar]
- Dandy, G.; Wu, W.; Simpson, A.; Leonard, M. A Review of Sources of Uncertainty in Optimization Objectives of Water Distribution Systems. Water 2023, 15, 136. [Google Scholar] [CrossRef]
- Lansey, K.E.; Duan, N.; Mays, L.W.; Tung, Y. Water Distribution System Design under Uncertainties. J. Water Resour. Plan. Manag. 1989, 115, 630–645. [Google Scholar] [CrossRef]
- Aklog, D.; Hosoi, Y. Reliability-Based Optimal Design of Water Distribution Networks. Water Sci. Technol. Water Supply 2003, 3, 11–18. [Google Scholar] [CrossRef]
- Xu, C.; Goulter, I.C. Reliability-Based Optimal Design of Water Distribution Networks. J. Water Resour. Plan. Manag. 1999, 125, 352–362. [Google Scholar] [CrossRef]
- Tolson, B.A.; Maier, H.R.; Simpson, A.R.; Lence, B.J. Genetic Algorithms for Reliability-Based Optimization of Water Distribution Systems. J. Water Resour. Plan. Manag. 2004, 130, 63–72. [Google Scholar] [CrossRef]
- Goulter, I.C.; Bouchart, F. Reliability-Constrained Pipe Network Model. J. Hydraul. Eng. 1990, 116, 211–229. [Google Scholar] [CrossRef]
- Wagner, J.M.; Shamir, U.; Marks, D.H. Water Distribution Reliability: Analytical Methods. J. Water Resour. Plan. Manag. 1988, 114, 253–275. [Google Scholar] [CrossRef]
- Su, Y.; Mays, L.W.; Duan, N.; Lansey, K.E. Reliability-Based Optimization Model for Water Distribution Systems. J. Hydraul. Eng. 1987, 113, 1539–1556. [Google Scholar] [CrossRef]
- Wagner, J.M.; Shamir, U.; Marks, D.H. Water Distribution Reliability: Simulation Methods. J. Water Resour. Plan. Manag. 1988, 114, 276–294. [Google Scholar] [CrossRef]
- Duan, N.; Mays, L.W.; Lansey, K.E. Optimal Reliability-Based Design of Pumping and Distribution Systems. J. Hydraul. Eng. 1990, 116, 249–268. [Google Scholar] [CrossRef]
- Gheisi, A.; Forsyth, M.; Naser, G. Water Distribution Systems Reliability: A Review of Research Literature. J. Water Resour. Plan. Manag. 2016, 142, 04016047. [Google Scholar] [CrossRef]
- Pasha, M.F.K.; Lansey, K. Analysis of Uncertainty on Water Distribution Hydraulics and Water Quality. In Impacts of Global Climate Change, Proceedings of the 2005 World Water and Environmental Resources Congress, Anchorage, AK, USA, 15–19 May 2005; American Society of Civil Engineers: Reston, VA, USA, 2005; Volume 10. [Google Scholar] [CrossRef]
- Pasha, M.F.K.; Lansey, K. Effect of Parameter Uncertainty on Water Quality Predictions in Distribution Systems-Case Study. J. Hydroinformatics 2010, 12, 1–21. [Google Scholar] [CrossRef]
- Kang, D.S.; Pasha, M.F.K.; Lansey, K. Approximate Methods for Uncertainty Analysis of Water Distribution Systems. Urban Water J. 2009, 6, 233–249. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, G. Fuzzy Credibility-Constrained Quadratic Optimization for Booster Chlorination of the Water Distribution System under Uncertainty. Aqua. Water Infrastruct. Ecosyst. Soc. 2022, 71, 608–627. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, G. Inexact Left-Hand Side Two-Stage Chance-Constrained Programming for Booster Optimization in Water Distribution System. J. Environ. Manag. 2021, 298, 113372. [Google Scholar] [CrossRef] [PubMed]
- Ben-Tal, A.; Nemirovski, A. Robust Convex Optimization. Math. Oper. Res. 1998, 23, 769–805. [Google Scholar] [CrossRef]
- El Ghaoui, L.; Lebret, H. Robust Solutions to Least-Squares Problems with Uncertain Data. SIAM J. Matrix Anal. Appl. 1997, 18, 1035–1064. [Google Scholar] [CrossRef]
- Ben-Tal, A.; Nemirovski, A. Robust Solutions of Uncertain Linear Programs. Oper. Res. Lett. 1999, 25, 1–13. [Google Scholar] [CrossRef]
- Ben-Tal, A.; El Ghaoui, L.; Nemirovski, A. Robust Optimization; Princeton University Press: Princeton, NJ, USA, 2009; ISBN 9780691143682. [Google Scholar]
- Boindala, S.P.; Ostfeld, A. Robust Multi-Objective Design Optimization of Water Distribution System under Uncertainty. Water 2022, 14, 2199. [Google Scholar] [CrossRef]
- Pankaj, B.S.; Jaykrishnan, G.; Ostfeld, A. Optimizing Water Quality Treatment Levels for Water Distribution Systems under Mixing Uncertainty at Junctions. J. Water Resour. Plan. Manag. 2022, 148, 04022013. [Google Scholar] [CrossRef]
- Housh, M.; Ostfeld, A.; Shamir, U. Optimal Multiyear Management of a Water Supply System under Uncertainty: Robust Counterpart Approach. Water Resour. Res. 2011, 47, W10515. [Google Scholar] [CrossRef]
- Schwartz, R.; Housh, M.; Ostfeld, A. Least-Cost Robust Design Optimization of Water Distribution Systems under Multiple Loading. J. Water Resour. Plan. Manag. 2016, 142, 04016031. [Google Scholar] [CrossRef]
- Perelman, L.; Housh, M.; Ostfeld, A. Robust Optimization for Water Distribution Systems Least Cost Design. Water Resour. Res. 2013, 49, 6795–6809. [Google Scholar] [CrossRef]
- Baron, O.; Milner, J.; Naseraldin, H. Facility Location: A Robust Optimization Approach. Prod. Oper. Manag. 2011, 20, 772–785. [Google Scholar] [CrossRef]
- Bertsimas, D.; Pachamanova, D.; Sim, M. Robust Linear Optimization under General Norms. Oper. Res. Lett. 2004, 32, 510–516. [Google Scholar] [CrossRef]
- Ewald, G.; Kurek, W.; Brdys, M.A. Grid Implementation of a Parallel Multiobjective Genetic Algorithm for Optimized Allocation of Chlorination Stations in Drinking Water Distribution Systems: Chojnice Case Study. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2008, 38, 497–509. [Google Scholar] [CrossRef]
- Kurek, W.; Ostfeld, A.; Asce, F. Multiobjective Water Distribution Systems Control of Pumping Cost, Water Quality, and Storage-Reliability Constraints. J. Water Resour. Plan. Manag. 2012, 140, 184–193. [Google Scholar] [CrossRef]
- Bragalli, C.; D’Ambrosio, C.; Lee, J.; Lodi, A.; Toth, P. Water Network Design by MINLP; IBM Research Report; IBM: Yorktown Heights, NY, USA, 2008. [Google Scholar]
- Ormsbee, L.; Hoagland, S.; Hernandez, E.; Hall, A.; Ostfeld, A. Hydraulic Model Database for Applied Water Distribution Systems Research. J. Water Resour. Plan. Manag. 2022, 148, 04022037. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boindala, S.P.; Jaykrishnan, G.; Ostfeld, A. Robust Optimal Booster Disinfectant Injection in Water Systems under Uncertainty. Water 2023, 15, 1777. https://doi.org/10.3390/w15091777
Boindala SP, Jaykrishnan G, Ostfeld A. Robust Optimal Booster Disinfectant Injection in Water Systems under Uncertainty. Water. 2023; 15(9):1777. https://doi.org/10.3390/w15091777
Chicago/Turabian StyleBoindala, Sriman Pankaj, G. Jaykrishnan, and Avi Ostfeld. 2023. "Robust Optimal Booster Disinfectant Injection in Water Systems under Uncertainty" Water 15, no. 9: 1777. https://doi.org/10.3390/w15091777