Pearson K-Mean Multi-Head Attention Model for Deformation Prediction of Super-High Dams in First Impoundments
Abstract
:1. Introduction
1.1. Literature Review
1.2. Problem Statement
- Traditional statistical models show poor robustness and transfer learning ability. In addition, they are frequently tailored to a specific project, which leads to less flexibility.
- The missing data in the dam monitoring system are normally compensated for through interpolation methods, which can generate misleading information.
- Deep learning models, such as LSTM and RNN, generally have poor interpretability.
1.3. Proposed Solution
- The attention mechanism of the deformation monitoring model for the first impoundment of super-high arch dams has been improved. Our proposed model not only enables the redistribution of the influence weights of environmental factors, but also visualisation operations. The model can also calculate the degree of interaction between the factors at each moment, which is more in line with the mechanics of dam deformation during the first renewal period of a very high arch dam.
- After the deformation measurement points are clustered and partitioned, when the deformation prediction model is constructed for a particular measurement point, the model imports the deformation data from the measurement points in the same partition, in addition to the traditional water level, temperature, and time-dependent factors. This allows the model to learn more accurate information.
- We have optimised the MultiheadAttention model to better match the deformation monitoring data for the first impoundment of a super-high arch dam. To the best of our knowledge, this is the first time that the MultiheadAttention model has been introduced into a first impoundment deformation prediction model for a super-high arch dam. The MultiheadAttention mechanism improves the optimisation of model parameters, enhances model performance, and increases model interpretability.
1.4. Symbols and Abbreviations
- (1)
- is the number of samples.
- (2)
- are the actual measurements.
- (3)
- are the model predictions of the prediction.
- (4)
- are the normalised monitoring data series.
- (5)
- are the Pearson correlation coefficients.
- (6)
- and are, respectively, standard deviations of the centroid and remaining variables.
- (7)
- are the input variables of the MA mechanism.
- (1)
- Multi-head attention—MA;
- (2)
- Pearson K-mean multi-head attention model—PKMA;
- (3)
- Long- and short-term memory—LSTM;
- (4)
- Mean absolute error—MAE;
- (5)
- Root mean square error—RMSE;
- (6)
- Mean square error—MSE;
- (7)
- Hydrostatic seasonal time—HST.
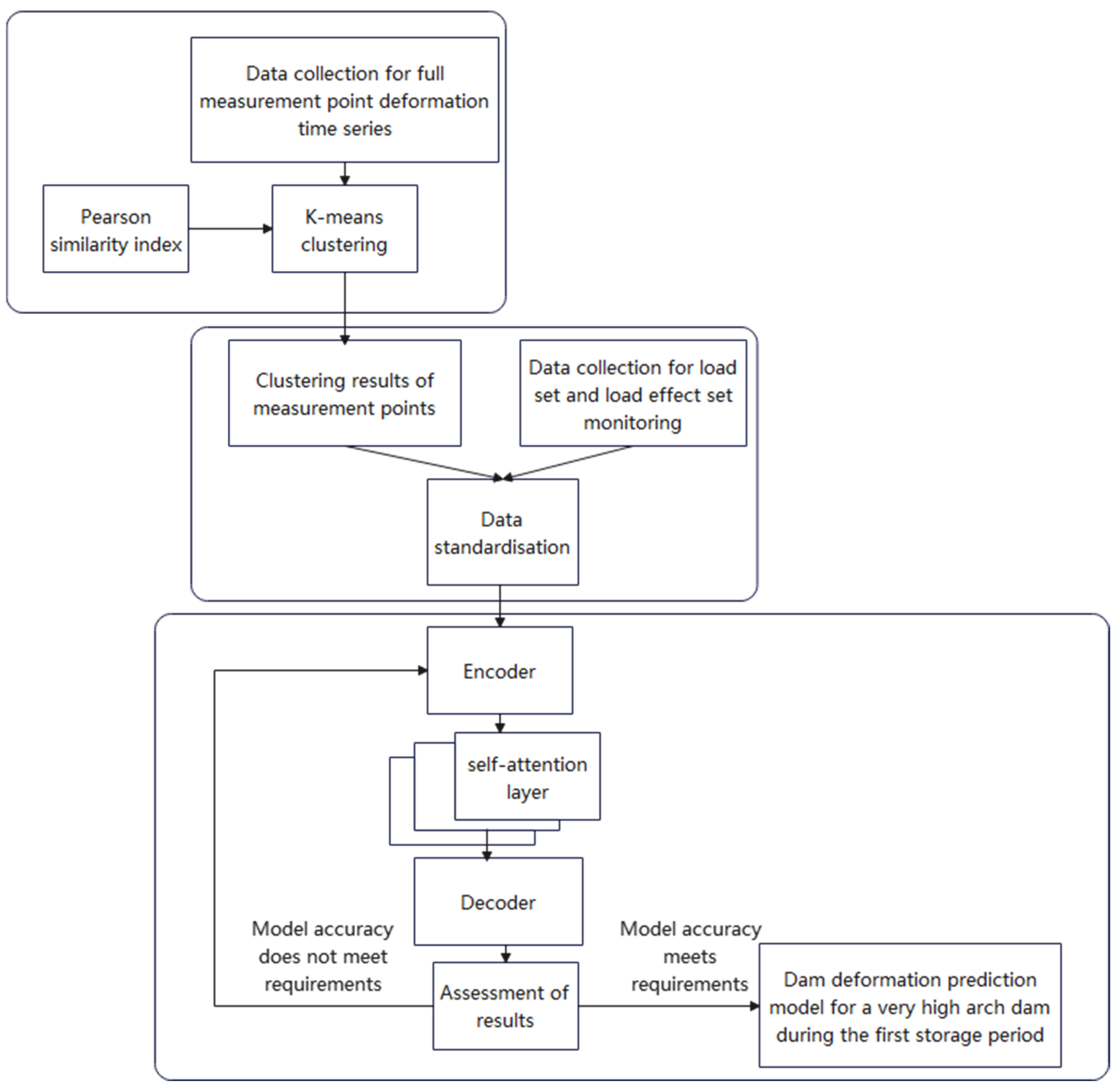
2. The Construction of the PKMA Model
2.1. The PKMA Model
2.2. K-means Clustering Based on Pearson Index
- (1)
- Let the data from candidate monitoring sets be after standardization, and the clustering procedures are given as follows:
- (2)
- Randomly select variables from as centroids, which behave as the predefined clusters.
- (3)
- Assign each of the remaining variables, based on its Pearson correlation coefficients from different centroids, to the centroid where is the highest.
- Place a new centroid for each cluster by calculating the sum of Pearson coefficients between the specific variable and the remaining variables in the cluster. The variable that contains the maximum sum is assigned as the new centroid.
- Repeat steps (2)–(3) until the centroids are no longer changed.
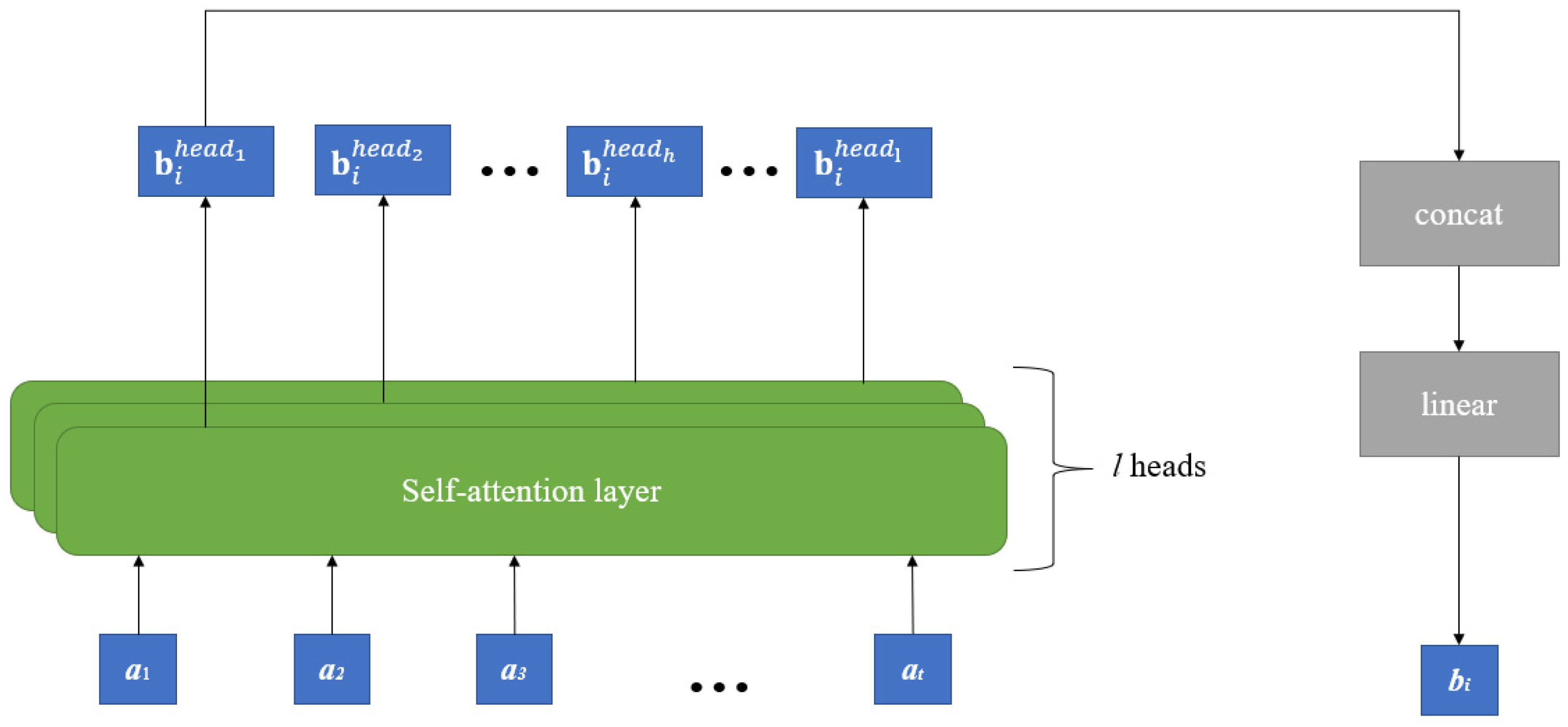
2.3. Multi-Head Self-Attention Mechanism
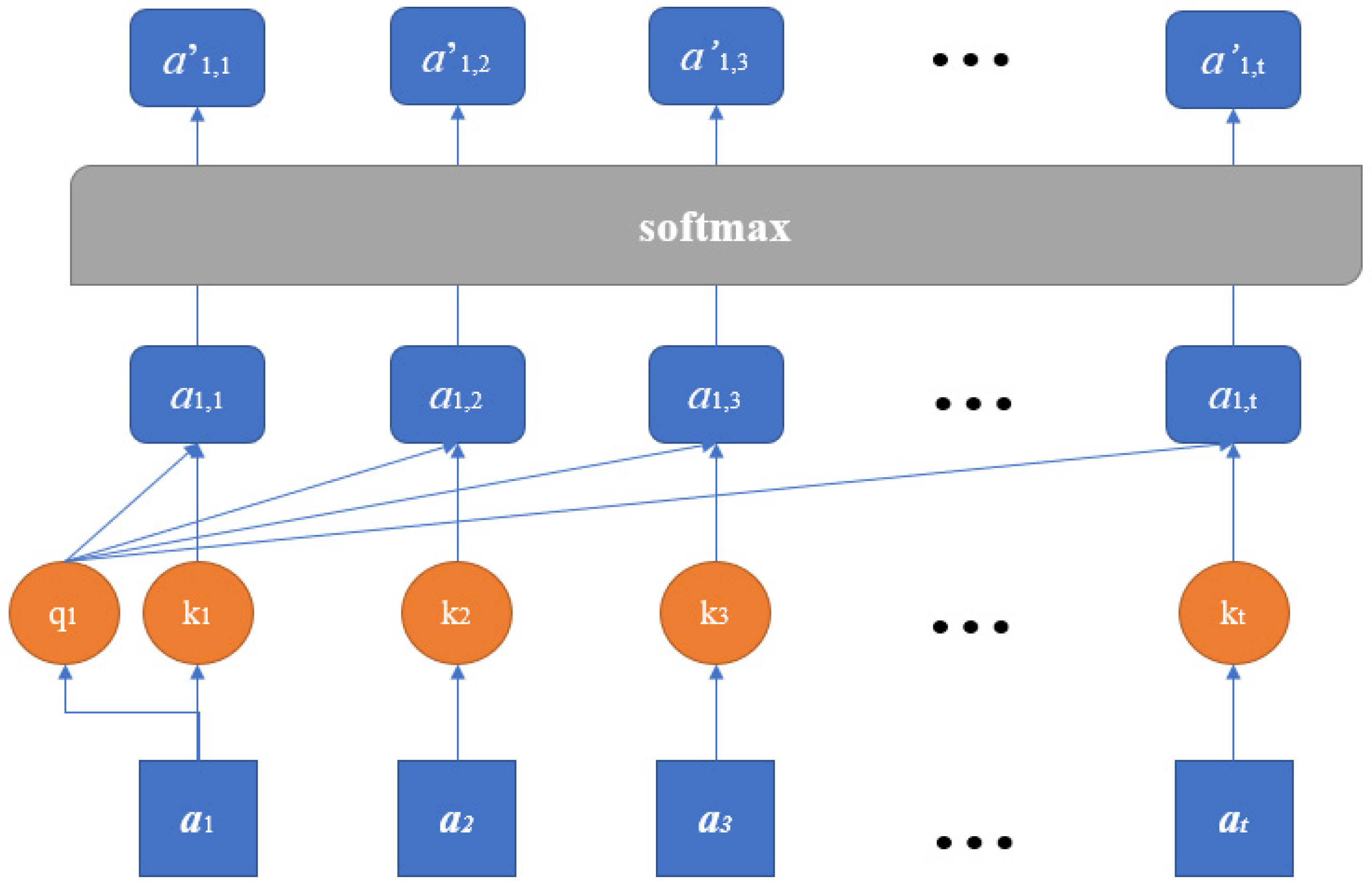
- Let be the input variables of the MA mechanism. Multiply by weight matrix for queries, for keys, and for values, respectively:where . is the number of heads used in the MA.
- For each head, calculate the weight matrix A by using the softmax function:where is the dimension of and .
- Thereby, head is obtained by summing the multiplication of and :
- The output of the MA is the multiplication of the concatenation of and the coefficient matrix
3. Case Study
3.1. Collection of the Candidate Inputs
3.1.1. Displacements along the River
3.1.2. Temperatures of the Dam Body and Foundation
3.1.3. Air Temperature and Water Levels
3.2. Selection of Inputs of the PKMA
3.2.1. Selection of Displacement of Plumb Lines
3.2.2. Selection of Dam Temperatures
3.2.3. Selection of Foundation Temperatures
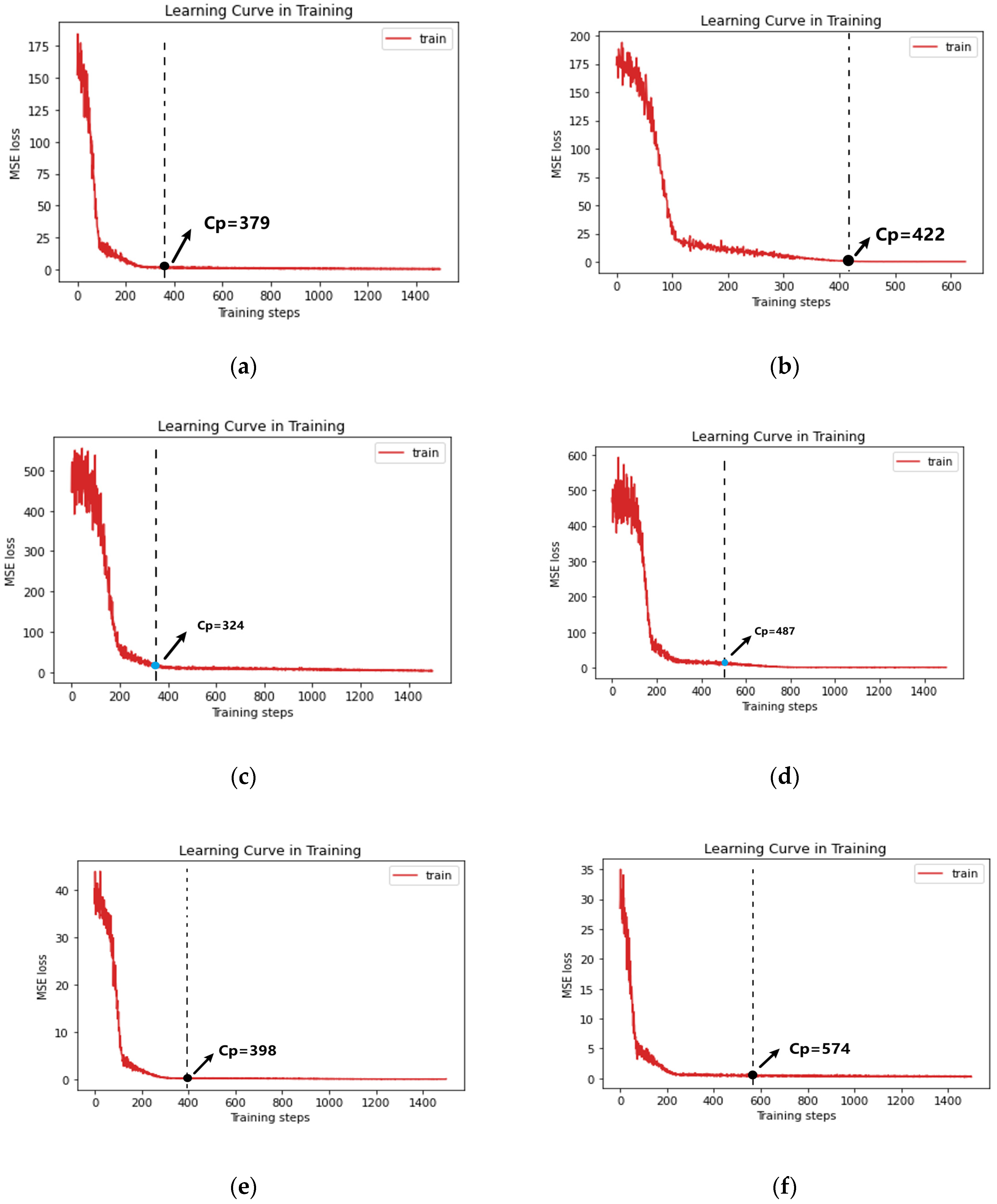
3.3. Hyperparameter Configuration
4. Results and Discussion
4.1. Model Performance
4.2. Model Interpretability
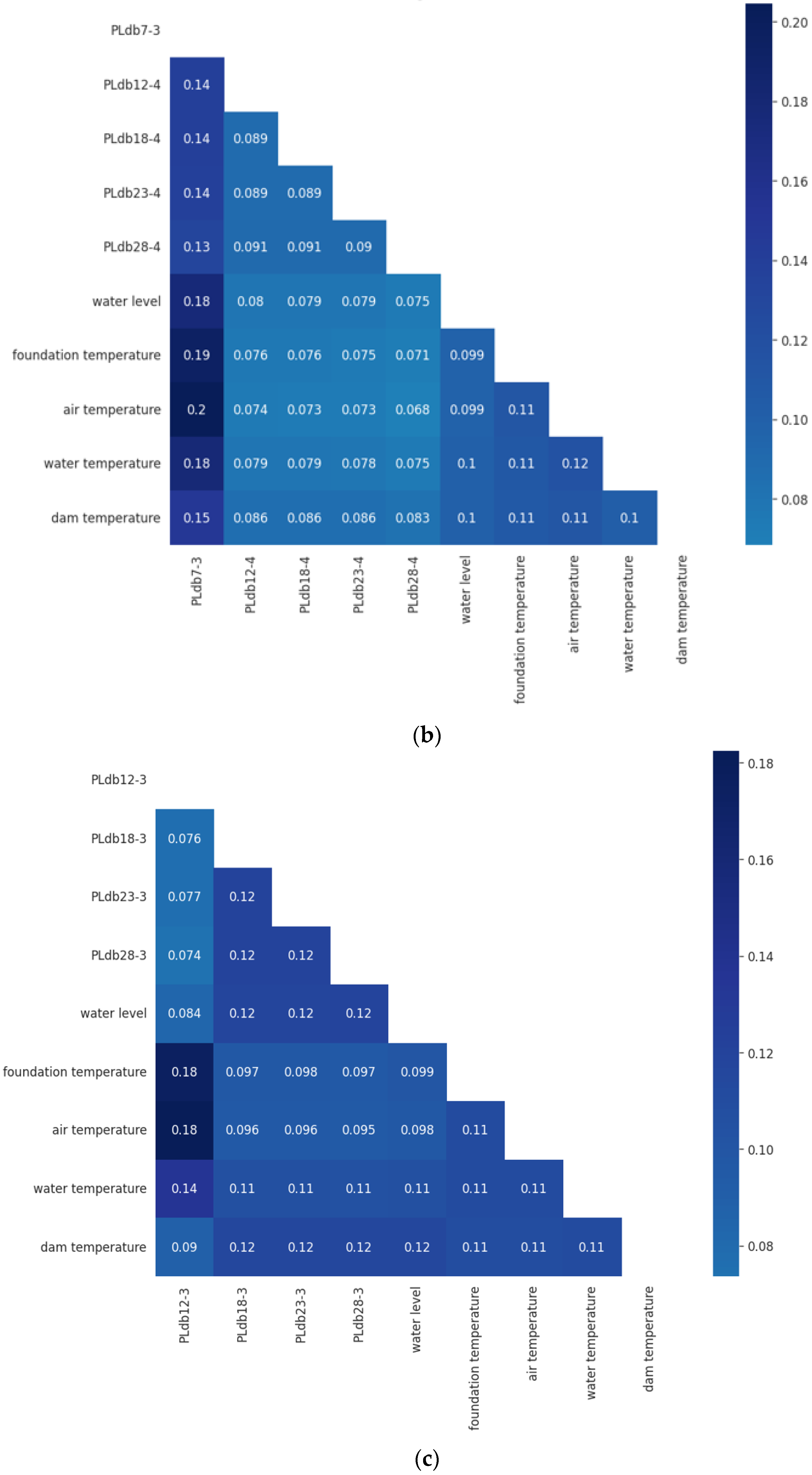
- The influences of the water level and temperature on the dam deformation are similar; the correlation coefficients between any two of them range from 0.075 to 0.18.
- The left bank measurement points, such as PLdb7-3, PLdb7-4, PLdb7-5, and PLdb12-3, are more sensitive to environmental factors than other measurement points.
- Compared to the temperatures of the water, air, and foundation, dam body temperature has a stronger impact on the dam deformation.
- The dam temperature, air temperature, water temperature, and bedrock temperature interact with each other, and their calculated weights are approximately the same.
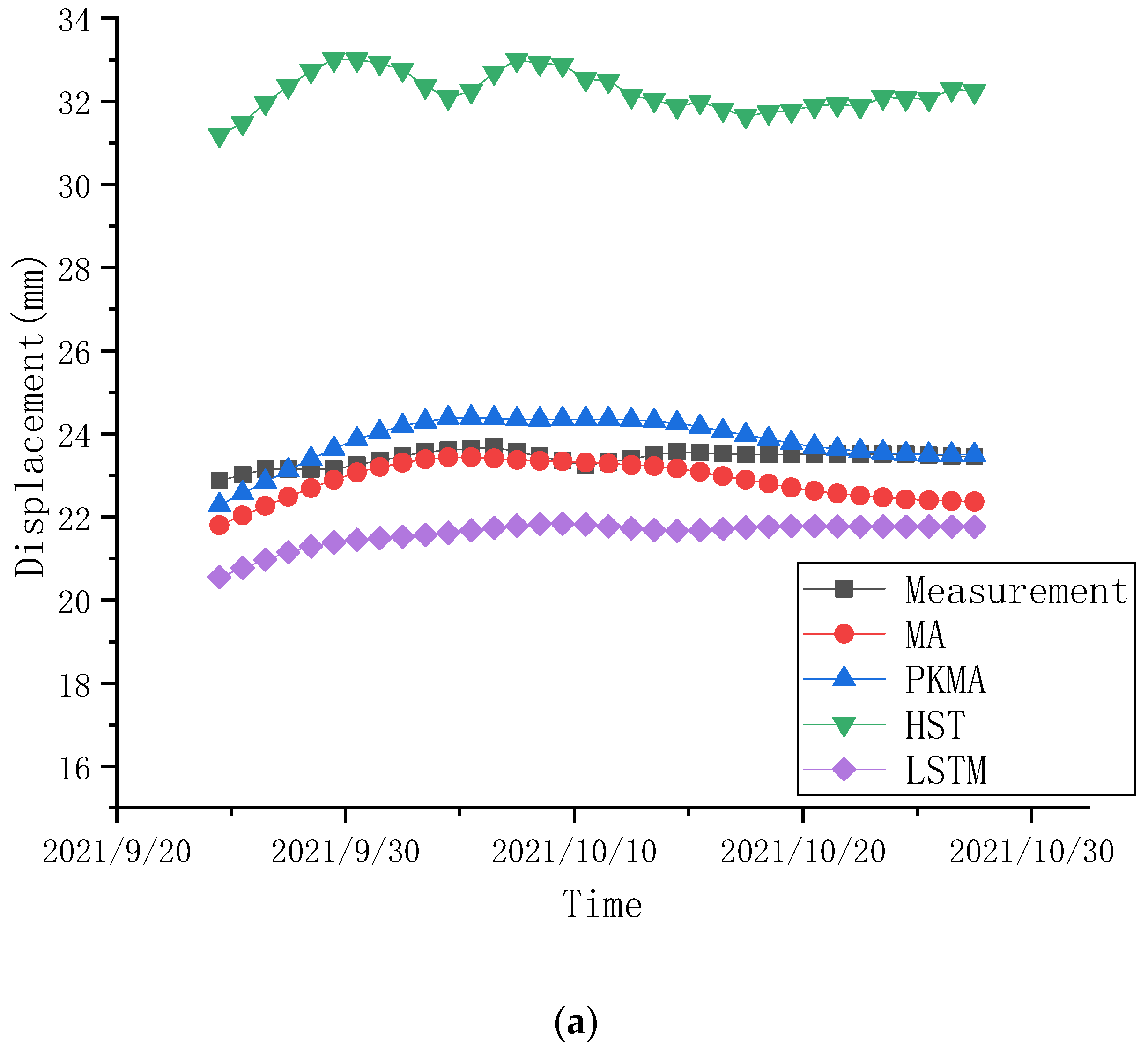
4.3. Prediction Comparisons
4.4. Transferability
5. Conclusions
- (1)
- The K-means clustering method based on Pearson metrics allows for the similarity in shape of the individual time-series curves to be taken into account, which leads to the method being able to further consider the deformation mechanism of each measurement point. This is because the reason for the slightly different time series curves of deformation at each measurement point is that the environmental factors at the location of each measurement point have different degrees of influence on their deformation. From the clustering results in this paper, the method succeeds in separately partitioning the measurement points in the shoreline dam section close to the structural weaknesses, which is more in line with the engineering reality and the deformation mechanism.
- (2)
- The PK clustering results adhere to the actual deformation mechanisms of different zones.
- (3)
- The application of the PK increases the fitting and prediction accuracy of the MA model, which makes the PKMA a satisfying solution for super-high dam deformation of the first impoundments.
- (4)
- The usage of the MA mechanism provides a way to explore the interactions between different inputs.
- (5)
- In addition to improving the accuracy of the model prediction for the first storage period of a very high arch dam, the multi-headed attention mechanism adopted in this paper also improves the interpretability of the model. Specifically, the multi-headed attention mechanism quantifies and visualizes the weights of each calculation step, providing a new way of thinking about the deformation-driven mechanism of the first storage period of a very high arch dam.
- (6)
- The PKMA model has superior transferability regarding training speed and prediction accuracy.
- (7)
- Given the powerful capabilities of the PKMA model proposed in this paper, we believe that it can be extended to other health monitoring problems for full-size structures with multi-factor effects, such as bridges, high-rise buildings, etc., in addition to its application to prediction models for dam deformation during the first storage period of extra-high arch dams.
- (8)
- The set of causal factors influencing the deformation during the first storage period of extra-high arch dams can be further determined in subsequent work, and more valid influencing factors can be accurately introduced into the model calculations.
- (9)
- Follow-up work should combine as many projects as possible, and a more comprehensive and systematic monitoring data mining system is expected in the future.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hu, B.; Liu, G.; Wu, Z. Analysis of dam foundation deformation characteristics during the first storage period of Xiaowan extra-high arch dam based on prototype monitoring. Hydropower Autom. Dam Monit. 2012, 36, 14–20. [Google Scholar]
- Wei, Y.; Hu, Y.; Wang, Y.; Tan, Y.; Liu, C.; Pei, L. A hybrid model approach for predicting deformation during the first storage period of Baihetan. J. Hydropower Gener. 2022, 41, 84–92. [Google Scholar]
- Zhang, X.L. Collection of typical cases of dam failures and accidents at hydropower stations. Dam Saf. 2015, 8, 13–16. [Google Scholar]
- Londe, P. The Malpasset Dam failure. Eng. Geol. 1987, 24, 295–329. [Google Scholar] [CrossRef]
- Alcrudo, F.; Gil, E. The malpasset dam-break case study. In Proceedings of the 4th Concerted Action on Dambreak Modelling Workshop, Zaragoza, Spain, 18 November 1999. [Google Scholar]
- Erpicum, S.; Archambeau, P.; Dewals, B.; Pirotton, M. Computation of the Malpasset dam break with a 2D conservative flow solver on a multiblock structured grid. In Proceedings of the 6th International Conference of Hydroinformatics, Singapore, 21–24 June 2004. [Google Scholar]
- Pan, J. Danger of arch dam. Knowl. Is Power 2003, 5, 53–55. [Google Scholar]
- Ghatak, A. Machine Learning with R; Springer: Singapore, 2017. [Google Scholar]
- Belmokre, A.; Mihoubi, M.K.; Santillán, D. Analysis of Dam Behavior by Statistical Models: Application of the Random Forest Approach. KSCE J. Civ. Eng. 2019, 23, 4800–4811. [Google Scholar] [CrossRef]
- Salazar, F.; Toledo, M.A.; Oñate, E.; Morán, R. An empirical comparison of machine learning techniques for dam behaviour modelling. Struct. Saf. 2015, 56, 9–17. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, A. Practical Time Series Analysis: Prediction with Statistics and Machine Learning; O’Reilly Media: Sebastopol, CA, USA, 2019. [Google Scholar]
- Li, B.; Yang, J.; Hu, D. Dam monitoring data analysis methods: A literature review. Struct. Control. Health Monit. 2019, 27, e2501. [Google Scholar] [CrossRef]
- Marius, B. Statistical Methods for Dam Behaviour Analysis; ETH Zurich: Zurich, Switzerland, 2018. [Google Scholar]
- Ren, Q.; Li, M.; Li, H.; Shen, Y. A novel deep learning prediction model for concrete dam displacements using interpretable mixed attention mechanism. Adv. Eng. Inform. 2021, 50, 101407. [Google Scholar] [CrossRef]
- Liu, C. Man-machine model: Pattern recognition and forecasts for complex structures supervised by multi-model ensembles. Struct. Saf. 2021, 88, 102022. [Google Scholar] [CrossRef]
- Gu, C.; Wu, Z. Theory and Method of Dam and Dam Foundation Safety Monitoring and Its Application; Hohai University Press: Nanjing, China, 2006. [Google Scholar]
- Hu, J.; Ma, F. Statistical modelling for high arch dam deformation during the initial impoundment period. Struct Control. Health Monit. 2020, 27, e2638. [Google Scholar] [CrossRef]
- Hu, J. Influence of Regenerated Crack to Arch Dam Deformation and Displacement Forecast. Water Resour. Power 2008, 6, 96–100. [Google Scholar]
- Wang, S.; Xu, C.; Gu, C.; Su, H.; Hu, K.; Xia, Q. Displacement monitoring model of concrete dams using the shape feature clustering-based temperature principal component factor. Struct Control Health Monit. 2020, 27, e2603. [Google Scholar] [CrossRef]
- Xu, C.; Wang, S.; Liu, Y.; Sui, X. Monitoring Model for Displacement of Arch Dams Considering Viscoelastic Hysteretic Effect. J. Yangtze River Sci. Res. Inst. 2022, 39, 67–72. [Google Scholar]
- Ren, Q.; Shen, Y.; Li, M.; Kong, R.; Li, H. Safety monitoring model of hydraulic structures and its optimization based on deep learning analysis. J. Hydraul. Eng. 2021, 52, 71–80. [Google Scholar]
- Chen, H.; Chen, X.; Guan, J.; Zhang, X.; Guo, J.; Yang, G.; Xu, B. A combination model for evaluating deformation regional characteristics of arch dams using time series clustering and residual correction. Mech. Syst. Signal Process. 2022, 179, 109397. [Google Scholar] [CrossRef]
- Ray, W.C. Advanced Engineering Mathematics; Mcgraw-Hill Book Company, Inc.: New York, NY, USA, 1960. [Google Scholar]
- Wu, Y. Exponential convergence rate of conditional mean absolute error for nonparametric regression kernel estimation. J. Jilin Univ. Med. Ed. 1986, 6, 186–194. [Google Scholar]
- Zhang, J. Probability Theory and Mathematical Statistics Tutorial; Zhejiang University Press: Hangzhou, China, 2006. [Google Scholar]
- Ren, Q.; Li, M.; Bai, S.; Shen, Y. A multiple-point monitoring model for concrete dam displacements based on correlated multiple-output support vector regression. Struct. Health Monit. 2022, 21, 2768–2785. [Google Scholar] [CrossRef]
- Penghai, H. Pearson correlation coefficient is applied to medical signal correlation measurement. Electron. World 2017, 1, 163. [Google Scholar]
- Neal, M. Bayesian Methods for Machine Learning. Nips Tutor. 2004, 13, 1–67. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Shen, X. Polynomial interpolation (I)-Lagrange interpolation. Prog. Math. 1983, 12, 193–214. [Google Scholar]
- Jaggi, R.; Morris, S. Rule of thumb. Can. Fam. Physician 2007, 1, 1309–1310. [Google Scholar]
- Zhou, L.; Gong, J.; He, J. Study on the expression of reasonable factor of time-dependent deformation of concrete dams. In Proceedings of the Technical Information Exchange Meeting of National Dam Safety Monitoring Technology Information Network National Dam Safety Monitoring Technology Information Network; 2007. Available online: https://www.fema.gov/sites/default/files/documents/fema_ndsp-report-congress-fy18-fy19.pdf (accessed on 5 April 2023).
- Pan, C. Experimental and Theoretical Study on Time-Dependent Deformation and Shear Performance of Concrete Structures; Southeast University: Dacca, Bangladesh, 2011. [Google Scholar]
- He, J.; Shi, Y.; Gong, J. Study on time-dependent deformation characteristics of concrete dams. J. Chang. Acad. Sci. 2010, 27, 5. [Google Scholar]
- Xu, C.; Wang, S.; Gu, C.; Su, H. A Probabilistic Prediction Model for Displacement of Super High Arch Dams Considering the Deformation Spatial Association; Geomatics and Information Science of Wuhan University: Wuhan, China, 2021. [Google Scholar] [CrossRef]
- Ren, Q.; Li, M.; Shen, Y.; Li, M. Dynamic monitoring model for dam deformation with spatiotemporal coupling correlation characteristics. J. Hydroelectr. Eng. 2021, 40, 160–172. [Google Scholar]
- Zhang, J.; Cao, X.; Xie, J.; Kou, P. An Improved Long Short-Term Memory Model for Dam Displacement Prediction. Math. Probl. Eng. 2019, 2019, 6792189. [Google Scholar] [CrossRef] [Green Version]
- Qu, X.; Yang, J.; Chang, M. A deep learning model for concrete dam deformation prediction based on RS-LSTM. J. Sens. 2019, 2019, 4581672. [Google Scholar] [CrossRef]
- Hu, J. Deformationforecasting model and its modeling method of super high arch dams during initial operation periods. Hydro-Sci. Eng. 2020, 5, 63–71. (In Chinese) [Google Scholar]
- Hu, B.; Liu, G.; Wu, Z. Study on deformation characteristics of dam foundation during the first storage period of Xiaowan extra-high arch dam based on prototype monitoring and numerical simulation tests. In Technical Advances in Reservoir Dam Construction and Management, Proceedings of the 2012 Annual Academic Conference of the China Dam Association, Denver, CO, USA, 16–20 September 2012; 2012; pp. 339–349. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=19a62e725bdffad616e01ed0cdc14fac&site=xueshu_se (accessed on 18 March 2023).
- Sundermeyer, M.; Schlüter, R.; Ney, H. LSTM Neural Networks for Language Modeling. In Proceedings of the Thirteenth Annual Conference of the International Speech Communication Association 2012 Interspeech, Portland, OR, USA, 9–13 September 2012. [Google Scholar]
- Mata, J.; Castro, A.T.D.; Costa, J.S.D. Constructing statistical models for arch dam deformation. Struct. Control Health Monit. 2014, 21, 423–437. [Google Scholar] [CrossRef] [Green Version]



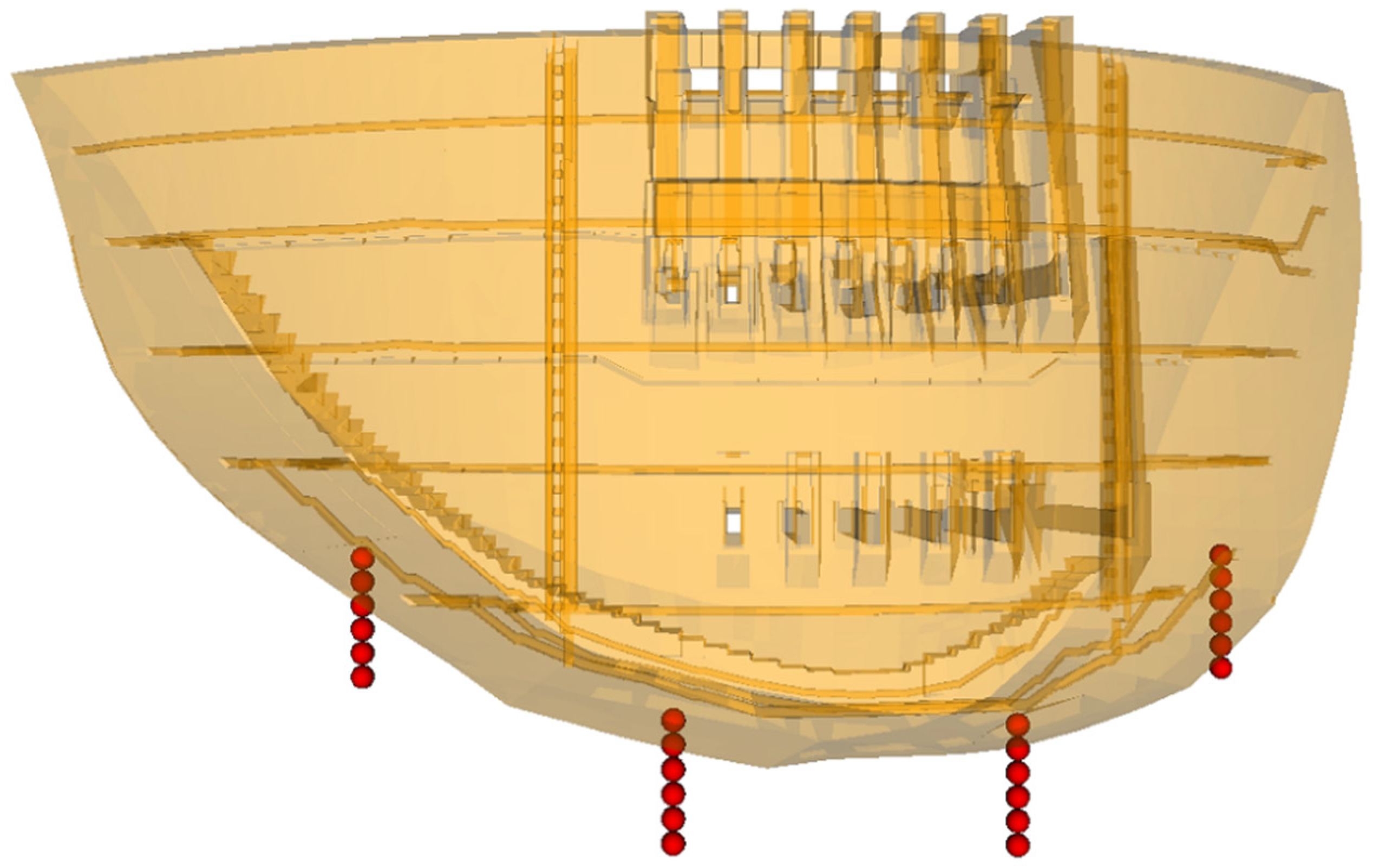





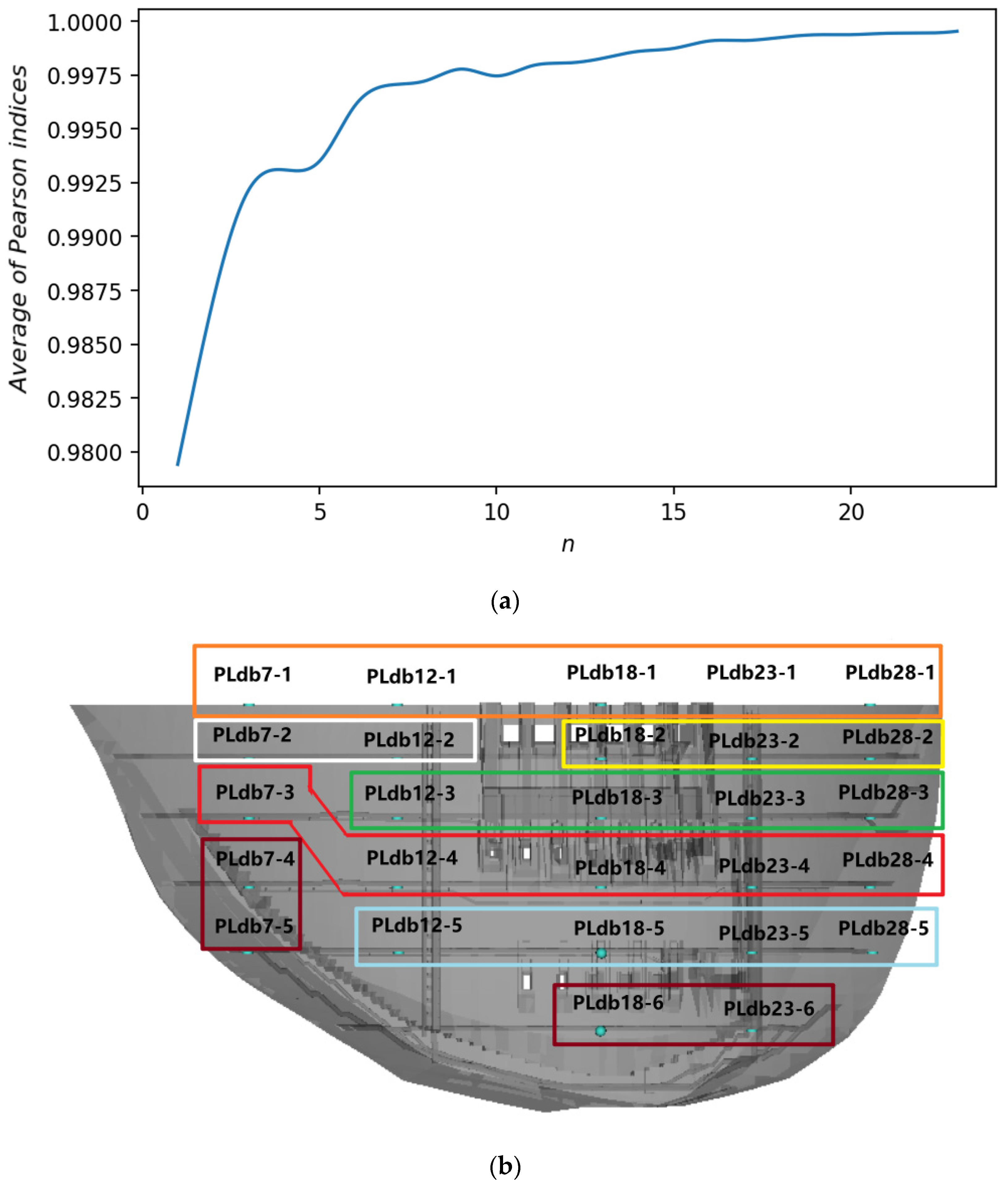
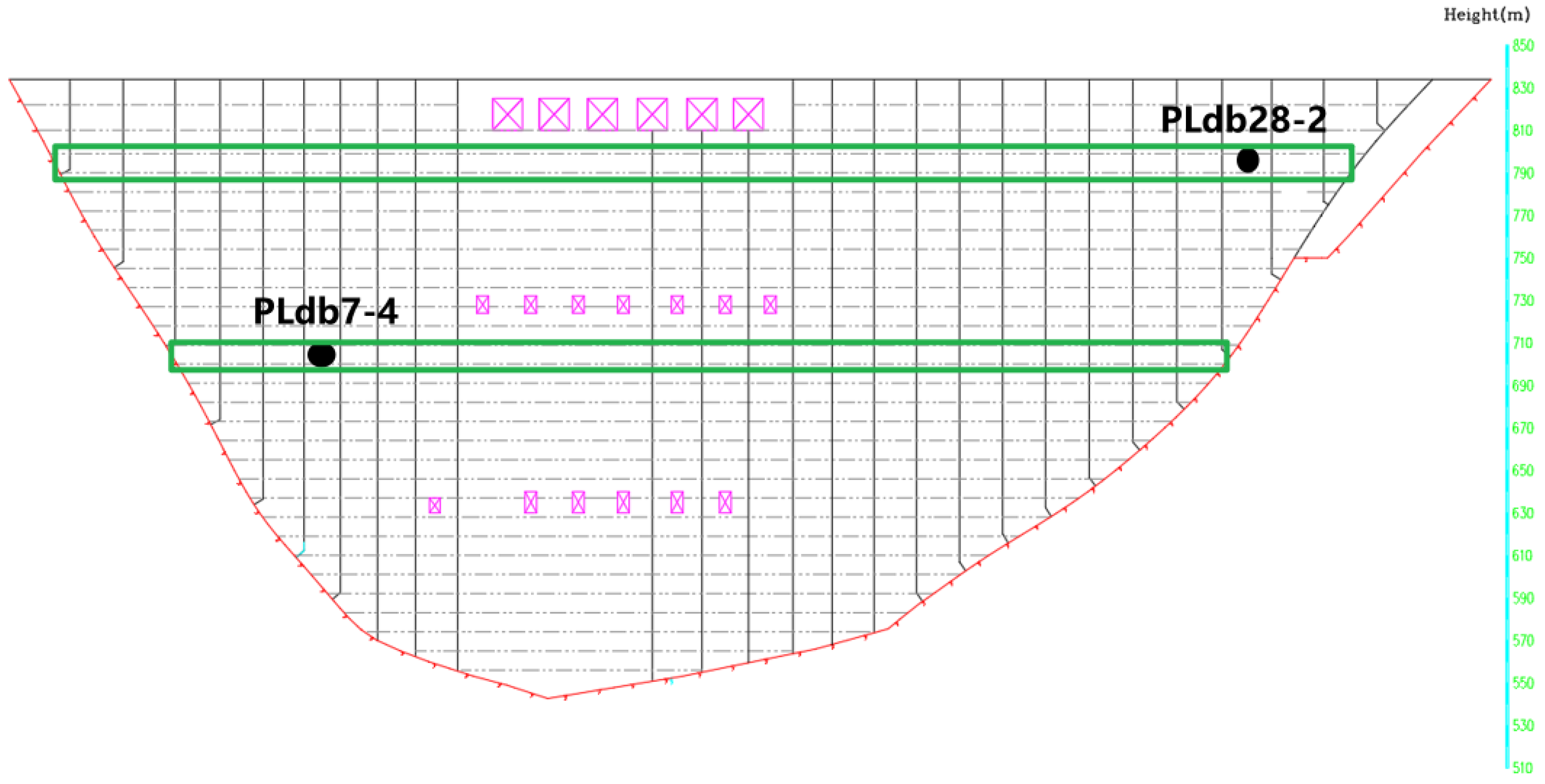
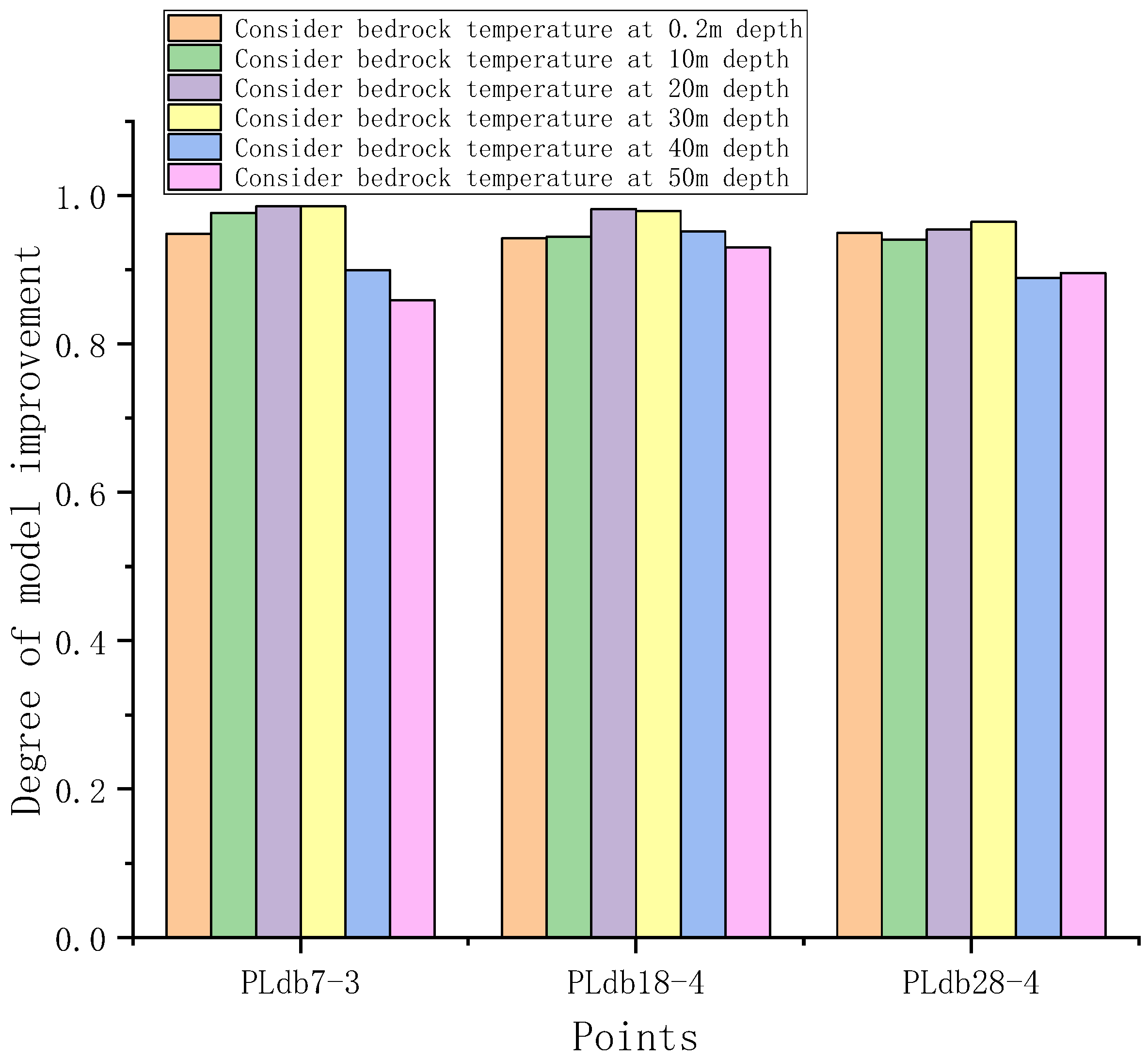









| Monitoring Types | Number of Monitoring Instruments | Number of Monitoring Data Values |
|---|---|---|
| Normal and inverted plumb lines | 51 | 33,762 |
| Observation piers located in the catwalk | 40 | 1360 |
| Gallery benchmarks | 162 | 8910 |
| Model | Hyperparameters |
|---|---|
| LSTM | batch size = 5, lr = 0.001 |
| MA | batch size = 5, lr = 0.001, heads = 3 |
| PKMA | batch size = 5, lr = 0.001, heads = 3 |
| Measuring Points | RMSE (mm) | MAE (mm) | MSE (mm) |
|---|---|---|---|
| PLdb7-4 | 0.3711 | 0.5010 | 0.6092 |
| PLdb18-4 | 1.1027 | 0.9017 | 1.2518 |
| PLdb28-3 | 0.2296 | 0.4189 | 0.4792 |
| Model | RMSE (mm) | MAE (mm) | MSE (mm) | |
|---|---|---|---|---|
| PLdb7-4 | LSTM vs. PKMA | 40.58% | 68.97% | 64.69% |
| MA vs. PKMA | 4.79% | 11.57% | 9.35% | |
| HST vs. PKMA | 57.59% | 72.42% | 82.01% | |
| PLdb18-4 | LSTM vs. PKMA | 63.98% | 47.64% | 87.02% |
| MA vs. PKMA | 50.62% | 69.02% | 75.61% | |
| HST vs. PKMA | 48.15% | 55.81% | 73.12% | |
| PLdb28-3 | LSTM vs. PKMA | 31.72% | 45.61% | 53.38% |
| MA vs. PKMA | 10.28% | 11.86% | 19.50% | |
| HST vs. PKMA | 12.66% | 5.69% | 23.71% |
| Model | RMSE (mm) | MAE (mm) | MSE (mm) | |
|---|---|---|---|---|
| PLdb7-4 | LSTM | 1.1650 | 1.3501 | 1.3573 |
| MA | 0.7270 | 0.4737 | 0.5286 | |
| HST | 1.6323 | 1.5191 | 2.6643 | |
| PKMA | 0.6922 | 0.4189 | 0.4792 | |
| PLdb18-4 | LSTM | 3.1057 | 1.7220 | 9.6455 |
| MA | 2.2656 | 2.9108 | 5.1330 | |
| HST | 2.1579 | 2.0404 | 4.6565 | |
| PKMA | 1.1188 | 0.9017 | 1.2518 | |
| PLdb28-3 | LSTM | 1.5639 | 1.8199 | 2.4457 |
| MA | 1.1902 | 1.1230 | 1.4165 | |
| HST | 1.2226 | 1.0495 | 1.4947 | |
| PKMA | 1.0678 | 0.9898 | 1.1403 |
| Prediction Targets | Model | RMSE (mm) | MAE (mm) | MSE (mm) |
|---|---|---|---|---|
| PLdb5-4 | PKMA with pre-training parameters | 1.094121 | 0.8339 | 1.1971 |
| PKMA without pre-training parameters | 1.155465 | 0.9619 | 1.3351 | |
| PLdb15-4 | PKMA with pre-training parameters | 1.070841 | 0.8375 | 1.1467 |
| PKMA without pre-training parameters | 1.176648 | 0.9926 | 1.3845 | |
| PLdb27-3 | PKMA with pre-training parameters | 1.740029 | 0.9745 | 3.0277 |
| PKMA without pre-training parameters | 2.025537 | 1.0575 | 4.1028 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Liu, C.; Duan, H.; Wang, Y.; Hu, Y.; Zhu, X.; Tan, Y.; Pei, L. Pearson K-Mean Multi-Head Attention Model for Deformation Prediction of Super-High Dams in First Impoundments. Water 2023, 15, 1734. https://doi.org/10.3390/w15091734
Wei Y, Liu C, Duan H, Wang Y, Hu Y, Zhu X, Tan Y, Pei L. Pearson K-Mean Multi-Head Attention Model for Deformation Prediction of Super-High Dams in First Impoundments. Water. 2023; 15(9):1734. https://doi.org/10.3390/w15091734
Chicago/Turabian StyleWei, Yilun, Chang Liu, Hang Duan, Yajun Wang, Yu Hu, Xuezhou Zhu, Yaosheng Tan, and Lei Pei. 2023. "Pearson K-Mean Multi-Head Attention Model for Deformation Prediction of Super-High Dams in First Impoundments" Water 15, no. 9: 1734. https://doi.org/10.3390/w15091734