Comprehensive Effects of Atmosphere and Soil Drying on Stomatal Behavior of Different Plant Types
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Methods
2.2.1. Estimation of the Stomatal Conductance
2.2.2. Calculation of Water Use Efficiency and Carbon Use Efficiency
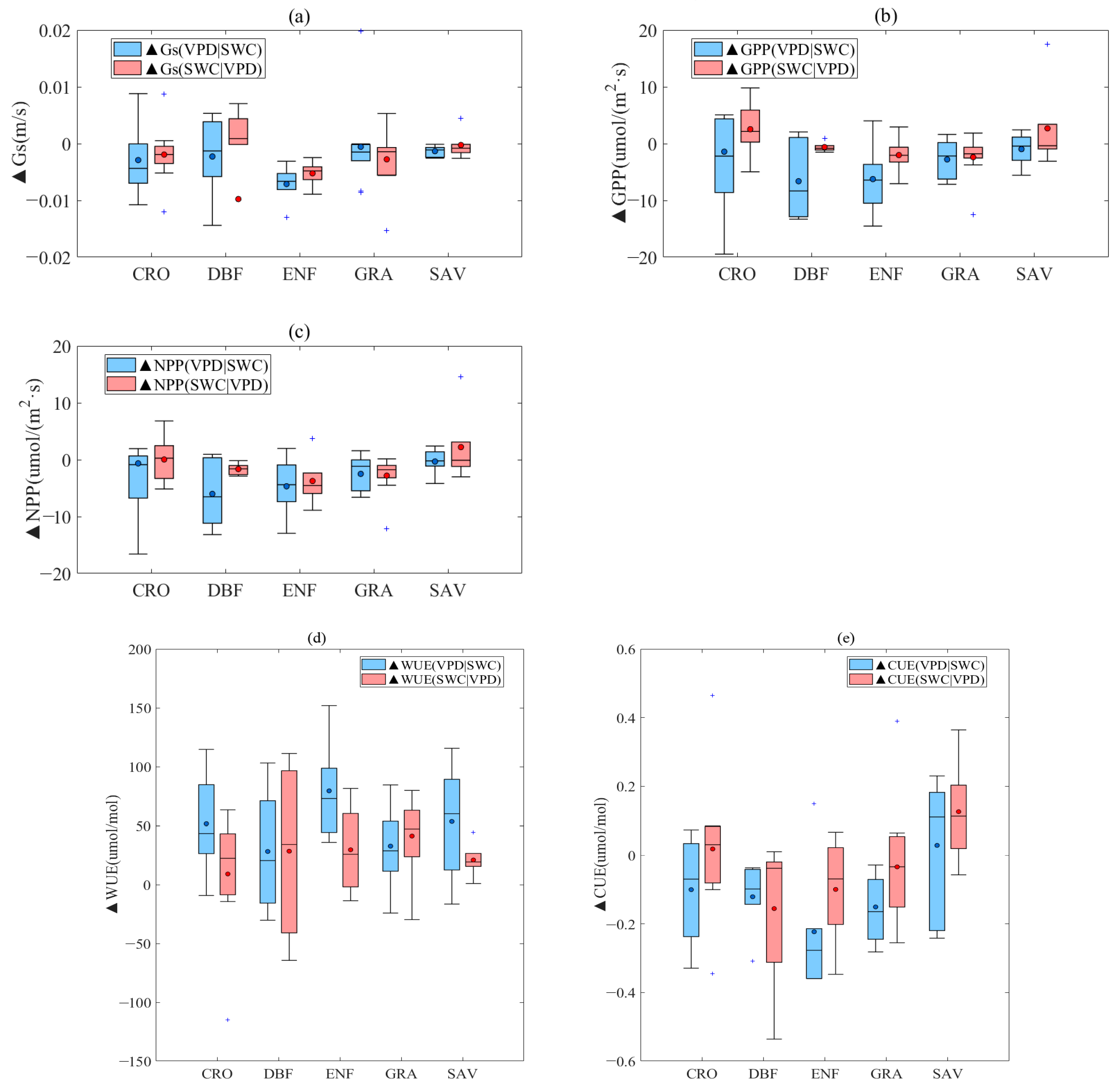
2.2.3. Separating the Relative Contribution of SWC and VPD to WUE and CUE
3. Results
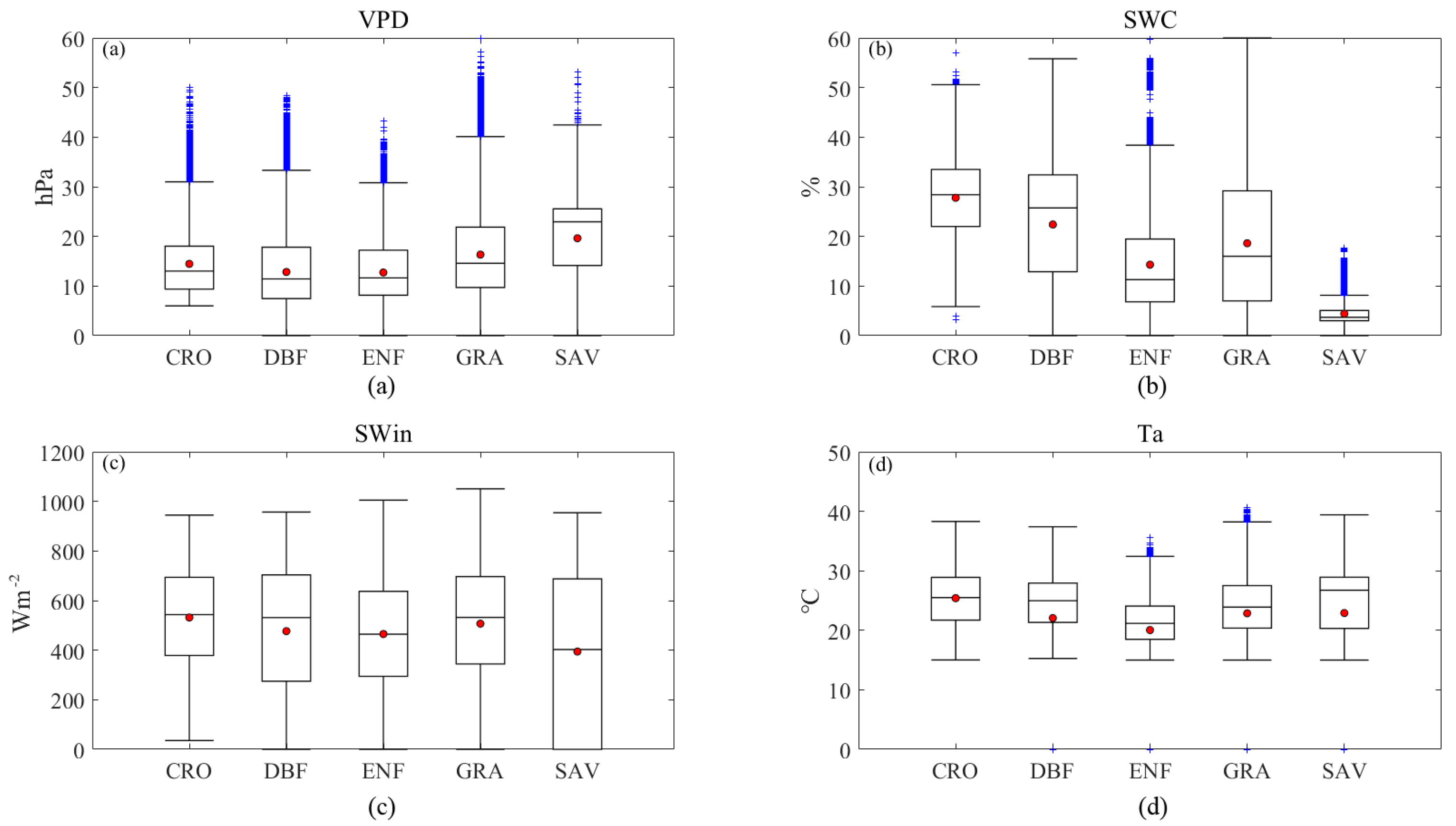
3.1. Meteorology Characteristics of Sites
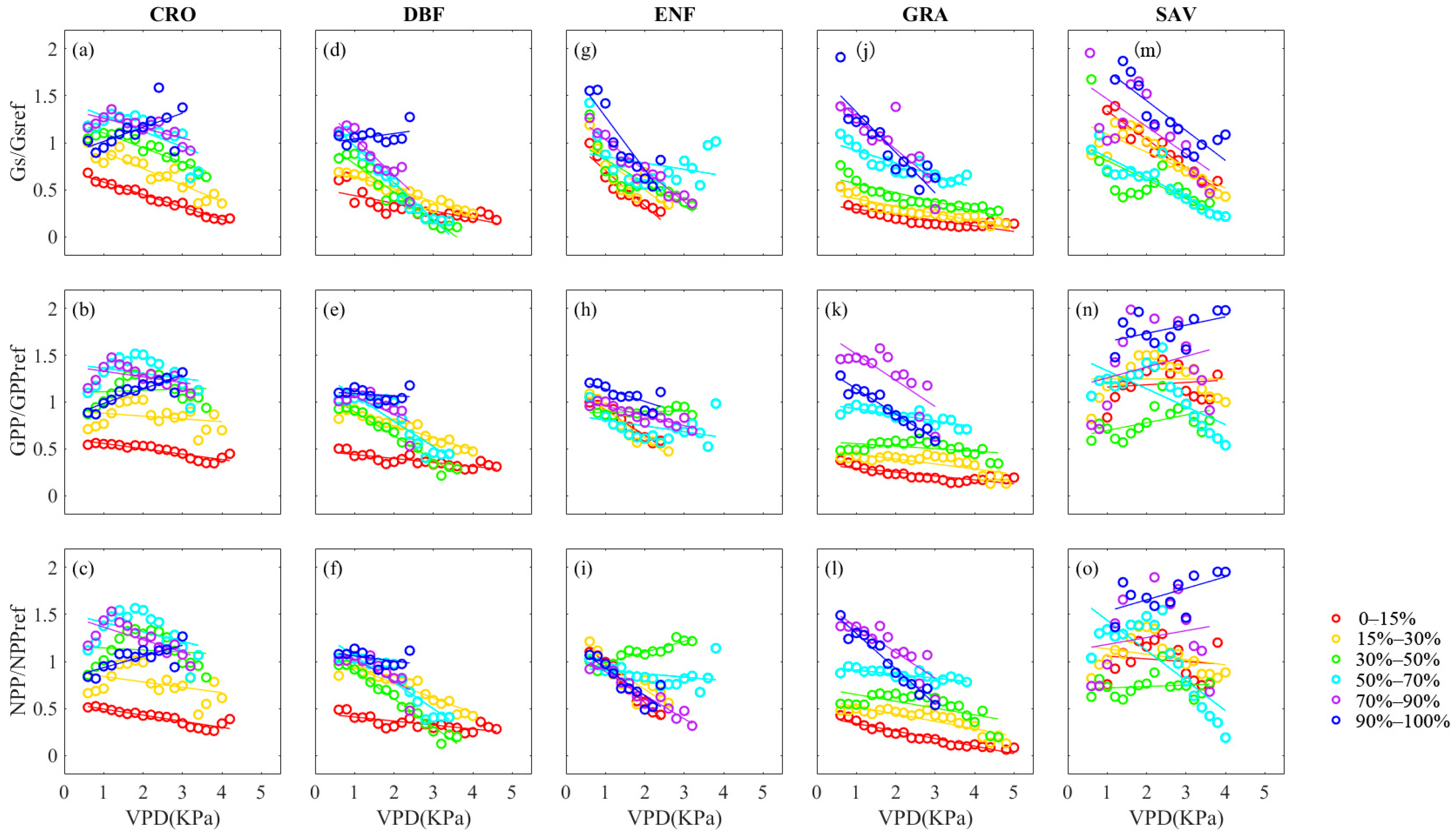
3.2. Effect of Decoupling VPD and SWC on Vegetation Stomatal Behavior
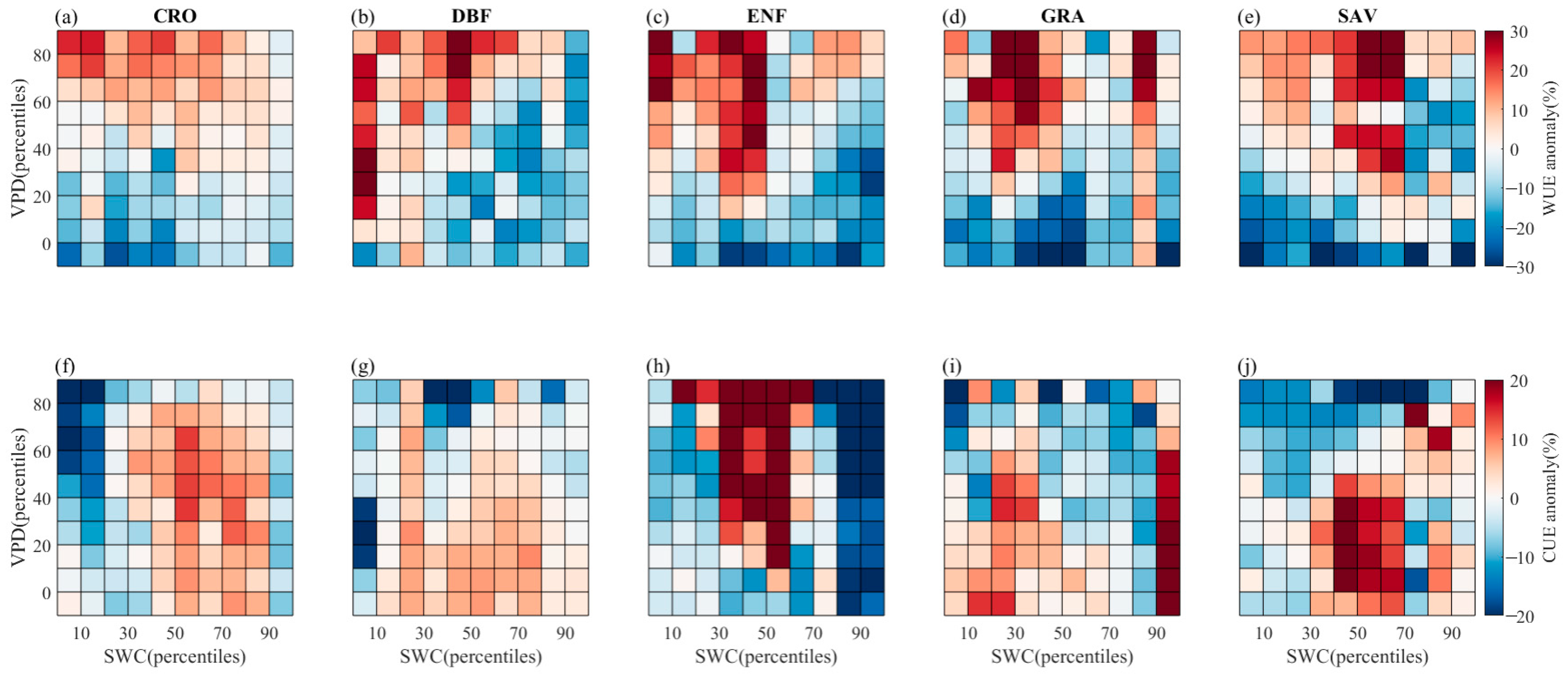
3.3. Influence of VPD and SWC on WUE and CUE of Different PFTs
4. Discussion
5. Conclusions
- (1)
- High VPD coupled with low SWC can restrict plant stomatal conductance, GPP, and NPP. However, in some vegetation types (CRO, DBF), high soil moisture content can offset the negative impact of high VPD, while low SWC limits vegetation stomatal conductance. Interestingly, in SAV, lower SWC levels (percentiles 0–30%) can lead to higher stomatal conductance and GPP than higher SWC levels (percentiles 30–70%). For certain PFTs, higher soil moisture levels can alleviate the limitation caused by high VPD and even partially promote GPP and NPP as VPD increases. Notably, there is an anomalous increase in NPP in the ENF vegetation type when soil moisture percentiles range between 30 and 50%, leading to a corresponding increase in CUE as soil moisture content increases with VPD.
- (2)
- Vegetation stomatal conductance and productivity have a direct impact on both WUE and CUE. Across the various vegetation types, an increase in VPD generally results in an increase in WUE, while the influence of SWC on WUE is less clear. Moreover, specific analyses reveal that the effect of VPD on WUE is more significant than that of SWC. The changes in WUE due to increasing VPD occur at an average WUE value of approximately 50 μmol/mol, with the ENF vegetation type being the most affected at 70 μmol/mol. Conversely, the changes in WUE due to decreasing SWC occur at an average WUE value of about 30μmol/mol.
- (3)
- The CUE of the CRO, DBF, ENF, and GRA vegetation types decreases as VPD increases, whereas the impact of SWC on these four types is relatively insignificant, with only a −0.05 μmol/μmol total change. In contrast, the SAV vegetation type’s CUE is affected differently by VPD and SWC, displaying an ascending tendency in CUE changes that are dominated by the rise in VPD and decline in SWC. This indicates that a decrease in SWC and increase in VPD foster the enhancement of CUE in the SAV vegetation type to some extent.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, L.; Gudmundsson, L.; Hauser, M.; Qin, D.; Li, S.; Seneviratne, S.I. Soil moisture dominates dryness stress on ecosystem production globally. Nat. Commun. 2020, 11, 1723–2041. [Google Scholar] [CrossRef] [PubMed]
- Madadgar, S.; AghaKouchak, A.; Farahmand, A.; Davis, S.J. Probabilistic estimates of drought impacts on agricultural production. Geophys. Res. Lett. 2017, 44, 7799–7807. [Google Scholar] [CrossRef]
- Sadras, V.O.; Milroy, S.P. Soil-water thresholds for the responses of leaf expansion and gas exchange: A review. Field Crops Res. 1996, 47, 253–266. [Google Scholar] [CrossRef]
- Huang, C.-W.; Domec, J.-C.; Ward, E.J.; Duman, T.; Manoli, G.; Parolari, A.J.; Katul, G.G. The effect of plant water storage on water fluxes within the coupled soil-plant system. New Phytol. 2016, 213, 1093–1106. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Vilalta, J.; Poyatos, R.; Aguadé, D.; Retana, J.; Mencuccini, M. A new look at water transport regulation in plants. New Phytol. 2014, 204, 105–115. [Google Scholar] [CrossRef]
- Grossiord, C.; Buckley, T.N.; Cernusak, L.A.; Novick, K.A.; Poulter, B.; Siegwolf, R.T.W.; Sperry, J.S.; McDowell, N.G. Plant responses to rising vapor pressure deficit. New Phytol. 2020, 226, 1550–1566. [Google Scholar] [CrossRef]
- Monteith, J.L. A reinterpretation of stomatal responses to humidity. Plant Cell Environ. 1995, 18, 357–364. [Google Scholar] [CrossRef]
- Zhou, S.; Williams, A.P.; Berg, A.M.; Cook, B.I.; Zhang, Y.; Hagemann, S.; Lorenz, R.; Seneviratne, S.I.; Gentine, P. Land–atmosphere feedbacks exacerbate concurrent soil drought and atmospheric aridity. Proc. Natl. Acad. Sci. USA 2019, 116, 18848–18853. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, Y.; Park Williams, A.; Gentine, P. Projected increases in intensity, frequency, and terrestrial carbon costs of compound drought and aridity events. Sci. Adv. 2019, 5, eaau5740. [Google Scholar] [CrossRef]
- Yuan, F.; Liu, J.; Zuo, Y.; Guo, Z.; Xu, X. Rising vegetation activity dominates growing water use efficiency in the asian permafrost region from 1900 to 2100. Sci. Total Environ. 2020, 736, 139587. [Google Scholar] [CrossRef]
- Zanotelli, D.; Montagnani, L.; Manca, G.; Tagliavini, M. Net primary productivity, allocation pattern and carbon use efficiency in an apple orchard assessed by integrating eddy-covariance, biometric and continuous soil chamber measurements. Biogeosci. Discuss 2013, 10, 3089–3108. [Google Scholar] [CrossRef]
- Zhao, Y.Y.; Amy, L.M.; Miao, F.F.; Chen, G.; Zhu, X.G. The evolution of stomatal traits along the trajectory toward c4 photosynthesis. Plant Physiol. 2022, 190, 441–458. [Google Scholar] [CrossRef] [PubMed]
- Novick, K.A.; Ficklin, D.L.; Stoy, P.C.; Williams, C.A.; Bohrer, G.; Oishi, A.C.; Papuga, S.A.; Blanken, P.D.; Noormets, A.; Sulman, B.N.; et al. The increasing importance of atmospheric demand for ecosystem water and carbon fluxes. Nat. Clim. Chang.f 2016, 6, 1023–1027. [Google Scholar] [CrossRef]
- Sulman, B.N.; Roman, D.T.; Yi, K.; Wang, L.; Phillips, R.P.; Novick, K.A. High atmospheric demand for water can limit forest carbon uptake and transpiration as severely as dry soil. Geophys. Res. Lett. 2016, 43, 9686–9695. [Google Scholar] [CrossRef]
- Kimm, H.; Guan, K.; Gentine, P.; Wu, J.; Bernacchi, C.J.; Sulman, B.N.; Griffis, T.J.; Lin, C. Redefining droughts for the U.S. Corn Belt: The dominant role of atmospheric vapor pressure deficit over soil moisture in regulating stomatal behavior of Maize and Soybean. Agric. For. Meteorol. 2020, 287, 107930. [Google Scholar] [CrossRef]
- Franks, P.J.; Adams, M.A.; Amthor, J.S.; Barbour, M.M.; Berry, J.A.; Ellsworth, D.S.; Farquhar, G.D.; Ghannoum, O.; Lloyd, J.; McDowell, N.; et al. Sensitivity of plants to changing atmospheric CO2concentration: From the geological past to the next century. New Phytol. 2013, 197, 1077–1094. [Google Scholar] [CrossRef]
- Nie, C.; Huang, Y.; Zhang, S.; Yang, Y.; Zhou, S.; Lin, C.; Wang, G. Effects of soil water content on forest ecosystem water use efficiency through changes in transpiration/evapotranspiration ratio. Agric. For. Meteorol. 2021, 308–309, 108605. [Google Scholar] [CrossRef]
- Zhang, Q.; Ficklin, D.L.; Manzoni, S.; Wang, L.; Way, D.; Phillips, R.P.; Novick, K.A. Response of ecosystem intrinsic water use efficiency and gross primary productivity to rising vapor pressure deficit. Environ. Res. Lett. 2019, 14, 074023. [Google Scholar] [CrossRef]
- Keenan, T.F.; Hollinger, D.Y.; Bohrer, G.; Dragoni, D.; Munger, J.W.; Schmid, H.P.; Richardson, A.D. Increase in forest water-use efficiency as atmospheric carbon dioxide concentrations rise. Nature 2013, 499, 324–327. [Google Scholar] [CrossRef]
- Knauer, J.; Zaehle, S.; Medlyn, B.E.; Reichstein, M.; Williams, C.A.; Migliavacca, M.; de Kauwe, M.G.; Werner, C.; Keitel, C.; Kolari, P.; et al. Towards physiologically meaningful water-use efficiency estimates from eddy covariance data. Glob. Chang. Biol. 2017, 24, 694–710. [Google Scholar] [CrossRef]
- Mastrotheodoros, T.; Pappas, C.; Molnar, P.; Burlando, P.; Keenan, T.F.; Gentine, P.; Gough, C.M.; Fatichi, S. Linking plant functional trait plasticity and the large increase in forest water use efficiency. J. Geophys. Res. Biogeosci. 2017, 122, 2393–2408. [Google Scholar] [CrossRef]
- Zhu, W.Z. Advances in the carbon use efficiency of forest. Chin. J. Ecol. 2014, 37, 1043–1058. [Google Scholar] [CrossRef]
- Stratton, L.C.; Goldstein, G. Carbon uptake, growth and resource-use efficiency in one invasive and six native hawaiian dry forest tree species. Tree Physiol. 2001, 21, 1327–1334. [Google Scholar] [CrossRef] [PubMed]
- Dong, G.; Guo, J.; Chen, J.; Ge, S.; Song, G.; Hu, L.; Wang, Y. Effects of spring drought on carbon sequestration, evapotranspiration and water use efficiency in the songnen meadow steppe in northeast China. Ecohydrology 2011, 4, 211–224. [Google Scholar] [CrossRef]
- Linares, J.C.; Delgado-Huertas, A.; Camarero, J.J.; Carreira, M. Competition and drought limit the response of water-use efficiency to rising atmospheric carbon dioxide in the mediterranean fir abies pinsapo. Oecologia 2009, 161, 611–624. [Google Scholar] [CrossRef]
- Zouaoui, R.; Ksontini, M.; Ourry, A.; Ferchichi, A. Effect of drought on leaf gas exchange, water-use efficiency and carbon isotope discrimination in two species (Rhus tripartitum (ucria) grande and Ziziphus lotus (L.)) in arid zone of tunisia threatened of disappearance. Int. J. Plant Prod. 2013, 4, 1616–1627. [Google Scholar]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. Climate extremes and the carbon cycle. Nature 2013, 500, 287–295. [Google Scholar] [CrossRef]
- Lin, C.; Gentine, P.; Huang, Y.; Guan, K.; Kimm, H.; Zhou, S. Diel ecosystem conductance response to vapor pressure deficit is suboptimal and independent of soil moisture. Agric. For. Meteorol. 2018, 250, 24–34. [Google Scholar] [CrossRef]
- Lyons, D.S.; Dobrowski, S.Z.; Holden, Z.A.; Maneta, M.P.; Sala, A. Soil moisture variation drives canopy water content dynamics across the western US. Remote Sens. Environ. 2021, 253, 112233. [Google Scholar] [CrossRef]
- Gentine, P.; Chhang, A.; Rigden, A.; Salvucci, G. Evaporation estimates using weather station data and boundary layer theory. Geophys. Res. Lett. 2016, 43, 11661–11670. [Google Scholar] [CrossRef]
- Green, J.K.; Konings, A.G.; Alemohammad, S.H.; Berry, J.; Entekhabi, D.; Kolassa, J.; Lee, J.-E.; Gentine, P. Regionally strong feedbacks between the atmosphere and terrestrial biosphere. Nat. Geosci. 2017, 10, 410–414. [Google Scholar] [CrossRef] [PubMed]
- Schwalm, C.R.; Williams, C.A.; Schaefer, K.; Baldocchi, D.; Black, T.A.; Goldstein, A.H.; Law, B.E.; Oechel, W.C.; Paw, U.K.T.; Scott, R.L. Reduction in carbon uptake during turn of the century drought in western North America. Nat. Geosci. 2012, 5, 551–556. [Google Scholar] [CrossRef]
- Anderegg, W.R.; Konings, A.G.; Trugman, A.T.; Yu, K.; Bowling, D.R.; Gabbitas, R.; Karp, D.S.; Pacala, S.; Sperry, J.S.; Sulman, B.N.; et al. Hydraulic diversity of forests regulates ecosystem resilience during drought. Nature 2018, 561, 538–541. [Google Scholar] [CrossRef] [PubMed]
- Pastorello, G.; Trotta, C.; Canfora, E.; Chu, H.; Christianson, D.; Cheah, Y.-W.; Poindexter, C.; Chen, J.; Elbashandy, A.; Humphrey, M.; et al. The FLUXNET2015 dataset and the ONEFlux processing pipeline for eddy covariance data. Nat. Publ. Group 2020, 7, 225. [Google Scholar] [CrossRef]
- Monteith, J. Evaporation and surface temperature. Q. J. R. Meteorol. Soc. 2007, 107, 1–27. [Google Scholar] [CrossRef]
- Pennypacker, S.; Baldocchi, D. Seeing the fields and forests: Application of surface-layer theory and flux-tower data to calculating vegetation canopy height. Bound.-Layer. Meteorol. 2016, 158, 165–182. [Google Scholar] [CrossRef]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the Separation of Net Ecosystem Exchange into Assimilation and Ecosystem Respiration: Review and Improved Algorithm. Glob. Chang. Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Chambers, J.Q.; Tribuzy, E.S.; Toledo, L.C.; Crispim, B.F.; Higuchi, N.; dos Santos, J.; Araújo, A.C.; Kruijt, B.; Nobre, A.D.; Trumbore, S.E. Respiration from a tropical forest ecosystem: Partitioning of sources and low carbon use efficiency. Ecol. Appl. 2004, 14, 72–88. [Google Scholar] [CrossRef]
- Green, J.K.; Seneviratne, S.I.; Berg, A.M.; Findell, K.L.; Hagemann, S.; Lawrence, D.M.; Gentine, P. Large influence of soil moisture on long-term terrestrial carbon uptake. Nature 2019, 565, 476–479. [Google Scholar] [CrossRef]
- Fu, Z.; Ciais, P.; Prentice, I.C.; Findell, K.L.; Hagemann, S.; Lawrence, D.M.; Gentine, P. Atmospheric dryness reduces photosynthesis along a large range of soil water deficits. Nat. Commun. 2022, 13, 989. [Google Scholar] [CrossRef]
- Wang, H.; Yan, S.; Ciais, P.; Wigneron, J.; Liu, L.; Li, Y.; Fu, Z.; Ma, H.; Liang, Z.; Wei, F.; et al. Exploring complex water stress–gross primary production relationships: Impact of climatic drivers, main effects, and interactive effects. Glob. Chang. Biol. 2022, 28, 4110–4123. [Google Scholar] [CrossRef] [PubMed]
- Qiu, M.; Hao, Z. Sensitivity to abscisic acid regulates stomatal oscillation and closure in arabidopsis thaliana. Pak. J. Bot. 2010, 42, 353–359. [Google Scholar]
- Kucera, B.; Cohn, M.A.; Leubner-Metzger, G. Plant hormone interactions during seed dormancy release and germination. Seed Sci. Res. 2005, 15, 281–307. [Google Scholar] [CrossRef]
- Leung, J.; Giraudat, J. Abscisic acid signal transduction. Ann. Rev. Plant Biol. 1998, 49, 199. [Google Scholar] [CrossRef]
- Yue, M.; Szostkiewicz, I.; Korte, A.; Moes, D.; Yang, Y.; Christmann, A.; Grill, E. Regulators of pp2c phosphatase activity function as abscisic acid sensors. Science 2009, 324, 1064–1068. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Tian, Y.; Liu, Z.; Xia, X. Comprehensive Effects of Atmosphere and Soil Drying on Stomatal Behavior of Different Plant Types. Water 2023, 15, 1675. https://doi.org/10.3390/w15091675
Xu Z, Tian Y, Liu Z, Xia X. Comprehensive Effects of Atmosphere and Soil Drying on Stomatal Behavior of Different Plant Types. Water. 2023; 15(9):1675. https://doi.org/10.3390/w15091675
Chicago/Turabian StyleXu, Zhi, Ye Tian, Zhiwu Liu, and Xinran Xia. 2023. "Comprehensive Effects of Atmosphere and Soil Drying on Stomatal Behavior of Different Plant Types" Water 15, no. 9: 1675. https://doi.org/10.3390/w15091675
APA StyleXu, Z., Tian, Y., Liu, Z., & Xia, X. (2023). Comprehensive Effects of Atmosphere and Soil Drying on Stomatal Behavior of Different Plant Types. Water, 15(9), 1675. https://doi.org/10.3390/w15091675




