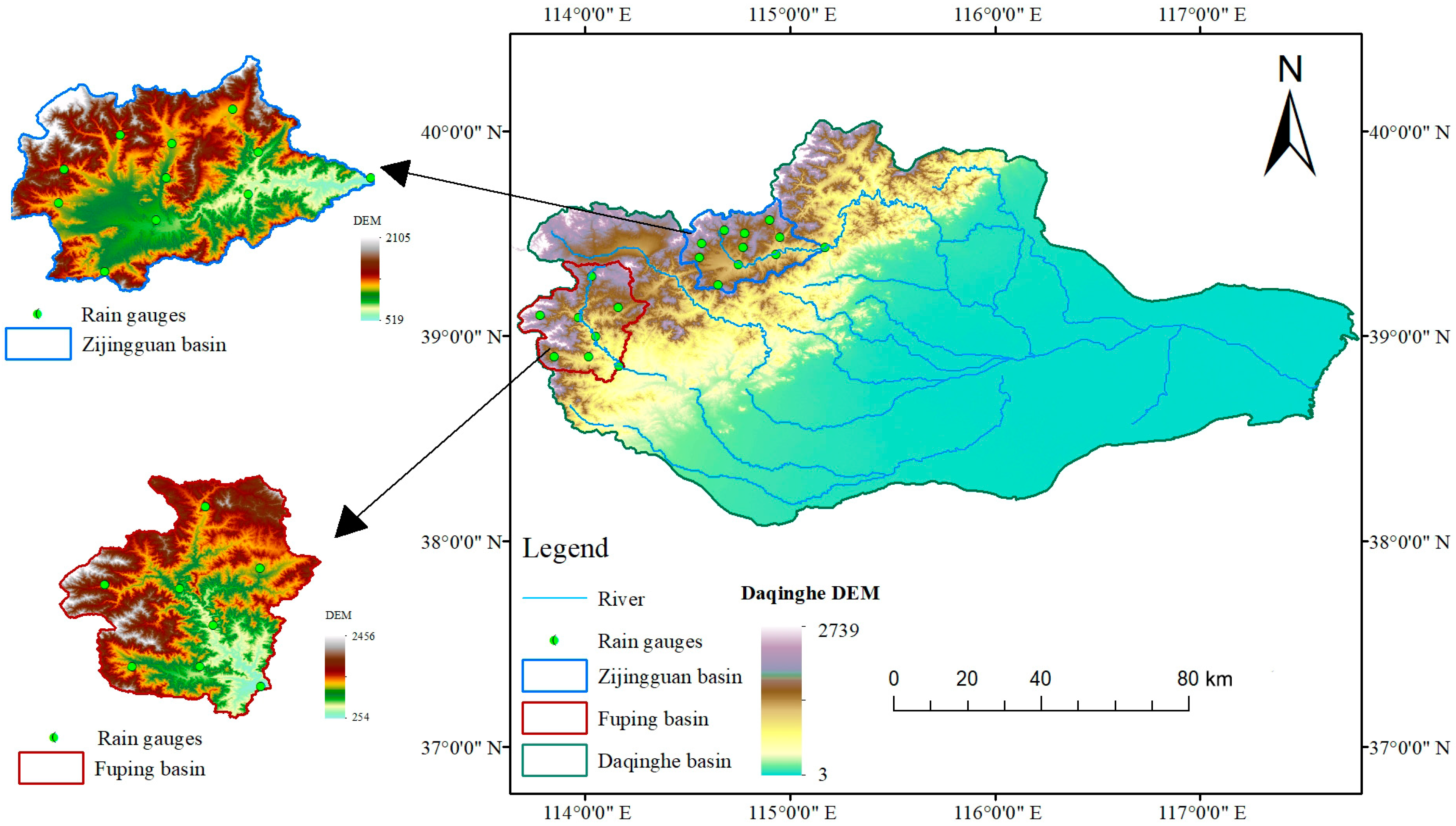
3.1. WRF Model Settings
To ensure that the spatial resolution of the nested grid set was as close as possible to that of the radar data, a three-layer nested grid was used. Setting the outermost grid range was conducive for assimilating large-scale GTS data, making the model operation more stable. The innermost grid covered the entire study area. The nesting ratio of the adjacent nesting layers was set to 1:3, and the grid sizes were 1, 3, and 9 km. The inner and outer grids provide two-way feedback in the WRF model. The grid center of the study area was 39°26′00″ N, 114°46′00″ E, and the innermost nested grid (Domain 3) was 145 × 115 km
2. The second-level nested grid (Domain 2) was 450 × 360 km
2, covering the radar scanning range, and the outermost nested grid (Domain 1) was 1260 × 1260 km
2. The nested grid and radar observation ranges in the study area are shown in
Figure 3 and
Table 3. The WRF model nested grid settings are shown. The three nested areas in this study were vertically divided into 40 layers. The top air pressure was 50 hPa [
30], and the WRF model integration time step was 6 s. The WRF model was set to output simulation results every 1 h. The precipitation output of the WRF model was used to drive the WRF-Hydro model. Because the study basins are located in the mid-latitude region, the Lambert projection was selected. The initial and lateral boundary conditions for forecasting were provided by the 1 × 1° Global Forecasting System (GFS). The GFS data are real-time data provided by the National Environmental Forecasting Center (NCEP) and are updated every 6 h. Because the GFS data are released in real time, they are often used as the initial driving force for precipitation forecasting in the WRF model [
31].
The simulation and forecasting capabilities of the model are highly dependent on the parameterization scheme. The scheme selected in this study may be applicable to precipitation processes in one region, but not to those in other regions [
32]. Because it is difficult to determine the most suitable scheme for future precipitation, the parameterization scheme is usually determined in advance for practical applications [
33]. In this study, the selection of the physical parameterization scheme was based on the sensitivity test results of the parameterization scheme for the same basin as that in Tian et al. [
34,
35]. The parameterization details that had a significant impact on the precipitation used in the assimilation test are listed in
Table 4. Details of the parameterizations used in the assimilation experiments are shown. Among them, the cumulus convection schemes for the 3 and 1 km grids were closed.
3.2. The 3Dvar Data Assimilation of WRF
Data assimilation combines observational data with the background forecasting of the mesoscale atmospheric model and their respective error statistics to improve the initial state of the atmosphere. Variational data assimilation is realized by the iterative minimization of specified functions. The initial state of the model is constantly adjusted by iteration, and the difference between forecasting and observation is reduced according to the following calculation correction:
The variational problem can be summarized by solving an analytical variable to make a target functional that measures the distance between the analytical variable and the background. The observation reaches the minimum; this occurs by finding the initial state
X of the model that minimizes
J(
x) (Equation (2)), which comprises the background component
Jb(
x) (Equation (3)) and observation component
Jo(
x) (Equation (4)) [
36], where
Xb is the background field,
B is the background error covariance matrix,
Y0 is the observation vector,
H is the observation operator projecting the model variable from the model space to the observation space through
y =
H(
x) for comparison with the observation results,
R is the observation error covariance matrix,
R =
E +
F,
E is the instrument observation error covariance matrix, and
F is the observation representative error covariance matrix.
The three-dimensional variational data assimilation method takes into account all observed data simultaneously, while ignoring changes over time during the assimilation process; hence, its operation is more efficient than that of the four-dimensional variational data assimilation. Assimilation algorithms in mesoscale numerical atmospheric models vary based on the observational data. For example, the 3Dvar assimilation system can assimilate 19 types of data, including conventional and unconventional observational data. When using the WRF model for precipitation forecasting, the most significant difference between introducing and not introducing data assimilation was whether the background was corrected and close to the real atmospheric state or not. The assimilation data used in this study were high-resolution observational, radar, and conventional meteorological data. The 3Dvar assimilation system processes the radar reflectivity and GTS data differently, primarily during the data preprocessing stage. GTS data assimilation follows a simpler principle than radar data assimilation. The assimilation of GTS data is based on the LITTLE_R format storage, and the ob.ascii file is obtained after running the file using obsproc.exe, and 3Dvar can easily recognize the downloaded GTS data. However, the principles of radar data assimilation are different. Radar reflectivity data are directly output after radar signal processing, and 3Dvar converts the assimilation of the rainwater mixing ratio (
qr) into an assimilation of reflectivity based on the observation operator of the radar reflectivity [
13].
where,
ρ is the air density and
Z is the radar reflectivity. This relation is derived analytically by assuming the Marshall–Palmer distribution of raindrop size. Simultaneously, the pixel-based radar reflectivity is assimilated directly into 3Dvar by stating the latitude and longitude of the pixel center and the height of the radar beam above that pixel.
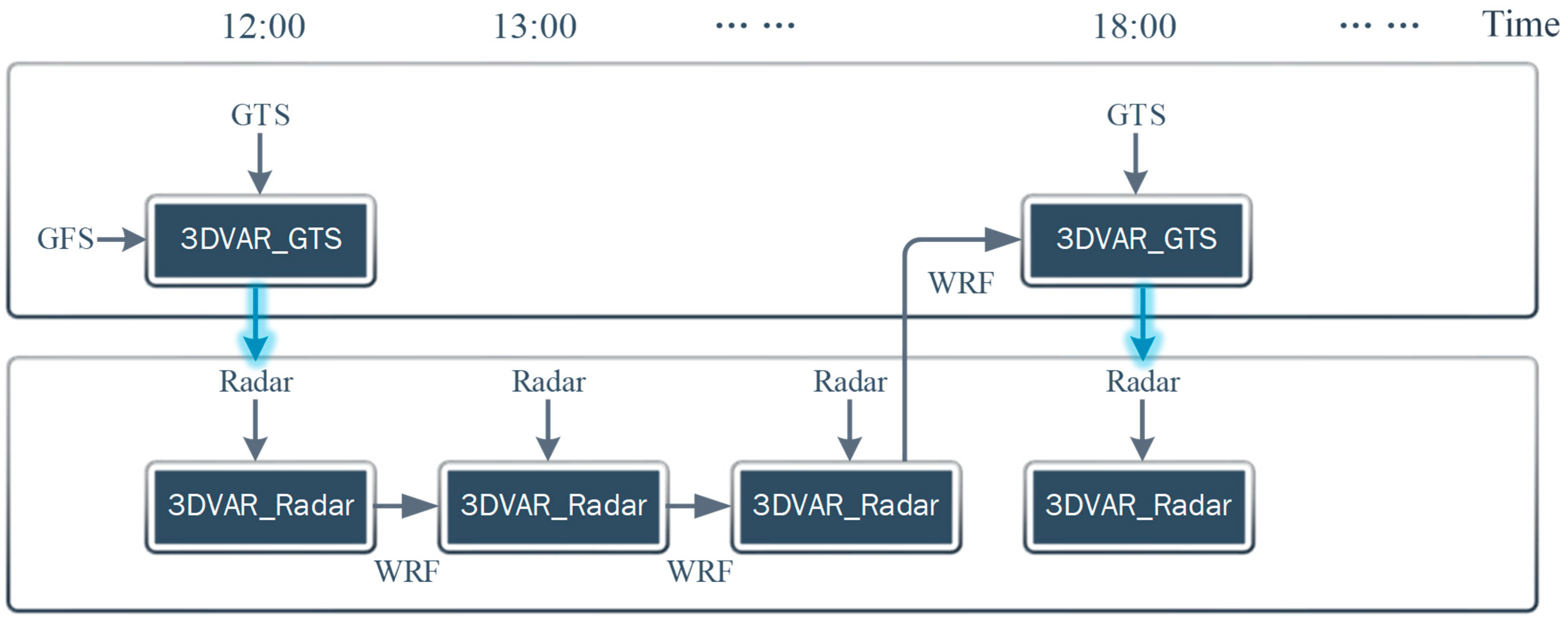
Although weather radar data can provide high-resolution instantaneous precipitation information, their coverage is limited compared to that of the GTS data; thus, they are more suitable for assimilation at small and medium scales. In this study, radar data were only assimilated in Domain 2, as the radar scanning radius used was 250 km, and its coverage area was between the outermost and innermost nested grids, similar to that of Domain 2. GTS data were complementary to the radar data, with wide coverage and low spatial density. Therefore, the GTS data were assimilated into Domain 1. As GTS data were updated every 6 h, in all assimilation schemes, GTS data were assimilated only at 6:00, 12:00, 18:00, and 24:00 after the beginning of precipitation, and radar data were assimilated every hour. Details can be seen in
Figure 4. In this study, CV3, which is the error covariance of the global background constructed by the NCEP, was selected because of its wide applicability and adaptability for numerical atmospheric forecasting in any region.
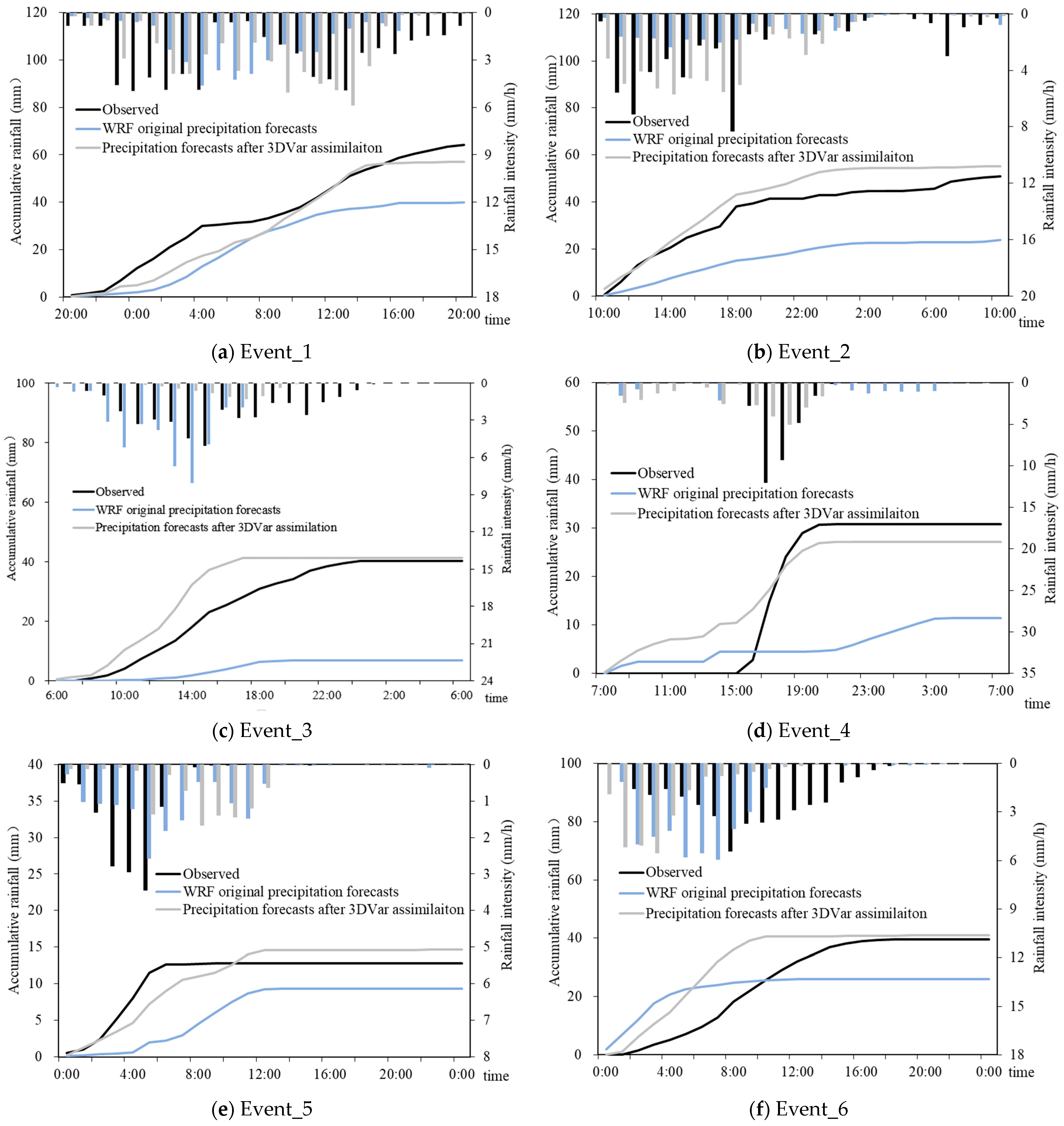
3.6. Evaluation Indicators
The root mean square error (
RMSE), mean bias error (
MBE), and critical success index (
CSI) were used to evaluate the simulated precipitation of the WRF (see Equations (6)–(8)).
RMSE and
MBE are the most widely used error metrics.
RMSE is used to measure the deviation between simulated and observed values. The lower the value of
RMSE, the more reliable the prediction, and
RMSE should be more useful when major errors are particularly undesirable [
43].
MBE represents the average degree of deviation between predicted and actual values, and is a quantitative indicator that can be used to represent the accuracy of the prediction model. After the analysis of the indices,
CSI/
RMSE was used as the comprehensive evaluation index to explore the more intuitive responses of different precipitation types to forecast errors at the temporal and spatial scales.
In Equations (6) and (7), for the spatial dimension,
Qi′ and
Qi denote the observed and forecasted accumulated 24 h rainfall, respectively, at each rain gauge
i.
M is the number of rain gauges, which is 8 for the Fuping catchment and 11 for the Zijingguan catchment. In the temporal dimension,
Qi′ and
Qi are the average areal precipitation of the observation and forecast, respectively, at each time step
i. Time
M was 24, thereby representing the number of time steps. The specific definitions are listed in
Table 7. The meanings of variables are depicted in Equations (6) and (7).
CSI [
44] denotes the percentage of correct simulations between forecast and observations, with 1 indicating a perfect score. The
CSI calculation depends on whether it rains. Because the essence of the WRF model simulation is to solve the equations, it is inevitable that the precipitation calculation result will be close to zero. The
CSI calculation was based on a rain/no rain contingency table (
Table 8).
The classified variables H, R, and S represent whether the forecasted and observed values in a certain observation period or position are greater than 0.01. If both the forecasted and observed values are greater than 0.01, i.e., precipitation is captured in the model, then H + 1; if the forecasted value is greater than 0.01 and the observed value is less than or equal to 0.01, i.e., the model misreports precipitation, then R + 1; if the forecasted value is less than or equal to 0.01 and the observed value is greater than 0.01, i.e., the precipitation is missed in the model, then S + 1. If both the forecasted and observed values are equal to 0.01, the model accurately forecasts a scenario without precipitation.
For the spatial dimension, the forecasted precipitation was compared with observations at rain gauge locations to calculate the indices
H,
R, and
S at time
i. Subsequently, the values of the indices at all times were averaged to obtain the
CSI according to Equation (8).
M is the total number of iterations. In this study, time
i was consistent with the output frequency of the model, which was 1 h. That is,
CSI is the average value of
H/(
H +
R +
S) for each hour of the 24 h precipitation duration. Similarly, for the temporal dimension, the indices in
Table 7 were calculated based on time-series data obtained for the simulated and observed areal precipitation at rain gauge
i. The values of the indices at all rain gauges were then averaged to produce the final
CSI value, based on Equation (8). Here,
M refers to the total number of rain gauges rather than the simulation time.
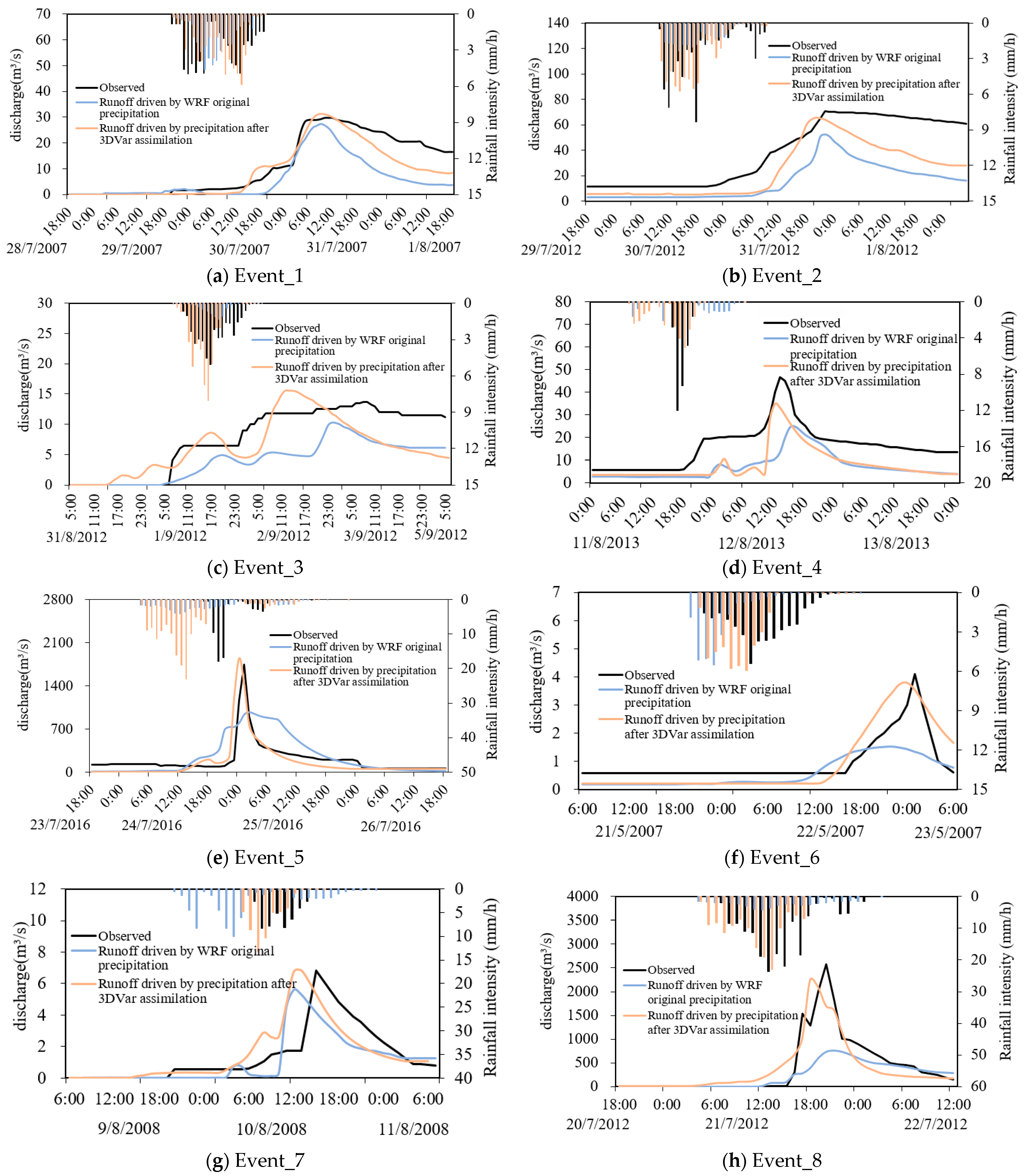
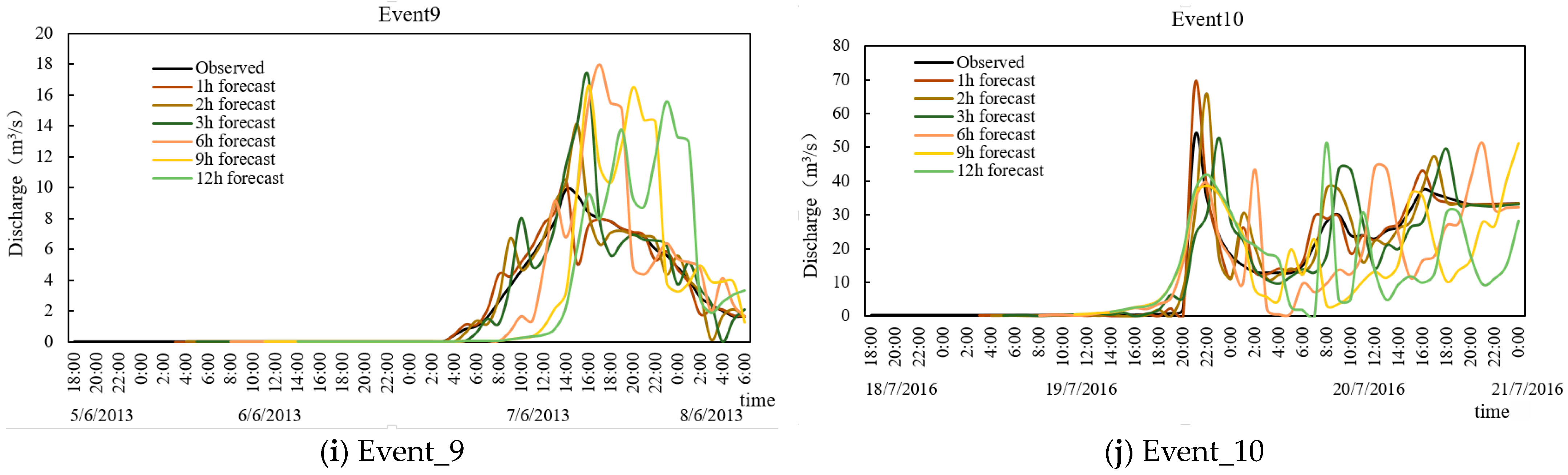
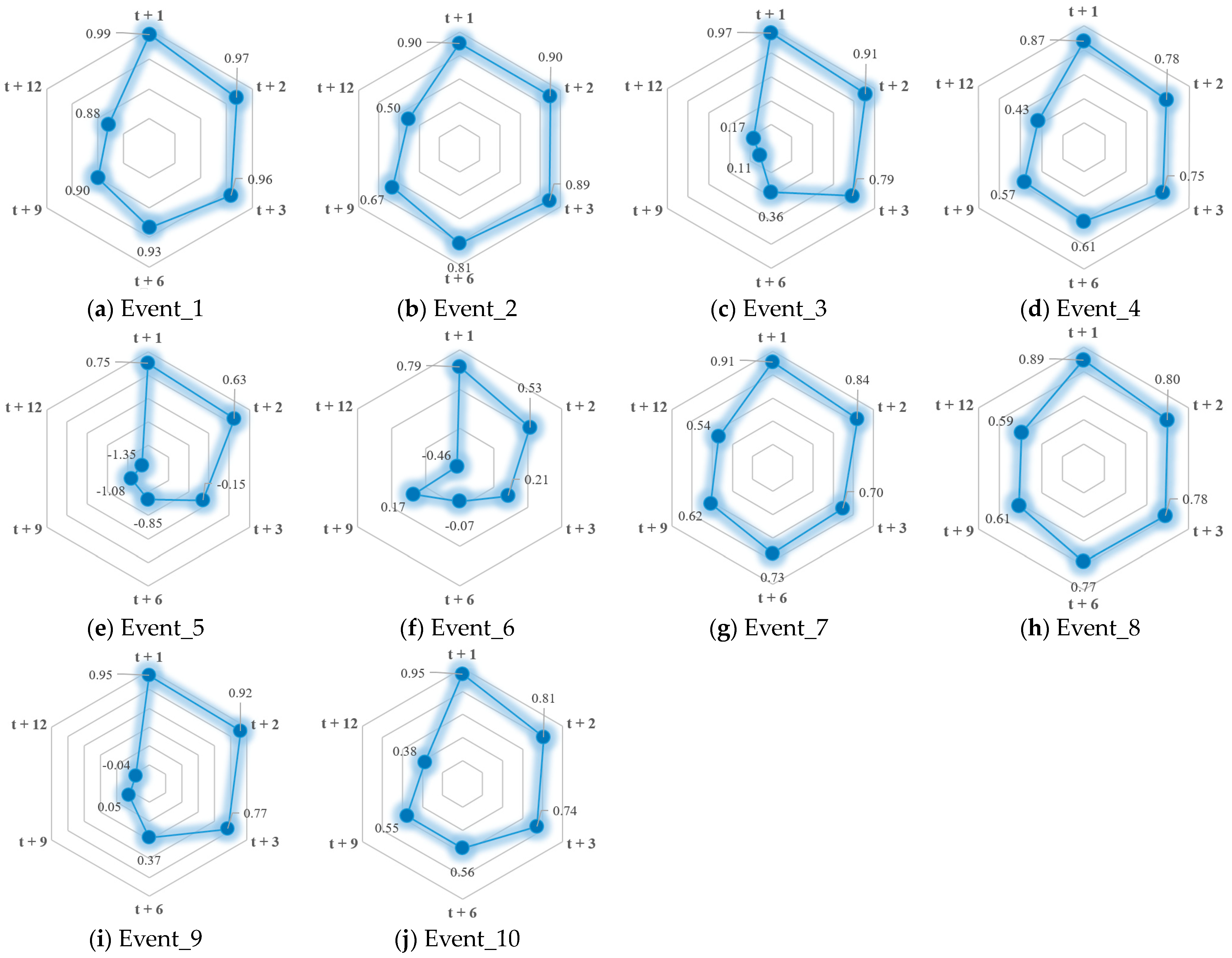
The Nash efficiency coefficient (
NSE), relative error of peak flow (
Rf), relative error of flood volume (
Rv) and absolute error of peak time (
T) were used to evaluate the runoff simulated by the WRF-Hydro model (see Equations (6)–(8)). The
NSE was used to verify the reliability of the hydrological model simulation results.
RMSE was used to measure the deviation between the forecasted and observed values.
Rf is the relative error of the flood peak reflecting the credibility of the simulated flood peak, and
Rv is the relative error of the flood volume reflecting the credibility of the simulated flood volume.
T is the time difference between the actual and forecasted peak times, which was used to represent the error in the peak time forecasting.
where
Ri′ is the runoff forecast value of the
ith hour in the flood process,
Ri is the measured runoff value in the
ith hour during the flood process,
N is the time step,
is the average value of
Ri,
Rf′ is the forecasted value of the peak flow of each flood,
Rf is the measured value of the peak flow of each flood,
Rv′ is the forecasted value of the flood volume of each flood, and
Rv is the measured value of flood volume of each flood.
T1 is the actual peak time;
T2 is the forecast peak time.