Assessment of the Midseason Crop Coefficient for the Evaluation of the Water Demand of Young, Grafted Hazelnut Trees in High-Density Orchards

Abstract

Knowledge of crop water requirements is important in supporting irrigation management. Evapotranspiration (ET) is commonly measured with a variety of instruments and field procedures, but it is also typically computed or modeled using the FAO56 or FAO66 methods. The adoption of this approach requires the assessment of the crop coefficients. Some data are available for own-rooted hazelnut trees, but no data have been reported for young and grafted hazelnut trees. There is a need to update nut–tree crop coefficients, especially considering modern cultivars and production systems, such as those with a high tree density per ha⁻¹. In this paper, the FAO66 crop transpiration coefficient K_c,Tr and the FAO56 dual crop coefficients K_cb were assessed for the mid-growing season of a young grafted hazelnut orchard. The field data were acquired manually and using UAV. The coefficients were determined for three tree densities and for two growing seasons. The crop coefficients, obtained using the FAO66 method, agreed with the literature data referring to low densities, while the FAO56 method could allow us to better define the crop coefficients for high-density hazelnut orchards.

1. Introduction

Water scarcity, in relation to climate change, has become the main barrier to maintaining crop production, especially in Mediterranean areas [1,2,3,4]. Therefore, it is important to develop sensible irrigation strategies to reduce water use while maintaining adequate yields [5]. Many studies on the crop water requirements of vegetables have been produced since the publication of the FAO56 guidelines in 1998 [6] and FAO66 guidelines in 2012 [7] for the yield response to the water of fruit trees and vines. A recent review has shown that the determination of crop evapotranspiration (ET_c), using the crop coefficient K_c—the reference evapotranspiration ET₀ approach—is the most widely used method for irrigation water management [8]. Another recent study reviewed [9] the research on the FAO56 crop coefficients of fruit trees and vines performed over the past twenty years. It showed that many studies have been published for table and wine grapes, oranges, and olives. In addition, a few recent studies have been conducted on almonds (Prunus dulcis Mill. D. A. Webb) [9].

To date, there is a lack of studies on the crop coefficients of hazelnuts (Corylus avellana L.), pecans (Carya illinoinensis L.), pistachios (Pistacia vera L.), and walnuts (Juglans regia L.) and their application in irrigation management. For hazelnut trees, only two recent studies have been identified [10,11]. The first one [10] was conducted on young trees from the “Itarski Dugi” cultivar in a micro-sprinkler orchard (833 plants ha⁻¹) in Serbia. In this work, the soil water balance (SWB) was used to measure the reference evapotranspiration (ET₀). The second [11] was conducted on hazelnut trees from the “Tonda Giffoni” cultivar in a drip-irrigated orchard (333 plants ha⁻¹) in the Maule region in Chile. In this work, the eddy covariance system was used to determine the K_c. Past works used lysimeters to determine the hazelnut coefficients K_c of the cultivar “Negret”, grown in a Spanish orchard with 500 plants ha⁻¹, and of the cultivars “Barcellona” and “Ennis”, which were grown in a French orchard with 416 plants ha⁻¹ [12,13]. However, in the FAO56 [6] tabulated single basal crop coefficients for use with the FAO Penman–Monteith ET₀, K_c values are not reported for hazelnuts, but only for walnuts and pistachios. In addition, all the aforementioned studies were carried out on own-rooted bush-trained hazelnut trees, produced by layering, with a low tree-planting density. Based on our knowledge, until now, no studies have been conducted on hazelnut trees grafted on not-suckering rootstock, such as “Corylus colurna” L., with a single trunk and a vase training system. A recent study showed that grafted plants may access deeper soil water layers in comparison with own-rooted ones and have the potential to more effectively tolerate thermal variations and drought conditions during the vegetative and productive seasons [14]. In light of the above factors, as already stressed by [9], there is a need to update nut trees’ crop coefficients, in particular for hazelnuts, while considering modern cultivars and production systems, especially those with increasing tree density.

The aim of this work was to assess and compare the FAO66 crop transpiration coefficient K_c,Tr, and the FAO56 dual crop coefficients, K_cb, for the mid-growing season of young, grafted hazelnuts from a new, recently patented cultivar (n. EU52157). We make reference to three tree densities, ranging from one that is more common in traditional growing areas (lowest density) to those with many more trees, which are common in modern hazelnut orchards, highly mechanized, and always irrigated [15].

2. Materials and Methods

2.1. Study Site Description and Tree Sampling

The research was carried out in an experimental orchard of the Department of Agricultural, Food, and Environmental Sciences of the University of Perugia, located in Central Italy (42°58′22.82″ N, 12°24′13.02″ E), 161 m a.s.l., during the growing season of 2021 and 2022. The orchard has an area of about 2300 m², and it is composed of 6 rows 4 m away from each other, each containing 43 trees divided into 3 plantation densities as follows:

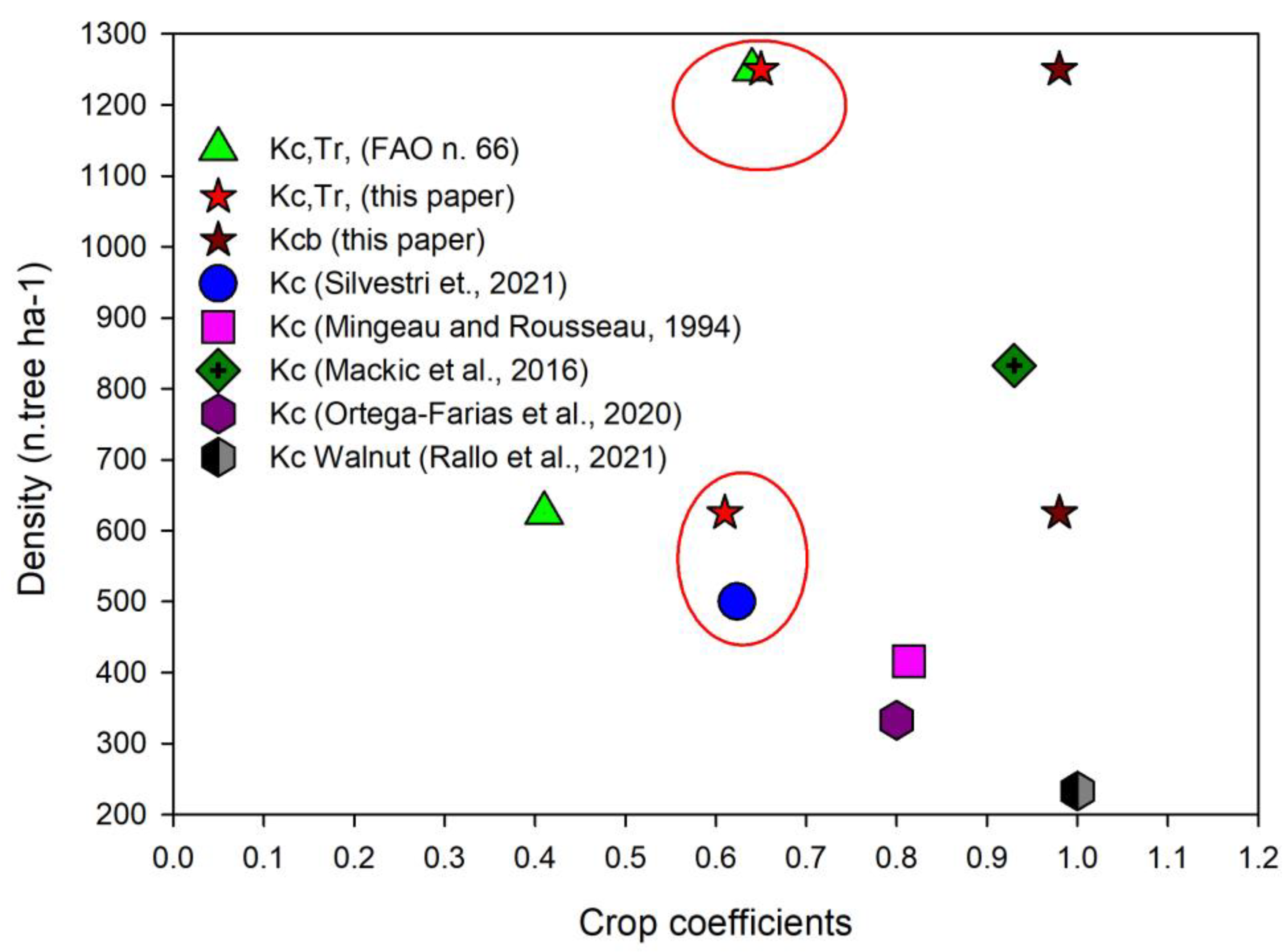
• 625 trees ha⁻¹, spaced 4 m between rows and 4 m on the row, used as a control treatment (the common density used by farmers);
• 1250 trees ha⁻¹, spaced 4 m × 2 m;
• 2500 trees ha⁻¹, spaced 4 m × 1 m.

The tree densities were chosen according to the past literature [12,16]. The low tree density is representative of traditional hazelnut orchards, while the medium and high densities are currently used in the new cultivation areas. Specifically, on the same row, the first 25 plants are spaced 1 m from each other, the next 12 are spaced 2 m apart, and the last 6 are placed 4 m apart. Each tree density is replicated three times, once per row.

All trees, grafted on no-suckering rootstock, were trained as single trunks with four main branches each.

The orchard is made up of trees belonging to two of the main Italian hazelnut cultivars, chosen for their higher productivity and early production: Tonda di Giffoni in the first three rows and Tonda Francescana^® in the next three rows.

In this paper, the trees studied belonged only to the hazelnut cultivar Tonda Francescana^®. The meteorological data were monitored using a Spectrum (Thayer Court, Aurora) WatchDog 2000 Series Weather Station [17] located within the experimental site and were recorded at a time resolution of 5 min.

The DJI (Shenzhen, China) Phantom 4 (P4) multispectral unmanned aerial vehicle UAV was used to assess the tree canopy and ground cover characteristics according to [18,19]. Moreover, the FAO66 procedure described in Section 2.3, calibrated for olives, was used to parametrize the K_c,Tr coefficients for the hazelnut orchard.

2.2. Manual Measurements

The following data were acquired to fill the equations reported in Section 2.3.

In other tree crops, corn (Zea mays L.), cotton (Gossypium arboretum L.), peanuts [20], soybean (Glycine max (L.) Merr.), and wheat (Triticum aestivum L.) LAI was remotely estimated using photogrammetry and UAVs; studies have been performed to extract the LAI [21]. Very few studies have been carried out on tree crops, mainly on vineyards using higher spatial resolution remote sensing. This species is trained with the vertical shoot position trellis system or pergola system with horizontal shoot position [21,22], while hazelnut plant has a unique plant architecture with bush growth habit and dense foliage, three or four main branches, and canopy shape similar to the cylinder; all of this makes it more difficult to implement LAI models using UAV. For these reasons, in the present study, data determined using UAV referred only to canopy characteristics such as tree height.

LAI_plant (the leaf area index, that is, the ratio of the plant leaf area to the canopy cross-sectional area), LAI_orchard (the ratio of the plant leaf area to the tree distance area), and LAD or DAF (the leaf area density) were measured and calculated following the procedure reported by [23] for 9 trees per growing season.

The LAI values were manually measured using an iron bar (2.5 m long, 0.1 m wide, 0.1 m thick) with holes, for a total of 25 measurements, positioned 10 cm apart when a metal rod is inserted at a perpendicular angle; the iron bar is equipped with a level to keep the rods perpendicular to the ground. The iron bar is moved from the trunk to the inter-row by an operator, who inserts the metal rods and counts the leaves at the intersection points on a grid set up in the canopy. Measurements with this instrument were performed in two canopy directions, to the east side and the west side. The mean leaf area per tree density plantation was calculated with SigmaScan Pro5 (Richmond, CA, USA) program [24] by measuring the area of 30 leaves (5 for each tree) collected from the whole canopy.

Moreover, ground cover was obtained as the ratio between the average canopy cross-sectional area and the ground area for each plant, equal to 16 m², 8 m², and 4 m², respectively, from the highest to the lowest tree density plantation. The average canopy cross-sectional areas were calculated as reported by [19].

The radiation intercepted from the tree Q_d was measured manually using a luxmeter; this is a kind of ceptometer but is larger in size, as it consists of metal bars: a fixed one that is planted on the ground and horizontal to it, which is 150 cm long, and another piece of furniture perpendicular to the first, which is 100 cm long. The latter has a support on top to hold a special bar equipped with a photosensitive sensor, which generally consists of a transducer (a photovoltaic cell). When reacting to light intensity, it generates an electric current that is detected by a specific galvanometer equipped with a screen and connected with cables calibrated in lux. The movable bar can therefore slide in different positions along the horizontal bar, from 0 cm (ground) to 50 cm or 100 cm, and it can also be increased in height by means of a screw, from 0 cm (ground) to 100 cm. In this way, the intensity of light is detected at different heights of the plant and is compared with the light measured in full sunlight, revealing the light interception by the tree canopy. This parameter is important because there is a direct relationship between cumulative ET and PAR (photosynthetically active radiation) light interception by the tree canopy; a higher PAR light interception value corresponds to higher ET [25]. To obtain an estimation of the light interception by the whole tree canopy, the canopy light interception is expressed as the mean value of all data recorded at different distances from the trunk and tree heights. A completely randomized design (CRD) is the model used so that each experimental unit has the same chance of receiving any one treatment. For the CRD, any difference among experimental units receiving the same treatment is considered an experimental error.

2.3. Evaluation of the Hazelnut Orchard’s Crop Coefficients Using the FAO66 Method

As assessed by FAO66 [7], the canopy size and stomatal conductance are the two main parameters that determine tree transpiration Tr. Therefore, the models needed to calculate Tr in different orchards, as a function of the size and conductance of the tree canopy, must be specific for each tree species. Orchard ET_c is considered the net irrigation requirement and, in well-managed irrigation systems, is the major component of the irrigation requirements. Orchard ET_c may be calculated using crop coefficients and ET₀, or by estimating its individual components, namely, transpiration and evaporation from the soil.

Orchard or vineyard ET_c may be calculated as the sum of four components [7]:

$${ET}_c=Tr+{Tr}_{CC}+E_{wz}+E_{dz}$$

(1)

where Tr is tree transpiration, Tr_cc is cover crop (or actively growing weed) transpiration, E_wz is the surface evaporation from the soil wetted by the emitters, and E_dz is the surface evaporation from the rest of the soil surface outside the emitter wetting pattern.

Evaluation of Tree Transpiration Tr

Steduto et al. [7] proposed a method to derive the tree transpiration Tr for an orchard, as follows:

$$Tr={ET}_0·K_{c,Tr}$$

(2)

where Tr is the tree transpiration (mm); ET₀ is the reference evapotranspiration (mm); and K_c,Tr is the transpiration coefficient, as follows:

$$K_{c,Tr}={(Q}_d·F1)·F2$$

(3)

F1 depends on tree density, i.e., F1 = 0.66 for tree densities > 250 trees/ha. F2 is the monthly tabulated coefficient; in this case, F2 = 1.25 for June and July, and F2 = 1.20 for August.

The parameter Q_d is the radiation intercepted by the tree (fraction), calculated as follows:

$$Q_d=1-e^{-K_{ext}{V}_u}$$

(4)

with

$$K_{ext}=0.52+0.00079·dp-0.76·e-1.25·DAF$$

(5)

K_ext is the radiation extinction coefficient; dp is the tree density (trees/ha); and DAF is the leaf area density:

$$DAF=2-0.53·(V_u-0.5), (\mathrm{note}:DAF \mathrm{must} \mathrm{be}<2)$$

(6)

with

$$V_u=V_0·\left(\frac{dp}{10000}\right)$$

(7)

where V_u is the canopy volume per unit ground surface (m³/m²), and V₀ is the canopy volume (m³/tree):

$$V_0=\frac{1}{6}·\pi ·D^2·H$$

(8)

where D is the canopy’s average diameter (m), H is the canopy height (m), and e is the exponent equal to 2.718.

The coefficients of Equations (5) and (6) were calibrated and tested for olives in a Mediterranean environment [26,27].

For a preliminary evaluation of the method, Equations (5) and (6) were applied to the hazelnut orchard.

In Equation (7), the canopy volume V₀ was substituted with the volume V_c, evaluated using the procedure described by [18,19]. Briefly, volume V_c was calculated considering the shape of the canopy obtained from the 3D point cloud reconstruction using a UAV survey. From the raster file of the canopy, the volume was obtained in a GIS environment by evaluating the volume between the DSM and a horizontal plane passing through the lowest point of the same. Thus, the evaluation of the canopy volume per unit ground surface $V_u^{\prime }$ (m³/m²) was made by substituting Equation (7) with the following formula:

$$V_u^{\prime }=V_c·\frac{dp}{10000}$$

(9)

The tree density, dp, was set to be equal to 625 trees/ha, 1250 trees/ha, and 2500 trees/ha.

The leaf area density, DAF_FAO, was evaluated using Equation (6) with $V_u^{\prime }$:

$${DAF}_{FAO}=2-0.53·(V_u^{\prime }-0.5)$$

(10)

The DAF_FAO was used for Equation (5), and by applying Equations (3) and (4), the $K_{c,Tr}$ was obtained.

As described above, the coefficients of Equations (5) and (6) were derived for the olive orchards. Using manual measurements of the leaf area density for each tree density and for the whole growing season (reported later), the coefficients of Equation (6) were derived. Therefore, manual measurements of the radiation intercepted by the tree, Q_d,m, were available. Thus, these were used in two ways:

• To calculate the $K_{c,Tr}$ using Equation (3);
• To derive the values of the product $\left(K_{ext}·V_u^{\prime }\right)$ from Equation (4). Substituting the $V_u^{\prime }$ values, obtained from Equation (9), the radiation extinction coefficients $K_{ext}$ were evaluated, and the coefficients of Equation (5) were determined for the hazelnut orchard.

Student’s t-test was conducted to evaluate the significant differences between results obtained for the different plant densities.

2.4. Estimation of the Hazelnut Orchard’s Crop Coefficients from the Fraction of Ground Cover and Height (Allen and Pereira [16])

The FAO56 procedure for the estimation of the dual crop coefficient K_cb shows that it is largely affected by the fraction of the soil surface covered by vegetation. Recently, Allen and Pereira [6,15] suggested using a density coefficient K_d as function of tree heights. Focusing on orchards, Allen et al. [28] and Allen and Pereira [15] combined the influence of crop density with standardized values for K_{cb full}, K_cmin, and K_{cb cover} to compute a K_cb value for orchards for both bare soil and active ground cover. This modification provided flexibility in adjusting the value for K_c and K_cb according to the fraction of ground shaded by canopy, which is highly variable between orchards [29].

The single K_c approach is not the most appropriate procedure for estimating crop ET for conditions with variable wetting of the soil surface, particularly when the ground cover is minimal. Changes in soil surface wetness are influenced by the frequency and duration of rainfall and irrigation events, as well as by the type of irrigation system or strategy employed, and these cannot be entirely accounted for using canopy cover estimates. This is particularly noticeable under the conditions of partial canopy cover, when soil evaporation (Es) is expected to be a considerable component of ET because increased energy reaches the soil’s surface. Due to this limitation, a dual K_c approach was developed to estimate crop ET_c, which splits the K_c into a T (K_cb) component and an Es (K_e) component [6]:

$${ET}_c=(K_{cb}+K_e)·{ET}_0$$

(11)

The basal crop coefficient K_cb is defined as the ratio of the crop evapotranspiration over the reference evapotranspiration (ET_c/ET₀) when the soil surface is dry, but transpiration is occurring at a potential rate, i.e., water is not limiting transpiration. Therefore, ‘K_cb · ET₀’ primarily represents the transpiration component of ET_c.

The basal K_cb is correlated with the amount of vegetation because it mostly represents transpiration. It can be expressed in terms of a density coefficient K_d, where [15]

$$K_{cb}=K_{cmin}+K_d·(K_{cbfull}-K_{cmin})$$

(12)

where K_cb is the approximation for conditions represented by the density coefficient K_d, K_{cb full} is the estimated basal K_c during peak plant growth under the condition of nearly full ground cover (or LAI > 3), and K_{c min} is the minimum basal K_c for bare soil (K_{c min} = 0.05 for orchards [30]). The coefficient K_{cb full} represents a general upper limit for tall vegetation with full ground cover and LAI > 3 under a full water supply; K_{cb full}, for use with ET₀, can be approximated as a function of the mean plant height and adjusted for climate following [6]:

$$K_{cbfull}=F_r·(\min \left(1.0+k_h·h,1.20\right)+[0.04·\left(u_2-2\right)-0.004·\left({RH}_{min}-45\right)]·{\left(\frac{h}{3}\right)}^{0.3})$$

(13)

where h is the mean maximum plant height (m), u₂ is the mean value for wind speed at the height of 2 m during the midseason (m/s), RH_min is the mean value for the minimum daily relative humidity during the midseason (%), and F_r is an adjustment factor relative to crop stomatal control, described below. As assessed by Pereira et al. [31], the effects of crop height are considered through the sum $(1.0+k_h·h)$, with k_h = 0.1 for tree crops.

For trees and vines, the parameter F_r is high when crops exhibit significant vegetative vigor and decreases with pruning and training, as well as with limited water supplies [29]. Adopting the definition in [6] for F_r, considering the variability of leaf resistance between annual and perennial crops, it is assumed that

$$F_r=\frac{∆+\gamma (1+0.34u_2)}{∆+\gamma (1+0.34u_2\frac{r_l}{r_{typ}})}$$

(14)

where r_l and r_typ are, respectively, the mean leaf resistance and the typical leaf resistance [s m⁻¹] for the vegetation in question, Δ is the slope of the saturation vapor pressure vs. the air temperature curve [kPa °C⁻¹], and γ is the psychrometric constant, kPa °C⁻¹, both relative to the period when K_{cb full} is computed. The original F_r was developed to empirically consider the effects of stomatal adjustment on K_{cb full} and, therefore, on K_cb, in response to water stress [6], since stomatal closure causes a decrease in transpiration and thus decreases K_cb and K_c. The stomatal adjustment process is well known for annual crops, while, for fruit trees, as for hazelnut orchards, it was less well known or unknown. Thus, the effect of the stomatal adjustment processes on transpiration could be characterized by the empirical adjustment of F_r. Some default F_r values were indicated by [15] for tree and vine crops.

The density coefficient K_d can be estimated as a function of the measured leaf area index, LAI [m² m⁻²], defined as the area of leaves per area of ground surface averaged over a large area:

$$K_d=(1-e^{\left[-0.7·LAI\right]})$$

(15)

As described by [13], where estimates of the fraction of the ground surface covered by vegetation, f_c, are available, the density coefficient K_d can be estimated as follows:

$$K_d=\mathrm{m}\mathrm{i}\mathrm{n}(1,M_L{f}_{ceff},{f_{ceff}}^{\left(\frac{1}{1+h}\right)})$$

(16)

where f_{c eff} is the effective fraction of ground covered or shaded by vegetation [0.01–1] near solar noon, M_L is a multiplier of f_{c eff} that describes the effect of the canopy density on shading and on the maximum relative ET per fraction of ground shaded [1.0–2.0], and h is the mean vegetation height (m). Thus, using the K_d values obtained from Equation (15) and the measurement data of f_{c eff} and h, the M_L coefficient was estimated.

3. Results

3.1. Application of the FAO66 Method

Using the measurements of the canopy’s average diameter D, the canopy height H, and the canopy volume obtained from the UAV survey [18,19], $V_u^{\prime }$, the equations from (3) to (6) were applied to the hazelnut orchard for each plant density (Figure S1). The mean value for the midseason (June, July, and August) of the coefficients $K_{c,Tr}$, evaluated using the coefficients tested for olive orchards [7] are reported in the first row of

Table 1. Values of the $K_{c,Tr}$ coefficients derived from the FAO66 method [7] and using the coefficients derived from the hazelnut orchard.

	625 Trees/ha	1250 Trees/ha	2500 Trees/ha
Equations (3)–(8)	0.41 c	0.64 a	0.61 b
Equations (3), (4), (17) and (18)	0.61 b	0.65 ab	0.74 a

Note: In each row, means followed by different letters are significantly different, with p < 0.05.

. The resulting coefficients were significantly different for all the densities; in fact, Student’s t-test showed that the means were significantly different (α = 0.05).

For a tree density of 625 trees/ha, the values of DAF_FAO were always higher than 2, and Equation (6) was set for DAF values lower than 2; as such, an adjustment of the coefficients of Equation (6) seems to be necessary. Using manual measurements of the leaf area density DAF_m for each tree density, as reported in

Table 2. Values of the manual measurements of leaf area density DAF_m, the intercepted radiation Q_d, and the ground fraction cover f_c.

	DAFm	Qd	fc
625 trees/ha	1.56	0.535	0.74
	2.54	0.635
	2.78	0.837
	2.66	0.835
	2.49	0.856
	2.38	0.799
	1.60	0.882
	2.47	0.856
	5.63	0.768
	3.99	0.644
	4.56	0.535
1250 trees/ha	3.13	0.863	0.795
	1.47	0.828
	1.48	0.714
	1.96	0.856
	2.35	0.737
	1.80	0.844
	2.40	0.934
	2.41	0.806
	5.89	0.532
	3.26	0.889
	7.01	0.748
2500 trees/ha	4.50	0.829	0.895
	6.41	0.858
	2.58	0.895
	4.48	0.902
	5.06	0.885
	3.51	0.912
	2.81	0.920
	4.26	0.943
	3.85	0.936
	4.09	0.935
	4.53	0.897
	3.62	0.824

, and for the whole mid-growing season, the coefficients of Equation (6) were derived:

$${DAF}_m=1.79+2.83·V_u^{\prime }$$

(17)

therefore, as described above, the manual measurements of the radiation intercepted by the tree, Q_d,m, were available (Figure S2). Therefore, Equation (5) could be modified for the evaluation of the radiation extinction coefficient, K_ext, as follows:

$$K_{ext}^{\prime }=0.385+0.0047·dp+4.67·e-0.909·DAF$$

(18)

where dp is the tree density (trees/ha), DAF is the leaf area density, and e is equal to 2.718.

From the application of Equations (3), (4), (17) and (18), the coefficients $K_{c,Tr}$ were evaluated and are reported in the second row of Table 1.

The coefficients were significantly different only between the densities of 625 trees/ha and 2500 trees/ha and between the densities of 1250 trees/ha and 2500 trees/ha, since Student’s t-test showed that the mean was significantly different from 0 (α = 0.05).

3.2. Application of the Allen and Pereira Method [15]

The procedure detailed in [15] was used to derive the K_cb. Equation (14) was not applicable because the value of the mean leaf resistance (r_l) is not available in the literature for hazelnut orchards. Due to these missing data, in this study, assuming a similarity in the water sensibility behaviors of hazelnut and walnut orchards [32], the F_r value of walnuts reported in Table 2 of [15] was used (F_r = 0.90). The values of the mean tree height measured using the UAV surveys [18,19] were used for the evaluation of K_{cb full} using Equation (13). The density coefficient K_d was calculated using the measurements of LAI conducted during the midseason and applied to Equation (15) (Figure S3). Thus, Equation (12) was used to estimate the values of K_cb, with K_{c min} = 0.05 [31]. The values obtained for the three tree densities (625 trees/ha, 1250 trees/ha, and 2500 trees/ha) are reported in

Table 3. Values of the coefficients $K_{cb}$ derived from the application of the Allen and Pereira [13] method ($K_{cb}$ A&P).

	625 trees/ha	1250 trees/ha	2500 trees/ha
Equation (13)	0.98 b	0.98 b	1.04 a

Note: Means followed by different letters are significantly different for p < 0.05.

.

From the values of the density coefficients K_d, calculated using Equation (15), Equation (16) was inverted to estimate the M_L coefficient as described by [8]. In particular, the f_{c eff} values were obtained from the following equation:

$$f_{ceff}=\frac{f_c}{\mathrm{s}\mathrm{i}\mathrm{n}\left(\beta \right)}$$

(19)

where β is the mean angle of the sun above the horizon during the period of maximum ET, evaluated using the procedure described by [6]; f_c is the fraction of the surface covered by the vegetation, measured from the UAV surveys, described in Vinci et al. [18,19]. The coefficients were significantly different only between the densities 625 trees/ha and 2500 trees/ha and between the densities 1250 trees/ha and 2500 trees/ha, since Student’s t-test showed that the mean was significantly different from 0 (α = 0.05).

The values of M_L obtained were M_L = 1.17 for 625 trees/ha, M_L = 1.09 for 1250 trees/ha, and M_L = 1.01 for 2500 trees/ha.

4. Discussion

Pereira et al. [8] suggest that the selection of F_r and M_L values is performed through a numerical search for the values of the parameters that make K_cb match the tabulated K_cb TAB values. However, as noted by Rallo et al. [9], studies for hazelnut trees are lacking, and K_cb tabulated values are not available for hazelnut orchards. The values of f_c measured and used for the analysis were in accordance with the values of f_c reported for walnut by [8], and for these values, the K_{c mid} was around 1 (Figure 1).

Figure 1 shows the crop coefficients reported for hazelnuts and for walnuts in the literature and those determined in this research, for several tree densities. The highest tree density of 2500 trees ha⁻¹, used in this study, was not reported in Figure 1 since it has never been used by farmers, and no data are available.

The K_c,Tr determined in this research for 625 trees ha⁻¹ density was similar to that reported by Silvestri et al. [12] for 500 trees ha⁻¹ for own-rooted young hazelnuts. On the other hand, it was higher than that suggested by FAO66 [7]; this may be because the K_c used was calibrated and tested for olives. In fact, olive trees are an evergreen and resilient species that are well adapted to the Mediterranean environment [26,27,33]; meanwhile, hazelnut is sensitive to water stress and prefers cooler and more humid environmental conditions [34,35]. However, for the medium density (1250 trees ha⁻¹), the K_c,Tr determined for hazelnut in this research was very similar to that of FAO66 [7]. This could be related to the species-specific physiological responses under changing light absorption conditions and nutrient availability. The values of the coefficients K_cb determined in this study by using the Allen and Pereira method [6] resulted in the highest values among those reported in the literature for hazelnuts (Figure 1). We suppose that, in applying this method, we overestimated the K_cb values for hazelnuts, with values very similar to those reported for walnuts (Figure 1).

Allen and Pereira [6] suggested a relationship between K_c and plant height in connection with the net radiation increment. However, we did not find any differences between the K_cb values of the two plant densities shown in Figure 1. This could be due to the specific training shape of hazelnut trees, which have four branches and no single axis. Therefore, the hazelnut tree’s height does not reflect the actual tree shape and canopy volume, especially in young trees. On the other hand, the K_c,Tr determined in this research for both crop densities was lower than the values reported in the literature for hazelnuts (Figure 1). The higher K_c values reported by Mačkić et al. [10] were probably due to the higher planting density and the specific orchard irrigation method. The higher K_c values reported by Mingeau and Rousseau [13] and by Ortega-Farias et al. [11] could be related to the specific orchard characteristics and management practices.

However, since the K_c,Tr determined in this research for grafted plants turned out to be lower (0.61–0.65), albeit with a higher planting density, than those reported in the literature for own-rooted plants (Figure 1), we cannot overlook the effect of grafting on hazelnut crop coefficients. In fact, as reported by Portarena et al. [14], the deeper root systems of grafted plants compared with own-rooted plants lead to differences in the depth of the root water uptake and in physiological functioning at the whole-plant level. It is likely that grafted hazelnut trees also have better radiation interception with a lower LAI (Figure S3) compared to those recorded for own-rooted trees of the same age by other authors [36]. All these factors reflect the stomatal control capacity of trees and the entire orchard’s water requirements, improving orchard sustainability.

5. Conclusions

For the first time for grafted hazelnut trees on non-suckering rootstock, K_cmid has been assessed for the evaluation of the water demand of young hazelnut trees in a high-density orchard.

The values of the density coefficient K_d did not differ among the three tested densities, a result that conflicted with the method of Allen and Pereira (2009), who suggested a relationship between K_d and the tree height. Moreover, the K_cb estimated in our grafted orchard was lower than the values reported in the literature for own-rooted hazelnuts. These lower values could be primarily related to the specific local environmental conditions, the cultivar, and the orchard management system, including the grafting practices employed.

Further studies are needed to determine the K_cb for grafted adult hazelnut trees. Against this background, further research will be conducted to evaluate the K_{c ini} and K_{c end} values of grafted hazelnut trees in order to schedule a well-planned and efficient irrigation practice based on the orchard’s water requirements.