Application of Optimization Techniques for Searching Optimal Reservoir Rule Curves: A Review
Abstract
:1. Introduction
2. Reservoir Simulation Models
3. Optimization Techniques for Reservoir Rule Curve Extraction
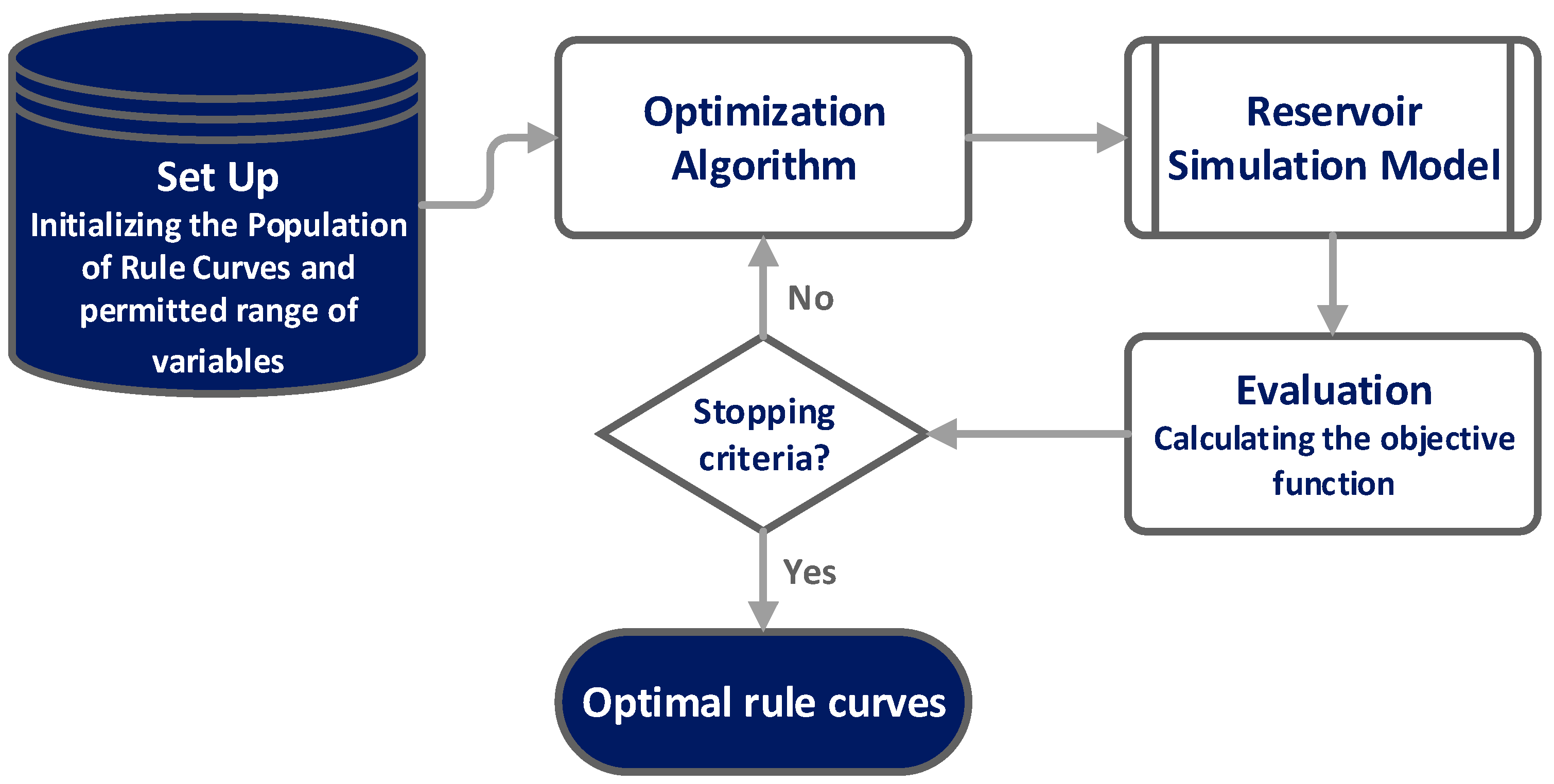
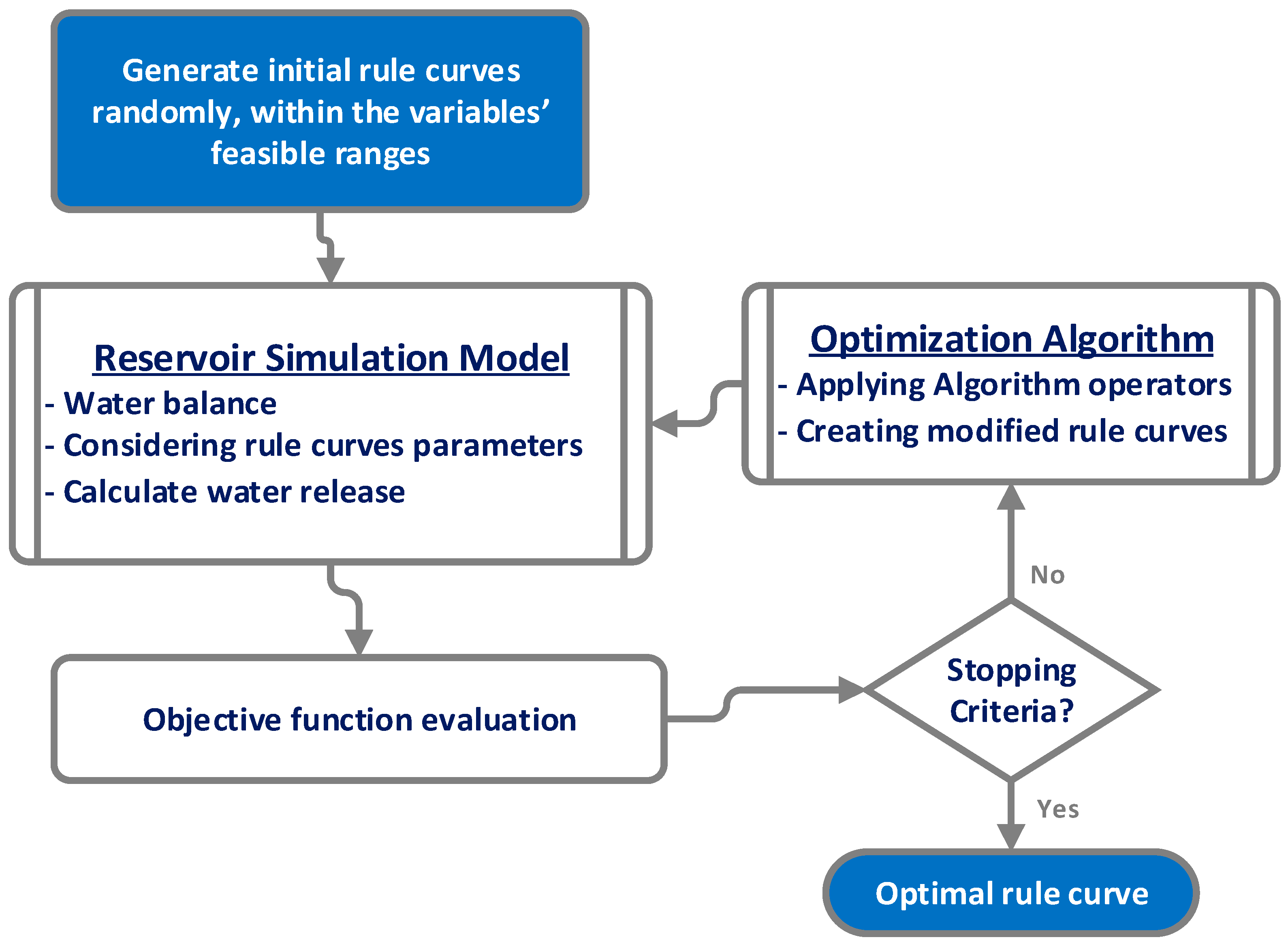
3.1. Integrating Optimization Techniques and the Reservoir Simulation Model
3.2. Objective Function of the Search Process
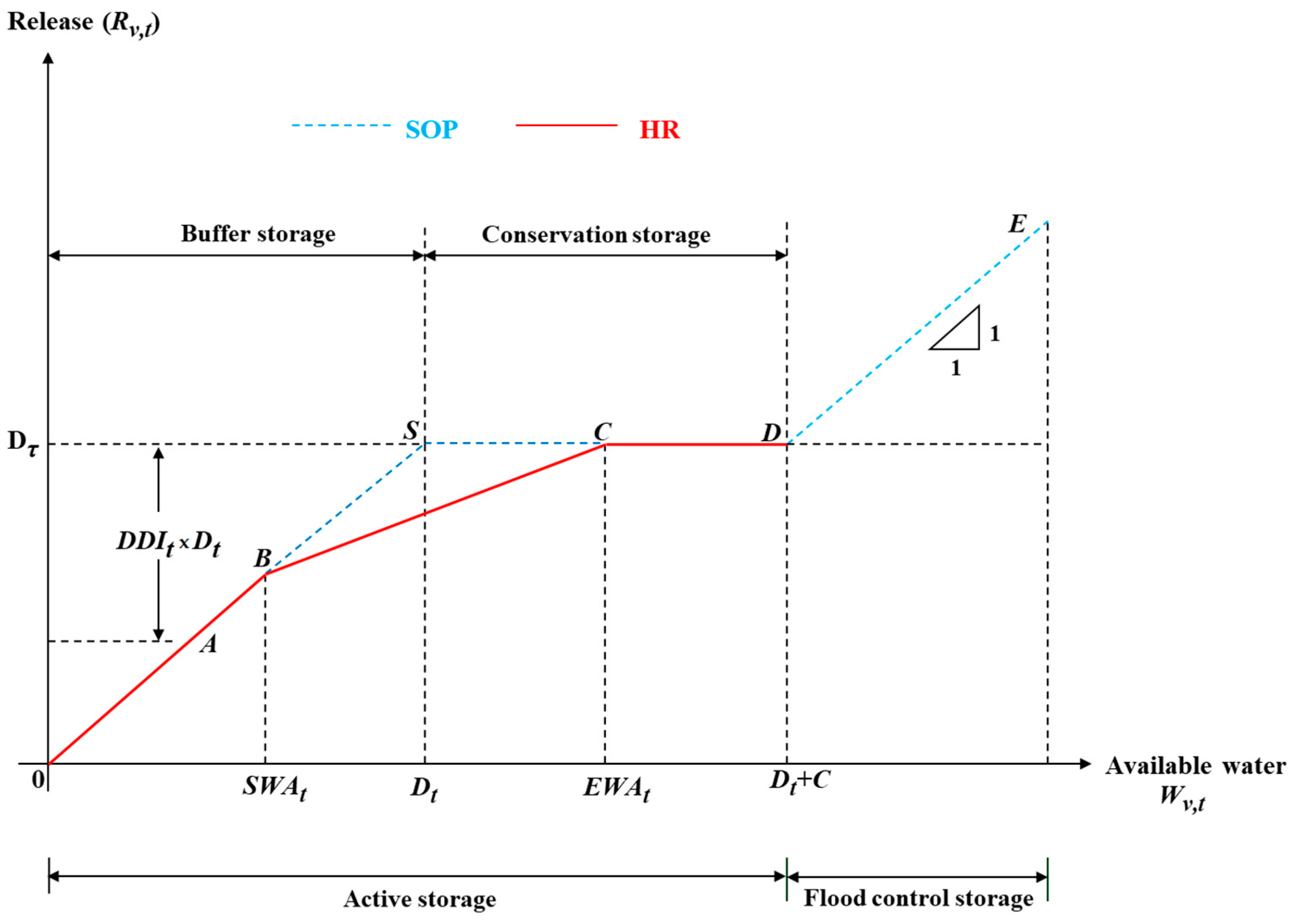
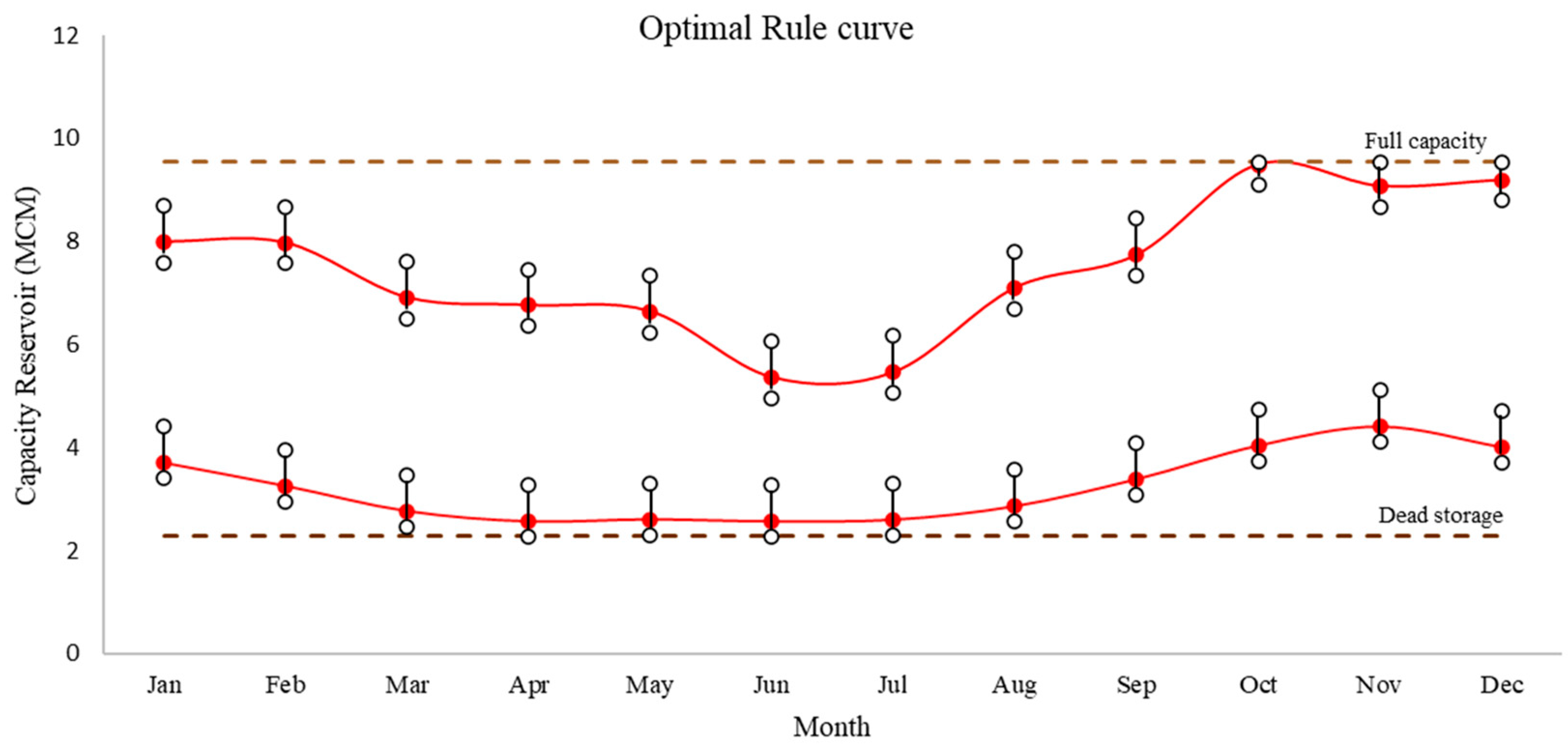
3.3. Optimizing the Points of the Rule Curves
4. Typically Applied Optimization Techniques
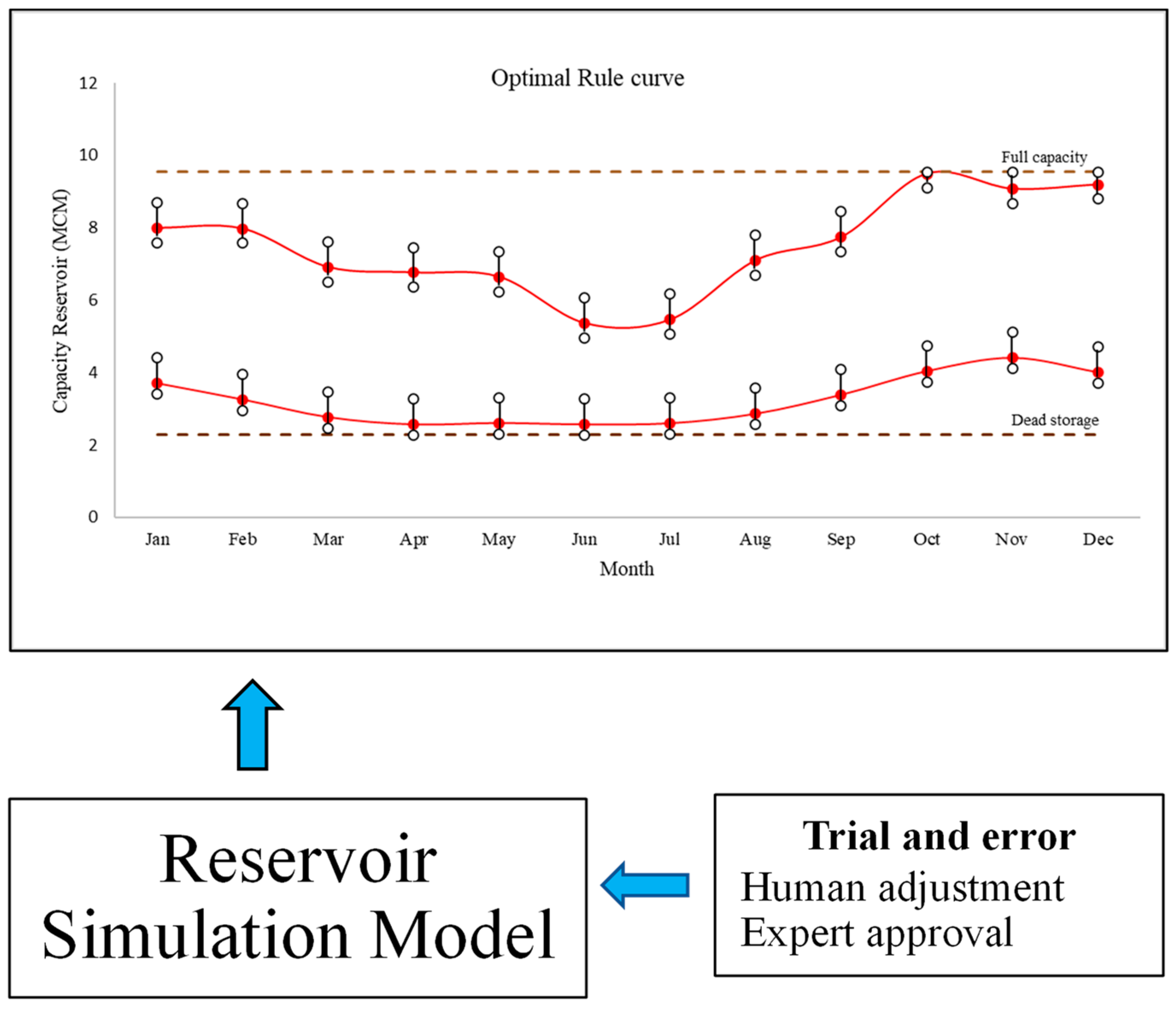
4.1. Trial and Error Technique with the Reservoir Simulation Model
4.2. Dynamic Programming
4.3. Heuristic and Metaheuristic Algorithms
4.3.1. Simulated Annealing Algorithm
4.3.2. The Shuffled Frog Leaping Algorithm
4.4. Evolutionary Algorithms
4.4.1. Genetic Algorithm
4.4.2. Differential Evolution
4.4.3. Genetic Programing
4.4.4. Cultural Algorithms
4.5. Swarm Algorithms
4.5.1. Particle Swam Optimization
4.5.2. Cuckoo Search
4.5.3. Tabu Search Algorithm
4.5.4. Firefly Algorithm
4.5.5. Flower Pollination Algorithm
4.5.6. Gray Wolf Optimizer
4.5.7. Wind-Driven Optimization
4.5.8. Ant Colony Optimization
4.5.9. Honey-Bee Mating Optimization
5. Suitable Future Rule Curves
5.1. Climate Change
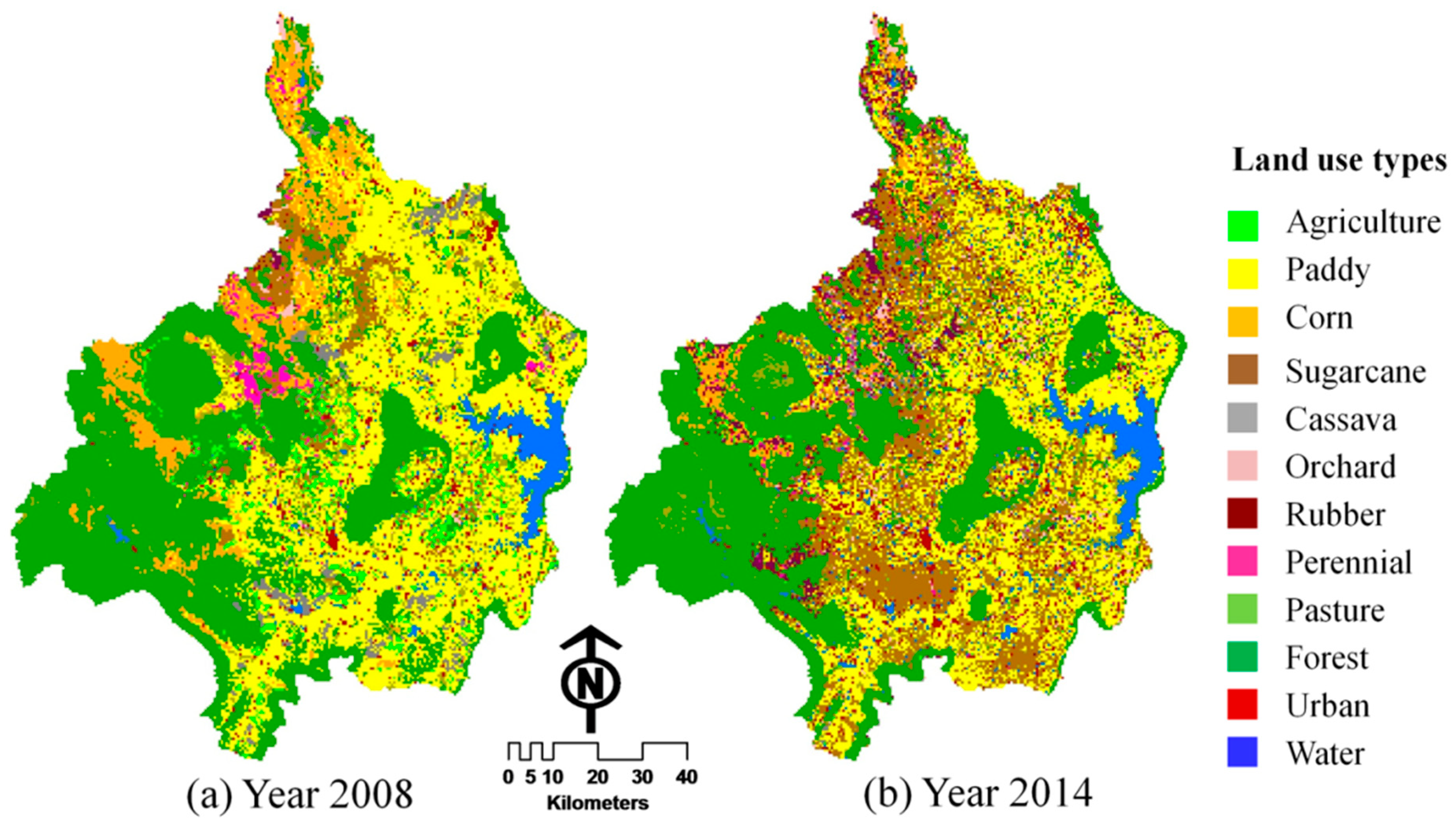
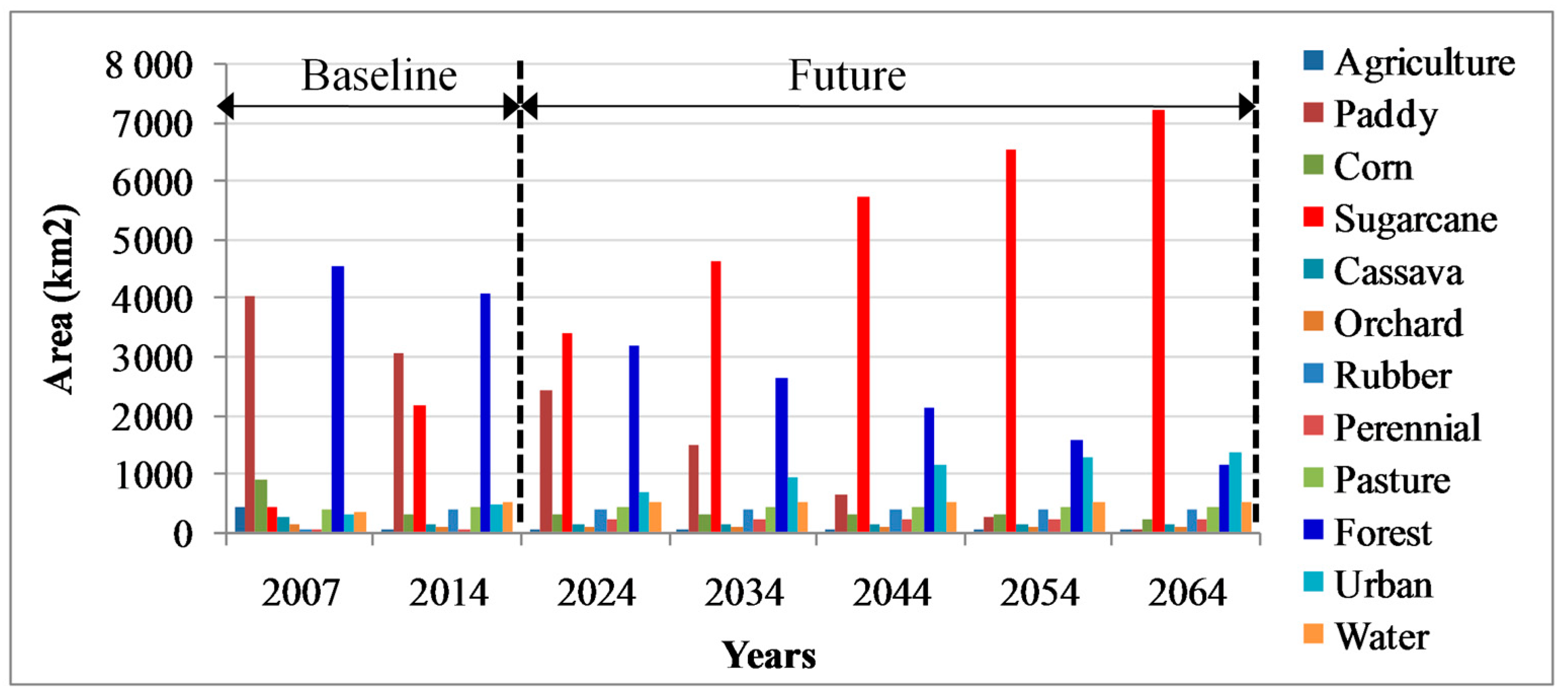
5.2. Land Use Changes
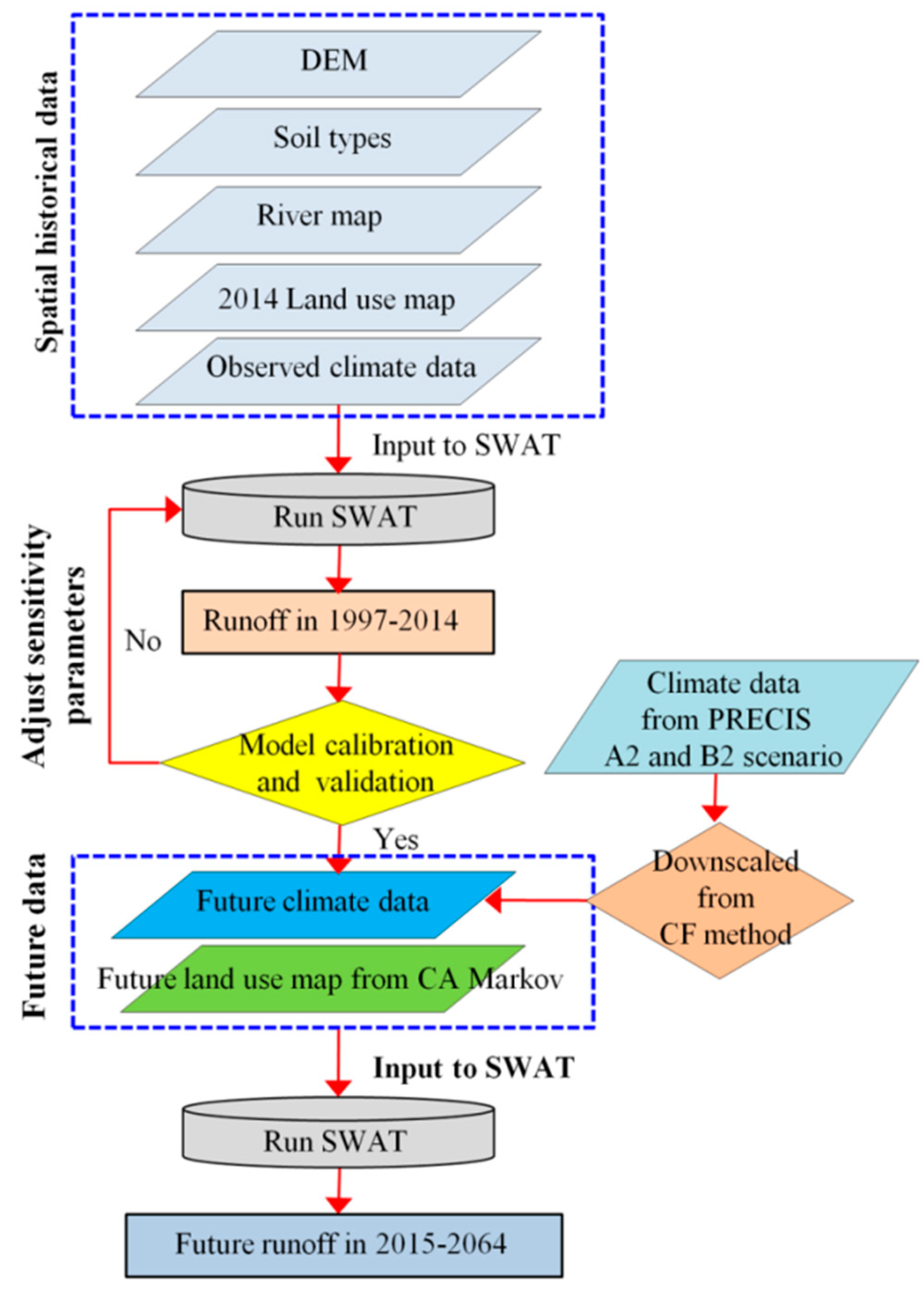
5.3. SWAT Model
5.4. Participation of Stakeholders
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shrestha, S. Assessment of Water Availability Under Climate Change Scenarios in Thailand. In Climate Change Impacts and Adaptation in Water Resources and Water Use Sectors; Springer Water; Springer: Cham, Switzerland, 2014; pp. 9–23. [Google Scholar] [CrossRef]
- Chen, J.; Shi, H.Y.; Sivakumar, B.; Peart, M.R. Population, water, food, energy and dams. Renew. Sust. Energ. Rev. 2016, 56, 18–28. [Google Scholar] [CrossRef]
- Shi, H.Y.; Li, T.J.; Wang, K.; Zhang, A.; Wang, G.Q.; Fu, X.D. Physically based simulation of the streamflow decrease caused by sediment-trapping dams in the middle Yellow River. Hydrol. Process. 2016, 30, 783–794. [Google Scholar] [CrossRef]
- Ashrafi, S.M. Two-stage metaheuristic mixed integer nonlinear programming approach to extract optimum hedging rules for multireservoir systems. J. Water Resour. Plan. Manag. 2021, 147, 04021070. [Google Scholar] [CrossRef]
- Beshavard, M.; Adib, A.; Ashrafi, S.M.; Kisi, O. Establishing effective warning storage to derive optimal reservoir operation policy based on the drought condition. Agric. Water Manag. 2022, 274, 107948. [Google Scholar] [CrossRef]
- EGAT (Electricity Generating Authority of Thailand). Manual for Operating the Bhumibol and Sirikit Reservoirs; EGAT Research Report; EGAT: Bangkok, Thailand, 2004. (In Thai) [Google Scholar]
- Georgakakos, A.P.; Yao, H.; Kistenmacher, M.; Georgakakos, K.P.; Graham, N.E.; Cheng, F.Y.; Spencer, C.; Shamir, E. Value of adaptive water resources management in Northern California under climatic variability and change: Reservoir management. J. Hydrol. 2012, 412–413, 34–46. [Google Scholar] [CrossRef]
- Thongwan, T.; Kangrang, A.; Prasanchum, H. Multi-objective future rule curves using conditional tabu search algorithm and conditional genetic algorithm for reservoir operation. Heliyon 2019, 5, e02401. [Google Scholar] [CrossRef]
- Kangrang, A.; Prasanchum, H.; Hormwichian, R. Active future rule curves for multi-purpose reservoir operation on the impact of climate and land use changes. J. Hydrol. Environ. Res. 2019, 24, 1–13. [Google Scholar] [CrossRef]
- Agramont Akiyama, A.; Peres-Cajías, G.; Villafuerte Philippsborn, L.; Van Cauwenbergh, N.; Craps, M.; van Griensven, A. Framing Water Policies: A Transdisciplinary Study of Collaborative Governance; the Katari River Basin (Bolivia). Water 2022, 14, 3750. [Google Scholar] [CrossRef]
- Mostaghimzadeh, E.; Ashrafi, S.M.; Adib, A.; Geem, Z.W. Investigation of Forecast Accuracy and its Impact on the Efficiency of Data-Driven Forecast-Based Reservoir Operating Rules. Water 2021, 13, 2737. [Google Scholar] [CrossRef]
- Jin, Y.; Lee, S.; Kang, T.; Kim, Y. A Dynamically Dimensioned Search Allowing a Flexible Search Range and Its Application to Optimize Discrete Hedging Rule Curves. Water 2022, 14, 3633. [Google Scholar] [CrossRef]
- Fang, H.B.; Hu, T.S.; Zeng, X.; Wu, F.Y. Simulation-optimization model of reservoir operation based on the target storage curves. Water Sci. Eng. 2014, 7, 433–445. [Google Scholar]
- Sullis, A. An optimisation model for reservoir operation. P. I. Civil Eng-Wat. M. 2017, 170, 175–183. [Google Scholar] [CrossRef]
- Tavoosi, N.; Hooshyaripor, F.; Noori, R.; Farokhnia, A.; Maghrebi, M.; Kløve, B.; Haghighi, A.T. Experimental-numerical simulation of soluble formations in reservoirs. Adv. Water Resour. 2022, 160, 104109. [Google Scholar] [CrossRef]
- Zhao, T.; Zhao, J. Optimizing operation of water supply reservoir: The role of constraints. Math. Probl. Eng. 2014, 2014, 853186. [Google Scholar] [CrossRef]
- Tayebiyan, A.; Mohammad, T.A.; Al-Ansari, N.; Malakootian, M. Comparison of optimal hedging policies for hydropower reservoir system operation. Water 2019, 11, 121. [Google Scholar] [CrossRef]
- Tayebiyan, A.; Mohammed Ali, T.A.; Ghazali, A.H.; Malek, M.A. Optimization of exclusive release policies for hydropower reservoir operation by using genetic algorithm. Water. Resour. Manag. 2016, 30, 1203–1216. [Google Scholar] [CrossRef]
- Thiha, S.; Shamseldin, A.Y.; Melville, B.W. Improving the summer power generation of a hydropower reservoir using the modified multi-step ahead time-varying hedging rule. Water. Resour. Manag. 2022, 36, 853–873. [Google Scholar] [CrossRef]
- Ngamsert, R.; Kangrang, A. Applying of marine predators algorithm linked with reservoir simulation model considering sedimentation for reservoir operation. Adv. Civ. Eng. 2022, 2022, 1631914. [Google Scholar] [CrossRef]
- Techarungruengsakul, R.; Kangrang, A. Application of Harris Hawks Optimization with Reservoir Simulation Model Considering Hedging Rule for Network Reservoir System. Sustainability 2022, 14, 4913. [Google Scholar] [CrossRef]
- Kangrang, A.; Chaleeraktrakoon, C. Genetic algorithms connected simulation with smoothing function for searching rule curves. Am. J. Appl. Sci. 2007, 42, 73–79. [Google Scholar] [CrossRef]
- Jain, S.K.; Goel, M.K.; Agarwal, P.K. Reservoir operation study of Sabamati system, India. J. Water Resour. Plan. Manag. 1998, 124, 31–38. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Yakowitz, S. Dynamic programming applications in water resources. Water Resour. Res. 1982, 18, 673–696. [Google Scholar] [CrossRef]
- Esogbue, A.O. A taxonomic treatment of dynamic programming models of water resources systems. In Dynamic Programming for Optimal Water Resources Systems Analysis; Prentice Hall: Upper Saddle River, NJ, USA, 1989; pp. 27–71. [Google Scholar]
- Labadie, J.W. Combining simulation and optimization in reservoir basin management. In Stochastic Hydrology and Its Use in Water Resources Systems Simulation and Optimization; Marco, J.B., Harboe, R.J., Salas, J.D., Eds.; NATO ASI Series; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1993; pp. 345–371. [Google Scholar]
- Larson, R. State Incremental Dynamic Programming; Elsevier Science: New York, NY, USA, 1968. [Google Scholar]
- Larson, R.E.; Korsak, A.J. A dynamic programming successive approximations technique with convergence proofs. Automatica 1970, 6, 245–252. [Google Scholar] [CrossRef]
- Hall, W.A.; Tauxe, G.W.; Yeh, W.W.-G. An alternate procedure for the optimization of operations for planning with multiple river, multiple purpose systems. Water Resour. Res. 1969, 5, 1367–1372. [Google Scholar] [CrossRef]
- Heidari, M.; Chow, V.T.; Kokotovic, P.V.; Meredith, D.D. Discrete differential dynamic programming approach to water resources systems optimization. Water Resour. Res. 1971, 7, 273–282. [Google Scholar] [CrossRef]
- Giles, J.E.; Wunderlich, W.O. Weekly multipurpose planning model for TVA reservoir system. J. Water Resour. Plan. Manag. 1981, 107, 495–511. [Google Scholar] [CrossRef]
- Kumar, D.; Baliarsingh, F. Folded dynamic programming for optimal operation of multireservoir system. Water. Resour. Manag. 2003, 17, 337–353. [Google Scholar] [CrossRef]
- Chaleeraktrakoon, C.; Kangrang, A. Dynamic programming with the principle of progressive optimality for searching rule curves. Can. J. Civ. Eng. 2007, 34, 170–176. [Google Scholar] [CrossRef]
- Huang, W.; Chen, D. An efficient heuristic algorithm for rectangle-packing problem. Simul. Model. Pract. Theory 2007, 15, 1356–1365. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Gharehpetian, G.B. A comprehensive review of heuristic optimization algorithms for optimal combined heat and power dispatch from economic and environmental perspectives. Renew. Sust. Energ. Rev. 2018, 81, 2128–2143. [Google Scholar] [CrossRef]
- Lourenço, H.R.; Martin, O.C.; Stützle, T. Iterated local search: Framework and applications. In Handbook of Metaheuristics; Springer: Cham, Switzerland, 2019; pp. 129–168. [Google Scholar]
- Ashrafi, S.M.; Dariane, A.B. Coupled operating rules for optimal operation of multi-reservoir systems. Water Resour. Manag. 2017, 31, 4505–4520. [Google Scholar] [CrossRef]
- Bashiri-Atrabi, H.; Qaderi, K.; Rheinheimer, D.E.; Sharifi, E. Application of harmony search algorithm to reservoir operation optimization. Water Resour. Manag. 2015, 29, 5729–5748. [Google Scholar] [CrossRef]
- Niu, W.J.; Feng, Z.K.; Jiang, Z.Q.; Wang, S.; Liu, S.; Guo, W.; Song, Z.G. Enhanced harmony search algorithm for sustainable ecological operation of cascade hydropower reservoirs in river ecosystem. Environ. Res. Lett. 2021, 16, 055013. [Google Scholar] [CrossRef]
- Ashrafi, S.M.; Mahmoudi, M. Developing a semi-distributed decision support system for great Karun water resources system. J. Appl. Res. Water Wastewater 2019, 6, 16–24. [Google Scholar]
- Ashrafi, S.M.; Ashrafi, S.F.; Moazami, S. Developing self-adaptive melody search algorithm for optimal operation of multi-reservoir systems. J. Hydraul. Struct. 2017, 3, 35–48. [Google Scholar]
- Kangrang, A.; Compliew, S.; Chaiyapoom, W. Heuristic algorithm with simulation model for searching optimal reservoir rule curves. Am. J. Appl. Sci. 2009, 6, 263–267. [Google Scholar] [CrossRef]
- Valeriano, O.C.S.; Koike, T.; Yang, K.; Yang, D. Optimal dam operation during flood season using a distributed hydrological model and a heuristic algorithm. J. Hydrol. Eng. 2010, 15, 580–586. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Locatelli, M. Simulated annealing algorithms for continuous global optimization: Convergence conditions. J. Optim. Theory Appl. 2000, 104, 121–133. [Google Scholar] [CrossRef]
- Teegavarapu, R.S.; Simonovic, S.P. Optimal operation of reservoir systems using simulated annealing. Water Resour. Manag. 2002, 16, 401–428. [Google Scholar] [CrossRef]
- Murray, D.M.; Yakowitz, S.J. Constrained differential dynamic programming and its application to multireservoir control. Water Resour. Res. 1979, 15, 1017–1027. [Google Scholar] [CrossRef]
- Tospornsampan, J.; Kita, I.; Ishii, M.; Kitamura, Y. Optimization of a multiple reservoir system using a simulated annealing—A case study in the Mae Klong system, Thailand. Paddy Water Environ. 2005, 3, 137–147. [Google Scholar] [CrossRef]
- Kangrang, A.; Compliew, S.; Hormwichian, R. Optimal reservoir rule curves using simulated annealing. P. I. Civil Eng.-Wat. M. 2011, 164, 27–34. [Google Scholar] [CrossRef]
- Georgiou, P.E.; Papamichail, D.M.; Vougioukas, S.G. Optimal irrigation reservoir operation and simultaneous multi-crop cultivation area selection using simulated annealing. Irrig. Drain. 2006, 55, 129–144. [Google Scholar] [CrossRef]
- Rouzegari, N.; Hassanzadeh, Y.; Sattari, M.T. Using the hybrid simulated annealing-M5 tree algorithms to extract the if-then operation rules in a single reservoir. Water Resour. Manag. 2019, 33, 3655–3672. [Google Scholar] [CrossRef]
- Azizipour, M.; Sattari, A.; Afshar, M.H.; Goharian, E.; Solis, S.S. Optimal hydropower operation of multi-reservoir systems: Hybrid cellular automata-simulated annealing approach. J. Hydroinform. 2020, 22, 1236–1257. [Google Scholar] [CrossRef]
- Eusuff, M.; Lansey, K.; Pasha, F. Shuffled frog-leaping algorithm: A memetic meta-heuristic for discrete optimization. Eng. Optim. 2006, 38, 129–154. [Google Scholar] [CrossRef]
- Elbeltagi, E.; Hegazy, T.; Grierson, D. A modified shuffled frog-leaping optimization algorithm: Applications to project management. Struct. Infrastruct. Eng. 2007, 3, 53–60. [Google Scholar] [CrossRef]
- Huynh, T.H. A modified shuffled frog leaping algorithm for optimal tuning of multivariable PID controllers. In Proceedings of the 2008 IEEE International Conference on Industrial Technology, Chengdu, China, 21–24 April 2008. [Google Scholar]
- Eusuff, M.M.; Lansey, K.E. Optimization of water distribution network design using the shuffled frog leaping algorithm. Water Resour. Plan. Manag. 2003, 129, 210–225. [Google Scholar] [CrossRef]
- Li, X.; Luo, J.; Chen, M.R.; Wang, N. An improved shuffled frog-leaping algorithm with extremal optimisation for continuous optimisation. Inf. Sci. 2012, 192, 143–151. [Google Scholar] [CrossRef]
- Kangrang, A.; Hormwichian, R. Optimal reservoir rule curves using conditional shuffled frog leaping algorithm and simulation. Int. J. Earth Sci. Eng. 2013, 6, 1392–1399. [Google Scholar]
- Sun, P.; Jiang, Z.Q.; Wang, T.T.; Zhang, Y.K. Research and application of parallel normal cloud mutation shuffled frog leaping algorithm in cascade reservoirs optimal operation. Water Resour. Manag. 2016, 30, 1019–1035. [Google Scholar] [CrossRef]
- Li, R.; Jiang, Z.; Li, A.; Yu, S.; Ji, C. An improved shuffled frog leaping algorithm and its application in the optimization of cascade reservoir operation. Hydrol. Sci. J. 2018, 63, 2020–2034. [Google Scholar] [CrossRef]
- Yeh, C.H. Applying multi-objective genetic algorithms for planning of flood detention dams system. Taiwan Water Conserv. 1997, 45, 70–81. [Google Scholar]
- Ahmed, J.A.; Sarma, A.K. Genetic algorithm for optimal operating policy of a multipurpose reservoir. Water Resour. Manag. 2005, 19, 145–161. [Google Scholar] [CrossRef]
- Hormwichian, R.; Kangrang, A.; Lamom, A. A conditional genetic algorithm model for searching optimal reservoir rule curves. J. Appl. Sci. 2009, 9, 3575–3580. [Google Scholar] [CrossRef]
- Chiamsathit, C.; Adeloye, A.; Soundharajan, B. Genetic algorithms optimization of hedging rules for operation of the multi-purpose Ubonratana Reservoir in Thailand. Proc. Int. Assoc. Hydrol. Sci. 2014, 364, 507–512. [Google Scholar] [CrossRef]
- Chang, F.J.; Chen, L.; Chang, L.C. Optimizing the reservoir operating rule curves by genetic algorithms. Hydrol. Process. 2005, 19, 2277–2289. [Google Scholar] [CrossRef]
- Fallah-Mehdipour, E.; Bozorg Haddad, O.; Mariño, M.A. Extraction of multicrop planning rules in a reservoir system: Application of evolutionary algorithms. J. Irrig. Drain. Eng. 2013, 139, 490–498. [Google Scholar] [CrossRef]
- Akbari-Alashti, H.; Bozorg Haddad, O.; Fallah-Mehdipour, E.; Marino, M.A. Multi-reservoir real-time operation rules: A new genetic programming approach. Proc. Inst. Civ. Eng. Water Manag. 2014, 167, 561–576. [Google Scholar] [CrossRef]
- Zhong, S.; Xie, X.; Lin, L.; Wang, F. Genetic algorithm optimized double-reservoir echo state network for multi-regime time series prediction. Neurocomputing 2017, 238, 191–204. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T. Optimization of hydropower reservoirs operation balancing generation benefit and ecological requirement with parallel multi-objective genetic algorithm. Energy 2018, 153, 706–718. [Google Scholar] [CrossRef]
- Prasanchum, H.; Kangrang, A. Optimal reservoir rule curves under climatic and land use changes for Lampao Dam using Genetic Algorithm. KSCE J. Civ. Eng. 2018, 22, 351–364. [Google Scholar] [CrossRef]
- Hormwichian, R.; Tongsiri, J.; Kangrang, A. Multipurpose rule curves for multipurpose reservoir by conditional genetic algorithm. Int. Rev. Civ. Eng. 2018, 9, 114–130. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Reddy, M.J.; Kumar, D.N. Evolving strategies for crop planning and operation of irrigation reservoir system using multi-objective differential evolution. Irrig. Sci. 2008, 26, 177–190. [Google Scholar] [CrossRef]
- Hormwichian, R.; Anongrit, K.; Alongkorn, L.; Chavalit, C.; Sanguan, P. Coupled-operations model and a conditional differential evolution algorithm for improving reservoir management. Int. J. Phys. Sci. 2012, 7, 5701–5710. [Google Scholar]
- Ahmadianfar, I.; Adib, A.; Salarijazi, M. Optimizing multireservoir operation: Hybrid of bat algorithm and differential evolution. J. Water Resour. Plann. Manag. 2016, 142, 05015010. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Samadi-Koucheksaraee, A.; Bozorg-Haddad, O. Extracting optimal policies of hydropower multi-reservoir systems utilizing enhanced differential evolution algorithm. Water Resour. Manag. 2017, 31, 4375–4397. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Kheyrandish, A.; Jamei, M.; Gharabaghi, B. Optimizing operating rules for multi-reservoir hydropower generation systems: An adaptive hybrid differential evolution algorithm. Renew. Energy 2021, 167, 774–790. [Google Scholar] [CrossRef]
- Willis, M.J.; Hiden, H.G.; Marenbach, P.; McKay, B.; Montague, G.A. Genetic programming: An introduction and survey of applications. In Proceedings of the Second International Conference on Genetic Algorithms in Engineering Systems: Innovations and Applications, Glasgow, UK, 2–4 September 1997. [Google Scholar]
- Ngamsert, R.; Kangrang, A. Estimation of Water Demand from Reservoir by Participation and Reservoir Operation. Master’s Thesis, Mahasarakham University, Maha Sarakham, April 2019. [Google Scholar]
- Fallah-Mehdipour, E.; Bozorg Haddad, O.; Mariño, M.A. Real-time operation of reservoir system by genetic programming. Water Resour. Manag. 2012, 26, 4091–4103. [Google Scholar] [CrossRef]
- Fallah-Mehdipour, E.; Bozorg Haddad, O.; Mariño, M.A. Developing reservoir operational decision rule by genetic programming. J. Hydroinform. 2013, 15, 103–119. [Google Scholar] [CrossRef]
- Ashlock, D.; Lathrop, J.I. A fully characterized test suite for genetic programming. In Evolutionary Programming VII; Springer: Berlin/Heidelberg, Germany, 1998; pp. 537–546. [Google Scholar]
- El-Dahshan, E.S.; Radi, A.; El-Bakry, M.Y. Genetic programing modeling for nucleus–nucleus collisions. Int. J. Mod. Phys. C 2009, 20, 1817–1825. [Google Scholar] [CrossRef]
- Reynolds, R.G. An introduction to cultural algorithms. In Proceedings of the Third Annual Conference on Evolutionary Programming; World Scientific: River Edge, NJ, USA, 1994; Volume 24, pp. 131–139. [Google Scholar]
- Reynolds, R.G.; Peng, B. Knowledge learning and social swarms in cultural systems. J. Math. Sociol. 2005, 29, 115–132. [Google Scholar] [CrossRef]
- Reynolds, R.G.; Ali, M.Z. Exploring knowledge and population swarms via an agent-based Cultural Algorithms Simulation Toolkit (CAT). In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007. [Google Scholar]
- Reynolds, R.; Ali, M. Embedding a social fabric component into cultural algorithms toolkit for an enhanced knowledge-driven engineering optimization. Int. J. Intell. Comput. Cybern. 2008, 1, 563–597. [Google Scholar] [CrossRef]
- Phumiphan, A.; Kangrang, A. Development of decision-making support tools for future reservoir management under climate and land cover variability: A case study. Int. Rev. Civ. Eng. 2021, 12, 271. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Ye, M. Parameter identification of dynamical systems based on improved particle swarm optimization. In Intelligent Control and Automation; Huang, D.S., Li, K., Irwin, G.W., Eds.; Springer: Heidelberg/Berlin, Germany, 2006; pp. 351–360. [Google Scholar]
- Pan, H.; Wang, L.; Liu, B. Particle swarm optimization for function optimization in noisy environment. Appl. Math. Comput. 2006, 181, 908–919. [Google Scholar] [CrossRef]
- Jamali, B.; Rasekh, M.; Jamadi, F.; Gandomkar, R.; Makiabadi, F. Using PSO-GA algorithm for training artificial neural network to forecast solar space heating system parameters. Appl. Therm. Eng. 2019, 147, 647–660. [Google Scholar] [CrossRef]
- Letting, L.K.; Munda, J.L.; Hamam, Y. Optimization of a fuzzy logic controller for PV grid inverter control using S-function based PSO. Sol. Energy 2012, 86, 1689–1700. [Google Scholar] [CrossRef]
- Nuannukul, N.; Kangrang, A.; Hormwichian, R. The Application of Particle Swarm Optimization for Searching Optimal Rule Curve of Lampao Reservoir. J. Sci. Technol. Mahasarakham Univ. 2015, 34, 1–9. [Google Scholar]
- Zhang, Z.; Jiang, Y.; Zhang, S.; Geng, S.; Wang, H.; Sang, G. An adaptive particle swarm optimization algorithm for reservoir operation optimization. Appl. Soft Comput. 2014, 18, 167–177. [Google Scholar] [CrossRef]
- Spiliotis, M.; Mediero, L.; Garrote, L. Optimization of hedging rules for reservoir operation during droughts based on particle swarm optimization. Water Resour. Manag. 2016, 30, 5759–5778. [Google Scholar] [CrossRef]
- Gong, Z.; Cheng, J.; Gong, Y.; Wang, L.; Wei, C. Modified particle swarm algorithm for the optimal water allocation of reservoir. Water Supply 2020, 20, 2875–2883. [Google Scholar] [CrossRef]
- Güvengir, U.; Savasaneril, S.; Altan-Sakarya, A.B.; Buhan, S. Short-term flood control and long-term energy maximization in multi-reservoir systems using improved particle swarm optimization. Water Resour. Manag. 2021, 35, 4293–4307. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing, Coimbatore, India, 9–11 December 2009. [Google Scholar]
- Yang, X.S.; Deb, S. Cuckoo search: Recent advances and applications. Neural. Comput. Appl. 2014, 24, 169–174. [Google Scholar] [CrossRef]
- Ming, B.; Chang, J.X.; Huang, Q.; Wang, Y.M.; Huang, S.Z. Optimal operation of multi-reservoir system based-on cuckoo search algorithm. Water Resour. Manag. 2015, 29, 5671–5687. [Google Scholar] [CrossRef]
- Yasar, M. Optimization of reservoir operation using cuckoo search algorithm: Example of Adiguzel Dam, Denizli, Turkey. Math. Probl. Eng. 2016, 2016, 1316038. [Google Scholar] [CrossRef]
- Ara, I.; Yasar, M. Optimization of the operation rule curves for cascade reservoirs using the cuckoo search algorithm. Adv. Civ. Eng. 2022, 2022, 8463358. [Google Scholar] [CrossRef]
- Kangrang, A.; Pakoktom, W.; Nuannukul, W.; Chaleeraktrakoon, C. Adaptive reservoir rule curves by optimisation and simulation. Proc. Inst. Civ. Eng. Water Manag. 2017, 170, 219–230. [Google Scholar] [CrossRef]
- Donyaii, A. Evaluation of climate change impacts on the optimal operation of multipurpose reservoir systems using cuckoo search algorithm. Environ. Earth Sci. 2021, 80, 663. [Google Scholar] [CrossRef]
- Li, W.D.; Ong, S.K.; Nee, A.Y.C. Optimization of process plans using a constraint-based tabu search approach. Int. J. Prod. Res. 2004, 42, 1955–1985. [Google Scholar] [CrossRef]
- da Silva, L.G.W.; Pereira, R.A.F.; Abbad, J.R.; Mantovani, J.R.S. Optimised placement of control and protective devices in electric distribution systems through reactive tabu search algorithm. Electr. Power Syst. Res. 2008, 78, 372–381. [Google Scholar] [CrossRef]
- da Conceicao Cunha, M.; Ribeiro, L. Tabu search algorithms for water network optimization. Eur. J. Oper. Res. 2004, 157, 746–758. [Google Scholar] [CrossRef]
- Faigle, U.; Kern, W. Some convergence results for probabilistic tabu search. ORSA J. Comput. 1992, 4, 32–37. [Google Scholar] [CrossRef]
- Glover, F. Tabu search and adaptive memory programming—Advances, applications and challenges. In Interfaces in Computer Science and Operations Research; Springer: Berlin/Heidelberg, Germany, 1997; pp. 1–75. [Google Scholar]
- Sa-Ngiamvibool, W.; Pothiya, S.; Ngamroo, I. Multiple tabu search algorithm for economic dispatch problem considering valve-point effects. Int. J. Electr. Power Energy Syst. 2011, 33, 846–854. [Google Scholar] [CrossRef]
- Kangrang, A.; Prasanchum, H.; Hormwichian, R. Development of future rule curves for multipurpose reservoir operation using conditional genetic and tabu search algorithms. Adv. Civ. Eng. 2018, 2018, 6474870. [Google Scholar] [CrossRef]
- Jeong, H.W.; Choi, S.A.; Kim, H.S.; Shim, M.P. Reservoir operation by Tabu search method during flood. J. Korea Water Resour. Assoc. 2005, 38, 761–770. [Google Scholar] [CrossRef]
- Wang, X.; Ruan, Q. Genetic algorithm and tabu search hybrid algorithm to co-scheduling model of Three Gorges-Gezhou Dam. In Advances in Neural Networks—ISNN 2009; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Mbeutcha, Y.; Gendreau, M.; Emiel, G. A hybrid dynamic programming-Tabu Search approach for the long-term hydropower scheduling problem. Comput. Manag. Sci. 2021, 18, 385–410. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly algorithms for multimodal optimization. In Stochastic Algorithms: Foundations and Applications; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Johari, N.F.; Zain, A.M.; Noorfa, M.H.; Udin, A. Firefly algorithm for optimization problem. Appl. Mech. Mater. 2013, 421, 512–517. [Google Scholar] [CrossRef]
- Hosseini-Moghari, S.M.; Banihabib, M.E. Optimizing operation of reservoir for agricultural water supply using firefly algorithm. J. Soil. Water. Conserv. 2014, 3, 17–31. [Google Scholar]
- Garousi-Nejad, I.; Bozorg-Haddad, O.; Loáiciga, H.A.; Mariño, M.A. Application of the firefly algorithm to optimal operation of reservoirs with the purpose of irrigation supply and hydropower production. J. Irrig. Drain. Eng. 2016, 142, 04016041. [Google Scholar] [CrossRef]
- Garousi-Nejad, I.; Bozorg-Haddad, O.; Loáiciga, H.A. Modified firefly algorithm for solving multireservoir operation in continuous and discrete domains. J. Water Resour. Plan. Manag. 2016, 142, 04016029. [Google Scholar] [CrossRef]
- Srikamol, N. Improvement of Rule Curves of Ubolrat and Nam Oon Reservoir Using Firefly Algorithm. Master’s Thesis, Mahasarakham University, Kantarawichai, Thailand, 2019. [Google Scholar]
- Yang, X.S. Flower pollination algorithm for global optimization. In Unconventional Computation and Natural Computation; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Yang, X.S.; Karamanoglu, M.; He, X. Flower pollination algorithm: A novel approach for multiobjective optimization. Eng. Optim. 2014, 46, 1222–1237. [Google Scholar] [CrossRef]
- Salgotra, R.; Singh, U. Application of mutation operators to flower pollination algorithm. Expert Syst. Appl. 2017, 79, 112–129. [Google Scholar] [CrossRef]
- Sriworamas, K.; Kangrang, A.; Thongwan, T.; Prasanchum, H. Optimal Reservoir of Small Reservoirs by Optimization Techniques on Reservoir Simulation Model. Adv. Civil Eng. 2021, 2021, 6625743. [Google Scholar] [CrossRef]
- Gupta, S.K.; Dalal, A. Optimization of hourly plants water discharges in hydrothermal scheduling using flower pollination algorithm. Int. J. Ambient. Energy 2022, 44, 686–692. [Google Scholar] [CrossRef]
- Tică, E.I.; Neagoe, A.; Popa, F.; Popa, B. Optimization of the operation of Drăgan-Iad hydropower development using Flower Pollination Algorithm. J. Phys. Conf. Ser. 2022, 2339, 012020. [Google Scholar] [CrossRef]
- El-Fergany, A.A.; Hasanien, H.M. Single and multi-objective optimal power flow using grey wolf optimizer and differential evolution algorithms. Electr. Power Compon. Syst. 2015, 43, 1548–1559. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z.; Mohamed, M.R.; Aliman, O. Using the gray wolf optimizer for solving optimal reactive power dispatch problem. Appl. Soft Comput. 2015, 32, 286–292. [Google Scholar] [CrossRef]
- Solomon Jebaraj, N.R.; Keshavan, H.R. Optimizing the ZigBee networks lifetime with a Grey Wolf algorithm. Asian J. Inf. Technol. 2017, 16, 472–478. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.Z.; Mirjalili, S.M. Evolutionary population dynamics and grey wolf optimizer. Neural Comput. Appl. 2015, 26, 1257–1263. [Google Scholar] [CrossRef]
- Choopan, Y.; Emami, S. Optimal operation of dam reservoir using gray wolf optimizer algorithm (case study: Urmia Shaharchay Dam in Iran). J. Soft Comput. Civ. Eng. 2019, 3, 47–61. [Google Scholar] [CrossRef]
- Donyaii, A.; Sarraf, A.; Ahmadi, H. Water reservoir multiobjective optimal operation using Grey Wolf optimizer. Shock Vib. 2020, 2020, 8870464. [Google Scholar] [CrossRef]
- Niu, W.J.; Feng, Z.K.; Liu, S.; Chen, Y.B.; Xu, Y.S.; Zhang, J. Multiple hydropower reservoirs operation by hyperbolic grey wolf optimizer based on elitism selection and adaptive mutation. Water Resour. Manag. 2021, 35, 573–591. [Google Scholar] [CrossRef]
- Masoumi, F.; Masoumzadeh, S.; Zafari, N.; Emami-Skardi, M.J. Optimal operation of single and multi-reservoir systems via hybrid shuffled grey wolf optimization algorithm (SGWO). Water Supply 2022, 22, 1663–1675. [Google Scholar] [CrossRef]
- Sinthuchai, N.; Kangrang, A. Improvement of Reservoir Rule Curve Using Grey Wolf Optimizer. Master’s Thesis, Mahasarakham University, Maha Sarakham, Thailand, May 2019. [Google Scholar]
- Pandey, A.; Parhi, D.R. Optimum path planning of mobile robot in unknown static and dynamic environments using Fuzzy-Wind Driven Optimization algorithm. Def. Technol. 2017, 13, 47–58. [Google Scholar] [CrossRef]
- Ghosh, T.K.; Das, S. Efficient job scheduling in computational grid systems using wind driven optimization technique. Int. J. Appl. Metaheuristic Comput. 2018, 9, 49–59. [Google Scholar] [CrossRef]
- Bayraktar, Z.; Komurcu, M.; Werner, D.H. Wind Driven Optimization (WDO): A novel nature-inspired optimization algorithm and its application to electromagnetics. In Proceedings of the 2010 IEEE Antennas and Propagation Society International Symposium, Toronto, ON, Canada, 11–17 July 2010. [Google Scholar]
- Bayraktar, Z.; Komurcu, M.; Jiang, Z.H.; Werner, D.H.; Werner, P.L. Stub-loaded inverted-F antenna synthesis via wind driven optimization. In Proceedings of the 2011 IEEE International Symposium on Antennas and Propagation, Spokane, WA, USA, 3–8 July 2011. [Google Scholar]
- Bayraktar, Z.; Komurcu, M.; Bossard, J.A.; Werner, D.H. The wind driven optimization technique and its application in electromagnetics. IEEE Trans. Antennas Propag. 2013, 61, 2745–2757. [Google Scholar] [CrossRef]
- Ho, S.L.; Yang, S.; Bai, Y.; Li, Y. A wind driven optimization-based methodology for robust optimizations of electromagnetic devices under interval uncertainty. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Kangrang, A.; Techarungruengsakul, R.; Hormwichian, R.; Sriwanpheng, O. Alternative approach of wind driven optimization for flood control rule curves. J. Eng. Appl. Sci. 2019, 14, 8026–8033. [Google Scholar] [CrossRef]
- Kosasaeng, S.; Yamoat, N.; Ashrafi, S.M.; Kangrang, A. Extracting Optimal Operation Rule Curves of Multi-Reservoir System Using Atom Search Optimization, Genetic Programming and Wind Driven Optimization. Sustainability 2022, 14, 16205. [Google Scholar] [CrossRef]
- Jalali, M.R.; Afshar, A.; Marino, M.A. Ant colony optimization algorithm (ACO); a new heuristic approach for engineering optimization. WSEAS Trans. Inf. Sci. Appl. 2005, 2, 606–610. [Google Scholar]
- Yin, P.Y.; Wang, J.Y. Ant colony optimization for the nonlinear resource allocation problem. Appl. Math. Comput. 2006, 174, 1438–1453. [Google Scholar] [CrossRef]
- Afshar, M.H. A parameter free continuous ant colony optimization algorithm for the optimal design of storm sewer networks: Constrained and unconstrained approach. Adv. Eng. Softw. 2010, 41, 188–195. [Google Scholar] [CrossRef]
- Kumar, D.N.; Reddy, M.J. Ant colony optimization for multi-purpose reservoir operation. Water Resour. Manag. 2006, 20, 879–898. [Google Scholar] [CrossRef]
- Moeini, R.; Afshar, M.H. Arc-based constrained ant colony optimisation algorithms for the optimal solution of hydropower reservoir operation problems. Can. J. Civ. Eng. 2011, 38, 811–824. [Google Scholar]
- Moeini, R.; Afshar, M.H. Extension of the constrained ant colony optimization algorithms for the optimal operation of multi-reservoir systems. J. Hydroinform. 2013, 15, 155–173. [Google Scholar] [CrossRef]
- Kangrang, A.; Lokham, C. Optimal reservoir rule curves considering conditional ant colony optimization with simulation model. J. Appl. Sci. 2013, 13, 154–160. [Google Scholar] [CrossRef]
- Afshar, A.; Massoumi, F.; Afshar, A.; Mariño, M.A. State of the art review of ant colony optimization applications in water resource management. Water Resour. Manag. 2015, 29, 3891–3904. [Google Scholar] [CrossRef]
- Haddad, O.B.; Afshar, A.; Mariño, M.A. Honey-bees mating optimization (HBMO) algorithm: A new heuristic approach for water resources optimization. Water Resour. Manag. 2006, 20, 661–680. [Google Scholar] [CrossRef]
- Afshar, A.; Haddad, O.B.; Mariño, M.A.; Adams, B.J. Honey-bee mating optimization (HBMO) algorithm for optimal reservoir operation. J. Franklin Inst. 2007, 344, 452–462. [Google Scholar] [CrossRef]
- Haddad, O.B.; Afshar, A.; Mariño, M.A. Honey-bee mating optimization (HBMO) algorithm in deriving optimal operation rules for reservoirs. J. Hydroinform. 2008, 10, 257–264. [Google Scholar] [CrossRef]
- Afshar, A.; Shafii, M.; Haddad, O.B. Optimizing multi-reservoir operation rules: An improved HBMO approach. J. Hydroinform. 2011, 13, 121–139. [Google Scholar] [CrossRef]
- Solgi, M.; Bozorg-Haddad, O.; Loáiciga, H.A. The enhanced honey-bee mating optimization algorithm for water resources optimization. Water Resour. Manag. 2017, 31, 885–901. [Google Scholar] [CrossRef]
- Songsaengrit, S.; Kangrang, A. Dynamic rule curves and streamflow under climate change for multipurpose reservoir operation using honey-bee mating optimization. Sustainability 2022, 14, 8599. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, X.; Xu, Q. Variation of runoff and sediment inflows to the Three Gorges Reservoir: Impact of upstream cascade reservoirs. J. Hydrol. 2021, 603, 126875. [Google Scholar] [CrossRef]
- Anache, J.A.; Flanagan, D.C.; Srivastava, A.; Wendland, E.C. Land use and climate change impacts on runoff and soil erosion at the hillslope scale in the Brazilian Cerrado. Sci. Total Environ. 2018, 622, 140–151. [Google Scholar] [CrossRef]
- Sriworamas, K.; Prasanchum, H.; Supakosol, J. The effect of forest rehabilitation on runoff and hydrological factors in the upstream area of the Ubolratana Reservoir in Thailand. J. Water Clim. Chang. 2020, 11, 1009–1020. [Google Scholar] [CrossRef]
- Castelletti, A.; Pianosi, F.; Soncini-Sessa, R. Integration, participation and optimal control in water resources planning and management. Appl. Math. Comput. 2008, 206, 21–33. [Google Scholar] [CrossRef]
- Ezekwe, J.N. Applied reservoir management principles with case histories. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 5–8 October 2003. [Google Scholar]
- Tong, S.T.; Sun, Y.; Ranatunga, T.; He, J.; Yang, Y.J. Predicting plausible impacts of sets of climate and land use change scenarios on water resources. Appl. Geogr. 2012, 32, 477–489. [Google Scholar] [CrossRef]
- Babel, M.S.; Agarwal, A.; Swain, D.K.; Herath, S. Evaluation of climate change impacts and adaptation measures for rice cultivation in Northeast Thailand. Clim. Res. 2011, 46, 137–146. [Google Scholar] [CrossRef]
- Lacombe, G.; Hoanh, C.T.; Smakhtin, V. Multi-year variability or unidirectional trends? Mapping long-term precipitation and temperature changes in continental Southeast Asia using PRECIS regional climate model. Clim. Chang. 2012, 113, 285–299. [Google Scholar] [CrossRef]
- Sentian, J.; Kong, S.S.K. High resolution climate change projection under SRES A2 scenario during summer and winter monsoons over Southeast Asia using PRECIS regional climate modeling system. SIJ Trans. Comput. Sci. Eng. Appl. (CSEA) 2013, 1, 163–173. [Google Scholar]
- Masud, M.B.; Soni, P.; Shrestha, S.; Tripathi, N.K. Changes in climate extremes over North Thailand. J. Climat. 2016, 2016, 1960–2099. [Google Scholar] [CrossRef]
- Plangoen, P.; Babel, M.S.; Clemente, R.S.; Shrestha, S.; Tripathi, N.K. Simulating the impact of future land use and climate change on soil erosion and deposition in the Mae Nam Nan sub-catchment, Thailand. Sustainability 2013, 5, 3244–3274. [Google Scholar] [CrossRef]
- Yang, X.; Zheng, X.Q.; Chen, R. A land use change model: Integrating landscape pattern indexes and Markov-CA. Ecol. Model. 2014, 283, 1–7. [Google Scholar] [CrossRef]
- Kumar, S.; Dirmeyer, P.A.; Merwade, V.; DelSole, T.; Adams, J.M.; Niyogi, D. Land use/cover change impacts in CMIP5 climate simulations: A new methodology and 21st century challenges. J. Geophys. Res. Atmos. 2013, 118, 6337–6353. [Google Scholar] [CrossRef]
- Du, J.; Qian, L.; Rui, H.; Zuo, T.; Zheng, D.; Xu, Y.; Xu, C.Y. Assessing the effects of urbanization on annual runoff and flood events using an integrated hydrological modeling system for Qinhuai River basin, China. J. Hydrol. 2012, 464, 127–139. [Google Scholar] [CrossRef]
- Li, Z.; Liu, W.Z.; Zhang, X.C.; Zheng, F.L. Impacts of land use change and climate variability on hydrology in an agricultural catchment on the Loess Plateau of China. J. Hydrol. 2009, 377, 35–42. [Google Scholar] [CrossRef]
- Mango, L.M.; Melesse, A.M.; McClain, M.E.; Gann, D.; Setegn, S. Land use and climate change impacts on the hydrology of the upper Mara River Basin, Kenya: Results of a modeling study to support better resource management. Hydrol. Earth Syst. Sci. 2011, 15, 2245–2258. [Google Scholar] [CrossRef]
- Zhang, L.; Nan, Z.; Xu, Y.; Li, S. Hydrological impacts of land use change and climate variability in the headwater region of the Heihe River Basin, Northwest China. PLoS ONE 2016, 11, e0158394. [Google Scholar] [CrossRef] [PubMed]
- Fazel, N.; Haghighi, A.T.; Kløve, B. Analysis of land use and climate change impacts by comparing river flow records for headwaters and lowland reaches. Glob. Planet. Chang. 2017, 158, 47–56. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development 1. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Lin, B.; Chen, X.; Yao, H.; Chen, Y.; Liu, M.; Gao, L.; James, A. Analyses of landuse change impacts on catchment runoff using different time indicators based on SWAT model. Ecol. Indic. 2015, 58, 55–63. [Google Scholar] [CrossRef]
- Yesuf, H.M.; Assen, M.; Alamirew, T.; Melesse, A.M. Modeling of sediment yield in Maybar gauged watershed using SWAT, northeast Ethiopia. CATENA 2015, 127, 191–205. [Google Scholar] [CrossRef]
- Xiong, L.; Xu, X.; Ren, D.; Huang, Q.; Huang, G. Enhancing the capability of hydrological models to simulate the regional agro-hydrological processes in watersheds with shallow groundwater: Based on the SWAT framework. J. Hydrol. 2019, 572, 1–16. [Google Scholar] [CrossRef]
- Emami, F.; Koch, M. Modeling the impact of climate change on water availability in the Zarrine River Basin and inflow to the Boukan Dam, Iran. Climate 2019, 7, 51. [Google Scholar] [CrossRef]
- Tian, J.; Guo, S.; Deng, L.; Yin, J.; Pan, Z.; He, S.; Li, Q. Adaptive optimal allocation of water resources response to future water availability and water demand in the Han River basin, China. Sci. Rep. 2021, 11, 7879. [Google Scholar] [CrossRef]
- Sun, J.; Yan, H.; Bao, Z.; Wang, G. Investigating Impacts of Climate Change on Runoff from the Qinhuai River by Using the SWAT Model and CMIP6 Scenarios. Water 2022, 14, 1778. [Google Scholar] [CrossRef]
- Tebakari, T.; Yoshitani, J.; Suvanpimol, P. Impact of large-scale reservoir operation on flow regime in the Chao Phraya River basin, Thailand. Hydrol. Process. 2012, 26, 2411–2420. [Google Scholar] [CrossRef]
- Ahmad, S.; Simonovic, S.P. System dynamics modeling of reservoir operations for flood management. J. Comput. Civ. Eng. 2000, 14, 190–198. [Google Scholar] [CrossRef]
- Kangrang, A.; Chaleeraktrakoon, C.; Patamatamkul, S.; Hormwichian, R. Expert participation with optimization technique for improving optimal rule curves of reservoir. Bulg. J. Agric. Sci. 2013, 19, 1140–1147. [Google Scholar]
- Song, X.; Mulder, K.; Frostell, B.; Ravesteijn, W.; Wennersten, R. Transition in public participation in Chinese water management. Proc. Inst. Civ. Eng.-Eng. Sustain. 2011, 164, 71–83. [Google Scholar] [CrossRef]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kangrang, A.; Prasanchum, H.; Sriworamas, K.; Ashrafi, S.M.; Hormwichian, R.; Techarungruengsakul, R.; Ngamsert, R. Application of Optimization Techniques for Searching Optimal Reservoir Rule Curves: A Review. Water 2023, 15, 1669. https://doi.org/10.3390/w15091669
Kangrang A, Prasanchum H, Sriworamas K, Ashrafi SM, Hormwichian R, Techarungruengsakul R, Ngamsert R. Application of Optimization Techniques for Searching Optimal Reservoir Rule Curves: A Review. Water. 2023; 15(9):1669. https://doi.org/10.3390/w15091669
Chicago/Turabian StyleKangrang, Anongrit, Haris Prasanchum, Krit Sriworamas, Seyed Mohammad Ashrafi, Rattana Hormwichian, Rapeepat Techarungruengsakul, and Ratsuda Ngamsert. 2023. "Application of Optimization Techniques for Searching Optimal Reservoir Rule Curves: A Review" Water 15, no. 9: 1669. https://doi.org/10.3390/w15091669







