IWQP4Net: An Efficient Convolution Neural Network for Irrigation Water Quality Prediction
Abstract
:1. Introduction
- Introduced an effective Irrigation Water Quality Prediction (IWQP) approach based on an efficient CNN architecture which comprises two convolution layers, a max-pooling layer, a dropout layer, and two dense layers;
- Examined and compared the performance of IWQP4Net with the LR, SVR, and kNN models using different evaluation measurements and visualizations methods;
- Demonstrated the efficiency of the developed IWQP4Net for IWQP and its superiority over the other competitive models.
2. Methods and Material
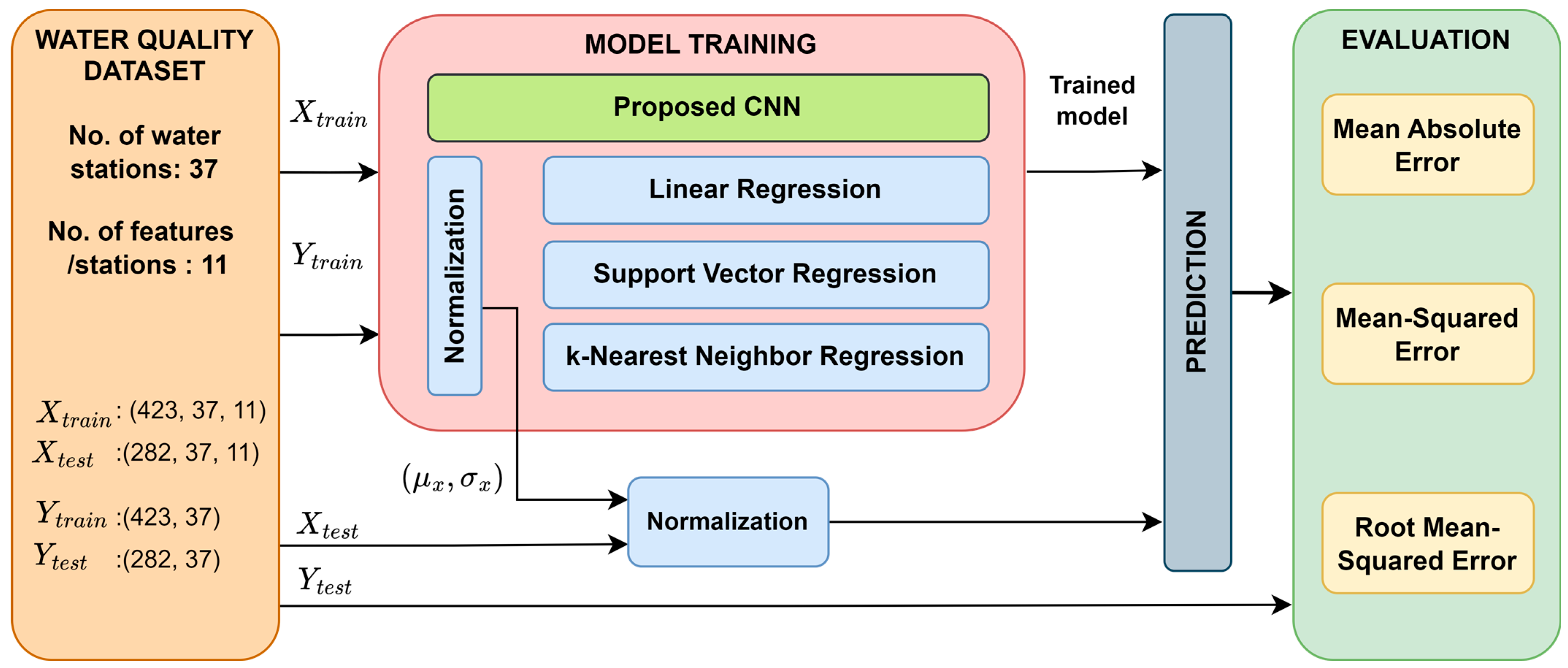
2.1. Dataset
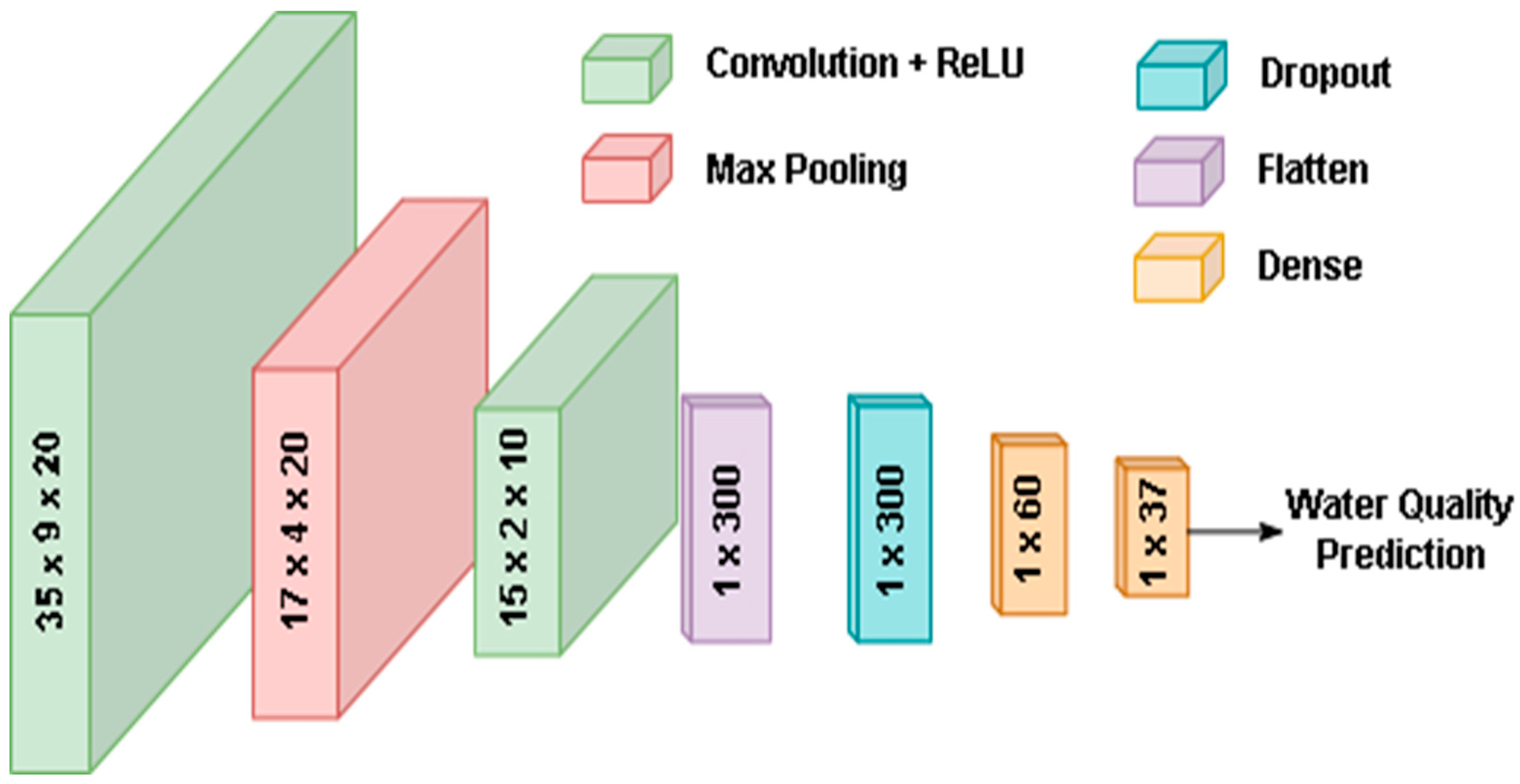
2.2. Proposed IWQP Approach
3. Evaluation Measurements
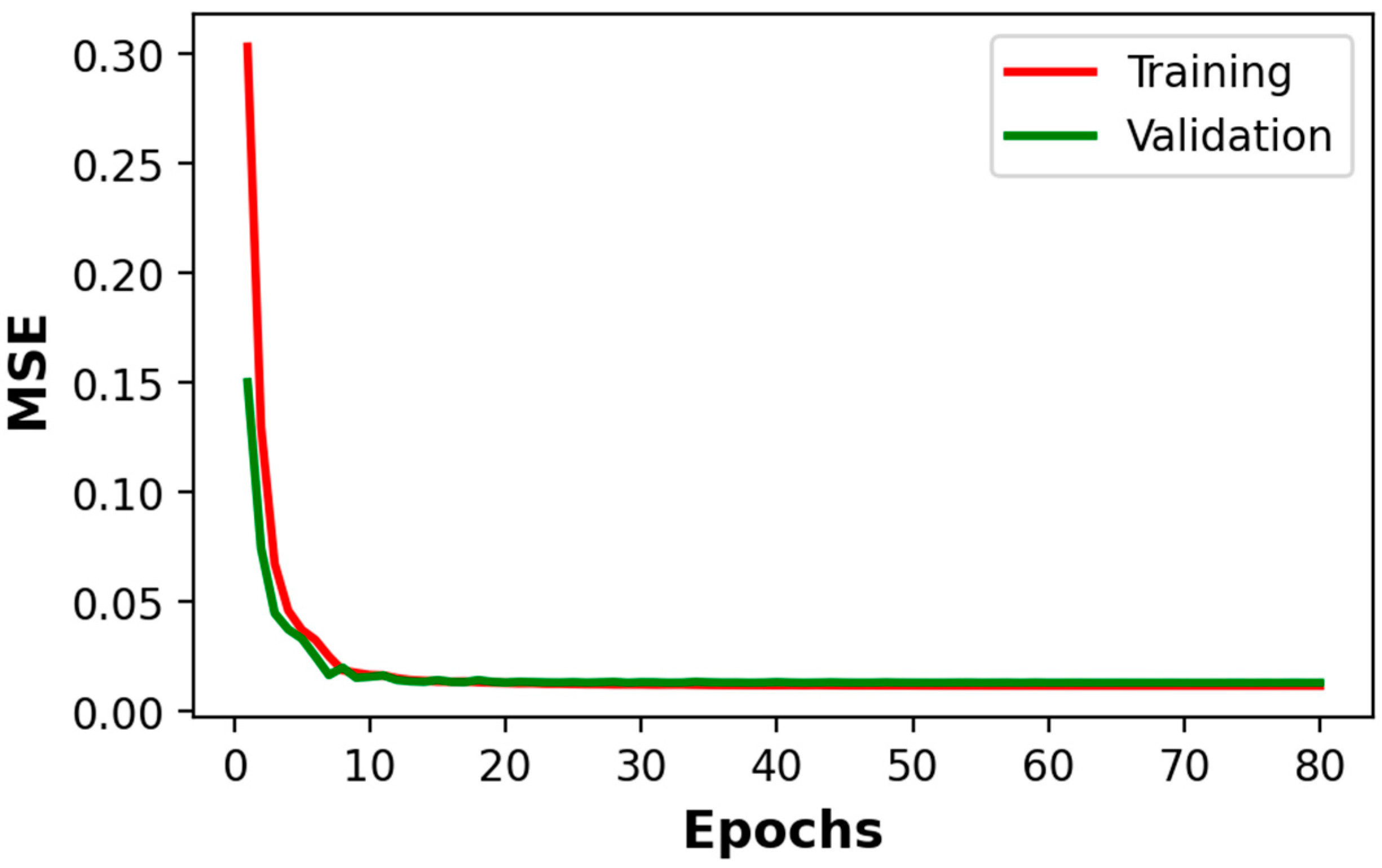
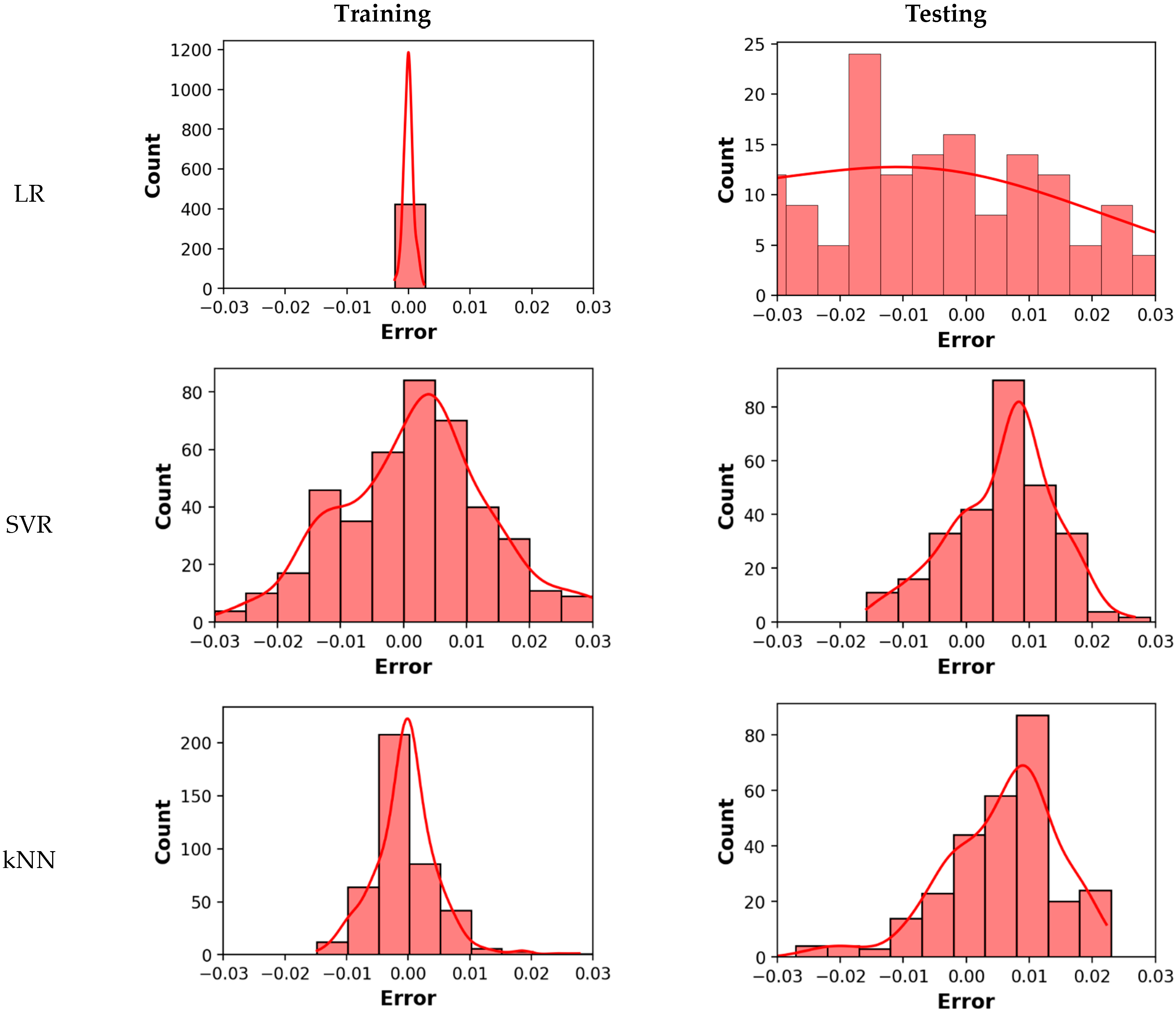
4. Experimental Results and Discussion
5. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, P.; Wu, J. Drinking Water Quality and Public Health. Expo. Health 2019, 11, 73–79. [Google Scholar] [CrossRef]
- Fadel, A.A.; Shujaa, M.I. Water Quality Monitoring System Based on IOT Platform. IOP Conf. Ser. Mater. Sci. Eng. 2020, 928, 032054. [Google Scholar] [CrossRef]
- National Institution for Transforming India (NITI) Aayog. Raising Agricultural Productivity and Making Farming Remunerative for Farmers; NITI Aayog, Government of India: New Delhi, India, 2015.
- Kondaveti, R.; Reddy, A.; Palabtla, S. Smart irrigation system using machine learning and IoT. In Proceedings of the 2019 International Conference on Vision Towards Emerging Trends in Communication and Networking (ViTECoN), Vellore, India, 30–31 March 2019. [Google Scholar]
- Goap, A.; Sharma, D.; Shukla, A.K.; Krishna, C.R. An IoT based smart irrigation management system using Machine learning and open source technologies. Comput. Electron. Agric. 2018, 155, 41–49. [Google Scholar] [CrossRef]
- Saraiva, M.; Protas, É.; Salgado, M.; Souza, C., Jr. Automatic mapping of center pivot irrigation systems from satellite images using deep learning. Remote Sens. 2020, 12, 558. [Google Scholar] [CrossRef]
- Chen, H.; Chen, A.; Xu, L.; Xie, H.; Qiao, H.; Lin, Q.; Cai, K. A deep learning CNN architecture applied in smart near-infrared analysis of water pollution for agricultural irrigation resources. Agric. Water Manag. 2020, 240, 106303. [Google Scholar] [CrossRef]
- Vianny, D.M.M.; John, A.; Mohan, S.K.; Sarlan, A.; Adimoolam; Ahmadian, A. Water optimization technique for precision irrigation system using IoT and machine learning. Sustain. Energy Technol. Assess. 2022, 52, 102307. [Google Scholar] [CrossRef]
- Kashyap, P.K.; Kumar, S.; Jaiswal, A.; Prasad, M.; Gandomi, A.H. Towards precision agriculture: IoT-enabled intelligent irrigation systems using deep learning neural network. IEEE Sens. J. 2021, 21, 17479–17491. [Google Scholar] [CrossRef]
- Iorliam, A.; Sylvester, B.U.M.; Aondoakaa, I.S.; Iorliam, I.B.; Shehu, Y. Machine Learning Techniques for the Classification of IoT-Enabled Smart Irrigation Data for Agricultural Purposes. Gazi Univ. J. Sci. Part A Eng. Innov. 2022, 9, 378–391. [Google Scholar] [CrossRef]
- Nayak, S. Assessment of Water Quality of Brahmani River Using Correlation and Regression Analysis. 2020. Available online: https://www.preprints.org/manuscript/202003.0088/v1 (accessed on 18 March 2023).
- Vij, A.; Vijendra, S.; Jain, A.; Bajaj, S.; Bassi, A.; Sharma, A. IoT and Machine Learning Approaches for Automation of Farm Irrigation System. Procedia Comput. Sci. 2020, 167, 1250–1257. [Google Scholar] [CrossRef]
- Sayari, S.; Mahdavi-Meymand, A.; Zounemat-Kermani, M. Irrigation water infiltration modeling using machine learning. Comput. Electron. Agric. 2020, 180, 105921. [Google Scholar] [CrossRef]
- Akshay, S.; Ramesh, T.K. Efficient machine learning algorithm for smart irrigation. In Proceedings of the 2020 International Conference on Communication and Signal Processing (ICCSP), Chennai, India, 28–30 July 2020; pp. 867–870. [Google Scholar]
- Saranya, T.; Deisy, C.; Sridevi, S.; Anbananthen, K.S.M. A comparative study of deep learning and Internet of Things for precision agriculture. Eng. Appl. Artif. Intell. 2023, 122, 106034. [Google Scholar] [CrossRef]
- Abdallah, E.B.; Grati, R.; Boukadi, K. A machine learning-based approach for smart agriculture via stacking-based ensemble learning and feature selection methods. In Proceedings of the 2022 18th International Conference on Intelligent Environments (IE), Biarritz, France, 20–23 June 2022; pp. 1–8. [Google Scholar]
- Lap, B.Q.; Phan, T.-T.; Du Nguyen, H.; Quang, L.X.; Hang, P.T.; Phi, N.Q.; Hoang, V.T.; Linh, P.G.; Hang, B.T.T. Predicting Water Quality Index (WQI) by feature selection and machine learning: A case study of An Kim Hai irrigation system. Ecol. Inform. 2023, 74, 101991. [Google Scholar] [CrossRef]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Short-term water quality variable prediction using a hybrid CNN–LSTM deep learning model. Stoch. Environ. Res. Risk Assess. 2020, 34, 415–433. [Google Scholar] [CrossRef]
- Zhao, L.; Gkountouna, O.; Pfoser, D. Spatial Auto-regressive Dependency Interpretable Learning Based on Spatial Topological Constraints. ACM Trans. Spat. Algorithms Syst. 2019, 5, 1–28. [Google Scholar] [CrossRef]
- Bianchi, V.; Bassoli, M.; Lombardo, G.; Fornacciari, P.; Mordonini, M.; De Munari, I. IoT Wearable Sensor and Deep Learning: An Integrated Approach for Personalized Human Activity Recognition in a Smart Home Environment. IEEE Internet Things J. 2019, 6, 8553–8562. [Google Scholar] [CrossRef]
- Minaee, S.; Boykov, Y.Y.; Porikli, F.; Plaza, A.J.; Kehtarnavaz, N.; Terzopoulos, D. Image segmentation using deep learning: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 3523–3542. [Google Scholar] [CrossRef] [PubMed]
- Gupta, A.; Anpalagan, A.; Guan, L.; Khwaja, A.S. Deep learning for object detection and scene perception in self-driving cars: Survey, challenges, and open issues. Array 2021, 10, 100057. [Google Scholar] [CrossRef]
- Zheng, Y.-Y.; Kong, J.-L.; Jin, X.-B.; Wang, X.-Y.; Su, T.-L.; Zuo, M. CropDeep: The Crop Vision Dataset for Deep-Learning-Based Classification and Detection in Precision Agriculture. Sensors 2019, 19, 1058. [Google Scholar] [CrossRef]
- Moshayedi, A.J.; Roy, A.S.; Kolahdooz, A.; Shuxin, Y. Deep Learning Application Pros and Cons over Algorithm. EAI Endorsed Trans. AI Robot. 2022, 1, 1–13. [Google Scholar] [CrossRef]
- Mathew, A.; Amudha, P.; Sivakumari, S. Deep learning techniques: An overview. In Advanced Machine Learning Technologies and Applications: Proceedings of AMLTA 2020; Springer: Singapore, 2021; pp. 599–608. [Google Scholar]
- Kim, T.Y.; Cho, S.B. Predicting the household power consumption using CNN-LSTM hybrid networks. In Proceedings of the Intelligent Data Engineering and Automated Learning–IDEAL 2018: 19th International Conference, Madrid, Spain, 21–23 November 2018; Part I; Springer International Publishing: Cham, Switzerland, 2018; Volume 19, pp. 481–490. [Google Scholar]
- Al-Shourbaji, I.; Kachare, P.H.; Abualigah, L.; Abdelhag, M.E.; Elnaim, B.; Anter, A.M.; Gandomi, A.H. A Deep Batch Normalized Convolution Approach for Improving COVID-19 Detection from Chest X-ray Images. Pathogens 2022, 12, 17. [Google Scholar] [CrossRef]
- Scott, D.W. On optimal and data-based histograms. Biometrika 1979, 66, 605–610. [Google Scholar] [CrossRef]

| Measure | Feat-1 | Feat-2 | Feat-3 | Feat-4 | Feat-5 | Feat-6 | Feat-7 | Feat-8 | Feat-9 | Feat-10 | Feat-11 | pH | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Training | Mean | 0.0652 | 0.8894 | 0.0290 | 0.0432 | 0.5678 | 0.8586 | 0.6049 | 0.5783 | 0.5571 | 0.5368 | 0.5532 | 0.6644 |
| S.D. | 0.1614 | 0.0348 | 0.1208 | 0.1333 | 0.1205 | 0.0311 | 0.1468 | 0.1718 | 0.2040 | 0.2123 | 0.1901 | 0.0293 | |
| Min | 0.0005 | 0.5769 | 0.0003 | 0.0005 | 0.1250 | 0.7195 | 0.0758 | 0.0315 | 0.0594 | 0.0256 | 0.0901 | 0.5741 | |
| Q1 | 0.0019 | 0.8718 | 0.0016 | 0.0018 | 0.4868 | 0.8415 | 0.5152 | 0.4803 | 0.3938 | 0.3654 | 0.3983 | 0.6481 | |
| Q2 | 0.0026 | 0.8974 | 0.0022 | 0.0024 | 0.5658 | 0.8537 | 0.6061 | 0.5906 | 0.5313 | 0.5096 | 0.5320 | 0.6667 | |
| Q3 | 0.0055 | 0.9103 | 0.0035 | 0.0048 | 0.6579 | 0.8780 | 0.7121 | 0.7087 | 0.7406 | 0.7244 | 0.7238 | 0.6759 | |
| Max | 1.0000 | 0.9872 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9630 | |
| Testing | Mean | 0.0813 | 0.8843 | 0.0340 | 0.0529 | 0.5256 | 0.8552 | 0.5556 | 0.5259 | 0.6352 | 0.6188 | 0.6244 | 0.6622 |
| S.D. | 0.1780 | 0.0360 | 0.1243 | 0.1415 | 0.1138 | 0.0312 | 0.1405 | 0.1695 | 0.1852 | 0.1929 | 0.1724 | 0.0294 | |
| Min | 0.0007 | 0.4103 | 0.0003 | 0.0007 | 0.1184 | 0.7317 | 0.0682 | 0.0315 | 0.0625 | 0.0224 | 0.1105 | 0.5741 | |
| Q1 | 0.0019 | 0.8590 | 0.0015 | 0.0018 | 0.4671 | 0.8415 | 0.5000 | 0.4646 | 0.5281 | 0.5032 | 0.5291 | 0.6481 | |
| Q2 | 0.0026 | 0.8846 | 0.0022 | 0.0024 | 0.5263 | 0.8537 | 0.5682 | 0.5512 | 0.6750 | 0.6571 | 0.6613 | 0.6574 | |
| Q3 | 0.0056 | 0.9103 | 0.0040 | 0.0050 | 0.5921 | 0.8780 | 0.6288 | 0.6142 | 0.7656 | 0.7532 | 0.7500 | 0.6759 | |
| Max | 1.0000 | 1.0000 | 0.8566 | 0.8633 | 0.9276 | 0.9878 | 0.9848 | 0.9606 | 1.0000 | 0.9936 | 0.9913 | 1.0000 |
| Layer Type | Kernel Parameters | Output Shape | Trainable Parameters |
|---|---|---|---|
| Input | - | (37, 11) | - |
| Convolution 2D | (3, 3, 20), ReLU | (35, 9, 20) | 200 |
| Max. Pooling 2D | (2, 2) | (17, 4, 20) | 0 |
| Convolution 2D | (3, 3, 10), ReLU | (15, 2, 10) | 1810 |
| Flatten | (1, 300) | (300) | 0 |
| Dropout | 0.4 | (300) | 0 |
| Dense | 60, ReLU | (60) | 18,060 |
| Dense | 37, ReLU | (37) | 2257 |
| Total trainable parameters | 22,327 | ||
| Measure | Definition | Equation | |
|---|---|---|---|
| RMSE | Root Mean Squared Error | (3) | |
| MAPE | Mean Absolute Percentage Error | (4) | |
| MAE | Mean Absolute Error | (5) | |
| Models | Hyper-Parameters and Value |
|---|---|
| LR | Fit intercept = True, Normalization = True |
| SVR | Kernel= Radial basis Function, Normalization = True, C = 1.0, epsilon = 0.2 |
| kNN | Neighbors = 5, weights = Uniform, leaf size = 30, metric = Minkowski |
| IWQP4Net | Loss = MSE, optimizer = Adam, learning rate = 0.01, batch size = 120, epochs = 80, validation split = 0.2 |
| Model | Data Subset | RMSE | MAPE | MAE |
|---|---|---|---|---|
| LR | Training | 0.0008 | 0.0009 | 0.0006 |
| Testing | 0.0549 | 0.0855 | 0.0406 | |
| SVR | Training | 0.0122 | 0.0251 | 0.0097 |
| Testing | 0.0100 | 0.0211 | 0.0085 | |
| kNN | Training | 0.0052 | 0.0085 | 0.0036 |
| Testing | 0.0108 | 0.0212 | 0.0090 | |
| IWQP4Net | Training | 0.0048 | 0.0078 | 0.0034 |
| Testing | 0.0080 | 0.0195 | 0.0068 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Shourbaji, I.; Duraibi, S. IWQP4Net: An Efficient Convolution Neural Network for Irrigation Water Quality Prediction. Water 2023, 15, 1657. https://doi.org/10.3390/w15091657
Al-Shourbaji I, Duraibi S. IWQP4Net: An Efficient Convolution Neural Network for Irrigation Water Quality Prediction. Water. 2023; 15(9):1657. https://doi.org/10.3390/w15091657
Chicago/Turabian StyleAl-Shourbaji, Ibrahim, and Salahaldeen Duraibi. 2023. "IWQP4Net: An Efficient Convolution Neural Network for Irrigation Water Quality Prediction" Water 15, no. 9: 1657. https://doi.org/10.3390/w15091657





