Time Series Analysis of Temperature and Rainfall in the Savannah Region in Togo, West Africa
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Study Area
2.2. Data Sources
2.3. Testing for Serial Correlation
2.4. Trend Tests
2.4.1. Mann–Kendall Trend Test
2.4.2. Sen’s Slope Estimator Test
2.4.3. Variance Correction Approaches
2.5. Variability Analysis
2.5.1. Coefficient of Variation (CoV %)
2.5.2. Rainfall Anomaly Index (RAI)
3. Results and Discussion
3.1. Annual and Seasonal Rainfall and Temperature Trend Analysis
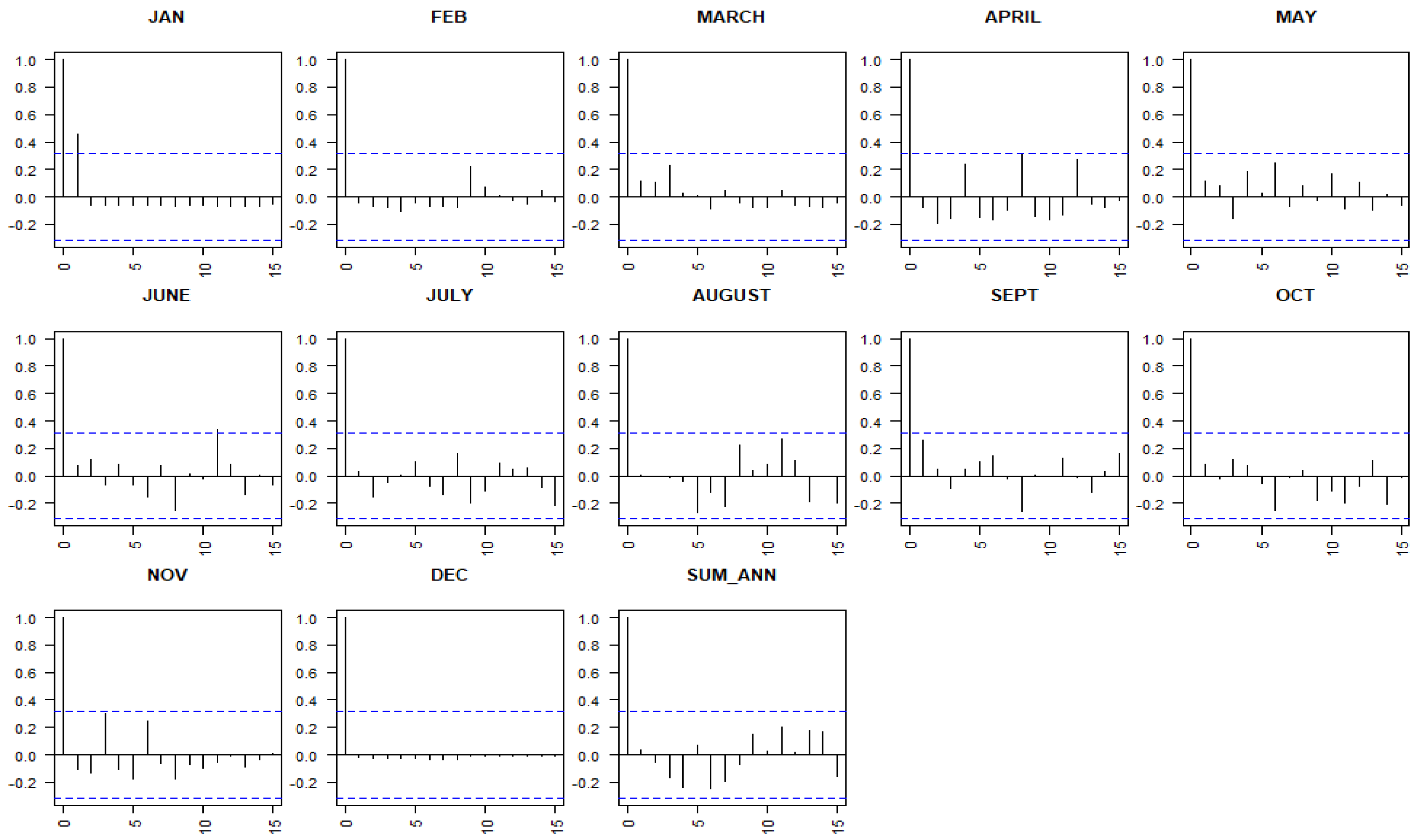
3.1.1. Serial Correlation Analysis
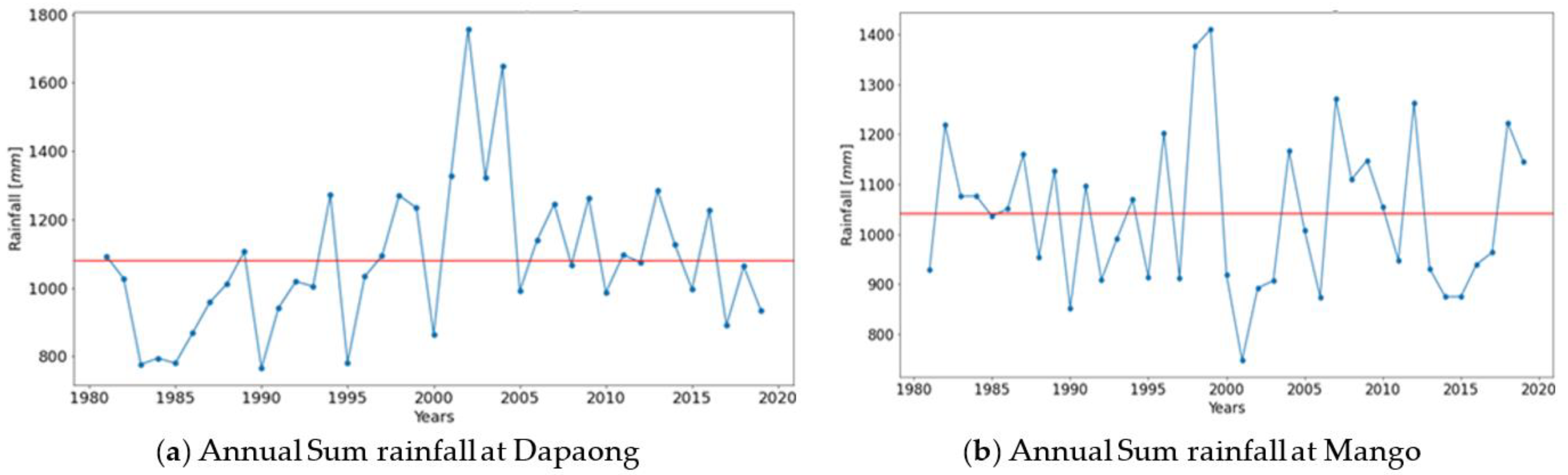
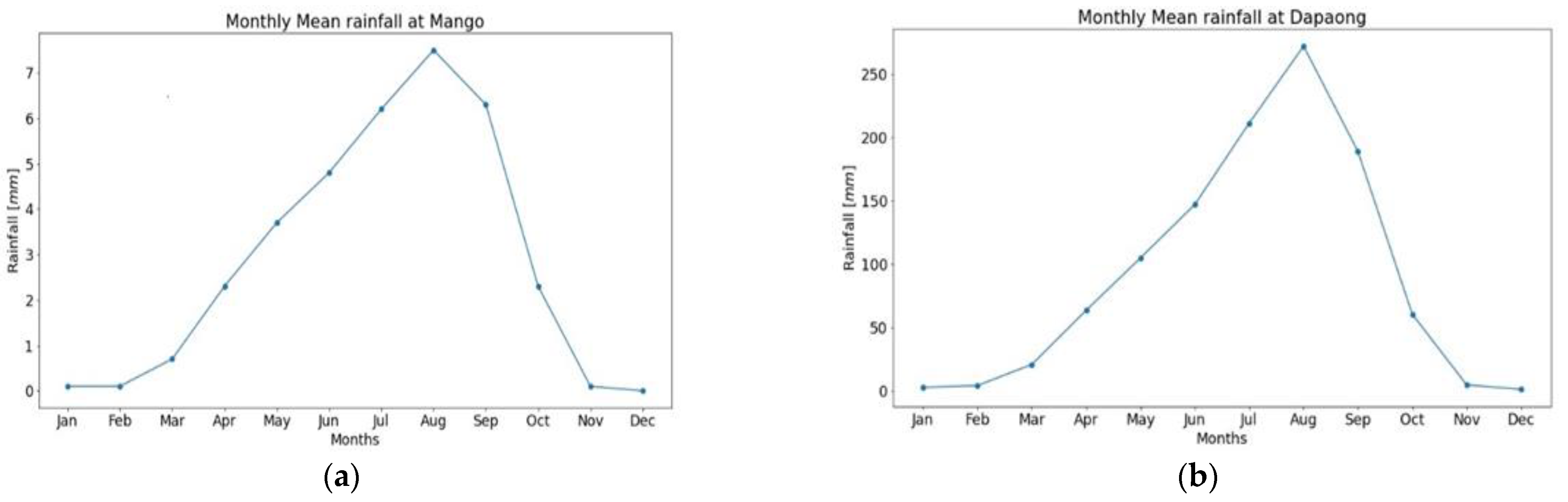
3.1.2. Annual Rainfall Trend Analysis
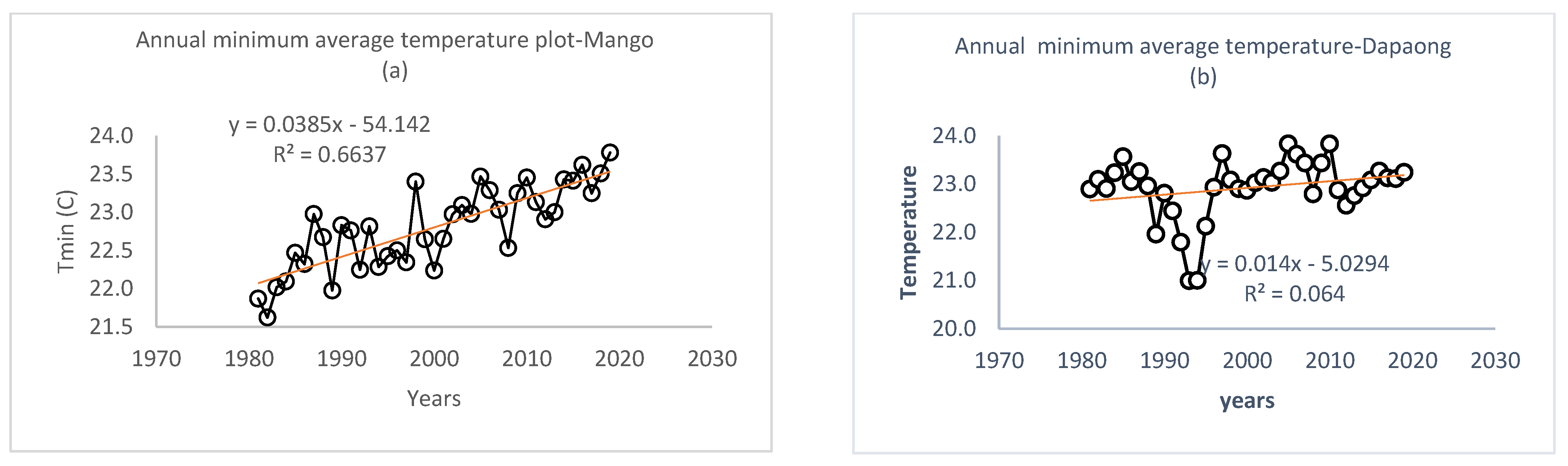
3.1.3. Annual Temperature Trend Analysis
3.1.4. Coefficient of Variation
3.2. Rainfall Anomaly Index
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IPCC. Intergovernmental Panel on Climate Change, Fourth Assessment Report: Climate Change 2007: Chapter 11-Regional Climate Projections; Cambridge University Press: Cambridge, UK, 2007; pp. 899–904. [Google Scholar]
- Malhi, Y.; Wright, J. Spatial patterns and recent trends in the climate of tropical rainforest regions. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2004, 359, 311–329. [Google Scholar] [CrossRef] [PubMed]
- Adeola, A.M.; Kruger, A.; Elias Makgoale, T.; Ondego Botai, J. Observed Trends and Projections of Tenmperature and Precipitation in the Olifants River Catchment in South Africa. PLoS ONE 2022, 17, e0271974. [Google Scholar] [CrossRef] [PubMed]
- Hulme, M.; Doherty, R.; Ngara, T.; New, M. Global warming and African climate change. In Climate Change and Africa; Low, P.S., Ed.; Cambridge University Press: Cambridge, UK, 2005; pp. 29–40. [Google Scholar]
- Chappell, A.; Agnew, C.T. Modelling climate change in West African Sahel rainfall (1931-90) as an artifact of changing station locations. Int. J. Climatol. 2004, 24, 547–554. [Google Scholar] [CrossRef]
- Dai, A.; Lamb, P.J.; Trenberth, K.E.; Hulme, M.; Jones, P.D.; Xie, P. The recent Sahel drought is real. Int. J. Climatol. 2004, 24, 1323–1331. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Selato, J.C. The influence of La Nina on African rainfall. Int. J. Climatol. 2000, 20, 1761–1776. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2007: Synthesis Report. Contribution of Working Groups I, II and III to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachauri, R.K., Reisinger, A., Eds.; IPCC: Geneva, Switzerland, 2014; 104p. [Google Scholar]
- Jalloh, A.; Nelson, G.C.; Thomas, T.S.; Zougmoré, R.; Roy-Macauley, H. West African Agriculture and Climate Change: A Comprehensive Analysis; IFPRI Research Monograph, International Food Policy Research: Washington, DC, USA, 2013. [Google Scholar]
- Lebel, T.; Ali, A. Recent trends in the Central and Western Sahel rainfall regime (1990–2007). J. Hydrol. 2009, 375, 52–64. [Google Scholar] [CrossRef]
- Ahokpossi, Y. Analysis of the Rainfall Variability and Change in the Republic of Benin (West Africa). Hydrol. Sci. J. 2018, 63, 2097–2123. [Google Scholar] [CrossRef]
- Adewi, E.; Badameli, K.M.S.; Dubreuil, V. Evolution des saisons des pluies potentiellement utiles au Togo de 1950 à 2000. Climatologie 2010, 7, 89–107. [Google Scholar] [CrossRef]
- Amegadje, M.K. Profil Environnemental du Togo; MERF: Lome, Togo, 2007. Climatologie 2010, 7, 89–107. [Google Scholar]
- Mcsweeney, C.; New, M.; Lizcano, G. UNDP Climate Change Country Profiles, Togo; School of 366 Geography and Environment, Oxford University: Oxford, UK, 2009. [Google Scholar]
- Rehmani, M.; Batebana, K.; Alex Ogwang, B.; Mie Mie Sein, Z.; Katchele Ogou, F.; Ongoma, V.; Ngarukiyimana, J.P. Rainfall Characteristics over Togo and their related Atmospheric circulation Anomalies. J. Environ. Agric. Sci. 2015, 5, 34–48. [Google Scholar]
- Djaman, K.; Sharma, V.; Rudnick, D.R.; Koudahe, K.; Irmak, S.; Adambounou, A.K.; Sodbedji, J.M. Spatial and Temporal Variation in Precipitation in Togo. Int. J. Hydrol. Res. 2017, 1, 97–105. [Google Scholar] [CrossRef]
- Gadedjisso-Tossou, A.; Adjegan, K.I.; Kablan, A.K.M. Rainfall and Temperature Trend Analysis by Mann–Kendall Test and Significance for Rainfed Cereal Yields in Northern Togo. Sci 2021, 3, 17. [Google Scholar] [CrossRef]
- Somiyabalo, P. Climate dynamics in Central and Northern Togo. Doctoral Dissertation, University of Lome, Lome, Togo, 2019. [Google Scholar]
- Onyutha, C. Statistical Uncertainty in Hydrometeorological Trend Analyses. Adv. Meteorol. 2016, 2016, 8701617. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Anderson, R.L. Distribution of the Serial Correlation Coefficient. Ann. Math. Stat. 1942, 13, 1–13. [Google Scholar] [CrossRef]
- Kendall, M.G.; Stuart, A. The Advanced Theory of Statistics; Charles Griffin & Company Ltd.: London, UK, 1968; Volume 2, ISBN 0-85264-069-2. [Google Scholar]
- Basistha, A.; Arya, D.S.; Goel, N.K. Analysis of historical changes in rainfall in the Indian Himalayas. Int. J. Climatol. 2009, 29, 555–572. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Edwards, D. Long-Term Trend Analysis of Precipitation and Air Temperature for Kentucky, United States. Climate 2016, 4, 10. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Charles Griffin: London, UK, 1955. [Google Scholar]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C.Y. The Mann-Kendall test modified by effective sample size to detect trend in serially correlated hydrological series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Hamed, K.H.; Ramachandra Rao, A. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Canchola, J.A.; Tang, S.; Hemyari, P.; Paxinos, E.; Marins, E. Correct Use of Percent Coefficient of Variation (%CV) Formula for Log-Transformed Data. MOJ Proteom. Bioinform. 2017, 6, 00200. [Google Scholar] [CrossRef]
- Van-rooy, M.P. A Rainfall Anomaly Index (RAI), Independent of the Time and Space. Notos 1965, 14, 43–48. [Google Scholar]
- Freitas, M. Um sistema de suporte à decisão para o monitoramento de secas meteorológicas em regiões semiáridas. Rev. Technol. 2005, 19, 84–95. [Google Scholar]
- Araújo, L.; Neto, J.; Sousa, F. Classificação da precipitação anual e da quadra chuvosa da bacia do rio Paraíba utilizando índice de Anomalia de Chuva (IAC). Ambiente Agua Interdiscip. J. Appl. Sci. 2009, 4, 93–110. [Google Scholar] [CrossRef]




| Stations | Latitude | Longitude | Elevation AMSL * (m) | Study Period | Number of Years |
|---|---|---|---|---|---|
| Mango | 10.22 | 0.28 | 146 | 1981–2019 | 39 |
| Dapaong | 10.51 | 0.12 | 300 | 1981–2019 | 39 |
| Emitter Type | Manufactures Coefficient | Interpretation |
|---|---|---|
| Point source | <0.05 | Excellent |
| 0.05–0.07 | Average | |
| 0.07–0.011 | Marginal | |
| 0.11–0.15 | Poor | |
| >0.15 | Unacceptable | |
| Line source | <0.10 | Good |
| 0.10–0.20 | Average | |
| >0.20 | Marginal to |
| RAI Range | Classification | |
|---|---|---|
| Rainfall Anomaly Index (RAI) | Above 4 | Extremely humid |
| 2 to 4 | Very humid | |
| 0 to 2 | Humid | |
| −2 to 0 | Dry | |
| −4 to −2 | Very dry | |
| Below −4 | Extremely dry |
| Period | Minimum (mm) | Maximum (mm) | Mean (mm) |
|---|---|---|---|
| January | 0 | 33.8 | 1.55 |
| February | 0 | 42.4 | 3.56 |
| March | 0 | 127.4 | 22.39 |
| April | 4.4 | 209.3 | 67.98 |
| May | 24.7 | 285.3 | 113.56 |
| June | 57.9 | 265.7 | 143.20 |
| July | 50.1 | 417.8 | 191.87 |
| August | 94.2 | 440 | 232.144 |
| September | 4.8 | 342.9 | 188.54 |
| October | 0 | 197.5 | 72.19 |
| November | 0 | 42.2 | 3.26 |
| December | 0 | 47.1 | 1.21 |
| Period | Minimum (mm) | Maximum (mm) | Mean (mm) |
|---|---|---|---|
| January | 0 | 98 | 2.54 |
| February | 0 | 70.1 | 3.93 |
| March | 0 | 220 | 20.53 |
| April | 0 | 196.8 | 63.35 |
| May | 22.5 | 306.9 | 104.8 |
| June | 68.1 | 247.1 | 147 |
| July | 54.7 | 984.4 | 211.3 |
| August | 4 | 784.7 | 272.2 |
| September | 3.5 | 348.8 | 189 |
| October | 0 | 182.8 | 60.3 |
| November | 0 | 51.1 | 4.44 |
| December | 0 | 29.8 | 0.95 |
| Time Series | p-Value | Sen’s Slope | MK | |||
|---|---|---|---|---|---|---|
| Dapaong | Mango | Dapaong | Mango | Dapaong | Mango | |
| April | 0.122 * | 0.943 * | 0.526 | 0.040 | 0.174 | 0.009 |
| May | 0.022 * | 0.010 * | 1.092 | 1.513 | 0.258 | 0.289 |
| June | 0.371 * | 0.141 * | 0.726 | −0.830 | 0.101 | −0.166 |
| July | 0.561 * | 0.471 * | −0.700 | 0.816 | −0.066 | 0.082 |
| August | 0.699 * | 0.486 * | 0.406 | 0.7 | 0.045 | 0.080 |
| September | 0.095 * | 0.014 * | 1.733 | −2.487 | 0.188 | −0.275 |
| October | 0.432 * | 0.121 * | 0.540 | 0.173 | 0.089 | 0.173 |
| ANNUAL | 0.050 * | 0.701 * | 5.500 | −0.937 | 0.220 | −0.045 |
| Time Series | Corrected Zc | New p-Value | Sen’s Slope | MMKY | ||||
|---|---|---|---|---|---|---|---|---|
| Dapaong | Mango | Dapaong | Mango | Dapaong | Mango | Dapaong | Mango | |
| April | 2.900 | 0.237 | 0.003 * | 0.812 * | 0.525 | 0.400 | 0.174 | 0.009 |
| May | 5.917 | 7.170 | 0.000 * | 0.000 * | 1.091 | 1.513 | 0.021 | 0.288 |
| June | 2.004 | −2.977 | 0.045 * | 0.002 * | 0.725 | −0.830 | 0.101 | −0.165 |
| July | −1.091 | 1.576 | 0.275 * | 0.114 * | −0.700 | 0.815 | −0.066 | 0.082 |
| August | 0.697 | 1.772 | 0.485 * | 0.076 * | 0.405 | 0.700 | 0.044 | 0.079 |
| September | 4.788 | −7.100 | 0.000 * | 0.000 * | 1.733 | −2.486 | 0.187 | −0.276 |
| October | 2.089 | 3.632 | 0.036 * | 0.000 * | 0.540 | 0.840 | 0.089 | 0.171 |
| ANNUAL | 2.551 | −1.236 | 0.010 * | 0.216 * | 5.500 | −0.937 | 0.219 | −0.039 |
| Time Series | p-Value (Two Tailed Test) | Sen’s Slope Estimate | Man Kendall Statistic (S) | |||
|---|---|---|---|---|---|---|
| Dapaong | Mango | Dapaong | Mango | Dapaong | Mango | |
| January | 0.133 * | 0.095 * | 0.029 | 0.032 | 0.169 | 0.188 |
| February | 0.240 * | 0.002 * | 0.027 | 0.053 | 0.132 | 0.340 |
| March | 0.008 * | 0.001 * | 0.029 | 0.058 | 0.299 | 0.417 |
| April | 0.529 * | 0.014 * | 0.006 | 0.030 | 0.071 | 0.275 |
| May | 0.536 * | 0.012 * | 0.004 | 0.033 | 0.070 | 0.280 |
| June | 0.203 * | 0.0001 * | 0.009 | 0.038 | 0.144 | 0.481 |
| July | 0.053 | 0.0001 * | 0.015 | 0.032 | 0.220 | 0.562 |
| August | 0.016 | 0.0001 * | 0.014 | 0.030 | 0.275 | 0.612 |
| September | 0.395 | 0.0001 * | 0.006 | 0.035 | 0.097 | 0.535 |
| October | 0.698 | 0.0001 * | 0.001 | 0.038 | 0.044 | 0.564 |
| November | 0.020 | 0.001 * | 0.026 | 0.056 | 0.263 | 0.357 |
| December | 0.255 | 0.040 * | 0.020 | 0.033 | 0.129 | 0.230 |
| ANNUAL | 0.143 | 0.0001 * | 0.008 | 0.040 | 0.164 | 0.625 |
| Time Series | p-Value (Two Tailed Test) | Sen’s Slope Estimate | Man Kendall Statistic (S) | |||
|---|---|---|---|---|---|---|
| Dapaong | Mango | Dapaong | Mango | Dapaong | Mango | |
| January | 0.270 * | 0.022 * | 0.017 | 0.040 | 0.125 | 0.255 |
| February | 0.164 * | 0.028 * | 0.023 | 0.040 | 0.157 | 0.246 |
| March | 0.023 * | 0.001 * | 0.030 | 0.048 | 0.260 | 0.389 |
| April | 0.309 * | 0.147 * | 0.014 | 0.027 | 0.114 | 0.162 |
| May | 0.467 * | 0.425 * | 0.012 | 0.014 | 0.082 | 0.089 |
| June | 0.255 * | 0.006 * | 0.040 | 0.034 | 0.129 | 0.304 |
| July | 0.167 * | 0.001 * | 0.015 | 0.040 | 0.156 | 0.397 |
| August | 0.244 * | 0.147 * | 0.010 | 0.014 | 0.133 | 0.162 |
| September | 0.594 * | 0.137 * | 0.005 | 0.010 | 0.060 | 0.166 |
| October | 0.771 * | 0.663 * | −0.005 | 0.004 | −0.033 | 0.049 |
| November | 0.011 * | 0.001 * | 0.040 | 0.039 | 0.286 | 0.378 |
| December | 0.018 * | 0.001 * | 0.043 | 0.056 | 0.267 | 0.386 |
| ANNUAL | 0.008 * | 0.0001 * | 0.022 | 0.032 | 0.295 | 0.455 |
| Mango Station | Dapaong Station | ||||
|---|---|---|---|---|---|
| Months | Stdev | CoV | Months | Stdev | CoV |
| Annual | 152.506 | 0.146 | Annual | 217.922 | 0.2017 |
| Jan | 6.798 | 4.375 | Jan | 15.688 | 6.161 |
| Feb | 9.441 | 2.647 | Feb | 12.829 | 3.262 |
| March | 29.342 | 1.310 | March | 39.254 | 1.912 |
| April | 48.14 | 0.708 | April | 39.074 | 0.61 |
| May | 50.845 | 0.448 | May | 50.047 | 0.478 |
| June | 54.783 | 0.383 | June | 54.313 | 0.372 |
| July | 75.284 | 0.392 | July | 143.15 | 0.677 |
| August | 72.261 | 0.311 | August | 126.07 | 0.463 |
| September | 73.853 | 0.392 | September | 73.224 | 0.388 |
| October | 51.601 | 0.715 | October | 41.836 | 0.694 |
| November | 7.884 | 2.417 | November | 10.454 | 2.353 |
| December | 7.541 | 6.205 | December | 4.8934 | 5.103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, K.M.A.; Kola, E.; Morenikeji, W.; Filho, W.L. Time Series Analysis of Temperature and Rainfall in the Savannah Region in Togo, West Africa. Water 2023, 15, 1656. https://doi.org/10.3390/w15091656
Yao KMA, Kola E, Morenikeji W, Filho WL. Time Series Analysis of Temperature and Rainfall in the Savannah Region in Togo, West Africa. Water. 2023; 15(9):1656. https://doi.org/10.3390/w15091656
Chicago/Turabian StyleYao, Komlagan Mawuli Apelete, Edinam Kola, Wole Morenikeji, and Walter Leal Filho. 2023. "Time Series Analysis of Temperature and Rainfall in the Savannah Region in Togo, West Africa" Water 15, no. 9: 1656. https://doi.org/10.3390/w15091656






